逻辑回归

逻辑回归（Logistic Regression）是机器学习中最基础且最常用的⼀种分类模型，尽管名字中有"回归"，但它实际上解决的是分类问题，特别是二分类问题。由于算法的简单和⾼效，在实际中应⽤⾮常⼴泛。

逻辑回归的应⽤场景

是否会⼴告点击
是否为垃圾邮件
是否患病
⾦融诈骗识别
虚假账号识别

看到上⾯的例⼦，我们可以发现其中的特点，那就是都属于两个类别之间的判断。逻辑回归就是解决⼆分类问题的利器

逻辑回归的原理

要想掌握逻辑回归，必须掌握两点：

逻辑回归中，其输⼊值是什么
如何判断逻辑回归的输出

输⼊

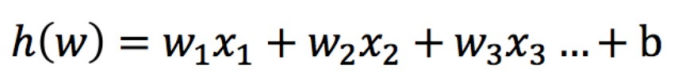
逻辑回归的输⼊就是⼀个线性回归的结果。

我们来看下图(下图中，设置阈值为0.6)：

核心思想

通过Sigmoid函数将线性回归的预测结果映射到(0,1)区间，转化为概率值：

等价写法：

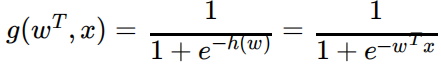
激活函数

sigmoid函数是一种激活函数也可以写作：

        1
f(z) = --------
       1 + e^{-z}

Sigmoid函数特性

将任意实数映射到(0,1)区间
z=0时概率为0.5
z→+∞时概率趋近1
z→-∞时概率趋近0

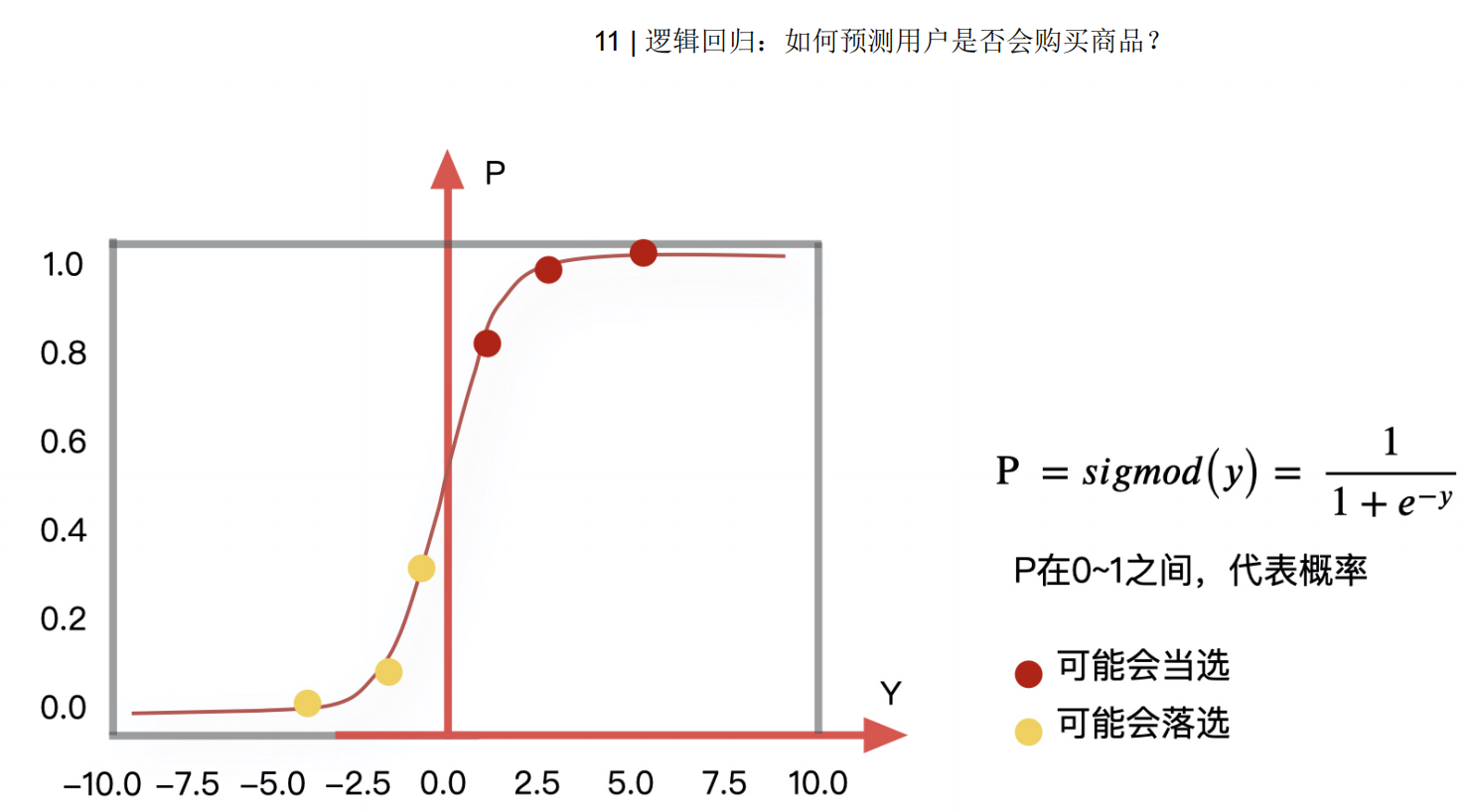
输出结果：[0, 1]区间中的⼀个概率值，默认为0.5为阈值

逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(正例),另外的⼀个类别会标记为0(反例)。（⽅便损失计算）

输出结果解释(重要)：假设有两个类别A，B，并且假设我们的概率值为属于A(1)这个类别的概率值。现在有⼀个样本的输⼊到逻辑回归输出结果0.55，那么这个概率值超过0.5，意味着我们训练或者预测的结果就是A(1)类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(0)类别。

关于逻辑回归的阈值是可以进⾏改变的，⽐如上⾯举例中，如果你把阈值设置为0.6，那么输出的结果0.55，就属于B类。

损失以及优化

如何计算逻辑回归的最优解？

在之前，我们⽤最⼩⼆乘法衡量线性回归的损失，从而计算线性回归最优解。

在逻辑回归中，当预测结果不对的时候，我们该怎么衡量其损失呢？

在逻辑回归里，我们一般会采用交叉熵函数的输出结果作为损失函数的评估目标，根据它来更新逻辑回归中的参数，再通过这些参数让整体的分布更加准确。

交叉熵损失函数一般是用来度量实际输出与期望输出之间的距离，交叉熵的值越小，两个概率分布就越接近，拟合得就更好。在我们的例子中，同样可以采用这个逻辑去分析样本真实分布和实际输出分布之间的误差。

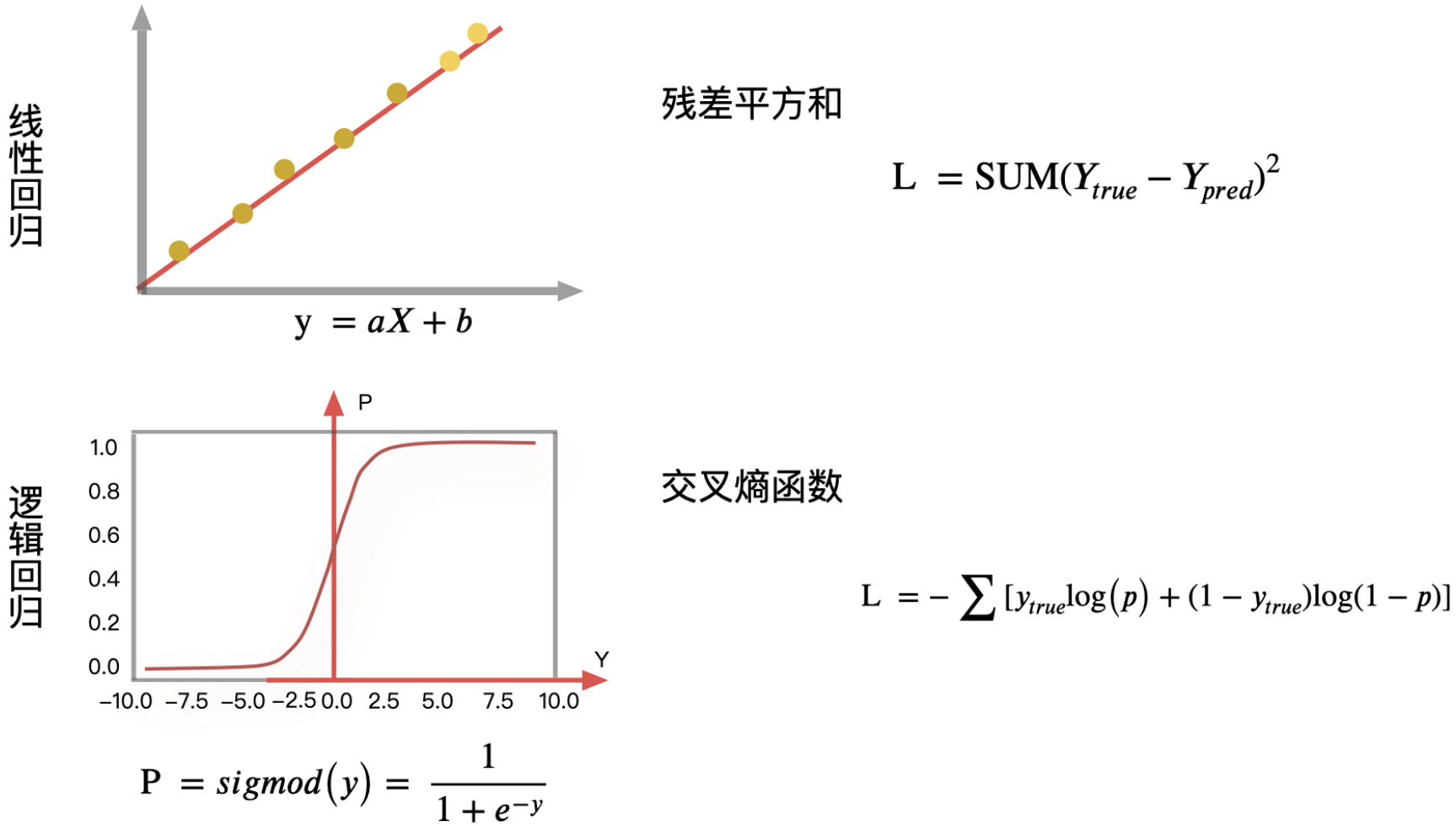
损失

逻辑回归的损失，称之为对数似然损失，公式如下：

分开类别：

怎么理解单个的式⼦呢？这个要根据log的函数图像来理解，当y=1时（也就是预测结果是1时）：

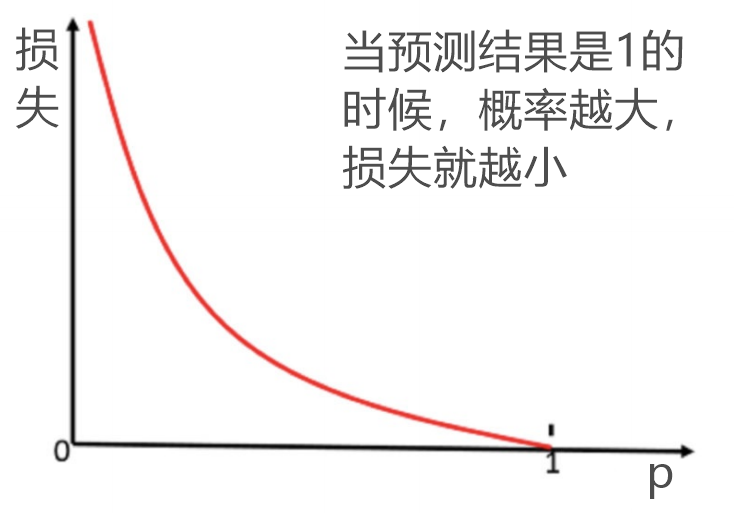
损失函数

⽆论何时，我们都希望损失函数值，越⼩越好

分情况讨论，对应的损失函数值：

当y=1时，我们希望p值越⼤越好；
当y=0时，我们希望p值越⼩越好

完整损失函数可以写作：

$y_{i}$ 是真实标签（0或1）

$p_{i}$ 是预测概率

$n$ 是样本数量

接下来我们呢就带⼊上⾯那个例⼦来计算⼀遍，就能理解意义了。

我们已经知道，-log(p), p值越⼤，结果越⼩，所以我们可以对着这个损失的式⼦去分析

优化

同样使⽤梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前⾯对应算法的权重参数。

为什么用交叉熵？

凸函数性质：保证梯度下降能找到全局最优解
概率解释：直接衡量预测概率与真实分布的差距
梯度友好：导数计算简单高效

API

核心API：LogisticRegression类

from sklearn.linear_model import LogisticRegression

关键参数解析

参数	默认值	选项	说明
`penalty`	'l2'	'l1','l2','elasticnet（弹性网络）','none'	正则化类型
`C`	1.0	>0的浮点数	正则化强度的倒数（C=1/λ，值越小正则化越强）
`solver`	'lbfgs'	'newton-cg','lbfgs','liblinear','sag','saga'	优化算法
`max_iter`	100	整数	最大迭代次数
`multi_class（弃用）`	'auto'	'ovr','multinomial','auto'	多分类策略
`class_weight`	None	None,'balanced',字典	类别权重设置（处理类不平衡）
`l1_ratio`	None	0-1之间的浮点数	elasticnet混合比例（仅当penalty='elasticnet'有效）

常用属性

model.coef_         # 特征系数数组 (n_classes, n_features)
model.intercept_    # 截距数组 (1,) or (n_classes,)
model.classes_      # 类别标签数组
model.n_iter_       # 实际迭代次数

solver（优化算法）选择指南

solver	支持的惩罚项	支持的多分类	适用场景	内存占用	速度
`liblinear`	l1, l2	仅ovr	小数据集	低	快
`newton-cg`	l2	ovr, multinomial	中小数据集	中	中
`lbfgs`	l2	ovr, multinomial	默认选择	中	中
`sag`	l2	ovr, multinomial	大数据集	低	快（收敛后）
`saga`	l1, l2, elasticnet	ovr, multinomial	超大数据集/弹性网	低	很快

使用建议：

小数据集：liblinear
中型数据集：lbfgs（默认）
大数据集：sag或saga
需要L1正则化：liblinear或saga
需要弹性网络：saga

基本使用代码示例

from sklearn.datasets import load_breast_cancer  # 威斯康星州乳腺癌（诊断）数据集https://archive.ics.uci.edu/dataset/17/breast+cancer+wisconsin+diagnostic
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

# 加载数据
data = load_breast_cancer()

# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2, random_state=42)

# 标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(x_train)
X_test_scalerd = scaler.transform(x_test)

# 创建模型
model = LogisticRegression(
    penalty='l2',
    C=0.1,
    solver='liblinear',
    max_iter=500,
    random_state=42  # 增加随机种子确保可复现性
)
# 模型训练
model.fit(X_train_scaled, y_train)

# 模型预测
score = model.score(X_test_scalerd, y_test)
print("准确率:", score)  # 模型得分: 0.9912280701754386
print("模型系数：",
      model.coef_)  # [[-0.35740273 -0.39859835  ... -0.38160644 -0.14069316 -0.39954273 -0.4478887  -0.4689656  -0.11858824]]
predict = model.predict(X_test_scalerd)
print("预测结果：", predict)
print("真实结果：", y_test)
print("是否正确", predict == y_test)
print("自行计算正确率", sum(y_test == predict) / len(y_test))  # 正确率 0.9912280701754386

获取样本属于各个类别的概率估计

# 获取样本属于各个类别的概率估计
probability=model.predict_proba(X_test_scalerd)

查看打印结果

 [[0.19 0.81]
 [1.   0.  ]
 [0.96 0.04]
 [0.02 0.98]
 [0.   1.  ]
 [1.   0.  ]
 [1.   0.  ]
 [0.87 0.13]
 [0.44 0.56]]

与相关方法的对比

方法	返回类型	关键特性	适用场景
`predict()`	类别标签	单值预测	只需要最终分类结果
`predict_proba()`	概率矩阵	概率估计	需要不确定性度量/阈值调整
`predict_log_proba()`	对数概率	数值稳定计算	概率乘积计算(如贝叶斯)
`decision_function()`	决策分数	原始模型输出	自定义阈值/模型诊断

理解：

其实就是返回上面提到的激活函数计算得到的概率值：

1. 二分类逻辑回归概率计算

2. 多分类逻辑回归概率计算

在很多分类场景当中我们不⼀定只关注预测的准确率！！！！！

⽐如以这个癌症举例⼦！！！我们并不关注预测的准确率，⽽是关注在所有的样本当中，癌症患者有没有被全部预测 （检测）出来。

所以关于分类模型的评估，需要通过混淆矩阵计算准确率，精确率，召回率，结合业务场景进行综合评判。此外，关于模型评估还可以通过AUC和KS值对模型预测效果进行评估。

超参数调优（交叉验证、网格搜索）

from sklearn.model_selection import GridSearchCV

param_grid = {
    'penalty': ['l1', 'l2'],
    'C': [0.001, 0.01, 0.1, 1, 10, 100],
    'solver': ['liblinear', 'saga'],
    'class_weight': [None, 'balanced']
}

grid_search = GridSearchCV(LogisticRegression(), param_grid, cv=5)
grid_search.fit(X_train, y_train)

print("最佳参数:", grid_search.best_params_)
print("最佳分数:", grid_search.best_score_)

处理类别不平衡数据

# 人工创建不平衡数据
from sklearn.datasets import make_classification

X, y = make_classification(
    n_samples=1000, 
    weights=[0.9, 0.1],  # 90%负类，10%正类
    random_state=42
)

# 1. 使用balanced模式自动加权
model_balanced = LogisticRegression(
    class_weight='balanced',
    solver='liblinear'
)

# 2. 手动设置权重（正类权重提高）
custom_weights = {0: 1, 1: 10}  # 正类的权重是负类的10倍
model_custom = LogisticRegression(
    class_weight=custom_weights,
    solver='liblinear'
)

多分类场景示例

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

# 加载鸢尾花数据集（3分类）
X, y = load_iris(return_X_y=True)

# 使用Pipeline确保正确处理
pipeline = make_pipeline(
    StandardScaler(),
    LogisticRegression(
        # 移除 multi_class 参数（未来版本默认使用'multinomial'）
        solver='lbfgs',     # 支持多分类的求解器
        max_iter=1000,      # 确保充分收敛
        random_state=42     # 保证可复现性
    )
)

# 划分训练测试集（更合理的评估）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 训练模型
pipeline.fit(X_train, y_train)

# 预测概率输出
probas = pipeline.predict_proba(X_test[:3])
print("修改后代码的预测概率:\n", probas)

# 额外评估指标
train_acc = pipeline.score(X_train, y_train)
test_acc = pipeline.score(X_test, y_test)
print(f"\n训练集准确率: {train_acc:.4f}")
print(f"测试集准确率: {test_acc:.4f}")

完整的多分类最佳实践

如果处理更复杂的多分类问题，考虑这些增强方案：

from sklearn.model_selection import GridSearchCV

# 设置参数网格（使用新版API规范）
param_grid = {
    'logisticregression__C': [0.01, 0.1, 1, 10, 100],
    'logisticregression__penalty': ['l2', 'none'],
    'logisticregression__solver': ['lbfgs', 'saga']
}

# 创建优化管道
tune_pipeline = make_pipeline(
    StandardScaler(),
    LogisticRegression(max_iter=1000, random_state=42)
)

# 网格搜索调优
grid_search = GridSearchCV(
    tune_pipeline,
    param_grid,
    cv=5,
    scoring='accuracy',
    n_jobs=-1
)
grid_search.fit(X_train, y_train)

# 输出最佳模型
print(f"最佳参数: {grid_search.best_params_}")
print(f"最佳得分: {grid_search.best_score_:.4f}")

# 使用最佳模型预测
best_model = grid_search.best_estimator_
best_probas = best_model.predict_proba(X_test[:3])
print("\n调优后预测概率:\n", best_probas)

弹性网络

elastic_model = LogisticRegression(
    penalty='elasticnet',
    solver='saga',
    l1_ratio=0.5,  # 0.5表示L1和L2各占一半
    C=0.1,
    max_iter=2000
)
elastic_model.fit(X_train, y_train)

与其他模型组合

1. 集成学习：Stacking

from sklearn.ensemble import StackingClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier

estimators = [
    ('svc', SVC(probability=True)),
    ('dt', DecisionTreeClassifier())
]

stacking_model = StackingClassifier(
    estimators=estimators,
    final_estimator=LogisticRegression(),
    cv=5
)
stacking_model.fit(X_train, y_train)

2. 特征转换：逻辑回归+多项式特征

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# 创建包含多项式特征的管道
poly_model = make_pipeline(
    PolynomialFeatures(degree=2, include_bias=False),
    StandardScaler(),
    LogisticRegression(solver='lbfgs', max_iter=1000)
)
poly_model.fit(X_train, y_train)

常见问题解决方案

1. 收敛警告处理

# 出现ConvergenceWarning时的优化方案
optimized_model = LogisticRegression(
    solver='saga',        # 换用更强的优化器
    max_iter=2000,        # 增加迭代次数
    tol=1e-4,             # 降低收敛阈值
    warm_start=True,      # 热启动继续优化
    n_iter_no_change=20   # 早停策略
)

2. 类别标签顺序问题

# 获取类别标签顺序
print("Classes:", model.classes_)  # 输出例如：[0, 1]

# 自定义类别顺序
custom_class_order = [1, 0]  # 将正类放在前面
model = LogisticRegression()
model.set_params(class_weight={custom_class_order[0]: 1, custom_class_order[1]: 2})
model.fit(X_train, y_train)

3. 特征重要性分析

import matplotlib.pyplot as plt

# 获取特征重要性（系数绝对值）
importance = np.abs(model.coef_[0])
features = data.feature_names if hasattr(data, 'feature_names') else [f'F_{i}' for i in range(len(importance))]

# 可视化
plt.figure(figsize=(10, 6))
sorted_idx = importance.argsort()[::-1]
plt.bar(range(len(sorted_idx)), importance[sorted_idx])
plt.xticks(range(len(sorted_idx)), [features[i] for i in sorted_idx], rotation=90)
plt.title("Feature Importance")
plt.tight_layout()
plt.show()

生产级部署技巧

1. 概率校准处理

from sklearn.calibration import CalibratedClassifierCV

# 原始模型（概率输出可能未校准）
base_model = LogisticRegression(solver='lbfgs')

# Platt Scaling校准
calibrated_platt = CalibratedClassifierCV(
    base_model, 
    method='sigmoid', 
    cv=3
)
calibrated_platt.fit(X_train, y_train)

# Isotonic校准（更强大但需要更多数据）
calibrated_iso = CalibratedClassifierCV(
    base_model, 
    method='isotonic', 
    cv=3
)
calibrated_iso.fit(X_train, y_train)

2. 模型持久化与API部署

import joblib
from flask import Flask, request, jsonify

# 保存模型
joblib.dump(model, 'logistic_model.pkl')

# Flask API部署
app = Flask(__name__)
model = joblib.load('logistic_model.pkl')

@app.route('/predict', methods=['POST'])
def predict():
    data = request.json
    features = data['features']
    prediction = model.predict([features]).tolist()
    probabilities = model.predict_proba([features]).tolist()[0]
    
    return jsonify({
        'prediction': prediction,
        'probabilities': probabilities
    })

if __name__ == '__main__':
    app.run(port=5000, debug=True)

3. 边缘设备部署优化

# 出现ConvergenceWarning时的优化方案
optimized_model = LogisticRegression(
    solver='saga',        # 换用更强的优化器
    max_iter=2000,        # 增加迭代次数
    tol=1e-4,             # 降低收敛阈值
    warm_start=True,      # 热启动继续优化
    n_iter_no_change=20   # 早停策略
)

最佳实践总结

数据预处理：始终标准化连续特征，处理缺失值
参数调优：使用网格搜索优化正则化参数C
类别平衡：设置class_weight='balanced'或自定义权重
模型诊断：绘制ROC曲线和PR曲线评估性能
概率校准：对概率敏感场景使用校准技术
特征选择：对高维数据使用L1正则化或特征重要性
算法选择：
- 二分类：liblinear或saga
- 多分类：lbfgs或saga
- 大数据集：sag或saga

逻辑回归API虽简单，但通过合理的参数配置和数据处理，可在许多实际场景达到与复杂模型媲美的效果，同时保持优秀的解释性和部署效率。

特征工程技巧

类别特征编码：
- 有序特征：Label Encoding
- 无序特征：One-Hot Encoding
- 高基数特征：Target Encoding
连续特征处理：
- 标准化： $σ x - μ$
- 分箱离散化
- 非线性变换：对数、平方等
特征交互：

# 创建交互特征
df['interaction'] = df['age'] * df['income']

4.特征选择方法：

- L1正则化自动特征选择
- 特征重要性排序
- 递归特征消除(RFE)

正则化技术

posted @ 2025-06-02 17:12 指尖下的世界阅读(36) 评论(0) 收藏举报

刷新页面返回顶部

指尖下的世界

今日事今日毕,今日无事早休息.