熵

熵

“熵”是一个非常重要的概念，在物理、信息论、机器学习等领域都有广泛应用。

一、熵的本质：衡量“不确定性”​​

​​熵（Entropy）的本质是描述一个系统的不确定性或混乱程度​​。

• ​​熵越高​​，系统越混乱、越难预测（比如抛一枚均匀硬币，结果最不确定）。
• ​​熵越低​​，系统越有序、越容易预测（比如一枚两面都是正面的硬币，结果完全确定）。

---

​​二、信息熵（Shannon Entropy）的公式​​

在信息论中，熵的数学定义是：

​​关键解读​​：

• p(x_i​) 是事件 xi​ 发生的概率。
• log_2​ 是为了以“比特”（二进制位）为单位衡量信息量。
• ​​熵的单位是比特（bit）​​，表示需要多少二进制位来描述系统的平均不确定性。

---

​​三、通过例子彻底理解熵​​

​​例1：抛硬币​​

• ​​情况1：均匀硬币​​（正反面概率各50%）

  

结果最不确定，熵=（1 bit）=最大熵。

最大熵

当所有事件概率相等时（如晴、雨、雪各占1/3），熵达到最大值：

此时系统不确定性最高，预测难度最大。

• ​​情况2：作弊硬币​​（正面概率100%，反面0%）

  
  

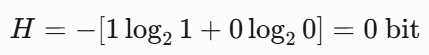
  结果完全确定，熵为0。

​​例2：天气预报​​

• 某地天气概率：晴（70%）、雨（20%）、雪（10%）。

• 熵值介于0和1.58（最大不确定性时的熵）之间，说明有一定可预测性。

 可预测性的解释​​

• ​​熵值为0​​：某天气概率为100%，完全确定（如100%晴天），可预测性最高。
• ​​熵为1.58​​：天气均匀分布（各1/3），完全不确定，可预测性最低。
• ​​实际熵1.16​​：介于0和1.58之间，表明系统存在偏向性（晴天占70%），不确定性较低，因此​​有一定可预测性​​。

---

​​常见困惑点解答​​

​​1. 为什么要用对数？​​

• 对数能将乘法转化为加法，符合信息量可加性（例如：两个独立事件联合信息量是各自信息量之和）。
• log₂​ 是为了二进制编码的直观解释，换底公式可转换为自然对数（$\ln$）或其他底数。

​​2. 为什么概率越高，熵越低？​​

• 系统越确定，提供的信息量越少。例如：“太阳每天升起”概率接近1，这句话几乎不提供新信息。

​​3. 熵和方差有什么区别？​​

• 方差描述数据的波动范围（适用于连续变量）。
• 熵描述概率分布的整体不确定性（适用于离散和连续变量）。

---

​​七、熵的扩展概念​​

​​1. 交叉熵（Cross-Entropy）​​

比较两个概率分布的差异：

• $p$ 是真实分布，$q$ 是预测分布。
• ​​机器学习中​​，交叉熵损失越小，说明预测越接近真实。

​​2. 相对熵（KL散度）​​

衡量两个分布的差异：

• 非对称性：

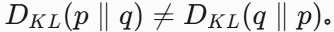
​​3. 条件熵​​

已知某个条件下，系统的剩余不确定性：

​​熵在不同领域的应用​​

​​1. 信息论​​

• 数据压缩：熵决定压缩极限（如ZIP、MP3）。
• 通信效率：信道容量与熵相关。

​​2. 机器学习​​

• ​​决策树​​：用信息增益（熵减少量）选择最佳特征划分数据。
• ​​交叉熵损失​​：衡量预测概率分布与真实分布的差异（常见于分类模型）。

​​3. 物理学​​

• 热力学熵：描述系统无序性（如冰块融化时熵增加）。
• ​​注意​​：物理熵与信息熵数学形式不同，但哲学内涵相通。