03-1概率论与数理统计-基本概念、各种概率计算方法

概率论与数理统计是研究随机现象规律性的数学分支

基本概念

样本空间

样本空间是概率论中的基础概念，指一个随机试验中所有可能结果的集合。它是定义概率模型的基础框架，用于描述随机现象的所有潜在结果。

1. 基本定义

符号表示：通常用 $Ω$ 或 $S$ 表示。
元素：样本空间中的每个结果称为样本点（Sample Point），记作 $ω \in Ω$ 。
核心要求：
- 互斥性：任意两个样本点不能同时发生。
- 完备性：包含所有可能结果，无遗漏。

2. 示例

随机试验	样本空间	样本点示例
抛一枚硬币	$Ω = {正面, 反面}$	正面、反面
掷一颗骰子	$Ω = {1, 2, 3, 4, 5, 6}$	点数为1、2、3、4、5、6
记录某日降雨量（mm）	$Ω = [0, + \infty)$	任意非负实数（如0、5.3、100）
两次抛硬币的结果	$Ω = {(H, H), (H, T), (T, H), (T, T)}$	(正面,反面)、(反面,正面)等

3. 分类

根据结果的可数性，样本空间分为两类：

(1) 离散样本空间

特点：结果可数（有限或无限可列）。
示例：
- 有限：骰子点数 ${1, 2, 3, 4, 5, 6}$ 。
- 无限可列：某客服中心一天接到的电话次数 ${0, 1, 2, \dots}$ 。

(2) 连续样本空间

特点：结果不可数，充满某个区间。
示例：
- 测量某物体的长度（单位：米）： $Ω = [0, 10]$ 。
- 某地区一天的温度变化： $Ω = [- 20, 40]$ （摄氏度）。

4. 事件（Event）与样本空间的关系

事件：样本空间的子集，表示某些结果的集合。
- 基本事件：仅包含一个样本点（如骰子点数为3）。
- 复合事件：包含多个样本点（如骰子点数为偶数 ${2, 4, 6}$ ）。
必然事件：整个样本空间 $Ω$ ，概率为1。
不可能事件：空集 $\emptyset$ ，概率为0。

6. 常见误区与注意事项

误区：混淆样本空间与事件空间。
- 纠正：样本空间是全体结果，事件空间是其子集的集合（即σ-代数）。

7. 总结

核心作用：为概率模型提供所有可能结果的定义域。

随机事件

随机事件是概率论中描述可能发生或不发生的结果集合的核心概念，是样本空间的子集。

1. 基本定义

数学定义：随机事件是样本空间 $Ω$ 的子集，记为 $A \subseteq Ω$ 。
发生条件：当试验结果 $ω \in A$ 时，称事件 $A$ 发生。
分类：
- 基本事件：仅含一个样本点的事件（如骰子点数为3）。
- 复合事件：由多个样本点组成的事件（如骰子点数为偶数）。
- 必然事件： $Ω$ （概率为1）。
- 不可能事件：空集 $\emptyset$ （概率为0）。

2. 事件的集合运算

通过集合操作可组合事件，对应概率的逻辑关系：

运算	符号	定义	概率意义
并（或）	$A \cup B$	$ω \in A$ 或 $ω \in B$	至少有一个事件发生。
交（与）	$A \cap B$	$ω \in A$ 且 $ω \in B$	两个事件同时发生。
差（非）	$A ∖ B$	$ω \in A$ 且 $ω \in / B$	事件A发生但B不发生。
补（对立）	$A^{c}$	$ω \in / A$	事件A不发生。

3. 事件的关系

关系	定义	示例
互斥（互不相容）	$A \cap B = \emptyset$	抛硬币得“正面”和“反面”是互斥事件。
独立	$P (A \cap B) = P (A) P (B)$	两次独立抛硬币的结果相互独立。
包含	$A \subseteq B$ → $A$ 发生必导致 $B$ 发生	骰子点数为2的事件包含于“点数小于3”。

事件的独立性

给定A、B两个事件，如果概率存在P(A,B)=P(A)P(B)（A、B事件的联合分布概率等于事件各自分布概率的积），则事件A和B相互独立。如果事件A、B相互独立，互不影响，那么存在P(A|B)=P(A)，P(B|A)=P(B)。

例1 袋中装有 4 个外形相同的球，其中三个球分别涂有红、白、黑色，另一个球涂有红、白、黑三种颜色．现从袋中任意取出一球，令：

A={ 取出的球涂有红色 }

B={ 取出的球涂有白色 }

C={ 取出的球涂有黑色 }

则：

这表明，A、B、C这三个事件是两两独立的，但不是相互独立的．

频率与概率

频率与概率是统计学中描述随机现象发生可能性的两种核心概念，分别对应实际观测结果与理论预期值。以下是两者的系统解析与对比：

1. 基本定义

概念	定义	数学形式
频率	在有限次试验中，某事件发生的次数与总试验次数的比值。	$f_{n} (A) = n 事件 A 发生次数$ 。
概率	描述事件发生的理论可能性，通常基于模型假设或公理化定义。	$P (A) \in [0, 1]$ ，满足概率三公理。

2. 核心区别

维度	频率	概率
性质	基于实际观测，随试验结果变化。	理论值，固定不变（假设模型正确）。
依赖条件	依赖具体试验数据。	依赖概率模型的定义（如均匀分布、正态分布）。
稳定性	试验次数较小时波动较大。	恒定值（如硬币正面的概率恒为0.5）。
极限关系	当试验次数 $n \to \infty$ ，频率趋近概率（大数定律）。	概率是频率的极限。

概率是频率的稳定值。

独立试验

重复独立试验：在相同的条件下，将试验E重复进行，且每次试验是独立进行的，即每次试验各种结果出现的概率不受其他各次试验结果的影响。

n重伯努利试验：若一试验的结果只有两个A和Ā, 在相同的条件下, 将试验独立地重复进行n次, 则称这n次试验所组成的试验为n重复伯努利试验或伯努利概型。

简单随机抽样

抽取的样本满足两点：

（1）样本X1，X2...Xn是相互独立的随机变量。

（2）样本X1，X2...Xn与总体X同分布。

联合分布函数：

联合概率密度：

排列数

从m个不同元素中取出n(n ≤ m)个元素(被取出的元素各不相同)，并按照一定的顺序排成一列(一般顺序是抽取出来的顺序)，叫做从m个不同元素中取出n个元素的一个排列。记作:A(m,n)

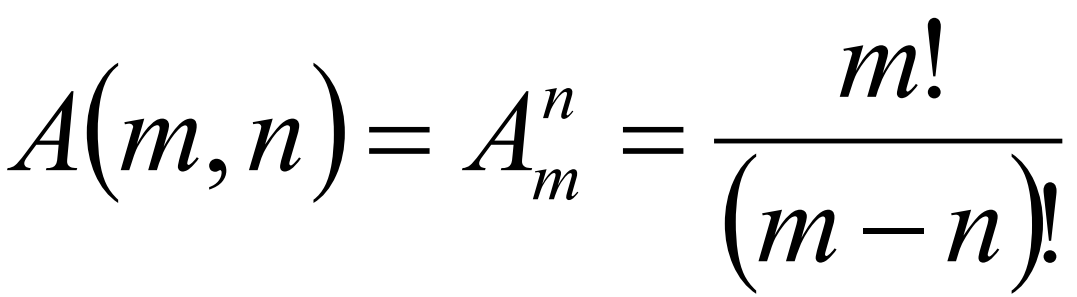
案例:

在一个盒子中有十个完全相同的球，其中每个球上编有一个编号，球的编号从0到9，求随机抽取3个球，可能出现的数字序列共有多少种?（备注：考虑数字的顺序，认为1、2、3和3、2、1是不一样的）。

总共10个球，抽取3个球的排列数：

第一步：从10个球中，获取一个球，有10种选择方式

第二步：从剩下的9个球中，获取一个球，有9种选择方式

第三步：从剩下的8个球中，获取一个球，有8种选择方式

合并这3步，就共有10 * 9 * 8种选择方式，即:

组合数

从m个不同元素中取出n(n ≤ m)个元素的所有组合的个数，叫做从m个不同元素中取出n个元素的组合数。记作:C(m,n)

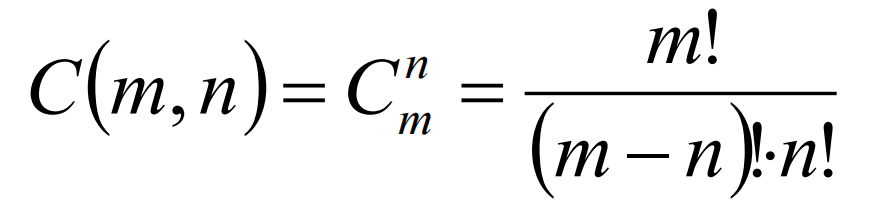
案例:

在一个盒子中有十个完全相同的球，其中每个球上编有一个编号，球的编号从0到9，求随机抽取3个球，可能出现的数字组合共有多少?

（备注：不考虑数字的顺序，认为1、2、3和3、2、1是一样的）。

总共10个球，抽取3个球的组合数：

抽取3个球的排列数为A(10, 3)
对于任意排列(a1 ,a2 ,a3 )都有3*2*1种相同元素的排列存在
其实组合就是在排列的基础上去掉相同元素后剩下的数量

即：

古典概率

概率是以假设为基础的，即假定随机现象所发生的事件是有限的、互不相容的，而且每个基本事件发生的可能性相等。一般来讲，如果在全部可能出现的基本事件范围内构成事件A的基本事件有a个，不构成事件A的有b个，那么事件A出现的概率为：

概率体现的是随机事件A发生可能的大小度量(数值)。

案例：

在一个盒子中有十个完全相同的球，其中五个黑球，五个白球，求事件A={从盒子中获取一个球，颜色是黑色}的概率。

基本的事件总数：10

抽取一个球是黑球的事件数：5

案例：

假设有n个人，每个人都等可能地被分配到N个房间中的任意一间去住(n≤N)，求事件A={恰好有n个房间，其中各住一个人}的概率。

每个人有N个房间可供选择，所以n个人住的方式共有Nⁿ种。

恰好n个房间表示这n个房间其实是从N个房间中任意抽取出来的，也就是从N个房间中抽取n个方法的组合总共有C(N,n)种。

对于n个房间来讲，n个人平均分配，那么总共有A(n,n)种入住方式。

生日问题：

某个班级有n个学生(n≤365)，问至少有两个人的生日在同一天的概率有多大?

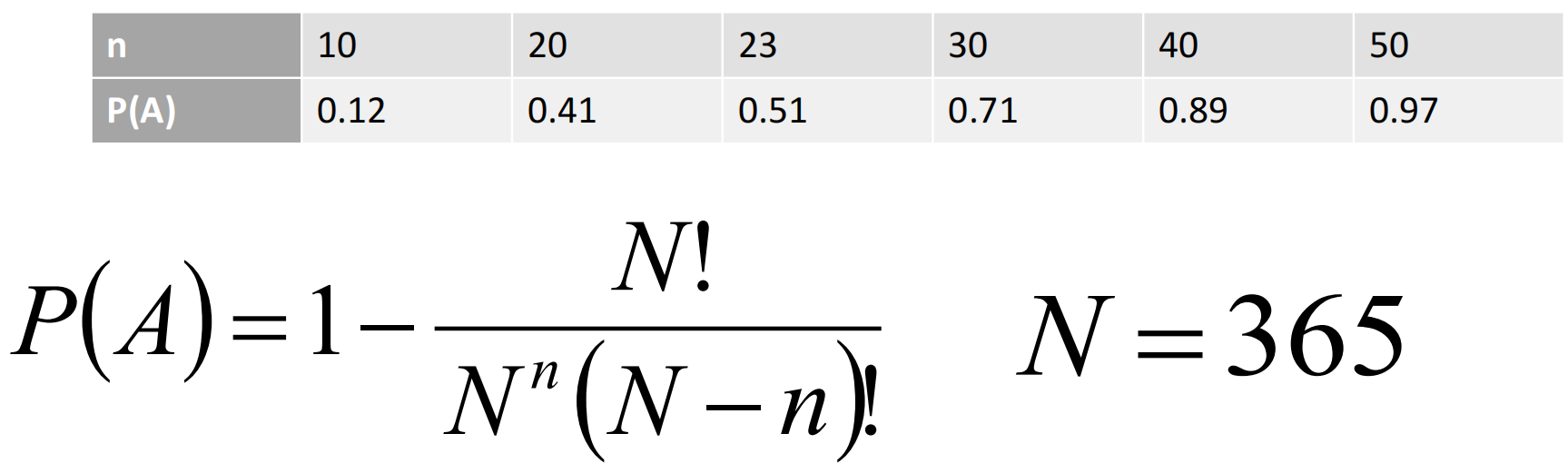
联合概率

表示两个事件共同发生的概率，事件A和事件B的共同概率记作：P(AB)、P(A,B)或者P(A∩B)，读作“事件A和事件B同时发生的概率”

独立事件： $P (A B) = P (A) \cdot P (B)$ 。例如多次抛硬币。
依赖事件： $P (A B) = P (A) \cdot P (B ∣ A)$ 或 $P (B) \cdot P (A ∣ B)$ 。
- 条件概率公式：当 $A$ 和 $B$ 不独立时，必须通过条件概率计算 $P (A B)$ 。
- 直观理解： $P (A B)$ 是 $A$ 发生的概率乘以在 $A$ 已发生时 $B$ 的条件概率。
特殊关系：
- 互斥事件： $P (A B) = 0$ ；
- 包含关系： $P (A B) = P (A)$ 或 $P (B)$ 。

条件概率

事件A在另外一个事件B已经发生的条件下的发生概率叫做条件概率，表示为P(A|B)，读作“在B条件下A发生的概率”

一般情况下P(A|B)≠P(A)，而且条件概率具有三个特性：

非负性
可列性
可加性

例 1 两台车床加工同一种零件共100个，结果如下

	合格品数	次品数	总计
第一台车床加工数	30	5	35
第二台车床加工数	50	15	65
总计	80	20	100

设 A={ 从100个零件中任取一个是合格品}

B={从100个零件中任取一个是第一台车床加工的 }

求：P(A),P(B),P(AB),P(A|B)

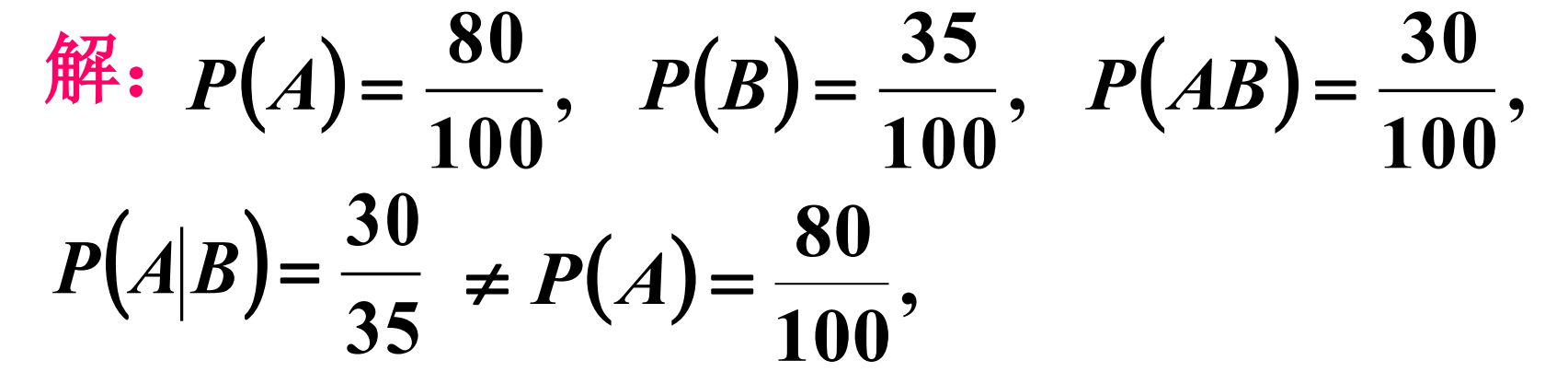
注意，P(AB)≠P(A)*P(B)；而是等于P(A)*（30/80）

例2 已知某家庭有3个小孩，且至少有一个是女孩，求该家庭至少有一个男孩的概率

解：设 A={ 3个小孩至少有一个女孩 }

B={ 3个小孩至少有一个男孩 }

将条件概率公式由两个事件推广到任意有穷多个事件时，可以得到如下公式，假设A1，A2，....，An为n个任意事件(n≥2)，而且P(A1A2 ...An )>0，则：

P(A₁A₂ ...A_n)=P(A₁)P(A₂|A₁)...P(An|A₁A₂...A_n-1)

例3 袋中有一个白球与一个黑球，现每次从中取出一球，若取出白球，则除把白球放回外再加进一个白球，直至取出黑球为止．求取了n 次都未取出黑球的概率．

例 4 设某光学仪器厂制造的透镜，第一次落下时打破的概率为 1/2 ，若第一次落下未打破，第二次落下打破的概率为 7/10 , 若前两次落下未打破，第三次落下打破的概率为 9/10 。求透镜落下三次而未打破的概率。

解：以 Ai ( i=1,2,3 ) 表示事件“透镜第 i 次落下打破”，以 B 表示事件“透镜落下三次而未打破”，

有：

全概率公式

全概率公式用于计算复杂事件概率，通过将事件分解为互斥且穷尽的情况来简化计算。

公式定义

设事件 $A_{1}, A_{2}, \dots, A_{n}$ 构成样本空间的一个划分（即互斥且穷尽），且 $P (A_{i}) > 0。$

（例如把365天划分成星期几，那么某一天不可能同时属于星期一又属于星期二）

则对任意事件 $B$ ，有：

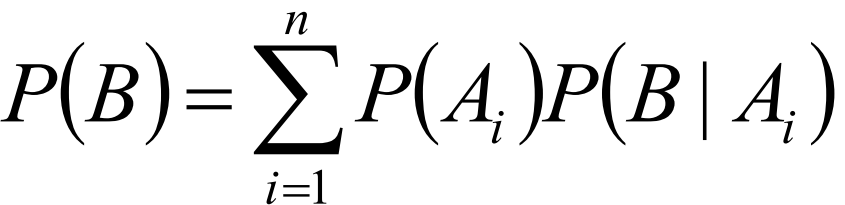
核心思想

分解复杂事件：将事件 $B$ 分解为多个互斥场景 $A_{1}, A_{2}, \dots, A_{n}$ 下的条件概率。
加权求和：每个场景的概率 $P (A_{i})$ 乘以该场景下 $B$ 发生的条件概率 $P (B ∣ A_{i})$ ，最后累加得到总概率。（发生A的概率乘以在发生A的条件下发生B的概率即 $P (B ∣ A_{i})$ ）

应用步骤

确定目标事件 $B$ ：明确需要计算概率的事件。
构造划分事件 $A_{1}, A_{2}, \dots, A_{n}$ ：确保这些事件互斥且覆盖所有可能。
计算每个 $A_{i}$ 的概率： $P (A_{1}), P (A_{2}), \dots, P (A_{n})$ 。
计算条件概率：针对每个 $A_{i}$ ，求 $P (B ∣ A_{i})$ 。
代入公式求和：将所有 $P (A_{i}) \cdot P (B ∣ A_{i})$ 相加。

经典示例

示例1：产品质量检测

场景：两个工厂生产产品，工厂A占60%，次品率1%；工厂B占40%，次品率2%。求随机抽取一件是次品的概率。
解：
- 划分事件： $A_{1}$ （来自工厂A）， $A_{2}$ （来自工厂B）。
- 计算： $P (次品) = P (A_{1}) \cdot P (次品 ∣ A_{1}) + P (A_{2}) \cdot P (次品 ∣ A_{2}) = 0.6 \times 0.01 + 0.4 \times 0.02 = 0.014.$

示例2：不放回抽球

场景：袋中有3红球和2蓝球，不放回抽两次，求第二次抽到红球的概率。
解：
- 划分事件： $A_{1}$ （第一次抽红球）， $A_{2}$ （第一次抽蓝球）。
- 计算：

例5 某小组有20名射手，其中一、二、三、四级射手分别为2、6、9、3名．又若选一、二、三、四级射手参加比赛，则在比赛中射中目标的概率分别为0.85、0.64、0.45、0.32，今随机选一人参加比赛，试求该小组在比赛中射中目标的概率．

扩展与注意事项

无限划分：当划分事件为可数无限个时，公式可推广为：

与贝叶斯定理的关系：全概率公式常用于计算贝叶斯定理中的分母 $P (B)$ ，例如：

验证划分的正确性：确保 $A_{1}, A_{2}, \dots, A_{n}$ 互斥且穷尽，避免遗漏或重叠。

总结

全概率公式通过分解复杂事件为互斥的简单场景，简化了概率计算。其核心在于正确构造划分事件并准确计算每个部分的概率。这一工具在统计推断、风险评估和决策分析中具有广泛应用。

贝叶斯公式

贝叶斯公式，用于在已知部分信息的条件下，更新事件发生的概率。它通过结合先验知识和新的证据，得出后验概率，广泛应用于统计学、机器学习、医学诊断等领域。

1. 公式定义

对于事件 $A$ 和 $B$ ，若 $P (B) > 0$ ，贝叶斯公式为：

关键概念：

先验概率 $P (A)$ ：在考虑证据 $B$ 之前，事件 $A$ 发生的初始概率(在没有数据支持下，A发生的概率)。
后验概率 $P (A ∣ B)$ ：在已知B发生后A发生的概率（在观察到 $B$ 后，事件 $A$ 发生的更新概率。）
似然概率 $P (B ∣ A)$ ：在 $A$ 发生的条件下，观察到 $B$ 的概率。又称似然函数。
边缘概率 $P (B)$ ：观察到 $B$ 的总概率，通常通过全概率公式计算。又称为证据。

2. 公式推导

贝叶斯公式源于条件概率的定义和乘法公式：

联立可得：

3. 应用场景

垃圾邮件过滤

- 问题：已知某关键词在垃圾邮件中的出现概率为 $10%$ ，在正常邮件中为 $1%$ ，且垃圾邮件的先验概率为 $20%$ 。若邮件包含该关键词，求其为垃圾邮件的概率。

设：

P(A)={邮件中出现关键词的概率}=0.10×0.20+0.01×0.80;

P(B)={任意邮件是垃圾邮件的概率}=0.20

P(B|A)=P(A|B)*P(B)/P(A):

一座房子在过去20年里一共发生过2次被盗案，房子的主人养了一条狗，狗平均每周晚上叫3次，在盗贼入侵时狗叫的概率估计为0.9，请求：在狗叫的时候发生入侵的概率是多少?

医学诊断

问题：已知某疾病患病率为 $1%$ ，检测准确率为 $99%$ （患病者 $99%$ 阳性，健康者 $99%$ 阴性）。若某人检测为阳性，求实际患病的概率。
解：
- 设 $A$ 为患病， $B$ 为检测阳性。
- 根据贝叶斯公式：

结论：检测为阳性时，患病概率仅为 $50%$ ，体现了先验概率的重要性。

例 6 用某种方法普查肝癌，设： A={ 用此方法判断被检查者患有肝癌 }， D={ 被检查者确实患有肝癌 }，

已知

而且已知：P(D)=0.0004

现有一人用此法检验患有肝癌，求此人真正患有肝癌的概率

数字特征

数字特征是描述随机变量或数据分布的核心统计量，用于量化其集中趋势、离散程度、形态特征等。以下是常见的数字特征及其详细解析：

1. 期望（Expectation，均值）

期望(mean)：也就是均值，是概率加权下的“平均值”，是每次可能结果的概率乘以其结果的总和，反映的实随机变量平均取值大小。

定义：随机变量所有可能取值的加权平均，权重为概率。
公式：
- 离散型：。
- 连续型：。
意义：反映数据的“中心位置”。
示例：
- 掷骰子的期望：。
性质：
- 线性性： $E (a X + b) = a E (X) + b$ 。
- 独立性：若 $X$ 与 $Y$ 独立，则 $E (X Y) = E (X) E (Y)$ 。

例：某城市有10万个家庭，没有孩子的家庭有1000个，有一个孩子的有9万个，有两个孩子的家庭有6000个，有三个孩子的家庭有3000个，问此城市一个家庭平均有小孩多少个？

例3 甲、乙两人射击，他们的射击水平由下表给出：

X：甲击中的环数；Y：乙击中的环数；

试问哪一个人的射击水平较高？

解：甲、乙的平均环数可写为

EX=8x0.1+9x0.3+10x0.6 =9.5
Ey=8x0.2+9x0.5+10x0.3-9.1

因此，从平均环数上看，甲的射击水平要比乙的好

2. 方差（Variance）与标准差（Standard Deviation）

方差：

定义：随机变量取值与期望的偏离程度的平方的期望。（衡量随机变量相对于数学期望的分散程度）
公式： $Var (X) = E [(X - E (X))^{2}] = E (X^{2}) - [E (X)]^{2}$ 。
意义：衡量数据的离散程度（值越大，数据越分散）。

性质：
- $Var (a X + b) = a^{2} Var (X)$ 。
- 独立性：若 $X$ 与 $Y$ 独立，则 $Var (X + Y) = Var (X) + Var (Y)$ 。

示例：
- 二项分布 $B (n, p)$ ： $Var (X) = n p (1 - p)$ 。

例：

甲、乙两人射击，他们的射击水平由下表给出：

X：甲击中的环数；

Y：乙击中的环数；

试问哪一个人的射击水平较高？

解：比较两个人的平均环数

甲的平均环数为：EX=8x0.3+9x0.2+10x0.5=9.2

乙的平均环数为：EY=8x0.2+9x0.4+10x0.4=9.2

因此，从平均环数上看，甲乙两人的射击水平是一样的，但两个人射击环数的方差分别为：

标准差：

定义：方差的平方根，与原始数据量纲一致。
标准差和方差的不同点在于，标准差和变量的计算单位是相同的，比方差清楚，因此在很多分析的时候使用的是标准差。
公式：

案例1

有甲乙两个单位愿意聘用你，而你能够获得的信息如下，请根据工资待遇的差异情况，您选择哪家单位？为什么？

已知随机变量X的分布列如下，分别求E(X)、E(2X+5)、D(X)、σ(X)的值

3. 协方差（Covariance）

- 定义：
  协方差常用于衡量两个变量的总体误差；当两个变量相同的情况下，协方差其实就是方差。
  
  如果X和Y是统计独立的，那么二者之间的协方差为零。如果协方差为零，那么X和Y是不相关的。
  衡量两个随机变量的线性相关性。

协方差是两个随机变量具有相同方向变化趋势的度量

1. 1. 若Cov(X,Y) > 0, 则X和Y的变化趋势相同
  2. 若Cov(X,Y) < 0, 则X和Y的变化趋势相反
  3. 若Cov(X,Y) = 0，则X和Y不相关，也就是变化没有什么相关性

- 公式： $Cov (X, Y) = E [(X - E (X)) (Y - E (Y))] = E (X Y) - E (X) E (Y)$ 。
- 意义：
  - 正值表示同向变化，负值表示反向变化。
  - 但数值大小受量纲影响，难以直接比较。
- 性质

假设C为一个常数，X和Y实两个随机变量，那么协方差有性质如下所示：

协方差矩阵

对于n个随机向量(X1 ,X2 ,X3 ....Xn ), 任意两个元素Xi和Xj都可以得到一个协方差，从而形成一个n*n的矩阵，该矩阵就叫做协方差矩阵，协方差矩阵为对称矩阵。

协方差的上界

4.相关系数（Correlation Coefficient）

- 定义：协方差的标准化形式，消除量纲影响。
  协方差可以描述X和Y的相关程度，但是协方差的值和X/Y的值采用的是不同的量纲，导致协方差在数值上表现出比较大的差异，因此可以引入相关系数来表示X和Y的相关性。
- 公式：。
- 范围： $- 1 \leq ρ_{X Y} \leq 1$ ，绝对值越大，线性相关性越强。

当p(X,Y)=0的时候，称X和Y不线性相关。

示例：
- 身高与体重的相关系数通常介于0.6~0.8，呈正相关。
注意：相关系数仅反映线性关系，非线性关联需其他方法（如互信息）。

5. 偏度（Skewness）

定义：描述数据分布不对称性的指标。

偏度系数(skewness)是描述分布偏离对称性程度的一个特征数，当分布左右对称的时候，偏度系数为0，当偏度系数大于0时候，即重尾在右侧时，该分布为右偏；当偏度系数小于0时候，即重尾在左侧时，该分布为左偏。

公式： $.$
随机变量的三阶中心矩与样本的平均离均差立方和的比值。
意义：
- 正偏（右偏）：右侧尾部更长，众数 < 中位数 < 均值。
- 负偏（左偏）：左侧尾部更长，均值 < 中位数 < 众数。
示例：
- 收入分布常右偏（少数高收入者拉高均值）。

6. 峰度（Kurtosis）

定义：描述数据分布尾部厚度的指标。

峰度(peakedness; kurtosis)又称峰态系数。表示了概率密度分布曲线在平均值处峰值高低的特征数，直观来讲，峰度反映的是峰部的尖度。

样本的峰度是和正态分布相比较而言的统计量，如果峰度值大于三，那么峰的形状比较尖，比正态分布峰要陡峭。反之亦然。

公式： $.$
意义：
- 尖峰（峰度 > 3）：尾部较厚，极端值概率高于正态分布（如金融收益率）。
- 低峰（峰度 < 3）：尾部较薄（如均匀分布）。
注意：常以正态分布的峰度为基准（3），计算超额峰度（Excess Kurtosis = 峰度 - 3）。

7. 矩（Moments）

原点矩： $E (X^{k})$ （k阶矩）。
中心矩： $E [(X - μ)^{k}]$ （k阶中心矩）。

若E{[X-c]^k}，k=1,2...存在，则称它为X关于点c的k阶矩。

若E{X^kY^p }，k、p=1,2...存在，则称它为X和Y的k+p阶混合原点矩。

若E{[X-E(X)]^k [Y-E(Y)]^p}，k、p=1,2...存在，则称它为X和Y的k+p阶混合中心矩。

意义：
- 一阶原点矩：期望。
- 二阶中心矩：方差。
- 三阶中心矩：用于计算偏度。
- 四阶中心矩：用于计算峰度。

X的数学期望E(X)是X的一阶原点矩。

X的方差D(X)是X的二阶中心矩。

X和Y的协方差Cov(X,Y)是X和Y的二阶混合中心矩。

8. 总结表

数字特征	公式	意义
期望（均值）		数据集中趋势
方差		数据离散程度
标准差		离散程度（与数据同量纲）
协方差		两变量线性相关性（带量纲）
相关系数		标准化线性相关性（无量纲）
偏度		分布不对称性
峰度		尾部厚度

8. 应用场景

数据分析：通过均值和方差快速描述数据集特征。
风险管理：用方差和协方差评估投资组合风险。
模型假设检验：通过偏度和峰度验证数据是否符合正态分布。
机器学习：特征工程中标准化数据（均值归零，方差归一）。

9. 注意事项

量纲影响：方差和协方差受量纲影响，比较不同量纲数据时需标准化。
异常值敏感度：均值和方差对异常值敏感，可结合中位数和四分位距分析。
非线性关系：相关系数仅捕捉线性关系，需结合散点图观察非线性模式。

总结

数字特征是统计学与概率论的基础工具，用于量化数据的分布特性。掌握这些特征的定义、计算及意义，能帮助快速理解数据规律，支撑科学决策与建模分析。

马尔科夫不等式

马尔可夫不等式是概率论中的基本工具，用于估计非负随机变量超过某阈值的概率，适用于任何非负随机变量，无需假设其方差或其他高阶矩存在。

1. 数学表述

对于任意非负随机变量 $X \geq 0$ 和正数 $a > 0$ ，有：

直观意义：随机变量取较大值的概率被其期望值控制。

例1：某公司员工月薪 $X$ （万元）的期望为 $E (X) = 1.5$ ，估计月薪超过3万元的概率。
解：由马尔可夫不等式：

即月薪超过3万元的概率不超过50%。

例2：随机变量 $X$ 表示灯泡寿命（小时），已知 $E (X) = 1000$ ，估计寿命不足200小时的概率。
解：马尔可夫不等式需针对 $X \geq a$ ，此处转换为 $P (X \leq 200) = 1 - P (X > 200)$ 。

若取 $a = 200$ ，则：

但概率值不可能超过 1，因此该结果无实际意义，仅说明马尔可夫不等式在 $a < E (X)$ 时无法提供有效上界。

5. 与其他不等式的关系

切比雪夫不等式：马尔可夫不等式的直接推论。
取 $Y = ∣ X - μ ∣$ ， $a = kσ$ ，则：

切比雪夫不等式/切比雪夫定理

切比雪夫不等式是概率论中用于估计随机变量偏离其均值的概率的重要工具，适用于任何具有有限均值和方差的分布。

1. 数学表述

对于任意随机变量 $X$ （无论离散型或连续型），若其均值 $μ = E (X)$ 、方差 $σ^{2} = Var (X)$ ，则对任意正数 $k > 0$ 或 $ϵ > 0$ ，有：

直观意义：数据偏离均值超过 $k$ 倍标准差的概率被方差控制。

2. 证明过程

切比雪夫不等式是马尔可夫不等式的直接推论：

例1：某考试分数服从均值 $μ = 75$ 、标准差 $σ = 10$ 的分布，估计分数在 55 到 95 之间的概率。

步骤：
- 计算偏离范围 $∣ X - 75∣ \leq 20$ （即 $ϵ = 20$ ）。
- 代入不等式：

- 结论：至少有 75% 的考生分数在 55 到 95 之间。

例2：某产品重量均值 $μ = 500 g$ ，标准差 $σ = 5 g$ ，估计重量在 490g 到 510g 之外的概率。

步骤：
- $∣ X - 500∣ \geq 10 g$ ，即 $k = 10/ 5 = 2$ 。
- 代入不等式：

- 结论：重量超出该范围的概率不超过 25%。

4. 与马尔可夫不等式的对比

性质	马尔可夫不等式	切比雪夫不等式
适用变量	非负随机变量（ $X \geq 0$ ）	任意随机变量（需存在方差）
依赖参数	仅需均值 $E (X)$	需均值 $μ$ 和方差 $σ^{2}$
估计对象	$P (X \geq a)$	P(\|(X- $μ)\|\geqk σ)$
精度	宽松（仅用一阶矩）	相对更紧（利用二阶矩）

6. 局限性

宽松性：实际概率通常远小于上界（如正态分布中 $P (∣ X - μ ∣ \geq 2 σ) \approx 5%$ ，但切比雪夫给出 25%）。
依赖方差：若方差不存在（如柯西分布），不等式失效。
对称性假设：对非对称分布的尾部概率估计可能不均衡。

7. 总结

核心公式：
核心价值：

为任意分布的尾部概率提供保守估计，仅依赖均值和方差。
使用建议：
- 适用于数据分布未知或验证假设的场景。
- 若已知分布类型（如正态分布），优先使用更精确的分布特性

大数定律

大数定律是概率论的核心定理之一，描述了随机变量的样本均值随样本量增大而稳定收敛于总体均值的现象。

在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。

设随机变量X1 ,X2 ,....,Xn是一列相互独立的随机变量(或者两两不相关)，并且分别存在期望E(X_k )和方差D(X_k )，对于任意小的正数ε，有：

当具有相同期望μ和方差为σ²的时候，对随机变量的均值:

则有：

大数定律的意义：随着样本容量n的增加，样本平均数将接近于总体平均数(期望μ)，所以在统计推断中，一般都会使用样本平均数估计总体平均数的值。

也就是我们会使用一部分样本的平均值来代替整体样本的期望/均值，出现偏差的可能是存在的，但是当n足够大的时候，偏差的可能性是非常小的，当n无限大的时候，这种可能性的概率基本为0。

大数定律的主要作用就是为使用频率来估计概率提供了理论支持。

中心极限定理

样本的平均值约等于总体的平均值。不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

描述的是一个实际的现象，有了这个定理就能解决很多问题了，比如我们可以通过对样本进行观察，得出总体的情况。

中心极限定理的意义：设从均值为μ、方差为σ²有限的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ、方差为σ² 的正态分布。

直观理解

核心意义：无论原始分布如何，样本均值的分布趋于正态。
几何解释：多因素独立作用的叠加效应会使总结果呈现对称性（类似抛硬币实验的极限行为）。
与大数定律的区别：
- 大数定律：样本均值依概率收敛于总体均值（收敛性）。
- 中心极限定理：描述样本均值收敛时的分布形态（正态性）。

参数估计

点估计

点估计是统计学中利用样本数据对总体参数进行单一数值估计的方法，旨在通过样本信息推断未知的总体参数（如均值、方差等）。

1. 基本概念

参数（Parameter）：总体的数字特征（如均值 $μ$ 、方差 $σ^{2}$ ）。
估计量（Estimator）：用于估计参数的统计量（如样本均值 $X ˉ$ 、样本方差 $S^{2}$ ）。
估计值（Estimate）：估计量的具体计算结果（如 $x ˉ = 5.2$ ）。

矩估计

矩估计是一种基于样本矩与总体矩匹配的参数估计方法，通过构建方程求解未知参数。其核心思想是利用样本数据计算出的矩（如均值、方差）来近似总体矩，从而推导出参数估计值。

1. 基本原理

矩的定义：

核心步骤：
1. 确定参数个数：假设待估参数有 $m$ 个。
2. 构建方程：令前 $m$ 个样本矩等于对应的总体矩，形成方程组。
3. 解方程组：求解得到参数的估计值。

2. 具体步骤

列出总体矩表达式：
根据分布类型，写出总体前 $m$ 阶矩的表达式（如均值 $μ$ 、方差 $σ^{2}$ ）。
计算样本矩：
用样本数据计算对应的样本矩（如样本均值 $X ˉ$ 、样本方差 $S^{2}$ ）。
建立方程：
令样本矩等于总体矩，得到方程组。
求解参数：
解方程组得到参数的矩估计值。

3. 示例分析

(1) 正态分布 $N (μ, σ^{2})$ 

待估参数： $μ$ （均值）和 $σ^{2}$ （方差）。
总体矩：
- 一阶原点矩： $E (X) = μ$ 。
- 二阶中心矩： $Var (X) = σ^{2}$ 。
样本矩：

(2) 指数分布 $Exp (λ)$ 

待估参数： $λ$ （速率参数）。

极大似然估计法

概率是求某件事情在某个条件下发生的可能性大小。

似然是某个事已经发生，求是在什么条件下发生的。

任取 1箱从中任取1 球已知取到红球问最有可能从何箱取P(红球/甲)= 0.99,P(红球/乙) =0.01

自然，认为从甲箱取更合理

又如，兔龟赛跑，得第一名的最有可能是谁？

在一次吃鸡比赛中，有两位选手，一个是职业选手，一个是菜鸟路人。

比赛结束后，公布结果有一位选手完成20杀，请问是哪个选手呢？

极大似然原理：一个随机试验有若干个可能结果A,B,C,…。若在一次试验中，结果A发生，则一般认为试验条件对A最有利，即A发生的概率P(A/θ)最大.(θ条件)

极大似然估计法是在总体的分布类型已知的条件下所使用的一种参数估计方法.

它首先是由德国数学家高斯在1821年提出的.

然而，这个方法常归功于英国统计学家费歇 .

费歇在1922年重新发现了这一方法，并首先研究了这种方法的一些性质 .

离散型似然函数的求法

概率密度函数：

表示在参数θ的下随机变量X取到x的可能性

如果有上式成立，则在参数θ1下随机变量X取到x值的可能性大于θ2

连续型总体似然函数的求法

如果X是连续随机变量给定足够小的ε>0，那么其在(x-ε,x+ε)内的概率为：

得到的结果与离散型一致！概率表达了在给定参数θ时X=x的可能性；（求概率）

而似然表示的是在给定样本X=x时，参数的可能性！（求“是在什么条件下发的”）

极⼤似然函数取对数的原因

减少计算量

在计算⼀个独⽴同分布数据集的联合概率时，如：

其联合概率是每个数据点概率的连乘：

两边取对数则可以将连乘化为连加：

乘法变成加法，从⽽减少了计算量；

同时，如果概率中含有指数项，如⾼斯分布，能把指数项也化为求和形式，进⼀步减少计算量；

另外，在对联合概率求导时，和的形式会⽐积的形式更⽅便。

2 利于结果更好的计算

但其实可能更重要的⼀点是，因为概率值都在[0,1]之间，因此，概率的连乘将会变成⼀个很⼩的值，可能会引起浮点数下溢，尤其是当数据集很⼤的时候，联合概率会趋向于0，⾮常不利于之后的计算。

3 取对数并不影响最后结果的单调性

因为相同的单调性，它确保了概率的最⼤对数值出现在与原始概率函数相同的点上。因此，可以⽤更简单的对数似然来代替原来的似然。

其他概念

二维随机变量

二维随机变量是研究两个随机变量联合行为的数学工具。

1. 定义与表示

定义：设 $(X, Y)$ 为定义在样本空间 $Ω$ 上的有序对，若对任意实数 $x, y$ ，集合 ${X \leq x, Y \leq y}$ 是随机事件，则称 $(X, Y)$ 为二维随机变量。
分类：
- 离散型： $X$ 和 $Y$ 均取有限或可列个值（如抛硬币和骰子的结果组合）。
- 连续型： $X$ 和 $Y$ 在区间上连续取值（如身高与体重）。

2. 联合分布函数（Joint CDF）

定义： $F (x, y) = P (X \leq x, Y \leq y) .$
性质：
1. 单调性：对任意 $x_{1} \leq x_{2}$ 和 $y_{1} \leq y_{2}$ ，有 $F (x_{1}, y_{1}) \leq F (x_{2}, y_{2})$ 。
2. 边缘分布： $F_{X} (x) = F (x, + \infty)$ ， $F_{Y} (y) = F (+ \infty, y)$ 。