02-3线性代数-矩阵
认识矩阵

矩阵(matrix)是线性代数的核心工具,是一个由数构成的二维数组。排列成 行 列,记作 。
和科学计算numpy里array的区别是,矩阵必须是2维的,但是array可以是多维的。
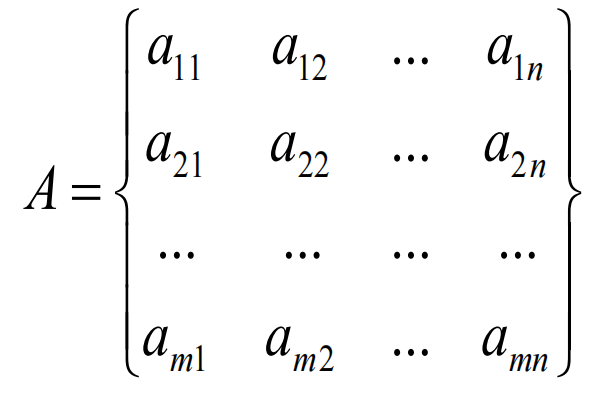
矩阵的维数:即行数×列数。
Aij 指第 i 行,第 j 列的元素。
例如下面这个是 3×2 矩阵,即 3 行 2 列
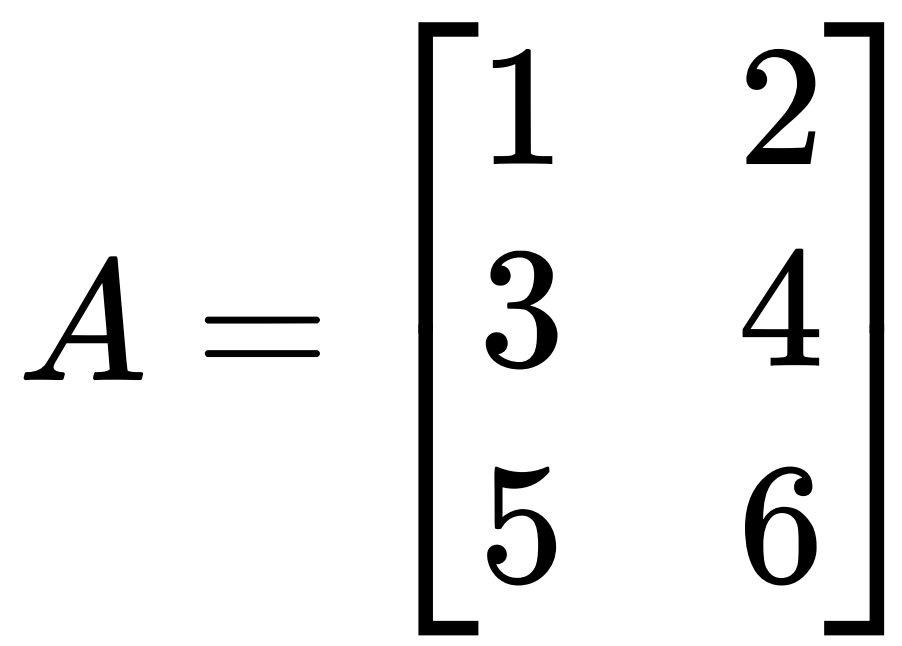
数域F中m*n个数排成m行n列,数域F上的矩阵,当F为实数域R时,A叫做实矩阵,当F为复数域C时,A叫做复矩阵。
矩阵和行列式

当矩阵是方阵的时候,它就有行列式:
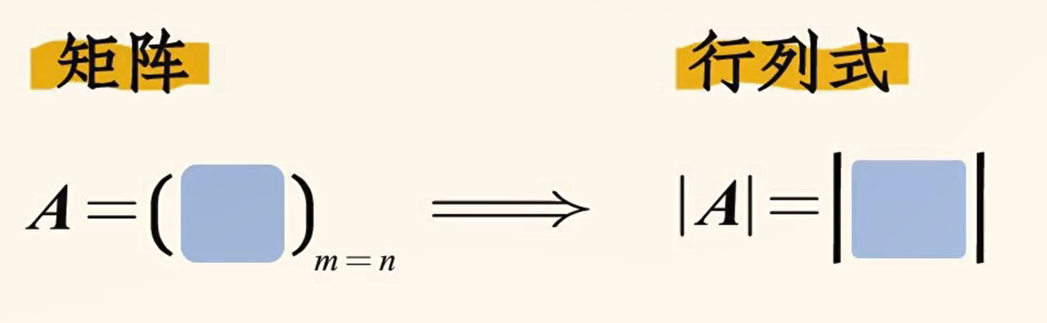
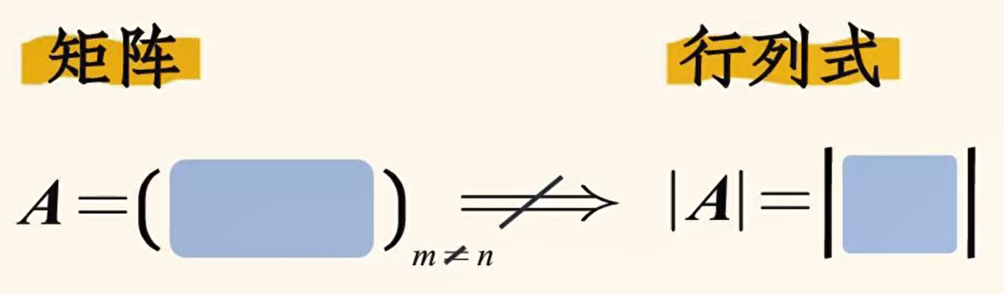
矩阵与向量
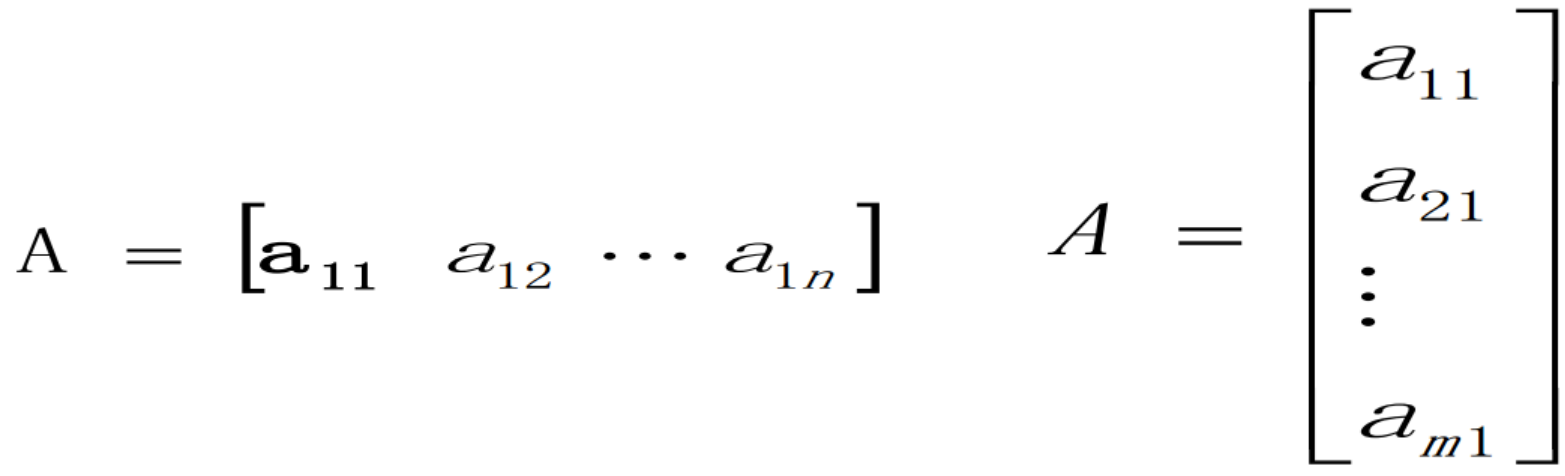
下面展示的就是三维列 向量(3×1)
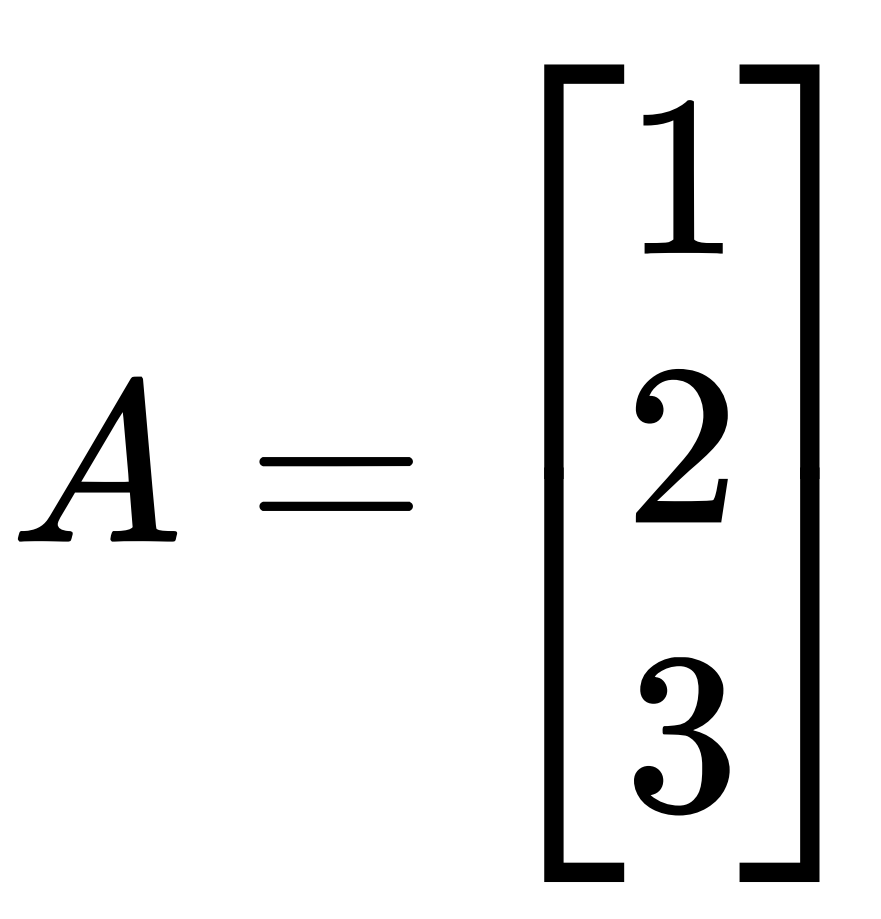
矩阵的应用
1.线性方程组求解
矩阵形式 可表示复杂方程组,通过高斯消元法或矩阵逆求解。
2.计算机图形学
- 变换矩阵(如旋转、平移、缩放)用于三维模型的位置和姿态调整。
- 例如,二维旋转矩阵:
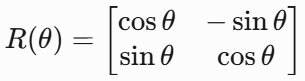
3.机器学习与数据科学
- 协方差矩阵:描述数据特征间的相关性。
- 权重矩阵:神经网络中连接不同层的参数。
4.量子力学
量子态和算符用矩阵表示,如泡利矩阵描述量子比特操作。
总结
- 核心作用:矩阵是表示线性变换、求解方程组、处理多维数据的通用工具。
- 关键性质:秩、行列式、特征值等不变量揭示了矩阵的深层结构。
- 应用广泛性:从物理学到人工智能,矩阵是建模与计算的基石。
通过掌握矩阵运算和分解方法,可以高效解决工程和科学中的复杂问题。建议结合实际问题(如数据降维、图像变换)进行练习,以深化理解。
矩阵同型与相等

特殊矩阵

负矩阵

零矩阵
如果矩阵A中的所有元素(m*n个)均为0,那么此时矩阵A叫做零矩阵,可以记作0。

方阵
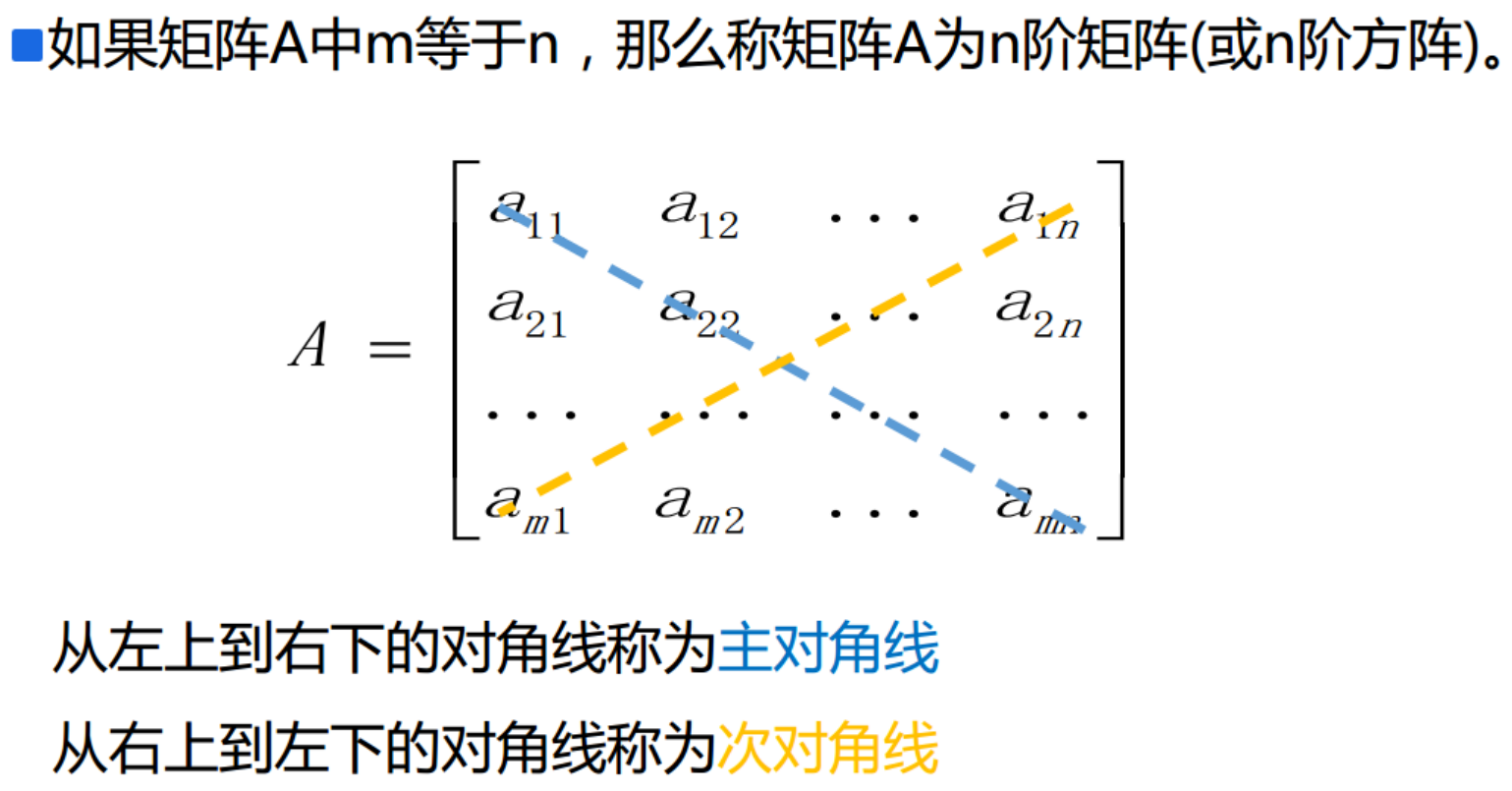
上三角矩阵、下三角矩阵
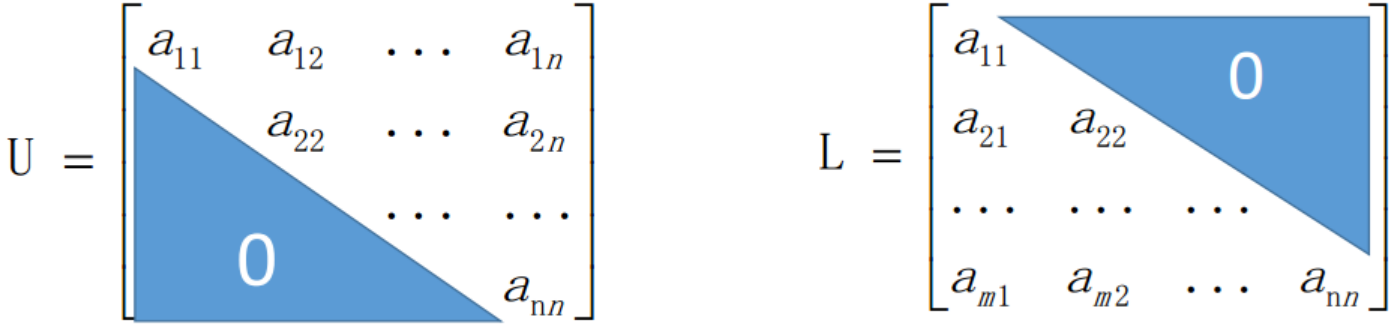
对角矩阵

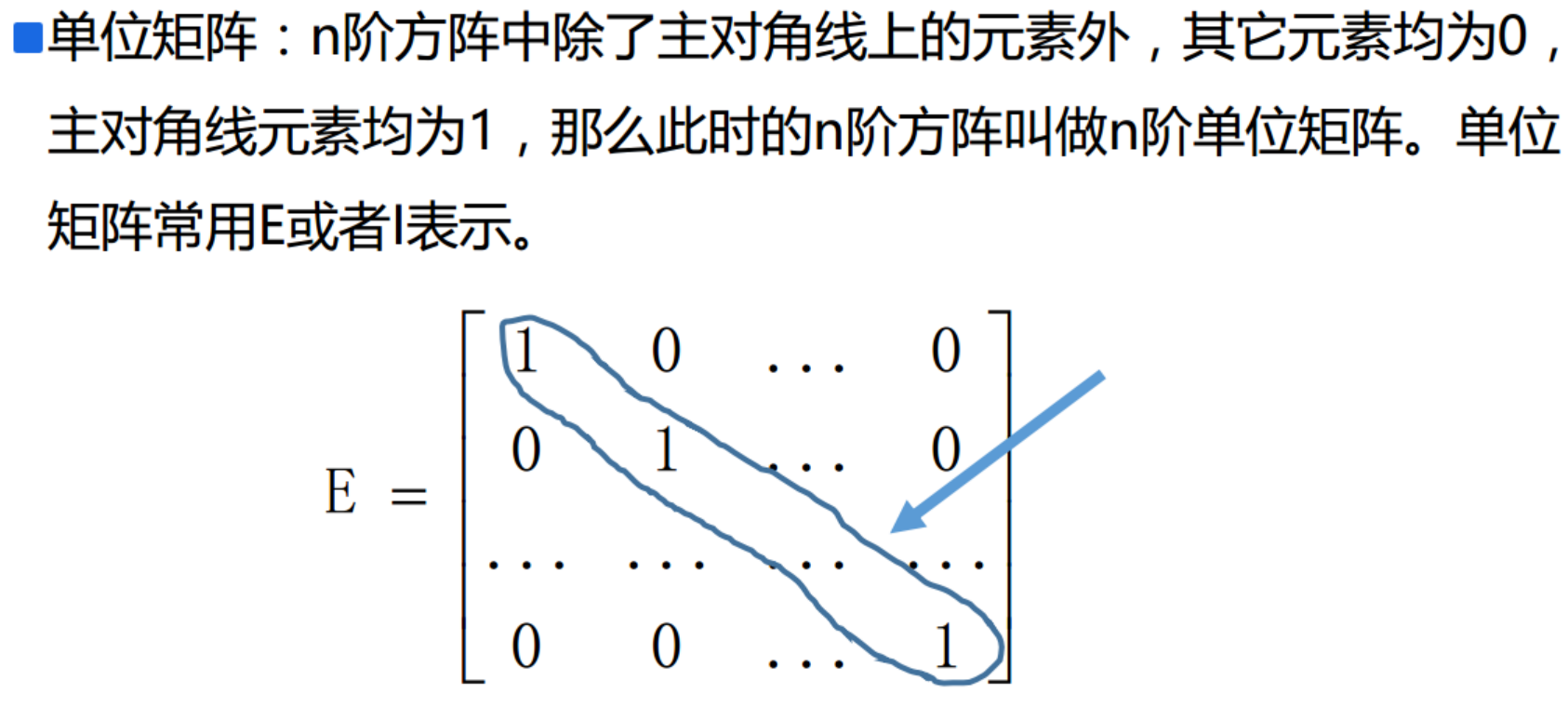
单位矩阵
数量矩阵
数量矩阵就是主对角线上都是K,任何矩阵乘以数量矩阵,都是原来的k倍,例如:
2 0 0
0 2 0
0 0 2
矩阵的基本运算
矩阵和标量的运算
1. 数学视角
- 严格线性代数:矩阵加法要求两个矩阵维度完全相同。标量无法直接与矩阵相加减乘除(除非显式将标量转换为同维矩阵)。
- 数值计算扩展:实际应用中,标量加矩阵通常表示将标量加减乘除到矩阵的每个元素上,即:

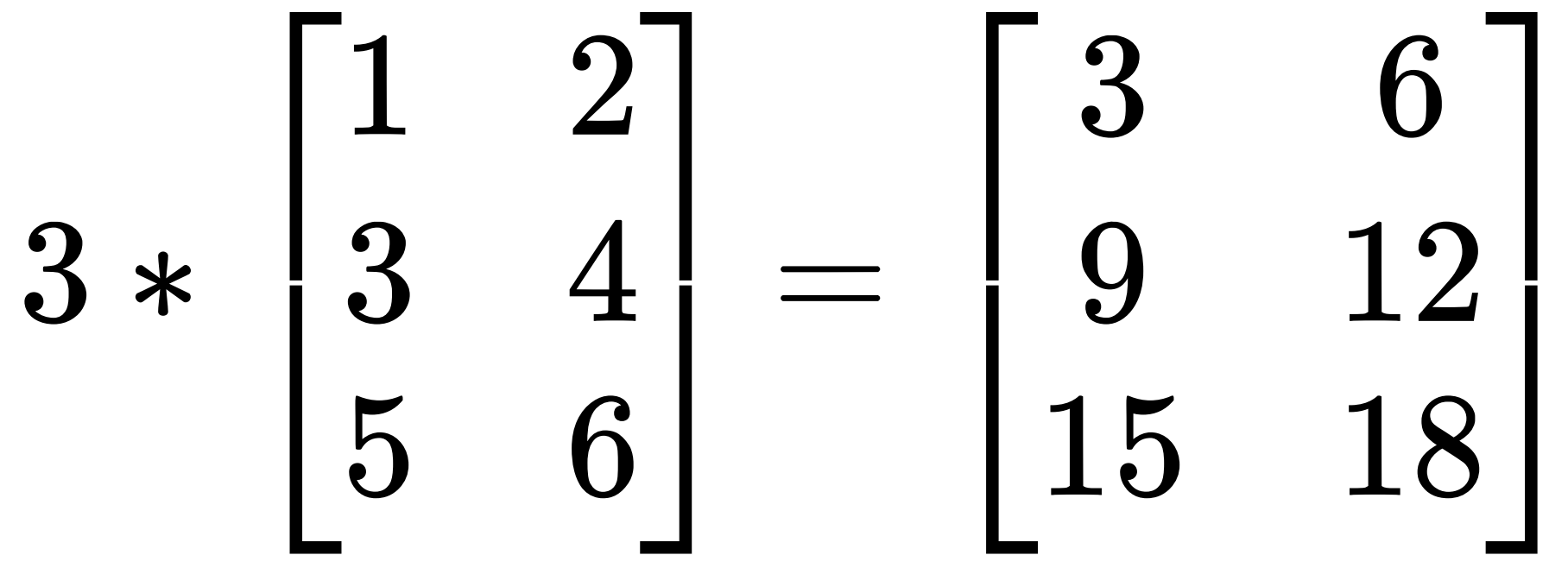
矩阵和矩阵的加法
只有当两个矩阵是同型矩阵时(行列数相等),才能进行加法 运算.
矩阵的加法与减法要求进行操作的两个矩阵A和B具有相同的阶,假设A为m*n阶矩阵,B为m*n阶矩阵,那么C=A±B也是m*n阶的矩阵,并且矩阵C的元素满足:cij =aij ±bij
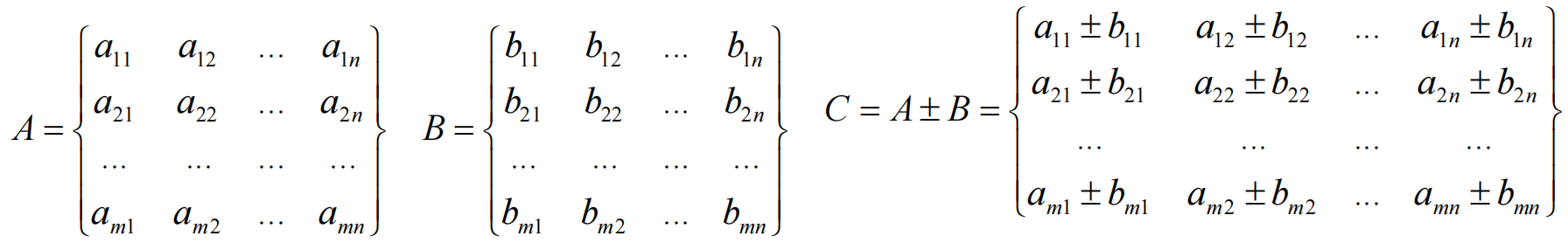
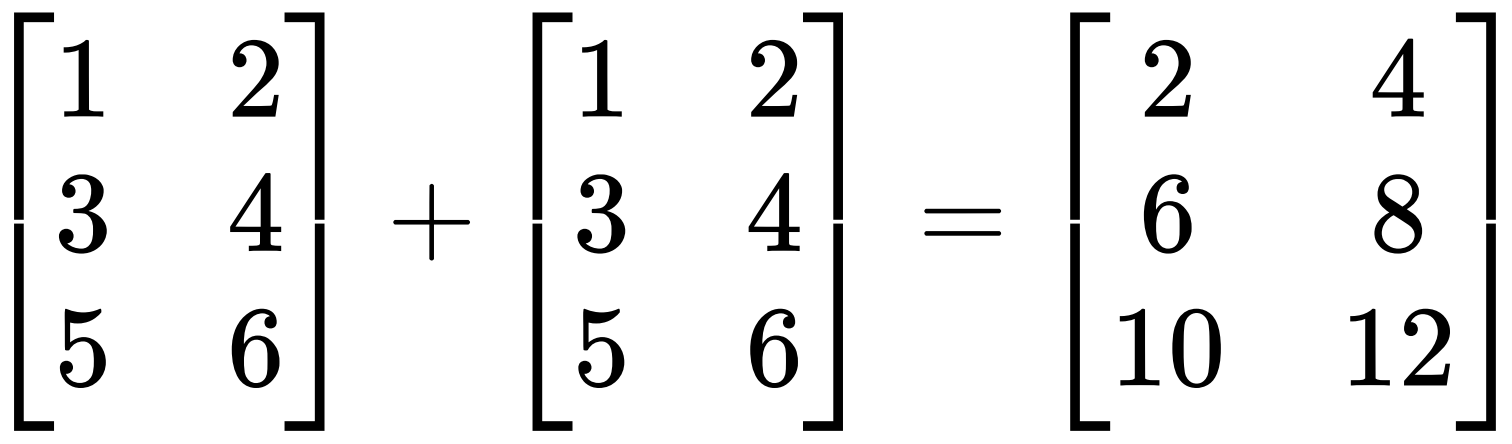
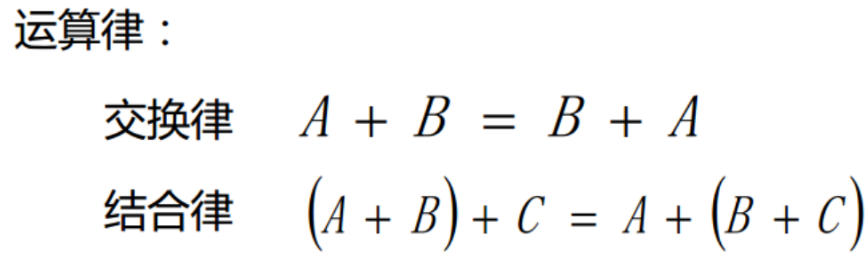
矩阵与数的乘
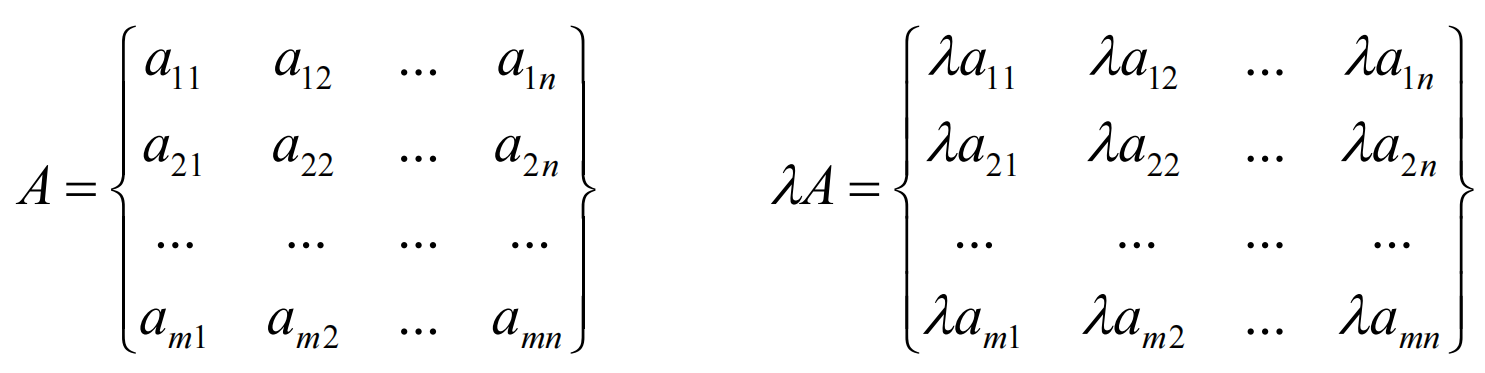
数乘:将数λ与矩阵A相乘,就是将数λ与矩阵A中的每一个元素相乘,记作λA;结果C=λA,并且C中的元素满足:cij =λaij
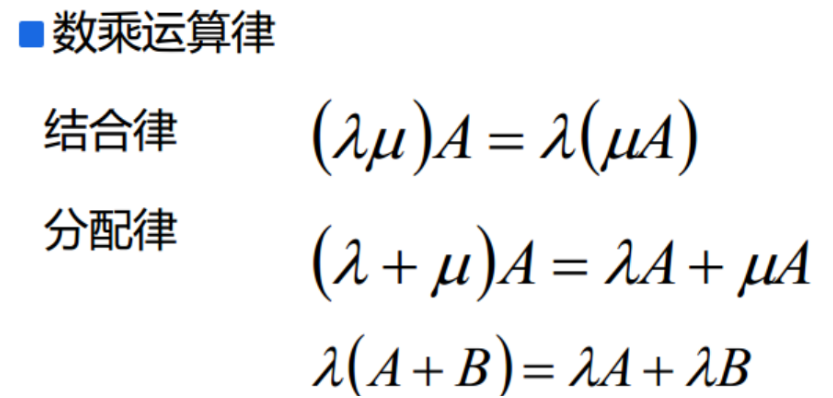
矩阵的数乘运算与行列式的数乘运算不同.(行列式如果乘以k,最后的值要乘以k平方)
矩阵与向量的乘法
矩阵与向量的乘法必须满足矩阵的列数等于向量的长度(即向量的维度)
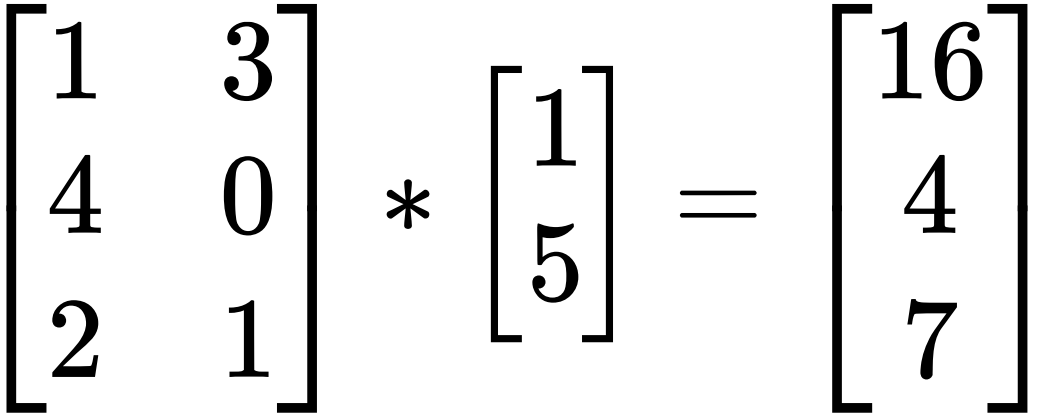
1*1+3*5 = 164*1+0*5 = 42*1+1*5 = 7
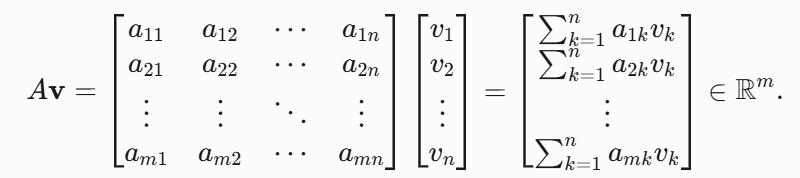
行向量与列向量的区别
- 列向量:维度为 ,可直接与 矩阵相乘。
- 行向量:维度为 ,需转置为列向量后才能与矩阵相乘。
例如:
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]]) # 3x2 矩阵
v_row = np.array([7, 8]) # 行向量 (1x2)
v_col = v_row.reshape(-1, 1) # 转换为列向量 (2x1)
result = A @ v_col # 正确:3x2 矩阵 × 2x1 向量 → 3x1 向量
# 错误示例:A @ v_row 会因维度不匹配报错矩阵与矩阵的乘法
矩阵的乘法仅当第一个矩阵A的列数和第二个矩阵B的行数相等时才能够定义,假设A为m*s阶矩阵,B为s*n阶矩阵,那么C=A*B是m*n阶矩阵。
矩阵乘法:其实就是拿A矩阵的每一行,和B矩阵的每一列相乘,得到C矩阵的每一个元素:
举例:A*B
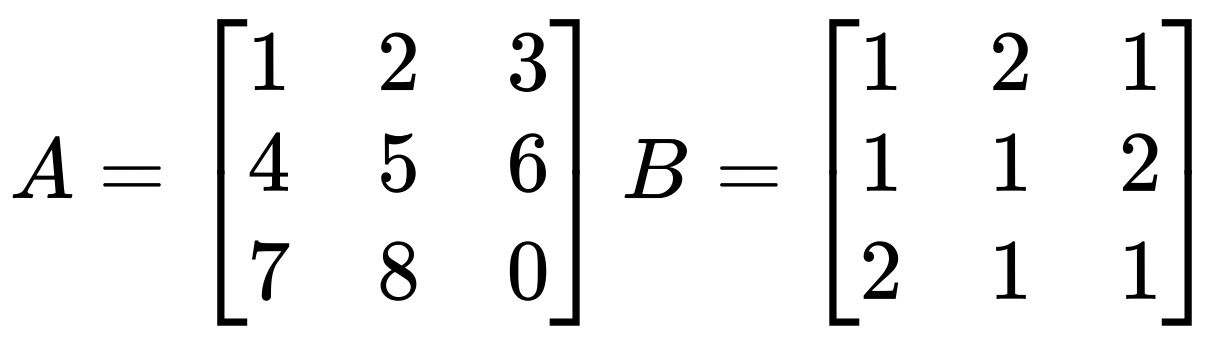
A的第一行和B的3个列分别相乘,得到C的第一行的3个数据C[0]=[(1*1+2*1+3*2),(1*2+2*1+3*1),(1*1+2*2+3*1)]
1 2 3 1 2 1 8 7 8
A=4 5 6 B= 1 1 2 C= x x x
7 8 0 2 1 1 x x x
![]()
结论:m×n 矩阵乘以 n×o 矩阵,变成 m×o 矩阵。即矩阵A的行数和矩阵B的列数。矩阵相乘不满足交换律。

举例:比如说现在有两个矩阵 A 和 B,那 么它们的乘积就可以表示为图中所示的形式。

练一练
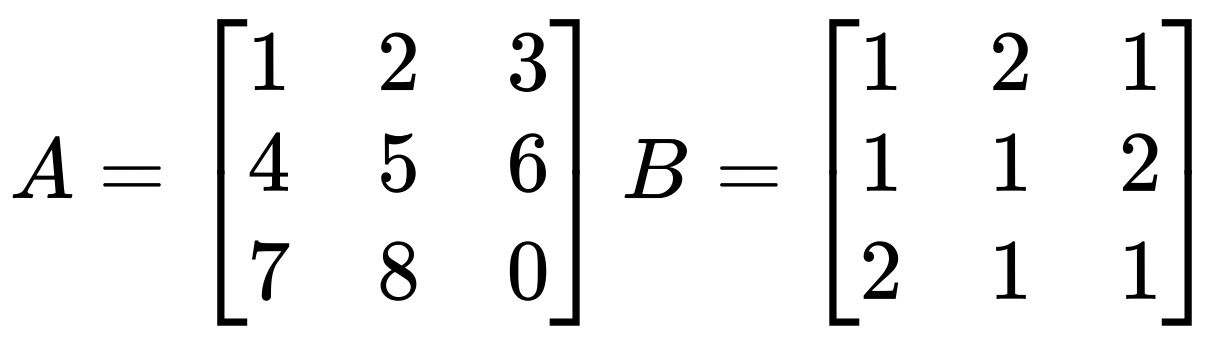
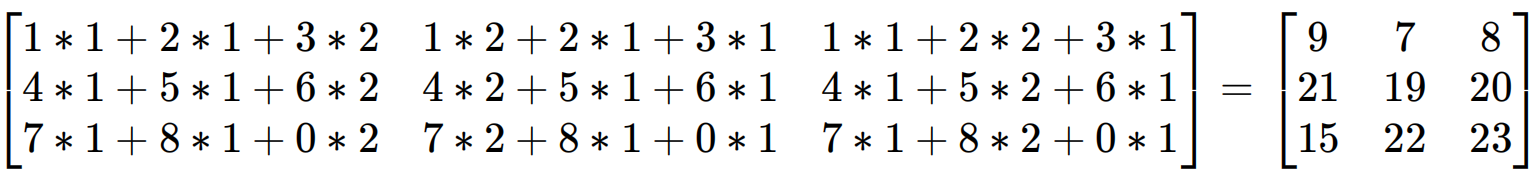
矩阵乘法的特点
- 不满足交换律:A×B≠B×A
- 不满足消去律:

- 满足结合律:A×(B×C)=(A×B)×C
- 满足分配律:
- 矩阵乘法中存在化零因子,而实数乘法中不存 在化零因子。
转置
矩阵的转置:把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵,这一过程叫做矩阵的转置。记 A T=B。 使用AT表示A的转置。
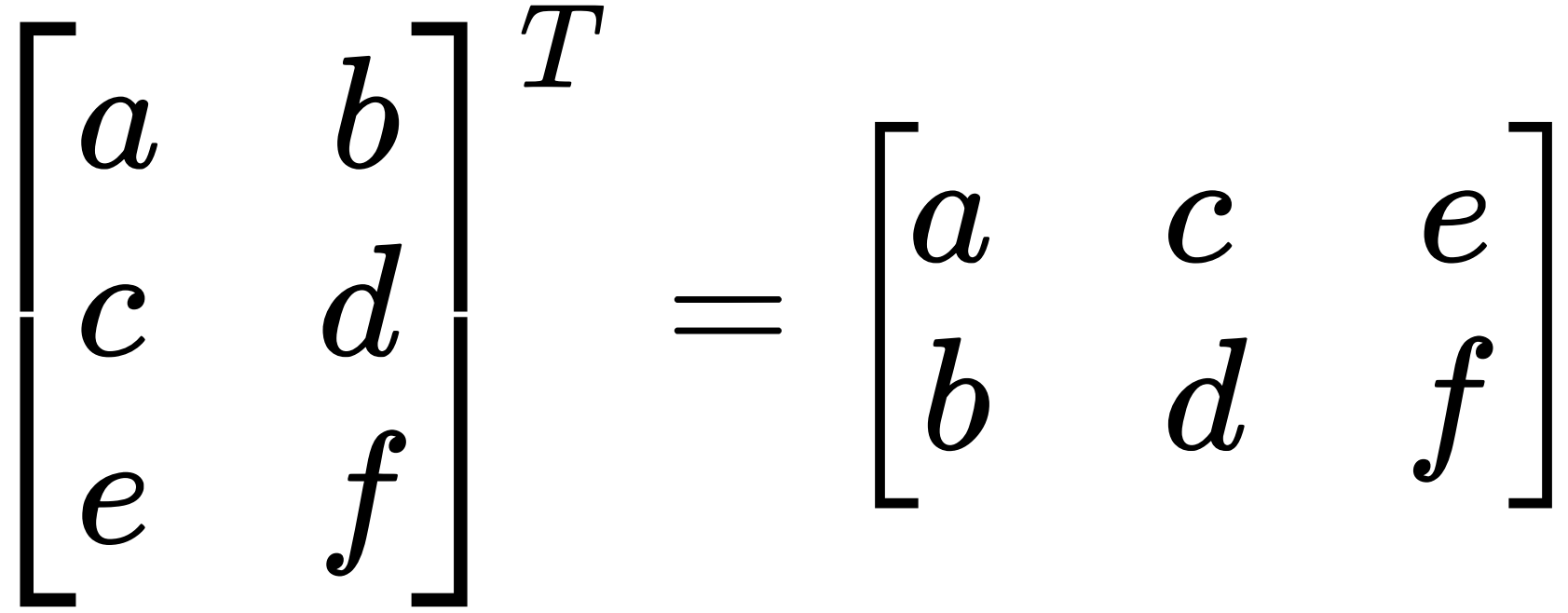


***方阵***
说明:以下这些概念仅适用于方阵:
| 概念 | 是否仅适用于方阵? | 说明 |
|---|---|---|
| 逆矩阵 | 是 | 只有方阵且可逆(行列式非零)时存在逆矩阵。 |
| 伴随矩阵 | 是 | 伴随矩阵是方阵的余因子矩阵转置,非方阵无定义。 |
| 行列式 | 是 | 行列式仅针对方阵定义,非方阵无行列式。 |
| 代数余子式 | 是 | 代数余子式基于子矩阵的行列式,仅方阵的元素有代数余子式。 |
| 上三角矩阵 | 是 | 严格定义为方阵中主对角线下方元素全为零的矩阵。 |
| 下三角矩阵 | 是 | 严格定义为方阵中主对角线上方元素全为零的矩阵。 |
| 单位矩阵 | 是 | 单位矩阵是主对角线为1、其余元素为0的方阵,非方阵无单位矩阵定义。 |
方阵的行列式

伴随矩阵A*
伴随矩阵(又称古典伴随矩阵)是方阵的重要概念,与矩阵求逆、行列式密切相关。伴随矩阵是原矩阵的代数余子式组成的矩阵的转置。伴随矩阵记作
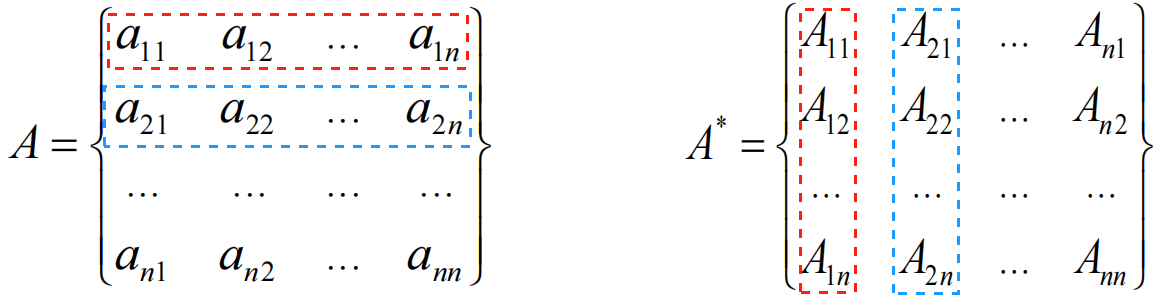
注意:A的代数余子式A*的元素排列顺序:A的行变成了A*的列

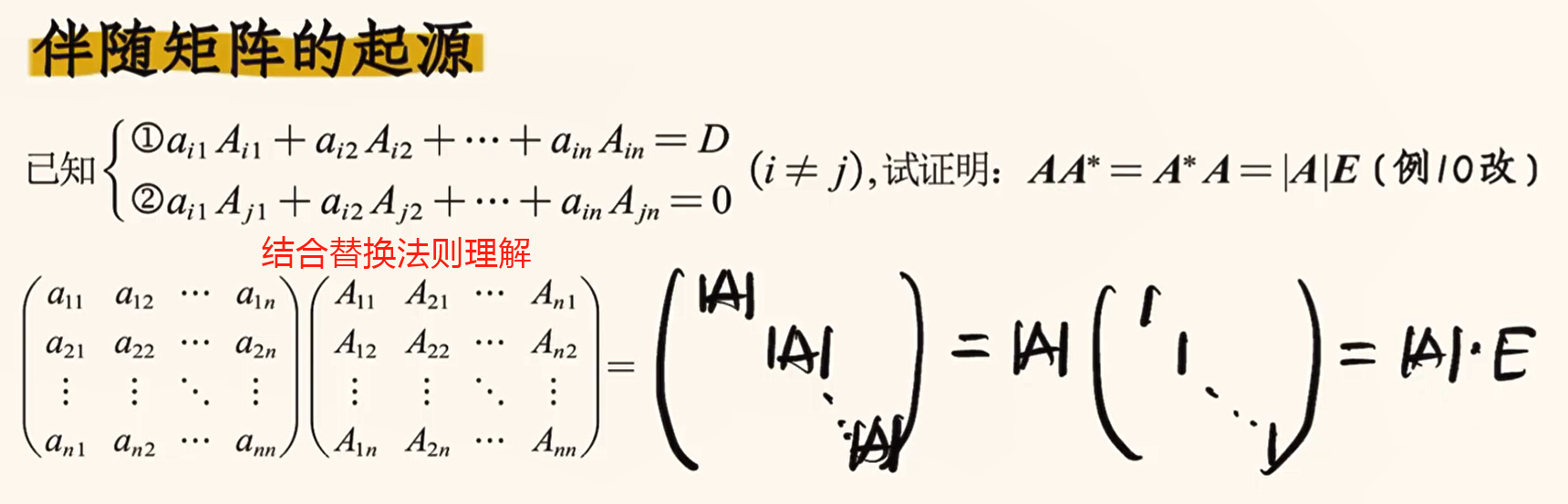
- A:矩阵
- A*:A的伴随矩阵
- |A|:A的行列式
- E:单位矩阵(主对角线元素都是1,其余元素均为0)
方阵的逆A-1

逆矩阵乘积=单位矩阵
而A被称为可逆矩阵或非奇异矩阵。
如果A不存在逆矩阵,那么A称为奇异矩阵。
举例子:
2 4 -1 1/2 1 0
A= A-1= A*A-1=
6 8 3/4 -1/4 0 1
矩阵A可逆的充要条件是行列式|A|不等于0:

逆矩阵性质

- 如果矩阵A是可逆的,那么矩阵A的逆矩阵是唯一的。
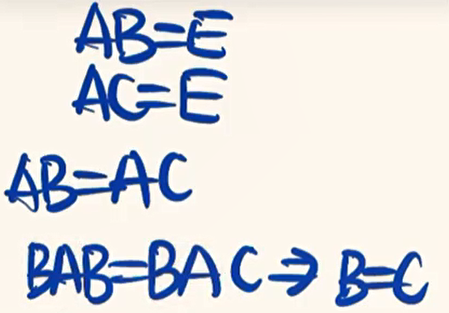
- 若矩阵A可逆,则矩阵A满足消去律,即AB=AC => B=C(A-1 AB=A-1 AC=>EB=EC)
求逆公式
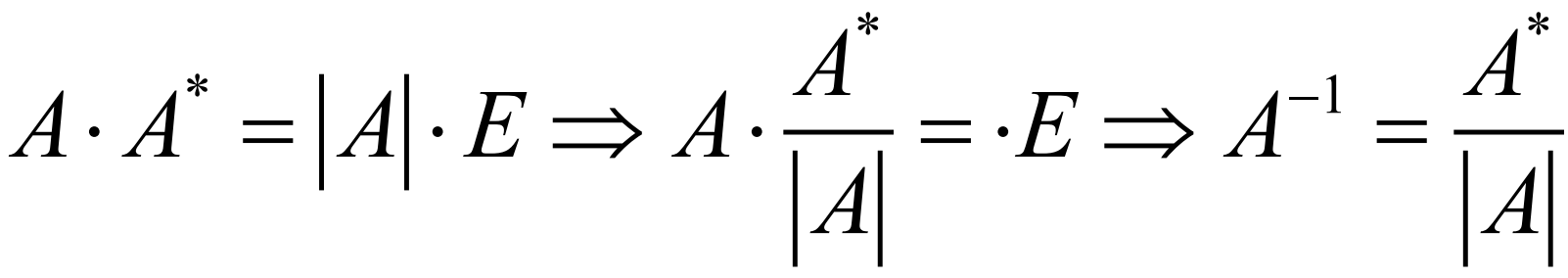
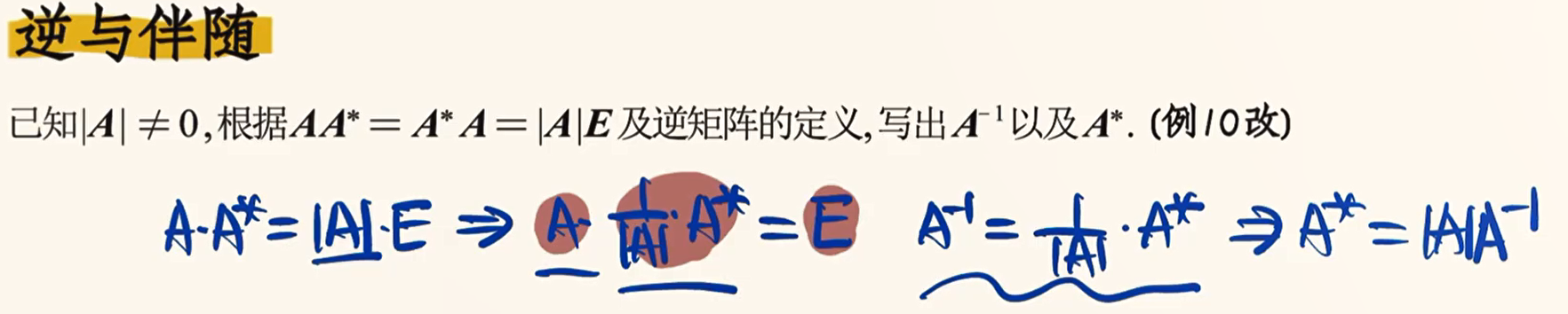

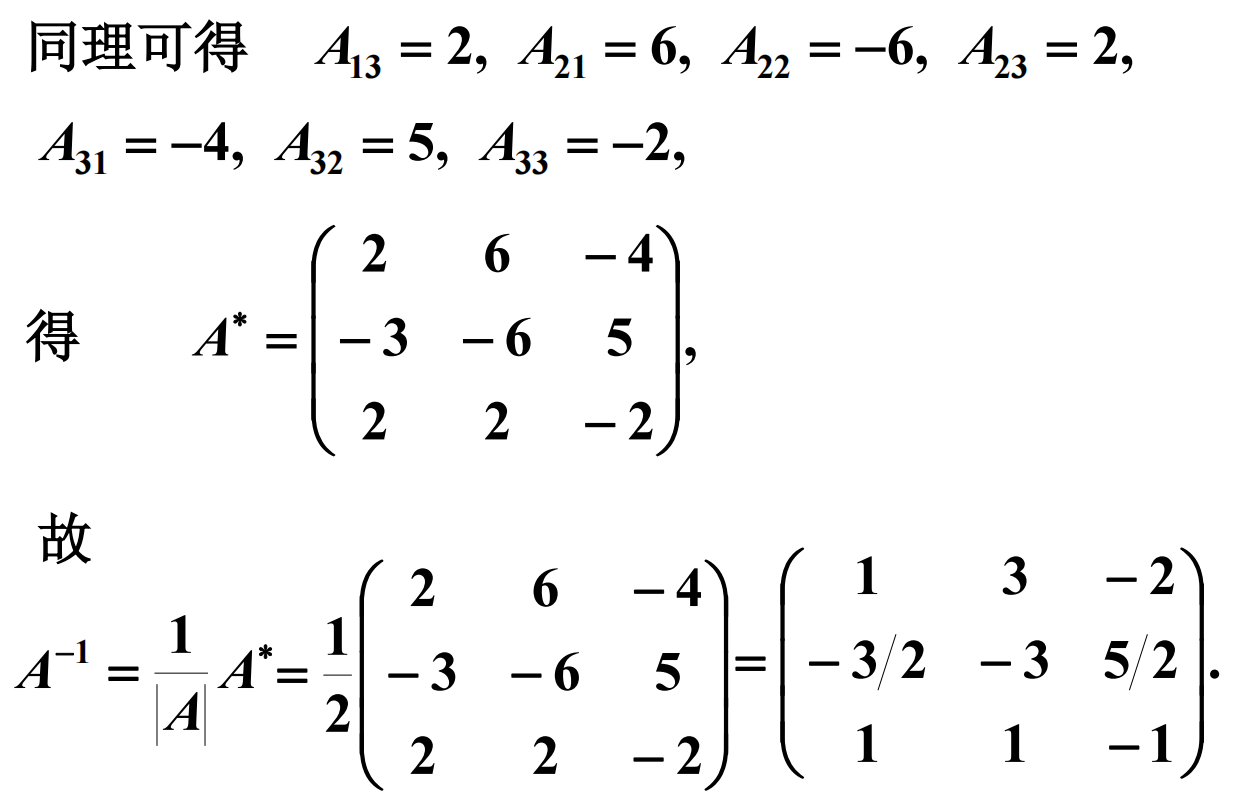

矩阵公式总结






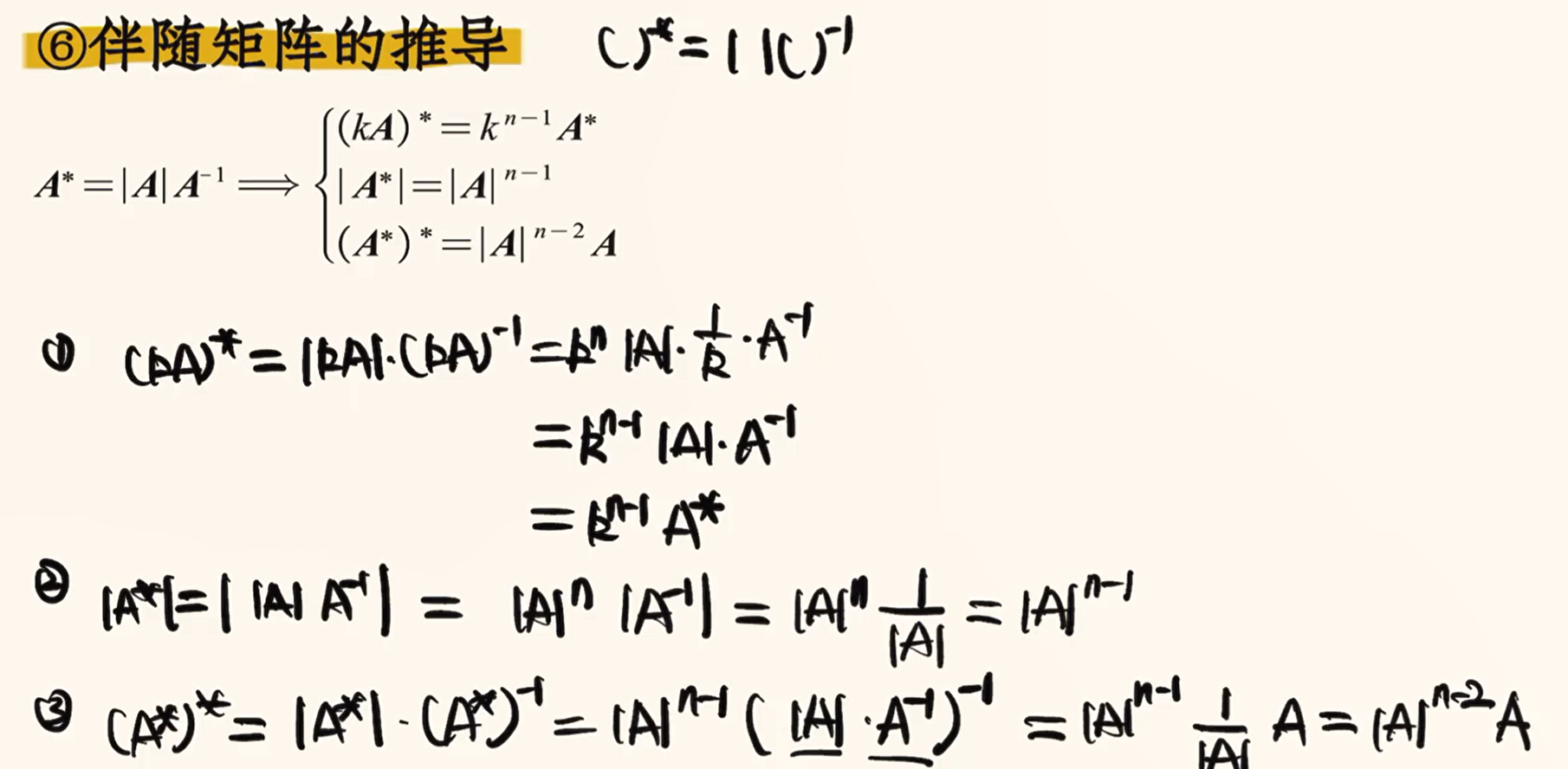
分块矩阵
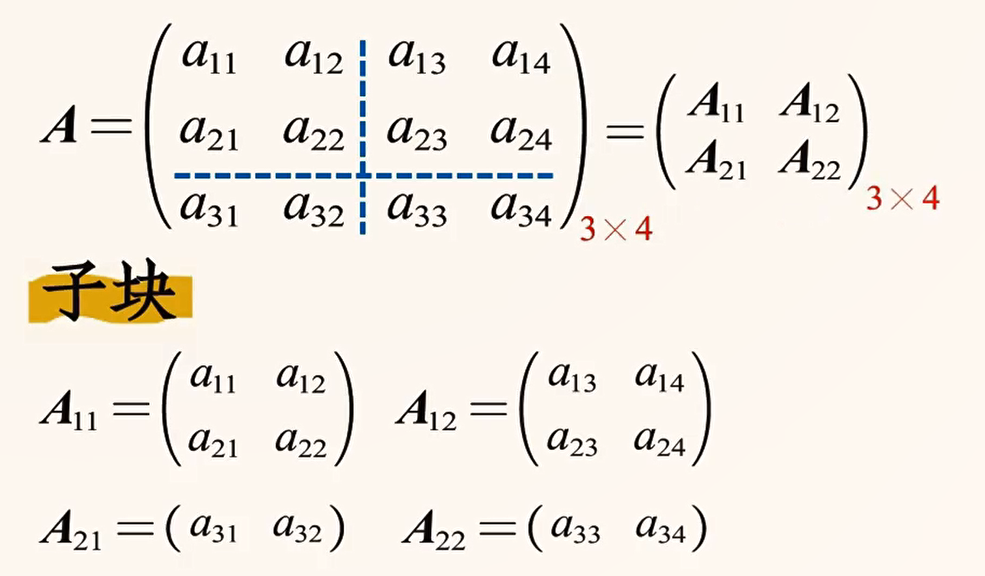


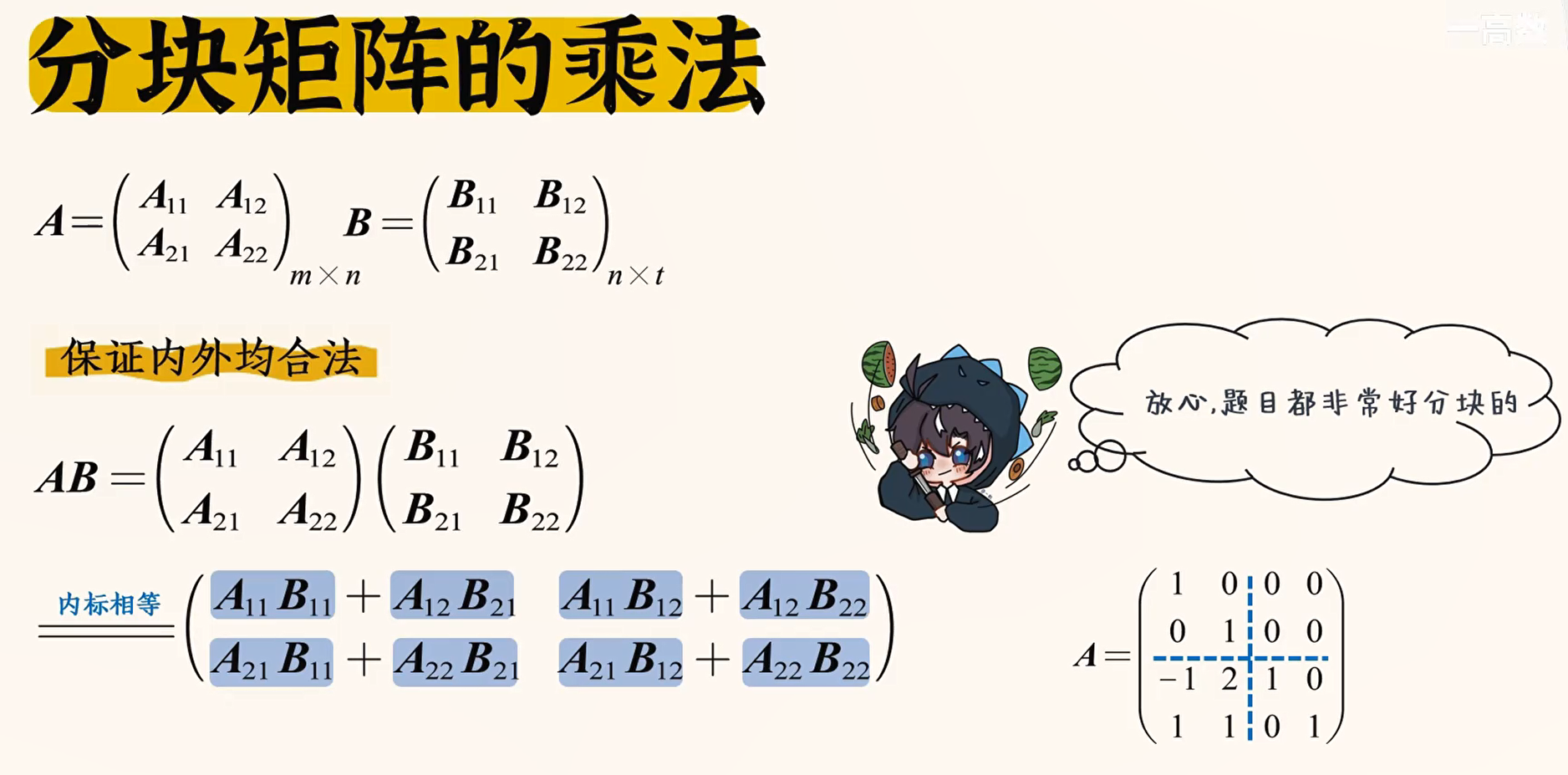


矩阵的初等变换
引例
消元法解方程。

注意:下面的消元法,需严格按顺序执行。要注意用于运算的行的值是否已经被改变(前面的步骤)





矩阵的初等变换定义




注意:初等列变换是不同解变换
初等行变换需严格按顺序执行,每次变换后的行会影响后续步骤。要注意用于运算的行的值是否已经被改变(前面的步骤)
用矩阵的初等行变换 解方程组
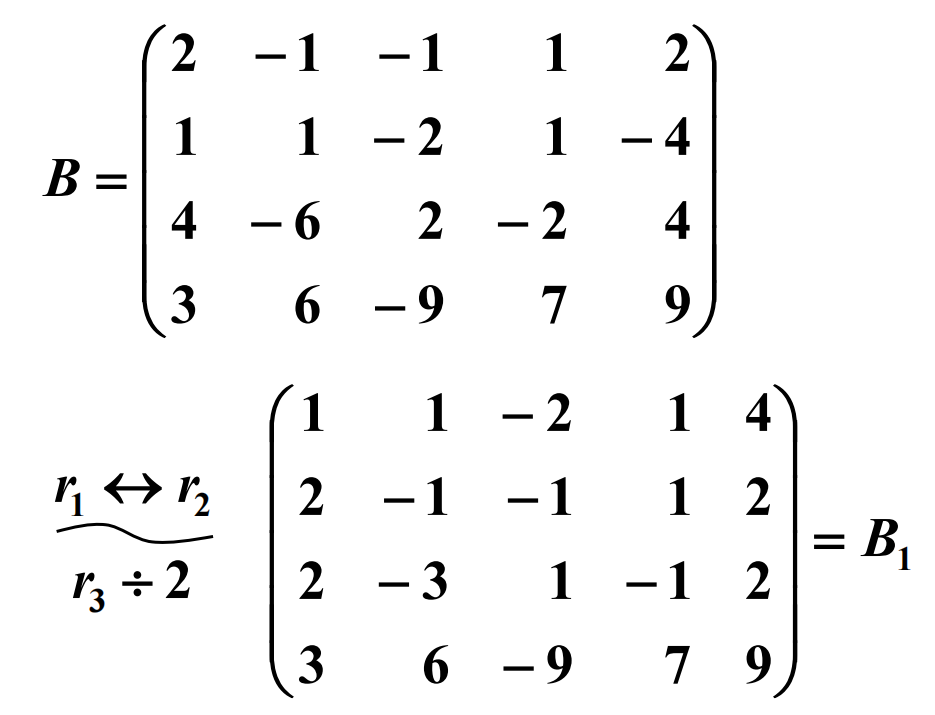 ⇒
⇒ ⇒
⇒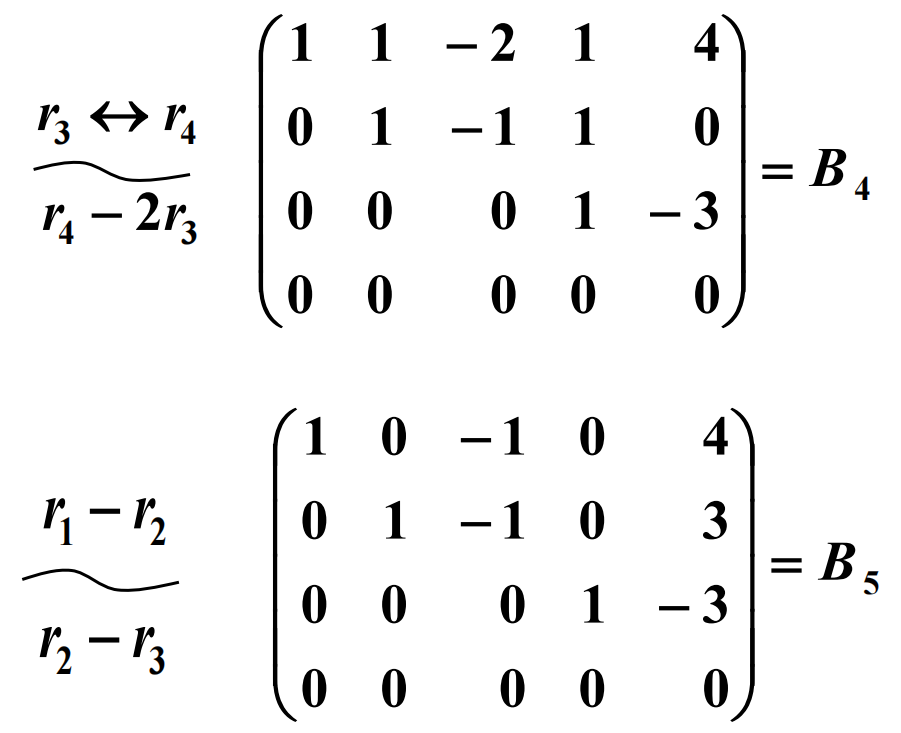
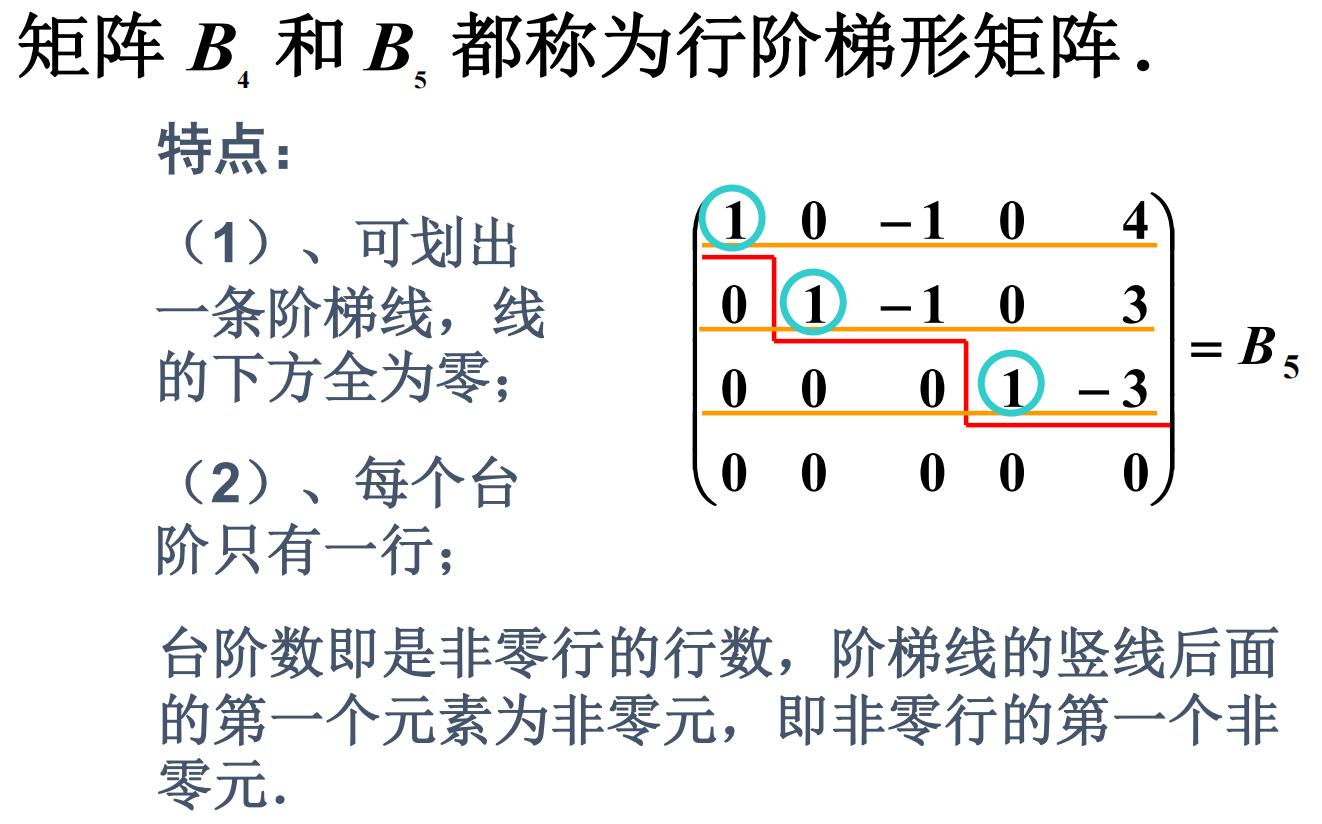
行阶梯形矩阵

行最简形矩阵
行阶梯形矩阵B5还称为行最简形矩阵

注:有效方程的个数=行阶梯/最简形矩阵非零行的行数=主元的个数我们把它称作为秩,用符号r表示
标准形矩阵
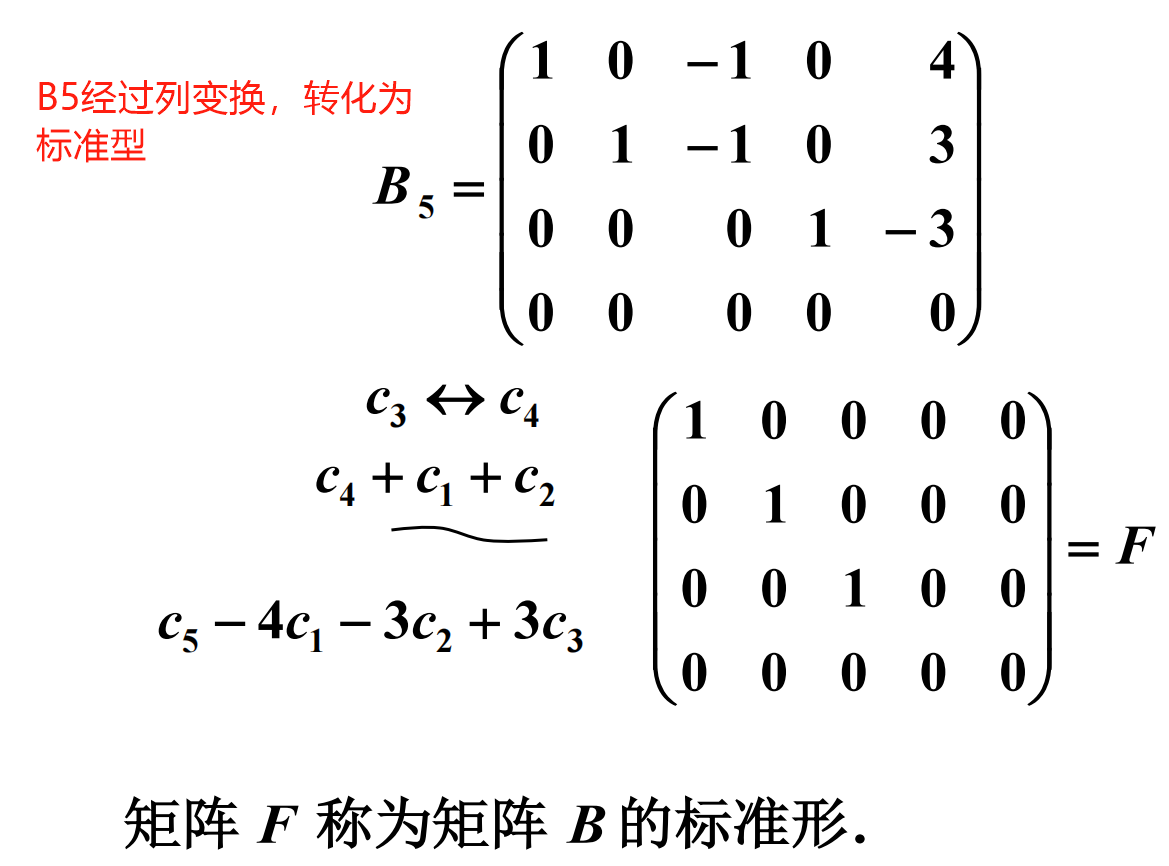
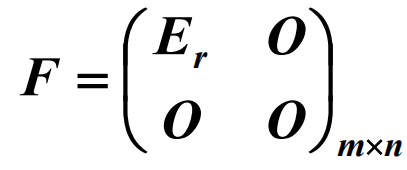
所有与矩阵A等价的矩阵组成的一个集合,称为一个等价类,标准形F是这个等价类中最简单的矩阵。

列变换与行变换的核心区别
- 行变换对应方程组的操作(如加减方程、缩放方程),保持方程组的解不变。
- 列变换对应变量的操作(如重新组合变量、缩放变量),会改变变量之间的关系,从而可能改变解的结构。
- 列变换可能改变变量的显式关系,但解空间的维度(即自由变量的个数)由秩决定,保持不变。
- 例如,若原方程组有1个自由变量,经过列变换后自由变量个数仍为1。
-
性质 行最简形 标准形(如 Smith 标准形) 变换类型 仅初等行变换 初等行变换和列变换 解的表达 直观,直接对应原始变量 变量可能被重新组合或缩放 核心不变量 秩、解空间维度 秩、行列式因子、模结构 应用场景 解线性方程组 矩阵结构分析、模论、编码理论
矩阵等价A~B


等价性的本质
- 等价类的核心是矩阵的秩和其他不变量(如行列式因子)相同,而非解的具体表达式不变。(列变换会导致对应方程组的解发生变化)
- 行最简形和标准形属于同一等价类,因为它们的秩和其他不变量相同。
- 解的具体形式可能因列变换而改变,但解空间的存在性和维度(由秩决定)不变,这是等价性的核心。
- 标准形的“最简单”体现在矩阵结构的清晰性,而非解的直接可读性。
用矩阵乘法表示初等变换
初等矩阵
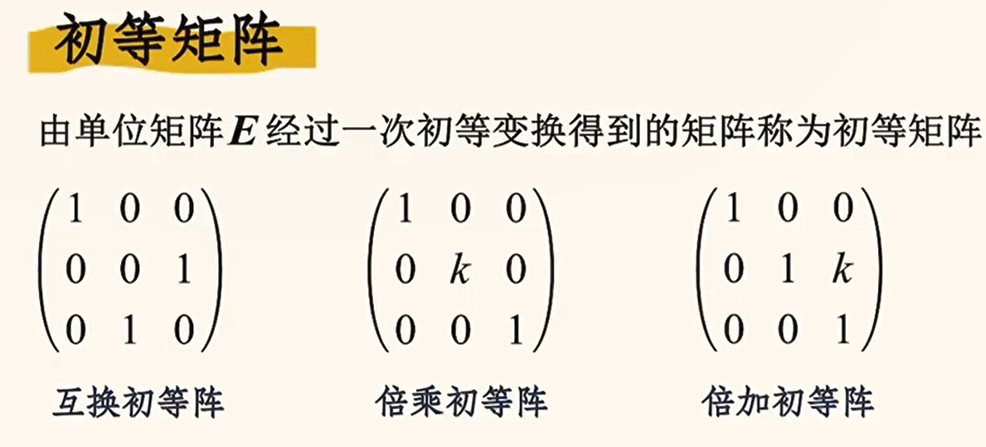


初等矩阵的逆
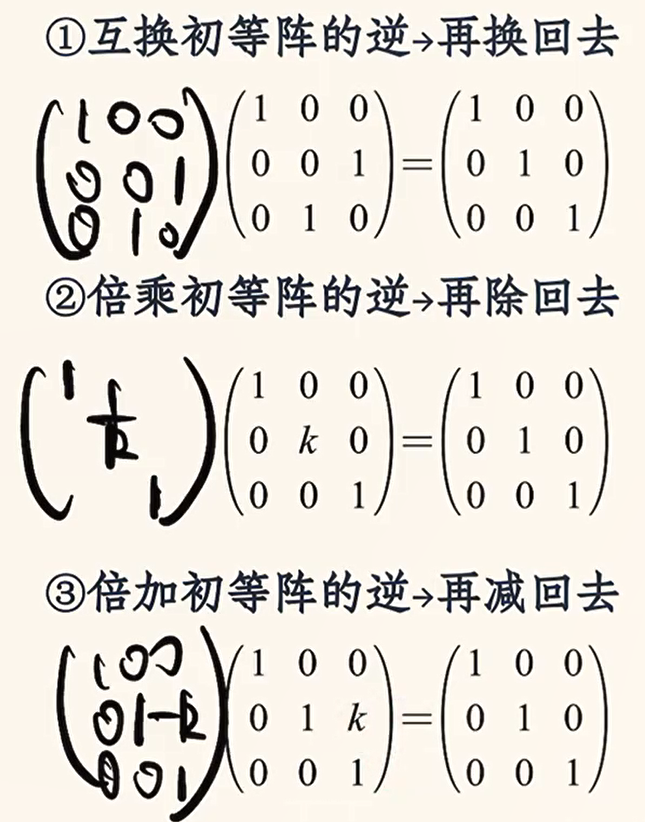
初等变换求逆


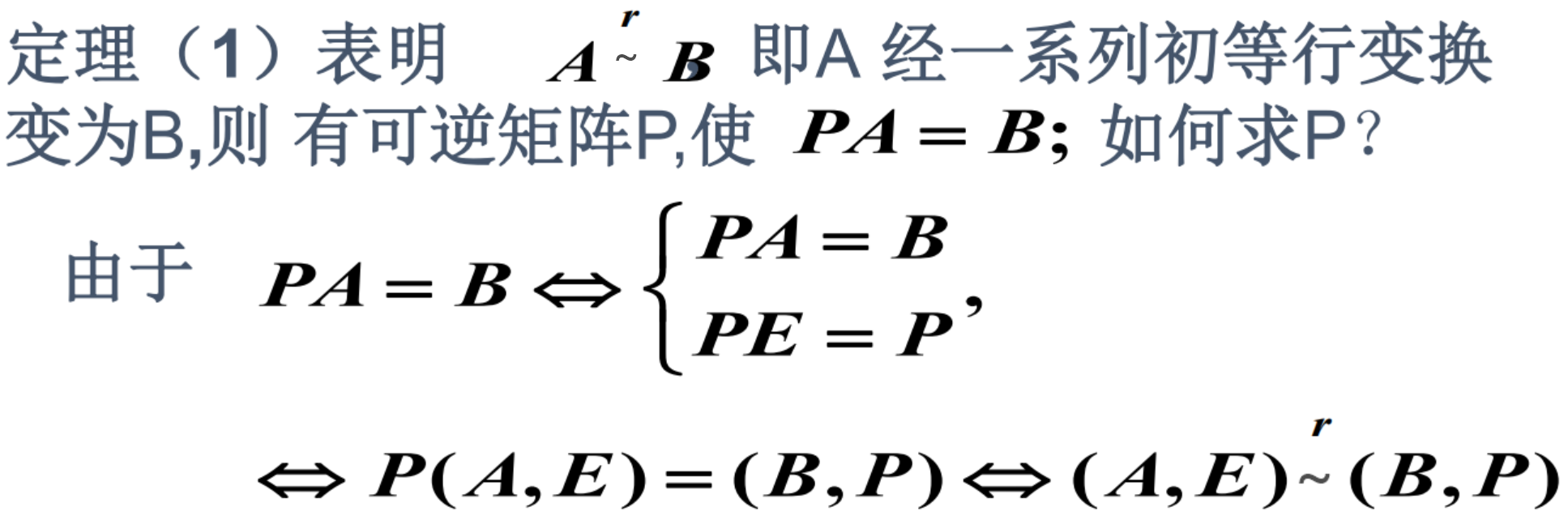




求解矩阵方程:

矩阵的秩
秩:反应矩阵本质不变的量
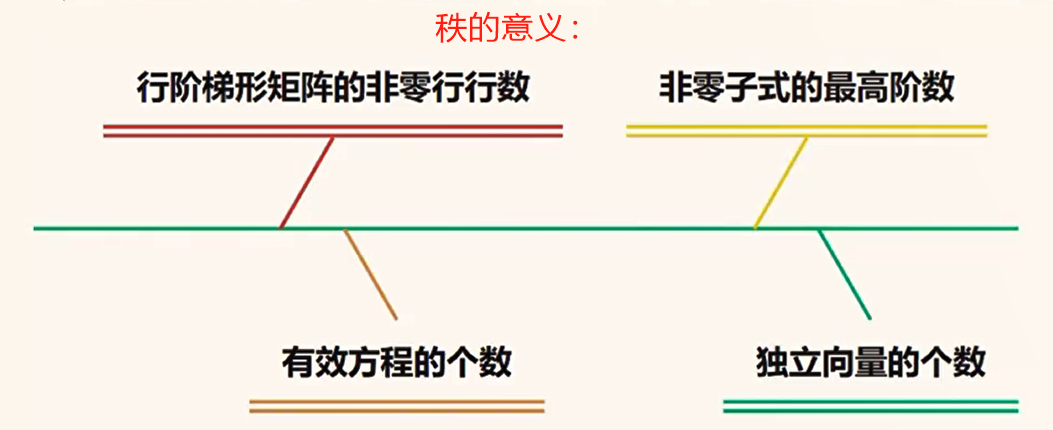
秩:非零子式的最高阶数
在m*n矩阵A中,任取k行k列,不改变这k 2个元素的在A中的次序,得到k阶方阵,称为矩阵A的k阶子式(是行列式)。
m*n阶矩阵A的k阶子式有![]() 个(在m行里取k行的情况数量*在n列里取k列的情况数量)
个(在m行里取k行的情况数量*在n列里取k列的情况数量)

设在矩阵A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在)全等于0,那么D称为矩阵A的最高阶非零子式,r称为矩阵A的秩,记作R(A)=r
- n*n的可逆矩阵,秩为n(因为他可以通过行初等变换为E,E的每一行都不是全为0的)
- 可逆矩阵又称为满秩矩阵
- 矩阵的秩等于它行(列)向量组的秩
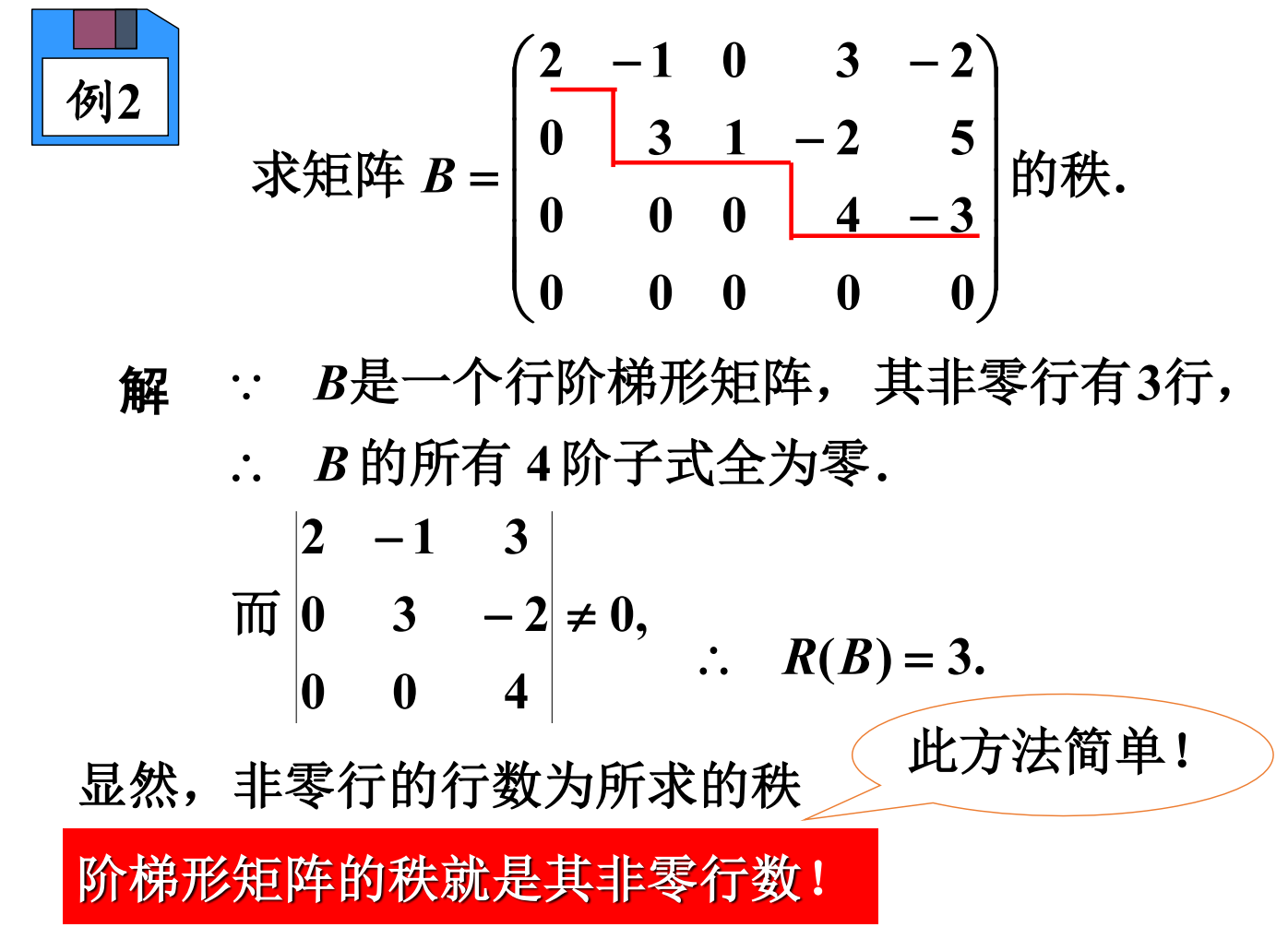
由上例可知行阶梯形矩阵的秩就等于其非零行的行数,一看便知不须计算。
因为对于任何矩阵Amxn,总可经过有限次初等行变换把他变为行阶梯形。
自然想到用初等行变换把矩阵化为行阶梯形矩阵,但两个等价矩阵的秩是否相等呢?
问题:经过初等变换矩阵的秩变吗?


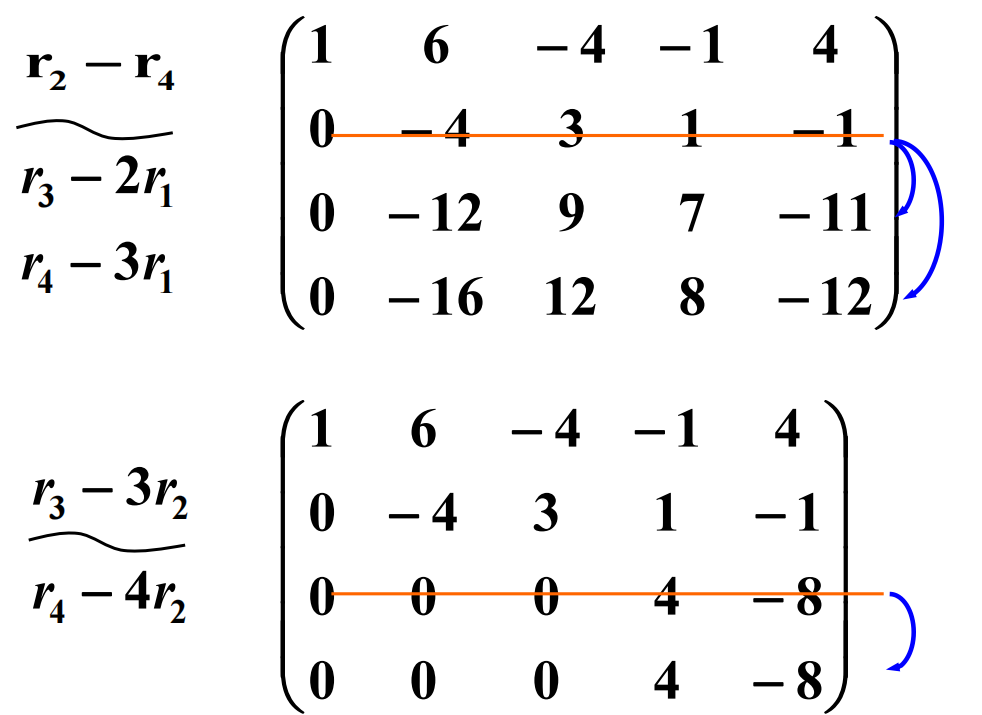


故 B中必有 3 阶非零子式. 且共有 4 个。
计算B的前三行构成的子式:
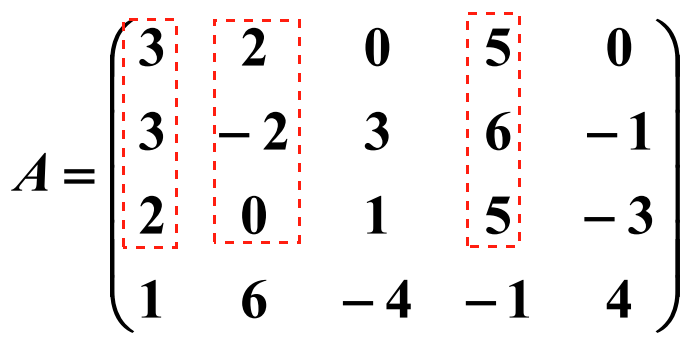

则这个子式便是 A 的一个最高阶非零子式
秩的公式总结










 浙公网安备 33010602011771号
浙公网安备 33010602011771号