02-1线性代数-向量
线性(linear)指量(变量)与量(变量)之间按比例、成直线关系,在数学上可以理解为一阶导数为常数的函数;
而非线性(non-linear)是指不成比例、没有直线关系,一阶导数不是常数的函数。
线性代数中的基本量指的是向量,基本关系是严格的线性关系;也就是可以简单的将线性代数理解为向量与向量之间的线性关系的映射。
向量(一维数组)
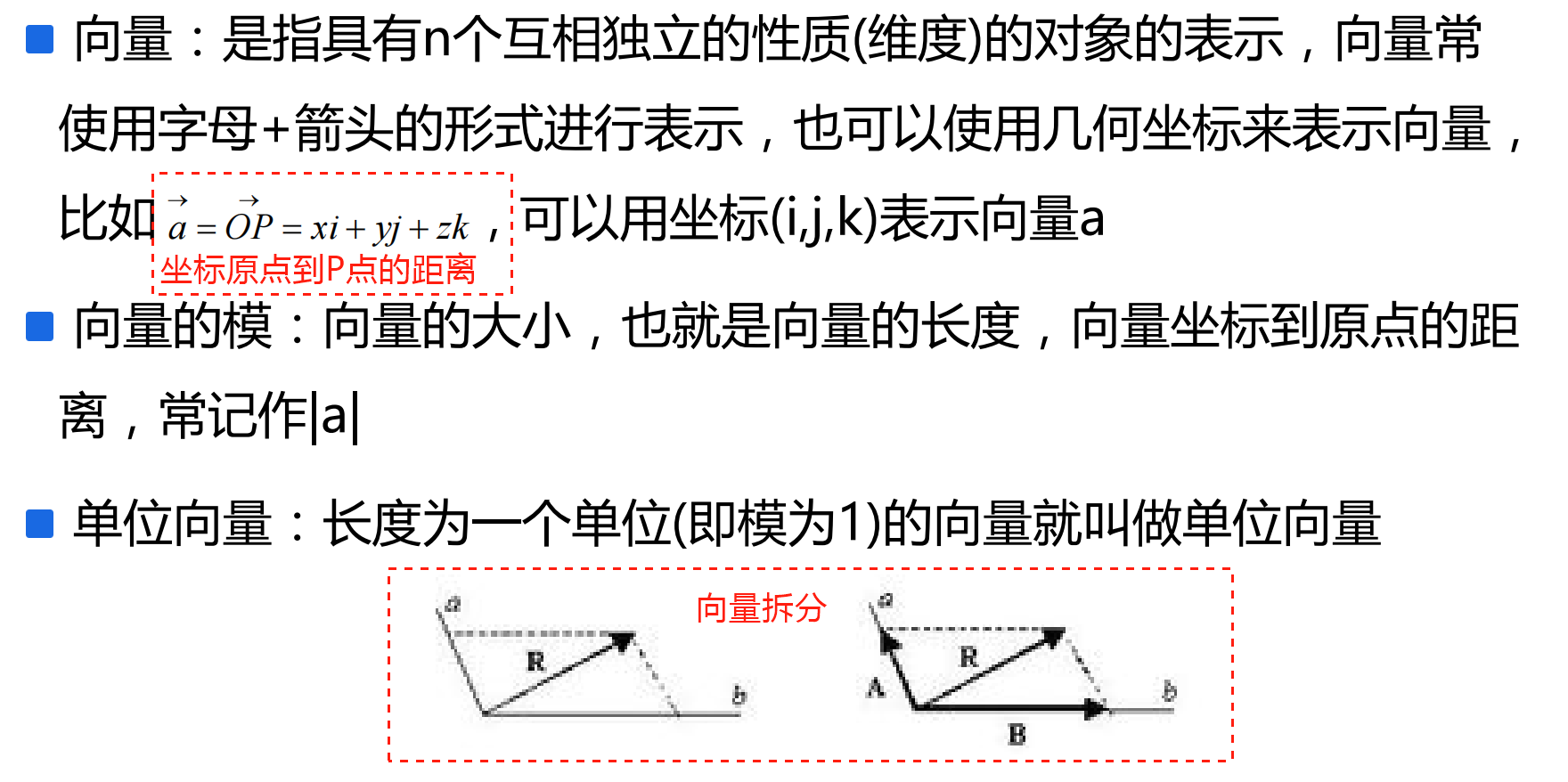
向量的运算
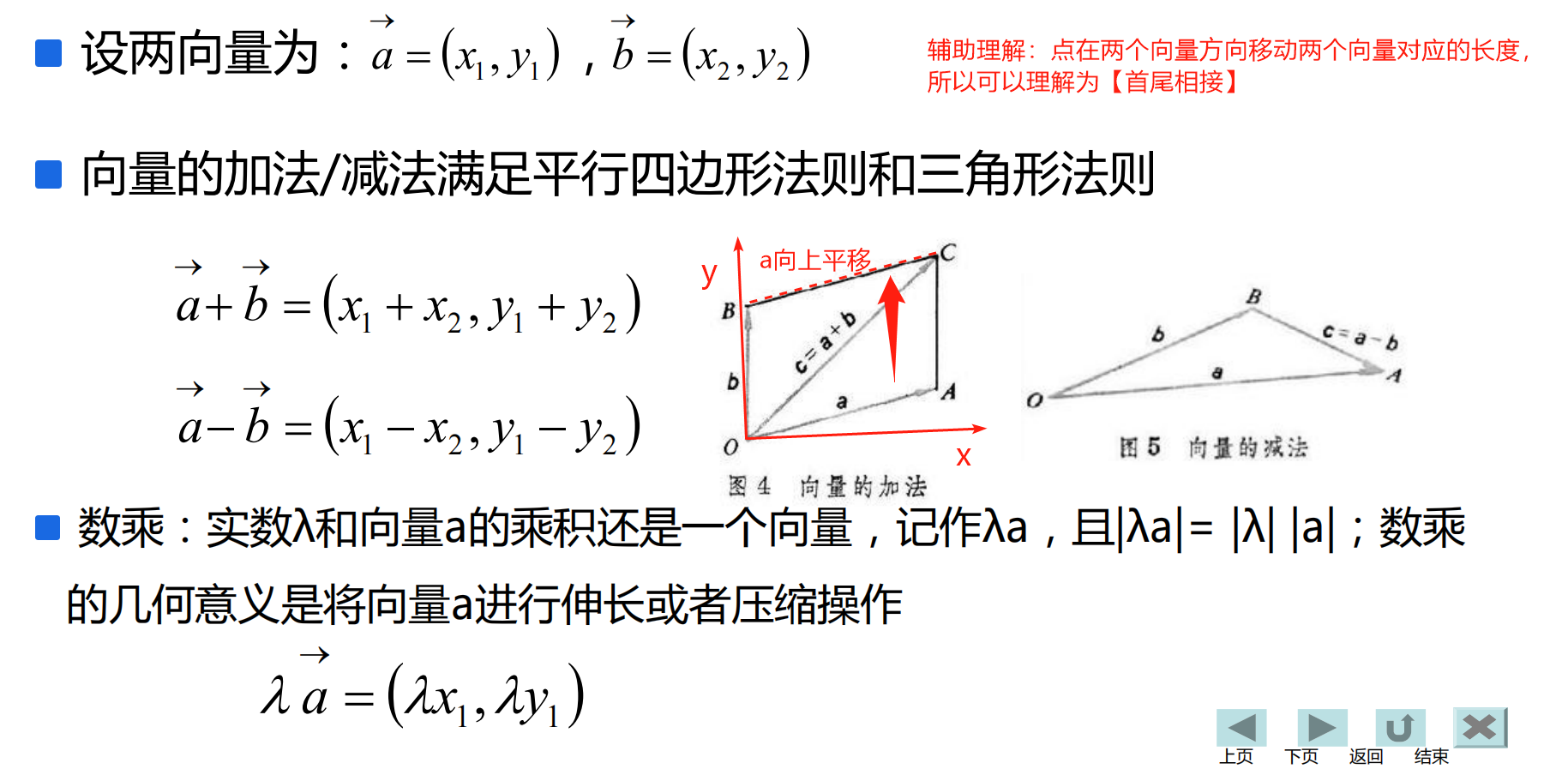
关于向量的运算,一般都会分为几何和代数两种处理方式。下面的数量积和向量积也不例外。

数量积
数量积(又称内积、点积)是向量间的标量运算,用于描述向量的投影关系和夹角特性,在几何、物理和工程中有广泛应用。
一、定义
设两个向量 和 ,它们的点乘结果为:
- 结果类型:标量(一个数)。
- 几何意义:
其中 为两向量夹角, 和 分别为向量的模长。(理解1:b向量的模,乘以向量a在向量b上的投影)

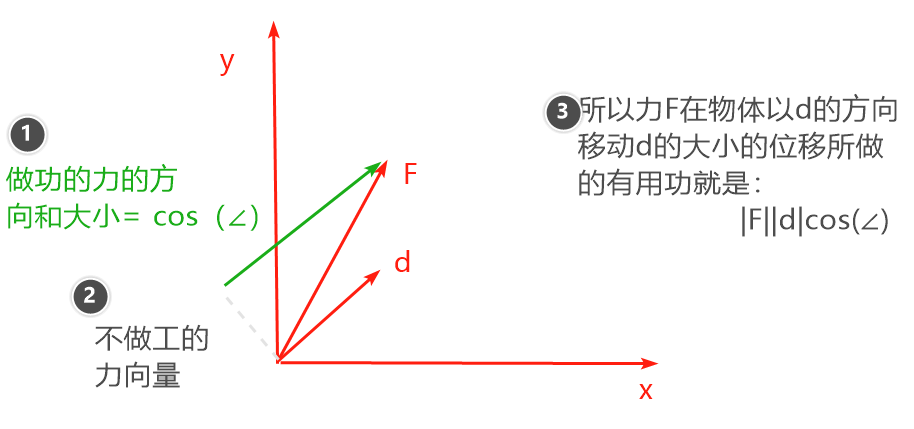
辅助理解:物理中的功计算
- 功的定义:力 在位移 方向上的分量所做的功:
- 实例:若力 牛,位移 米,则功为:
夹角计算:
- 通过点乘可求两向量夹角:
- 特例:
- (向量垂直)
- (锐角)
- (钝角)
核心应用场景
-
判断向量方向关系
- 垂直检测:若 ,则两向量垂直。
- 实例:检测三维坐标系中坐标轴的正交性(如 )。
- 垂直检测:若 ,则两向量垂直。
-
物理中的功计算
- 功的定义:力 在位移 方向上的分量所做的功:
-
- 实例:若力 牛,位移 米,则功为:
数据科学中的相似度度量
- 余弦相似度:通过点乘计算向量方向的一致性:

实例:文本分类中,文档向量的余弦相似度用于衡量内容相关性。
数量积运算律:

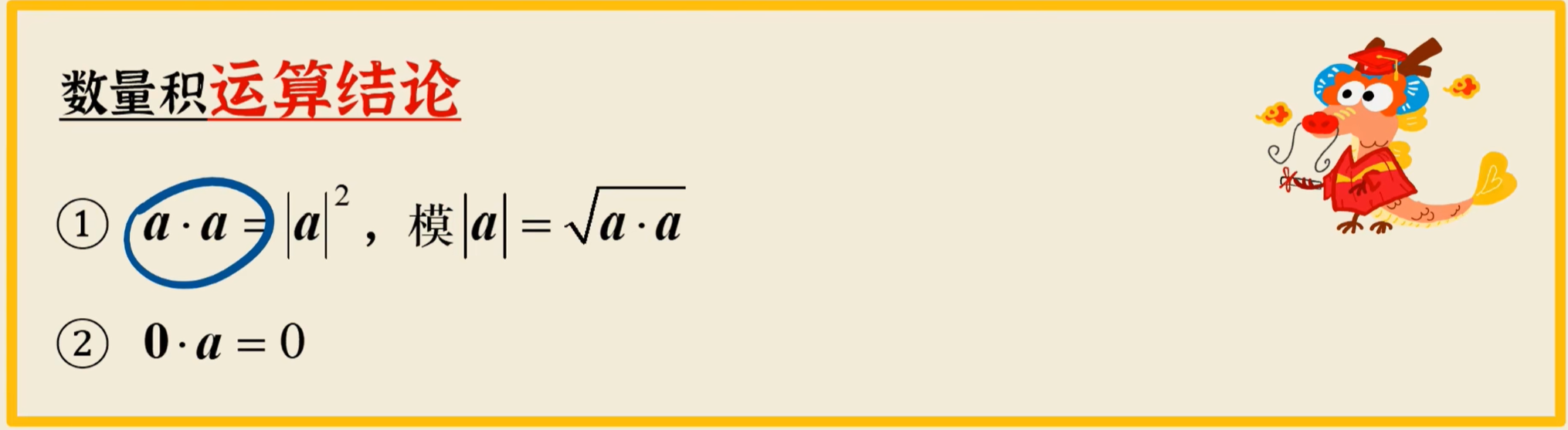
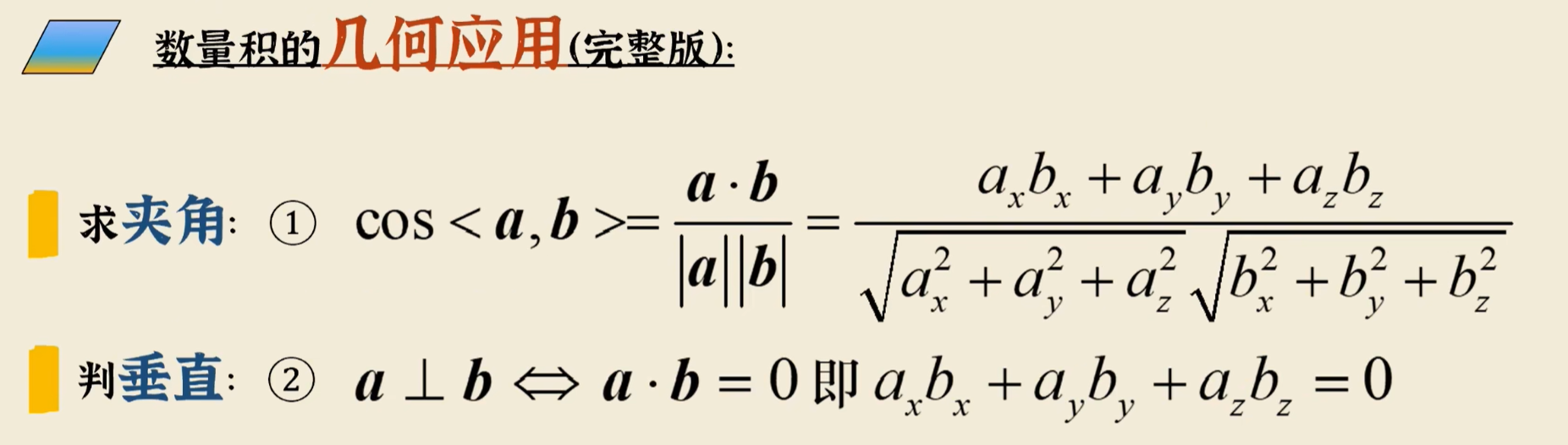
实例详解
例1:判断向量垂直
设 ,,则:
两向量不垂直。
例2:计算夹角
设 ,,则:
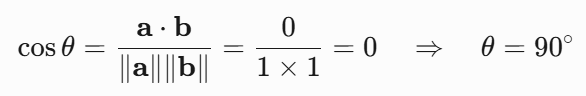
两向量垂直。
正交向量
正交向量:如果两个向量的点积为零,那么称这两个向量互为正交向量;在几何意义上来讲,正交向量在二维/三维空间上其实就是两
个向量垂直。
如果两个或者多个向量,它们的点积均为0,那么它们互相称为正交向量。

总结
- 核心作用:描述向量间的投影关系和夹角特性,适用于任意维度的向量运算。
向量积
在学习向量积之前要先搞明白力矩
力矩

力矩是描述力对物体产生转动效果大小的物理量,衡量力改变物体转动状态的能力。其核心是力与力臂的乘积,方向遵循右手螺旋定则。
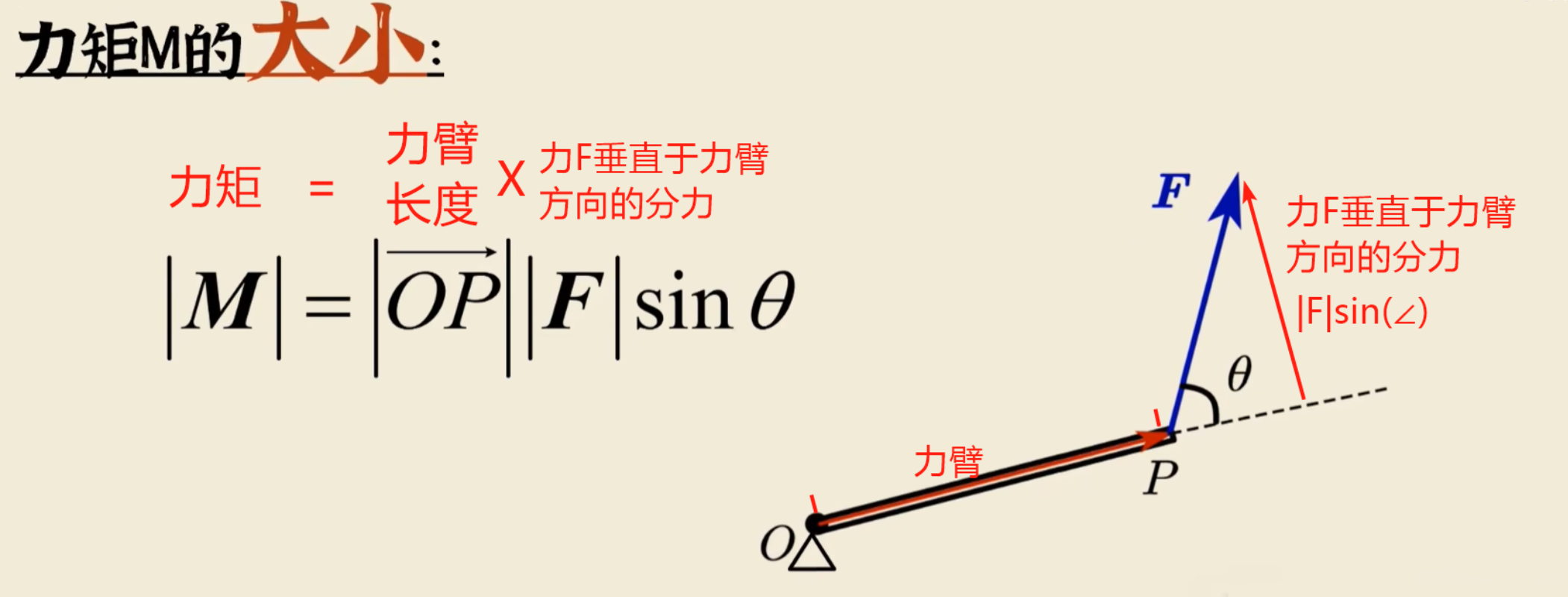
力矩既有大小又有方向。(理解:物体旋转过程中,力的方向一直是变动的,但是物体确一直沿着逆时针(或顺时针)旋转,也就是旋转方向没有变,说明力矩一直没变,那么力矩的方向也只能是垂直于力臂所旋转的平面)


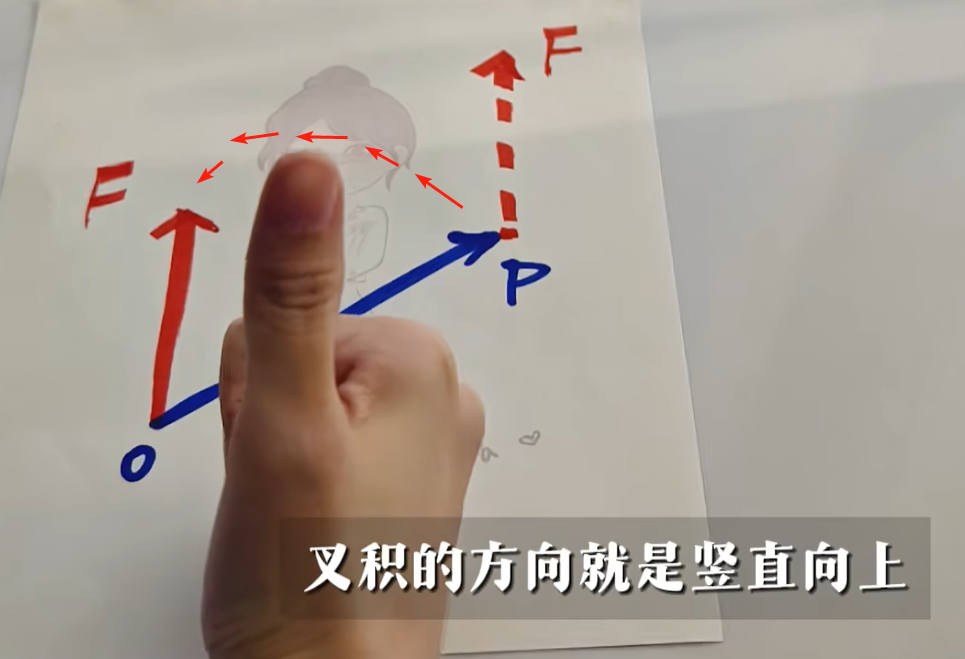


向量积的理解
向量积(又称外积、叉积)是三维向量之间的重要运算,其结果为垂直于原向量的新向量,具有明确的几何和物理意义。
注意:数量积和向量积公式对比!
设两个向量 和
数量积(积之后得到的是数量):
a⋅b=|a||b|cosθ
结果是一个数字(标量)
向量积(积之后得到的是向量):
a×b=((a2b3−a3b2),−(a1b3−a3b1),(a1b2−a2b1))(由三阶行列式运算所得,下面细讲)
结果是一个向量,并且方向垂直于a和b构成的平面(具体方向由右手定则判定)
注意,axb的模为:
|a×b|=|a||b|sinθ(几何意义:即a和b构成的平行四边形的面积)
向量积计算公式
设两个三维向量 和 ,它们的叉乘结果为(三阶行列式运算):

注:不要以为三阶行列式、二阶行列式,是什么高级复杂的东西,就是一个运算规则(加减乘除也是计算规则),把数字套进去,就会按照指定规则运算,得出相应的结果。
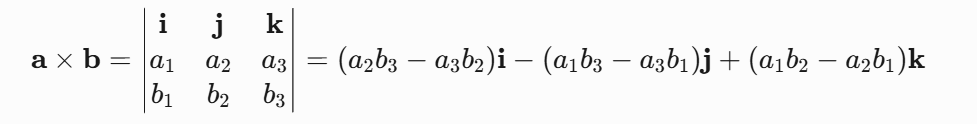
i,j,k:叫基本单位向量,(又叫标准正交基),对应方向分别是X轴,Y轴,Z轴。
公式记忆技巧:

向量积运算律


例题求三角形面积:

对比
| 特性 | 数量积(点乘) | 向量积(叉乘) |
|---|---|---|
| 结果类型 | 标量 | 向量 |
| 几何意义 | 投影长度,夹角余弦乘积 | 垂直向量,大小为面积 |
| 交换律 | 满足() | 不满足() |
| 应用场景 | 判断正交性、计算功、相似度度量 | 计算面积、力矩、法向量方向 |
| 适用空间 | 任意维度 | 仅三维空间 |
混合积(选修)





上题所求结果方程,其实就是ABC三点所在平面的平面方程

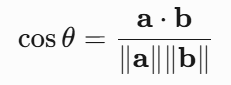



 浙公网安备 33010602011771号
浙公网安备 33010602011771号