01-5高等数学-多元函数极限、偏导数、方向导数、梯度

多元函数的极限

多元函数的概念

二元函数的定义

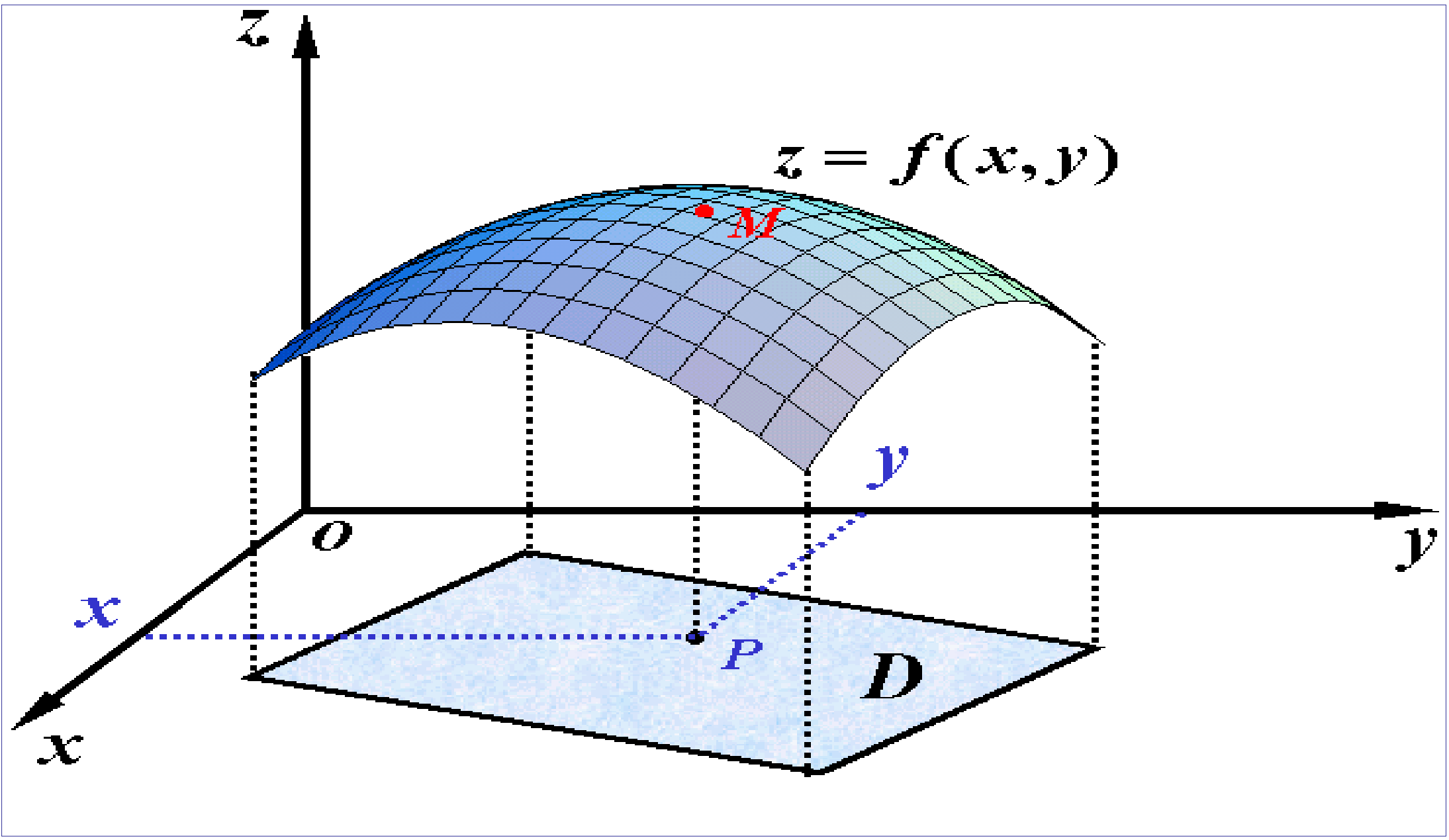
二元函数的图形通常是一张曲面。

多元函数的极限

多元函数偏导数

举例理解：一次对付一个不法分子，各个击破。

高阶偏导数

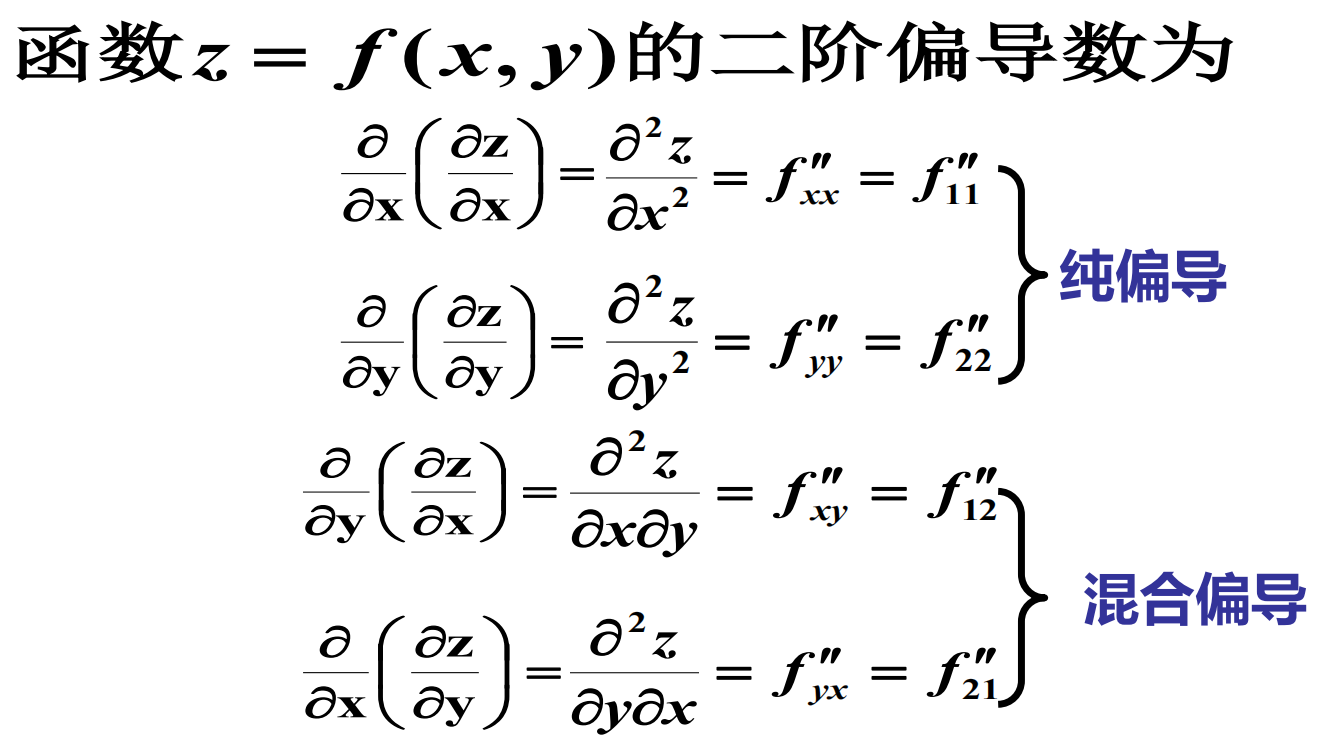
解释：纯偏导：一次只谈有一个女朋友

方向导数

方向导数，和各学科交叉都无敌好用的微积分知识。

方向导数定义

理解：

Δy小于0时：

偏导数是双侧极限，方向导数是单侧的;

偏导数只看两个方向，方向导数可指定任意方向

方向导数计算公式

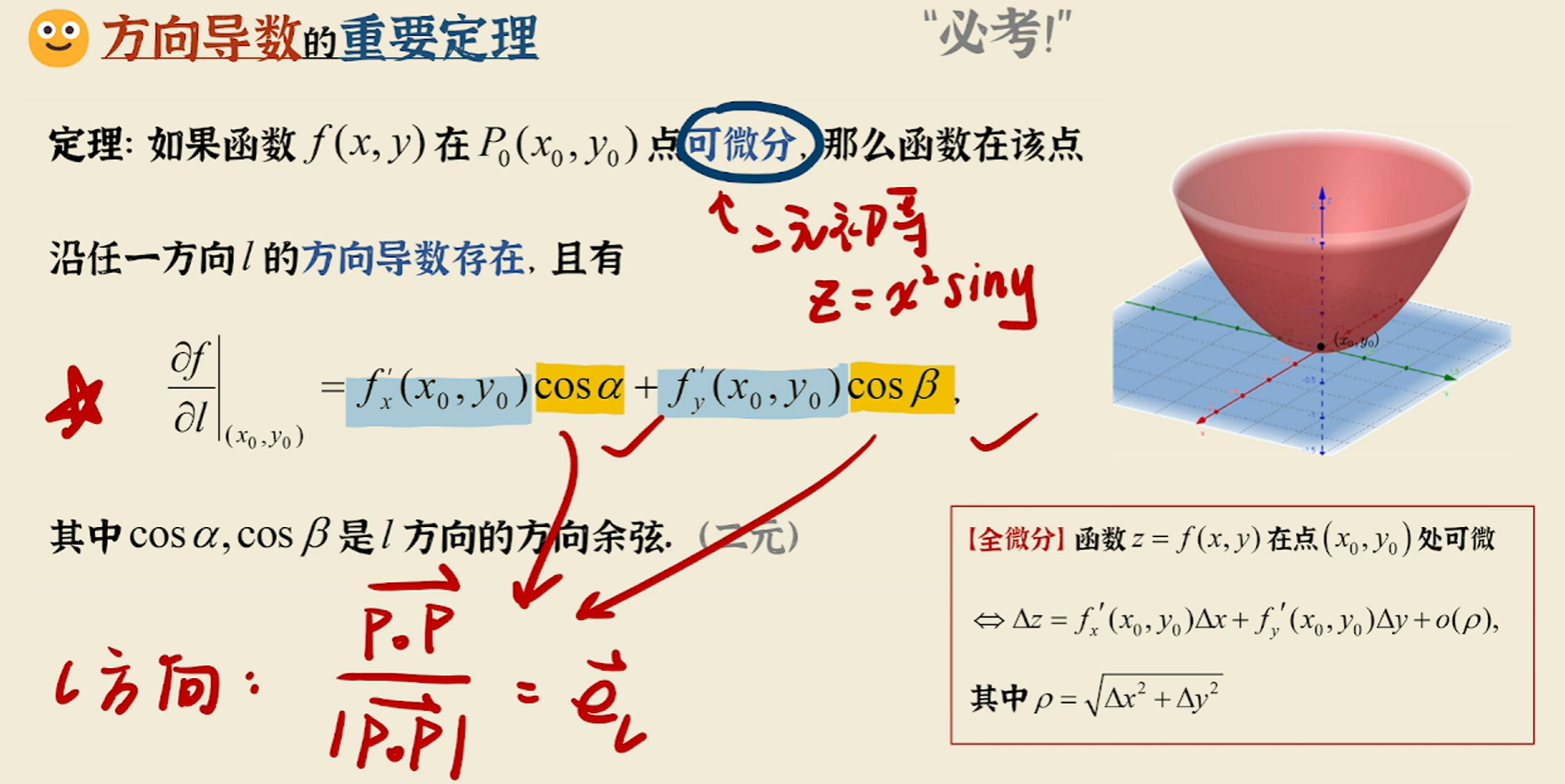
注：ο(ρ)是ρ的高阶无穷小

方向导数计算公式证明

总结：求偏导的步骤就是：

1.收集两个偏导（相对于x和y）；

2.把方向向量单位化，获取到（cos（α）和cos（β））

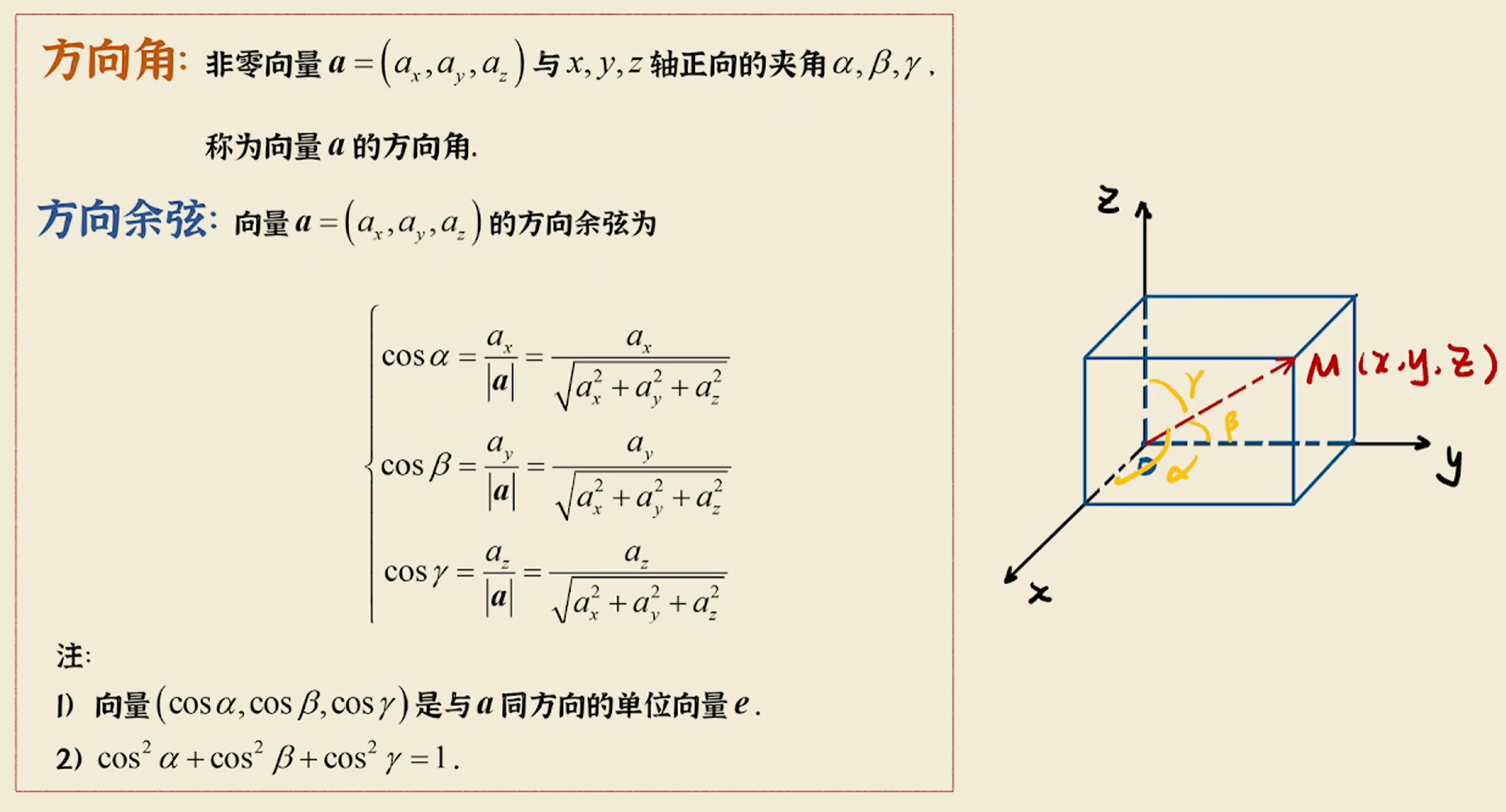
三元函数的方向导数

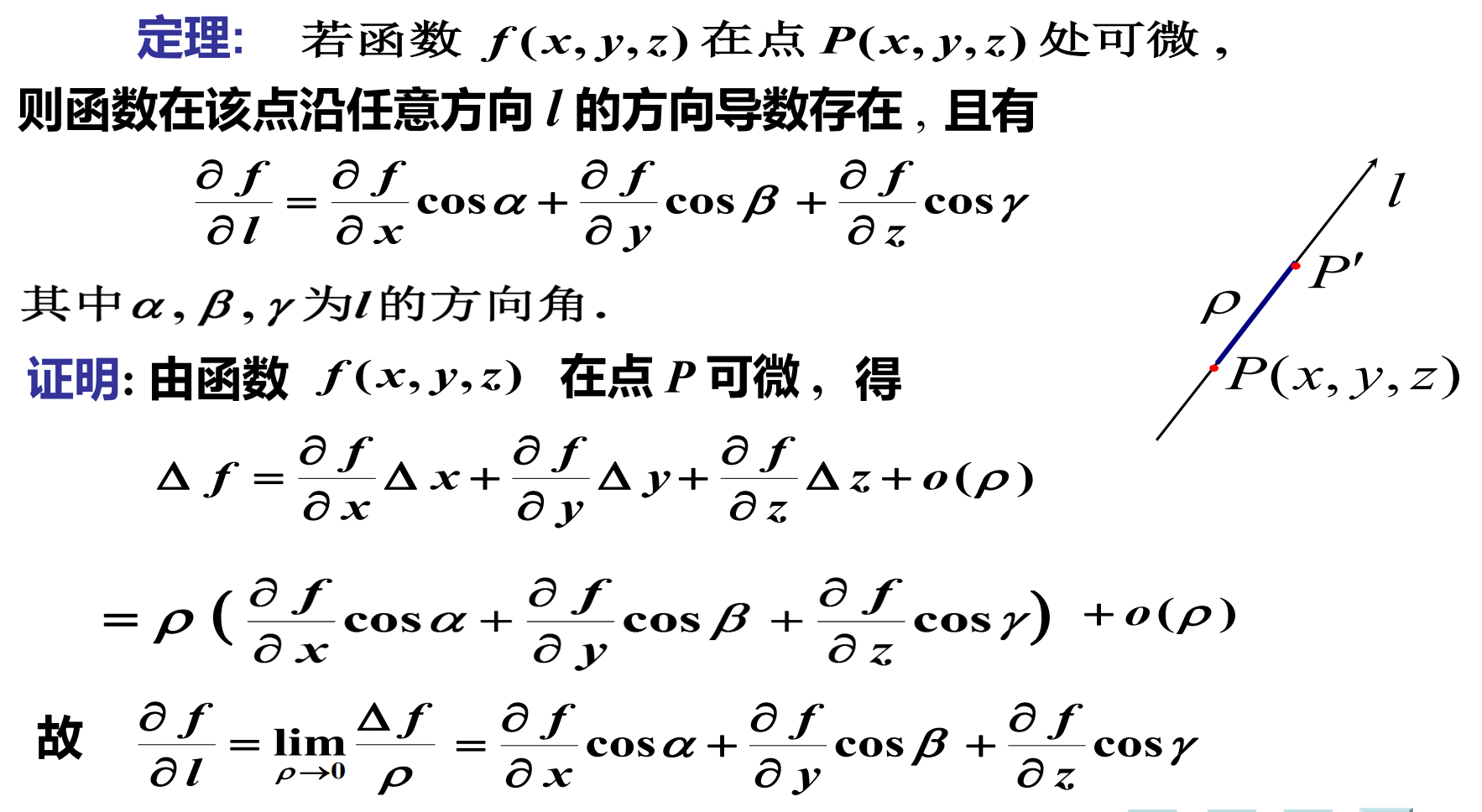
梯度（是一个向量：是方向导数值（函数值变化率）最大的时候的方向，以及最大的值）

我们发现，函数在X0，Y0的方向向量，等于函数分别在x方向和y方向的偏导数组成的向量与单位向量e的点积：

∇读作“nabla”‌。这个符号在数学中常用于表示向量微分算符，特别是在高数中代表梯度算符。

求梯度练习

 

梯度和方向导数的关系

梯度和等位线关系

1. ​​等高（位）线的定义​​
   等高线是函数值相等的点的集合（如 $f(x,y)=c$）。

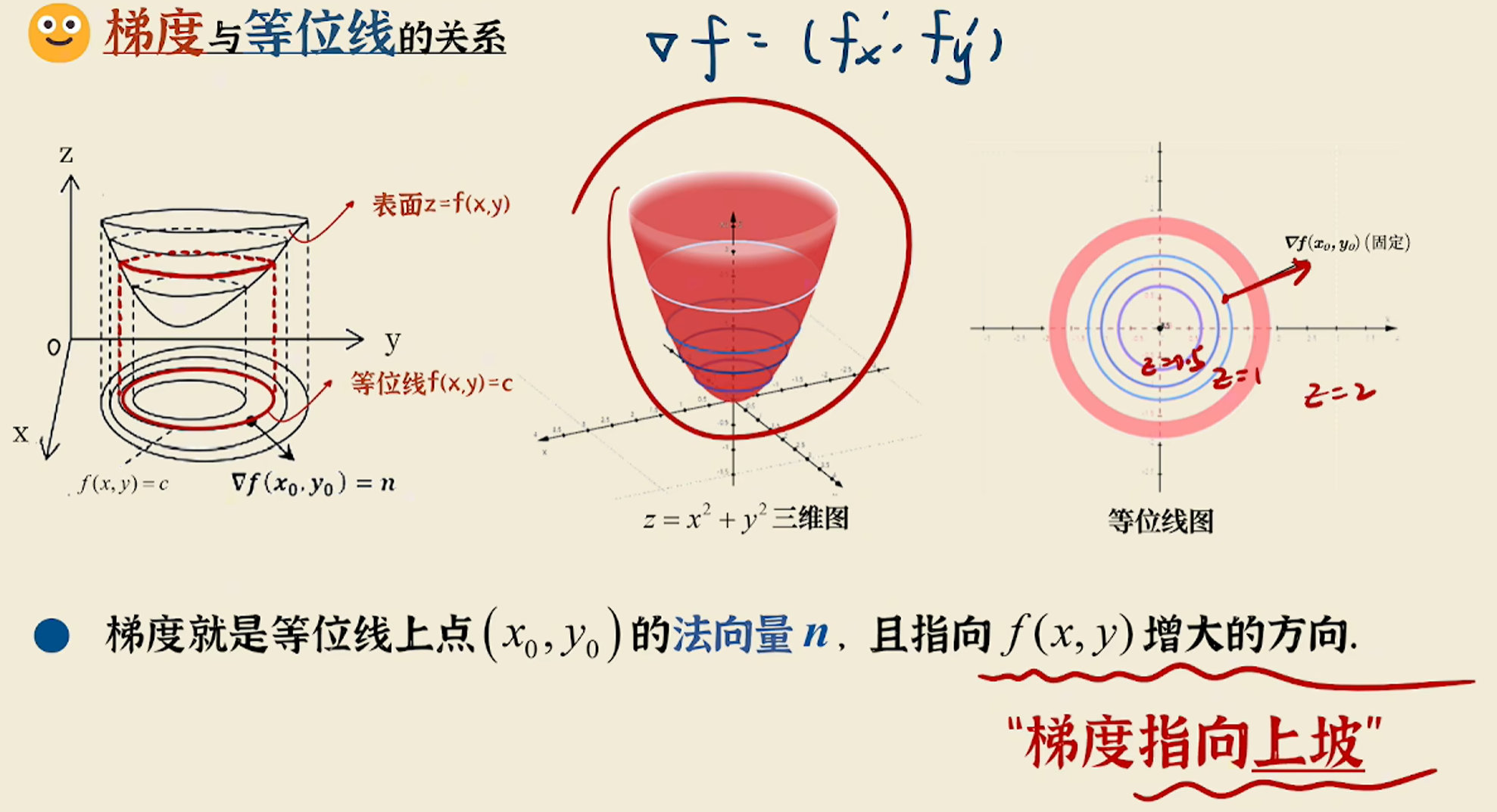
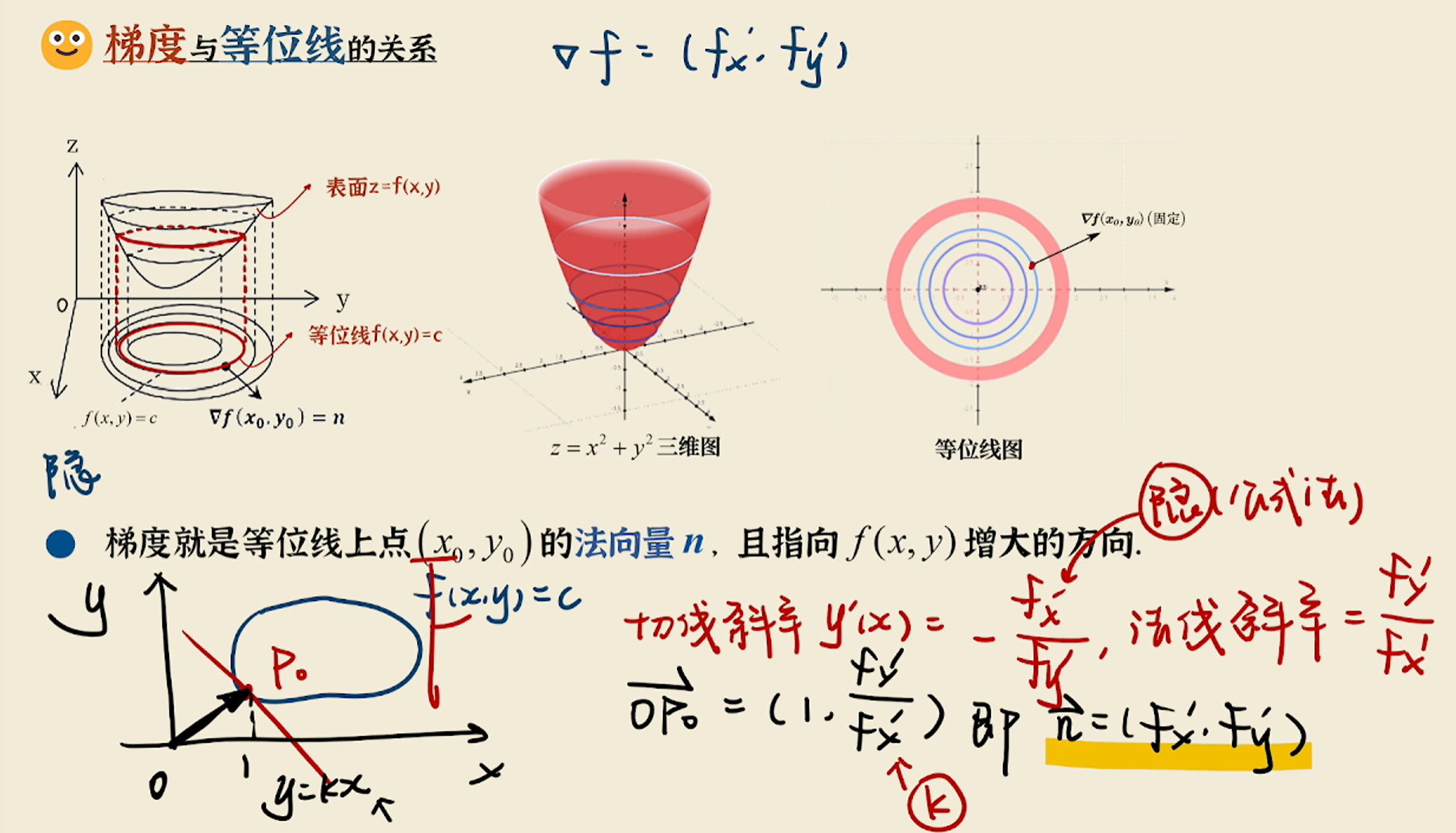
2. ​​梯度与等高线的关系​​

   • 沿等高线方向移动时，函数值不变，方向导数为零。
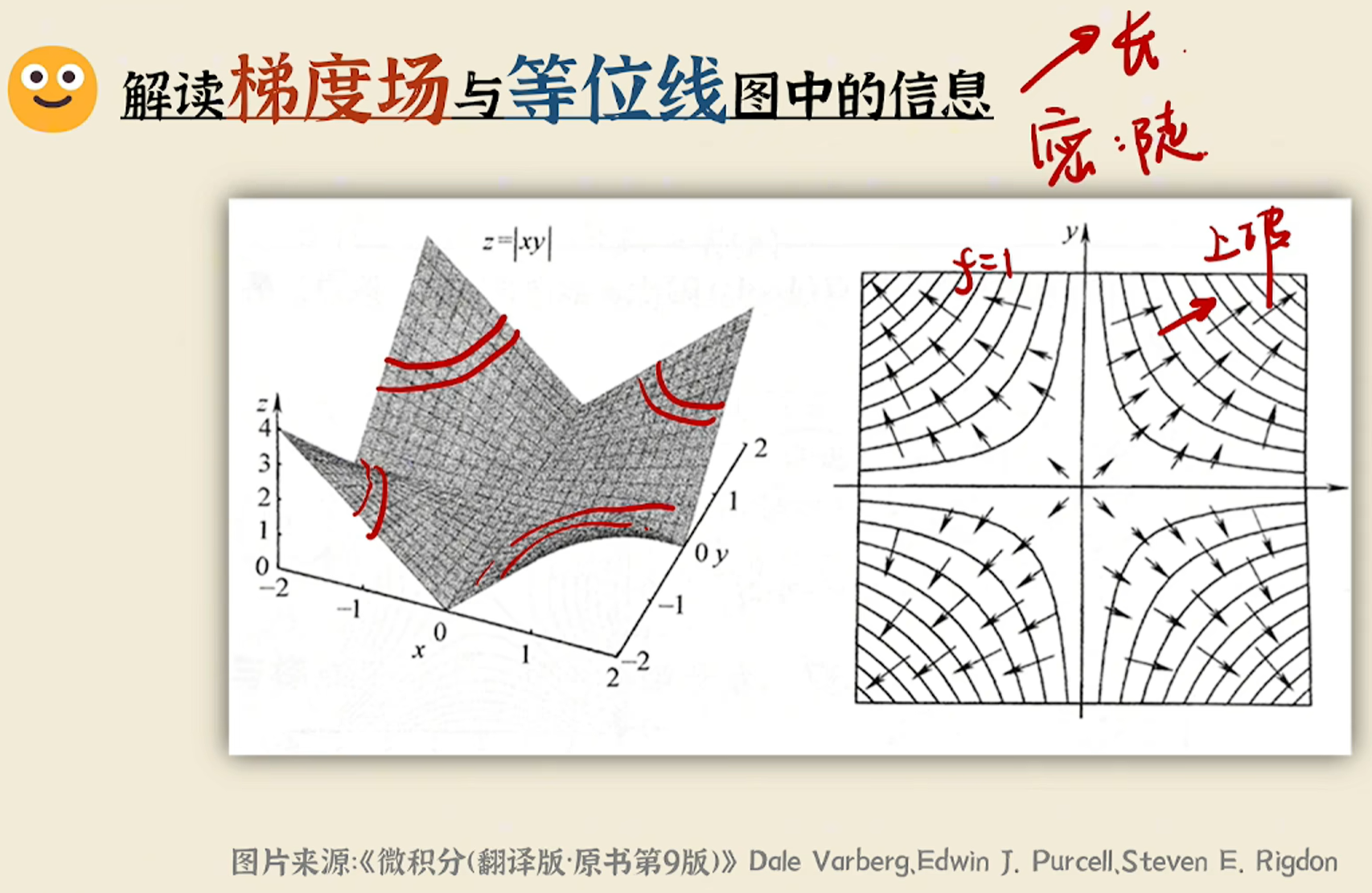
   • 梯度方向与等高线垂直（法向量），指向函数值增大的区域。

   ​​示例​​：
   对于 f(x,y)=x²+y²，等高线为同心圆，梯度 $\nabla f=(2x,2y)$ 始终指向外侧（远离原点）。

注意

梯度（​​Gradient​​）是​​多变量函数​​的概念

1. 严格数学定义​​

• ​​梯度​​：
  仅适用于​​多元函数​​（如 $f(x,y,z)$）。梯度是一个向量，方向指向函数在该点​​增长最快的方向​​，模长表示最大增长率。
  例如：f(x,y)=x²+y² 的梯度为 $\nabla f=(2x,2y)$。

• ​​一元函数​​：
  单变量函数 $f(x)$ 的导数 f′(x) 是​​标量​​，表示函数在某一点的​​瞬时变化率​​（斜率）。
  例如：f(x)=x² 的导数为 f′(x)=2x。

​​结论​​：严格来说，一元函数​​没有梯度​​，只有导数。

---

​​2. 术语的泛用场景​​

在​​优化算法​​（如梯度下降法）或​​机器学习​​中，术语“梯度”可能被泛化，用于单变量情况：

• ​​梯度下降法​​中，即使对于单变量函数 $f(x)$，也会称 f′(x) 为“梯度”，因为算法在多变量和单变量场景下逻辑一致。
• ​​代码实现​​中，梯度计算函数可能统一处理单变量和多变量情况，例如在 Python 的深度学习框架（如 PyTorch）中，对单变量张量求梯度时，返回的 grad 属性即为导数值。