03数据特征、样本,以及标签(目标值)
数据简介
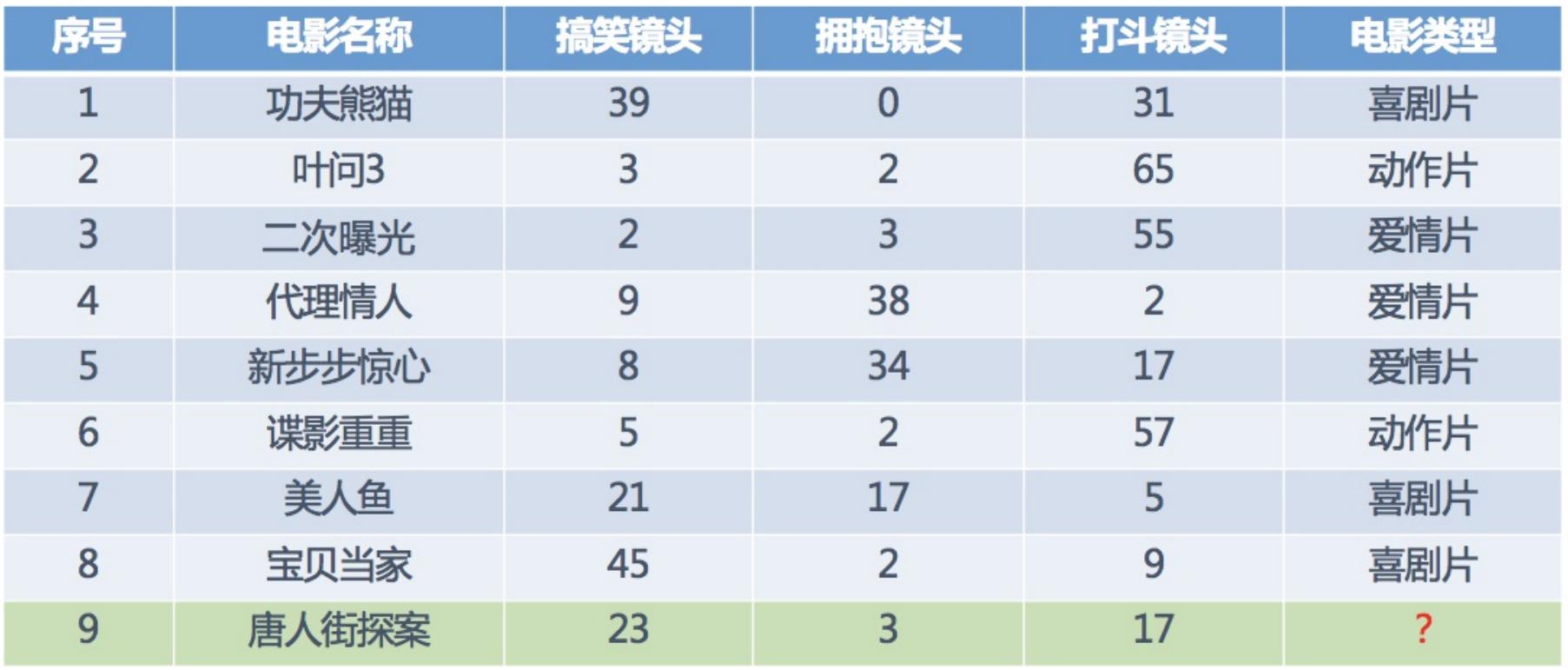
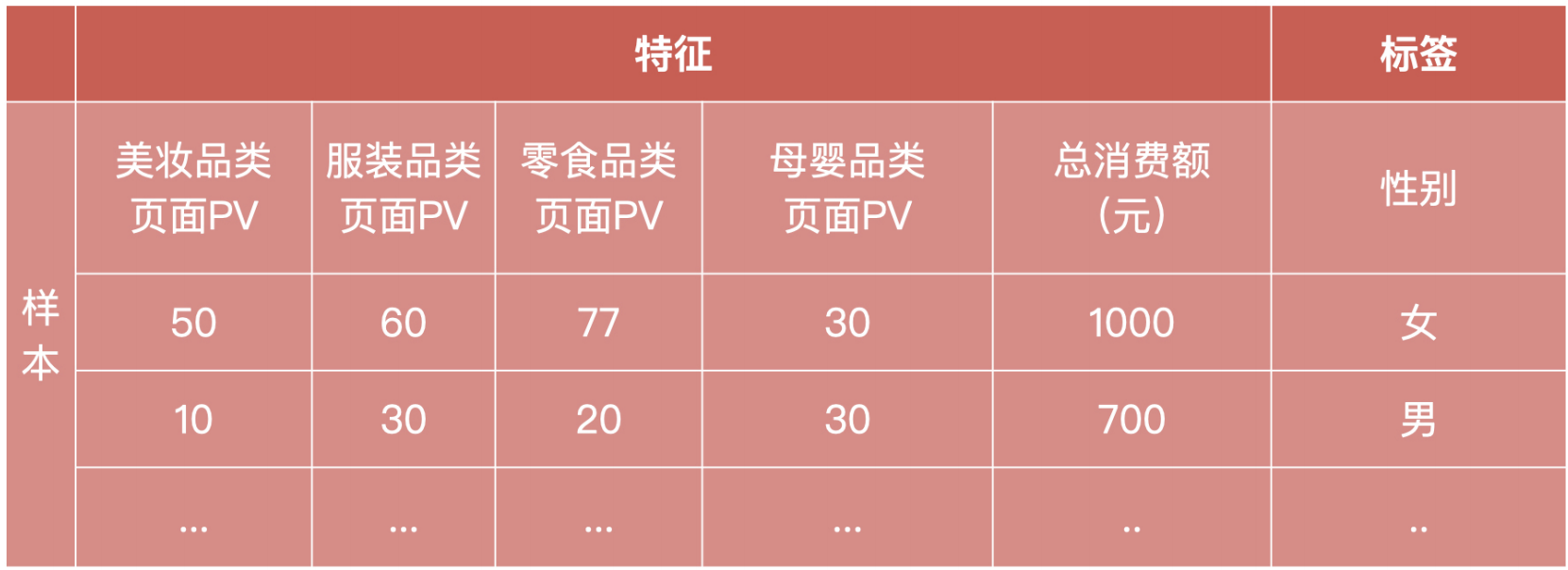
- 一行数据我们称为一个样本
- 一列数据我们称为一个特征
- 有些数据有目标值(标签值),有些数据没有目标值(如上表中,电影类型就是这个数据集的标签(目标值))
- 数据类型一:特征值+目标值(目标值是连续的和离散的)
- 数据类型二:只有特征值,没有目标值
- 机器学习一般的数据集会划分为两个部分:
- 训练数据(训练集):用于训练,构建模型
- 测试数据(测试集):在模型检验时使用,用于评估模型是否有效
- 划分比例:
- 训练集:70% 80% 75%
- 测试集:30% 20% 25%
详述
在机器学习和数据科学中,数据特征、样本和标签是构建模型的核心概念,理解它们的关系是学习的基础。以下是详细解释:
1. 特征(Features)
-
定义:
特征是描述数据的属性或变量,用于表征数据的某种特性。它们是模型学习的输入(X)。 -
示例:
-
房价预测中,特征可能是:
房屋面积、房间数量、地理位置、建造年份等。 -
图像分类中,特征可以是每个像素的数值(如RGB值)。
-
-
特点:
-
可以是数值型(如温度、价格)、类别型(如性别、颜色)或文本型。
-
特征工程(如归一化、编码、特征选择)直接影响模型性能。
-
2. 样本(Sample/Instance)
-
定义:
样本是数据集中的一个独立个体或观察对象,由一组特征值组成。每个样本对应模型的一条输入数据。 -
示例:
-
房价预测中,一个样本可能表示为:
[120平方米, 3室, 北京市海淀区, 2010年]。 -
图像分类中,一张图片的所有像素值构成一个样本。
-
-
特点:
-
在数据集中,样本通常以行的形式存储(表格数据中每一行是一个样本)。
-
样本数量决定数据集的大小(如10,000个样本)。
-
3. 标签(Label/Target)
-
定义:
标签是监督学习中样本的“正确答案”,是模型需要预测的目标变量(Y)。样本可以带标签,也可以不带标签。带标签的样本用于模型的训练,不带标签的样本用于模型的预测。在无监督学习中,标签不存在。 -
示例:
-
房价预测中,标签是房屋的实际售价(如
650万元)。 -
图像分类中,标签是图片的类别(如
猫、狗)。
-
-
特点:
-
标签可以是连续值(回归任务,如价格)或离散类别(分类任务,如类别)。
-
标签的质量直接影响模型的监督学习效果。
-
三者的关系
结构示意图
| 样本(行) | 特征1(面积) | 特征2(房间数) | 特征3(位置) | 标签(房价) |
|---|---|---|---|---|
| 样本1 | 120㎡ | 3室 | 海淀区 | 650万元 |
| 样本2 | 80㎡ | 2室 | 朝阳区 | 480万元 |
-
监督学习:模型通过特征(X)预测标签(Y)。
-
无监督学习:只有特征(X),没有标签(Y),模型需自行发现规律(如聚类)。
不同场景中的具体示例
1. 房价预测(结构化数据)
-
特征:面积、房间数、地理位置、房龄
-
样本:每个房子的数据(如一行数据)
-
标签:房价(监督学习中的目标值)
2. 图像分类(非结构化数据)
-
特征:图像像素的数值(如28x28像素的784个数值)
-
样本:单张图片的所有像素值
-
标签:图片类别(如“猫”或“狗”)
3. 无监督学习(如客户分群)
-
特征:用户的年龄、消费金额、活跃频率
-
样本:每个用户的数据
-
标签:无(模型需自动将用户分组)
常见误区
-
特征 vs 标签:
-
特征是输入,标签是输出(仅在监督学习中存在)。
-
例如:预测学生成绩时,
学习时长是特征,考试成绩是标签。
-
-
样本 vs 特征:
-
样本是完整的个体数据,特征是描述样本的维度。
-
例如:一个患者(样本)的
年龄、血压、病史是特征。
-
-
无监督学习没有标签:
-
如聚类任务中,模型仅通过特征发现数据内在结构。
-
总结
-
特征:数据的属性,模型学习的输入。
-
样本:单个数据点,由多个特征组成。
-
标签:监督学习中的目标值,模型需要预测的结果。
-
关键关系:特征和标签共同构成监督学习的数据集,样本是数据的基本单位。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号