初中数学一本通

实数：与数轴上的点一一对应

　　有理数：有限小数或无限循环小数

　　　　自然数：0、1、2、3、……

　　无理数：无限不循环小数

相反数：a -a；导数：a 1/a；绝对值|a|=

数的大小比较：①作差法a-b；②正数作商法>1；③利用数轴比较：数轴左边的数总是比右边的数小；④平方法（放大）⑤估算法；⑥特殊值法

 

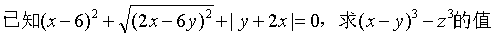
代数式：用运算符号把数或表示数的字母连接而成的式子。一个数或字母也是代数式；

单项式：表示数或字母的乘积的代数式，单独的一个数或字母也是单项式；

多项式：几个单项式的和叫做多项式；

整式：单项式和多项式统称整式。字母不能做分母

分式：A/B 且B中含有字母

分式方程：分母中含有未知数的方程。增根问题

同底指数幂运算：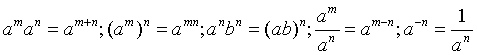

反比例函数k的几何意义：过双曲线上任意一点分别做x轴y轴的垂线，所得的矩形面积均为|k|

二次函数：一般式：y=ax²+bx+c(a≠0)；顶点式：y=a(x-h)²+k；交点式：y=a(x-x₁)(x-x₂)；

顶点坐标公式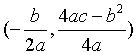：； |a|越大开口越小；

********************************************

 几何部分：

平行线的判定：同位角相等，两直线平行；　　内错角相等，两直线平行；　　同旁内角互补，两直线平行；

平行线的性质：两直线平行，同位角相等；　　两直线平行，内错角相等；　　两直线平行，同旁内件互补；

命题：判断一件事的语句，叫做命题。由题设和结论两部分组成。　　命题的表达形式：如果……那么……　　命题的种类：真命题（判断是正确的）；假命题（判断是错误的）
互逆命题：两个命题，如果一个命题的条件和结论分别是另一个命题的结论和条件，那么这两个命题叫做互逆命题。
定义：对名词或术语的含义加以描述，做出明确的规定，即给出定义。
公理：在实践中总结出来的公认的真命题叫做公理。　　定理：从公理或已知的真命题出发，用逻辑推理的方法推导出来的真命题叫做定理　　推论：由定理直接推出的结论（真命题）叫做推论。
互逆定理：如果一个定理的逆命题也是正确的，那么这两个定理互为逆定理
证明：判断命题正确性的推导过程叫做证明。

三角形：不在同一直线上的三条线段首尾顺次连接所组成的图形叫做三角形。
三角形性质：①稳固性②两个和大于第三边，两边差小于第三边③内角和为180°④一个外角等于与它不相邻的两个内角和⑤等角对等边，大角对长边⑥直角三角形斜边上的中线等于斜边的一半⑦直角三角形30角所对的边等于斜边的一半

勾股定理（毕达哥拉斯定理）：a²+b²=c²；

三角形全等判定：①SSS②SAS③ASA④AAS⑤HL斜边直角边对应相等的两个直角三角形全等

尺规作图：用没有刻度的直尺和圆规来作图的方法叫做尺规作图。

 

 

 

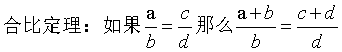
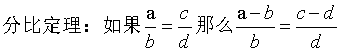
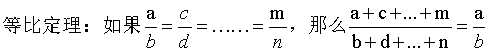
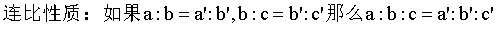
 黄金分割：AB/AC=AC/BC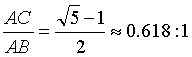　　

 

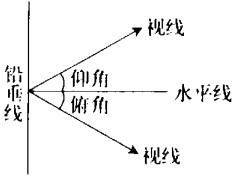
  相似三角形：对应角相等，对应边成比例的三角形叫做相似三角形。

 相似三角形的判定：①三边对应成比例的两个三角形相似②两边对应成比例且夹角相等的两个三角形相似③两角对应相等，两个三角形相似

 位似图形：如果两个图形不仅是相似图形，而且每组对应点所在的直线都经过同一点P，那么这样的两个图形叫做位似图形。这个点P称为位似中心；位似中心可以在图形的内部或外部。位似比等于相似比；

三角函数：sin²A+cos²B=1　　tanA=sinA/cosA

n边形的内角和：(n-2)×180° 　　多边形外角和：360° 　　n边形有(n-3)条对角线，将多边形分成(n-2)个三角形　　n边形共有n(n-3)/2条对角线

平行四边形：两组对边分别平行的四边形叫做平行四边形；（一组对比平行且相等的四边形）；中心对称图形；面积=底×高
平行四边形性质：对边平行且相等；对象相等，邻角互补；对角线互相平分；
平行四边形的判定：①两组对边分别平行的四边形是平行四边形②两组对边分别相等的四边形是平行四边形③一组对边平行且相等的四边形是平行四边形④两组对角分别相等的四边形是平行四边形⑤对角线互相平分的四边形是平行四边形

矩形：有一个角是直角的平行四边形是矩形。
矩形性质：①具有平行四边形所有性质②四个角都是直角③对角线相等④是轴对称图形也是中心对称图形
矩形的判定：①有一个角是直角的平行四边形②对角线相等的平行四边形③有三个角是直角的四边形
菱形：有一组邻边相等的平行四边形叫做菱形。
菱形性质：①具有平行四边形的一切性质②对角线互相垂直平分③四条边都相等④是轴对称图形也是中心对称图形
菱形的判定：①一组邻边相等的平行四边形是菱形②对角线互相垂直的四边形是菱形③对角线互相垂直平分的四边形是菱形④四条边都相等的四边形是菱形

正方形：有个角是直角的菱形叫做正方形；具有平行四边形、矩形、菱形的所有性质；对角线垂直平分

梯形：一组对边平行，另一组对边不平行的四边形叫做梯形。面积S=(上底+下底)×高/2
梯形中位线：平行于两底且等于两底和的一半。

圆：平面内到定点O的距离等于定长r的点的集合。
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。
推论：①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。②圆的两条平行弦所夹的弧相等
圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角相等，且都等于这条弧所对圆心角的一半
圆的内接四边形对角互补
不共线的三点确定一个圆。
圆切线的性质定理：圆的切线垂直于过切点的半径。
圆的切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角。
圆外切四边形的性质定理：圆的外切四边形的两组对边之和相等。
圆的切割线定理：从圆外一点引圆的切线和割线，切线长是这点与圆相交的两点线段的比例中项。PA²=PB*PC
割线定理：PA*PB=PC*PD 相交弦定理：PA*PB=PC*PD 弦切角定理：弦切角等于所夹弧所对的圆周角
圆与圆的位置关系判断：设R，r（R>r）分别为两个圆的半径，d为圆心距，那么：
①d>R+r两圆外离②d=R+r两圆外切③R-r<d<R+r两圆相交④d=R-r两圆内切⑤0≤d<R-r两圆内含

弧长和扇形面积：弧长l=nπR/180　　扇形面积S=nπR²/360=lR/2　　S_圆锥侧=πRl　　

轴对称图案设计：平移、旋转、翻折、拼接、分割
中心对称图形：对应点连线中点是对称中心，全等形

********************

数据的收集与整理
数据处理过程：收集数据-整理数据-描述数据-分析数据-得出结论。
数据的收集过程：明确调查的问题-确定调查对象-选择调查的方式-展开调查-记录结果-得出结论。
数据的收集方式：调查（民意调查、实地调查、全面调查、抽样调查）；查阅资料/上网查询；试验等
全面调查：为了某一特定目的而考察全体对象的调查，叫做全面调查/普查。 优点：获得总体情况，资料全面、可靠；缺点：费时费力；
抽样调查：为了某一特定目的而考察部分对象的调查，叫做抽样调查。优点：调查范围小，节省时间、人力、物力和财力； 缺点：调查结果往往不如全面调查得到的结果准确。 //要注意样本的代表性和广泛性。

总体：在一个统计问题中，所要考察对象的全体叫做总体。
个体：总体中的每一个考察对象叫做个体。
样本：从总体中抽取的一部分个体叫做总体的一个样本。 
样本容量：样本中个体的数目叫做样本容量。（只是一个数字，没有单位）

数据的描述方式：条形图、扇形图、折线图和直方图
组数：把数据分组，组的个数称为组数。
组距：把所有数据分成若干组，每个小组的两个端点之间的距离（即组内数据的取值范围）称为组距。
频数：将一组数据分组后，落在各个小组内数据的个数叫做该组数据的频数。各组数据的频数之和等于数据总数。
频率：数据的频数与总数的比值叫做这组数据的频率。各组数据的频数之和等于1

数据的分析：算术平均数、加权平均数、中位数、众数（可以不存在，也可以不唯一）

数据的波动
极差：一组数据中最大数据与最小数据的差叫做这组数据的极差。极差=最大数据-最小数据　　//极差越小数据波动越小
方差：各数据与它们平均数的差的平方的平均数叫做这组数据的方差。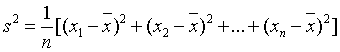　　//方差越小数据波动越小

标准差：方差的算术平方根叫做这组数据的标准差，记作s.　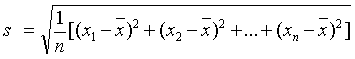　　　//标准差越小，数据波动越小

 

 随机事件与概率

必然事件：在一定条件下，有些事必然会发生，这样的事件称为必然事件。
不可能事件：在一定条件下，有些事情必然不会发生，这样的事件称为不可能事件。
确定事件：必然事件与不可能事件统称为确定事件。
随机事件/不确定事件：在一定条件下，可能发生也可能不发生的事件，称为随机事件/不确定事件

概率：一般地，在大量重复试验中，如果事件A发生的频率m/n会稳定在某个常数p附近，那么这个常数p就叫做事件A发生的概率，记作P(A)=p.

当A是不可能事件时P(A)=0；当A是必然事件时P(A)=1；当A是随机事件时0<P(A)<1

概率的求解方法：列举法求概率；列表法求概率；树状图法求概率；用频率估计概率

概率的应用：几何概率：用部分线段的长度/部分区域的面积和整条线段的长度/整个区域的面积的比来表示。　　游戏公平性需要概率来衡量

计数原理
分类加法计数原理：完成一件事有n类办法，在第一类办法中有m₁种不同的方法，在第二类办法中有m₂种不同的方法…在第n类办法中有m_n种不同的方法，那么完成这件事共有N=m₁+m₂+……+m_n种不同的方法。

//在所有两位数中，个位的数大于十位的数的两位数共有多少个？

分步乘法计数原理：完成一件事，需要分n个步骤，做第1步有m₁种不同的方法，做第2步有m₂种不同的方法…做第n步有m_n种不同的方法，那么完成这件事共有N=m₁*m₂*……*m_n种不同的方法。

//三张卡片的正反面分别写有1、2、3和4、5、6，若将这三张卡片并列，可得到多少个不同的三位数（6不能作9用）？

*******数学竞赛知识********

代数式：

带余除式定理：设f(x)，g(x)是两个关于x的多项式，且g(x)≠0，则有带余除式：f(x)=g(x)q(x)+r(x)，其中f(x)，g(x)，q(x)，r(x)分别代表被除式、除式、商式和余式。

余式定理：多项式f(x)除以x-a所得的余式为f(a).　　因式定理：x-a是多项式f(x)的一个因式，当且仅当f(a)=0.　　相等的多项式对应项系数相等；

待定系数法；拆项；添项；分离常数法；

几何：

重心：三角形三条中线的交点，顶点到重心的距离是重心到对边距离的2倍。x=(x1+x2+x3)/3  y=(y1+y2+y3)/3

垂心：三角形三条高线的的交点；

内心：三角形三条内角平分线的交点；

外心：三角形三边的垂直平分线的交点；

旁心：三角形一内角平分线和另外两顶点处的外角平分线的交点（旁切圆的圆心）；

费马点：在一个三角形中，到三个顶点距离之和最小的点叫做这个三角形的费马点。若∠A≥120°，则A为费马点；若三个内角都小于120°，则在三角形内部与三边张角都为120°的点为费马点。内角都小于120°，则分别以三边向外做正三角形，三个顶点的交点为费马点

欧拉定理：△ABC的外心O，重心G，垂心H依次位于同一直线上，且OG=GH/2

欧拉线：△ABC的外心O，重心G，垂心H所在的直线叫做欧拉线。　　九点圆（欧拉圆、费尔巴哈圆）

三角形面积：ah/2=absinC/2=(a+b+c)r/2=sqrt(p(p-a)(p-b)(p-c))；其中p=三角形周长的一半

数论：倍数、约数（因数）、偶数、奇数、质数、合数、公约数、公倍数

数学思想：数形结合、分类讨论、函数与方程思想、化归与转化思想、整体思想、模型思想

数学方法：换元法、消元法、待定系数法、配方法、赋值法、比较法、同一法、类比法、归纳法、反证法、综合法、构造法、面积法