LoRA-《LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS》论文解读

LoRA

主流的大模型训练范式之一便是“Pre-train + Finetune”，即“通用能力的学习+下游任务的适配”两个环节，而在下游任务适配这一环节中，似乎全参数的微调成本随着模型规模的增大而逐渐变得难以接受，部分研究者也针对这个问题进行了一些高效适配方案的研究

目前主流的下游任务高效适配方案主要分为两大类：1、在Transformer中加入Adapter层；2、优化输入层激活的某些部分（e.g. Prefix-tuning、Prompt-tuning ）。前者会引入推理延迟，尽管 Adapter 参数量很少（通常 <1%），但由于其增加了新的计算层，在在线推理场景下，尤其是batch size 很小时，推理延迟显著增加（如下图所示），尤其是在分布式训练中，当模型需要进行分片并行时，Adapter 的额外深度会增加 GPU 间同步操作的次数，进一步拖慢推理；后者直接优化Prompt，难以训练收敛，且随着可训练参数数量的变化，性能并不单调提升。其中，prefix-tuning 需要占用一部分输入序列长度来表示任务特征，从而减少了可用于实际任务的输入空间，影响下游性能

Aghajanyan等人和Li等人的工作早已揭晓如下事实：即深度学习模型或者如今的LLM，在一个低维子空间进行学习也能达到全参数学习的性能。于是作者提出了如下假设："在模型适配微调的过程中，“权重的变化”这个事情本身同样也具有低秩结构"，即权重具有“内部秩”（intrinsic rank），换句话说，模型的更新总是集中在那么几个方向上

根据上述假设，作者提出了LoRA（Low-Rank Adaptation），在微调时冻结预训练模型的权重，将权重的更新部分建模为可训练的低秩分解矩阵（如下图所示），数学表达为：\(W' = W + \Delta W\)，此处的待训练的低秩分解矩阵即\(\Delta W\)。即给定一个下游数据集\(Z=\{(x_i, y_i)\}_{i=1}^N\)，从原来的全参数微调目标：\(\max_{\theta} \sum_{(x, y) \in Z}\sum_{t=1}^{|y|}\log P_{\Theta}(y_t \mid x, y_{<t})\tag{1}\)变为LoRA的微调目标：\(\max_{\theta} \sum_{(x, y) \in Z}\sum_{t=1}^{|y|}\log P_{\Theta_0 + \Delta \Theta(\theta)}(y_t \mid x, y_{<t})\tag{2}\)

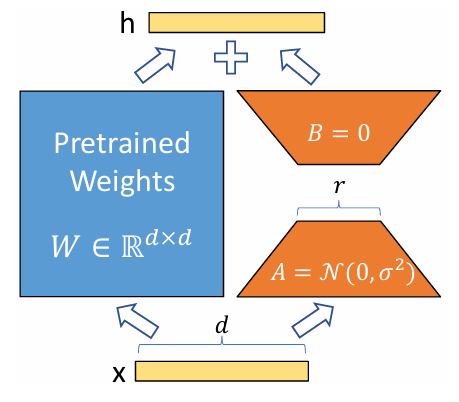
对于权重\(W_0 \in \mathbb{R}^{d \times k}\)，前文提到提到对该权重的更新部分进行低秩分解：\(\Delta W = BA\)，其中\(B \in \mathbb{R}^{d \times r}\)、\(A \in \mathbb{R}^{r \times k}\)，\(r \ll min(d, k)\)。在初始化时，将\(A\)初始化为高斯随机噪声，\(B\)初始化为全零矩阵，即初始时刻\(\Delta W = 0\)，那么在前向传播中就有：

\(h = W_0 x + \Delta W x = W_0 x + B A x \tag{3}\)

LoRA与全量微调的关系

可以注意到，当\(\Delta W\)为full-rank时（\(rank(ΔW)=min(d,k)\)），此时不再受限于低秩近似，可以覆盖整个参数空间，此时LoRA退化为全量微调

无推理延迟

当\(B\)、\(A\)训练完成后，我们在推理前可以预先计算\(\widetilde{W} = W_0 + BA\)，而后每一步的推理就按微调前的模型推理进行：\(h = \widetilde{W} x\)，推理速度不会造成影响

LoRA在Transformer中的应用

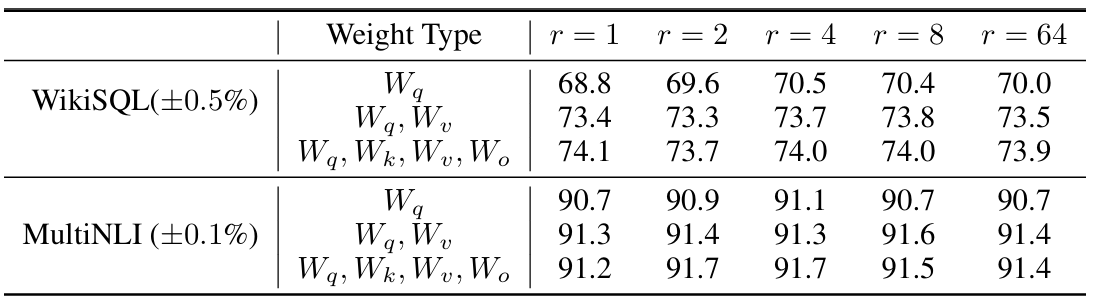
在Transformer中，一个Self-attetion模块通常涉及四个权重矩阵：\(W_q\)、\(W_k\)、\(W_v\)、\(W_o\)，还包含扩张和收缩两个MLP层，文中作者选择只在\(W_q\)、\(W_k\)、\(W_v\)、\(W_o\)上进行LoRA性能比较实验，而其他权重选择冻结，对比实验结果如下图所示。可分析得到两个结论：1、在表中，选择\(W_q\)和\(W_v\)进行LoRA是性能最优的；2、“对单个矩阵进行较高值的低秩分解”性能不及“对多个矩阵进行较低值的低秩分解”

如何找到LoRA最优的秩r？

对于这个问题，作者基于上述的设置又进行了如下表所示的对比实验，可以得到如下几个结论：1、在秩非常低时（\(r\)=1、2）已经能够取得较好的性能，继续增大秩并不能带来显著的性能提升；2、对\(W_q\)和\(W_v\)进行LoRA时，较小的秩下性能更为稳定；3、仅对\(W_q\)进行LoRA时，模型性能对于秩的设置十分敏感，波动不规律

不同秩之间的子空间相似度

作者在文中提出了以下问题：当我们使用不同的秩（比如\(r = 8\)/\(r=64\)）时，模型学习到的\(\Delta W\)的特征空间是否相同？

文中通过计算一个空间重叠度来衡量这种相似性：比如对于\(r=8\)和\(r=64\)，对LoRA得到的矩阵\(A_{r=8}\)和\(A_{r=64}\)进行SVD，由于SVD的右矩阵体现了输入空间的主要方向，我们选取右矩阵结果\(U_{A_{r=8}}\)和\(U_{A_{r=64}}\)，我们想要弄清楚，\(r=8\)的前\(top-i\)个奇异向量（\(1 \leq i \leq 8\)）有多少被包含在\(r64\)的前\(top-j\)个奇异向量（\(1 \leq j \leq 64\)）中？

对于上述这类问题，我们可以使用Grassmann距离进行衡量，可以计算为：

\(\Phi(A_{r=8}, A_{r=64}, i, j)=\frac{||U_{A_{r=8}}^{iT}U_{A_{r=64}}^{j}||^2_F}{min(i,j)} \in [0, 1] \tag{4}\)

该距离取值范围为0到1，0表示彻底独立的两个子空间，1表示完全重叠的两个子空间，实验结果如下图所示，其中右边图3图4为左边图1图2左下角的放大

由图可知，\(r=8\)和\(r=64\)的top几个方向颜色较浅，说明\(r=8\)和\(r=64\)的top几个方向重叠度较高；而右下角颜色较深，说明\(r=64\)高秩的部分没有和\(r=8\)的top部分产生很强的相关性，也就是说top方向的作用最大，其他更多的多余方向可能会引入更多的噪声。尤其是\(i=j=1\)的方向，重叠度超过了0.5，这解释了为什么 \(r=1\) 时也能在 GPT-3 上取得不错效果，也就是说，更新矩阵的大部分有效信息集中在这个最重要的方向上，即\(\Delta W\)具有很小的内部秩

随机种子验证

为了验证上述关于内部秩的结论，文中在相同的预训练模型上，用两个不同随机种子进行\(r=64\)的LoRA，然后对比两次训练学到的\(A_{r=64}\)的子空间相似度，如果两个训练结果的子空间相似度很高，说明模型确实倾向学习到相同的低秩结构（而不是噪声），也就是计算：

\(S(A_{r=64}^{(Seed1)},A_{r=64}^{(Seed2)}) \tag{5}\)

实验结果如下图所示，结果显示，\(\Delta W_q\)的内部秩比\(\Delta W_v\)的内部秩更高，且相似度更高，这说明了两个现象：1、不论在什么随机种子下进行训练，\(\Delta W_q\)得到的top个向量方向都更为一致且稳定；2、内部秩高代表了\(W_q\)这个模块在任务中起到的作用更关键，它的有效子空间更为复杂。此外，实验还分析了高斯噪声，由于噪声不具备相关性，所以自然呈现的是纯黑的样子

\(\Delta W\)和\(W\)的关系

作者针对\(\Delta W\)和\(W\)的关系这个角度提出了如下问题：1、\(\Delta W\)和\(W\)是否方向相似？（或者说，\(\Delta W\)是否主要分布在\(W\)的top个奇异方向上？）2、LoRA 在这些主要方向上的更新幅度有多大？

文中利用SVD的角度对这个问题进行了分析，首先，对\(\Delta W\)进行奇异值分解：\(\Delta W = U \Sigma V^T\)，而后将\(W\)投影到\(\Delta W\)的\(r\)维空间中：\(U^TWV^T\)，随后我们比较\(\Delta W\)和\(U^TWV^T\)的Frobenius 范数（计算方式：对于一个矩阵\(A = [a_{ij}] \in \mathbb{R}^{m \times n}\)，其Frobenius 范数计算为\(||A||_F = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij}^2}\)）

这样做的理由是什么呢？我们假设矩阵\(A和\)\(B\)两者主方向完全重合，有：\(A = \alpha \cdot B\)，那么我们也先对\(B\)进行SVD，按上述公式求两者的范数比值则为：\(\frac{|| U^T A V^T ||_F}{||B||_F}\)，由于正交矩阵不影响范数的大小，所以可以推导得到：\(\frac{|| U^T A V^T ||_F}{||B||_F} = \frac{|| U^T (\alpha \cdot B) V^T ||_F}{||B||_F} = |\alpha| \tag{6}\)

可见如果两个矩阵的主方向重合时，根据上述公式得到的为一个大于0的值\(\alpha\)，这个值反映了如果\(A\)中有主方向与\(B\)中主方向重合时，\(A\)在幅度上对其的放大程度是多少。而如果假设\(A\)和\(B\)方向毫无关联，接近正交，那么此时\(U^T A V^T \approx 0\)，导致比值为0。也就是说，我们可以通过这个比值的大小来判断两个矩阵是否主方向关联

文中的实验结果如下表所示，作者分别利用\(W_q\)、\(\Delta W_q\)和\(Random\)三种不同的矩阵进行SVD后对\(W_q\)进行转换，在\(r=4\)和\(r=64\)的条件下重复实验。可以观察得到几个现象：

1、\(W_q\)在自己的特征空间下主方向重合度是最高的，这很直观，自己与自己当然最一致；

2、相比于\(W_q\)与随机矩阵而言，\(W_q\)与\(\Delta W_q\)的比值更大，也就是说\(W_q\)与\(\Delta W_q\)之间存在一定的联系，\(\Delta W\)的更新包含了一部分\(W\)中的特征；

3、\(W_q\)与\(\Delta W_q\)的比值远小于\(W_q\)与自身的比值，这说明LoRA中\(delta W\)并不是简单重复更新原矩阵的主方向，而是重点增强那些在\(W\)中没有被强调的方向，换句话说，LoRA能够补充模型的“盲区”或“弱特征”，从而修正模型对下游任务敏感的方向；

4、可以观察到，在\(r=4\)时，\(\Delta W\)中对于与\(W\)中相关的主方向的放大倍数为\(\alpha = 6.91 / 0.32 \approx 21.5\)，意味着低秩情况下，\(\Delta W\)对于主方向的增强还是很明显的。而当秩增大\(r=64\)时，这个增强效果反而减弱了，这是因为当\(r\)增大时，每个方向的增强幅度分散了，导致整体放大因子变小（作者还做了一些实验验证这个部分，具体可以参考原文，这里不展开说了）

参考资料

• 《LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS》
• https://baike.baidu.com/item/奇异值分解/4968432