Adam(Adaptive Moment Estimation)
Adam是一种自适应地优化算法,结合了Momentum和RMSProp的特点,在优化过程中自适应地调整优化的学习率,其组成部分主要分为一阶矩估计和二阶矩估计
1、一阶矩估计表示为\(m_t\) ,计算公式如下:
\(m_t=\beta_1m_{t-1}+(1-\beta_1)\nabla_{\theta_t}L(\theta_t)\) 2、二阶矩估计表示为\(v_t\) ,计算公式如下:
\(v_t=\beta_2v_{t-1}+(1-\beta_2)[\nabla_{\theta_t}L(\theta_t)]^2\) 其中,\(\nabla_{\theta_t}L(\theta_t)\) 为损失函数关于优化参数的梯度、\(\beta_1\) 、\(\beta_2\) 为用于控制一阶、二阶矩指数衰减率的超参数,一般设置为\(0.9\) 和\(0.999\) 。由于优化初始时刻,\(m_t\) 和\(v_t\) 的值较小,会在初始阶段被低估,此时需要引入一个偏差校正的环节:\(\hat{m_t}=\frac{m_t}{1-\beta_1^t}\) 、\(\hat{v_t}=\frac{v_t}{1-\beta_2^t}\) ,那么给定初始学习率\(\eta\) ,Adam优化过程可以描述为:
\(\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t}\) 在优化过程中,一阶矩我们称为动量项,它通过累计加权累计历史梯度,从而表示一个平均的梯度方向,这个梯度方向象征了一个好的优化倾向。例如参数维度为3,每一个epoch如果都向梯度方向\([1,1,1]\) 进行优化,那么平均值\([1,1,1]\) 则证明该方向的梯度是值得采用的
而二阶矩对历史梯度的平方和进行累计,反映了梯度大小的累积幅度。如果以往的梯度累积幅度过大,说明该方向变化快或者敏感,如果每次按梯度原值更新,容易“跳过最优点”,此时则需要基于二阶矩减小学习率,使优化过程更为稳定
Adam结合了一阶矩和二阶矩,实现了自适应学习率,对于那些不经常更新的参数,会给予更大的学习率,很好地处理了稀疏问题。且相比于SGD需要精心选择学习率和动量参数,Adam无需手动调整太多学习率参数,在大多数情况下对超参数(尤其是学习率)的选择不那么敏感,通常默认参数就能取得不错的效果
在实际应用中,通常\(\beta_1\) 设置成0.9,\(\beta_2\) 设置成0.999,这么做的目的是因为\(v_t\) 项是对Hessian矩阵的一种近似,Hessian 是损失函数的全局曲率性质,它变化相对缓慢,不会像随机梯度那样剧烈波动,为了准确估计一个稳定的全局量,我们需要一个长期、平滑的估计,减少随机梯度噪声的影响;而\(m_t\) 项聚合历史梯度方向来加速收敛并减少振荡,在随机优化中,如果已经接近最优点,或者在不同区域梯度方向变化很大,长期的平均梯度\(E[g_t]\) 会趋近于0,如果太过关注全局,会导致出现更新停滞的问题,因此这部分平均应该更“局部”,关注近期的梯度方向,以便快速响应曲面的变化
AdamW
由于在深度学习模型特别是大模型中,模型通常有大量的参数。如果模型参数过多且训练数据不足,模型就可能过度学习训练数据中的噪声和特有模式,而不是学习到数据的普遍规律。这导致模型过拟合。过拟合的模型往往具有非常大或非常小的权重,因为这些大权重使得模型对训练数据中的微小变化过于敏感,而 Weight decay 的目标就是抑制这种大权重的出现
而在原始的Adam中,Weight decay的实现是在损失中加上正则化项\(g_t=\nabla_{\theta_t}L(\theta_t)+\lambda\theta_t\) ,而这样的形式在Adam中则会被卷入了自适应缩放,使得正则化效果被压缩不能很好地起效果
AdamW的做法则是,将这一项移出了梯度缩放部分:
\(\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t} - \eta\lambda\theta_t\) 一阶梯度与二阶梯度
不论是Adam、AdamW、SGD+Momentum,这些方法都是基于一阶梯度进行的优化计算,根据一阶梯度来确定优化方向。而一阶梯度如同山坡的坡度一般,是有变化的,即逐渐变陡或变缓。当前坡度信息无法预测这种变化,根据当前坡度来确定步子大小就会产生一些问题
拿一个二维的目标函数为例,其表达式为\(L(x,y)=100x^2+y^2\) ,等高线为椭圆,其一阶梯度为\([200x, 2y]\) ,二阶梯度为\([200, 2]\) ,假设待更新参数\(x_t, y_t\) ,根据一阶梯度更新公式为:\(x_{t+1}=x_t - 200 \eta x_t\) 、\(y_{t+1}=y_t - 2 \eta y_t\) ,此时若学习率稍微设置的大一些,为\(\eta=0.01\) ,则有\(x_{t+1}=-x_t\) ,\(y_{t+1}=0.98y_t\) 。可以看见\(x\) 维度上,其梯度变化率为200,即更为陡峭,而只依赖于一阶梯度进行更新则没有考虑这个信息,会在陡峭的维度上来回大幅度变化震荡,而在平缓的维度\(y\) 上则又变化十分微小,如下图蓝线所示,而二阶梯度则能给出了一条直达最优处的直线,如红线所示:
而如果我们能够引入二阶梯度信息,相当于得到了坡度的变化信息,可以利用二阶梯度的信息来提升优化性能。比如经典牛顿法:\(\theta_{t+1} = \theta_t - \eta H^{-1}g\) ,\(H\) 为Hessian矩阵,可以写为特征分解的形式:\(H=Q \Lambda Q^T\) ,\(Q\) 包含了若干特征向量\(q_i\) ,\(\Lambda\) 包含了若干特征值\(\lambda_i\) ,则形式可变换为:\(\theta_{t+1} = \theta_t - \eta Q \Lambda^{-1} Q^T g\)
这里简单说明一下,给定一个方向向量\(v\) ,那么函数在该方向上的二阶变化率可以表示为:\(v^THv\) 。如果这个方向\(v\) 取特征向量\(q_i\) 的话,则有\(v^THv=q_i^THq_i=q_i^T(\lambda_iq_i)=\lambda_i(q_i^Tq_i)=\lambda_i\) ,由此可以发现,Hessian 的特征值\(\lambda_i\) 就是函数在特征方向\(q_i\) 上的二阶导数,也就是曲率
回到式子\(\theta_{t+1} = \theta_t - \eta Q \Lambda^{-1} Q^T g\) ,\(Q^Tg\) 就相当于将梯度从原始坐标系拉到了Hessian 的特征坐标系;而后\(\Lambda^{-1}\) 相当于在每个转换后的主方向上除以特征值也就是曲率,对Hessian特征坐标系下的梯度进行约束,带来的影响就是,陡峭方向走得更小,平缓方向走得更大;最后\(Q\) 再变换回原始坐标系。这就很好地利用二阶信息提升了优化过程,精确地沿特征方向下降
虽然基于二阶梯度进行优化的方法收敛性很好,但是其计算量限制了实际的应用。每次梯度更新的时候都会带来平方级别的空间复杂度和立方级别的时间复杂度,因此这些方法在现在的深度学习优化方法中并不常见。可以由上述内容得知,如果在深度学习中要应用类似于牛顿法的方法,对Hessian矩阵做比较大的简化假设,比如对角矩阵或者低秩矩阵
Shamppo
Google Research在2018年提出了一种名为Shamppo的高效近似二阶优化算法,其目标为利用二阶信息加速收敛,同时避免 Hessian 维度太大带来的计算负担,其核心思想是不直接计算或储存 Hessian,而是利用参数张量的结构(例如矩阵、卷积核等的维度)来做 Kronecker 分解近似。在简述Shamppo原理之前,需要简单介绍两个东西(省去一些复杂的推导,有兴趣可自己搜索查看):
1、Kronecker分解:Kronecker分解思想可以简单概述如下:对于一个大方阵\(H \in \mathbb{R}^{mn \times mn}\) ,如果能找到两个较小的矩阵\(A \in \mathbb{R}^{m \times m}\) 、\(B \in \mathbb{R}^{n \times n}\) ,使得\(H \approx A \bigotimes B\) ,那么就可以用\(A\) 和\(B\) 来描述\(H\) ,其中\(\bigotimes\) 称为Kronecker积,定义为:
这样进行分解后,矩阵的存储量从原始的\((mn)^2\) 减少到了\(m^2 + n^2\) ,大大减小了空间复杂度,且还可以推导得到如下性质:\(H^{-1} \approx A^{-1} \bigotimes B^{-1}\) ,这样可以从求一个大矩阵的逆转换为求两个小矩阵的逆,大大减小了计算的时间复杂度
2、现有的Adagrad/Adam/RMSProp只是利用历史梯度平方的累积来近似 Hessian 的对角线元素,为什么这么说呢?由泰勒展开式可以得知:\(f(\theta) \approx f(\theta^*)+\frac{1}{2}H(\theta-\theta^*)^2\) ,那么两边求导得到:\(g = \frac{\partial{f}}{\partial{\theta}}=H(\theta-\theta^*)\) ,两边平方:\(g^2 = H^2(\theta-\theta^*)^2\) ,求期望:\(E[g^2] = H^2E[(\theta-\theta^*)^2]\) 。如果训练过程中的参数\(\theta\) 在最优点附近上下波动,那么可以认为\((\theta-\theta^*)^2\) 的期望是某个小常数,代表你在局部的探索范围,那么此时可得到:\(E[g^2] \propto H^2\) 。在多维场景下,则需要假设各维度独立(即不同维度之间的协方差很小),则可以得到:\(E[g_i^2] \propto H_{ii}^2\) 。此时再使用牛顿法:\(\delta\theta = -H^{-1}g\) -> \(\delta\theta = -\frac{1}{H_{ii}}g\) ,这就与Adam和RMSProp中的概念一致了
此处博客从Hessian近似看自适应学习率优化器 \(gg^T\) ,只不过缓存外积空间成本太大,所以实践中改为Hadamard积\(g⊙g\) ,也即是上述所谓的“历史梯度平方”
在Shamppo中,假设模型某层权重参数矩阵为\(W \in \mathbb{R}^{m \times n}\) ,其中\(m\) 为输出维度,\(n\) 为输入维度。参数梯度则为\(G_t = \delta_tx_t^T\) ,其中\(x_t \in \mathbb{R}^n\) 为激活后的输入(列方向),\(\delta_t \in \mathbb{R}^m\) 为反向传播的误差信号(行方向)。由上述可知,可以使用梯度外积对Hessian进行近似:
\(vec(G_t) = x_t \bigotimes \delta_t\) 那么:\(E[vec(G_t)vec(G_t)^T] = E[(x_tx_t^T) \bigotimes (\delta_t \delta_t^T)]\)
令\(R_t =E[x_tx_t^T]\) , \(L_t=E[\delta_t\delta_t^T]\) ,可得到:\(H_t^2 \approx R_t \bigotimes L_t\) 。在实际应用中使用统计均值代替期望,可以换一个表达方式:\(L_t \approx \frac{1}{t} \sum_{\tau = 1}^t G_{\tau}G_{\tau}^T \in \mathbb{R}^{m \times m}\) 、\(R_t \approx \frac{1}{t} \sum_{\tau = 1}^t G_{\tau}^TG_{\tau} \in \mathbb{R}^{n \times n}\) ,由于\(\frac{1}{t}\) 作为一个常量,只算是一个时间衰减因子,后续可以结合在学习率中从而去除,于是写成:\(L_t \propto \sum_{\tau = 1}^t G_{\tau}G_{\tau}^T \in \mathbb{R}^{m \times m}\) 、\(R_t \propto \sum_{\tau = 1}^t G_{\tau}^TG_{\tau} \in \mathbb{R}^{n \times n}\)
有了Hessian的近似表达后,我们可以进一步推导得到:\(H_t \approx R_t^{- 1/2} \bigotimes L_t^{- 1/2}\) 。而后按照Adagrad中描述的更新范式进行更新:\(\theta_t - \eta H_t^{- 1/2}g_t\) 进行更新,最终的表达式为:\(\theta_{t+1} = \theta_t - \eta L_t^{-1/4}G_tR_t^{-1/4}\)
在实际应用中,\(R_t\) 和\(L_t\) 采用指数平均的方式进行更新:
\(L_{t+1} = \beta L_t + G_{t+1}G_{t+1}^T\) \(R_{t+1} = \beta R_t + G_{t+1}^TG_{t+1}\) Shamppo中,默认\(\beta\) 为1
Shamppo算法距离实际应用还有几个难点:1、预条件子的计算和存储的巨大消耗;2、\(L\) 、\(R\) 矩阵的求逆与求根的巨大消耗;3、神经网络加速器通常是定制的,其加速器设计倾向于低精度(8bit/16bit),能够满足现有的方案。而Shamppo需要双精度运算,因此已有的加速器甚至都不会启动。现有深度学习库提供的最优化器 API 适应于一阶梯度下降模式。而二阶优化器需要与训练循环做交互,因此从实现上需要对框架底层做出修正。Google在后续的工作中提出了相应的算法和组件上的优化,使得Shamppo二阶优化器在大模型上成功work
Muon(MomentUm Orthogonalized by Newton-schulz)
对于矩阵参数\(W \in \mathbb{R}^{m \times n}\) 而言,Muon的更新公式为:
\(M_t = \beta M_{t-1} + G_t\) \(W_t = W_{t-1} - \eta [msign(M_t) + \lambda W_{t-1}]\) 其中,\(msign\) 是矩阵符号函数,是sign函数的矩阵化推广,它跟SVD的关系是:\(SVD(M)= U\Sigma V^T\) ,\(msign(M) = U_{[:,:r]}V_{[:,:r]}^T\) ,其中\(r\) 为\(M\) 的秩。在SVD中,将一个矩阵\(M\) 看成输入空间到输出空间的线性变换,\(V\) 为输入空间的主方向,\(U\) 为输出空间的主方向,而\(\Sigma\) 则代表转换到输入空间后沿每个方向的拉伸幅度大小,这个拉伸程度的不同体现了SVD的“各向异性”。而对于\(msign\) 而言,相当于只保留了方向映射,将所有方向拉至单位长度
苏神这篇博客写得很深入,推荐大家去阅读:Muon优化器赏析:从向量到矩阵的本质跨越 ,其中谈到,像Adagrad、RMSprop、Adam等自适应学习率优化器主要有两个特点:1、损失函数的常数缩放不影响优化轨迹;2、每个参数分量的更新幅度尽可能一致。而Muon则满足这两点要求:1、假设进行SVD,损失函数乘以\(\lambda\) ,\(M\) 也会乘以\(\lambda\) ,结果是\(\Sigma\) 被乘以\(\lambda\) ,但Muon最后的更新量是将\(\Sigma\) 变为单位矩阵,所以不会产生任何影响;2、Muon的“各向同性“也起到了同步更新幅度的作用
实际应用中,如果每一步都对\(M\) 进行SVD求解\(msign(M)\) 的话,计算成本相对较大,我们可以利用SVD得到如下公式:\(msign(M) = (MM^T)^{-1/2}M = M(M^TM)^{-1/2}\) ,将\((M^TM)^{-1/2}\) 在\(M^TM=I\) 处展开得到:\(msign(M) \approx \frac{8}{15} M - \frac{5}{4}M(M^TM) + \frac{3}{8}M(M^TM)^2\) ,如果\(X_t\) 为\(msign(M)\) 某个近似,基于Newton-schulz迭代可以得到一个更优的近似:\(X_{t+1} \approx \frac{8}{15} X_t - \frac{5}{4}X_t(X_t^TX_t) + \frac{3}{8}X_t(X_t^TX_t)^2\)
Muon和Shamppo之间的联系:Shamppo中也涉及到了一部分矩阵的幂运算,而不是采用Newton-schulz迭代这类迭代算法,而是采用SVD进行运算,这样会相比之下产生更多的计算量,因此Shamppo中\(R_t\) 、\(L_t\) 的更新是以一定的步数间隔来更新的。由上述Shamppo的指数平均的更新公式可以推导,当\(\beta = 0\) 时,有\((GG^T)^{-1/4}G(G^TG)^{-1/4} = msign(G)\) ,这时候两者等价
PS:感觉有部分地方还是有点半知半解,后续还是要持续学习(˘•ω•˘)
参考资料
posted @
2025-10-12 23:23
Luna-Evelyn
阅读(
8 )
评论()
收藏
举报

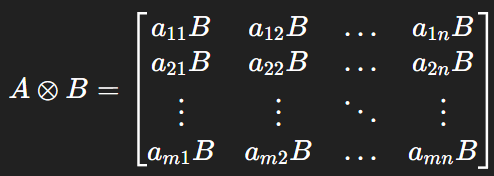


 浙公网安备 33010602011771号
浙公网安备 33010602011771号