Post-norm和Pre-norm
Post-norm
- 在传统的transformer中,layer normalization一般发生在残差之后,即在add之后再进行norm,如果令
F为MHAorFFN,那么post-norm则有:Xo = LN(Xi + F(Xi))。post-norm可以使得每个神经网络层的输出都在相似的尺度上,保持了每个模块的一致性,稳定了前向传播的方差。在残差之后进行归一化,保证了模块的输入输出的分布相似性,从而在前向传播中避免特征能量发散

- 但是Post-norm也存在以下问题:
- (1)假设x的方差是
1,F(x)的方差是σ,Norm 操作就相当于除以sqrt(1+σ^2)。如果σ比较小,那么残差中这条x的岔路的权重则非常接近于1,这说明其能够作为一条恒久的路存在下去从而发挥残差的作用,,模型在初始阶段就越接近一个恒等函数,越不容易梯度消失。但是,参数的随机初始化可以认为x与F(x)是两个相互独立的随机向量。假设它们各自的方差是1,则x+F(x)的方差是2,而Norm操作负责将方差重新变为1,那么在初始化阶段,Norm操作就相当于除以了根号2,x->x/根号2。这个例子证明,post-norm中会削弱残差分支,且在浅层输入时更为严重,还是不太好训练 - (2)当进行梯度传播时,有如下计算公式:

-
也就是说LN会根据输入方差对梯度进行缩放,当输入方差较小(深层残差信号被削弱时),梯度会被放大,且越靠近输出层,残差信号经过多层叠加和削弱,梯度被显著放大;而对于输入层,bp时经过多层连乘和残差结构的失效后会削弱梯度,造成浅层可能出现梯度消失情况。这表明了post-norm对参数非常敏感,在没有任何调整的情况下使用较大的学习率训练的效果会非常差。抑制高层剧烈更新,保证梯度信号稳定。此时我们需要进行warm up操作,缓慢提高学习率,这样高层不会因梯度大+学习率大而剧烈震荡,而低层接收到的反向梯度方向更加平滑、稳定,可以安全积累小幅更新
-
Adam通过计算梯度的一阶矩(均值)和二阶矩(方差),实现自适应学习率调整。不像传统SGD的参数更新严格与梯度大小成正比,梯度太小则更新量几乎为零,导致训练停滞。只要梯度幅度大于噪声水平,Adam 都能保证参数获得一定量级的更新,避免梯度过小导致的停滞。因此post-norm还是有机会得到有效训练,但是对层数高的post-norm而言,确实非常难训练。不过,对于finetune而言,需要的是优先调整靠近输出层的参数,快速适应新任务;保持靠近输入层的参数稳定,避免破坏预训练的底层特征,这么看来post-norm似乎相当适合进行微调
Pre-norm

- pre-norm在进行非线性操作
F前对输入进行LN,即“将要被使用时才进行归一化” - 在进行函数计算前进行LN,能够使得模型更有效地控制输入特征的尺度,且保留原始输入的直接传递通道,降低深层网络的优化难度
Post-norm v.s. Pre-norm
- 在苏神的文章中,讨论了这一问题:“Post Norm的结构迁移性能更加好,也就是说在Pretraining中,Pre Norm和Post Norm都能做到大致相同的结果,但是Post Norm的Finetune效果明显更好”
- 为什么呢?知乎 @唐翔昊给出了分析:,一个L层的Pre Norm模型,其实际等效层数不如L层的Post Norm模型。对于Pre-norm,我们可以推导得到:
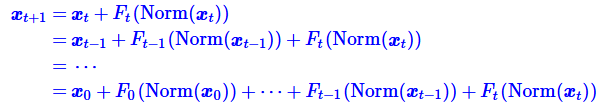
- 输入经过LN后量级大致相同,且Attetion、MLP这两个函数操作通常不会大幅改变输入数值的整体量级(幅值、方差),输出和输入的量级大致相同。经过上述两点分析,也就是说第t+1层跟第t层的差别当t较大时,两者的相对差别是很小的。因此可得到如下结论:

- 上述公式可知,经过近似后,输入xt连续经过t和t+1层,等价于xt经过一个更宽一些的t层。所以在Pre Norm中多层叠加的结果更多是增加宽度而不是深度,层数越多,这个层数就越“虚假”,模型退化为浅且宽的模型。而对于模型而言,深度的增加等价于函数复合次数增加,深度的增加能以指数级提升函数表示能力,而宽度的增加只能线性提升容量,所以模型的能力也随之变弱。而在上述的分析中,post-norm每Norm一次就削弱一次恒等分支x的权重,所以它反而是更突出残差分支F(x)的,因此Post Norm中的层数更加真实,一旦训练好之后效果更优


 浙公网安备 33010602011771号
浙公网安备 33010602011771号