万门大学-人工智能、大数据与复杂系统-04.高等数学——元素和极限

1、定义实数

 

戴德金原理(Dedekind principle)亦称戴德金分割：

定义1 若将实数集R分成两个子集S和T，它们满足：

(1)；

(2)；

(3)，

总有x<y(称S为左集，T为右集)则称为实数集R的一个“戴德金分划”，记作(S，T)

无理数为无理戴德金分割的点；

 

2、元素的个数

自然数的个数=整数个数，即使自然数是整数的真子集；

通过比势：一一对应的则为等势；

 

整数个数与有理数个数相同

 

自然数个数少于实数个数

证明：反证法

阿涅夫集合

习惯上习惯把阿列夫作为无穷基数的代名词， 可以看成一个定义域为序数列 ord，陪域为无穷基数类的双射类函数：

满足下列条件：

1、是自然数集的基数；

2、对任何 

3、若β 是极限基数，则

其中，α⁺ 是α 的后继序数， 是 的后记基数。

 

无穷大的比较：

 

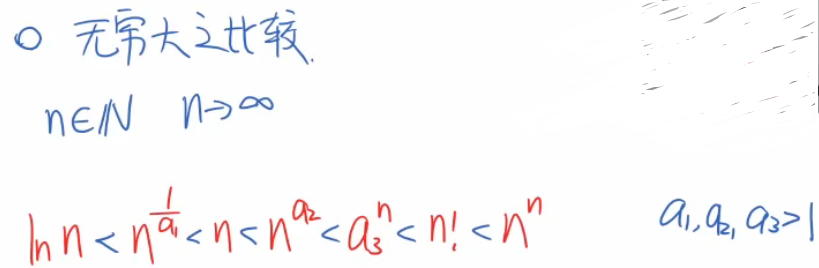
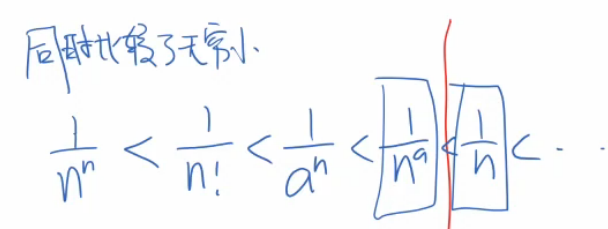
无穷小比较：收敛和不收敛的分界线

 

 

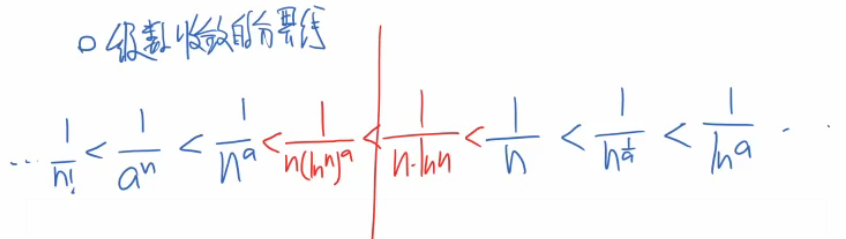
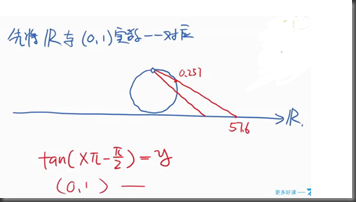
3、极限定义

1、极限的定义采用：要想任意近，只要足够近的思维定义。

 

 

2、极限的四则运算&极限的复合

 

 

 3、连续性