一些关于1+1的有趣问题

0x00 如何用高等数学证明1+1=2

\(\ \ \ \ 1+1\)
\(=( \sin \dfrac{\pi}{2}-\sin 0)+(\cos 0- \cos \dfrac{\pi}{2})\)

\(=\sin x \Bigg|^{\frac{\pi}{2}}_0+\cos x \Bigg|^{0}_\frac{\pi}{2}\)

\(=\displaystyle \int^{\frac{\pi}{2}}_0\cos x \text{d}x+\int^{0}_{\frac{\pi}{2}}(-\sin x)\text{d}x\)

\(=\displaystyle \int^{\frac{\pi}{2}}_0 (\cos x+\sin x)\text{d}x\)

\(=\displaystyle \int^\frac{\pi}{2}_0 \sqrt 2\sin \left( x+ \dfrac{\pi}{4}\right)\text{d}x\)

\(=-\sqrt 2\cos \left( x+\dfrac{\pi}{4} \right)\Bigg|^{\frac{\pi}{2}}_0\)

\(=-\sqrt 2\left[\cos \left( \dfrac{\pi}{2}+\dfrac{\pi}{4}\right)-\cos \dfrac{\pi}{4}\right]\)

\(=-\sqrt 2\left( -\sin \dfrac{\pi}{4}-\cos \dfrac{\pi}{4}\right)\)

\(=\sqrt 2\left (\sin \dfrac{\pi}{4} + \cos \dfrac{\pi}{4} \right)\)

\(=\sqrt 2\times \sqrt 2\ sin \left(\dfrac{\pi}{4}+\dfrac{\pi}{4}\right)\)

\(=2\sin \left[\dfrac{\pi}{4}(1+1)\right]\)

由上可知

\[1+1=2\sin \left[\dfrac{\pi}{4}(1+1)\right] \]

\(令 x=1+1\)

\[x=2\sin\dfrac{\pi}{4}x \]

图像法解方程

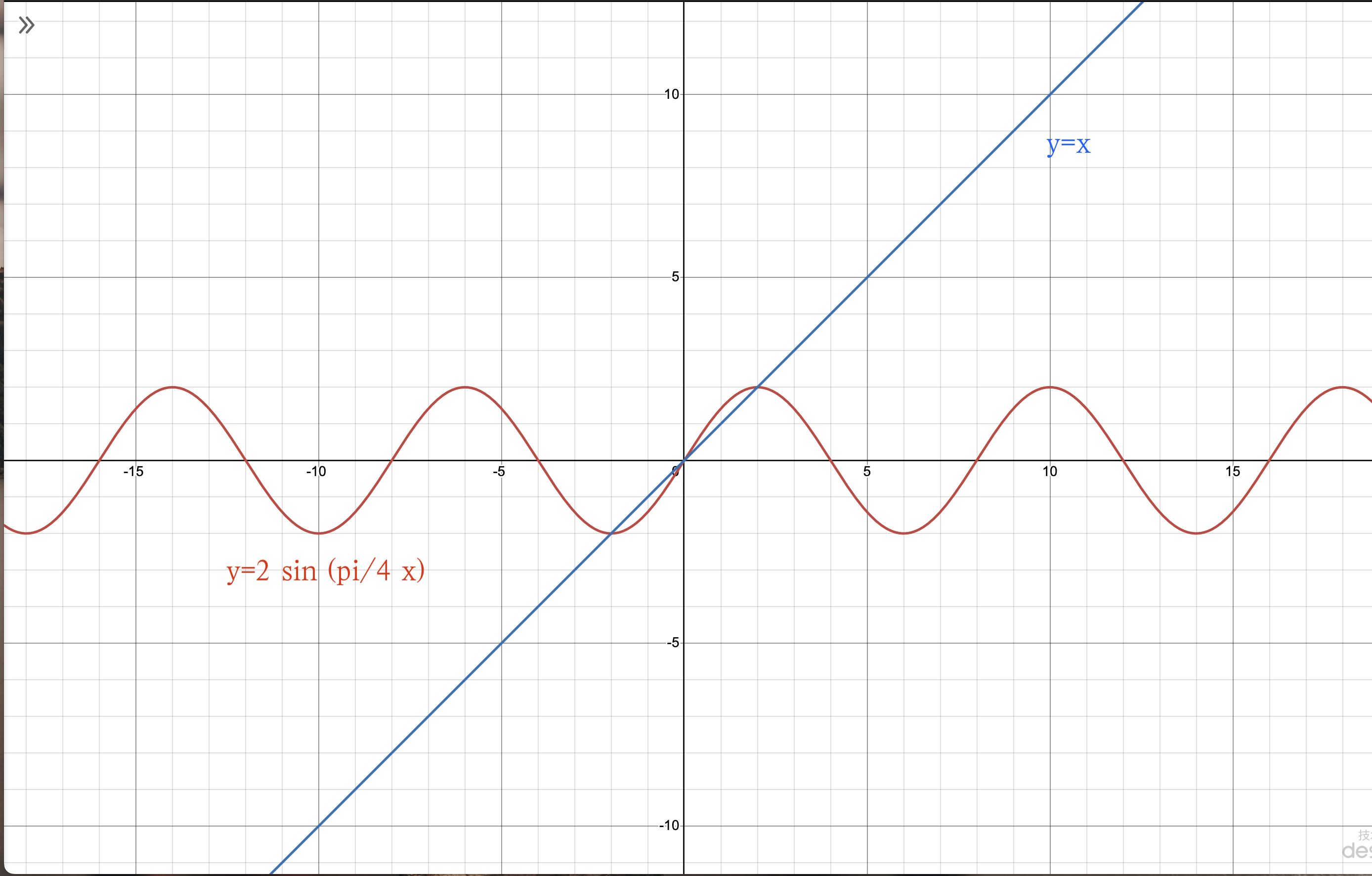
解得 \(x=-2,0,2\)

\(\therefore 1+1 =-2,0,2\)

\(\because 1+1\ge 2\sqrt{1\times 1}=2\)

\(\therefore 1+1=2\)

0x01 证明1+1=3的方法

\(\ \ \ \ 1+1\)
\(=4-0-2\)
\(=4-\dfrac{9}{2}+\dfrac{9}{2}-2\)

\(=\sqrt{\left(4-\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=\sqrt{4^2-2\times4\times\dfrac{9}{2}+\left(\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=\sqrt{4^2-4\times9+\left(\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=\sqrt{16-36+\left(\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=\sqrt{-20+\left(\dfrac{9}{2}\right)}+\dfrac{9}{2}-2\)

\(=\sqrt{25-45+\left(\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=\sqrt{5^2-2\times5\times\dfrac{9}{2}+\left(\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=\sqrt{\left(5-\dfrac{9}{2}\right)^2}+\dfrac{9}{2}-2\)

\(=5-\dfrac{9}{2}+\dfrac{9}{2}-2\)

\(=5-2\)

\(=3\)