决策树(基于增益率)之python实现
如图,为使用到的公式,信息熵表明样本的混乱程度,增益表示熵减少了,即样本开始分类,增益率是为了平衡增益准则对可取值较多的属性的偏好,同时增益率带来了对可取值偏小的属性的偏好,实际中,先用增益进行筛选,选取大于增益平均值的,然后再选取其中增益率最高的。
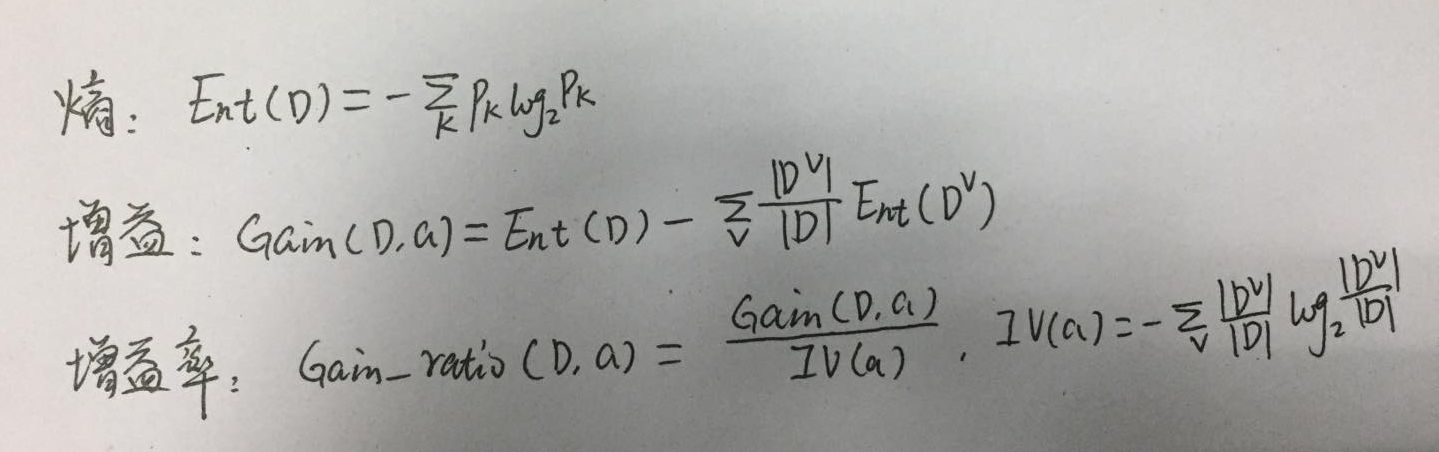
以下代码纯粹手写,未参考其他人代码,如果问题,请不吝赐教。
1,计算信息熵的函数
import numpy as np
# 计算信息熵 # data:like np.array # data.shape=(num_data,data_features+1) 即属性与label放一起了 def entropy(data,num_class): class_set=list(set(data[:,-1])) result=0 length=len(data) # 这里修改一下,不使用num_class for i in range(len(class_set)): l=len(data[data[:,-1]==class_set[i]]) p=l/length result-=p*np.log2(p) return result
2,计算增益及属性a的固有值(IV)
# 计算不同属性的信息增益 # detail_features:特征构成的list,每个特征的可取值构成list元素,即也是list def calculate_gain(data,detail_features,num_class):
'''返回各属性对应的信息增益及平均值''' result=[] ent_data=entropy(data,num_class) for i in range(len(detail_features)): res=ent_data for j in range(len(detail_features[i])): part_data=data[data[:,i]==detail_features[i][j]] length=len(part_data) res-=length*entropy(part_data,num_class)/len(data) result.append(res) return result,np.array(result).mean() # 计算某个属性的固有值 def IVa(data,attr_index): attr_values=list(set(data[:,attr_index])) v=len(attr_values) res=0 for i in range(v): part_data=data[data[:,attr_index]==attr_values[i]] p=len(part_data)/len(data) res-=p*np.log2(p) return res
3,构建节点类,以便构建树
class Node: def __init__(self,key,childs): self.childs=[] self.key=key def add_node(self,node): self.childs.append(node)
4,构建树
# 判断数据是否在所有属性的取值都一样,以致无法划分 def same_data(data,attrs): for i in range(len(attrs)): if len(set(data[:,i]))>1: return False return True # attrs:属性的具体形式 def create_tree(data,attrs,num_class,root): # 注意这里3个退出条件 # 1,如果数据为空,不能划分,此时这个叶节点不知标记为哪个分类了 if len(data)==0: return # 2,如果属性集为空,或所有样本在所有属性的取值相同,无法划分,返回样本最多的类别 if len(attrs)==0 or same_data(data,attrs): class_set=list(set(data[:,-1])) max_len=0 index=0 for i in range(len(class_set)): if len(data[data[:,-1]==class_set[i]])>max_len: max_len=len(data[data[:,-1]==class_set[i]]) index=i root.key=root.key+class_set[index] return # 3,如果当前节点包含同一类的样本,无需划分 if len(set(data[:,-1]))==1: root.key=root.key+data[0,-1] return ent=entropy(data,num_class) gain_result,mean=calculate_gain(data,attrs,num_class) max=0 max_index=-1 # 求增益率最大 for i in range(len(gain_result)): if gain_result[i]>=mean: iva=IVa(data,i) if gain_result[i]/iva>max: max=gain_result[i]/iva max_index=i for j in range(len(attrs[max_index])): part_data=data[data[:,max_index]==attrs[max_index][j]] # 删除该列特征 part_data=np.delete(part_data,max_index,axis=1) # 添加节点 root.add_node(Node(key=attrs[max_index][j],childs=[])) # 删除某一类已判断属性 new_attrs=attrs[0:max_index] new_attrs.extend(attrs[max_index+1:]) create_tree(part_data,new_attrs,num_class,root.childs[j])
5,使用西瓜数据集2.0测试,数据这里就手写了,比较少
def createDataSet(): """ 创建测试的数据集 :return: """ dataSet = [ # 1 ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'], # 2 ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'], # 3 ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'], # 4 ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'], # 5 ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'], # 6 ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'], # 7 ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'], # 8 ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'], # ---------------------------------------------------- # 9 ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'], # 10 ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'], # 11 ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'], # 12 ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'], # 13 ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'], # 14 ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'], # 15 ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'], # 16 ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'], # 17 ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'] ] # 特征值列表 labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感'] # 特征对应的所有可能的情况 labels_full = [] for i in range(len(labels)): items=[item[i] for item in dataSet] uniqueLabel = set(items) labels_full.append(list(uniqueLabel)) return np.array(dataSet), labels, labels_full
6,开始构建树
dataset,labels,labels_full=createDataSet() root=Node('',[]) create_tree(dataset, labels_full, 2, root)
7,打印树结构
def print_root(n,root):print(n,root.key) for node in root.childs: print_root(n+1,node) print_root(0,root)
打印结果为:数字表示层次
0
1 模糊坏瓜
1 稍糊
2 硬滑坏瓜
2 软粘好瓜
1 清晰
2 硬滑好瓜
2 软粘
3 青绿
4 稍蜷好瓜
4 蜷缩
4 硬挺坏瓜
3 乌黑坏瓜
3 浅白
8,绘制树形结构,这里我就手动绘制了。图中有2个叶节点为空白,即模型不知道该推测其为好瓜还是坏瓜。这里我暂时没有好的思路解决,只能随机处理?

9,总结
首先,暂时没有添加predict函数。其次,这是个简陋版的实现,有很多待优化的地方,如连续值处理、缺失值处理、剪枝防止过拟合,树的创建使用的是递归(样本大导致栈溢出,改成队列实现较好),也有基于基尼指数的实现,还有多变量决策树(可实现复杂的分类边界)。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号