密码学|实验三 RSA算法
实验目的:
掌握模幂和模逆的实现算法;通过 RSA 加密和签名算法,了解基于大数分解问题的公钥密码。
实验内容:
- 实现模幂和模逆算法
- 实现 RSA 加密算法
- 实现 RSA 签名算法
实验步骤:
- 采用从右到左算法实现模幂运算。
- 采用扩展欧几里得算法实现模逆运算。
- 生成公私钥对。
- 对消息 m,利用模幂程序得到 RSA 密文 c,再验证 c 解密后验证是否为 m
- 对消息 m,得到 RSA 签名 s,再验证 s 的正确性。
- 改变密钥对和消息,重复上述过程,将实验结果填入表
实验过程
使用Miller-Rabin素性测试确保生成大素数
生成素数
import random
def Miller_Rabin_is_prime(n, k=5):
"""Miller-Rabin素性测试"""
if n <= 1:
return False
elif n <= 3:
return True
elif n % 2 == 0:
return False
d = n - 1
s = 0
while d % 2 == 0:
d //= 2
s += 1
for _ in range(k):
a = random.randint(2, n - 2)
x = pow(a, d, n)
if x == 1 or x == n - 1:
continue
for __ in range(s - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
def generate_prime(bits):
"""生成指定位数的素数"""
while True:
p = random.getrandbits(bits)
p |= (1 << bits - 1) | 1
if Miller_Rabin_is_prime(p):
return p
使用拓展欧几里得算法实现模逆运算
拓展欧几里得算法
def extended_gcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = extended_gcd(b % a, a)
return (g, x - (b // a) * y, y)
def mod_inverse(a, m):
g, x, y = extended_gcd(a, m)
if g != 1:
raise ValueError("模逆不存在")
else:
return x % m
实现快速模幂运算
快速模幂运算
def fast_modular_exponentiation(m, d, n):
"""
快速模幂运算
"""
# 将指数d转换为二进制字符串
binary_d = bin(d)[2:]
k = len(binary_d)
x = 1
y = m % n
for i in range(k):
a_i = int(binary_d[i])
if a_i == 1:
x = (x * y) % n
y = (y * y) % n
else:
y = (y * y) % n
return x
密钥生成
def generate_keypair(bits=1024):
p = generate_prime(bits // 2)
q = generate_prime(bits // 2)
while p == q:
q = generate_prime(bits // 2)
n = p * q
phi = (p - 1) * (q - 1)
print(f"φ(n) = {phi}")
while True:
try:
e = int(input("输入e值(建议为65537): "))
if math.gcd(e, phi) != 1:
print("Error,e必须与φ(n)互质")
elif e < 2 or e >= phi:
print("Error,e必须在2和φ(n)-1之间")
else:
break
except ValueError:
print("错误:请输入一个有效的整数。")
d = mod_inverse(e, phi)
public_key = (e, n)
private_key = (d, n)
return public_key, private_key
完成具体RSA功能
RSA功能实现
def rsa_encrypt(public_key, plaintext):
e, n = public_key
if plaintext >= n:
raise ValueError("明文必须小于n")
return fast_modular_exponentiation(plaintext, e, n)
def rsa_decrypt(private_key, ciphertext):
d, n = private_key
return fast_modular_exponentiation(ciphertext, d, n)
def rsa_sign(private_key, message):
return rsa_encrypt(private_key, message)
def rsa_verify(public_key, signature, message):
decrypted = rsa_decrypt(public_key, signature)
return decrypted == message
实验结果
| n | e | d | m | s 签名 | c | decrypt |
|---|---|---|---|---|---|---|
| 6607361578056698093 | 65537 | 743236179797604353 | 231213 | 4782700734081529582 | 2836956322425680191 | 231213 |
| 5872539187104964069 | 65537 | 896154300040522913 | 12345 | 2830542832659584526 | 2830542832659584526 | 12345 |
| 52259664338030243 | 65537 | 12057591550917377 | 231213 | 14506512871382930 | 14506512871382930 | 231213 |
| 26487264889 | 65537 | 1181337469 | 10101100 | 10505105852 | 10505105852 | 10101100 |
| 50665843 | 15647509 | 3856949 | 250616 | 38387790 | 38387790 | 250616 |
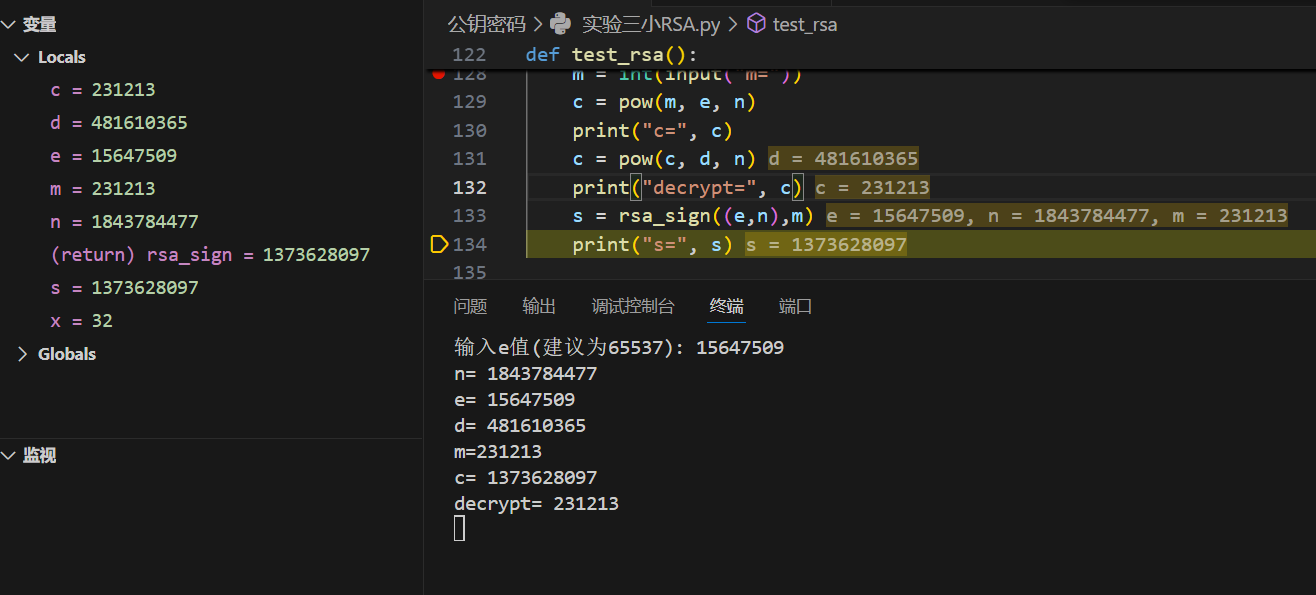
实验代码
import math
import random
def Miller_Rabin_is_prime(n, k=5):
"""Miller-Rabin素性测试"""
if n <= 1:
return False
elif n <= 3:
return True
elif n % 2 == 0:
return False
d = n - 1
s = 0
while d % 2 == 0:
d //= 2
s += 1
for _ in range(k):
a = random.randint(2, n - 2)
x = pow(a, d, n)
if x == 1 or x == n - 1:
continue
for __ in range(s - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
def generate_prime(bits):
"""生成指定位数的素数"""
while True:
p = random.getrandbits(bits)
p |= (1 << bits - 1) | 1
if Miller_Rabin_is_prime(p):
return p
def extended_gcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = extended_gcd(b % a, a)
return (g, x - (b // a) * y, y)
def mod_inverse(a, m):
g, x, y = extended_gcd(a, m)
if g != 1:
raise ValueError("模逆不存在")
else:
return x % m
def fast_modular_exponentiation(m, d, n):
"""
快速模幂运算
"""
# 将指数d转换为二进制字符串
binary_d = bin(d)[2:]
k = len(binary_d)
x = 1
y = m % n
for i in range(k):
a_i = int(binary_d[i])
if a_i == 1:
x = (x * y) % n
y = (y * y) % n
else:
y = (y * y) % n
return x
def generate_keypair(bits=1024):
p = generate_prime(bits // 2)
q = generate_prime(bits // 2)
while p == q:
q = generate_prime(bits // 2)
n = p * q
phi = (p - 1) * (q - 1)
print(f"φ(n) = {phi}")
while True:
try:
e = int(input("输入e值(建议为65537): "))
if math.gcd(e, phi) != 1:
print("Error,e必须与φ(n)互质")
elif e < 2 or e >= phi:
print("Error,e必须在2和φ(n)-1之间")
else:
break
except ValueError:
print("错误:请输入一个有效的整数。")
d = mod_inverse(e, phi)
public_key = (e, n)
private_key = (d, n)
return public_key, private_key
def rsa_encrypt(public_key, plaintext):
e, n = public_key
if plaintext >= n:
raise ValueError("明文必须小于n")
return fast_modular_exponentiation(plaintext, e, n)
def rsa_decrypt(private_key, ciphertext):
d, n = private_key
return fast_modular_exponentiation(ciphertext, d, n)
def rsa_sign(private_key, message):
return rsa_encrypt(private_key, message)
def rsa_verify(public_key, signature, message):
decrypted = rsa_decrypt(public_key, signature)
return decrypted == message
def main():
print("\n生成RSA密钥对")
public_key, private_key = generate_keypair()
print(f"\n公钥 (e, n): {public_key}")
print(f"私钥 (d, n): {private_key}")
while True:
print("\n请选择操作:")
print("1. 加密")
print("2. 解密")
print("3. 签名")
print("4. 验证签名")
print("5. 退出")
choice = input("请输入选项(1-5): ")
if choice == '1':
try:
plaintext = int(input("请输入要加密的明文: "))
ciphertext = rsa_encrypt(public_key, plaintext)
print(f"加密结果: {ciphertext}")
except ValueError as e:
print(f"错误: {e}")
elif choice == '2':
try:
ciphertext = int(input("请输入要解密的密文: "))
plaintext = rsa_decrypt(private_key, ciphertext)
print(f"解密结果: {plaintext}")
except ValueError as e:
print(f"错误: {e}")
elif choice == '3':
try:
message = int(input("请输入要签名的消息: "))
signature = rsa_sign(private_key, message)
print(f"签名结果: {signature}")
except ValueError as e:
print(f"错误: {e}")
elif choice == '4':
try:
signature = int(input("请输入要验证的签名: "))
message = int(input("请输入原始消息: "))
if rsa_verify(public_key, signature, message):
print("验证成功: 签名有效")
else:
print("验证失败: 签名无效")
except ValueError as e:
print(f"错误: {e}")
elif choice == '5':
print("退出系统。")
break
else:
print("无效选项,请重新输入。")
def test_rsa():
x = int(input("请输入素数位数:"))
(e,n),(d,n) = generate_keypair(x)
print("n=", n)
print("e=", e)
print("d=", d)
m = int(input("m="))
c = fast_modular_exponentiation(m, e, n)
print("c=", c)
c = fast_modular_exponentiation(c, d, n)
print("decrypt=", c)
s = rsa_sign((e,n),m)
print("s=", s)
if __name__ == "__main__":
test_rsa()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号