实验四 阿巴阿巴

ex1

1.函数声明可以放main函数前也可以是后，由    返回值类型（不需要用void）   函数名 （形参）构成

形参可以是变量，字符，数列

根不能设计成函数返回值的方式给主调函数

2.x1，x2

3.把函数声明去掉，将其余加入double a,b,c;后

// 一元二次方程求解 （函数实现方式） 
// 重复执行， 直到按Ctrl+Z结束 

#include <math.h>
#include <stdio.h>

// 函数声明
void solve(double a, double b, double c);

// 主函数 
int main() {
    double a, b, c;
    
    printf("Enter a, b, c: ");
    while(scanf("%lf%lf%lf", &a, &b, &c) != EOF) {
        solve(a, b, c);  // 函数调用 
        printf("Enter a, b, c: ");
    }
    
    return 0;
}

// 函数定义
// 功能：求解一元二次方程，打印输出结果
// 形式参数：a,b,c为一元二次方程系数 
void solve(double a, double b, double c) {
    double x1, x2;
    double delta, real, imag;
    
    if(a == 0) 
        printf("not quadratic equation.\n");
    else {
        delta = b*b - 4*a*c;
        
        if(delta >= 0) {
            x1 = (-b + sqrt(delta)) / (2*a);
            x2 = (-b - sqrt(delta)) / (2*a);
            printf("x1 = %f, x2 = %f\n", x1, x2);
        }
        else {
            real = -b/(2*a);
            imag = sqrt(-delta) / (2*a);
            printf("x1 = %f + %fi, x2 = %f - %fi\n", real, imag, real, imag);
        }
    }    
}

 

ex2

// 利用局部static变量计算阶乘
 
#include <stdio.h>
long long fac(int n);  // 函数声明 

int main() {
    int i,n;
    
    printf("Enter n: ");
    scanf("%d", &n);
    
    for(i=1; i<=n; ++i) 
        printf("%d! = %lld\n", i, fac(i)); 
    
    return 0;
}

// 函数定义 
long long fac(int n) {
    static long long p = 1;
    printf("p=%d\n",p);
    p = p*n;
    
    return p;
}

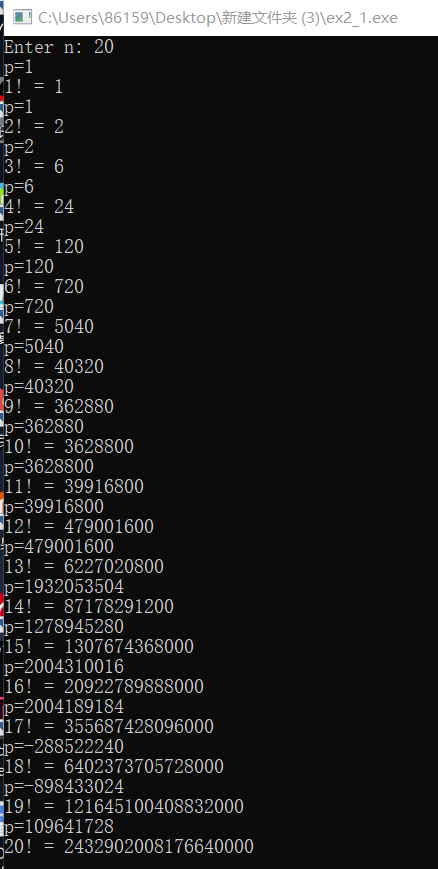
一致

 

ex3

//寻找两个整数之间的所有素数(包括这两个整数),把结果保存在数组bb中,函数返回素数的个数。
// 例如，输入6和21,则输出为:7 11 13 17 19。

#include <stdio.h>

#define N 1000
int fun(int n,int m,int bb[N]) {
    int i,j,k=0,flag;
    
    for(j=n;j<=m;j++) {
          flag=1;   
        for(i=2;i<j;i++)
            if(j%i==0) {  
               flag=0;
               break;
        }
        if(flag==1) 
           bb[k++]=j;
    }
    return k;
}

int main(){
    int n=0,m=0,i,k,bb[N];
    
    scanf("%d",&n);
    scanf("%d",&m);
    
    for(i=0;i<m-n;i++)
        bb[i]=0;
        
    k=fun(n,m,bb); 
    
    for(i=0;i<k;i++)
        printf("%4d",bb[i]);
        
    return 0;
}

 

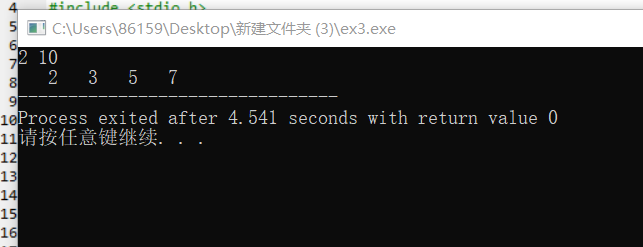
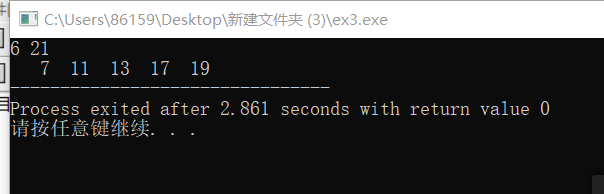
ex4

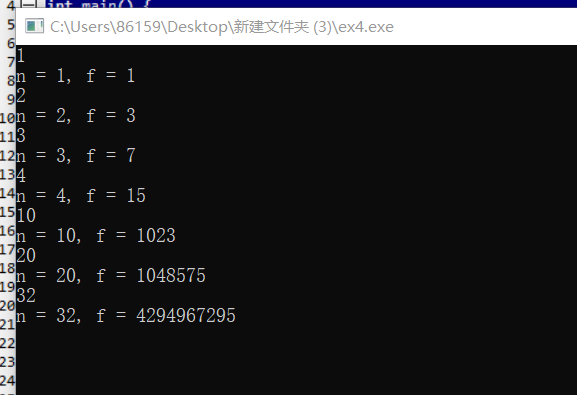
这部分的f（n-1）我还是不太会用，最后想到了用for循环去计算2的多次方

#include <stdio.h>
long long fun(int n);   // 函数声明 

int main() {
    int n;
    long long f;
    
    while(scanf("%d", &n) != EOF) {
        f = fun(n);  // 函数调用 
        printf("n = %d, f = %lld\n", n, f);
    }
    
    return 0;
}

// 函数定义
long long fun(int n){
    int i;
    long long sum=1;
   for(i=1;i<=n;i++)
   {
       sum*=2;
   }
   sum=sum-1;
   return sum;
   
}
 

 

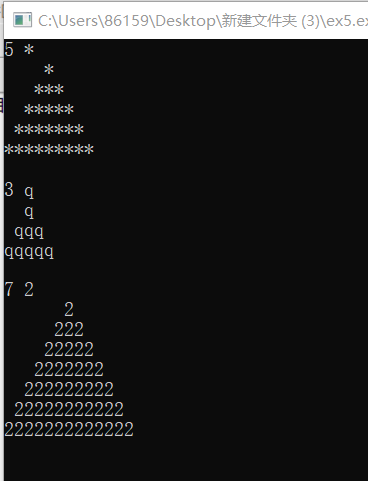
ex5

刚开始打把空格的“ “给忘了，试了好多回才发现，害。。

 

总结

到了实验四我才把函数给大致搞懂了，用起来是要便捷很多，然后还是太马虎了，每个实验都要试好久改好多次，就还是不太熟练，不如if语句的{}老是会忘记打。