具有神经网络思维的Logistic回归
使用Numpy的基础Python、logistic回归
import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import math
Part 1:Python Basics with Numpy
1 - Building basic functions with numpy
1.1 - sigmoid function, np.exp()
Exercise: Build a function that returns the sigmoid of a real number x. Use math.exp(x) for the exponential function.
def sig_function(x):
s = 1.0 / (1 + 1/math.exp(x))
return s
sig_function(3)
0.9525741268224334
Exercise: Implement the sigmoid function using numpy.
def sig_function_by_np(x):
s = 1.0 / (1 + 1/np.exp(x))
return s
x = np.array([1, 2, 3])
sig_function_by_np(x)
array([0.73105858, 0.88079708, 0.95257413])
1.2 - Sigmoid gradient
Exercise: Implement the function sigmoid_grad() to compute the gradient of the sigmoid function with respect to its input x.
# 对sigmoid函数求导
def sigmoid_grad(x):
s = 1.0 / (1 + 1/np.exp(x))
ds = s * (1 - s)
return ds
sigmoid_grad(x)
array([0.19661193, 0.10499359, 0.04517666])
1.3 - Reshaping arrays
Exercise: Implement image2vector() that takes an input of shape (length, height, 3) and returns a vector of shape (lengthheight3, 1).
def image2vector(image):
v = image.reshape((image.shape[0] * image.shape[1] * image.shape[2], 1))
return v
image = np.array([[[ 0.67826139, 0.29380381],
[ 0.90714982, 0.52835647],
[ 0.4215251 , 0.45017551]],
[[ 0.92814219, 0.96677647],
[ 0.85304703, 0.52351845],
[ 0.19981397, 0.27417313]],
[[ 0.60659855, 0.00533165],
[ 0.10820313, 0.49978937],
[ 0.34144279, 0.94630077]]])
print ("image2vector(image) = " + str(image2vector(image)))
image2vector(image) = [[0.67826139]
[0.29380381]
[0.90714982]
[0.52835647]
[0.4215251 ]
[0.45017551]
[0.92814219]
[0.96677647]
[0.85304703]
[0.52351845]
[0.19981397]
[0.27417313]
[0.60659855]
[0.00533165]
[0.10820313]
[0.49978937]
[0.34144279]
[0.94630077]]
1.4 - Normalizing rows
Exercise: Implement normalizeRows() to normalize the rows of a matrix.
np.linalg.norm(x, ord=None, axis=None, keepdims=False)
- axis=1表示按行向量处理;axis=0表示按列向量处理
- keepding:是否保持矩阵的二维特性
x = np.array([
[0, 3, 4],
[1, 6, 4]])
np.linalg.norm(x, ord=1, axis=1, keepdims=True)
array([[ 7.],
[11.]])
def normalizeRows(x):
x_norm = np.linalg.norm(x, axis=1, keepdims=True) # 计算每一行的长度
return x / x_norm # 利用numpy的广播,用矩阵与列向量相除
normalizeRows(x)
array([[0. , 0.6 , 0.8 ],
[0.13736056, 0.82416338, 0.54944226]])
1.5 - Broadcasting and the softmax function
Exercise: Implement a softmax function using numpy.
def softmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp, axis=1, keepdims=True)
s = x_exp / x_sum
return s
x = np.array([
[9, 2, 5, 0, 0],
[7, 5, 0, 0 ,0]])
print("softmax(x) = " + str(softmax(x)))
softmax(x) = [[9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04
1.21052389e-04]
[8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04
8.01252314e-04]]
2 - Vectorization
2.1 Implement the L1 and L2 loss functions
Exercise: Implement the numpy vectorized version of the L1 loss.
def L1(yhat, y):
loss = np.sum(np.abs(y-yhat))
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))
L1 = 1.1
Exercise: Implement the numpy vectorized version of the L2 loss.
def L2(yhat, y):
loss = np.sum(np.power((y-yhat),2))
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))
L2 = 0.43
Part 2: Logistic Regression with a Neural Network Mindset
Code
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
2 - Overview of the Problem set
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
index = 25
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) +
", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")
y = [1], it's a 'cat' picture.

print(train_set_y.shape)
print(train_set_y[:,25]) # 相当与一维
print(np.squeeze(train_set_y[:,25]))
(1, 209)
[1]
1
classes[1].decode("utf-8")
'cat'
Exercise: Find the values for:
- m_train (number of training examples)
- m_test (number of test examples)
- num_px ( height and width of a training image)
Remember that train_set_x_orig is a numpy-array of shape (m_train, num_px, num_px, 3).
m_train = train_set_y.shape[1]
m_test = test_set_y.shape[1]
num_px = train_set_x_orig.shape[1]
print(m_train)
print(m_test)
print(num_px)
209
50
64
Exercise: Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape.
列是训练集的样本数量:
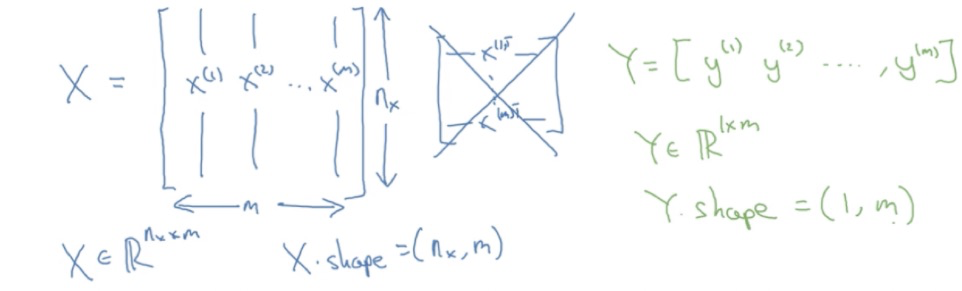
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[1]*train_set_x_orig.shape[2]
*train_set_x_orig.shape[3], train_set_x_orig.shape[0])
test_set_x_flatten = test_set_x_orig.reshape(m_test, -1).T # -1让程序帮忙算,最后程序算出来时12288列,最后用一个T表示转置
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)
彩色图像的像素值实际上是从0到255范围内的三个数字的向量。机器学习中一个常见的预处理步骤是对数据集进行居中和标准化,这意味着可以减去每个示例中整个numpy数组的平均值,然后将每个示例除以整个numpy数组的标准偏差。但对于图片数据集,可以将数据集的每一行除以255(像素通道的最大值),因为在RGB中不存在比255大的数据,所以除以255让标准化的数据位于[0,1]之间,现在标准化我们的数据集:
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
3 - General Architecture of the learning algorithm
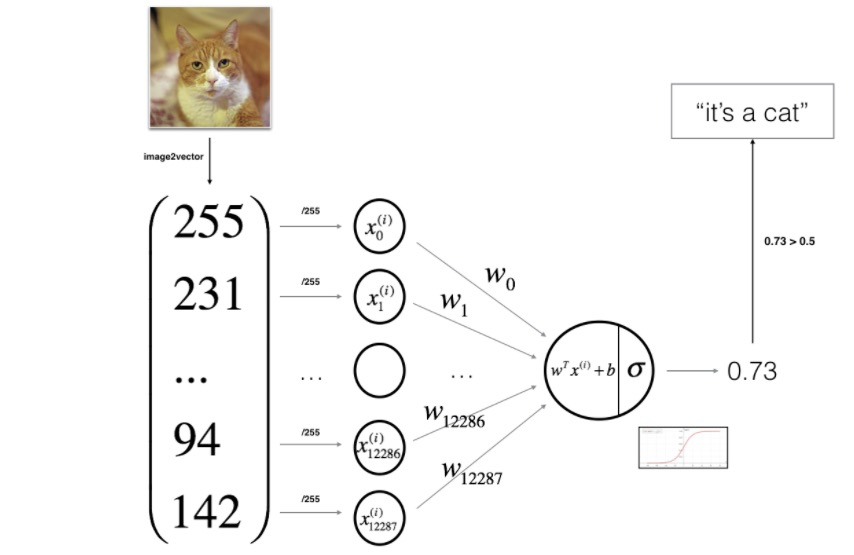
4 - Building the parts of our algorithm
Exercise: Using your code from “Python Basics”, implement sigmoid().
def sigmoid(z):
s = 1 / (1 + np.exp(-z))
return s
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
sigmoid([0, 2]) = [0.5 0.88079708]
Exercise: Implement parameter initialization in the cell below.
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
w = np.zeros((dim, 1))
b = 0
# 使用断言来确保我要的数据是正确的
assert(w.shape == (dim, 1)) # w的维度是(dim,1)
assert(isinstance(b, float) or isinstance(b, int)) # b的类型是float或者是int
return w, b
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))
w = [[0.]
[0.]]
b = 0
Exercise: Implement a function propagate() that computes the cost function and its gradient.

梯度就是导数,这里全都是算出来的:
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
"""
m = X.shape[1]
A = sigmoid(np.dot(w.T, X) + b)
cost = -(1/m) * np.sum(Y * np.log(A) + (1 - Y)*np.log(1 - A))
dw = (1.0/m)*np.dot(X,(A-Y).T)
db = (1.0/m)*np.sum(A-Y)
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())a
grads = {"dw": dw,
"db": db}
return grads, cost
w, b, X, Y = np.array([[1.],[2.]]), 2., np.array([[1.,2.,-1.],[3.,4.,-3.2]]), np.array([[1,0,1]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
dw = [[0.99845601]
[2.39507239]]
db = 0.001455578136784208
cost = 5.801545319394553
Exercise: Write down the optimization function.
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads['dw']
db = grads['db']
w = w - dw*learning_rate
b = b - db*learning_rate
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples
if (print_cost) and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
params = {'w':w, 'b':b}
grads = {'dw':dw, 'db':db} # for循环不是一个函数体,所以for循环中的变量i的作用域其实和for循环同级
"""
def foo():
i=None
for i in range(1,5,2):
pass
print(i)
foo() # 结果为3,即循环结束i的最终值
"""
return params, grads, costs
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
w = [[0.19033591]
[0.12259159]]
b = 1.9253598300845747
dw = [[0.67752042]
[1.41625495]]
db = 0.21919450454067652
Exercise: The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the predict() function.
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1, m))
w = w.reshape(X.shape[0],1) # 确保维数正确?
A = sigmoid(np.dot(w.T, X) + b)
for i in range(A.shape[1]):
if A[0, i] > 0.5:
Y_prediction[0, i] = 1
else:
Y_prediction[0, i] = 0
assert(Y_prediction.shape == (1, m))
return Y_prediction
w = np.array([[0.1124579],[0.23106775]])
b = -0.3
X = np.array([[1.,-1.1,-3.2],[1.2,2.,0.1]])
print ("predictions = " + str(predict(w, b, X)))
predictions = [[1. 1. 0.]]
5 - Merge all functions into a model
Exercise: Implement the model function.
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
w, b = initialize_with_zeros(X_train.shape[0])
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
w = parameters['w']
b = parameters['b']
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
d = model(train_set_x, train_set_y, test_set_x, test_set_y,
num_iterations = 2000, learning_rate = 0.005, print_cost = True)
迭代的次数: 0 , 误差值: 0.693147
迭代的次数: 100 , 误差值: 0.709726
迭代的次数: 200 , 误差值: 0.657712
迭代的次数: 300 , 误差值: 0.614611
迭代的次数: 400 , 误差值: 0.578001
迭代的次数: 500 , 误差值: 0.546372
迭代的次数: 600 , 误差值: 0.518331
迭代的次数: 700 , 误差值: 0.492852
迭代的次数: 800 , 误差值: 0.469259
迭代的次数: 900 , 误差值: 0.447139
迭代的次数: 1000 , 误差值: 0.426262
迭代的次数: 1100 , 误差值: 0.406617
迭代的次数: 1200 , 误差值: 0.388723
迭代的次数: 1300 , 误差值: 0.374678
迭代的次数: 1400 , 误差值: 0.365826
迭代的次数: 1500 , 误差值: 0.358532
迭代的次数: 1600 , 误差值: 0.351612
迭代的次数: 1700 , 误差值: 0.345012
迭代的次数: 1800 , 误差值: 0.338704
迭代的次数: 1900 , 误差值: 0.332664
train accuracy: 91.38755980861244 %
test accuracy: 34.0 %
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
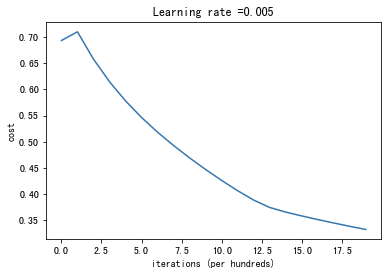
6 - Further analysis
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
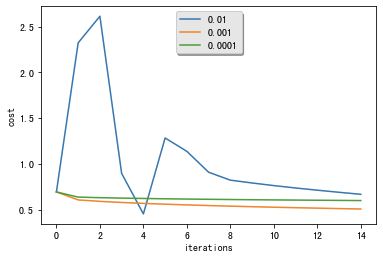
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
learning rate is: 0.01
train accuracy: 71.29186602870814 %
test accuracy: 74.0 %
-------------------------------------------------------
learning rate is: 0.001
train accuracy: 74.16267942583733 %
test accuracy: 34.0 %
-------------------------------------------------------
learning rate is: 0.0001
train accuracy: 66.02870813397129 %
test accuracy: 34.0 %
-------------------------------------------------------


 浙公网安备 33010602011771号
浙公网安备 33010602011771号