卷积
一.互相关运算(原矩阵乘以卷积核)
X为原矩阵,K为卷积核,Y 为结果。shape[0]表示行数,h行数,w列数
import torch
def corr2d(X,K):
h,w=K.shape #获得卷积核的行数h,列数w
Y=torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1)) #Y为结果,先构造为0矩阵
#遍历Y进行计算赋值
for i in range (Y.shape[0]):
for j in range (Y.shape[1]):
Y[i,j]=(X[i:i+h,j:j+w]*K).sum() #Y[i,j]表示第i行第j列那个元素
#X[i:i+h,j:j+w]只能这么写表示切片矩阵,切出来大小为h*w
return Y
X=torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
K=torch.tensor([[0.0,1.0],[2.0,3.0]])
print(corr2d(X,K))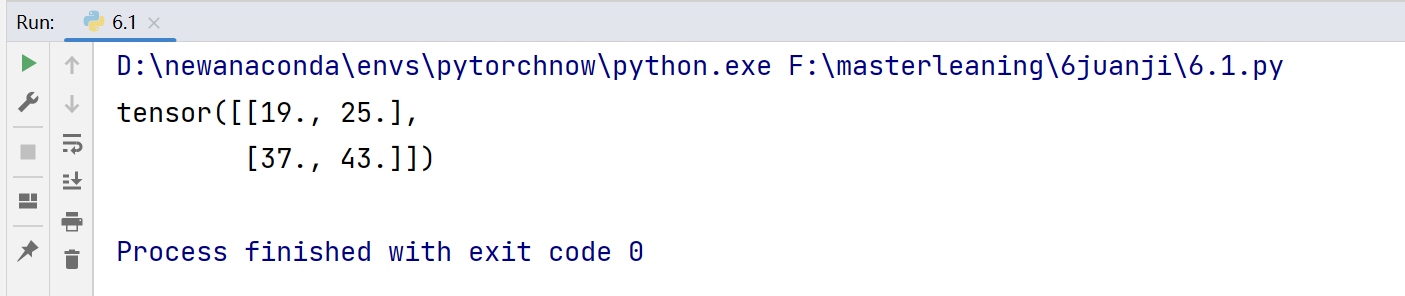
二.利用互相关运算实现边缘检测
import torch
def corr2d(X,K):
h,w=K.shape #获得卷积核的行数h,列数w
Y=torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1)) #Y为结果,先构造为0矩阵
#遍历Y进行计算赋值
for i in range (Y.shape[0]):
for j in range (Y.shape[1]):
Y[i,j]=(X[i:i+h,j:j+w]*K).sum() #Y[i,j]表示第i行第j列那个元素
#X[i:i+h,j:j+w]只能这么写表示切片矩阵,切出来大小为h*w
return Y
X=torch.ones((6,8)) #构造一个6行8列的全是1的矩阵
X[:,2:6]=0 #将2-5列元素都变为0
K=torch.tensor([[1.0,-1.0]]) #卷积核,这里是默认,接下来会学习如何学习这个核。注意要是二维
print(X)#0->1或1->0表示边缘
#调用上面的互相关运算corr2d
print(corr2d(X,K))#边缘所得乘积结果为非0原X

构造边缘,中间4列变为0

检测边缘,结果为非0就是边缘
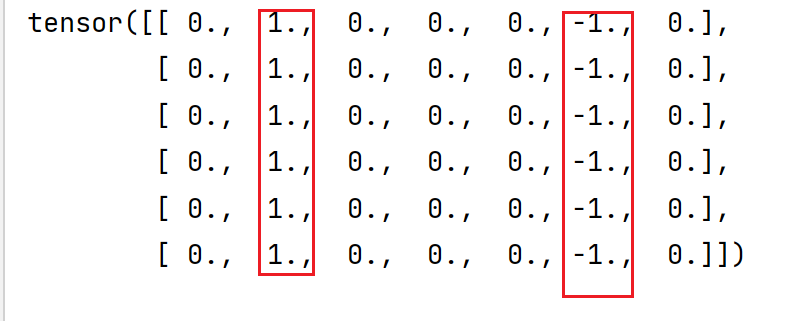
注意:[[1.0,-1.0]]这个卷积核只能检测垂直边缘,不能检测到水平边缘
import torch
def corr2d(X,K):
h,w=K.shape #获得卷积核的行数h,列数w
Y=torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1)) #Y为结果,先构造为0矩阵
#遍历Y进行计算赋值
for i in range (Y.shape[0]):
for j in range (Y.shape[1]):
Y[i,j]=(X[i:i+h,j:j+w]*K).sum() #Y[i,j]表示第i行第j列那个元素
#X[i:i+h,j:j+w]只能这么写表示切片矩阵,切出来大小为h*w
return Y
X=torch.ones((6,8))
print(X)
X[:,2:6]=0
K=torch.tensor([[1.0,-1.0]])
# print(X)
# print(corr2d(X,K))
a=X.t()
print(a)
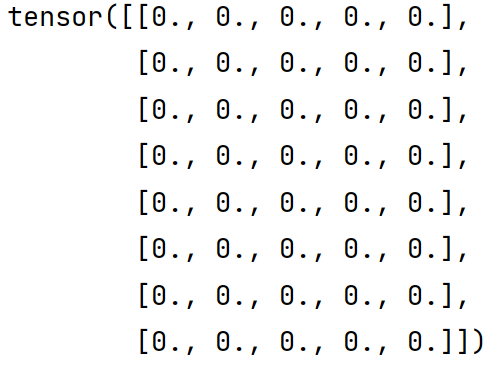
print(corr2d(a,K))
和[[1.0,-1.0]]做互相关运算结果->说明这个卷积核不可以检测水平边缘
三.卷积层
import torch
#在torch里面nn模块用于构建神经网络
from torch import nn
#其实这个互相关运算和卷积层Corr2d只是为了便于理解。实际使用直接调用nn.Conv2d实现卷积
def corr2d(X,K):#互相关运算
h,w=K.shape #获得卷积核的行数h,列数w
Y=torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1)) #Y为结果,先构造为0矩阵
#遍历Y进行计算赋值
for i in range (Y.shape[0]):
for j in range (Y.shape[1]):
Y[i,j]=(X[i:i+h,j:j+w]*K).sum() #Y[i,j]表示第i行第j列那个元素
#X[i:i+h,j:j+w]只能这么写表示切片矩阵,切出来大小为h*w
return Y
class Corr2d(nn.Module):#构建卷积层,继承自nn.Module
def __init__(self,kernel_size):
super().__init__()
self.weight=nn.Parameter(torch.rand(kernel_size))#weight定义一个随机值等会儿会更新
self.bias=nn.Parameter(torch.zeros(1))
def forward(self,x):#x是原矩阵,前向传播。self是核
return corr2d(x,self.weight)+self.bias
#已知输入X,输出Y->学习卷积核k
#X为1个6行8列的矩阵,中间4列为0
X=torch.ones((6,8))
X[:,2:6]=0
print(X)
X=X.reshape(1,1,6,8)#将二维改成4维 (批量大小, 通道数, 高度, 宽度)
Y=torch.zeros((6,7))#已知输出Y,边缘分界线是1和-1
Y[:,1:2]=1
Y[:,5:6]=-1
print(Y)
Y=Y.reshape(1,1,6,7)
#卷积层
conv2d=nn.Conv2d(1,1,(1,2),bias=False)#这是直接用pytorch下封装好的nn下的卷积Conv2d实现,上面手写 Corr2d只是为了理解卷积的含义
learning_rate=3e-2 #学习率
for i in range (10):
Y_hat=conv2d(X)#预测值
l=(Y_hat-Y)**2#损失平方差
conv2d.zero_grad()#清空梯度避免梯度积累
l.sum().backward()#损失平方差累积并反向传播
conv2d.weight.data[:]-=learning_rate*conv2d.weight.grad#权值的更新,权值=权值-学习率*梯度
print(f'第{i+1}次的循环,损失是{l.sum()}')#输出当前损失平方差
print(f'当前卷积核{conv2d.weight.data}')#输出学习出来的核k步幅和填充
1.填充
import torch
from torch import nn
def compare_conv2d(conv2d,X):#该方法为了检验卷积后输出的结果
X=X.reshape((1,1)+X.shape)#(1,1)批量,通道。这里用reshape因为输入是2维
Y=conv2d(X)#做卷积
return Y.reshape(Y.shape[2:])#返回是reshape后的Y,只取Y的后两维,因为前两维是批量和通道。Y.shape返回的是元组表示张量的大小。
conv2d=nn.Conv2d(1,1,(3,3),padding=1)#卷积定义,前两维表示输入输出通道
X=torch.rand((8,8))#生成随机X
print(compare_conv2d(conv2d,X).shape)两个维度填充的大小不同
import torch
from torch import nn
def com(conv2d,X):#conv2d表示卷积,X表示输入张量
X=X.reshape((1,1)+X.shape)
Y=conv2d(X)
return Y.reshape(Y.shape[2:])
X=torch.rand((8,8))
conv2d=nn.Conv2d(1,1,(5,3),padding=(2,1))
print(com(conv2d,X).shape)#返回卷积后输出的结果张量总结:
如果要保证输出张量和原张量一样大:
ph=核高-1
pw=核宽-1
如果卷积核高宽是奇数(常见)
填充高:ph/2
填充宽:pw/2
如果卷积核高宽是偶数,则/2后顶部和左边向上取整,右下向下取整
2.步幅

import torch
from torch import nn
def com(conv2d,X):#conv2d表示卷积,X表示输入张量
X=X.reshape((1,1)+X.shape)
Y=conv2d(X)
return Y.reshape(Y.shape[2:])
X=torch.rand((8,8))
conv2d=nn.Conv2d(1,1,(5,3),padding=(2,1),stride=(2,3))
print(com(conv2d,X).shape)#返回卷积后输出的结果张量输出:

原因:
padding=(2,1)
所以:
ph=2*2=4
pw=2*1=2
输出形状:
宽w=(8-5+4+2)/2向下取整=4
高h=(8-3+2+3)/3向下取整=3
6.4多输入输出通道
一.多输入通道
import torch
from d2l import torch as d2l #d2l是深度学习这本书对应下载的库。
def mul_input(X,K):
return sum(d2l.corr2d(x,k)for x,k in zip(X,K))#x是每个输入通道里的一个个小矩阵,k是对应卷积核,做互相关运算(已封装到d2l)
X=torch.tensor([[[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]],
[[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]]])#输入,两个输入通道,每个输入通道是二维(3*3)
K=torch.tensor([[[0.0,1.0],[2.0,3.0]],[[1.0,2.0],[3.0,4.0]]])#卷积核,因为有两个输入通道,所以有两个卷积核(每个核都是2*2)
print(mul_input(X,K))#输出卷积结果二.多输入输出通道
import torch
from d2l import torch as d2l
def mul_input(X,K):#多输入通道。
return sum(d2l.corr2d(x,k)for x,k in zip(X,K))
def mul_inout(X,K):#多输入多输出通道的互相关运算
return torch.stack([mul_input(X,k) for k in K],0)
X=torch.tensor([[[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]],
[[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]]])#输入,两个输入通道,每个输入通道是二维(3*3)
K=torch.tensor([[[0.0,1.0],[2.0,3.0]],[[1.0,2.0],[3.0,4.0]]])
K=torch.stack((K,K+1,K+2),0)#沿着维度 0(新创建的维度)将这三个张量堆叠起来
print(K.shape)
print(K)
print(mul_inout(X,K))stack后K的形状变为
![]()
表示3个输出通道,输入通道2个,每个卷积核2*2
K原来:

堆叠:

输出结果:

核心代码解释:;
def mul_inout(X,K):#多输入多输出通道的互相关运算
return torch.stack([mul_input(X,k) for k in K],0)
用中括号,因为要生成列表,stack是对一个个张量堆叠。
三.1*1卷积
1*1卷积等价于全连接
import torch
from d2l import torch as d2l
def mul_input(X,K):
return sum(d2l.corr2d(x,k)for x,k in zip(X,K))
def mul_inout(X,K):
return torch.stack([mul_input(X,k) for k in K],0)
def mul_inout1x1(X,K):#1*1矩阵乘法。X为输入矩阵,K为卷积核
c_i,h,w=X.shape#c_i输入通道数,h行数,w列数
c_o=K.shape[0]#卷积核的0维表示输出通道数
X=X.reshape((c_i,h*w))#将输入转为c_i*hw
K=K.reshape((c_o,c_i))#只保留前两维
Y=torch.matmul(K,X)
return Y.reshape((c_o,h,w))#输出结果
X=torch.normal(0,1,(3,3,3))#输入通道数为3
K=torch.normal(0,1,(2,3,1,1))#输出通道数2
Y1=mul_inout(X,K)#卷积
Y2=mul_inout1x1(X,K)#做
print(Y1)
print(Y2)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6#assert是当条件不满足时抛出异常,如果正常无抛出综上:conv2d=nn.Conv2d(1,1,(3,3),padding=1)#卷积定义,前两维表示输入、输出通道,()卷积核大小,padding填充,stride步幅
直接调用torch下的nn下的卷积Conv2d即可





 浙公网安备 33010602011771号
浙公网安备 33010602011771号