P2831 愤怒的小鸟
知识点: 状压DP , 简单数学
原题面
题目要求:
平面直角坐标系 的 第一象限中 , 有一些点,
构造尽可能少的, 解析式为 \(y=ax^2 + bx\) 形式的抛物线
使所有的点都被 至少经过一次
求最少的抛物线 数量.
分析题意:
观察数据范围: \(n\le18\), 可以跑些复杂度较高 的 算法.
对于每个点 , 只有两种情况 : 被经过过/未被经过
考虑状压 \(DP\).
通过观察抛物线的解析式 ,
发现只要确定两点, 就可以确定一条抛物线 .
那么根据上述性质 ,
设 \(map[i][j]\) , 表示一条经过 \(i,j\) 两点的抛物线 , 能经过的点的集合 .
-
获得 \(map\) 数组:
-
两层循环枚举 \(i,j\) , 将 \(i,j\) 两点加入点集,
并将 \(i,j\) 两点的坐标代入解析式中 -
模拟手算过程 , 解二元一次方程组 , 得到 经过 \(i,j\) 两点的抛物线解析式 .
手算过程: \(\text{获得各项系数}\Rightarrow \text{乘} 10^k , \text{将系数转化为整数}\Rightarrow\text{相减消元}\) -
枚举 所有点 , 将被此抛物线经过的点加入点集 .
-
-
对于 \(i,j\) 两点 , 有一种不合法,要舍弃的情况 (不可能在同一抛物线上) :
若 \(x[i]\ge x[j]\) 且 \(y[i]>y[j]\) 时, \(i\) 的斜率 大于 \(j\) 的斜率即图中情况 \((1,1)\) 和 \((1.2,2)\) :
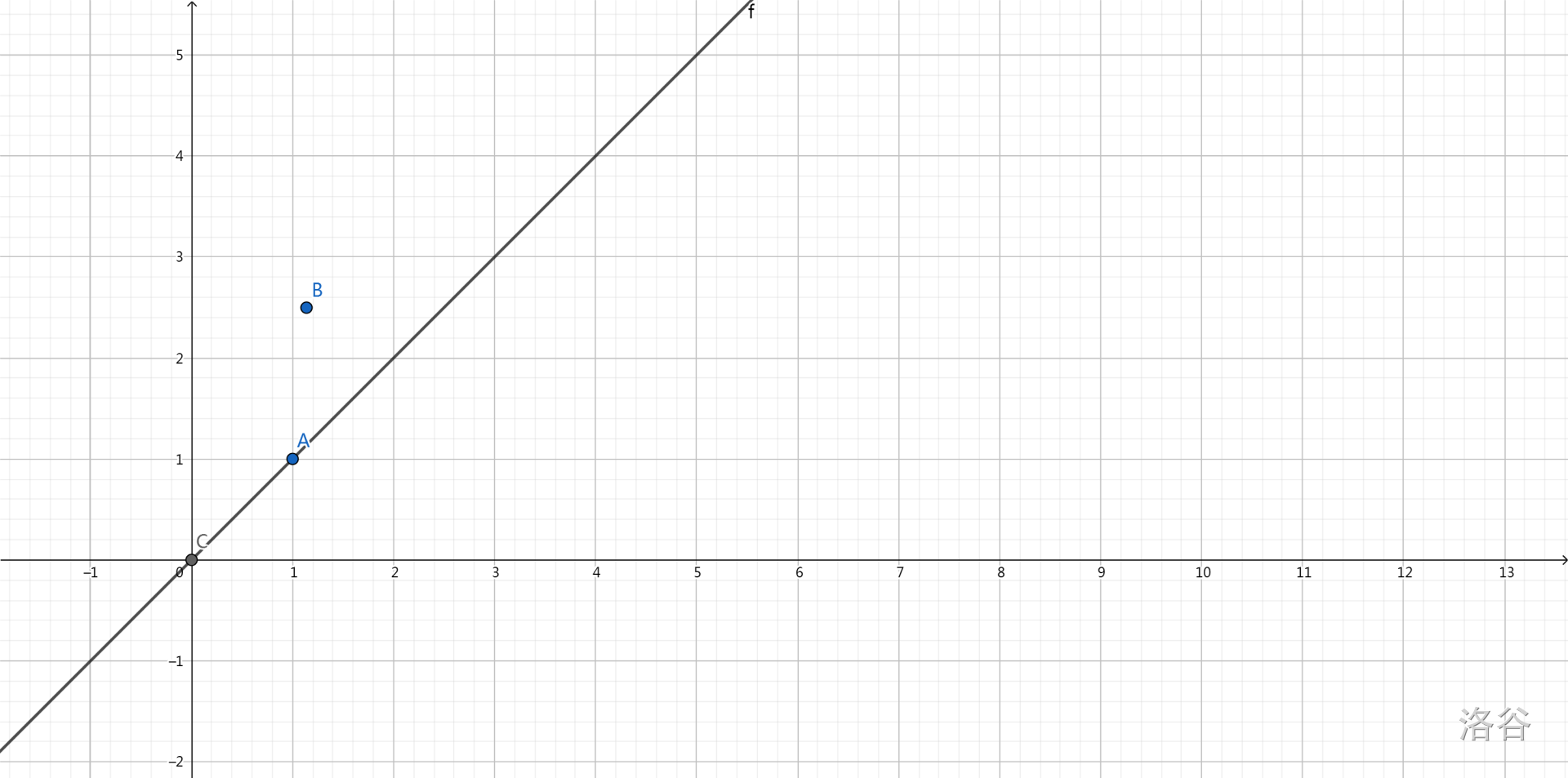
可以发现,对于同时经过原点 和 \(A\) 点的抛物线 ,
不可能出现一个 在抛物线上的点 , 在图示直线上方的区域 . -
注意预处理出 只经过一个点 的抛物线 .
可以设 \(map[i][n]\) = 点集\(\{i\}\) , 代表此抛物线只经过第 \(i\) 个点.
得到预处理后的 \(map\) 数组后,
就可以简单地进行状压 \(DP\) .
设 \(ans[s]\) 为 经过的点 构成的 点集 \(s\) , 所需要的最少抛物线数.
则有 状态转移方程式 :
\(ans[\ s | map[j][k]\ ] = min( ans[\ s | map[j][k]\ ] , ans[s]+1)\ (j\notin \text{点集}s)\)
最后输出 构造全集 的代价即可.
复杂度 \(O(Tn^2\ 2^n)\)
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctype.h>
#define min(a,b) a<b?a:b
#define lb long double
const lb eps = 1e-12;//极小值(0的近似值
//=============================================================
int T,n,m,all , map[20][20],ans[524288];
lb x[20],y[20];//横纵坐标
//=============================================================
inline int read()
{
int s=1, w=0; char ch=getchar();
for(; !isdigit(ch);ch=getchar()) if(ch=='-') s =-1;
for(; isdigit(ch);ch=getchar()) w = w*10+ch-'0';
return s*w;
}
int gcd(int a, int b) {return b?gcd(b,a%b):a;}
void get_ab(int fir,int sec,lb &a, lb &b)//求解 二元一次方程组
{
lb x1=x[fir],x12=x1*x1,y1=y[fir] , x2=x[sec],x22=x2*x2,y2=y[sec];//初始各系数的值
x1*=100000,x12*=100000,y1*=100000,x2*=100000,x22*=100000,y2*=100000;//将各系数转化为整数
int t1=x1,t12=x12,tt1=y1,t2=x2,t22=x22,tt2=y2 , d=gcd(t12,t22),l=(t12/d*t22);//赋给整形变量
t1*=(l/t12),tt1*=(l/t12) , t2*=(l/t22),tt2*=(l/t22),t12=t22=l;//进行通分,以进行相减消元
b = ((tt2-tt1)*1.0)/((t2-t1)*1.0);//获得a,b的值
a = (tt1*1.0-t1*b)/t12;
}
void prepare()
{
memset(ans,127,sizeof(ans)); ans[0]=0;//初始化ans为极大值
memset(map,0,sizeof(map));
n=read(),m=read(); all=(1<<n)-1;
for(int i=0; i<n; i++) scanf("%Lf%Lf",&x[i],&y[i]);
for(int i=0; i<n; i++) map[i][n] = (1<<i);//只经过一个点的抛物线
for(int i=0; i<n; i++)//枚举 抛物线经过的两个点
for(int j=i+1; j<n; j++)
{
//不合法的点对
if(x[i]>=x[j] && y[i]>y[j] && y[i]/x[i]>=y[j]/x[j]) continue;
if(x[j]>=x[i] && y[j]>y[i] && y[j]/x[j]>=y[i]/x[i]) continue;
lb a,b; map[i][j]|=(1<<i),map[i][j]|=(1<<j);//加入点集
get_ab(i,j,a,b);//求解a,b
for(int k=0; k<n; k++)//将被此抛物线经过的 其他点加入点集
if(fabs(a*x[k]*x[k]+b*x[k] - y[k]) <= eps)
map[i][j]|= (1<<k);
}
}
//=============================================================
signed main()
{
T=read();
for(;T;T--)
{
prepare();
for(int i=0; i<all; i++)//枚举点集
for(int j=0,sum=1; sum<=(1<<j); j++,sum<<=1)
if(!(i&(1<<j)))//枚举不在点集中的点
for(int k=j+1; k<=n; k++)//构造新的抛物线,并构造新的点集.
ans[i|map[j][k]] = min(ans[i|map[j][k]],ans[i]+1);
printf("%d\n",ans[all]);
}
}
\(\text{Updata on 2019.10.15 :}\)
考虑优化 :
以上复杂度为 \(O(Tn^2\ 2^n)\) 的算法 , 在 \(\text{CCF}\) 的速龙240上是跑不过去的= =
在 \(\text{Luogu}\) 上也只是 勉强卡过
在题解的帮助下 考虑 继续进行优化 :
-
假设 当前对 点集 \(S\) 进行转移 :
设 \(x\) 为满足 \(S\&(1<<(x-1))=0\) 的最小正整数,则由 \(S\) 转移的所有线都要经过 \(x\)正确性很显然 ,
若在此次转移中 , 构造的抛物线不经过 \(x\) ,
则 在之后的 某次转移中 也要经过 \(x\) .
则 在此次转移中 , 先经过 \(x\) , 答案不会变劣 -
则可以 进行预处理 ,
预处理出 每一个点集 , 满足 \(S\&(1<<(x-1))=0\) 的最小正整数 ,
转移时 只枚举经过此点的 抛物线 即可
由于 经过一个点的 抛物线最多只有 \(n\) 条
则复杂度变为 \(O(Tn\ 2^n)\) , 稳过
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctype.h>
#define min(a,b) a<b?a:b
#define lb long double
const lb eps = 1e-12;//极小值(0的近似值
//=============================================================
int T,n,m,all , map[20][20],ans[524288],lowbit[524288];
lb x[20],y[20];//横纵坐标
//=============================================================
inline int read()
{
int s=1, w=0; char ch=getchar();
for(; !isdigit(ch);ch=getchar()) if(ch=='-') s =-1;
for(; isdigit(ch);ch=getchar()) w = w*10+ch-'0';
return s*w;
}
int gcd(int a, int b) {return b?gcd(b,a%b):a;}
void get_ab(int fir,int sec,lb &a, lb &b)//求解 二元一次方程组
{
lb x1=x[fir],x12=x1*x1,y1=y[fir] , x2=x[sec],x22=x2*x2,y2=y[sec];//初始各系数的值
x1*=100000,x12*=100000,y1*=100000,x2*=100000,x22*=100000,y2*=100000;//将各系数转化为整数
int t1=x1,t12=x12,tt1=y1,t2=x2,t22=x22,tt2=y2 , d=gcd(t12,t22),l=(t12/d*t22);//赋给整形变量
t1*=(l/t12),tt1*=(l/t12) , t2*=(l/t22),tt2*=(l/t22),t12=t22=l;//进行通分,以进行相减消元
b = ((tt2-tt1)*1.0)/((t2-t1)*1.0);//获得a,b的值
a = (tt1*1.0-t1*b)/t12;
}
void prepare()
{
memset(ans,127,sizeof(ans)); ans[0]=0;//初始化ans为极大值
memset(map,0,sizeof(map));
n=read(),m=read(); all=(1<<n)-1;
for(int i=0; i<n; i++) scanf("%Lf%Lf",&x[i],&y[i]);
for(int i=0; i<n; i++) map[i][n] = (1<<i);//只经过一个点的抛物线
for(int i=0; i<n; i++)//枚举 抛物线经过的两个点
for(int j=i+1; j<n; j++)
{
//不合法的点对
if(x[i]>=x[j] && y[i]>y[j] && y[i]/x[i]>=y[j]/x[j]) continue;
if(x[j]>=x[i] && y[j]>y[i] && y[j]/x[j]>=y[i]/x[i]) continue;
lb a,b; map[i][j]|=(1<<i),map[i][j]|=(1<<j);//加入点集
get_ab(i,j,a,b);//求解a,b
for(int k=0; k<n; k++)//将被此抛物线经过的 其他点加入点集
if(fabs(a*x[k]*x[k]+b*x[k] - y[k]) <= eps)
map[i][j]|= (1<<k);
}
}
//=============================================================
signed main()
{
for(int i=0; i<(1<<18); i++)//预处理 每个点集 最低位的0 (未被经过的点)
for(int j=1 ;j <= 18 && i & (1<<(j-1)); j++);
lowbit[i] = j;
T=read();
for(;T;T--)
{
prepare();
for(int i=0; i<all; i++)//枚举点集
{
int bit = lowbit[i]-1;//当前点集 中未被经过的点
for(int k=1; k<=n; k++)//构造新的抛物线, 并构造新的点集.
ans[i|map[bit][k]] = min(ans[i|map[bit][k]],ans[i]+1);
}
printf("%d\n",ans[all]);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号