189. 旋转数组

一、题目

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。
示例 :

输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

说明:

• 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
• 要求使用空间复杂度为 O(1) 的 原地 算法。

---

二、解决方案

方案一：暴力法

旋转 k 次，每次将数组旋转 1 个元素。
代码如下：

void rotate(int* nums, int numsSize, int k) {
    for (int i = 0; i < k; i++)
    {
        int temp = 0;
        temp = nums[numsSize - 1];
        for (int j = numsSize - 1; j > 0; j--)
        {
            nums[j] = nums[j - 1];
        }
        nums[0] = temp;
    }
}

复杂度分析

• 时间复杂度：\(O(n*k)\)。每个元素都被移动 1 步\(（O(n)）\)k次\(（O(k)）\)。
• 空间复杂度：\(O(1)\)。没有额外空间被使用。

---

方案二：使用额外数组——空间换取时间

使用一个额外的数组将每个元素放到正确的位置上。
也就是原本数组里下标为 \(i\) 的我们将其放到\((i + k)%数组长度\)的位置。然后把新的数组拷贝到原数组中。
代码如下：

void rotate(int* nums, int numsSize, int k) {

    int* a = (int*)malloc(numsSize * sizeof(int));

    for (int i = 0; i < numsSize; i++)
    {
        a[(i + k) % numsSize] = nums[i];
    }

    for (int i = 0; i < numsSize; i++)
    {
        nums[i] = a[i];
    }
}

复杂度分析：

• 时间复杂度：\(O(n)\)。将数字放到新的数组中需要一遍遍历，另一边来把新数组的元素拷贝回原数组。
• 空间复杂度：\(O(n)\)。另一个数组需要原数组长度的空间。

---

方案三：使用环状替换

算法描述：如果我们直接把每一个数字放到它最后的位置，但这样的后果是遗失原来的元素。因此，把需要被替换的数字保存在变量 temp 里面并可解决该问题。然后，我们将被替换数字（temp）放到它正确的位置，并继续这个过程 n 次，n 是数组的长度。这是因为我们需要将数组里所有的元素都移动。但是，这种方法可能会有个问题，如果 n%k0，其中 k=k%n （因为如果 k 大于 n ，移动 k 次实际上相当于移动 k%n次）。这种情况下，我们会发现在没有遍历所有数字的情况下回到出发数字。此时，我们应该从下一个数字开始再重复相同的过程。
算法证明：假设，数组里我们有 n 个元素并且 k 是要求移动的次数。并且假设 n%k=0。第一轮中，所有移动数字的下标 i 满足 i%k0 。这是因为我们每跳 k 步，我们只会到达相距为 k 个位置下标的数。每一轮，我们都会移动 \(\frac{n}{k}\) 个元素。下一轮中，我们会移动满足 i%k1 的位置的数。这样的轮次会一直持续到我们再次遇到 i%k0 的地方为止，此时 i=k。此时在正确位置上的数字共有 \(k \times \frac{n}{k}=n\) 个。因此所有数字都在正确位置上。

下面让我们看一个例子，以更好地说明这个过程：
nums = [1, 2, 3, 4, 5, 6]
k = 2

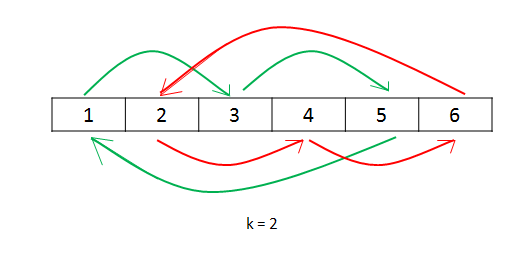
代码如下：

void rotate(int* nums, int numsSize, int k) {
    k = k % numsSize;
    int count = 0;
    for (int start = 0; count < numsSize; start++)
    {
        int current = start;
        int prev = nums[start];
        do
        {
            int next = (current + k) % numsSize;
            int temp = nums[next];
            nums[next] = prev;
            prev = temp;
            current = next;
            count++;
        } while (start != current);
    }
}

复杂度分析

• 时间复杂度：\(O(n)\)。只遍历了每个元素一次。
• 空间复杂度：\(O(1)\)。使用了常数个额外空间。

---

方案4：使用反转

算法：这个方法基于这个事实：当我们旋转数组 k 次， k%n 个尾部元素会被移动到头部，剩下的元素会被向后移动。在这个方法中，我们首先将所有元素反转。然后反转前 k 个元素，再反转后面 n−k 个元素，就能得到想要的结果。
假设 n=7 且 k=3。

原始数组                  : 1 2 3 4 5 6 7
反转所有数字后             : 7 6 5 4 3 2 1
反转前 k 个数字后          : 5 6 7 4 3 2 1
反转后 n-k 个数字后        : 5 6 7 1 2 3 4 --> 结果

代码如下：

void reverse(int* nums, int start, int end)
{
    while (start < end)
    {
        int temp = nums[start];
        nums[start] = nums[end];
        nums[end] = temp;
        start++;
        end--;
    }
}

void rotate(int* nums, int numsSize, int k) 
{
    k %= numsSize;
    reverse(nums, 0, numsSize - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, numsSize - 1);    
}

复杂度分析

• 时间复杂度：\(O(n)\) 。 n 个元素被反转了总共 3 次。
• 空间复杂度：\(O(1)\) 。 没有使用额外的空间。