数据结构 : Hash Table [I]
引子
这篇仍然不讲并行/并发。
Hash table,国内相当一部分书籍将其直译为哈希表,但博主本人喜欢称其为散列表。
散列表支持任何基于 Key-Value 对的插入,检索,删除操作。
比如在 .NET 1.x 版本下,我们可以这样使用:
10 namespace Lucifer.CSharp.Sample
11 {
12 class Program
13 {
14 public static void Main()
15 {
16 Hashtable table = new Hashtable();
17
18 //插入操作
19 table[1] = "A";
20 table.Add(2, "B");
21 table[3] = "C";
22
23 //检索操作
24 string a = (string)table[1];
25 string b = (string)table[2];
26 string c = (string)table[3];
27
28 //删除操作
29 table.Remove(1);
30 table.Remove(2);
31 table.Remove(3);
32 }
33 }
34 }
而在 .NET 2.0 及以上版本下,我们则这样使用:
10 namespace Lucifer.CSharp.Sample
11 {
12 class Program
13 {
14 public static void Main()
15 {
16 Dictionary<int, string> table =
17 new Dictionary<int, string>();
18
19 //插入操作
20 table[1] = "A";
21 table.Add(2, "B");
22 table[3] = "C";
23
24 //检索操作
25 string a = table[1];
26 string b = table[2];
27 string c;
28 table.TryGetValue(3, out c);
29
30 //删除操作
31 table.Remove(1);
32 table.Remove(2);
33 table.Remove(3);
34 }
35 }
36 }
众所周知,假如在数组中知道了某个索引的话,也就知道了该索引位置上的值。同理,在散列表中,我们所要做的就是根据 Key 来知道 Value 在表中的位置 。 Key 的作用只不过用来指示位置。而通过 Key 来查找位置,意味着查找时间从顺序查找的 O(N),折半查找的 O(lgN) 骤减至 O(1)。
那么我们如何把可能是字符串,数字等的某 Key 转换成表的索引呢?这一步,在 .NET 中由 GetHashCode 方法来完成。当然在散列表内还需要根据 Hash Code 来进一步计算,但我们现在暂且认为通过 Key 的 GetHashCode 方法我们已经可以找到 Value 了。实际上,对于外部开发人员来说的确不需要再做别的工作了。而这也是 Object 类带有 GetHashCode 虚方法的原因。当我们在使用 Stack<T>,List<T>,Queue<T> 等集合时,根本不需要在乎有没有 GetHashCode 方法,但是如果你想使用 Dictionary<TKey, TValue>,HashSet<T>(.NET 3.5新增) 等集合时,则必须正确重写 GetHashCode 方法,否则这些集合不能正常工作。当然,使用.NET基元类型没有任何问题,因为 Microsoft 已经为这些类型实现了良好的重载。
而在讲解数据结构的书籍里,把 GetHashCode 方法完成的工作称为“散列函数(hash function)”。
散列函数
那么散列函数是如何工作的呢?通常来说,它会把某个数字或者能够转换成数字的类型映射成固定位数的数字。比如 .NET 的 GetHashCode 方法返回 32 位有符号整型。当我们把64 位或更多位数字映射成 32 位时,很显然,这带来了一个复杂问题:两个或多个不同的 Key 可能被散列到同一位置,引起碰撞冲突。这种情况很难避免,因为 Key 的个数比位置要多。当然,如果能够避免碰撞冲突,那就完美了。我们把能够完成这种情况的散列函数叫做完全散列函数(perfect hash function)。
从定义和实现来看,散列函数其实就是伪随机数生成器(PRNG)。总的来说,散列函数的性能通常可以接受,而且也可以把散列函数当作 PNRG 来进行比较。理论上,存在一个完全散列函数。它从不会让数据发生碰撞冲突。实际上,要找到这样的散列函数以及应用该散列函数的实际应用程序太困难了。即使是它最低限度的变体,也相当有限。
实践中,有很多种数据排列。有一些非常随机,另外一些则相当的格式化。一种散列函数很难概括所有的数据类型,即使针对某种数据类型也很困难。我们所能做的就是通过不断尝试来寻找最适合我们需要的散列函数。这也是必须重写 GetHashCode 方法的原因之一。
下面是我们分析选择散列函数的两大要素:
- 数据分布。这是衡量散列函数生成散列值好坏的尺度。分析这个需要知道在数据集内发生碰撞冲突的数量,即非唯一的散列值。
- 散列函数的效率。这是衡量散列函数生成散列值快慢的尺度。理论上,散列函数非常快。但是也应当注意到,散列函数并不总是保持 O(1) 的时间复杂度。
那么如何来实现散列函数呢?基本上有以下两大方法论:
- 加法和乘法。这个方法的主要思想是通过遍历数据,然后以某种计算形式来构造散列值。通常情况下是乘以某个素数的乘法形式。如下图所示:
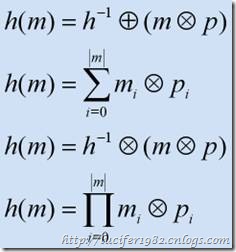
目前来说,还没有数学方法能够证明素数和散列函数之间的关系。不过在实践中利用一些素数可以得到很好的结果。
- 位移。顾名思义,散列值是通过位移处理获得的。每一次的处理结果都累加,最后返回该值。如下图所示:
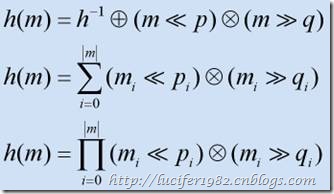
此外,还有很多方法可以用来计算散列值。不过这些方法也不外乎是上述两种的变种或综合运用。老实说,一个良好的散列函数很大程度上是靠经验得来。除此之外,别无良方。幸运的是,前人留下了许多经典的散列函数实现。接下来,我们就来了解下这些经典的散列函数。注意,本文所介绍的散列函数均不能使用在诸如加密,数字签名等领域。
关于整型和浮点类型的散列函数,因为都很简单,在这里就不再详细阐述。有兴趣的可以使用 Reflector 等反编译工具自行查看其 GetHashCode 实现。值得一提的是浮点类型要注意使 +0.0 和 -0.0 的散列值结果一致,还有就是 128 位的 Decimal 类型实现。
接下来将详细介绍几个字符串散列函数。
先看下 Java 的字符串散列函数是什么样。注意,本文代码均以C#写就,下同。代码如下:
8 public int JavaHash(string str)
9 {
10 int hashCode = 0;
11 for (int i = 0; i < str.Length; i++)
12 {
13 hashCode = 31 * hashCode + str[i];
14 }
15 return hashCode;
16 }
上述散列函数,一般来讲已经相当好。不过如果字符串很长,我们可能需要对它进行修改。它实际上来自于 K & R 的《The C Programming Language》。其中我们使用的素数 31 可以替换成 31, 131, 1313, 13131, 131313,... 等。看起来,它跟下面这个散列函数很相似。
18 public int DJBHash(string str)
19 {
20 int hashCode = 5381;
21 for (int i = 0; i < str.Length; i++)
22 {
23 hashCode = ((hashCode << 5) + hashCode)
24 + str[i];
25 }
26 return hashCode;
27 }
该函数最早由 Daniel J. Bernstein 教授展示于新闻组 comp.lang.C 上,是最有效率的散列函数之一。
我们再来看看 .NET 中的字符串散列函数。代码如下:
29 public unsafe int DotNetHash(string str)
30 {
31 fixed(char* charPtr = new String(str.ToCharArray()))
32 {
33 int hashCode = (5381 << 16) + 5381;
34 int numeric = hashCode;
35 int* intPtr = (int*)charPtr;
36
37 for (int i = str.Length; i > 0; i -= 4)
38 {
39 hashCode = ((hashCode << 5) + hashCode +
40 (hashCode >> 27)) ^ intPtr[0];
41 if (i <= 2)
42 {
43 break;
44 }
45 numeric = ((numeric << 5) + numeric +
46 (numeric >> 27)) ^ intPtr[1];
47 intPtr += 2;
48 }
49 return hashCode + numeric * 1566083941;
50 }
51 }
上述代码实际上是大牛唐纳德在他的《The Art Of Computer Programming Volume 3》中的变种。因为老唐的散列函数在某些情况下会有问题,所以 .NET 没有完全采用老唐的办法。老唐提供的散列函数如下:
53 public int DEKHash(string str)
54 {
55 int hashCode = str.Length;
56 for (int i = 0; i < str.Length; i++)
57 {
58 hashCode = ((hashCode << 5) ^ (hashCode >> 27))
59 ^ str[i];
60 }
61 return hashCode;
62 }
此外在Unix平台上还有一种广泛采用的散列函数。代码如下:
64 public int ELFHash(string str)
65 {
66 int hashCode = 0;
67 int numeric = 0;
68 for (int i = 0; i < str.Length; i++)
69 {
70 hashCode = (hashCode << 4) + str[i];
71 if ((numeric = hashCode & 0xF0000000L) != 0)
72 {
73 hashCode ^= (hashCode >> 24);
74 }
75 hashCode &= ~numeric;
76 }
77 return hashCode;
78 }
前文讲过,散列函数会带来碰撞冲突,那如何解决这种情况呢?敬请下回分解。
最后给大家提个问题:乘法运算快呢,还是位移运算快?



