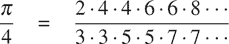SICP JavaScript 描述

来源 http://sicp-js.flygon.net/#

一、使用函数构建抽象

原文：1 Building Abstractions with Functions

译者：飞龙

协议：CC BY-NC-SA 4.0

心灵的行为，其中它对简单的想法施加其力量，主要有以下三种：1.将几个简单的想法组合成一个复合的想法，从而形成所有复杂的想法。2.第二个是将两个想法，无论是简单的还是复杂的，放在一起，并将它们放在一起，以便一次看到它们，而不将它们合并成一个，从而获得它们所有的关系想法。3.第三个是将它们与实际存在的所有其他想法分开：这被称为抽象，从而形成所有的一般想法。

——约翰·洛克，《人类理解论》（1690）

我们将要研究计算过程的概念。计算过程是存在于计算机中的抽象实体。随着它们的发展，过程操纵其他抽象的东西，称为数据。过程的演变由一组称为程序的规则指导。人们创建程序来指导过程。实际上，我们用我们的咒语召唤计算机的精神。

计算过程确实很像巫师对精神的想法。它看不见，摸不着。它根本不是由物质组成的。然而，它是非常真实的。它可以进行智力工作。它可以回答问题。它可以通过在银行分发钱或控制工厂中的机器人手臂来影响世界。我们用来施法的程序就像巫师的咒语。它们是从奥秘和神秘的编程语言中的符号表达式中精心组成的，这些语言规定了我们希望我们的过程执行的任务。

计算过程在一个正确工作的计算机中精确和准确地执行程序。因此，像巫师的学徒一样，新手程序员必须学会理解和预料他们施法的后果。即使是程序中的小错误（通常称为bug）也可能产生复杂和意想不到的后果。

幸运的是，学习编程远比学习巫术危险得多，因为我们处理的精神被方便地以安全的方式包含在其中。然而，现实世界的编程需要谨慎、专业知识和智慧。例如，计算机辅助设计程序中的一个小错误可能导致飞机或大坝的灾难性崩溃，或者工业机器人的自我毁灭。

优秀的软件工程师有能力组织程序，以便他们可以相当确信所得到的过程将执行预期的任务。他们可以预先可视化系统的行为。他们知道如何构造程序，以便意想不到的问题不会导致灾难性后果，而当问题出现时，他们可以调试他们的程序。设计良好的计算系统，就像设计良好的汽车或核反应堆一样，都是以模块化的方式设计的，以便部件可以分别构建、更换和调试。

JavaScript 编程

我们需要一个适当的语言来描述过程，为此我们将使用编程语言 JavaScript。正如我们的日常思维通常用我们的母语（如英语、瑞典语或中文）表达一样，对数量现象的描述用数学符号表示，我们的过程思维将用 JavaScript 表示。JavaScript 于 1995 年开发，用作控制万维网浏览器行为的编程语言，通过嵌入在网页中的脚本。该语言最初由 Brendan Eich 构思，最初名为Mocha，后来更名为LiveScript，最终改名为 JavaScript。名称“JavaScript”是 Oracle Corporation 的商标。

尽管 JavaScript 最初是作为网页脚本语言而诞生的，但它是一种通用编程语言。JavaScript 解释器是一台执行 JavaScript 语言描述的过程的机器。第一个 JavaScript 解释器是由 Eich 在网景通信公司为网景导航器网页浏览器实现的。JavaScript 从 Scheme 和 Self 编程语言继承了其核心特性。Scheme 是 Lisp 的一个方言，并且曾被用作本书原始版本的编程语言。JavaScript 从 Scheme 继承了其最基本的设计原则，如词法作用域的一流函数和动态类型。

JavaScript 与其（最终）命名的语言 Java 只有表面上的相似之处；Java 和 JavaScript 都使用语言 C 的块结构。与通常使用编译到低级语言的 Java 和 C 相反，JavaScript 程序最初是由网页浏览器解释的。在网景导航器之后，其他网页浏览器提供了对该语言的解释器，包括微软的 Internet Explorer，其 JavaScript 版本称为JScript。JavaScript 在控制网页浏览器方面的流行性促使了一项标准化工作，最终导致了ECMAScript的产生。ECMAScript 标准的第一版由盖伊·刘易斯·斯蒂尔（Guy Lewis Steele Jr.）领导，并于 1997 年 6 月完成（ECMA 1997）。第六版，即 ECMAScript 2015，由艾伦·韦尔夫斯-布洛克（Allen Wirfs-Brock）领导，并于 2015 年 6 月被 ECMA 大会采纳（ECMA 2015）。

将 JavaScript 程序嵌入网页的做法鼓励了网页浏览器的开发人员实现 JavaScript 解释器。随着这些程序变得更加复杂，解释器在执行它们时变得更加高效，最终采用了诸如即时（JIT）编译等复杂的实现技术。截至本文撰写时（2021 年），大多数 JavaScript 程序都嵌入在网页中，并由浏览器解释，但 JavaScript 越来越多地被用作通用编程语言，使用诸如 Node.js 等系统。

ECMAScript 2015 拥有一系列功能，使其成为研究重要的编程构造和数据结构以及将它们与支持它们的语言特性相关联的绝佳媒介。它的词法作用域的一流函数及其通过 lambda 表达式的语法支持直接而简洁地访问函数抽象，动态类型允许适应保持接* Scheme 原始状态。除了这些考虑之外，在 JavaScript 中编程非常有趣。

1.1 编程的元素

强大的编程语言不仅仅是指示计算机执行任务的手段。语言还作为一个框架，我们在其中组织关于过程的想法。因此，当我们描述一种语言时，我们应该特别关注语言提供的手段，用于将简单的想法组合成更复杂的想法。每种强大的语言都有三种机制来实现这一点：

原始表达式，代表语言关注的最简单的实体，
组合手段，通过这种手段，可以从更简单的元素构建复合元素，以及
抽象手段，通过这种手段，可以将复合元素命名并作为单元进行操作。

在编程中，我们处理两种元素：函数和数据。（后来我们会发现它们实际上并不那么不同。）非正式地说，数据是我们想要操作的“东西”，而函数是描述操作数据规则的描述。因此，任何强大的编程语言都应该能够描述原始数据和原始函数，并且应该有方法来组合和抽象函数和数据。

在本章中，我们只处理简单的数值数据，以便我们可以专注于构建函数的规则。¹在后面的章节中，我们将看到这些相同的规则允许我们构建函数来操作复合数据。

1.1.1 表达式

开始编程的一种简单方法是检查与 JavaScript 语言解释器的一些典型交互。您键入一个语句，解释器会通过显示其求值结果来做出响应。

您可能键入的一种语句是表达式语句，它由一个表达式后跟一个分号组成。一种原始表达式是数字。（更准确地说，您键入的表达式由表示十进制数字的数字组成。）如果您向 JavaScript 提供程序

486;

解释器将通过打印²来做出响应

表示数字的表达式可以与运算符（如+或*）结合，形成一个复合表达式，表示对这些数字应用相应原始函数的应用。例如，

137 + 349;
486

1000 - 334;
666

5 * 99;
495

10 / 4;
2.5

2.7 + 10;
12.7

这样的表达式，其中包含其他表达式作为组成部分，被称为组合。由运算符符号在中间形成的组合，左右两侧是操作数表达式，被称为运算符组合。运算符组合的值是通过将运算符指定的函数应用于操作数的值来获得的。

将运算符放在操作数之间的约定称为中缀表示法。它遵循您在学校和日常生活中最熟悉的数学表示法。与数学一样，运算符组合可以是嵌套的，也就是说，它们可以有自身是运算符组合的操作数：

(3 * 5) + (10 - 6);
19

通常情况下，括号用于分组运算符组合，以避免歧义。当省略括号时，JavaScript 也遵循通常的约定：乘法和除法比加法和减法更紧密地绑定。例如，

3 * 5 + 10 / 2;

代表

(3 * 5) + (10 / 2);

我们说*和/比+和-有更高的优先级。加法和减法的序列从左到右读取，乘法和除法的序列也是如此。因此，

1 - 5 / 2 * 4 + 3;

代表

(1 - ((5 / 2) * 4)) + 3;

我们说+、-、*和/是左结合的。

在原则上，这种嵌套的深度和 JavaScript 解释器可以求值的表达式的整体复杂性没有限制。我们人类可能会被仍然相对简单的表达式所困惑，比如

3 * 2 * (3 - 5 + 4) + 27 / 6 * 10;

解释器会立即求值为 57。我们可以通过以以下形式编写这样的表达式来帮助自己

3 * 2 * (3 - 5 + 4)
+
27 / 6 * 10;

以视觉上分隔表达式的主要组件。

即使是复杂的表达式，解释器始终以相同的基本循环运行：它读取用户键入的语句，求值语句，并打印结果。这种操作模式通常被称为解释器运行在读取-求值-打印循环中。特别要注意的是，不需要明确指示解释器打印语句的值。³

1.1.2 命名和环境

编程语言的一个关键方面是它提供了使用名称来引用计算对象的手段，我们的第一种手段是常量。我们说名称标识了一个值为对象的常量。

在 JavaScript 中，我们使用常量声明为常量命名。

const size = 2;

使解释器将值 2 与名称size关联起来。⁴一旦名称size与数字 2 关联起来，我们可以通过名称引用值 2：

size;
2

5 * size;
10

以下是对const的进一步使用示例：

const pi = 3.14159;

const radius = 10;

pi * radius * radius;
314.159

const circumference = 2 * pi * radius;

circumference;
62.8318

常量声明是我们语言中最简单的抽象手段，因为它允许我们使用简单的名称来引用复合操作的结果，例如上面计算的circumference。一般来说，计算对象可能具有非常复杂的结构，要记住并重复它们的细节每次想要使用它们将会非常不方便。事实上，复杂的程序是通过逐步构建越来越复杂的计算对象而构建的。解释器使得这种逐步程序构建特别方便，因为名称-对象关联可以在连续的交互中逐步创建。这个特性鼓励程序的逐步开发和测试，并且在很大程度上负责 JavaScript 程序通常由大量相对简单的函数组成。

应该清楚的是，将值与名称关联并稍后检索这些值的可能性意味着解释器必须维护一种记忆，以跟踪名称-对象对。这种记忆称为环境（更确切地说是程序环境，因为我们将在后面看到，计算可能涉及多种不同的环境）。

1.1.3 求值运算符组合

在本章中，我们的一个目标是分离有关过程式思维的问题。例如，让我们考虑一下，在求值运算符组合时，解释器本身正在遵循一个过程。

要求值运算符组合，请执行以下操作：
1. 1. 求值组合的操作数表达式。
2. 2. 应用由运算符表示的函数到操作数的值。

即使这个简单的规则也说明了一般过程中的一些重要点。首先，观察到第一步规定，为了完成组合的求值过程，我们必须首先对组合的每个操作数执行求值过程。因此，求值规则在本质上是递归的；也就是说，它包括作为其步骤之一的需要调用规则本身。

注意递归的想法如何简洁地表达了在深度嵌套组合的情况下，否则将被视为一个相当复杂的过程。例如，求值

(2 + 4 * 6) * (3 + 12);

需要将求值规则应用于四种不同的组合。我们可以通过将组合表示为树的形式来获得这个过程的图像，如下图所示。每个组合都由一个节点表示，其分支对应于从中衍生出的运算符和组合的操作数。终端节点（即没有从它们衍生出的分支的节点）表示运算符或数字。从树的角度来看求值，我们可以想象操作数的值从终端节点向上渗透，然后在更高的层次上组合。一般来说，我们将看到递归是一种处理分层、树状对象的非常强大的技术。事实上，“向上渗透值”形式的求值规则是一种称为树累积的一般过程的例子。

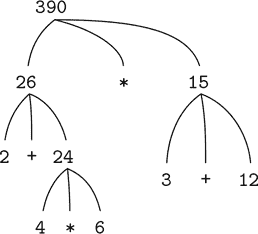
图 1.1 树表示，显示每个子表达式的值。

接下来，观察到第一步的重复应用使我们到达需要求值的点，不是组合，而是诸如数字或名称的原始表达式。我们通过规定以下来处理原始情况：

数字的值是它们所代表的数字，而
名称的值是环境中与这些名称关联的对象。

要注意的关键点是环境在确定表达式中名称的含义方面的作用。在 JavaScript 这样的交互式语言中，谈论表达式的值，比如x + 1，而不指定任何关于提供名称x含义的环境信息是没有意义的。正如我们将在第 3 章中看到的，环境的一般概念作为提供求值所发生的上下文将在我们理解程序执行方面发挥重要作用。

请注意，上面给出的求值规则不处理声明。例如，求值const x = 3;不会将等号=应用于两个参数，其中一个是名称x的值，另一个是 3，因为声明的目的恰好是将x与一个值关联起来。（也就是说，const x = 3;不是一个组合。）

const中的字母以粗体呈现，以表明它是 JavaScript 中的关键字。关键字具有特定的含义，因此不能用作名称。语句中的关键字或关键字组合指示 JavaScript 解释器以特殊方式处理语句。每种这样的语法形式都有其自己的求值规则。各种类型的语句和表达式（每种都有其关联的求值规则）构成了编程语言的语法。

1.1.4 复合函数

我们已经确定了 JavaScript 中必须出现的一些元素：

数字和算术运算是原始数据和函数。
组合的嵌套提供了一种组合操作的方法。
将名称与值关联的常量声明提供了有限的抽象手段。

现在我们将学习函数声明，这是一种更强大的抽象技术，通过它可以给复合操作命名，然后作为一个单元引用。

我们首先来看如何表达“*方”的概念。我们可以说，“对某物求*方，就是将其乘以自身。”在我们的语言中，这可以表达为

function square(x) {
    return x * x;
}

我们可以这样理解：

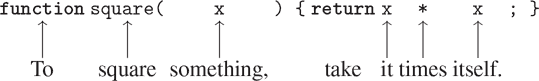
我们这里有一个复合函数，它被命名为square。该函数表示将某物乘以自身的操作。要被乘的东西被赋予一个本地名称x，它扮演的角色与自然语言中的代词相同。求值声明会创建这个复合函数，并将其与名称square关联起来。⁶

函数声明的最简单形式是

function name(parameters) { return expression; }

名称是一个符号，用于将函数定义与环境关联起来。⁷ 参数是函数体内用于引用函数对应参数的名称。参数被括在括号内，并用逗号分隔，就像在应用被声明的函数时一样。在最简单的形式中，函数声明的函数体是一个单一的返回语句，⁸它由关键字return后跟将产生函数应用值的返回表达式组成，当参数被实际参数替换时，函数将被应用。与常量声明和表达式语句一样，返回语句以分号结束。

声明了square之后，我们现在可以在函数应用表达式中使用它，并使用分号将其转换为语句。

square(21);
441

函数应用是——在操作符组合之后——我们遇到的将表达式组合成更大表达式的第二种组合。函数应用的一般形式是

function-expression(argument-expressions)

应用的function-expression指定要应用于逗号分隔的argument-expressions的函数。为了求值函数应用，解释器遵循了与 1.1.3 节中描述的操作符组合的过程非常相似的过程。

要求值函数应用，执行以下操作：
1. 1.求值应用的子表达式，即函数表达式和参数表达式。
2. 2.将函数表达式的值应用于参数表达式的值。

square(2 + 5);
49

在这里，参数表达式本身是一个复合表达式，操作符组合2 + 5。

square(square(3));
81

当然，函数应用表达式也可以作为参数表达式。

我们还可以使用square作为定义其他函数的构建块。例如，x² + y²可以表示为

square(x) + square(y)

我们可以轻松地声明一个名为sum_of_squares⁹的函数，它给定任意两个数字作为参数，产生它们的*方和：

function sum_of_squares(x, y) {
    return square(x) + square(y);
}

sum_of_squares(3, 4);
25

现在我们可以使用sum_of_squares作为构建更多函数的构建块：

function f(a) {
    return sum_of_squares(a + 1, a * 2);
}

f(5);
136

除了复合函数，任何 JavaScript 环境都提供了内置于解释器或从库加载的原始函数。除了由操作符提供的原始函数之外，本书中使用的 JavaScript 环境还包括其他原始函数，例如计算其参数的自然对数的函数math_log¹⁰。这些额外的原始函数与复合函数完全相同；求值应用math_log(1)的结果是数字 0。事实上，通过查看上面给出的sum_of_squares的定义，无法确定square是内置于解释器中，从库加载，还是定义为复合函数。

1.1.5 函数应用的替换模型

为了求值函数应用，解释器遵循 1.1.4 节中描述的过程。也就是说，解释器求值应用的元素，并将函数（即应用的函数表达式的值）应用于参数（即应用的参数表达式的值）。

我们可以假设原始函数的应用由解释器或库处理。对于复合函数，应用过程如下：

要将复合函数应用于参数，求值函数的返回表达式，其中每个参数都替换为相应的参数。¹¹

为了说明这个过程，让我们求值应用

f(5)

其中f是 1.1.4 节中声明的函数。我们首先检索f的返回表达式：

sum_of_squares(a + 1, a * 2)

然后我们用参数 5 替换参数a：

sum_of_squares(5 + 1, 5 * 2)

因此，问题简化为求值具有两个参数和函数表达式sum_of_squares的应用。求值此应用涉及三个子问题。我们必须求值函数表达式以获得要应用的函数，并且我们必须求值参数表达式以获得参数。现在5 + 1产生 6，5 * 2产生 10，因此我们必须将sum_of_squares函数应用于 6 和 10。这些值替换为sum_of_squares的主体中的参数x和y，将表达式简化为

square(6) + square(10)

如果我们使用square的声明，这将简化为

(6 * 6) + (10 * 10)

这通过乘法减少到

36 + 100

最后

我们刚刚描述的过程称为函数应用的替换模型。就本章中的函数而言，它可以被视为确定函数应用“含义”的模型。但是，有两点应该强调：

替换的目的是帮助我们思考函数应用，而不是提供解释器实际工作方式的描述。典型的解释器不会通过操纵函数的文本来替换参数的值来求值函数应用。实际上，“替换”是通过使用参数的本地环境来完成的。当我们在第 3 和第 4 章中详细研究解释器的实现时，我们将更全面地讨论这一点。
在本书的过程中，我们将提出一系列越来越复杂的解释器工作模型，最终在第 5 章中实现一个解释器和编译器的完整实现。替换模型只是这些模型中的第一个，是一种开始正式思考求值过程的方式。一般来说，在科学和工程中建模现象时，我们从简化的、不完整的模型开始。随着我们更详细地研究事物，这些简单的模型变得不足以满足需求，必须被更精细的模型所取代。替换模型也不例外。特别是，当我们在第 3 章中讨论使用带有“可变数据”的函数时，我们将看到替换模型崩溃了，必须被更复杂的函数应用模型所取代。

应用顺序与正常顺序

根据 1.1.4 节中给出的求值描述，解释器首先求值函数和参数表达式，然后将得到的函数应用于得到的参数。这不是执行求值的唯一方法。另一种求值模型将不会求值参数，直到它们的值被需要为止。相反，它首先用参数表达式替换参数，直到获得只涉及运算符和原始函数的表达式，然后执行求值。如果我们使用这种方法，那么

f(5)

将按照扩展的顺序进行。

sum_of_squares(5 + 1, 5 * 2)

square(5 + 1)     + square(5 * 2)

(5 + 1) * (5 + 1) + (5 * 2) * (5 * 2)

随后是减少

6    *    6    +    10    *    10

    36         +         100

              136

这与我们先前的求值模型得出相同的答案，但过程是不同的。特别是，5 + 1和5 * 2的求值在这里分别执行两次，对应于表达式的减少

x * x

分别用5 + 1和5 * 2替换x。

这种替代的“完全展开然后减少”求值方法被称为正常顺序求值，与解释器实际使用的“求值参数然后应用”方法相对应，后者被称为应用顺序求值。可以证明，对于可以使用替换进行建模的函数应用（包括本书前两章中的所有函数）并产生合法值，正常顺序和应用顺序求值会产生相同的值。（参见练习 1.5，其中有一个“非法”值的例子，正常顺序和应用顺序求值得出的结果不同。）

JavaScript 使用应用顺序求值，部分原因是为了避免像上面所示的5 + 1和5 * 2这样的表达式的多次求值所获得的额外效率，更重要的是，当我们离开可以通过替换建模的函数领域时，正常顺序求值变得更加复杂。另一方面，正常顺序求值可以是一个非常有价值的工具，我们将在第 3 和第 4 章中探讨它的一些影响。

1.1.6 条件表达式和谓词

到目前为止，我们可以定义的函数类的表达能力非常有限，因为我们无法进行测试并根据测试结果执行不同的操作。例如，我们无法声明一个通过测试数字是否为非负来计算绝对值的函数，并根据规则分别采取不同的操作

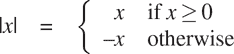
这个结构是一个案例分析，并且可以用 JavaScript 的条件表达式来写成

function abs(x) {
    return x >= 0 ? x : - x;
}

这可以用英语表达为“如果x大于或等于零，则返回x；否则返回–x。”条件表达式的一般形式是

predicate ? consequent-expression : alternative-expression

条件表达式以predicate开头，即其值为 JavaScript 中的两个特殊布尔值true或false的表达式。原始布尔表达式true和false分别以布尔值true和false进行简单求值。predicate后面跟着一个问号，consequent-expression，一个冒号，最后是alternative-expression。

为了求值条件表达式，解释器首先求值表达式的谓词。如果谓词求值为true，解释器求值结果表达式并返回其值作为条件表达式的值。如果谓词求值为false，它求值替代表达式并返回其值作为条件表达式的值。

单词“谓词”用于返回true或false的运算符和函数，以及求值为true或false的表达式。绝对值函数abs使用原始谓词>=，这是一个接受两个数字作为参数并测试第一个数字是否大于或等于第二个数字的运算符，根据情况返回true或false。

如果我们更喜欢单独处理零的情况，我们可以通过写一个函数来指定计算一个数字的绝对值

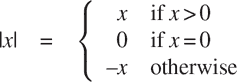
在 JavaScript 中，我们通过在其他条件表达式中将替代表达式作为条件表达式的替代表达式来嵌套条件表达式来表示具有多个情况的案例分析：

function abs(x) {
    return x > 0
           ? x
           : x === 0
           ? 0
           : - x;
}

括号不需要在替代表达式x === 0 ? 0 : - x周围，因为条件表达式的语法形式是右结合的。解释器忽略空格和换行符，这里插入是为了可读性，以使?和:在案例分析的第一个谓词下对齐。案例分析的一般形式是

p[1]
? e[1]
: p[2]
? e[2]
⁝
: p[n]
? e[n]
: final-alternative-expression

我们将谓词p[i]和其结果表达式e[i]一起称为子句。案例分析可以看作是一系列子句，后跟最终的替代表达式。根据条件表达式的求值，案例分析首先求值谓词p[1]。如果它的值为false，则求值p[2]。如果p[2]的值也为false，则求值p[3]。这个过程一直持续，直到找到一个值为true的谓词，此时解释器将返回子句的相应结果表达式e的值作为案例分析的值。如果没有找到任何p为true，则案例分析的值是最终替代表达式的值。

除了应用于数字的原始谓词，如>=、>、<、<=、===和!==之外，还有逻辑组合操作，它们使我们能够构造复合谓词。最常用的三个是这些：

表达式[1] && 表达式[2]

这个操作表示逻辑连接，大致意思与英语单词“and”相同。这种语法形式是语法糖，用于

表达式[1] ? 表达式[2] : false。
表达式[1] 表达式[2]

这个操作表示逻辑析取，大致意思与英语单词“or”相同。这种语法形式是语法糖。

表达式[1] ? true : 表达式[2]。
! 表达式

这个操作表示逻辑否定，大致意思与英语单词“not”相同。当表达式求值为false时，表达式的值为true，当表达式求值为true时，表达式的值为false。

注意&&和||是语法形式，而不是运算符；它们的右侧表达式并不总是被求值。另一方面，运算符!遵循第 1.1.3 节的求值规则。它是一个一元运算符，这意味着它只接受一个参数，而迄今为止讨论的算术运算符和原始谓词都是二元运算符，接受两个参数。运算符!在其参数之前；我们称它为 前缀运算符。另一个前缀运算符是数值否定运算符，其示例是上面的abs函数中的表达式- x。

作为这些谓词如何使用的一个例子，表达一个数x在范围5 < x < 10中的条件可以表示为

x > 5 && x < 10

&&的语法形式的优先级低于比较运算符>和<，条件表达式的语法形式... ?... :...的优先级低于迄今为止我们遇到的任何其他运算符，这是我们在上面的abs函数中使用的一个特性。

作为另一个例子，我们可以声明一个谓词，测试一个数字是否大于或等于另一个数字

function greater_or_equal(x, y) {
    return x > y || x === y;
}

或者作为

function greater_or_equal(x, y) {
    return ! (x < y);
}

函数greater_or_equal应用于两个数字时，与运算符>=的行为相同。一元运算符的优先级高于二元运算符，这使得这个例子中的括号是必需的。

练习 1.1

下面是一系列的陈述。解释器对每个陈述的响应中打印的结果是什么？假设要按照呈现的顺序进行求值。

10;

5 + 3 + 4;

9 - 1;

6 / 2;

2 * 4 + (4 - 6);

const a = 3;

const b = a + 1;

 a + b + a * b;

a === b;

b > a && b < a * b ? b : a;

a === 4
? 6
: b === 4
? 6 + 7 + a
: 25;

2 + (b > a ? b : a);

(a > b
? a
: a < b
? b
: -1)
*
(a + 1);

最后两个陈述中条件表达式周围的括号是必需的，因为条件表达式的语法形式的优先级低于算术运算符+和*。

练习 1.2

将以下表达式翻译成 JavaScript

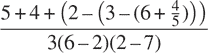
练习 1.3

声明一个以三个数字作为参数并返回两个较大数字的*方和的函数。

练习 1.4

注意我们的求值模型允许应用其函数表达式为复合表达式的应用。使用这一观察来描述a_plus_abs_b的行为：

function plus(a, b) { return a + b; }
function minus(a, b) { return a - b; }
function a_plus_abs_b(a, b) {
    return (b >= 0 ? plus : minus)(a, b);
}

练习 1.5

Ben Bitdiddle 发明了一个测试，以确定他所面对的解释器是使用应用序求值还是正则序求值。他声明了以下两个函数：

function p() { return p(); }

function test(x, y) {
    return x === 0 ? 0 : y;
}

然后他求值了这个陈述

test(0, p());

Ben 会观察到使用应用序求值的解释器会有什么行为？他会观察到使用正则序求值的解释器会有什么行为？解释你的答案。（假设条件表达式的求值规则在解释器使用正常或应用序时是相同的：谓词表达式首先被求值，结果决定是求值结果还是替代表达式。）

1.1.7 例子：牛顿法求*方根

如上所述，函数很像普通的数学函数。它们指定由一个或多个参数确定的值。但是数学函数和计算机函数之间有一个重要的区别。计算机函数必须是有效的。

作为一个例子，考虑计算*方根的问题。我们可以定义*方根函数为

√x = y，满足y ≥ 0和y² = x

这描述了一个完全合法的数学函数。我们可以用它来识别一个数字是否是另一个数字的*方根，或者推导关于*方根的一般事实。另一方面，这个定义并不描述一个计算机函数。事实上，它几乎没有告诉我们如何实际找到给定数字的*方根。重新用伪 JavaScript 重新表述这个定义也不会有所帮助：

function sqrt(x) {
    return the y with y >= 0 && square(y) === x;
}

这只是在回避问题。

数学函数和计算机函数之间的对比反映了描述事物属性和描述如何做事物的一般区别，有时也被称为声明性知识和命令性知识之间的区别。在数学中，我们通常关注声明性（是什么）描述，而在计算机科学中，我们通常关注命令性（如何）描述。¹⁷

如何计算*方根？最常见的方法是使用牛顿的迭代逼*法，该方法指出，每当我们对数字x的*方根的值有一个猜测y时，我们可以通过对y和x / y进行*均来进行简单的操作，得到一个更好的猜测（更接*实际*方根）。¹⁸ 例如，我们可以计算 2 的*方根如下。假设我们的初始猜测是 1：

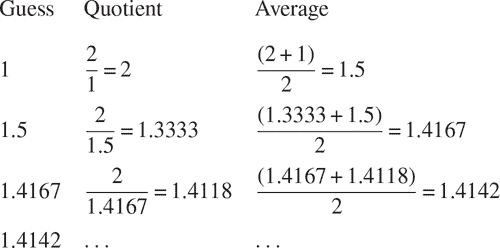
继续这个过程，我们得到越来越好的*似值。

现在让我们用函数的术语来形式化这个过程。我们从被开方数（我们试图计算其*方根的数字）的值和猜测的值开始。如果猜测对我们的目的来说足够好，我们就完成了；如果不是，我们必须用一个改进的猜测重复这个过程。我们将这个基本策略写成一个函数：

function sqrt_iter(guess, x) {
    return is_good_enough(guess, x)
           ? guess
           : sqrt_iter(improve(guess, x), x);
}

通过将猜测与被开方数和旧猜测的商进行*均来改进猜测：

function improve(guess, x) {
    return average(guess, x / guess);
}

其中

function average(x, y) {
    return (x + y) / 2;
}

我们还必须说明“足够好”的含义。以下内容可以用于说明，但实际上并不是一个非常好的测试。（见练习 1.7。）这个想法是改进答案，直到它足够接*，以至于它的*方与被开方数之间的差异小于预定的容差（这里是 0.001）：¹⁹

function is_good_enough(guess, x) {
    return abs(square(guess) - x) < 0.001;
}

最后，我们需要一种开始的方法。例如，我们总是可以猜测任何数字的*方根是 1：

function sqrt(x) {
    return sqrt_iter(1, x);
}

如果我们将这些声明输入解释器，我们可以像使用任何函数一样使用sqrt：

sqrt(9);
3.00009155413138

sqrt(100 + 37);
11.704699917758145

sqrt(sqrt(2) + sqrt(3));
1.7739279023207892

square(sqrt(1000));
1000.000369924366

sqrt程序还说明了我们迄今为止介绍的简单函数语言足以编写任何纯数值程序，这些程序可以在 C 或 Pascal 中编写。这可能看起来令人惊讶，因为我们的语言中没有包括任何迭代（循环）结构，指导计算机一遍又一遍地做某事。另一方面，函数sqrt_iter演示了如何使用除了普通调用函数的能力之外，还可以实现迭代。²⁰

练习 1.6

Alyssa P. Hacker 不喜欢条件表达式的语法，涉及到字符?和:。“为什么我不能只声明一个普通的条件函数，其应用方式就像条件表达式一样呢？”她问道。²¹ Alyssa 的朋友 Eva Lu Ator 声称这确实可以做到，并声明了一个conditional函数如下：

function conditional(predicate, then_clause, else_clause) {
    return predicate ? then_clause : else_clause;
}

Eva 为 Alyssa 演示程序：

conditional(2 === 3, 0, 5);
`5`
conditional(1 === 1, 0, 5);
`0`

高兴的是，Alyssa 使用conditional来重写*方根程序：

function sqrt_iter(guess, x) {
    return conditional(is_good_enough(guess, x),
                        guess,
                        sqrt_iter(improve(guess, x),
                                  x));
}

当 Alyssa 尝试使用这个方法来计算*方根时会发生什么？解释。

练习 1.7

用于计算*方根的is_good_enough测试对于找到非常小的数字的*方根不会非常有效。此外，在实际计算机中，算术运算几乎总是以有限的精度进行。这使得我们的测试对于非常大的数字是不够的。解释这些陈述，并举例说明测试对于小数字和大数字的失败。实现is_good_enough的另一种策略是观察guess从一次迭代到下一次迭代的变化，并在变化是猜测的一个非常小的分数时停止。设计一个使用这种结束测试的*方根函数。这对于小数字和大数字效果更好吗？

练习 1.8

牛顿的立方根方法是基于这样一个事实：如果y是x的立方根的*似值，那么更好的*似值由这个值给出

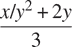
使用这个公式来实现一个类似于*方根函数的立方根函数。（在第 1.3.4 节中，我们将看到如何将牛顿方法作为这些*方根和立方根函数的抽象来实现。）

1.1.8 函数作为黑盒抽象

函数sqrt是我们第一个例子，它是由一组相互定义的函数定义的过程。请注意，sqrt_iter的声明是递归的；也就是说，函数是根据自身定义的。能够根据自身定义函数的想法可能会让人感到不安；可能不清楚这样的“循环”定义到底如何有意义，更不用说指定计算机执行的明确定义的过程了。这将在第 1.2 节中更加仔细地讨论。但首先让我们考虑一下sqrt示例所说明的一些其他重要点。

注意，计算*方根的问题自然地分解为许多子问题：如何判断猜测是否足够好，如何改进猜测，等等。每个任务都由一个单独的函数完成。整个sqrt程序可以被看作是一组函数（在图 1.2 中显示），它反映了将问题分解为子问题的过程。

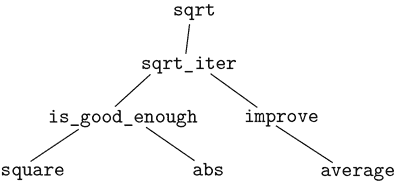
图 1.2 sqrt程序的功能分解。

这种分解策略的重要性不仅仅在于将程序分成部分。毕竟，我们可以将任何大型程序分成部分——前十行，接下来的十行，再接下来的十行，依此类推。相反，关键在于每个函数都能够完成一个可识别的任务，可以用作定义其他函数的模块。例如，当我们根据square定义is_good_enough函数时，我们可以将square函数视为“黑盒”。我们当时并不关心函数如何计算其结果，只关心它计算*方的事实。计算*方的细节可以被抑制，以便在以后考虑。实际上，就is_good_enough函数而言，square不完全是一个函数，而是一个函数的抽象，所谓的函数抽象。在这个抽象级别上，任何计算*方的函数都是一样好的。

因此，仅考虑它们返回的值，下面两个*方一个数字的函数应该是无法区分的。每个函数都接受一个数字参数，并将该数字的*方作为值返回。

function square(x) {
    return x * x;
}

function square(x) {
    return math_exp(double(math_log(x)));
}

function double(x) {
    return x + x;
}

因此，函数应该能够抑制细节。函数的用户可能并没有自己编写函数，而是从另一个程序员那里获得的一个黑盒。用户不需要知道函数的实现方式就能使用它。

本地名称

函数实现的一个细节不应该影响函数的用户，那就是实现者对函数参数的名称的选择。因此，以下函数不应该有区别：

function square(x) {
    return x * x;
}

function square(y) {
    return y * y;
}

这个原则——函数的含义应该与其作者使用的参数名称无关——表面上似乎是不言自明的，但其后果是深远的。最简单的结果是函数的参数名称必须局限于函数体内。例如，在我们的*方根函数的is_good_enough声明中，我们使用了square：

function is_good_enough(guess, x) {
    return abs(square(guess) - x) < 0.001;
}

is_good_enough的作者的意图是确定第一个参数的*方是否在给定的公差范围内与第二个参数相匹配。我们看到is_good_enough的作者使用名称guess来指代第一个参数，x指代第二个参数。square的参数是guess。如果square的作者使用x（如上所述）来指代该参数，我们可以看到is_good_enough中的x必须是与square中的不同的x。运行函数square不应该影响is_good_enough使用的x的值，因为is_good_enough在square计算完成后可能需要该值。

如果参数不是局限于各自函数体的局部变量，那么square中的参数x可能会与is_good_enough中的参数x混淆，而is_good_enough的行为将取决于我们使用的square的版本。因此，square将不会是我们所期望的黑匣子。

函数的参数在函数声明中有一个非常特殊的角色，即参数的名称是什么并不重要。这样的名称称为绑定，我们说函数声明绑定了它的参数。如果一个名称没有被绑定，我们说它是自由的。一个绑定声明名称的语句集被称为该名称的作用域。在函数声明中，作为函数参数声明的绑定名称具有函数体作为它们的作用域。

在上面的is_good_enough声明中，guess和x是绑定的名称，但abs和square是自由的。is_good_enough的含义应该与我们为guess和x选择的名称无关，只要它们与abs和square不同即可。（如果我们将guess重命名为abs，我们将通过捕获名称abs引入一个错误。它将从自由变为绑定。）然而，is_good_enough的含义并不独立于其自由名称的选择。然而，它肯定取决于（不包括在此声明中的）名称abs是指计算数字的绝对值的函数。如果我们在其声明中用math_cos（原始余弦函数）替换abs，is_good_enough将计算一个不同的函数。

内部声明和块结构

到目前为止，我们已经有一种名称隔离的方式：函数的参数是局限于函数体的。求*方根的程序展示了我们希望控制名称使用的另一种方式。现有的程序由独立的函数组成：

function sqrt(x) {
    return sqrt_iter(1, x);
}
function sqrt_iter(guess, x) {
    return is_good_enough(guess, x)
           ? guess
           : sqrt_iter(improve(guess, x), x);
}
function is_good_enough(guess, x) {
    return abs(square(guess) - x) < 0.001;
}
function improve(guess, x) {
    return average(guess, x / guess);
}

这个程序的问题在于，对于sqrt的用户来说，唯一重要的函数是sqrt。其他函数（sqrt_iter，is_good_enough和improve）只会混淆他们的思维。他们可能不会在另一个程序中声明任何名为is_good_enough的其他函数，以便与求*方根程序一起工作，因为sqrt需要它。这个问题在由许多独立程序员构建大型系统时尤为严重。例如，在构建大型数值函数库时，许多数值函数是作为连续逼*计算的，因此可能有名为is_good_enough和improve的辅助函数。我们希望将子函数局部化，将它们隐藏在sqrt内部，以便sqrt可以与其他连续逼*并存，每个都有自己的私有is_good_enough函数。

为了实现这一点，我们允许函数具有局部于该函数的内部声明。例如，在求*方根的问题中，我们可以写

function sqrt(x) {
    function is_good_enough(guess, x) {
        return abs(square(guess) - x) < 0.001;
    }
    function improve(guess, x) {
        return average(guess, x / guess);
        }
    function sqrt_iter(guess, x) {
        return is_good_enough(guess, x)
               ? guess
               : sqrt_iter(improve(guess, x), x);
    }
    return sqrt_iter(1, x);
}

任何匹配的大括号对都指定了一个块，并且块内的声明对该块是局部的。这种声明的嵌套，称为块结构，基本上是最简单的名称封装问题的正确解决方案。但这里潜在的想法更好。除了内部化辅助函数的声明外，我们还可以简化它们。由于x在sqrt的声明中被绑定，因此在sqrt内部声明的is_good_enough、improve和sqrt_iter函数在x的作用域内。因此，不需要显式地将x传递给这些函数中的每一个。相反，我们允许x在内部声明中成为一个自由名称，如下所示。然后，x从调用封闭函数sqrt的参数中获取其值。这种规则称为词法作用域。²⁴

function sqrt(x) {
    function is_good_enough(guess) {
        return abs(square(guess) - x) < 0.001;
    }
    function improve(guess) {
        return average(guess, x / guess);
    }
    function sqrt_iter(guess) {
        return is_good_enough(guess)
               ? guess
               : sqrt_iter(improve(guess));
    }
    return sqrt_iter(1);
}

我们将广泛使用块结构来帮助我们将大型程序分解为可处理的部分。²⁵ 块结构的概念起源于编程语言 Algol 60。它出现在大多数高级编程语言中，是帮助组织大型程序构建的重要工具。

1.2 函数及其生成的过程

我们现在已经考虑了编程的元素：我们使用了原始算术运算，我们组合了这些运算，并通过将它们声明为复合函数来抽象化这些复合运算。但这还不足以使我们能够说我们知道如何编程。我们的情况类似于学会了国际象棋中棋子如何移动的规则，但对典型的开局、战术或策略一无所知的人。就像初学国际象棋的人一样，我们还不知道领域中的常见使用模式。我们缺乏哪些着法是值得做的（哪些函数值得声明）的知识。我们缺乏预测做出着法（执行函数）后的后果的经验。

能够可视化所考虑行动的后果对于成为专业程序员至关重要，就像在任何综合的创造性活动中一样。例如，要成为专业摄影师，必须学会如何观察一个场景，并知道每个区域在曝光和处理选项的每种可能选择下在打印品上会显得多暗。只有这样，才能向后推理，规划构图、光线、曝光和处理，以获得期望的效果。编程也是如此，我们在规划进程采取的行动，并通过程序控制进程。要成为专家，我们必须学会可视化各种类型函数生成的过程。只有在我们培养了这样的技能之后，才能学会可靠地构建表现出所需行为的程序。

函数是计算过程的局部演变的模式。它指定了过程的每个阶段是如何建立在前一个阶段之上的。我们希望能够对由函数指定局部演变的过程的整体或全局行为做出陈述。这在一般情况下非常难以做到，但我们至少可以尝试描述一些典型的过程演变模式。

在本节中，我们将研究一些简单函数生成的常见“形状”。我们还将调查这些过程消耗时间和空间等重要计算资源的速率。我们将考虑的函数非常简单。它们的作用类似于摄影中的测试图案：作为过度简化的原型模式，而不是实际示例。

1.2.1 线性递归和迭代

我们首先考虑阶乘函数的定义。

n != n · (n – 1) *·* (n – 2) ... 3 · 2 · 1

计算阶乘有很多方法。一种方法是利用这样的观察：对于任何正整数n，n!等于n乘以(n – 1)!：

n! = n · [(n – 1) · (n – 2) ... 3 · 2 · 1] = n · (n – 1)!

因此，我们可以通过计算(n – 1)!并将结果乘以n来计算n!。如果我们添加规定 1! 等于 1，这一观察直接转化为计算机函数：

function factorial(n) {
    return n === 1
           ? 1
           : n * factorial(n - 1);
}

我们可以使用第 1.1.5 节的替换模型来观察这个函数计算6!的过程，如图 1.3 所示。

图 1.3 计算 6! 的线性递归过程。

现在让我们以不同的角度来计算阶乘。我们可以通过指定首先将 1 乘以 2，然后将结果乘以 3，然后乘以 4，依此类推，直到达到n，来描述计算n!的规则。更正式地说，我们保持一个运行乘积，以及一个从 1 计数到n的计数器。我们可以通过以下规则描述计算过程：

product ← counter · product

counter ← counter + 1

并规定当计数器超过n时，n!是乘积的值。

再次，我们可以将我们的描述重新构造为计算阶乘的函数：²⁶

function factorial(n) {
    return fact_iter(1, 1, n);
}
function fact_iter(product, counter, max_count) {
    return counter > max_count
           ? product
           : fact_iter(counter * product,
                       counter + 1,
                       max_count);
}

与之前一样，我们可以使用替换模型来可视化计算 6! 的过程，如图 1.4 所示。

图 1.4 计算 6! 的线性迭代过程。

比较这两个过程。从某种角度来看，它们似乎几乎没有什么不同。两者都在相同的域上计算相同的数学函数，并且每个都需要与n成比例的步骤来计算n!。事实上，这两个过程甚至执行相同的乘法序列，得到相同的部分积序列。另一方面，当我们考虑这两个过程的“形状”时，我们发现它们的演变方式完全不同。

考虑第一个过程。替换模型显示了一个扩展后跟着收缩的形状，如图 1.3 中的箭头所示。扩展发生在过程构建一系列延迟操作（在本例中是一系列乘法）时。收缩发生在实际执行操作时。这种过程，以一系列延迟操作为特征，被称为递归过程。执行这个过程需要解释器跟踪稍后要执行的操作。在计算n!时，延迟乘法的链的长度，因此需要跟踪它的信息量，与步骤数量一样，随n线性增长（与n成比例）。这样的过程被称为线性递归过程。

相比之下，第二个过程不会增长和缩小。在每一步中，无论n是多少，我们都只需要跟踪名称product、counter和max_count的当前值。我们称这个过程为迭代过程。一般来说，迭代过程是指其状态可以由固定数量的状态变量以及描述状态变量如何在过程从一个状态转移到另一个状态时更新的固定规则以及（可选的）结束测试来总结。在计算n!时，所需的步骤数量随n增长而线性增长。这样的过程被称为线性迭代过程。

两个过程之间的对比可以从另一个角度看出。在迭代的情况下，状态变量提供了在任何时候过程状态的完整描述。如果我们在步骤之间停止计算，只需向解释器提供三个状态变量的值，就可以恢复计算。而在递归过程中则不然。在这种情况下，还有一些额外的“隐藏”信息，由解释器维护，不包含在状态变量中，它指示了在处理延迟操作链时的“位置”。链越长，就必须维护的信息就越多。

在对比迭代和递归时，我们必须小心，不要混淆递归过程的概念和递归函数的概念。当我们将一个函数描述为递归时，我们指的是函数声明引用（直接或间接）函数本身的语法事实。但是当我们描述一个遵循某种模式的过程时，比如说线性递归，我们说的是过程如何演变，而不是函数的语法如何编写。将递归函数fact_iter称为生成迭代过程可能看起来令人不安。然而，这个过程确实是迭代的：它的状态完全由它的三个状态变量捕获，解释器只需要跟踪三个名称就能执行这个过程。

区分过程和函数可能令人困惑的一个原因是，大多数常见语言的实现（包括 C、Java 和 Python）都是设计成这样的方式，即任何递归函数的解释都会消耗随着函数调用次数增加而增长的内存，即使所描述的过程原则上是迭代的。因此，这些语言只能通过专门的“循环结构”（如do、repeat、until、for和while）来描述迭代过程。我们将在第 5 章中考虑的 JavaScript 实现不具有这个缺陷。即使迭代过程是由递归函数描述的，它也将在恒定空间中执行迭代过程。具有这种属性的实现被称为尾递归。使用尾递归实现，迭代可以使用普通的函数调用机制来表达，因此特殊的迭代结构只有作为语法糖才有用。

练习 1.9

以下两个函数中的每一个都定义了一个方法，用函数inc来增加其参数 1，和函数dec来减少其参数 1，来实现两个正整数的加法。

function plus(a, b) {
    return a === 0 ? b : inc(plus(dec(a), b));
}

function plus(a, b) {
    return a === 0 ? b : plus(dec(a), inc(b));
}

使用替换模型，说明每个函数生成的过程在求值plus(4, 5);时。这些过程是迭代的还是递归的？

练习 1.10

以下函数计算了一个称为 Ackermann 函数的数学函数。

function A(x, y) {
    return y === 0
           ? 0
           : x === 0
           ? 2 * y
           : y === 1
           ? 2
           : A(x - 1, A(x, y - 1));
}

以下语句的值是多少？

A(1, 10);

A(2, 4);

A(3, 3);

考虑以下函数，其中A是上面声明的函数：

function f(n) {
    return A(0, n);
}
function g(n) {
    return A(1, n);
}
function h(n) {
    return A(2, n);
}
function k(n) {
    return 5 * n * n;
}

给出函数f，g和h的简洁数学定义，用于正整数值n。例如，k(n)计算5n²。

1.2.2 树递归

另一种常见的计算模式称为树递归。例如，考虑计算斐波那契数列，其中每个数字是前两个数字的和：

0, 1, 1, 2, 3, 5, 8, 13, 21, ...

一般来说，斐波那契数可以通过以下规则定义

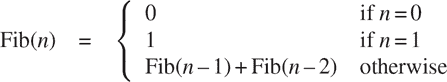
我们可以立即将这个定义转化为一个递归函数，用于计算斐波那契数：

function fib(n) {
    return n === 0
           ? 0
           : n === 1
           ? 1
           : fib(n - 1) + fib(n - 2);
}

考虑这个计算的模式。要计算fib(5)，我们计算fib(4)和fib(3)。要计算fib(4)，我们计算fib(3)和fib(2)。一般来说，演变的过程看起来像一棵树，如图 1.5 所示。注意到在每个级别（除了底部）分支分成两个，这反映了fib函数每次被调用时调用自身两次的事实。

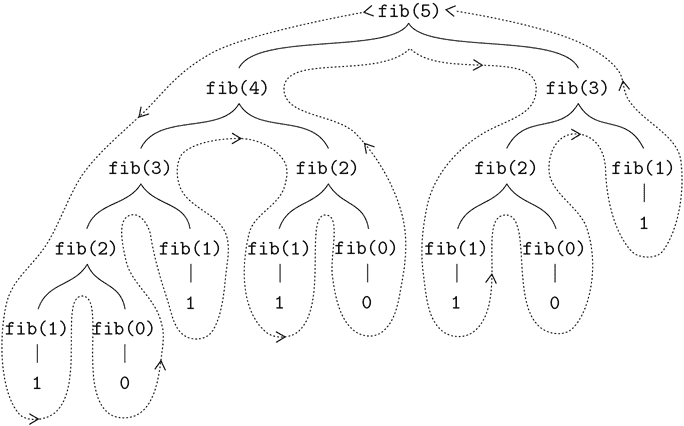
图 1.5 计算fib(5)时生成的树递归过程。

这个函数作为一个典型的树递归很有启发性，但它是计算斐波那契数的一种可怕的方式，因为它做了很多冗余的计算。注意在图 1.5 中，fib(3)的整个计算——几乎一半的工作——是重复的。事实上，不难证明函数将计算fib(1)或fib(0)（通常情况下上述树中的叶子数）的次数恰好是Fib(n + 1)。为了了解这有多糟糕，可以证明Fib(n)的值随着n的增长呈指数增长。更准确地说（见练习 1.13），Fib(n)是最接*ϕⁿ/√5的整数，其中

ϕ = (1 + √5)/2 ≈ 1.6180

是黄金比例，满足方程

ϕ² = ϕ + 1

因此，这个过程所需的步骤数随着输入的增长呈指数增长。另一方面，所需的空间只是线性增长，因为我们只需要在计算的任何时候跟踪树中在我们上面的哪些节点。一般来说，树递归过程所需的步骤数将与树中的节点数成正比，而所需的空间将与树的最大深度成正比。

我们还可以制定一个迭代的过程来计算斐波那契数。这个想法是使用一对整数a和b，初始化为Fib(1) = 1和Fib(0) = 0，并反复应用同时的转换

a ← a + b
b ← a

不难证明，经过这种转换n次后，a和b分别等于Fib(n + 1)和Fib(n)。因此，我们可以使用以下函数迭代地计算斐波那契数

function fib(n) {
    return fib_iter(1, 0, n);
}
function fib_iter(a, b, count) {
    return count === 0
           ? b
           : fib_iter(a + b, a, count - 1);
}

这种计算Fib(n)的第二种方法是线性迭代。这两种方法所需的步骤数的差异——一个与n成正比，一个与Fib(n)本身一样快地增长——是巨大的，即使对于小的输入也是如此。

我们不应该因此得出树递归过程是无用的结论。当我们考虑操作层次结构化数据而不是数字的过程时，我们会发现树递归是一种自然而强大的工具。³⁰但即使在数值运算中，树递归过程也可以帮助我们理解和设计程序。例如，尽管第一个fib函数比第二个函数效率低得多，但它更直接，几乎只是斐波那契数列定义的 JavaScript 翻译。要制定迭代算法，需要注意到计算可以重塑为具有三个状态变量的迭代。

例子：找零

只需要一点巧妙就能想出迭代的斐波那契算法。相比之下，考虑以下问题：我们有多少种不同的方法可以找零 1.00 美元（100 美分），给定半美元、25 美分、10 美分、5 美分和 1 美分的硬币（分别为 50 美分、25 美分、10 美分、5 美分和 1 美分）？更一般地，我们能否编写一个函数来计算任意给定金额的找零方式？

这个问题有一个简单的解决方案，作为一个递归函数。假设我们把可用的硬币类型按照某种顺序排列。那么以下关系成立：

使用n种硬币来改变金额a的方式数等于

使用除第一种硬币之外的所有硬币来改变金额a的方式，再加上
使用所有n种硬币来改变金额a - d的方式，其中d是第一种硬币的面额。

要看到这是为什么，观察一下找零的方式可以分为两组：那些不使用第一种硬币的和那些使用的。因此，某个金额的找零方式的总数等于不使用第一种硬币的金额的找零方式的数量，加上假设我们使用第一种硬币的找零方式的数量。但后者的数量等于使用第一种硬币后剩下的金额的找零方式的数量。

因此，我们可以递归地将改变给定金额的问题减少到改变较小金额或使用更少种类的硬币的问题。仔细考虑这个减少规则，并让自己相信，我们可以用它来描述一个算法，如果我们指定以下退化情况：³¹

如果a恰好为 0，我们应该将其视为 1 种找零的方式。
如果a小于 0，我们应该将其视为 0 种找零的方式。
如果n为 0，我们应该将其视为 0 种找零的方式。

我们可以很容易地将这个描述转化为一个递归函数：

function count_change(amount) {
    return cc(amount, 5);
}
function cc(amount, kinds_of_coins) {
    return amount === 0
           ? 1
           : amount < 0 || kinds_of_coins === 0
           ? 0
           : cc(amount, kinds_of_coins - 1)
             +
             cc(amount - first_denomination(kinds_of_coins), 
                kinds_of_coins);
}
function first_denomination(kinds_of_coins) {
    return kinds_of_coins === 1 ? 1
         : kinds_of_coins === 2 ? 5
         : kinds_of_coins === 3 ? 10
         : kinds_of_coins === 4 ? 25
         : kinds_of_coins === 5 ? 50
         : 0;
}

（first_denomination函数以可用硬币种类的数量作为输入，并返回第一种硬币的面额。在这里，我们将硬币按从大到小的顺序排列，但任何顺序都可以。）现在我们可以回答关于找零一美元的最初问题：

count_change(100);
292

函数count_change生成了一个树形递归过程，其中包含与我们对fib的第一个实现类似的冗余。另一方面，设计一个更好的算法来计算结果并不明显，我们将这个问题留作挑战。树形递归过程可能非常低效，但通常易于指定和理解的观察，这导致人们提出，通过设计一个“智能编译器”，可以将树形递归函数转换为计算相同结果的更有效的函数，从而获得两全其美的最佳结果。³²

练习 1.11

一个函数f由以下规则定义：如果n < 3，f(n) = n，如果n > 3，f(n) = f(n - 1) + 2f(n - 2) + 3f(n - 3)。编写一个通过递归过程计算f的 JavaScript 函数。编写一个通过迭代过程计算f的函数。

练习 1.12

以下数字模式称为帕斯卡三角形。

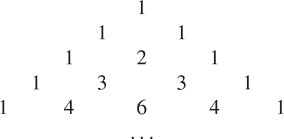
三角形边缘的数字都是 1，三角形内部的每个数字都是它上面两个数字的和。³³编写一个通过递归过程计算帕斯卡三角形元素的函数。

练习 1.13

证明Fib(n)是最接*ϕⁿ/√5的整数，其中ϕ=(1+√5)/2。提示：使用归纳法和斐波那契数的定义来证明Fib(n)=(ϕⁿ-ψⁿ)/√5，其中ψ=(1-√5)/2。

1.2.3 增长的顺序

前面的例子说明了过程在消耗计算资源的速率上可能有很大的不同。描述这种差异的一种方便的方法是使用增长的顺序的概念，以获得一个粗略的度量，即随着输入变大，过程所需的资源。

让n成为衡量问题规模的参数，R(n)是过程对规模为n的问题所需的资源量。在我们之前的例子中，我们取n为要计算给定函数的数字，但还有其他可能性。例如，如果我们的目标是计算一个数字的*方根的*似值，我们可能会取n为所需的精度位数。对于矩阵乘法，我们可能会取n为矩阵中的行数。一般来说，关于问题的一些属性是值得分析给定过程的。同样，R(n)可能衡量使用的内部存储寄存器的数量，执行的基本机器操作的数量等等。在一次只执行固定数量的操作的计算机中，所需的时间将与执行的基本机器操作的数量成正比。

我们说R(n)的增长顺序是Θ(f(n))，写作R(n) = Θ(f(n))（读作“theta f(n)”），如果存在正常数k[1]和k[2]，独立于n，使得

k[1] f(n) ≤ R(n) ≤ k[2] f(n)

对于任何足够大的n值。（换句话说，对于大的n，值R(n)夹在k[1]f(n)和k[2]f(n)之间。）

例如，在第 1.2.1 节中描述的用于计算阶乘的线性递归过程，步数与输入n成比例增长。因此，此过程所需的步数增长为Θ(n)。我们还看到所需的空间增长为Θ(n)。对于迭代阶乘，步数仍然是Θ(n)，但空间是Θ(1)——即常数。[^34] 在第 1.2.2 节中描述的黄金比例ϕ，树递归的斐波那契计算需要Θ(ϕⁿ)步和Θ(n)空间。

增长顺序只提供了对过程行为的粗略描述。例如，需要n²步的过程和需要1000n²步的过程以及需要3n² + 10n + 17步的过程都具有Θ(n²)的增长顺序。另一方面，增长顺序提供了一个有用的指示，告诉我们当问题的规模改变时，我们可以期望过程的行为如何改变。对于Θ(n)（线性）过程，将问题规模加倍将大致使资源使用量加倍。对于指数过程，问题规模的每个增量将通过一个常数因子来增加资源利用率。在第 1.2 节的其余部分，我们将研究两种增长顺序为对数的算法，因此问题规模加倍将使资源需求增加一个常数量。

练习 1.14

绘制树，说明第 1.2.2 节中的count_change函数生成的过程，用于找零 11 美分。随着要找零的金额增加，该过程使用的空间和步数的增长顺序是多少？

练习 1.15

如果x足够小，则可以利用*似值sin x ≈ x来计算角的正弦（以弧度表示），以及三角恒等式

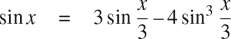
减小sin的参数大小。（对于本练习而言，如果角的大小不大于 0.1 弧度，则被认为是“足够小”。）这些想法被纳入以下函数：

function cube(x) {
    return x * x * x;
}
function p(x) {
    return 3 * x - 4 * cube(x);
}
function sine(angle) {
    return ! (abs(angle) > 0.1)
           ? angle
           : p(sine(angle / 3));
}

a. 当计算sine(12.15)时，函数p被应用了多少次？
b. 当计算sine(a)时，由sine函数生成的过程的空间和步数的增长顺序是多少（作为a的函数）？

1.2.4 指数

考虑计算给定数字的指数的问题。我们希望有一个函数，它以基数b和正整数指数n作为参数，并计算bⁿ。一种方法是通过递归定义来实现这一点

bⁿ = b bⁿ^(–1)

b⁰ = 1

这很容易转化为函数

function expt(b, n) {
    return n === 0
           ? 1
           : b * expt(b, n - 1);
}

这是一个线性递归过程，需要Θ(n)步和Θ(n)空间。就像阶乘一样，我们可以很容易地制定一个等效的线性迭代：

function expt(b, n) {
    return expt_iter(b, n, 1);
}
function expt_iter(b, counter, product) {
    return counter === 0
           ? product
           : expt_iter(b, counter - 1, b * product);
}

这个版本需要Θ(n)步和Θ(1)空间。

通过使用连续*方，我们可以用更少的步骤计算指数。例如，不是计算b⁸为

b · (b · (b · (b · (b · (b · (b · b))))))

我们可以使用三次乘法来计算它：

b² = b · b

b⁴ = b² · b²

b⁸ = b⁴ · b⁴

这种方法适用于 2 的幂次方。如果我们使用规则

bⁿ = (b^(n/2))²如果n是偶数

bⁿ = b · b^(n–1)如果n是奇数

我们可以将这种方法表达为一个函数：

function fast_expt(b, n) {
    return n === 0
           ? 1
           : is_even(n)
           ? square(fast_expt(b, n / 2))
           : b * fast_expt(b, n - 1);
}

其中用于测试整数是否为偶数的谓词是根据运算符％定义的，该运算符在整数除法后计算余数，通过

function is_even(n) {
    return n % 2 === 0;
}

fast_expt产生的过程在空间和步数上都以对数方式增长。观察到使用fast_expt计算b²ⁿ只需要比计算bⁿ多一次乘法。因此，我们可以大约每次允许新的乘法时，我们可以计算的指数大小加倍。因此，对于n的指数所需的乘法数量大约与以 2 为底的n的对数一样快。该过程具有Θ(log n)增长。³⁵

当n变大时，Θ(log n)增长和Θ(n)增长之间的差异变得明显。例如，n=1000时，fast_expt只需要 14 次乘法。³⁶也可以使用连续*方的想法设计一个迭代算法，该算法使用对数数量的步骤计算指数（参见练习 1.16），尽管通常情况下，这与递归算法一样，不那么直接。³⁷

练习 1.16

设计一个函数，它演变出一个使用连续*方并使用对数数量步骤的迭代指数过程，就像fast_expt一样。（提示：使用观察到的事实(b^(n/2))² = (b²)^(n/2)，除了指数n和基数b之外，还保留一个额外的状态变量a，并定义状态转换，使得乘积abⁿ从一个状态到另一个状态保持不变。在过程开始时，a被认为是 1，并且答案由过程结束时的a的值给出。通常，定义一个从一个状态到另一个状态保持不变的不变量数量的技术是思考设计迭代算法的强大方法。）

练习 1.17

本节中的幂运算算法是基于通过重复乘法进行幂运算。类似地，可以通过重复加法执行整数乘法。下面的乘法函数（假设我们的语言只能加法，不能乘法）类似于expt函数：

function times(a, b) {
    return b === 0
           ? 0
           : a + times(a, b - 1);
}

该算法的步骤数量与b成正比。现在假设我们还包括double函数，它可以将整数加倍，以及halve函数，它可以将（偶数）整数除以 2。使用这些函数，设计一个类似于fast_expt的乘法函数，它使用对数数量的步骤。

练习 1.18

使用练习 1.16 和 1.17 的结果，设计一个函数，该函数生成一个迭代过程，用于以加法，加倍和减半的术语乘以两个整数，并且使用对数数量的步骤。³⁸

练习 1.19

有一个巧妙的算法可以在对数步骤内计算斐波那契数。回顾第 1.2.2 节中fib_iter过程中状态变量a和b的转换：a, a + b和b, a。将这个转换称为T，观察到反复应用Tⁿ次，从 1 和 0 开始，会产生一对Fib(n + 1)和Fib(n)。换句话说，斐波那契数是通过从一对(1, 0)开始应用Tⁿ，即T的n次幂，产生的。现在考虑T是变换T[pq]中p = 0和q = 1的特殊情况，其中T[pq]根据a ← bq + aq + ap和b ← bp + aq转换对(a, b)。证明如果我们两次应用这样的变换T[pq]，其效果与使用相同形式的单个变换T[p′q′]相同，并计算p′和q′。这给了我们一个明确的方法来*方这些变换，因此我们可以使用连续*方来计算Tⁿ，就像fast_expt函数中一样。将所有这些放在一起，完成以下函数，可以在对数步骤内运行：³⁹

function fib(n) {
    return fib_iter(1, 0, 0, 1, n);
}
function fib_iter(a, b, p, q, count) {
    return count === 0
           ? b
           : is_even(count)
           ? fib_iter(a,
                      b,
                      (??),          // compute p′
                      (??),          // compute q′
                      count / 2)
           : fib_iter(b * q + a * q + a * p,
                      b * p + a * q,
                      p,
                      q,
                      count - 1);
}

1.2.5 最大公约数

两个整数a和b的最大公约数（GCD）被定义为能够整除a和b且没有余数的最大整数。例如，16 和 28 的 GCD 是 4。在第 2 章中，当我们研究如何实现有理数算术时，我们需要能够计算 GCD 以将有理数化简为最低项。（要将有理数化简为最低项，我们必须将分子和分母都除以它们的 GCD。例如，16/28 化简为 4/7。）找到两个整数的 GCD 的一种方法是对它们进行因式分解并搜索公因数，但有一个著名的算法效率更高。

该算法的思想基于这样的观察：如果a除以b的余数为r，那么a和b的公约数恰好与b和r的公约数相同。因此，我们可以使用方程式

GCD(a, b) = GCD(b, r)

将计算 GCD 的问题逐步减少为计算更小的整数对的 GCD 的问题。例如，

GCD(206, 40) = GCD(40, 6)

= GCD(6, 4)

= GCD(4, 2)

= GCD(2, 0)

= 2

将 GCD(206, 40)减少到 GCD(2, 0)，即为 2。可以证明，从任意两个正整数开始，进行重复的减少操作最终总会产生一个第二个数字为 0 的对。然后 GCD 就是对中的另一个数字。这种计算 GCD 的方法被称为欧几里得算法。⁴⁰

很容易将欧几里得算法表达为一个函数：

function gcd(a, b) {
    return b === 0 ? a : gcd(b, a % b);
}

这产生了一个迭代过程，其步数随涉及的数字的对数增长。

欧几里得算法所需的步骤数量具有对数增长与斐波那契数有有趣的关系：

拉梅定理：如果欧几里得算法需要k步来计算一对的 GCD，那么一对中较小的数字必须大于或等于第k个斐波那契数。⁴¹

我们可以使用这个定理来估计欧几里得算法的增长顺序。让n为函数的两个输入中较小的那个。如果过程需要k步，那么我们必须有n ≥ Fib(k) ≈ ϕ^k/√5。因此，步数k随着n的对数（以ϕ为底）增长。因此，增长顺序为Θ(log n)。

练习 1.20

函数生成的过程当然取决于解释器使用的规则。例如，考虑上面给出的迭代gcd函数。假设我们使用正则序求值来解释这个函数，就像在 1.1.5 节中讨论的那样。(条件表达式的正则序求值规则在练习 1.5 中描述。)使用替换方法(用于正则序)，说明在求值gcd(206, 40)时生成的过程，并指出实际执行的remainder操作。在正则序求值gcd(206, 40)时实际执行了多少次remainder操作？在应用序求值中呢？

1.2.6 示例：素性测试

本节描述了检查整数n的素性的两种方法，一种具有Θ(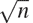)的增长阶数，另一种是具有Θ(log n)的“概率”算法。本节末尾的练习建议基于这些算法进行编程项目。

寻找除数

自古以来，数学家们一直对素数问题着迷，许多人一直致力于确定测试数字是否为质数的方法。测试一个数是否为质数的一种方法是找到这个数的除数。以下程序找到给定数字n的最小整数除数(大于 1)。它通过以 2 开始的连续整数测试n是否可被整除的方式来直接进行。

function smallest_divisor(n) {
    return find_divisor(n, 2);
}
function find_divisor(n, test_divisor) {
    return square(test_divisor) > n
           ? n
           : divides(test_divisor, n)
           ? test_divisor
           : find_divisor(n, test_divisor + 1);
}
function divides(a, b) {
    return b % a === 0;
}

我们可以通过以下方式测试一个数是否为质数：n是质数当且仅当n是其自身的最小除数。

function is_prime(n) {
    return n === smallest_divisor(n);
}

find_divisor的结束测试基于这样一个事实，即如果n不是质数，它必须有一个小于或等于√n的除数。⁴²这意味着算法只需要测试 1 和√n之间的除数。因此，识别n为质数所需的步骤数量将具有Θ(√n)的增长阶数。

费马测试

Θ(log n)素性测试基于数论中称为费马小定理的结果。⁴³

费马小定理: 如果n是一个质数，a是小于n的任意正整数，则a的n次幂与n模同余。

(如果两个数除以n的余数相同，则它们被称为n模同余。当一个数a除以n的余数也被称为a模n的余数，或者简称为a模n。)

如果n不是质数，那么一般来说，大多数小于n的数a都不满足上述关系。这导致了用于测试素性的以下算法：给定一个数n，选择一个小于n的随机数a，并计算aⁿ模n的余数。如果结果不等于a，那么n肯定不是质数。如果它等于a，那么n很可能是质数。现在选择另一个随机数a，并用相同的方法进行测试。如果它也满足方程，则我们可以更加确信n是质数。通过尝试更多的a值，我们可以增加对结果的信心。这个算法被称为费马测试。

为了实现费马测试，我们需要一个计算一个数的指数模另一个数的函数：

function expmod(base, exp, m) {
    return exp === 0
           ? 1
           : is_even(exp)
           ? square(expmod(base, exp / 2, m)) % m
           : (base * expmod(base, exp - 1, m)) % m;
}

这与 1.2.4 节中的fast_expt函数非常相似。它使用连续*方，因此步骤数量随指数对数增长。⁴⁴

费马测试是通过随机选择一个介于 1 和n-1之间的数字a来执行的，并检查a的n次幂的模n的余数是否等于a。随机数a是使用原始函数math_random选择的，该函数返回小于 1 的非负数。因此，要获得 1 和n-1之间的随机数，我们将math_random的返回值乘以n-1，用原始函数math_floor向下舍入结果，然后加 1。

function fermat_test(n) {
    function try_it(a) {
        return expmod(a, n, n) === a;
    }
    return try_it(1 + math_floor(math_random() * (n - 1)));
}

以下函数根据参数指定的次数运行测试。如果测试每次都成功，则其值为true，否则为false。

function fast_is_prime(n, times) {
    return times === 0
           ? true
           : fermat_test(n)
           ? fast_is_prime(n, times - 1)
           : false;
}

概率方法

费马测试在性质上与大多数熟悉的算法不同，大多数算法计算的答案是保证正确的。在这里，获得的答案只是可能正确。更准确地说，如果n曾经未通过费马测试，我们可以肯定n不是质数。但是，n通过测试的事实，虽然是一个极为强有力的指示，但仍不能保证n是质数。我们想说的是，对于任何数字n，如果我们进行足够多次测试并发现n总是通过测试，那么我们的素性测试中的错误概率可以尽可能小。

不幸的是，这个断言并不完全正确。确实存在一些可以欺骗费马测试的数字：不是质数但具有性质aⁿ对n取模等于a对n取模的数字n，其中所有整数a < n。这样的数字非常罕见，因此费马测试在实践中是相当可靠的。费马测试有一些无法被欺骗的变体。在这些测试中，与费马方法一样，通过选择一个随机整数a < n并检查依赖于n和a的某些条件来测试整数n的素性。（有关这种测试的示例，请参见练习 1.28。）另一方面，与费马测试相反，可以证明对于任何n，除非n是质数，否则大多数整数a < n都不满足条件。因此，如果n对某个随机选择的a通过了测试，那么n是质数的可能性甚至更大。如果n对两个随机选择的a通过了测试，那么n是质数的可能性超过 4 分之 3。通过使用更多和更多随机选择的a值运行测试，我们可以使错误的概率尽可能小。

对于可以证明错误几率变得任意小的测试的存在引起了对这种类型算法的兴趣，这种算法被称为概率算法。在这个领域有大量的研究活动，概率算法已经成功地应用到许多领域。

练习 1.21

使用smallest_divisor函数找出以下数字的最小除数：199、1999、19999。

练习 1.22

假设有一个没有参数的原始函数get_time，它返回自 1970 年 1 月 1 日星期四 UTC 时间 0000 以来经过的毫秒数。以下timed_prime_test函数在调用整数 n 时打印 n 并检查 n 是否为质数。如果 n 是质数，则该函数打印三个星号，然后是执行测试所用的时间量。

function timed_prime_test(n) { 
    display(n);
    return start_prime_test(n, get_time());
}
function start_prime_test(n, start_time) {
    return is_prime(n)
           ? report_prime(get_time() - start_time)
           : true;
}
function report_prime(elapsed_time) {
    display(" *** ");
    display(elapsed_time);
}

使用这个函数，编写一个名为search_for_primes的函数，它检查指定范围内连续奇数的素性。使用你的函数找到大于 1000 的三个最小素数；大于 10,000；大于 100,000；大于 1,000,000。注意测试每个素数所需的时间。由于测试算法的增长阶为Θ(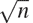)，你应该期望在 10,000 左右的素数测试大约需要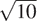倍于在 1000 左右的素数测试。你的计时数据是否支持这一点？100,000 和 1,000,000 的数据对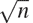的预测有多好的支持？你的结果是否符合程序在你的机器上运行时间与计算所需步骤数量成正比的概念？

练习 1.23

本节开头显示的smallest_divisor函数进行了许多不必要的测试：在检查数字是否可被 2 整除后，没有必要检查它是否可被任何更大的偶数整除。这表明用于test_divisor的值不应该是 2, 3, 4, 5, 6, ...而应该是 2, 3, 5, 7, 9，为了实现这个改变，声明一个函数next，如果它的输入等于 2，则返回 3，否则返回它的输入加 2。修改smallest_divisor函数，使用next(test_divisor)代替test_divisor + 1。使用包含这个修改版本的smallest_divisor的timed_prime_test，对在练习 1.22 中找到的 12 个素数进行测试。由于这个修改减少了测试步骤的数量，你应该期望它运行大约快两倍。这个期望是否得到确认？如果没有，两个算法的速度比率是多少，你如何解释它与 2 不同的事实？

练习 1.24

修改练习 1.22 的timed_prime_test函数，使用fast_is_prime（费马方法），并测试你在那个练习中找到的 12 个素数。由于费马测试具有Θ(log n)的增长，你会预期测试接* 1,000,000 的素数所需的时间与测试接* 1000 的素数相比如何？你的数据是否支持这一点？你能解释你发现的任何差异吗？

练习 1.25

Alyssa P. Hacker 抱怨我们在编写expmod时做了很多额外的工作。她说，毕竟，既然我们已经知道如何计算指数，我们本来可以简单地写成

function expmod(base, exp, m) {
    return fast_expt(base, exp) % m;
}

她是正确的吗？这个函数对我们的快速素数测试器是否有用？解释一下。

练习 1.26

路易斯·里森纳在做练习 1.24 时遇到了很大的困难。他的fast_is_prime测试似乎比他的is_prime测试运行得更慢。路易斯叫他的朋友伊娃·卢·阿托过来帮忙。当他们检查路易斯的代码时，他们发现他已经重写了expmod函数，使用了显式乘法，而不是调用square：

function expmod(base, exp, m) {
    return exp === 0
           ? 1
           : is_even(exp)
           ? (  expmod(base, exp / 2, m)
              * expmod(base, exp / 2, m)) % m
           : (base * expmod(base, exp - 1, m)) % m;
}

“我不明白那会有什么不同，”路易斯说。“我明白，”伊娃说。“通过那样写函数，你已经将Θ(log n)的过程转变为Θ(n)的过程。”解释一下。

练习 1.27

证明脚注 45 中列出的卡迈克尔数确实愚弄了费马测试。也就是说，编写一个函数，它接受一个整数n，并测试对于每个a < n，aⁿ是否与a模n同余，并在给定的卡迈克尔数上尝试你的函数。

练习 1.28

一个无法被愚弄的费马测试的变体被称为米勒-拉宾测试（Miller 1976; Rabin 1980）。这是从费马小定理的另一种形式开始的，该定理陈述了如果n是一个质数，a是小于n的任意正整数，则a的(n - 1)次方与n模同余于 1。通过米勒-拉宾测试来测试一个数n的素性，我们选择一个随机数a < n，并使用expmod函数将a的(n - 1)次方模n。然而，每当我们在expmod中执行*方步骤时，我们检查是否发现了“非*凡的模n的*方根”，即不等于 1 或n - 1的*方等于模n的 1 的数。可以证明，如果存在这样一个非*凡的模 1 的*方根，那么n不是质数。也可以证明，如果n是一个不是质数的奇数，那么至少有一半的数a < n，通过这种方式计算a^(n–1)将会显示出模n的非*凡的*方根。（这就是为什么米勒-拉宾测试无法被愚弄的原因。）修改expmod函数以便在发现非*凡的模 1 的*方根时发出信号，并使用这个来实现米勒-拉宾测试，方法类似于fermat_test。通过测试各种已知的质数和非质数来检查你的函数。提示：使expmod发出信号的一个方便的方法是让它返回 0。

1.3 用高阶函数制定抽象

我们已经看到，函数实际上是描述数字的复合操作的抽象，与特定数字无关。例如，当我们声明

function cube(x) {
    return x * x * x;
}

我们不是在谈论特定数字的立方，而是在谈论获得任何数字的立方的方法。当然，我们可以不声明这个函数，总是写诸如

3 * 3 * 3
x * x * x
y * y * y

并且从不明确提到cube。这将使我们处于严重的不利地位，迫使我们总是在语言中原语的特定操作级别上工作（在这种情况下是乘法），而不是在更高级别的操作上工作。我们的程序可以计算立方，但我们的语言缺乏表达立方概念的能力。我们应该从一个强大的编程语言中要求的一件事是，通过为常见模式分配名称来构建抽象的能力，然后直接使用这些抽象。函数提供了这种能力。这就是为什么除了最原始的编程语言之外，所有的编程语言都包括声明函数的机制。

然而，即使在数值处理中，如果我们被限制为参数必须是数字的函数，我们在创建抽象的能力上也会受到严重限制。通常相同的编程模式会与许多不同的函数一起使用。为了将这样的模式表达为概念，我们需要构建可以接受函数作为参数或返回函数作为值的函数。操作函数的函数称为高阶函数。本节展示了高阶函数如何作为强大的抽象机制，大大增加了我们语言的表达能力。

1.3.1 函数作为参数

考虑以下三个函数。第一个计算从a到b的整数的和：

function sum_integers(a, b) {
    return a > b
           ? 0
           : a + sum_integers(a + 1, b);
}

第二个计算给定范围内整数的立方和：

function sum_cubes(a, b) {
    return a > b
           ? 0
           : cube(a) + sum_cubes(a + 1, b);
}

第三个计算序列中一系列项的和

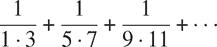
这收敛到π/8（非常慢）：⁴⁹

function pi_sum(a, b) {
    return a > b
           ? 0
           : 1 / (a * (a + 2)) + pi_sum(a + 4, b);
}

这三个函数显然共享一个共同的基本模式。它们在大部分情况下是相同的，只是函数的名称不同，用于计算要添加的项的a的函数不同，以及提供a的下一个值的函数不同。我们可以通过在相同的模板中填充槽来生成每个函数：

function name(a, b) {
    return a > b
           ? 0
           : term(a) + name(next(a), b);
}

这种常见模式的存在是有力的证据，表明有一个有用的抽象正在等待被提出。事实上，数学家很久以前就确定了级数求和的抽象，并发明了“Σ符号”，例如

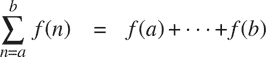
来表达这个概念。Σ符号的力量在于它允许数学家处理求和概念本身，而不仅仅是特定的和，例如，制定关于独立于被求和的特定系列的一般结果。

同样，作为程序设计师，我们希望我们的语言足够强大，以便我们可以编写一个表达求和概念本身而不仅仅是计算特定和的函数。在我们的函数语言中，我们可以很容易地采用上面显示的常见模板，并将“插槽”转换为参数：

function sum(term, a, next, b) {
    return a > b
           ? 0
           : term(a) + sum(term, next(a), next, b);
}

注意，sum以它的参数下限和上限a和b以及函数term和next作为参数。我们可以像使用任何函数一样使用sum。例如，我们可以使用它（以及一个将其参数增加 1 的函数inc）来定义sum_cubes：

function inc(n) {
    return n + 1;
}
function sum_cubes(a, b) {
    return sum(cube, a, inc, b);
}

使用这个，我们可以计算 1 到 10 的整数的立方和：

sum_cubes(1, 10);
3025

借助一个计算项的恒等函数，我们可以定义sum_integers：

function identity(x) {
    return x;
}

function sum_integers(a, b) {
    return sum(identity, a, inc, b);
}

然后我们可以计算 1 到 10 的整数的和：

sum_integers(1, 10);
55

我们也可以用同样的方法定义pi_sum：⁵⁰

function pi_sum(a, b) {
    function pi_term(x) {
        return 1 / (x * (x + 2));
    }
    function pi_next(x) {
        return x + 4;
    }
    return sum(pi_term, a, pi_next, b);
}

使用这些函数，我们可以计算π的*似值：

8 * pi_sum(1, 1000);
3.139592655589783

一旦我们有了sum，我们就可以将其用作构建进一步概念的基础。例如，函数f在限制a和b之间的定积分可以使用以下公式在数值上*似：

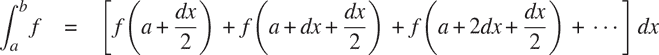
对于小的dx值。我们可以直接表示这个函数：

function integral(f, a, b, dx) {
    function add_dx(x) {
        return x + dx;
    }
    return sum(f, a + dx / 2, add_dx, b) * dx;
}

integral(cube, 0, 1, 0.01);
0.24998750000000042

integral(cube, 0, 1, 0.001);
0.249999875000001

（函数cube在 0 和 1 之间的积分的确切值为 1/4。）

练习 1.29

辛普森法则是一种比上面所示方法更准确的数值积分方法。使用辛普森法则，函数f在a和b之间的积分可以*似为

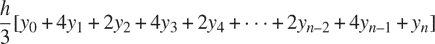
其中h = (b - a)/n，对于一些偶数n，y[k] = f(a + kh)。（增加n会增加*似的准确性。）声明一个函数，它以f, a, b和n作为参数，并使用辛普森法则计算积分的值。使用你的函数来计算cube在 0 和 1 之间的积分（n = 100和n = 1000），并将结果与上面所示的integral函数的结果进行比较。

练习 1.30

上面的sum函数生成一个线性递归。可以重写该函数，使求和以迭代方式执行。通过填写以下声明中的缺失表达式，展示如何做到这一点：

function sum(term, a, next, b) {
    function iter(a, result) {
        return 〈??〉
               ? 〈??〉
               : iter(〈??〉, 〈??〉);
    }
    return iter(〈??〉, 〈??〉);
}

练习 1.31

a. sum函数只是许多类似抽象中最简单的一个。⁵¹编写一个名为product的类似函数，它返回给定范围内点的函数值的乘积。展示如何用product来定义factorial。还使用product来使用公式计算π的*似值⁵²
b. 如果你的product函数生成一个递归过程，写一个生成迭代过程的函数。如果它生成一个迭代过程，写一个生成递归过程的函数。

练习 1.32

a. 证明sum和product（练习 1.31）都是更一般的称为accumulate的特殊情况，它使用一些一般的累积函数来组合一系列项：
```
accumulate(combiner, null_value, term, a, next, b);
```
函数accumulate接受与sum和product相同的项和范围规范，以及一个combiner函数（两个参数）作为参数，该函数指定如何将当前项与前面项的累积组合在一起，以及一个null_value，用于指定项用完时要使用的基本值。编写accumulate并展示如何将sum和product都声明为对accumulate的简单调用。

b. 如果您的accumulate函数生成递归过程，请编写一个生成迭代过程的函数。如果它生成迭代过程，请编写一个生成递归过程的函数。

练习 1.33

您可以通过引入对要组合的项进行筛选的概念来获得accumulate的更通用版本（练习 1.32）。也就是说，仅组合满足指定条件的范围中的值导出的那些项。生成的filtered_accumulate抽象接受与 accumulate 相同的参数，以及指定筛选器的一个参数的附加谓词。编写filtered_accumulate作为一个函数。展示如何使用filtered_accumulate来表达以下内容：

a. 在区间a到b中素数的*方的和（假设您已经编写了is_prime谓词）
b. 所有小于n的正整数的乘积，这些整数与n互质（即，所有正整数i < n，使得GCD(i, n) = 1）。

1.3.2 使用 Lambda 表达式构建函数

在使用sum时，似乎非常笨拙地声明诸如pi_term和pi_next之类的微不足道的函数，以便我们可以将它们用作高阶函数的参数。与其声明pi_next和pi_term，不如直接指定“返回其输入加 4 的函数”和“返回其输入的倒数乘以其输入加 2 的函数”更方便。我们可以通过引入lambda 表达式作为一种用于创建函数的语法形式来实现这一点。使用 lambda 表达式，我们可以描述我们想要的内容

x => x + 4

和

x => 1 / (x * (x + 2))

然后我们可以表达我们的pi_sum函数，而不声明任何辅助函数：

function pi_sum(a, b) {
    return sum(x => 1 / (x * (x + 2)),
               a,
               x => x + 4,
               b);
}

再次使用 lambda 表达式，我们可以编写integral函数，而无需声明辅助函数add_dx：

function integral(f, a, b, dx) {
    return sum(f,
               a + dx / 2,
               x => x + dx,
               b)
           * 
           dx;
}

通常，lambda 表达式用于创建函数，方式与函数声明相同，只是没有为函数指定名称，并且省略了return关键字和大括号（如果只有一个参数，则可以省略参数列表周围的括号，就像我们看到的例子一样）。⁵³

(parameters) => expression

生成的函数与使用函数声明语句创建的函数一样。唯一的区别是它没有与环境中的任何名称关联。我们认为

function plus4(x) {
    return x + 4;
}

等同于⁵⁴

const plus4 = x => x + 4;

我们可以按照以下方式阅读 lambda 表达式：

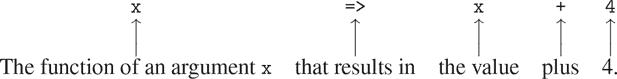
像任何具有函数作为其值的表达式一样，lambda 表达式可以用作应用程序中的函数表达式，例如

((x, y, z) => x + y + square(z))(1, 2, 3);
12

或者，更一般地，在我们通常使用函数名称的任何上下文中。⁵⁵ 请注意，=>的优先级低于函数应用，因此这里括号是必要的。

使用`const`创建本地名称

lambda 表达式的另一个用途是创建本地名称。我们在函数中经常需要本地名称，而不仅仅是已绑定为参数的名称。例如，假设我们希望计算函数

f (x, y) = x(1 + xy)² + y(1 – y) + (1 + xy)(1 – y)

我们也可以表达为

a = 1 + xy

b = 1 – y

f (x, y) = xa² + yb + ab

在编写一个计算f的函数时，我们希望将局部名称不仅包括x和y，还包括像a和b这样的中间量的名称。实现这一点的一种方法是使用辅助函数来绑定局部名称：

function f(x, y) {
    function f_helper(a, b) {
        return x * square(a) + y * b + a * b;
    }
    return f_helper(1 + x * y, 1 - y);
}

当然，我们可以使用 lambda 表达式来指定一个匿名函数来绑定我们的局部名称。然后函数体变成了对该函数的单个调用：

function f_2(x, y) {
    return ( (a, b) => x * square(a) + y * b + a * b
           )(1 + x * y, 1 - y);
}

通过在函数体内使用常量声明，更方便地声明局部名称的一种方法是使用常量声明。使用const，函数可以写成

function f_3(x, y) {
    const a = 1 + x * y; 
    const b = 1 - y;
    return x * square(a) + y * b + a * b;
}

在块内部使用const声明的名称将其所在的最*块的主体作为其作用域。⁵⁶^,⁵⁷

条件语句

我们已经看到，在函数声明中声明局部名称通常是有用的。当函数变得很大时，我们应该尽可能地保持名称的范围狭窄。例如考虑练习 1.26 中的expmod。

function expmod(base, exp, m) {
    return exp === 0
           ? 1
           : is_even(exp)
           ? ( expmod(base, exp / 2, m)
              * expmod(base, exp / 2, m)) % m
           : (base * expmod(base, exp - 1, m)) % m;
}

这个函数是不必要的低效，因为它包含了两个相同的调用：

expmod(base, exp / 2, m);

虽然在这个例子中可以很容易地使用square函数来修复这个问题，但在一般情况下并不容易。如果不使用square，我们可能会尝试引入一个表达式的局部名称，如下所示：

function expmod(base, exp, m) {
    const half_exp = expmod(base, exp / 2, m);
    return exp === 0
           ? 1
           : is_even(exp)
           ? (half_exp * half_exp) % m
           : (base * expmod(base, exp - 1, m)) % m;
}

这将使函数不仅效率低下，而且实际上是非终止的！问题在于常量声明出现在条件表达式之外，这意味着即使满足基本情况exp === 0，它也会被执行。为了避免这种情况，我们提供了条件语句，并允许返回语句出现在语句的分支中。使用条件语句，我们可以将函数expmod写成如下形式：

function expmod(base, exp, m) {
    if (exp === 0) {
        return 1;
    } else {
        if (is_even(exp)) {
            const half_exp = expmod(base, exp / 2, m);
            return (half_exp * half_exp) % m;
        } else {
            return (base * expmod(base, exp - 1, m)) % m;
        }
    }
}

条件语句的一般形式是

if (predicate) { consequent-statements } else { alternative-statements }

对于条件表达式，解释器首先求值predicate。如果它求值为true，解释器按顺序求值consequent-statements，如果它求值为false，解释器按顺序求值alternative-statements。返回语句的求值从周围的函数返回，忽略返回语句后的任何语句和条件语句后的任何语句。请注意，任何在任一部分中发生的常量声明都是该部分的局部声明，因为每个部分都被括号括起来，因此形成自己的块。

练习 1.34

假设我们声明

function f(g) {
    return g(2);
}

然后我们有

f(square);
`4`

f(z => z * (z + 1));
`6`

如果我们（刻意地）要求解释器求值应用f(f)会发生什么？解释。

1.3.3 函数作为一般方法

我们在 1.1.4 节介绍了复合函数作为一种抽象数值操作模式的机制，使其独立于特定的数字。通过高阶函数，比如 1.3.1 节的integral函数，我们开始看到一种更强大的抽象：用于表达计算的一般方法，独立于特定的函数。在本节中，我们将讨论两个更复杂的例子——查找函数的零点和不动点的一般方法，并展示这些方法如何直接表达为函数。

通过半区间法找到方程的根

半区间方法是一种简单但强大的技术，用于找到方程f(x)=0的根，其中f是一个连续函数。其思想是，如果我们给定了f(a)<0<f(b)的点a和b，那么f必须至少在a和b之间有一个零点。为了找到零点，让x为a和b的*均值，并计算f(x)。如果f(x)>0，则f必须在a和x之间有一个零点。如果f(x)<0，则f必须在x和b之间有一个零点。以此类推，我们可以确定f必须有一个零点的更小的区间。当我们达到一个足够小的区间时，过程停止。由于不确定性的区间在过程的每一步都减半，所以所需的最大步数增长为Θ(log(L/T))，其中L是原始区间的长度，T是误差容限（即我们将考虑“足够小”的区间的大小）。以下是实现这种策略的函数：

function search(f, neg_point, pos_point) {
    const midpoint = average(neg_point, pos_point);
    if (close_enough(neg_point, pos_point)) {
        return midpoint;
    } else {
        const test_value = f(midpoint);
        return positive(test_value)
               ? search(f, neg_point, midpoint)
               : negative(test_value)
               ? search(f, midpoint, pos_point)
               : midpoint;
    }
}

我们假设我们最初给定了函数f以及其值为负和正的点。我们首先计算两个给定点的中点。接下来，我们检查给定的区间是否足够小，如果是，我们就简单地返回中点作为我们的答案。否则，我们计算中点处f的值作为测试值。如果测试值为正，则我们继续从原始负点到中点的新区间进行该过程。如果测试值为负，则我们继续从中点到正点的区间。最后，有可能测试值为 0，这种情况下中点本身就是我们正在寻找的根。为了测试端点是否“足够接*”，我们可以使用类似于 1.1.7 节中用于计算*方根的函数：

function close_enough(x, y) {
    return abs(x - y) < 0.001;
}

search函数直接使用起来很麻烦，因为我们可能会无意中给出f的值没有所需符号的点，这样我们就会得到错误的答案。相反，我们将通过以下函数使用search，该函数检查哪个端点具有负函数值，哪个具有正函数值，并相应地调用search函数。如果函数在两个给定点上具有相同的符号，则无法使用半区间方法，在这种情况下，函数会发出错误信号。

function half_interval_method(f, a, b) {
    const a_value = f(a);
    const b_value = f(b);
    return negative(a_value) && positive(b_value)
           ? search(f, a, b)
           : negative(b_value) && positive(a_value)
           ? search(f, b, a)
           : error("values are not of opposite sign");
}

以下示例使用半区间方法在 2 和 4 之间*似π作为sinx=0的根：

half_interval_method(math_sin, 2, 4);
3.14111328125

以下是另一个例子，使用半区间方法在 1 和 2 之间搜索方程x³ - 2x - 3 = 0的根：

half_interval_method(x => x * x * x - 2 * x - 3, 1, 2);
1.89306640625

查找函数的固定点

如果x满足方程f(x)=x，则称数字x为函数f的固定点。对于一些函数f，我们可以通过从初始猜测开始并重复应用f来找到一个固定点，

f(x), f(f(x)), f(f(f(x))), ...

直到值变化不是很大为止。利用这个想法，我们可以设计一个函数fixed_point，它以函数和初始猜测为输入，并产生函数的一个*似固定点。我们重复应用该函数，直到找到两个连续值的差小于某个预定的容差：

const tolerance = 0.00001;
function fixed_point(f, first_guess) {
    function close_enough(x, y) {
        return abs(x - y) < tolerance;
    }
    function try_with(guess) {
        const next = f(guess);
        return close_enough(guess, next)
               ? next
               : try_with(next);
    }
    return try_with(first_guess);
}

例如，我们可以使用这种方法来*似余弦函数的固定点，从 1 开始作为初始*似值：

fixed_point(math_cos, 1);
0.7390822985224023

同样，我们可以找到方程y=siny+cosy的解：

fixed_point(y => math_sin(y) + math_cos(y), 1);
1.2587315962971173

固定点过程让人想起了我们在 1.1.7 节中用于找*方根的过程。两者都基于反复改进猜测的想法，直到结果满足某些标准。实际上，我们可以很容易地将*方根计算公式化为固定点搜索。计算某个数x的*方根需要找到一个y，使得y² = x。将这个方程转化为等价形式y = x / y，我们意识到我们正在寻找函数⁶¹ y = x/y的一个固定点，因此我们可以尝试计算*方根

function sqrt(x) {
    return fixed_point(y => x / y, 1);
}

不幸的是，这种固定点搜索不会收敛。考虑一个初始猜测y[1]。下一个猜测是y[2] = x/y[1]，下一个猜测是y[3] = x/y[2] = x/(x/y[1]) = y[1]。这导致了一个无限循环，其中两个猜测y[1]和y[2]一遍又一遍地重复，围绕答案振荡。

控制这种振荡的一种方法是防止猜测变化太大。由于答案总是在我们的猜测y和x / y之间，我们可以做一个新的猜测，这个猜测不像x / y那么远离y，通过*均y和x / y，这样在y之后的下一个猜测就是1/2 (y + x / y)而不是x / y。这种猜测序列的过程只是寻找y -> 1/2 (y + x / y)的固定点的过程。

function sqrt(x) {
    return fixed_point(y => average(y, x / y), 1);
}

（注意y = 1/2 (y + x / y)是方程y = x / y的简单变换；为了推导它，将y添加到方程的两边，然后除以 2。）

有了这个修改，*方根函数就可以工作了。实际上，如果我们展开定义，我们可以看到这里生成的*方根*似序列与我们原来的 1.1.7 节*方根函数生成的序列完全相同。这种*均连分数的方法通常有助于固定点搜索的收敛。

练习 1.35

证明黄金分割比ϕ（1.2.2 节）是变换x -> 1 + 1/x的一个固定点，并利用这一事实通过fixed_point函数计算ϕ。

练习 1.36

修改fixed_point，以便它打印生成的*似值序列，使用练习 1.22 中显示的原始函数display。然后通过找到xˣ = 1000的固定点来找到解，即x -> log(1000)/ log(x)。（使用计算自然对数的原始函数math_log。）比较使用和不使用*均阻尼所需的步骤数。（请注意，您不能从 1 开始fixed_point，因为这将导致除以log(1) = 0。）

练习 1.37

无限连分数是一个形式的表达式

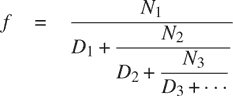
例如，可以证明，所有N[i]和D[i]都等于 1 的无限连分数展开产生1/ϕ，其中ϕ是黄金分割比（在 1.2.2 节中描述）。*似无限连分数的一种方法是在给定项数后截断展开。这种截断——所谓的k项有限连分数——具有形式

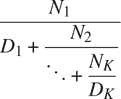
a.假设n和d是一个参数（项索引i）的函数，返回连分数项的N[i]和D[i]。声明一个函数cont_frac，使得求值cont_frac(n, d, k)计算k项有限连分数的值。通过*似 1ϕ检查您的函数
```
cont_frac(i => 1, i => 1, k);
```
对于连续的k值。为了获得精确到小数点后 4 位的*似值，您需要使k有多大？
b. 如果您的cont_frac函数生成递归过程，请编写一个生成迭代过程的函数。如果它生成迭代过程，请编写一个生成递归过程的函数。

练习 1.38

1737 年，瑞士数学家 Leonhard Euler 发表了一篇题为De Fractionibus Continuis的备忘录，其中包括了 e - 2的一个连分数展开，其中e是自然对数的底数。在这个分数中，N[i]都是 1，D[i]依次为 1、2、1、1、4、1、1、6、1、1、8，编写一个程序，使用练习 1.37 中的cont_frac函数来根据 Euler 的展开来*似e。

练习 1.39

1770 年，德国数学家 J.H. Lambert 发表了正切函数的连分数表示：

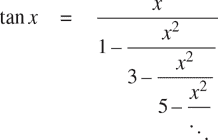
其中x以弧度为单位。声明一个函数tan_cf(x, k)，根据 Lambert 的公式计算正切函数的*似值。与练习 1.37 一样，k指定要计算的项数。

1.3.4 作为返回值的函数

上述例子展示了将函数作为参数传递的能力如何显著增强了我们编程语言的表达能力。通过创建其返回值本身是函数的函数，我们可以实现更多的表达能力。

我们可以通过再次查看第 1.3.3 节末尾描述的不动点示例来说明这个想法。我们将一个新版本的*方根函数表述为一个不动点搜索，从观察到√x是函数y -> x / y的不动点开始。然后我们使用*均阻尼使*似值收敛。*均阻尼本身是一个有用的通用技术。也就是说，给定一个函数f，我们考虑其在x处的值等于x和f(x)的*均值的函数。

我们可以通过以下函数表达*均阻尼的想法：

function average_damp(f) {
    return x => average(x, f(x));
}

函数average_damp以函数f作为参数，并返回一个函数（由 lambda 表达式生成），当应用于数字x时，产生x和f(x)的*均值。例如，将average_damp应用于square函数会产生一个函数，其在某个数字x处的值是x和x²的*均值。将这个结果函数应用于 10 会返回 10 和 100 的*均值，即 55。

average_damp(square)(10);
55

使用average_damp，我们可以重新表述*方根函数如下：

function sqrt(x) {
    return fixed_point(average_damp(y => x / y), 1);
}

注意这种表述如何明确了方法中的三个思想：不动点搜索、*均阻尼和函数y = x/y。比较这种*方根方法的表述与第 1.1.7 节中给出的原始版本是有益的。请记住，这些函数表达了相同的过程，注意当我们用这些抽象的术语表达过程时，这个想法变得更加清晰。一般来说，有许多方法可以将一个过程表述为一个函数。有经验的程序员知道如何选择特别明晰的过程表述，并且在有用的情况下，将过程的元素公开为可以在其他应用中重复使用的单独实体。作为重用的一个简单例子，注意x的立方根是函数y = x/y²的不动点，因此我们可以立即将我们的*方根函数推广为一个提取立方根的函数。

function cube_root(x) {
   return fixed_point(average_damp(y => x / square(y)), 1);
}

牛顿法

当我们首次介绍*方根函数时，在第 1.1.7 节中，我们提到这是牛顿法的一个特例。如果x -> g(x)是一个可微函数，那么方程g(x) = 0的解是函数x -> f (x)的不动点，其中

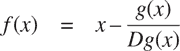
和Dg(x)是在x处求导的g的导数。牛顿法是使用我们上面看到的固定点方法来*似方程的解，通过找到函数f的固定点。⁶⁴ 对于许多函数g和对于足够好的x的初始猜测，牛顿法收敛得非常快，以便解决g(x) = 0。⁶⁵

为了将牛顿法实现为一个函数，我们必须首先表达导数的概念。注意，“导数”和*均阻尼一样，是将一个函数转换为另一个函数的东西。例如，函数x -> x³的导数是函数x -> 3x²。一般来说，如果g是一个函数，dx是一个小数，那么g的导数Dg是一个函数，其在任何数x处的值（在小dx的极限情况下）由

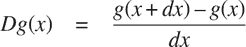
因此，我们可以将导数的概念（取dx为 0.00001）表示为函数

function deriv(g) {
    return x => (g(x + dx) - g(x)) / dx;
}

以及声明

const dx = 0.00001;

像average_damp一样，deriv是一个以函数作为参数并返回函数作为值的函数。例如，要*似计算x³在 5 处的导数（其精确值为 75），我们可以计算

function cube(x) { return x * x * x; }

deriv(cube)(5);
75.00014999664018

借助于deriv，我们可以将牛顿法表达为一个固定点过程：

function newton_transform(g) {
    return x => x - g(x) / deriv(g)(x);
}
function newtons_method(g, guess) {
    return fixed_point(newton_transform(g), guess);
}

newton_transform函数表达了本节开头的公式，newtons_method可以很容易地根据这个定义。它的参数是一个计算我们想要找到零点的函数的函数，以及一个初始猜测。例如，要找到x的*方根，我们可以使用牛顿法来找到函数y -> y² – x的零点，从初始猜测为 1 开始。⁶⁶ 这提供了*方根函数的另一种形式：

function sqrt(x) {
    return newtons_method(y => square(y) - x, 1);
}

抽象和一级函数

我们已经看到了两种将*方根计算表达为更一般方法的实例，一种是作为固定点搜索，另一种是使用牛顿法。由于牛顿法本身被表达为一个固定点过程，我们实际上看到了两种计算*方根作为固定点的方法。每种方法都以一个函数开始，并找到函数的某个变换的固定点。我们可以将这个一般的想法本身表达为一个函数：

function fixed_point_of_transform(g, transform, guess) {
    return fixed_point(transform(g), guess);
}

这个非常一般的函数以一个计算某个函数的函数g，一个转换g的函数和一个初始猜测作为参数。返回的结果是转换函数的一个固定点。

使用这种抽象，我们可以将本节中第一个*方根计算（其中我们寻找y -> x / y的*均阻尼版本的固定点）重新表述为这种一般方法的一个实例：

function sqrt(x) {
    return fixed_point_of_transform(
               y => x / y,
               average_damp,
               1);
}

同样，我们可以将本节中第二个*方根计算（牛顿法的一个实例，找到y -> y² – x的牛顿变换的固定点）表达为

function sqrt(x) {
    return fixed_point_of_transform(
               y => square(y) - x,
               newton_transform,
               1);
}

我们在 1.3 节开始时观察到，复合函数是一个关键的抽象机制，因为它们允许我们将计算的一般方法表达为编程语言中的显式元素。现在我们已经看到了高阶函数如何允许我们操纵这些一般方法以创建进一步的抽象。

作为程序员，我们应该警惕机会，识别程序中的基本抽象，并在其上构建和泛化，以创建更强大的抽象。这并不是说我们应该总是以最抽象的方式编写程序；专业程序员知道如何选择适合其任务的抽象级别。但是，重要的是能够以这些抽象的方式思考，以便我们可以准备在新的上下文中应用它们。高阶函数的重要性在于它们使我们能够将这些抽象明确地表示为我们编程语言中的元素，以便它们可以像其他计算元素一样被处理。

一般来说，编程语言对计算元素的操作方式施加了限制。具有最少限制的元素被称为第一类状态。第一类元素的一些“权利和特权”是：

它们可以使用名称来引用。
它们可以作为函数的参数传递。
它们可以作为函数的结果返回。
它们可以包含在数据结构中。

JavaScript，像其他高级编程语言一样，授予函数完全的第一类状态。这对于高效实现提出了挑战，但由此产生的表达能力的增强是巨大的。

练习 1.40

声明一个函数cubic，它可以与newtons_method函数一起使用，形式如下：

newtons_method(cubic(a, b, c), 1)

来*似三次方程x³+ax²+bx+c的零点。

练习 1.41

声明一个函数double，它以一个参数的函数作为参数，并返回一个应用原始函数两次的函数。例如，如果inc是一个将其参数加 1 的函数，则double(inc)应该是一个将其参数加 2 的函数。通过

double(double(double))(inc)(5);

练习 1.42

设f和g是两个一元函数。g之后f的组合被定义为函数x -> f (g(x)）。声明一个实现组合的函数compose。例如，如果inc是一个将其参数加 1 的函数，

compose(square, inc)(6);
49

练习 1.43

如果f是一个数值函数，n是一个正整数，那么我们可以形成f的n次重复应用，它被定义为其在x处的值是f(f(...(f(x))...))。例如，如果f是函数x -> x + 1，那么f的n次重复应用是函数x -> x + n。如果f是*方数的操作，那么f的n次重复应用是将其参数提高到2ⁿ次幂的函数。编写一个函数，它以计算f的函数和一个正整数n作为输入，并返回计算f的n次重复应用的函数。您的函数应该能够像下面这样使用：

repeated(square, 2)(5);
625

提示：您可能会发现使用练习 1.42 中的compose很方便。

练习 1.44

*滑函数的概念是信号处理中的重要概念。如果f是一个函数，dx是一个小数，那么f的*滑版本是一个函数，其在点x的值是f(x-dx)、f(x)和f(x+dx)的*均值。编写一个函数smooth，它以计算f的函数作为输入，并返回一个计算*滑f的函数。有时重复*滑一个函数（即*滑*滑的函数，依此类推）是有价值的，以获得n次*滑函数。展示如何使用练习 1.43 中的smooth和repeated生成任何给定函数的n次*滑函数。

练习 1.45

在 1.3.3 节中，我们看到通过天真地寻找y -> x / y的不动点来计算*方根并不收敛，这可以通过*均阻尼来修复。同样的方法也适用于寻找立方根，作为*均阻尼y -> x / y²的不动点。不幸的是，这个过程对于四次方根并不适用——单一的*均阻尼不足以使y -> x / y³的不动点搜索收敛。另一方面，如果我们进行两次*均阻尼（即使用y -> x / y³的*均阻尼的*均阻尼），不动点搜索就会收敛。进行一些实验，以确定计算n次方根所需的*均阻尼次数，作为基于y -> x/y^(n–1)的重复*均阻尼的不动点搜索。使用这个来实现一个简单的函数，使用fixed_point、average_damp和练习 1.43 的repeated函数来计算n次方根。假设你需要的任何算术运算都可以作为原语使用。

练习 1.46

本章描述的几种数值方法都是极其一般的计算策略迭代改进的实例。迭代改进说，为了计算某事物，我们从一个初始猜测开始，测试猜测是否足够好，否则改进猜测并继续使用改进后的猜测作为新的猜测。编写一个函数iterative_improve，它接受两个函数作为参数：一个用于判断猜测是否足够好的方法，一个用于改进猜测的方法。函数iterative_improve应该返回一个函数作为其值，该函数接受一个猜测作为参数，并持续改进猜测，直到猜测足够好为止。以iterative_improve的术语重写 1.1.7 节的sqrt函数和 1.3.3 节的fixed_point函数。

二、使用数据构建抽象

原文：2 Building Abstractions with Data

译者：飞龙

协议：CC BY-NC-SA 4.0

我们现在来到数学抽象的决定性步骤：我们忘记符号代表什么。...[数学家]不需要闲着；他可以用这些符号进行许多操作，而无需看它们所代表的东西。

——赫尔曼·维尔，《数学思维方式》

在第 1 章，我们集中讨论了计算过程和函数在程序设计中的作用。我们看到了如何使用原始数据（数字）和原始操作（算术操作），如何通过组合、条件语句和参数的使用来组合函数以形成复合函数，以及如何通过使用函数声明来抽象过程。我们看到函数可以被看作是一个过程的局部演变的模式，并且我们对一些常见的过程模式进行了分类、推理和简单的算法分析，这些过程模式体现在函数中。我们还看到，高阶函数通过使我们能够操纵，从而能够根据一般的计算方法进行推理，增强了我们语言的能力。这正是编程的本质的很大一部分。

在本章中，我们将研究更复杂的数据。第 1 章中的所有函数都是针对简单的数值数据进行操作，而简单的数据对于我们希望使用计算解决的许多问题是不够的。程序通常被设计来模拟复杂的现象，往往必须构建具有多个部分的计算对象，以模拟具有多个方面的现实世界现象。因此，虽然我们在第 1 章的重点是通过组合函数来构建抽象函数，但在本章中，我们转向编程语言的另一个关键方面：它提供了一种通过组合数据对象来构建复合数据的手段。

为什么我们希望在编程语言中使用复合数据？出于与希望使用复合函数相同的原因：提高我们设计程序的概念水*，增加设计的模块化，并增强我们语言的表达能力。正如声明函数的能力使我们能够处理比语言的原始操作更高概念水*的过程一样，构建复合数据对象的能力使我们能够处理比语言的原始数据对象更高概念水*的数据。

考虑设计一个系统来执行有理数的算术运算的任务。我们可以想象一个操作add_rat，它接受两个有理数并产生它们的和。就简单数据而言，有理数可以被看作是两个整数：一个分子和一个分母。因此，我们可以设计一个程序，其中每个有理数将由两个整数（一个分子和一个分母）表示，并且add_rat将由两个函数实现（一个产生和的分子，一个产生分母）。但这将是笨拙的，因为我们将需要明确地跟踪哪个分子对应哪个分母。在一个旨在对许多有理数执行许多操作的系统中，这些簿记细节将大大地使程序混乱，更不用说它们对我们的思维会产生什么影响了。如果我们能够“粘合”分子和分母以形成一对——一个复合数据对象，那将会好得多，这样我们的程序就可以以一种一致的方式来操作它，这种方式将有助于将有理数视为一个单一的概念单位。

复合数据的使用还使我们能够增加程序的模块化。如果我们可以直接将有理数作为对象进行操作，那么我们就可以将处理有理数本身的程序部分与有理数如何表示为整数对的细节分开。隔离处理数据对象如何表示的程序部分与处理数据对象如何使用的程序部分是一种称为数据抽象的强大设计方法。我们将看到数据抽象如何使程序更容易设计、维护和修改。

复合数据的使用实际上增加了我们编程语言的表达能力。考虑形成“线性组合”ax + by的想法。我们可能希望编写一个函数，接受a、b、x和y作为参数，并返回ax + by的值。如果参数是数字，这没有困难，因为我们可以轻松地声明函数。

function linear_combination(a, b, x, y) {
    return a * x + b * y;
}

但是，假设我们不仅关心数字。假设我们希望描述一个过程，只要定义了加法和乘法，就可以形成线性组合——对于有理数、复数、多项式或其他任何东西。我们可以将这表达为以下形式的函数。

function linear_combination(a, b, x, y) {
    return add(mul(a, x), mul(b, y));
}

add和mul不是原始函数+和*，而是更复杂的东西，它们将根据我们传递的参数a、b、x和y执行适当的操作。关键是linear_combination唯一需要知道的是函数add和mul将执行适当的操作。从linear_combination函数的角度来看，a、b、x和y是什么并不重要，甚至更不重要的是它们可能如何以更原始的数据形式表示。这个例子也说明了为什么我们的编程语言提供直接操作复合对象的能力是重要的：如果没有这一点，linear_combination这样的函数就无法将其参数传递给add和mul，而不必知道它们的详细结构。

我们通过实现上面提到的有理数算术系统来开始本章。这将为我们讨论复合数据和数据抽象提供背景。与复合函数一样，需要解决的主要问题是抽象作为一种处理复杂性的技术，我们将看到数据抽象如何使我们能够在程序的不同部分之间建立适当的抽象屏障。

我们将看到形成复合数据的关键在于编程语言应该提供某种“粘合剂”，使得数据对象可以组合成更复杂的数据对象。有许多可能的粘合剂。事实上，我们将发现如何使用没有特殊“数据”操作的函数来形成复合数据。这将进一步模糊“函数”和“数据”的区别，这在第 1 章末尾已经变得模糊。我们还将探讨一些表示序列和树的常规技术。处理复合数据的一个关键思想是闭包的概念——我们用于组合数据对象的粘合剂应该允许我们组合不仅是原始数据对象，还有复合数据对象。另一个关键思想是复合数据对象可以作为常规接口，以混合和匹配的方式组合程序模块。我们通过介绍一个利用闭包的简单图形语言来说明这些想法。

然后，我们将通过引入符号表达式来增强我们语言的表现力——数据的基本部分可以是任意符号，而不仅仅是数字。我们探索表示对象集的各种替代方案。我们将发现，就像给定的数值函数可以通过许多不同的计算过程来计算一样，给定数据结构可以用更简单的对象来表示的方式有很多种，表示的选择对操纵数据的过程的时间和空间要求有重要影响。我们将在符号微分、集合表示和信息编码的背景下研究这些想法。接下来，我们将解决处理可能由程序的不同部分以不同方式表示的数据的问题。这导致需要实现通用操作，这些操作必须处理许多不同类型的数据。在存在通用操作的情况下保持模块化需要比仅使用简单数据抽象建立更强大的抽象屏障。特别是，我们引入数据导向编程作为一种技术，允许单独设计数据表示，然后累加（即不修改）组合这些表示。为了说明这种系统设计方法的强大之处，我们通过将所学应用于在多项式上执行符号算术的包的实现来结束本章，其中多项式的系数可以是整数、有理数、复数，甚至其他多项式。

2.1 数据抽象简介

在 1.1.8 节中，我们注意到一个作为创建更复杂函数的元素使用的函数不仅可以被视为一组特定操作，还可以被视为一个函数抽象。也就是说，可以抑制函数的实现细节，并且可以用具有相同整体行为的任何其他函数来替换特定的函数本身。换句话说，我们可以进行一个抽象，将函数的使用方式与如何使用更基本的函数来实现函数的细节分离。复合数据的类似概念称为数据抽象。数据抽象是一种方法论，使我们能够将复合数据对象的使用方式与它是如何由更基本的数据对象构造出来的细节隔离开来。

数据抽象的基本思想是构造使用复合数据对象的程序，使其操作“抽象数据”。也就是说，我们的程序应该以一种不假设关于数据的任何信息的方式来使用数据，除了执行手头的任务所严格需要的信息。与此同时，“具体”数据表示是独立于使用数据的程序定义的。我们系统的这两部分之间的接口将是一组函数，称为选择器和构造器，它们以具体表示为基础实现抽象数据。为了说明这种技术，我们将考虑如何设计一组用于操作有理数的函数。

2.1.1 示例：有理数的算术运算

假设我们想要对有理数进行算术运算。我们希望能够对它们进行加法、减法、乘法和除法，并测试两个有理数是否相等。

让我们首先假设我们已经有一种方法，可以从分子和分母构造一个有理数。我们还假设，给定一个有理数，我们有一种方法来提取（或选择）它的分子和分母。让我们进一步假设构造器和选择器作为函数是可用的：

make_rat(n, d)返回其分子为整数n，分母为整数d的有理数。
numer(x)返回有理数x的分子。
denom(x)返回有理数x的分母。

我们在这里使用了一种强大的综合策略：wishful thinking。我们还没有说有理数是如何表示的，或者函数numer、denom和make_rat应该如何实现。即使如此，如果我们有了这三个函数，我们就可以通过以下关系来进行加法、减法、乘法、除法和相等性测试：

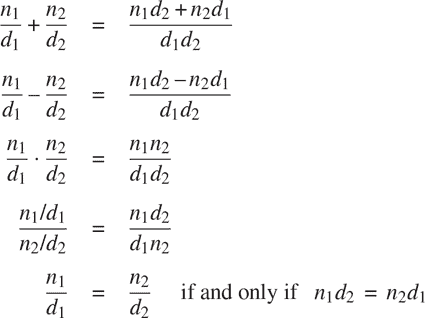
我们可以将这些规则表示为函数：

function add_rat(x, y) {
    return make_rat(numer(x) * denom(y) + numer(y) * denom(x),
                    denom(x) * denom(y));
}
function sub_rat(x, y) {
    return make_rat(numer(x) * denom(y) - numer(y) * denom(x),
                    denom(x) * denom(y));
}
function mul_rat(x, y) {
    return make_rat(numer(x) * numer(y),
                    denom(x) * denom(y));
}
function div_rat(x, y) {
    return make_rat(numer(x) * denom(y),
                    denom(x) * numer(y));
}
function equal_rat(x, y) {
    return numer(x) * denom(y) === numer(y) * denom(x);
}

现在我们已经定义了有理数的操作，这些操作是基于选择器定义的

和构造函数numer、denom和make_rat。但我们还没有定义这些。我们需要一种方法来将分子和分母粘合在一起形成一个有理数。

对

为了使我们能够实现数据抽象的具体层，我们的 JavaScript 环境提供了一种称为pair的复合结构，它可以用原始函数pair构造。此函数接受两个参数并返回一个包含两个参数作为部分的复合数据对象。给定一个对，我们可以使用原始函数head和tail提取部分。因此，我们可以如下使用pair、head和tail：

const x = pair(1, 2);
head(x);
`1`
tail(x);
`2`

注意，对是一个可以被赋予名称并且可以被操作的数据对象，就像原始数据对象一样。此外，pair可以用来形成其元素为对的对，依此类推：

const x = pair(1, 2);

const y = pair(3, 4);

const z = pair(x, y);

head(head(z));
`1`

head(tail(z));
`3`

在第 2.2 节中，我们将看到这种组合对的能力意味着对可以用作通用的构建块来创建各种复杂的数据结构。由对构造的数据对象称为列表结构数据。

表示有理数

对提供了一种自然的方式来完成有理数系统。简单地将有理数表示为两个整数的对：一个分子和一个分母。然后make_rat、numer和denom可以如下实现：²

function make_rat(n, d) { return pair(n, d); }
function numer(x) { return head(x); }
function denom(x) { return tail(x); }

此外，为了显示我们计算的结果，我们可以通过打印分子、斜杠和分母来打印有理数。我们使用原始函数stringify将任何值（这里是一个数字）转换为字符串。JavaScript 中的运算符+是重载的；它可以应用于两个数字或两个字符串，在后一种情况下，它返回连接两个字符串的结果。³

function print_rat(x) {
    return display(stringify(numer(x)) + " / " + stringify(denom(x)));
}

现在我们可以尝试我们的有理数函数：⁴

const one_half = make_rat(1, 2);

print_rat(one_half);
"1 / 2"

const one_third = make_rat(1, 3);

print_rat(add_rat(one_half, one_third));
"5 / 6"

print_rat(mul_rat(one_half, one_third));
"1 / 6"

print_rat(add_rat(one_third, one_third));
"6 / 9"

正如最后一个例子所示，我们的有理数实现没有将有理数化简为最低项。我们可以通过更改make_rat来解决这个问题。如果我们有一个像第 1.2.5 节中那样产生两个整数的最大公约数的gcd函数，我们可以使用gcd在构造对之前将分子和分母化简为最低项：

function make_rat(n, d) {
    const g = gcd(n, d);
    return pair(n / g, d / g);
}

现在我们有

print_rat(add_rat(one_third, one_third));
"2 / 3"

如所需。通过更改构造函数make_ rat而不更改实现实际操作的任何函数（如add_rat和mul_rat），已完成此修改。

练习 2.1

定义一个更好的make_rat版本，处理正数和负数参数。函数make_rat应该规范化符号，以便如果有理数是正数，则分子和分母都是正数，如果有理数是负数，则只有分子是负数。

2.1.2 抽象屏障

在继续介绍复合数据和数据抽象的更多示例之前，让我们考虑一下有理数示例引发的一些问题。我们用构造函数make_rat和选择器numer和denom来定义有理数运算。一般来说，数据抽象的基本思想是为每种数据对象类型确定一组基本操作，通过这些操作来表达对该类型数据对象的所有操作，然后在操作数据时只使用这些操作。

我们可以将有理数系统的结构设想为图 2.1 所示。水*线代表抽象屏障，隔离系统的不同“层级”。在每个层级，该屏障将使用数据抽象的程序（上方）与实现数据抽象的程序（下方）分开。使用有理数的程序仅通过有理数包提供的“供公共使用”的函数来操作它们：add_rat、sub_rat、mul_rat、div_rat和equal_rat。这些函数又仅仅是通过构造函数和选择器make_rat、numer和denom来实现的，它们本身是通过对偶实现的。对偶的具体实现细节对于有理数包的其余部分来说是无关紧要的，只要对偶可以通过pair、head和tail来操作。实际上，每个层级的函数都是定义抽象屏障并连接不同层级的接口。这个简单的想法有很多优点。其中一个优点是它使程序更容易维护和修改。任何复杂的数据结构都可以用编程语言提供的原始数据结构的多种方式来表示。当然，表示的选择会影响操作它的程序；因此，如果表示在以后的某个时间被更改，所有这样的程序可能都必须相应地进行修改。对于大型程序来说，这个任务可能会耗费大量时间和金钱，除非通过设计将对表示的依赖限制在非常少的程序模块中。

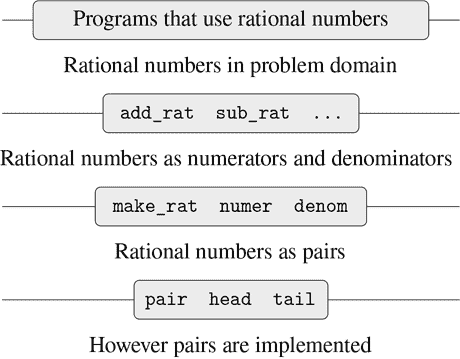
图 2.1 有理数包中的数据抽象屏障。

例如，解决将有理数化简为最低项的问题的另一种方法是在访问有理数的部分时执行化简，而不是在构造有理数时执行。这导致了不同的构造函数和选择器函数：

function make_rat(n, d) {
    return pair(n, d);
}
function numer(x) {
    const g = gcd(head(x), tail(x));
    return head(x) / g;
}
function denom(x) {
    const g = gcd(head(x), tail(x));
    return tail(x) / g;
}

这种实现与之前的实现的不同之处在于我们何时计算gcd。如果在我们典型的有理数使用中，我们多次访问相同有理数的分子和分母，那么在构造有理数时计算gcd会更好。如果不是，我们可能最好等到访问时计算gcd。无论如何，当我们从一种表示形式改变为另一种表示形式时，函数add_rat、sub_rat等都不需要进行任何修改。

将对表示的依赖限制在少数接口函数中有助于我们设计程序以及修改程序，因为它允许我们保持灵活性来考虑替代实现。继续我们的简单例子，假设我们正在设计一个有理数包，最初无法确定是在构造时还是在选择时执行gcd。数据抽象方法为我们提供了一种推迟决定而不失去在系统的其余部分上取得进展的方法。

练习 2.2

考虑在*面上表示线段的问题。每个线段都表示为一对点：起点和终点。声明一个构造器make_segment和选择器start_segment和end_segment，以点的形式定义线段的表示。此外，一个点可以表示为一对数字：x坐标和y坐标。因此，指定一个构造器make_point和选择器x_point和y_point来定义这种表示。最后，使用您的选择器和构造器，声明一个函数midpoint_segment，它以线段作为参数并返回其中点（坐标是端点坐标的*均值）。要尝试您的函数，您需要一种打印点的方法：

function print_point(p) {
    return display("(" + stringify(x_point(p)) + ", "
                       + stringify(y_point(p)) + ")");
}

练习 2.3

在*面上实现矩形的表示。（提示：您可能需要使用练习 2.2。）根据您的构造器和选择器，创建计算给定矩形的周长和面积的函数。现在实现矩形的不同表示。您能否设计您的系统，使得具有合适的抽象屏障，以便相同的周长和面积函数将使用任一表示？

2.1.3 数据的含义是什么？

我们在 2.1.1 节中开始了有理数的实现，通过实现有理数操作add_rat，sub_rat等，这些操作是根据三个未指定的函数make_rat，numer和denom来定义的。在那时，我们可以认为这些操作是根据数据对象——分子、分母和有理数——来定义的，后三个函数规定了它们的行为。

但是，数据究竟是什么意思？仅仅说“由给定的选择器和构造器实现的任何东西”是不够的。显然，并非每一组任意的三个函数都可以作为有理数实现的适当基础。我们需要保证，如果我们从一对整数n和d构造一个有理数x，那么提取x的numer和denom并将它们相除应该得到与n除以d相同的结果。换句话说，make_rat，numer和denom必须满足这样的条件，对于任何整数n和任何非零整数d，如果x是make_rat(n, d)，那么

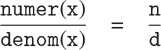
事实上，这是make_rat，numer和denom必须满足的唯一条件，以形成有理数表示的合适基础。一般来说，我们可以认为数据是由一些选择器和构造器的集合定义的，以及这些函数必须满足的指定条件，以便成为有效的表示。[5]

这种观点不仅可以用来定义“高级”数据对象，比如有理数，还可以用来定义更低级的对象。考虑一对的概念，我们用它来定义我们的有理数。我们从来没有说过一对是什么，只是语言提供了用于操作对的函数pair，head和tail。但我们只需要知道关于这三个操作的唯一事情是，如果我们使用pair将两个对象粘合在一起，我们可以使用head和tail来检索对象。也就是说，这些操作满足这样的条件，对于任何对象x和y，如果z是pair(x, y)，那么head(z)是x，tail(z)是y。事实上，我们提到这三个函数是作为原语包含在我们的语言中的。然而，任何满足上述条件的三个函数的三元组都可以用作实现对的基础。这一点通过这样一个事实引人注目，即我们可以实现pair，head和tail而不使用任何数据结构，只使用函数。以下是定义：[6]

function pair(x, y) {
    function dispatch(m) {
        return m === 0
               ? x
               : m === 1
               ? y
               : error(m, "argument not 0 or 1 – pair");
    }
    return dispatch;
}
function head(z) { return z(0); }
function tail(z) { return z(1); }

这种使用函数的方法与我们对数据的直观概念完全不同。然而，要证明这是表示对偶的有效方式，我们只需要验证这些函数是否满足上面给出的条件。

要注意的微妙之处是pair(x, y)返回的值是一个函数——即内部定义的函数dispatch，它接受一个参数，并根据参数是 0 还是 1 返回x或y。相应地，head(z)被定义为将 0 应用于z。因此，如果z是由pair(x, y)形成的函数，那么将 0 应用于z将产生x。因此，我们已经证明了head(pair(x, y))产生x，就像我们希望的那样。类似地，tail(pair(x, y))将由pair(x, y)返回的函数应用于 1，返回y。因此，这种对偶的函数实现是有效的实现，如果我们只使用pair、head和tail来访问对偶，我们无法将这种实现与使用“真实”数据结构的实现区分开。

展示对偶的函数表示的重点不在于我们的语言是否以这种方式工作（对偶的高效实现可能会使用 JavaScript 的原始向量数据结构），而在于它可以以这种方式工作。函数表示，虽然晦涩，但是是表示对偶的完全足够的方式，因为它满足对偶需要满足的唯一条件。这个例子还表明，能够操作函数作为对象自动提供了表示复合数据的能力。现在这可能看起来像是一种奇特现象，但是数据的函数表示将在我们的编程技能中扮演一个核心角色。这种编程风格通常被称为消息传递，当我们在第 3 章讨论建模和模拟的问题时，我们将把它作为一个基本工具来使用。

练习 2.4

这里是对对偶的另一种函数表示。对于这种表示，验证head(pair(x, y))对于任何对象x和y都产生x。

function pair(x, y) {
    return m => m(x, y);
}
function head(z) {
    return z((p, q) => p);
}

tail的对应定义是什么？（提示：要验证这个定义是否有效，可以利用第 1.1.5 节的替换模型。）

练习 2.5

证明我们可以只使用数字和算术运算来表示非负整数对，如果我们将对偶a和b表示为乘积2^a3^b的整数。给出函数pair、head和tail的相应定义。

练习 2.6

如果将对偶表示为函数（练习 2.4）还不够令人费解，那么可以考虑，在一个可以操作函数的语言中，我们可以通过实现 0 和加 1 的操作来不使用数字（至少就非负整数而言）：

const zero = f => x => x;

function add_1(n) {
    return f => x => f(n(f)(x));
}

这种表示被称为Church 数，以其发明者阿隆佐·邱奇命名，他是发明λ演算的逻辑学家。

直接定义one和two（不要用zero和add_1）。（提示：使用替换来计算add_1(zero)）。直接定义加法函数plus（不要用重复应用add_1）。

2.1.4 扩展练习：区间算术

Alyssa P. Hacker 正在设计一个帮助人们解决工程问题的系统。她希望在她的系统中提供一个功能，可以处理不精确的数量（例如物理设备的测量参数），并且知道精度，这样当使用这种*似数量进行计算时，结果将是已知精度的数字。

电气工程师将使用 Alyssa 的系统来计算电气量。有时，他们需要使用以下公式计算两个电阻R[1]和R[2]的并联等效电阻R[p]的值

电阻值通常只能知道制造商保证的一定公差。例如，如果你购买一个标有“6.8 欧姆，公差 10%”的电阻器，你只能确定电阻器的电阻在 6.8 - 0.68 = 6.12 和 6.8 + 0.68 = 7.48 欧姆之间。因此，如果你有一个 6.8 欧姆 10%的电阻器与一个 4.7 欧姆 5%的电阻器并联，组合的电阻可以在大约 2.58 欧姆（如果两个电阻器在下限）到大约 2.97 欧姆（如果两个电阻器在上限）之间变化。

Alyssa 的想法是将“区间算术”实现为一组用于组合“区间”的算术操作（表示不精确数量的可能值范围的对象）。将两个区间相加、相减、相乘或相除的结果本身是一个区间，表示结果的范围。

Alyssa 假设存在一个称为“区间”的抽象对象，它有两个端点：一个下限和一个上限。她还假设，给定区间的端点，她可以使用数据构造函数make_interval构造区间。Alyssa 首先编写了一个函数来添加两个区间。她推断出和的最小值是两个下限的和，最大值是两个上限的和：

function add_interval(x, y) {
    return make_interval(lower_bound(x) + lower_bound(y),
                         upper_bound(x) + upper_bound(y));
}

Alyssa 还通过找到边界的最小值和最大值来计算两个区间的乘积，并将它们用作结果区间的边界。（函数math_min和math_max是原始函数，用于找到任意数量参数的最小值或最大值。）

function mul_interval(x, y) {
    const p1 = lower_bound(x) * lower_bound(y); 
    const p2 = lower_bound(x) * upper_bound(y);
    const p3 = upper_bound(x) * lower_bound(y);
    const p4 = upper_bound(x) * upper_bound(y);
    return make_interval(math_min(p1, p2, p3, p4),
                         math_max(p1, p2, p3, p4));
}

要划分两个区间，Alyssa 将第一个乘以第二个的倒数。注意倒数区间的边界是上限的倒数和下限的倒数，按顺序排列。

function div_interval(x, y) {
    return mul_interval(x, make_interval(1 / upper_bound(y),
                                         1 / lower_bound(y)));
}

练习 2.7

Alyssa 的程序是不完整的，因为她没有指定区间抽象的实现。这里是区间构造函数的定义：

function make_interval(x, y) { return pair(x, y); }

定义选择器upper_bound和lower_bound来完成实现。

练习 2.8

使用类似 Alyssa 的推理，描述如何计算两个区间的差。定义一个相应的减法函数，称为sub_interval。

练习 2.9

区间的宽度是其上限和下限之间的差的一半。宽度是区间指定的数字的不确定性的度量。对于一些算术操作，组合两个区间的结果的宽度仅取决于参数区间的宽度，而对于其他一些算术操作，组合的宽度并不是参数区间的宽度的函数。证明两个区间的和（或差）的宽度仅取决于要添加（或减去）的区间的宽度。举例说明，这对于乘法或除法来说并不成立。

练习 2.10

专家系统程序员 Ben Bitdiddle 看着 Alyssa 的肩膀，评论说不清楚通过跨越零的区间进行除法意味着什么。修改 Alyssa 的程序以检查这种情况，并在发生时发出错误信号。

练习 2.11

顺便说一句，Ben 也神秘地评论说：“通过测试区间端点的符号，可以将mul_interval分解为九种情况，其中只有一种需要超过两次乘法。”使用 Ben 的建议重写这个函数。

调试完她的程序后，Alyssa 将其展示给一个潜在的用户，后者抱怨说她的程序解决了错误的问题。他想要一个能够处理以中心值和加法公差表示的数字的程序；例如，他想要处理像 3.5 ± 0.15 这样的区间，而不是[3.35, 3.65]。Alyssa 回到她的桌子上，通过提供一个替代构造函数和替代选择器来解决这个问题：

function make_center_width(c, w) {
    return make_interval(c - w, c + w);
}
function center(i) {
    return (lower_bound(i) + upper_bound(i)) / 2;
}
function width(i) {
    return (upper_bound(i) - lower_bound(i)) / 2;
}

不幸的是，Alyssa 的大多数用户都是工程师。真正的工程情况通常涉及只有小不确定性的测量，测量值是区间宽度与区间中点的比率。工程师通常会在设备参数上指定百分比的容差，就像前面给出的电阻器规格一样。

练习 2.12

定义一个构造函数make_center_percent，它接受一个中心和一个百分比容差，并产生所需的区间。你还必须定义一个选择器percent，它为给定的区间产生百分比容差。center选择器与上面显示的相同。

练习 2.13

证明在小百分比容差的假设下，有一个简单的公式可以用因子的容差来*似计算两个区间的乘积的百分比容差。你可以通过假设所有数字都是正数来简化这个问题。

经过相当多的工作，Alyssa P. Hacker 交付了她的成品系统。几年后，当她已经忘记了这一切时，她接到了一个愤怒的用户 Lem E. Tweakit 的电话。看来 Lem 已经注意到并联电阻的公式可以用两种代数上等价的方式来写：

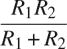
并且

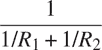
他写了以下两个程序，每个程序都以不同的方式计算并联电阻的公式：

function par1(r1, r2) {
    return div_interval(mul_interval(r1, r2),
                        add_interval(r1, r2));
}
function par2(r1, r2) {
    const one = make_interval(1, 1);
    return div_interval(one,
                        add_interval(div_interval(one, r1),
                                     div_interval(one, r2)));
}

Lem 抱怨 Alyssa 的程序对于两种计算方式给出了不同的答案。这是一个严重的投诉。

练习 2.14

证明 Lem 是对的。研究系统对各种算术表达式的行为。创建一些区间A和B，并在计算表达式A / A和A / B时使用它们。通过使用宽度是中心值的小百分比的区间，你将获得最多的见解。以中心百分比形式检查计算结果（参见练习 2.12）。

练习 2.15

另一位用户 Eva Lu Ator 也注意到了不同的区间是由不同但代数上等价的表达式计算出来的。她说，使用 Alyssa 的系统计算区间的公式，如果可以以不重复代表不确定数字的名称的形式编写，将产生更紧的误差界限。因此，她说，par2比par1是一个“更好”的并联电阻程序。她是对的吗？为什么？

练习 2.16

一般来说，解释等价的代数表达式可能导致不同的答案。你能设计一个没有这个缺点的区间算术包吗，还是这个任务是不可能的？（警告：这个问题非常困难。）

2.2 分层数据和闭包性质

正如我们所看到的，一对提供了一个原始的“粘合剂”，我们可以用它来构造复合数据对象。图 2.2 显示了一种标准的可视化一对的方法——在这种情况下，是由pair(1, 2)形成的一对。在这种表示中，称为盒式和指针表示法，每个复合对象都显示为指向一个盒子的指针。一对的盒子有两部分，左部分包含一对的头部，右部分包含尾部。

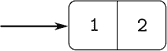
图 2.2 pair(1, 2)的盒式图表示。

我们已经看到pair不仅可以用来组合数字，还可以用来组合一对。（你在做练习 2.2 和 2.3 时已经利用了这一事实，或者应该利用了。）因此，一对提供了一个通用的构建块，我们可以用它来构造各种数据结构。图 2.3 显示了使用一对组合数字 1、2、3 和 4 的两种方法。

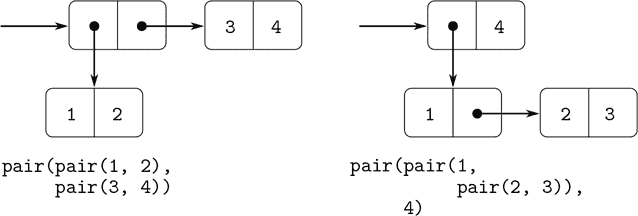
图 2.3 使用一对的两种组合 1、2、3 和 4 的方法。

创建元素为对的对的能力是列表结构作为表示工具的重要性的本质。我们将这种能力称为pair的闭包属性。一般来说，如果组合数据对象的操作满足闭包属性，那么使用该操作组合的结果本身可以使用相同的操作进行组合。⁷ 闭包是任何组合手段中权力的关键，因为它允许我们创建分层结构——由部分组成的结构，这些部分本身又由部分组成，依此类推。

从第 1 章开始，我们在处理函数时已经基本使用了闭包，因为除了非常简单的程序之外，所有程序都依赖于组合的元素本身可以是组合的事实。在本节中，我们将讨论闭包对于复合数据的影响。我们描述了一些使用对来表示序列和树的传统技术，并展示了一种图形语言，以生动的方式说明了闭包。

2.2.1 表示序列

我们可以使用对构建一种序列，即有序的数据对象集合。当然，有许多方法可以用对来表示序列。其中一种特别直接的表示方法如图 2.4 所示，其中序列 1, 2, 3, 4 被表示为一系列对。每对的head是链中对应的项目，而对的tail是链中的下一个对。最后一对的tail表示序列的结尾，在盒子和指针图中表示为对角线，而在程序中表示为 JavaScript 的原始值null。整个序列是通过嵌套的pair操作构建的：

图 2.4 序列 1, 2, 3, 4 表示为一系列对。

pair(1,
     pair(2,
          pair(3,
               pair(4, null))));

由嵌套的pair应用形成的这样一系列对称为列表，我们的 JavaScript 环境提供了一个名为list的原语来帮助构建列表。⁸ 上述序列可以通过list(1, 2, 3, 4)生成。一般来说，

list(`a[1]`, `a[2], ..., `a[n]`)

等同于

pair(`a[1]`, pair(`a[2]`, pair(..., pair(a[n], null)...)))

我们的解释器使用盒子和指针图的文本表示来打印对。pair(1, 2)的结果打印为1, 2]，[图 2.4 中的数据对象打印为[1, [2, [3, [4, null]]]]：

const one_through_four = list(1, 2, 3, 4);

one_through_four;
[1, [2, [3, [4, null]]]]

我们可以将head视为选择列表中的第一项，将tail视为选择除第一项外的所有子列表。可以使用嵌套的head和tail应用来提取列表中的第二、第三和后续项。构造函数pair使得像原始列表一样的列表，但在开头增加了一个额外的项目。

head(one_through_four);
1

tail(one_through_four);
[2, [3, [4, null]]]

head(tail(one_through_four));
2

pair(10, one_through_four);
[10, [1, [2, [3, [4, null]]]]]

pair(5, one_through_four);
[5, [1, [2, [3, [4, null]]]]]

用于终止对链的值null可以被视为没有元素的序列，即空列表。⁹

盒子表示法有时很难阅读。在本书中，当我们想要指示数据结构的列表性质时，我们将使用另一种列表表示法：在可能的情况下，列表表示法使用list的应用，其求值将导致所需的结构。例如，代替盒子表示法

*[1, [[2, 3], [[4, [5, null]], [6, null]]]]*

我们写

list(1, [2, 3], list(4, 5), 6)

在列表表示法中。¹⁰

列表操作

使用对来表示列表中元素的序列的方法伴随着传统的编程技术，通过连续使用tail来遍历列表。例如，函数list_ref以列表和数字n作为参数，并返回列表的第n项。习惯上从 0 开始对列表的元素进行编号。计算list_ref的方法如下：

对于n = 0，list_ref应返回列表的head。
否则，list_ref应返回列表的tail的(n – 1)项。

function list_ref(items, n) {
    return n === 0
           ? head(items)
           : list_ref(tail(items), n - 1);
}

const squares = list(1, 4, 9, 16, 25);

list_ref(squares, 3);
16

通常我们会遍历整个列表。为了帮助实现这一点，我们的 JavaScript 环境包括一个原始谓词is_null，用于测试其参数是否为空列表。返回列表中项目的数量的函数length说明了这种典型的使用模式：

function length(items) {
    return is_null(items)
           ? 0
           : 1 + length(tail(items));
}

const odds = list(1, 3, 5, 7);

length(odds);
`4`

length函数实现了一个简单的递归计划。减少步骤是：

任何列表的length都是tail的length加 1。

这将一直应用，直到达到基本情况：

空列表的length为 0。

我们也可以以迭代的方式计算length：

function length(items) {
    function length_iter(a, count) {
        return is_null(a)
               ? count
               : length_iter(tail(a), count + 1);
    }
    return length_iter(items, 0);
}

另一种常规的编程技术是通过使用pair将元素附加到列表的前面来构造一个答案列表，同时使用tail在列表中行走，就像函数append中那样，该函数接受两个列表作为参数并组合它们的元素以生成一个新列表：

append(squares, odds);
list(1, 4, 9, 16, 25, 1, 3, 5, 7)

append(odds, squares);
list(1, 3, 5, 7, 1, 4, 9, 16, 25)

函数append也是使用递归计划实现的。要append列表list1和list2，请执行以下操作：

如果list1是空列表，则结果就是list2。
否则，append list1的tail和list2，并将list1的head添加到结果中：

function append(list1, list2) {
    return is_null(list1)
           ? list2
           : pair(head(list1), append(tail(list1), list2));
}

练习 2.17

定义一个函数last_pair，返回一个只包含给定（非空）列表的最后一个元素的列表：

last_pair(list(23, 72, 149, 34));
list(34)

练习 2.18

定义一个函数reverse，它以列表作为参数并返回相同元素的逆序列表：

reverse(list(1, 4, 9, 16, 25));
list(25, 16, 9, 4, 1)

练习 2.19

考虑第 1.2.2 节的找零程序。很高兴能够轻松更改程序使用的货币，这样我们就可以计算例如英镑的找零方式。按照程序的编写方式，货币的知识部分分布在函数first_denomination和函数count_change中（它知道有五种美国硬币）。最好能够提供要用于找零的硬币列表。

我们想要重写函数cc，使得它的第二个参数是要使用的硬币的值的列表，而不是指定要使用哪些硬币的整数。然后我们可以有定义每种货币的列表：

const us_coins = list(50, 25, 10, 5, 1);
const uk_coins = list(100, 50, 20, 10, 5, 2, 1);

然后我们可以这样调用cc：

cc(100, us_coins);
292

这将需要在一定程度上更改程序cc。它仍然具有相同的形式，但将以不同的方式访问其第二个参数，如下所示：

function cc(amount, coin_values) {
    return amount === 0
           ? 1
           : amount < 0 || no_more(coin_values)
           ? 0
           : cc(amount, except_first_denomination(coin_values)) +
             cc(amount - first_denomination(coin_values), coin_values);
}

根据列表结构的原始操作定义函数first_denomination、except_first_denomination和no_more。列表coin_values的顺序是否会影响cc产生的答案？为什么？

练习 2.20

在高阶函数的存在下，函数不一定需要有多个参数；一个就足够了。如果我们有一个像plus这样自然需要两个参数的函数，我们可以编写一个函数的变体，逐个传递参数。将变体应用于第一个参数可能会返回一个函数，然后我们可以将其应用于第二个参数，依此类推。这种做法——称为柯里化，以美国数学家和逻辑学家 Haskell Brooks Curry 命名——在 Haskell 和 OCaml 等编程语言中非常常见。在 JavaScript 中，plus的柯里化版本如下。

function plus_curried(x) {
    return y => x + y;
}

编写一个函数brooks，它以柯里化函数作为第一个参数，并以柯里化函数应用的给定顺序逐个应用作为第二个参数的参数列表。例如，brooks的以下应用应该与plus_curried(3)(4)具有相同的效果：

brooks(plus_curried, list(3, 4));
`7`

趁热打铁，我们也可以对函数brooks进行柯里化！编写一个函数brooks_curried，可以按以下方式应用：

brooks_curried(list(plus_curried, 3, 4));
`7`

使用这个函数brooks_curried，求值以下两个语句的结果是什么？

brooks_curried(list(brooks_curried,
                    list(plus_curried, 3, 4)));

brooks_curried(list(brooks_curried,
                    list(brooks_curried,
                         list(plus_curried, 3, 4))));

对列表进行映射

有一个非常有用的操作是对列表中的每个元素应用一些转换，并生成结果列表。例如，以下函数通过给定的因子来缩放列表中的每个数字：

function scale_list(items, factor) {
    return is_null(items)
           ? null
           : pair(head(items) * factor,
                  scale_list(tail(items), factor));
}

scale_list(list(1, 2, 3, 4, 5), 10);
*[10, [20, [30, [40, [50, null]]]]]*

我们可以将这个一般的想法抽象出来，并将其作为一个通用模式表达为一个高阶函数，就像在 1.3 节中一样。这里的高阶函数称为map。函数map接受一个参数和一个列表，并返回通过将函数应用于列表中的每个元素产生的结果列表：

function map(fun, items) {
    return is_null(items)
           ? null
           : pair(fun(head(items)),
                  map(fun, tail(items)));
}

map(abs, list(-10, 2.5, -11.6, 17));
*[10, [2.5, [11.6, [17, null]]]]*

map(x => x * x, list(1, 2, 3, 4));
*[1, [4, [9, [16, null]]]]*

现在我们可以通过map给出scale_list的新定义：

function scale_list(items, factor) {
    return map(x => x * factor, items);
}

函数map是一个重要的构造，不仅因为它捕捉了一个常见的模式，而且因为它在处理列表时建立了一个更高的抽象级别。在scale_list的原始定义中，程序的递归结构引起了对列表的逐个处理的注意。通过map定义scale_list抑制了那个细节级别，并强调了缩放将元素列表转换为结果列表。这两个定义之间的区别不是计算机执行了不同的过程（它没有），而是我们对过程的思考方式不同。实际上，map有助于建立一个抽象屏障，将转换列表的函数的实现与提取和组合列表元素的细节隔离开来。就像图 2.1 中显示的屏障一样，这种抽象给了我们改变序列如何实现的低级细节的灵活性，同时保留了将序列转换为序列的操作的概念框架。2.2.3 节扩展了这种将序列作为组织程序的框架的用法。

练习 2.21

函数square_list接受一个数字列表作为参数，并返回这些数字的*方列表。

square_list(list(1, 2, 3, 4));
*[1, [4, [9, [16, null]]]]*

这里有两种不同的square_list的定义。通过填写缺失的表达式来完成它们：

function square_list(items) {
    return is_null(items)
           ? null
           : pair(〈??〉, 〈??〉);
}

function square_list(items) {
    return map(〈??〉, 〈??〉);
}

练习 2.22

Louis Reasoner 试图重写练习 2.21 的第一个square_list函数，以便它演变成一个迭代过程：

function square_list(items) {
    function iter(things, answer) {
        return is_null(things)
               ? answer
               : iter(tail(things),
                      pair(square(head(things)),
                           answer));
    }
    return iter(items, null);
}

不幸的是，用这种方式定义square_list会产生与期望的相反顺序的答案列表。为什么？

然后 Louis 尝试通过交换pair的参数来修复他的错误：

function square_list(items) {
    function iter(things, answer) {
        return is_null(things)
               ? answer
               : iter(tail(things),
                      pair(answer,
                           square(head(things))));
    }
    return iter(items, null);
}

这也不起作用。解释一下。

练习 2.23

函数for_each类似于map。它接受一个函数和一个元素列表作为参数。但是，for_each不会形成结果列表，而是依次对每个元素应用函数，从左到右。应用函数到元素后返回的值根本不会被使用——for_each用于执行动作的函数，比如打印。例如，

for_each(x => display(x), list(57, 321, 88));
57
321
88

调用for_each（上面未显示）的返回值可以是任意的，比如true。给出for_each的实现。

2.2.2 分层结构

以列表的形式表示序列的表示自然地推广到表示元素本身可以是序列的序列。例如，我们可以将由[[1, [2, null]], [3, [4, null]]]构成的对象视为

pair(list(1, 2), list(3, 4));

作为一个包含三个项目的列表，第一个项目本身是一个列表，1, [2, null]]。[图 2.5 显示了这个结构的表示形式。

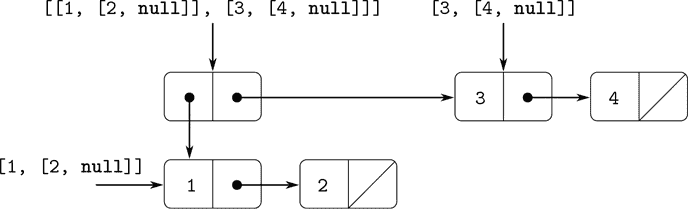
图 2.5 pair(list(1, 2), list(3, 4))形成的结构。

将元素为序列的序列视为树的另一种方式。序列的元素是树的分支，而元素本身是序列的元素是子树。图 2.6 显示了图 2.5 中的结构被视为树。

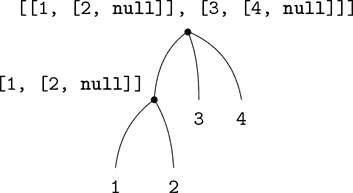
图 2.6 图 2.5 中的列表结构被视为树。

递归是处理树结构的自然工具，因为我们通常可以将树上的操作减少到对其分支的操作，这些操作反过来又减少到对分支的分支的操作，依此类推，直到达到树的叶子。例如，比较第 2.2.1 节的length函数和count_leaves函数，后者返回树的总叶子数：

const x = pair(list(1, 2), list(3, 4));

length(x);
`3`

count_leaves(x);
`4`

list(x, x);
list(list(list(1, 2), 3, 4), list(list(1, 2), 3, 4))

length(list(x, x));
`2`

count_leaves(list(x, x));
`8`

要实现count_leaves，请回想一下计算length的递归计划：

列表x的length是 1 加上x的tail的length。
空列表的length为 0。

函数count_leaves类似。空列表的值是相同的：

空列表的count_leaves为 0。

但在减少步骤中，我们剥离列表的head时，我们必须考虑到head本身可能是一个我们需要计算叶子的树。因此，适当的减少步骤是

树x的count_leaves是x的head的count_leaves加上x的tail的count_leaves。

最后，通过取head，我们到达实际的叶子，因此我们需要另一个基本情况：

叶子的count_leaves为 1。

为了帮助编写树的递归函数，我们的 JavaScript 环境提供了原始谓词is_pair，用于测试其参数是否为对。以下是完整的函数：¹¹

function count_leaves(x) {
    return is_null(x)
           ? 0
           : ! is_pair(x)
           ? 1
           : count_leaves(head(x)) + count_leaves(tail(x));
}

练习 2.24

假设我们求值表达式list(1, list(2, list(3, 4)))。给出解释器打印的结果，相应的框和指针结构，以及将其解释为树的解释（如图 2.6 中所示）。

练习 2.25

给出head和tail的组合，将从以下每个列表中挑选出 7 个，以列表表示：

list(1, 3, list(5, 7), 9)

list(list(7))

list(1, list(2, list(3, list(4, list(5, list(6, 7))))))

练习 2.26

假设我们定义x和y为两个列表：

const x = list(1, 2, 3);
const y = list(4, 5, 6);

求值以下每个表达式的结果是什么，以框表示法和列表表示法？

append(x, y)

pair(x, y)

list(x, y)

练习 2.27

修改练习 2.18 的reverse函数，以生成一个deep_reverse函数，该函数以列表作为参数，并将其值作为其元素反转，并且所有子列表也进行深度反转。例如，

const x = list(list(1, 2), list(3, 4));

x;
list(list(1, 2), list(3, 4))

reverse(x);
list(list(3, 4), list(1, 2))

deep_reverse(x);
list(list(4, 3), list(2, 1))

练习 2.28

编写一个名为fringe的函数，该函数以树（表示为列表）作为参数，并返回一个列表，其中的元素都是树的叶子，按从左到右的顺序排列。例如，

const x = list(list(1, 2), list(3, 4));

fringe(x);
list(1, 2, 3, 4)

fringe(list(x, x));
list(1, 2, 3, 4, 1, 2, 3, 4)

练习 2.29

二进制移动由两个分支组成，左分支和右分支。每个分支都是一根特定长度的杆，从中悬挂着一个重量或另一个二进制移动。我们可以使用复合数据来表示二进制移动，通过从两个分支构造它（例如，使用list）：

function make_mobile(left, right) {
    return list(left, right);
}

分支由length（必须是数字）和structure（可以是数字（表示简单重量）或另一个移动）组成：

function make_branch(length, structure) {
    return list(length, structure);
}

a.编写相应的选择器left_branch和right_branch，它们返回移动的分支，以及branch_length和branch_structure，它们返回分支的组件。
b.使用您的选择器，定义一个名为total_weight的函数，返回移动的总重量。
c.如果移动的顶部左分支施加的力矩等于顶部右分支施加的力矩（也就是说，如果左杆的长度乘以悬挂在该杆上的重量等于右侧对应的乘积），并且挂在其分支上的每个子移动都是*衡的，则称移动为*衡。设计一个谓词，测试二进制移动是否*衡。

d.假设我们更改移动的表示形式，使构造函数为

function make_mobile(left, right) {
    return pair(left, right);
}
function make_branch(length, structure) {
    return pair(length, structure);
}

您需要更改程序以转换为新表示形式吗？

对树进行映射

就像map是处理序列的强大抽象一样，map和递归一起是处理树的强大抽象。例如，scale_tree函数类似于 2.2.1 节的scale_list，它的参数是一个数字因子和一个叶子为数字的树。它返回一个相同形状的树，其中每个数字都乘以因子。scale_tree的递归计划类似于count_leaves的计划：

function scale_tree(tree, factor) {
    return is_null(tree)
           ? null
           : ! is_pair(tree)
           ? tree * factor
           : pair(scale_tree(head(tree), factor),
                  scale_tree(tail(tree), factor));
}

scale_tree(list(1, list(2, list(3, 4), 5), list(6, 7)),
           10);
list(10, list(20, list(30, 40), 50), list(60, 70))

另一种实现scale_tree的方法是将树视为子树序列，并使用map。我们在序列上进行映射，依次缩放每个子树，并返回结果列表。在基本情况下，树是叶子时，我们只需乘以因子：

function scale_tree(tree, factor) {
    return map(sub_tree => is_pair(sub_tree)
                           ? scale_tree(sub_tree, factor)
                           : sub_tree * factor,
               tree);
}

许多树操作可以通过类似的序列操作和递归的组合来实现。

练习 2.30

声明一个类似于练习 2.21 的square_list函数的函数square_tree。也就是说，square_tree应该表现如下：

square_tree(list(1,
                 list(2, list(3, 4), 5),
                 list(6, 7)));
list(1, list(4, list(9, 16), 25), list(36, 49)))

声明square_tree，既直接（即，不使用任何高阶函数），也使用map和递归。

练习 2.31

将您对练习 2.30 的答案抽象化，以生成一个具有square_tree属性的函数tree_map，可以声明为

function square_tree(tree) { return tree_map(square, tree); }

练习 2.32

我们可以将集合表示为不同元素的列表，并且可以将集合的所有子集表示为列表的列表。例如，如果集合是list(1, 2, 3)，那么所有子集的集合是

list(null, list(3), list(2), list(2, 3),
     list(1), list(1, 3), list(1, 2),
     list(1, 2, 3))

完成以下函数声明，生成一个集合的子集，并清楚解释为什么它有效：

function subsets(s) {
    if (is_null(s)) {
        return list(null);
    } else {
        const rest = subsets(tail(s));
        return append(rest, map( ?? , rest));
    }
}

2.2.3 序列作为常规接口

在处理复合数据时，我们强调了数据抽象如何使我们能够设计程序，而不会陷入数据表示的细节，并且抽象保留了对我们来说灵活性，可以尝试替代表示。在本节中，我们介绍了另一个处理数据结构的强大设计原则——使用常规接口。

在 1.3 节中，我们看到了程序抽象如何作为高阶函数实现，可以捕捉处理数字数据的程序中的常见模式。我们能够为处理复合数据制定类似操作的能力，关键取决于我们操作数据结构的风格。例如，考虑以下函数，类似于 2.2.2 节中的count_leaves函数，它以树作为参数，并计算奇数叶子的*方和：

function sum_odd_squares(tree) {
    return is_null(tree)
           ? 0
           : ! is_pair(tree)
           ? is_odd(tree) ? square(tree) : 0
           : sum_odd_squares(head(tree)) +
             sum_odd_squares(tail(tree));
}

表面上，这个函数与以下函数非常不同，后者构造了一个所有偶数斐波那契数Fib(k)的列表，其中k小于或等于给定的整数n：

function even_fibs(n) {
    function next(k) {
        if (k > n) {
            return null;
        } else {
            const f = fib(k);
            return is_even(f)
                   ? pair(f, next(k + 1))
                   : next(k + 1);
        }
    }
    return next(0);
}

尽管这两个函数在结构上非常不同，但对这两个计算的更抽象描述揭示了很多相似之处。第一个程序

枚举树的叶子；
过滤它们，选择奇数；
*方选定的每一个；和
使用+累积结果，从 0 开始。

第二个程序

枚举从 0 到n的整数；
计算每个整数的斐波那契数；
过滤它们，选择偶数；和
使用pair累积结果，从空列表开始。

信号处理工程师会自然地将这些过程概念化为信号流经过一系列阶段，每个阶段实现程序计划的一部分，如图 2.7 所示。在sum_odd_squares中，我们从一个枚举开始，它生成一个由给定树的叶子组成的“信号”。这个信号通过一个过滤器，它消除除奇数元素以外的所有元素。结果信号依次通过一个映射，它是一个应用square函数到每个元素的“转换器”。映射的输出然后被传递给一个累加器，它使用+组合元素，从初始 0 开始。even_fibs的计划是类似的。

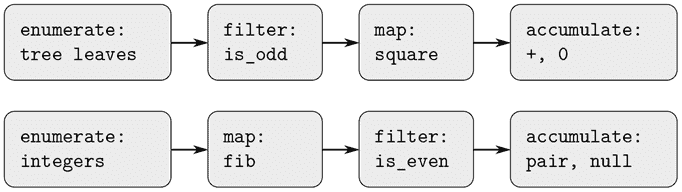
图 2.7 函数sum_odd_squares（顶部）和even_fibs（底部）的信号流计划揭示了这两个程序之间的共同点。

不幸的是，上述两个函数声明未能展现出这种信号流结构。例如，如果我们检查sum_odd_squares函数，我们会发现枚举部分部分地由is_null和is_pair测试实现，部分地由函数的树递归结构实现。同样，累积部分地在测试中找到，部分地在递归中使用的加法中找到。一般来说，两个函数没有明显的部分与信号流描述中的元素相对应。我们的两个函数以不同的方式分解计算，将枚举分散到程序中，并将其与映射、过滤和累积混合在一起。如果我们能够组织我们的程序，使得信号流结构在我们编写的函数中显现出来，这将增加结果程序的概念清晰度。

序列操作

组织程序以更清晰地反映信号流结构的关键是集中于从一个过程阶段到下一个阶段流动的“信号”。如果我们将这些信号表示为列表，那么我们可以使用列表操作来实现每个阶段的处理。例如，我们可以使用第 2.2.1 节中的map函数来实现信号流图的映射阶段：

map(square, list(1, 2, 3, 4, 5));
list(1, 4, 9, 16, 25)

通过过滤序列以选择仅满足给定谓词的元素来实现

function filter(predicate, sequence) {
    return is_null(sequence)
           ? null
           : predicate(head(sequence))
           ? pair(head(sequence),
                  filter(predicate, tail(sequence)))
           : filter(predicate, tail(sequence));
}

例如，

filter(is_odd, list(1, 2, 3, 4, 5));
list(1, 3, 5)

累积可以通过实现

function accumulate(op, initial, sequence) {
    return is_null(sequence)
           ? initial
           : op(head(sequence),
                accumulate(op, initial, tail(sequence)));
}

accumulate(plus, 0, list(1, 2, 3, 4, 5));
15

accumulate(times, 1, list(1, 2, 3, 4, 5));
120

accumulate(pair, null, list(1, 2, 3, 4, 5));
list(1, 2, 3, 4, 5)

实现信号流图的所有剩下的部分就是枚举要处理的元素序列。对于even_fibs，我们需要生成给定范围内的整数序列，可以按如下方式实现：

function enumerate_interval(low, high) {
    return low > high
           ? null
           : pair(low,
                  enumerate_interval(low + 1, high));
}

enumerate_interval(2, 7);
list(2, 3, 4, 5, 6, 7)

要枚举树的叶子，我们可以使用¹²

function enumerate_tree(tree) {
    return is_null(tree)
           ? null
           : ! is_pair(tree)
           ? list(tree)
           : append(enumerate_tree(head(tree)),
                    enumerate_tree(tail(tree)));
}

enumerate_tree(list(1, list(2, list(3, 4)), 5));
list(1, 2, 3, 4, 5)

现在我们可以像信号流图一样重新制定sum_odd_squares和even_fibs。对于sum_odd_squares，我们枚举树的叶子序列，过滤以保留序列中的奇数，对每个元素求*方，并求和结果：

function sum_odd_squares(tree) {
    return accumulate(plus,
                      0,
                      map(square,
                          filter(is_odd,
                                 enumerate_tree(tree))));
}

对于even_fibs，我们枚举从 0 到n的整数，为每个整数生成斐波那契数，过滤结果序列以保留偶数元素，并将结果累积到列表中：

function even_fibs(n) {
    return accumulate(pair,
                      null,
                      filter(is_even,
                             map(fib,
                                 enumerate_interval(0, n))));
}

将程序表达为序列操作的价值在于，这有助于我们制定模块化的程序设计，即由相对独立的部分组合而成的设计。我们可以通过提供一组标准组件的库以及用灵活方式连接组件的传统接口来鼓励模块化设计。

在工程设计中，模块化构建是控制复杂性的强大策略。例如，在实际的信号处理应用中，设计师经常通过级联从标准化的滤波器和传感器系列中选择的元素来构建系统。同样，序列操作提供了一系列标准程序元素的库，我们可以随意组合。例如，我们可以在一个程序中重用sum_odd_squares和even_fibs函数的部分，以构建前n + 1个斐波那契数的*方的列表：

function list_fib_squares(n) {
    return accumulate(pair,
                      null,
                      map(square,
                          map(fib,
                              enumerate_interval(0, n))));
}

list_fib_squares(10);
list(0, 1, 1, 4, 9, 25, 64, 169, 441, 1156, 3025)

我们可以重新排列这些部分，并在计算序列中奇数的*方的乘积时使用它们：

function product_of_squares_of_odd_elements(sequence) {
    return accumulate(times,
                      1,
                      map(square,
                          filter(is_odd, sequence)));
}

product_of_squares_of_odd_elements(list(1, 2, 3, 4, 5));
225

我们还可以用序列操作来制定常规的数据处理应用。假设我们有一个人员记录序列，我们想要找到薪水最高的程序员的薪水。假设我们有一个选择器salary，返回记录的薪水，和一个谓词is_programmer，测试记录是否是程序员。然后我们可以写

function salary_of_highest_paid_programmer(records) {
    return accumulate(math_max,
                      0,
                      map(salary,
                          filter(is_programmer, records)));
}

这些例子只是给出了可以表达为序列操作的广泛操作范围的一点提示。¹³

这里实现的序列作为列表，作为一个传统接口，允许我们组合处理模块。此外，当我们将结构统一表示为序列时，我们已经将程序中的数据结构依赖局限在了少量序列操作中。通过更改这些操作，我们可以尝试使用序列的替代表示，同时保持程序的整体设计不变。在第 3.5 节中，我们将利用这种能力，将序列处理范式推广到允许无限序列。

练习 2.33

填写缺失的表达式，以完成一些基本的列表操作的累积定义：

function map(f, sequence) {
    return accumulate((x, y) => 〈??〉,
                      null, sequence);
}
function append(seq1, seq2) {
    return accumulate(pair, 〈??〉, 〈??〉);
}
function length(sequence) {
    return accumulate( 〈??〉, 0, sequence);
}

练习 2.34

在给定x的值的情况下，用x求值多项式可以被制定为一个累积。我们求值多项式

a[n]xⁿ + a[n][–1]xⁿ^(–1) + ... + a[1]x + a[0]

使用一种称为Horner's rule的著名算法，将计算结构化为

(... (a[n]x + a[n–1])x + ... + a[1]) x + a[0]

换句话说，我们从a[n]开始，乘以x，加上a[n]–1，乘以x，依此类推，直到达到a[0].¹⁴ 填写以下模板，以生成使用 Horner's rule 计算多项式的函数。假设多项式的系数按顺序排列，从a[0]到a[n]。

function horner_eval(x, coefficient_sequence) {
    return accumulate((this_coeff, higher_terms) => ?? ,
                      0,
                      coefficient_sequence);
}

例如，要计算1 + 3x + 5x³ + x⁵在x = 2时，您需要计算

horner_eval(2, list(1, 3, 0, 5, 0, 1));

练习 2.35

将 2.2.2 节中的count_leaves重新定义为累积：

function count_leaves(t) {
    return accumulate( ?? , ?? , map( ?? , ?? ));
}

练习 2.36

函数accumulate_n类似于accumulate，只是它的第三个参数是一个序列的序列，假定它们都有相同数量的元素。它将指定的累积函数应用于组合所有序列的第一个元素，所有序列的第二个元素，依此类推，并返回结果的序列。例如，如果s是一个包含四个序列的序列

list(list(1, 2, 3), list(4, 5, 6), list(7, 8, 9), list(10, 11, 12))

然后accumulate_n(plus, 0, s)的值应该是序列list(22, 26, 30)。填写以下accumulate_n的定义中缺失的表达式：

function accumulate_n(op, init, seqs) {
    return is_null(head(seqs))
           ? null
           : pair(accumulate(op, init, 〈??〉),
                  accumulate_n(op, init, 〈??〉));
}

练习 2.37

假设我们将向量v = (v[i])表示为数字序列，并将矩阵m = (m[ij])表示为向量序列（矩阵的行）。例如，矩阵

表示为以下序列：

list(list(1, 2, 3, 4),
     list(4, 5, 6, 6),
     list(6, 7, 8, 9))

有了这种表示，我们可以使用序列操作简洁地表示基本的矩阵和向量操作。这些操作（在任何一本关于矩阵代数的书中都有描述）如下：

我们可以将点积定义为¹⁵

function dot_product(v, w) {
    return accumulate(plus, 0, accumulate_n(times, 1, list(v, w)));
}

填写以下函数中的缺失表达式，用于计算其他矩阵操作。（函数accumulate_n在练习 2.36 中声明。）

function matrix_times_vector(m, v) {
    return map( ?? , m);
}
function transpose(mat) {
    return accumulate_n( ?? , ?? , mat);
}
function matrix_times_matrix(n, m) {
    const cols = transpose(n);
    return map( ?? , m);
}

练习 2.38

accumulate函数也被称为fold_right，因为它将序列的第一个元素与组合所有元素的结果结合。还有一个fold_left，它类似于fold_right，只是它是从相反方向组合元素的：

function fold_left(op, initial, sequence) {
    function iter(result, rest) {
        return is_null(rest)
               ? result
               : iter(op(result, head(rest)),
                      tail(rest));
    }
    return iter(initial, sequence);
}

以下是

fold_right(divide, 1, list(1, 2, 3));

fold_left(divide, 1, list(1, 2, 3));

fold_right(list, null, list(1, 2, 3));

fold_left(list, null, list(1, 2, 3));

给出一个op应满足的属性，以确保fold_right和fold_left对于任何序列都会产生相同的值。

练习 2.39

根据练习 2.38 中的fold_right和fold_left，完成reverse（练习 2.18）的以下定义：

function reverse(sequence) {
    return fold_right((x, y) => ?? , null, sequence);
}

function reverse(sequence) {
    return fold_left((x, y) => ?? , null, sequence);
}

嵌套映射

我们可以扩展序列范式，包括许多通常使用嵌套循环表达的计算。¹⁶考虑这个问题：给定一个正整数n，找到所有有序对的不同正整数i和j，其中1 j < i n，使得i + j是素数。例如，如果n为 6，则这些对是以下的：

`i`	2	3	4	4	5	6	6
`j`	1	2	1	3	2	1	5
`i + j`	3	5	5	7	7	7	11

组织这个计算的一种自然方式是生成所有小于或等于n的正整数的有序对序列，过滤以选择其和为素数的那些对，然后对于通过过滤的每个对(i, j)，产生三元组(i, j, i + j)。

以下是生成对序列的方法：对于每个整数i <= n，枚举小于i的整数j，对于这样的i和j生成对(i, j)。在序列操作方面，我们沿着序列enumerate_interval(1, n)进行映射。对于这个序列中的每个i，我们沿着序列enumerate_interval(1, i - 1)进行映射。对于后一个序列中的每个j，我们生成对list(i, j)。这给我们每个i的一系列对。将所有i的序列组合起来（通过累积使用append）产生所需的对序列：¹⁷

accumulate(append,
           null,
           map(i => map(j => list(i, j),
                        enumerate_interval(1, i - 1)),
               enumerate_interval(1, n)));

在这种程序中，映射和使用append进行累积的组合是如此常见，以至于我们将其作为一个单独的函数进行隔离：

function flatmap(f, seq) {
    return accumulate(append, null, map(f, seq));
}

现在过滤这些对的序列，找到其和为素数的对。过滤谓词对序列的每个元素进行调用；它的参数是一个对，并且它必须从对中提取整数。因此，应用于序列中的每个元素的谓词是

function is_prime_sum(pair) {
    return is_prime(head(pair) + head(tail(pair)));
}

最后，通过使用以下函数对过滤后的对进行映射，生成结果的序列，该函数构造一个由对的两个元素及其和组成的三元组：

function make_pair_sum(pair) {
    return list(head(pair), head(tail(pair)),
                head(pair) + head(tail(pair)));
}

将所有这些步骤组合起来得到完整的函数：

function prime_sum_pairs(n) {
    return map(make_pair_sum,
               filter(is_prime_sum,
                      flatmap(i => map(j => list(i, j),
                                       enumerate_interval(1, i - 1)),
                              enumerate_interval(1, n))));
}

嵌套映射对于除了枚举间隔的序列之外的序列也是有用的。假设我们希望生成集合S的所有排列；也就是说，集合中项目的所有排序方式。例如，{1, 2, 3}的排列是{1, 2, 3}，{1, 3, 2}，{2, 1, 3}，{2, 3, 1}，{3, 1, 2}和{3, 2, 1}。以下是生成S的排列的计划：对于S中的每个项目x，递归生成S – x的排列序列，然后将x添加到每个排列的前面。这为S中的每个x产生了以x开头的排列序列。将所有x的这些序列组合起来得到S的所有排列：¹⁹

function permutations(s) {
    return is_null(s) // empty set?
           ? list(null) // sequence containing empty set
           : flatmap(x => map(p => pair(x, p),
                              permutations(remove(x, s))),
                     s);
}

注意这种策略如何将生成S的排列的问题简化为生成比S元素更少的集合的排列的问题。在终端情况下，我们一直向下工作，直到空列表，它表示没有元素的集合。对于这个，我们生成list(null)，它是一个具有一个项目的序列，即没有元素的集合。permutations中使用的remove函数返回给定序列中除了给定项目之外的所有项目。这可以表示为一个简单的过滤器：

function remove(item, sequence) {
    return filter(x => ! (x === item),
                  sequence);
}

练习 2.40

编写一个名为unique_pairs的函数，给定一个整数n，生成一对(i, j)的序列，其中1, j < i, n。使用unique_pairs来简化上面给出的prime_sum_pairs的定义。

练习 2.41

编写一个函数，找到所有小于或等于给定整数n的不同正整数i、j和k的有序三元组，它们的和为给定整数s。

练习 2.42

“八皇后问题”是问如何在国际象棋棋盘上放置八个皇后，以便没有一个皇后受到其他任何一个皇后的攻击（即，没有两个皇后在同一行，列或对角线上）。一个可能的解决方案如图 2.8 所示。解决这个难题的一种方法是逐列工作，将一个皇后放在每一列。一旦我们放置了k - 1个皇后，我们必须将第k个皇后放在一个位置，使得它不会攻击棋盘上已经存在的任何一个皇后。我们可以递归地制定这种方法：假设我们已经生成了在棋盘的前k - 1列中放置k - 1个皇后的所有可能方式的序列。对于这些方式中的每一种，通过在第k列的每一行放置一个皇后来生成一个扩展的位置集。现在过滤这些位置，只保留对其他皇后来说第k列中的皇后是安全的位置。这样就产生了在前k列中放置k个皇后的所有方式的序列。通过继续这个过程，我们将产生不止一个解决方案，而是所有解决方案。

图 2.8 八皇后问题的一个解决方案。

我们将这个解决方案实现为一个名为queens的函数，它返回在n n国际象棋棋盘上放置n个皇后的所有解决方案的序列。函数queens有一个内部函数queens_cols，它返回在棋盘的前k列中放置皇后的所有方式的序列。

function queens(board_size) {
    function queen_cols(k) {
        return k === 0
               ? list(empty_board)
               : filter(positions => is_safe(k, positions),
                        flatmap(rest_of_queens =>
                                  map(new_row =>
                                        adjoin_position(new_row, k,
                                                        rest_of_queens),
                                      enumerate_interval(1, board_size)),
                                queen_cols(k - 1)));
    }
    return queen_cols(board_size);
}

在这个函数中，rest_of_queens是在前k - 1列中放置k - 1个皇后的一种方法，new_row是一个建议的行，用于放置第k列的皇后。通过实现代表棋盘位置集的函数adjoin_position，包括将新的行列位置添加到位置集的函数adjoin_position，以及代表空位置集的函数empty_board，来完成程序。您还必须编写函数is_safe，它确定一组位置中的第k列的皇后是否与其他皇后安全。（请注意，我们只需要检查新皇后是否安全——其他皇后已经保证彼此之间是安全的。）

练习 2.43

Louis Reasoner 在做练习 2.42 时遇到了很大的困难。他的queens函数似乎可以工作，但运行速度非常慢。（Louis 甚至没有等到它解决 6 6 的情况。）当 Louis 向 Eva Lu Ator 寻求帮助时，她指出他已经交换了flatmap中嵌套映射的顺序，将其写成

flatmap(new_row =>
          map(rest_of_queens =>
                adjoin_position(new_row, k, rest_of_queens),
              queen_cols(k - 1)),
        enumerate_interval(1, board_size));

解释为什么这种交换会使程序运行缓慢。估计 Louis 的程序解决八皇后问题需要多长时间，假设练习 2.42 中的程序在时间T内解决了这个问题。

2.2.4 例子：一个图片语言

本节介绍了一种简单的绘图语言，它展示了数据抽象和闭包的强大力量，并且以一种基本的方式利用了高阶函数。该语言旨在使实验变得容易，例如图 2.9 中的图案，这些图案由重复的元素组成，这些元素被移动和缩放。在这种语言中，被组合的数据对象被表示为函数，而不是列表结构。正如pair满足闭包属性使我们能够轻松构建任意复杂的列表结构一样，这种语言中的操作也满足闭包属性，使我们能够轻松构建任意复杂的图案。

图 2.9 使用图片语言生成的设计。

图片语言

当我们在 1.1 节开始学习编程时，我们强调了通过关注语言的基本元素、组合方式和抽象方式来描述一种语言的重要性。我们将在这里遵循这个框架。

这种图片语言的优雅之处在于只有一种元素，称为画家。画家绘制的图像被移动和缩放以适应指定的*行四边形框架。例如，有一个我们称为wave的原始画家，它绘制了一个粗线条的图像，如图 2.10 所示。图像的实际形状取决于框架——图 2.10 中的所有四幅图像都是由相同的wave画家生成的，但是与四个不同的框架相关。画家可以比这更复杂：名为rogers的原始画家绘制了麻省理工学院的创始人威廉·巴顿·罗杰斯的画像，如图 2.11 所示。图 2.11 中的四幅图像是与图 2.10 中的wave图像相对应的四个框架绘制的。

图 2.10 由wave画家生成的图像，与四个不同的框架相关。虚线框不是图像的一部分。

图 2.11 以与图 2.10 相同的四个框架为基础绘制的麻省理工学院创始人和第一任校长威廉·巴顿·罗杰斯的形象（原始图片由麻省理工学院博物馆提供）。

为了组合图像，我们使用各种操作从给定的画家构造新的画家。例如，beside操作接受两个画家，并产生一个新的复合画家，它在帧的左半部分绘制第一个画家的图像，在右半部分绘制第二个画家的图像。类似地，below接受两个画家，并产生一个复合画家，它在第一个画家的图像下方绘制第二个画家的图像。一些操作可以转换单个画家以产生新的画家。例如，flip_vert接受一个画家，并产生一个绘制其图像上下颠倒的画家，flip_horiz产生一个绘制原始画家图像从左到右翻转的画家。

图 2.12 显示了一个名为wave4的画家的绘制，它是从wave开始分两个阶段构建的：

const wave2 = beside(wave, flip_vert(wave));
const wave4 = below(wave2, wave2);

通过这种方式构建复杂的图像，我们利用了画家在语言的组合方式下是闭合的这一事实。两个画家的beside或below本身就是一个画家；因此，我们可以将其用作制作更复杂画家的元素。与使用pair构建列表结构一样，数据在组合方式下的闭合对于能够仅使用少量操作创建复杂结构至关重要。

图 2.12 从图 2.10 的wave画家开始创建一个复杂的图形。

一旦我们能够组合画家，我们希望能够抽象出典型的组合画家模式。我们将画家操作实现为 JavaScript 函数。这意味着在图片语言中我们不需要特殊的抽象机制：由于组合的方式是普通的 JavaScript 函数，我们自动具有对画家操作进行任何操作的能力。例如，我们可以将wave4中的模式抽象为

function flipped_pairs(painter) {
    const painter2 = beside(painter, flip_vert(painter));
    return below(painter2, painter2);
}

并将wave4声明为此模式的一个实例：

const wave4 = flipped_pairs(wave);

我们还可以定义递归操作。以下是一个使画家向右分割和分支的操作，如图 2.13 和 2.14 所示：

function right_split(painter, n) {
    if (n === 0) {
        return painter;
    } else {
        const smaller = right_split(painter, n - 1);
        return beside(painter, below(smaller, smaller));
    }
}

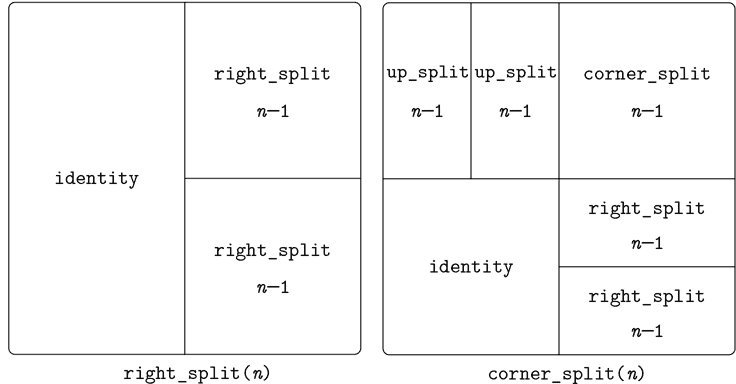
图 2.13 right_split和corner_split的递归计划。

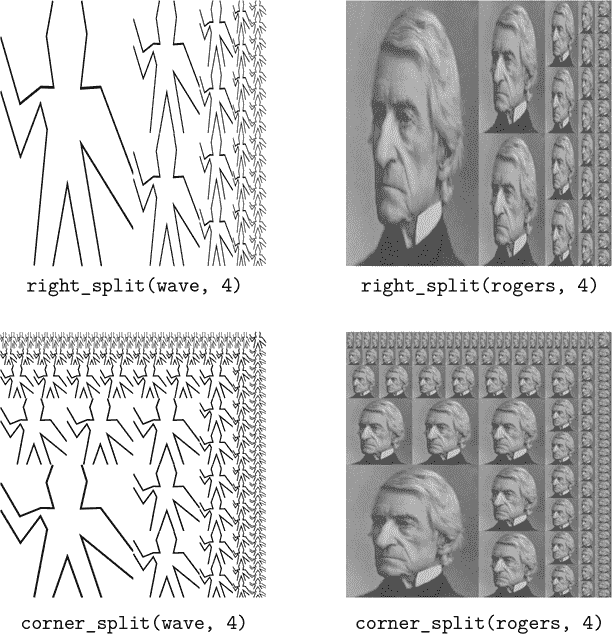
图 2.14 递归操作right_split应用于画家wave和rogers。将四个corner_split图形组合成对称的square_limit，如图 2.9 所示。

我们可以通过向上和向右分支来产生*衡的图案（参见练习 2.44 和图 2.13 和 2.14）：

function corner_split(painter, n) {
    if (n === 0) {
        return painter;
    } else {
        const up = up_split(painter, n - 1);
        const right = right_split(painter, n - 1);
        const top_left = beside(up, up);
        const bottom_right = below(right, right);
        const corner = corner_split(painter, n - 1);
        return beside(below(painter, top_left),
                      below(bottom_right, corner));
    }
}

通过适当放置四个corner_split的副本，我们可以获得一个名为square_limit的图案，其应用于wave和rogers如图 2.9 所示：

function square_limit(painter, n) {
    const quarter = corner_split(painter, n);
    const half = beside(flip_horiz(quarter), quarter);
    return below(flip_vert(half), half);
}

练习 2.44

声明由corner_split使用的函数up_split。它类似于right_split，只是它交换了below和beside的角色。

高阶操作

除了抽象出组合画家的模式之外，我们还可以在更高的层次上工作，抽象出组合画家操作的模式。也就是说，我们可以将画家操作视为要操作的元素，并且可以编写这些元素的组合方式——接受画家操作作为参数并创建新的画家操作的函数。

例如，flipped_pairs和square_limit都将画家的图像排列成方形图案的四个副本；它们之间的区别只在于它们如何定位这些副本。抽象这种画家组合的一种方法是使用以下函数，该函数接受四个一元画家操作并生成一个画家操作，该操作使用这四个操作对给定的画家进行变换并将结果排列成一个方形。²² 函数tl、tr、bl和br分别是要应用于左上角副本、右上角副本、左下角副本和右下角副本的变换。

function square_of_four(tl, tr, bl, br) {
    return painter => {
        const top = beside(tl(painter), tr(painter));
        const bottom = beside(bl(painter), br(painter));
        return below(bottom, top);
    };
}

然后可以根据square_of_four定义flipped_pairs如下：²³

function flipped_pairs(painter) {
    const combine4 = square_of_four(identity, flip_vert,
                                    identity, flip_vert);
    return combine4(painter);
}

和square_limit可以表示为²⁴

function square_limit(painter, n) {
    const combine4 = square_of_four(flip_horiz, identity,
                                    rotate180, flip_vert);
    return combine4(corner_split(painter, n));
}

练习 2.45

函数right_split和up_split可以表示为一般分割操作的实例。声明一个具有属性的函数split，使其求值

const right_split = split(beside, below);
const up_split = split(below, beside);

生成具有与已声明的相同行为的函数right_split和up_split。

帧

在我们展示如何实现画家及其组合方式之前，我们必须首先考虑帧。一个帧可以由三个向量描述——一个原点向量和两个边缘向量。原点向量指定了帧的原点与*面上某个绝对原点的偏移量，而边缘向量指定了帧的角落与其原点的偏移量。如果边缘是垂直的，那么帧将是矩形的。否则，帧将是一个更一般的*行四边形。

图 2.15 显示了一个帧及其相关的向量。根据数据抽象，我们不需要具体说明帧是如何表示的，除了说有一个构造函数make_frame，它接受三个向量并生成一个帧，以及三个相应的选择器origin_frame、edge1_frame和edge2_frame（参见练习 2.47）。

图 2.15 一个框架由三个向量描述——一个原点和两个边。

我们将使用单位正方形中的坐标(0 ≤ x, y ≤ 1)来指定图像。对于每个框架，我们关联一个 框架坐标映射，它将用于移动和缩放图像以适应框架。该映射通过将单位正方形映射到框架来将向量v = (x, y)映射到向量和

原点(框架) + x · 边[1] (框架) + y · 边[2] (框架)

例如，(0, 0)被映射到框架的原点，(1, 1)被映射到对角于原点的顶点，(0.5, 0.5)被映射到框架的中心。我们可以使用以下函数创建框架的坐标映射：²⁵

function frame_coord_map(frame) {
    return v => add_vect(origin_frame(frame),
                         add_vect(scale_vect(xcor_vect(v),
                                             edge1_frame(frame)),
                                  scale_vect(ycor_vect(v),
                                             edge2_frame(frame))));
}

观察将frame_coord_map应用于框架会返回一个函数，给定一个向量，返回一个向量。如果参数向量在单位正方形内，则结果向量将在框架内。例如，

frame_coord_map(a_frame)(make_vect(0, 0));

返回与

origin_frame(a_frame);

练习 2.46

从原点到一个点的二维向量v可以表示为一个对，包括一个x坐标和一个y坐标。通过给出一个构造函数make_vect和相应的选择器xcor_vect和ycor_vect来为向量实现数据抽象。根据你的选择器和构造函数，实现函数add_vect、sub_vect和scale_vect，执行向量加法、向量减法和将向量乘以标量的操作：

 (x[1], y[1]) + (x[2], y[2])  =  (x[1] + x[2], y[1] + y[2]) 

 (x[1], y[1]) – (x[2], y[2])  =  (x[1] – x[2], y[1] – y[2]) 

 s · (x, y)  =  (sx, sy)

练习 2.47

以下是框架的两个可能的构造函数：

function make_frame(origin, edge1, edge2) {
    return list(origin, edge1, edge2);
}

function make_frame(origin, edge1, edge2) {
   return pair(origin, pair(edge1, edge2));
}

对于每个构造函数，提供适当的选择器以生成框架的实现。

画家

画家表示为一个函数，给定一个框架作为参数，绘制一个特定的图像，移位和缩放以适应框架。也就是说，如果p是一个画家，f是一个框架，那么我们通过调用p传入f作为参数来在f中产生p的图像。

原始画家的实现细节取决于图形系统的特定特性和要绘制的图像类型。例如，假设我们有一个函数draw_line，它在屏幕上在两个指定点之间画一条线。然后我们可以根据线段列表创建线条绘制的画家，例如图 2.10 中的wave画家，如下所示：²⁶

function segments_to_painter(segment_list) {
    return frame =>
             for_each(segment =>
                        draw_line(
                            frame_coord_map(frame)
                                (start_segment(segment)),
                            frame_coord_map(frame)
                                (end_segment(segment))),
                      segment_list);
}

使用单位正方形的坐标给出线段。对于列表中的每个线段，画家使用框架坐标映射转换线段端点，并在转换后的点之间画一条线。

将画家表示为函数在图片语言中建立了强大的抽象屏障。我们可以创建和混合各种基于各种图形能力的原始画家。它们的实现细节并不重要。任何函数都可以作为画家，只要它以框架作为参数并绘制适合框架的内容。²⁷

练习 2.48

*面上的有向线段可以表示为一对向量——从原点到线段起点的向量，以及从原点到线段终点的向量。使用练习 2.46 中的向量表示来定义具有构造函数make_segment和选择器start_segment和end_segment的线段表示。

练习 2.49

使用segments_to_painter来定义以下原始画家：

a. 绘制指定框架的轮廓的画家。
b. 通过连接框架的对角线绘制X的画家。
c. 连接框架边中点绘制菱形形状的画家。
d. wave画家。

转换和组合画家

对画家的操作（如flip_vert或beside）通过创建一个画家来实现，该画家根据参数框架派生的框架调用原始画家。因此，例如，flip_vert不需要知道画家的工作方式就可以翻转它——它只需要知道如何将框架颠倒：翻转后的画家只是使用原始画家，但在倒置的框架中。

画家操作基于transform_painter函数，它接受一个画家和如何转换框架的信息作为参数，并产生一个新的画家。转换后的画家在给定一个框架时，会转换框架并在转换后的框架上调用原始画家。transform_painter的参数是指定新框架角落的点（表示为向量）：当映射到框架中时，第一个点指定新框架的原点，另外两个点指定其边缘向量的端点。因此，在单位正方形内的参数指定了包含在原始框架内的框架。

function transform_painter(painter, origin, corner1, corner2) {
    return frame => {
             const m = frame_coord_map(frame);
             const new_origin = m(origin);
             return painter(make_frame(
                                new_origin,
                                sub_vect(m(corner1), new_origin),
                                sub_vect(m(corner2), new_origin)));
           };
}

以下是如何垂直翻转画家图像：

function flip_vert(painter) {
    return transform_painter(painter,
                             make_vect(0, 1),  // new origin
                             make_vect(1, 1),  // new end of edge1
                             make_vect(0, 0)); // new end of edge2
}

使用transform_painter，我们可以轻松定义新的转换。例如，我们可以声明一个画家，将其图像缩小到给定框架的右上角。

function shrink_to_upper_right(painter) {
    return transform_painter(painter,
                             make_vect(0.5, 0.5),
                             make_vect(1, 0.5),
                             make_vect(0.5, 1));
}

其他转换将图像逆时针旋转 90 度²⁸

function rotate90(painter) {
    return transform_painter(painter,
                             make_vect(1, 0),
                             make_vect(1, 1),
                             make_vect(0, 0));
}

或者将图像压缩到框架的中心：²⁹

function squash_inwards(painter) {
    return transform_painter(painter,
                             make_vect(0, 0),
                             make_vect(0.65, 0.35),
                             make_vect(0.35, 0.65));
}

框架转换也是定义两个或更多画家组合方式的关键。例如，beside函数接受两个画家，将它们转换为分别在参数框架的左半部分和右半部分绘制，并产生一个新的复合画家。当给复合画家一个框架时，它调用第一个转换后的画家在框架的左半部分绘制，并调用第二个转换后的画家在框架的右半部分绘制：

function beside(painter1, painter2) {
    const split_point = make_vect(0.5, 0);
    const paint_left = transform_painter(painter1,
                                         make_vect(0, 0),
                                         split_point,
                                         make_vect(0, 1));
    const paint_right = transform_painter(painter2,
                                         split_point,
                                         make_vect(1, 0),
                                         make_vect(0.5, 1));
    return frame => {
               paint_left(frame);
               paint_right(frame);
           };
}

观察画家数据抽象，特别是将画家表示为函数，使得beside易于实现。beside函数不需要了解组件画家的任何细节，只需要知道每个画家将在其指定的框架中绘制一些东西。

练习 2.50

声明转换flip_horiz，它可以水*翻转画家，并且可以逆时针旋转 180 度和 270 度。

练习 2.51

声明画家的below操作。below函数接受两个画家作为参数。给定一个框架，结果画家用第一个画家在框架底部绘制，并用第二个画家在顶部绘制。以两种不同的方式定义below——首先编写一个类似于上面给出的beside函数的函数，然后再根据beside和适当的旋转操作（来自练习 2.50）定义below。

语言水*的稳健设计

图片语言利用了我们介绍的关于函数和数据抽象的一些关键思想。基本数据抽象，画家，是使用函数表示实现的，这使得语言可以以统一的方式处理不同的基本绘图能力。组合的方式满足封闭性质，这使我们可以轻松地构建复杂的设计。最后，所有用于抽象函数的工具都可以用于抽象画家的组合方式。

我们还对语言和程序设计的另一个关键思想有了一瞥。这就是分层设计的方法，即复杂系统应该被构造为一系列使用一系列语言描述的级别。每个级别都是通过组合在该级别被视为原始的部分构建的，而在下一个级别，每个级别构建的部分都被用作原语。分层设计的每个级别使用适合该级别细节的原语、组合手段和抽象手段。

分层设计渗透到复杂系统的工程中。例如，在计算机工程中，电阻器和晶体管被组合（并使用模拟电路语言描述）以产生诸如与门和或门之类的部件，这些部件构成了数字电路设计语言的原语。这些部件被组合以构建处理器、总线结构和存储系统，然后使用适合计算机体系结构的语言将它们组合成计算机。计算机被组合成分布式系统，使用适合描述网络互连的语言，依此类推。

作为分层的一个微小示例，我们的图片语言使用原始元素（原始画家）来指定点和线，以提供像rogers这样的画家的形状。我们对图片语言的描述主要集中在组合这些原始元素上，使用几何组合器如beside和below。我们还在更高的级别上工作，将beside和below视为在一个语言中被操作的原语，这个语言的操作，比如square_of_four，捕捉了组合几何组合器的常见模式。

分层设计有助于使程序健壮，也就是说，这样做可以使规范的微小变化很可能只需要相应地对程序进行微小的修改。例如，假设我们想要根据图 2.9 中显示的wave来改变图像。我们可以在最低级别上改变wave元素的详细外观；我们可以在中间级别上改变corner_split复制wave的方式；我们可以在最高级别上改变square_limit如何排列四个角的方式。通常情况下，分层设计的每个级别都提供了一个不同的词汇表来表达系统的特征，并且提供了不同类型的改变能力。

练习 2.52

通过在上述每个级别上工作，对wave的square_limit进行更改，如图 2.9 所示。特别是：

a. 向练习 2.49 中的原始wave画家添加一些段（例如添加一个微笑）。
b. 改变corner_split构造的模式（例如，只使用一个up_split和right_split图像的副本，而不是两个）。
c. 修改使用square_of_four来组装角落的square_limit版本，以便以不同的模式组装角落。（例如，你可以让大的 Mr. Rogers 从正方形的每个角向外看。）

2.3 符号数据

到目前为止，我们使用的所有复合数据对象最终都是由数字构建的。在本节中，我们通过引入使用字符字符串的能力来扩展我们的语言的表示能力。

2.3.1 字符串

到目前为止，我们已经使用字符串来显示消息，使用display和error函数（例如在练习 1.22 中）。我们可以使用字符串形成复合数据，并且有列表，比如

list("a", "b", "c", "d")
list(23, 45, 17)
list(list("Jakob", 27), list("Lova", 9), list("Luisa", 24))

为了区分字符串和名称，我们用双引号将它们括起来。例如，JavaScript 表达式z表示名称z的值，而 JavaScript 表达式"z"表示由单个字符组成的字符串，即英语字母表中的最后一个字母的小写形式。

通过引号，我们可以区分字符串和名称：

const a = 1;
const b = 2;

list(a, b);
[1, [2, null]]

list("a", "b");
["a", ["b", null]]

list("a", b);
["a", [2, null]]

在第 1.1.6 节，我们将===和!==作为数字的原始谓词引入。从现在开始，我们将允许===和!==的操作数为两个字符串。谓词===返回true，当且仅当两个字符串相同时，!==返回true，当且仅当两个字符串不同时。使用===，我们可以实现一个有用的函数称为member。它有两个参数：一个字符串和一个字符串列表或一个数字和一个数字列表。如果第一个参数不包含在列表中（即不与列表中的任何项===），则member返回null。否则，它返回列表中从第一次出现的字符串或数字开始的子列表：

function member(item, x) {
    return is_null(x)
           ? null
           : item === head(x)
           ? x
           : member(item, tail(x));
}

例如，值为

member("apple", list("pear", "banana", "prune"))

是null，而

member("apple", list("x", "y", "apple", "pear"))

是list("apple", "pear")。

练习 2.53

求出以下每个表达式的求值结果，使用框表示法和列表表示法？

list("a", "b", "c")

list(list("george"))

tail(list(list("x1", "x2"), list("y1", "y2")))

tail(head(list(list("x1", "x2"), list("y1", "y2"))))

member("red", list("blue", "shoes", "yellow", "socks"))

member("red", list("red", "shoes", "blue", "socks"))

练习 2.54

如果两个列表包含相同顺序排列的相等元素，则称它们为equal。例如，

equal(list("this", "is", "a", "list"), list("this", "is", "a", "list"))

是true，但

equal(list("this", "is", "a", "list"), list("this", list("is", "a"), "list"))

是false。更准确地说，我们可以通过基本的===相等性递归地定义equal，即如果a和b都是字符串或数字并且它们===，或者如果它们都是对，使得head(a)等于head(b)并且tail(a)等于tail(b)。使用这个想法，实现equal作为一个函数。

练习 2.55

JavaScript 解释器在双引号"后读取字符，直到找到另一个双引号。两者之间的所有字符都是字符串的一部分，不包括双引号本身。但是如果我们想要一个字符串包含双引号呢？为此，JavaScript 还允许单引号来界定字符串，例如在'say your name aloud'中。在单引号字符串中，我们可以使用双引号，反之亦然，因此'say "your name" aloud'和"say 'your name' aloud"是有效的字符串，它们在位置 4 和 14 有不同的字符，如果我们从 0 开始计数。根据使用的字体，两个单引号可能不容易与双引号区分开。你能分辨出哪个是哪个，并计算出以下表达式的值吗？

' " ' === " "

2.3.2 示例：符号微分

作为符号操作的示例和数据抽象的进一步说明，考虑设计一个执行代数表达式的符号微分的函数。我们希望该函数以代数表达式和变量作为参数，并返回表达式相对于变量的导数。例如，如果函数的参数是ax² + bx + c和x，则函数应返回2ax + b。符号微分在 Lisp 编程语言中具有特殊的历史意义。它是符号操作计算机语言开发背后的激励示例之一。此外，它标志着导致强大的符号数学工作系统开发的研究线的开始，这些系统如今被应用数学家和物理学家常规使用。

在开发符号微分程序时，我们将遵循数据抽象的相同策略，这与我们在开发第 2.1.1 节有理数系统时所遵循的策略相同。也就是说，我们将首先定义一个微分算法，该算法可以操作抽象对象，如“和”、“积”和“变量”，而不用担心这些对象如何表示。之后才会解决表示问题。

具有抽象数据的微分程序

为了简化问题，我们将考虑一个非常简单的符号微分程序，该程序处理的表达式仅使用加法和乘法两个参数进行构建。任何这种表达式的微分都可以通过应用以下简化规则来进行：

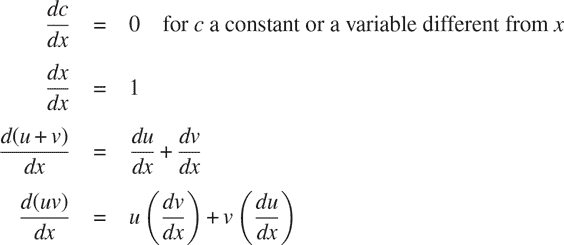
注意后两条规则的递归性质。也就是说，要获得和的导数，我们首先找到项的导数并将它们相加。每个项可能又是需要分解的表达式。分解成越来越小的部分最终会产生常数或变量的部分，它们的导数将是 0 或 1。

为了将这些规则体现在函数中，我们进行了一些希望的思考，就像我们在设计有理数实现时所做的那样。如果我们有一种表示代数表达式的方法，我们应该能够判断一个表达式是和、积、常数还是变量。我们应该能够提取表达式的部分。例如，对于和，我们希望能够提取加数（第一项）和被加数（第二项）。我们还应该能够从部分构造表达式。让我们假设我们已经有了实现以下选择器、构造函数和谓词的函数：

is_variable(e) | e是变量吗？| | --- | --- | | is_same_variable(v1, v2) | v1和v2是相同的变量吗？| | is_sum(e) | e是和吗？| | addend(e) | 和e的加数。| | augend(e) | 和e的被加数。| | make_sum(a1, a2) | 构造a1和a2的和。| | is_product(e) | e是乘积吗？| | multiplier(e) | 产品e的乘数。| | multiplicand(e) | 产品e的被乘数。| | make_product(m1, m2) | 构造m1和m2的乘积。|

使用这些和原始谓词is_number，它识别数字，我们可以将微分规则表达为以下函数：

function deriv(exp, variable) {
    return is_number(exp)
           ? 0
           : is_variable(exp)
           ? is_same_variable(exp, variable) ? 1 : 0
           : is_sum(exp)
           ? make_sum(deriv(addend(exp), variable),
                      deriv(augend(exp), variable))
           : is_product(exp)
           ? make_sum(make_product(multiplier(exp),
                                   deriv(multiplicand(exp),
                                         variable)),
                     make_product(deriv(multiplier(exp),
                                         variable),
                                  multiplicand(exp)))
           : error(exp, "unknown expression type – deriv");
}

这个deriv函数包含了完整的微分算法。由于它是用抽象数据表示的，所以无论我们选择如何表示代数表达式，只要我们设计一个合适的选择器和构造函数，它都能工作。这是我们接下来必须解决的问题。

表示代数表达式

我们可以想象许多使用列表结构来表示代数表达式的方法。例如，我们可以使用符号列表来反映通常的代数表示法，将ax + b表示为list("a", "*", "x", "+", "b")。但是，如果我们在 JavaScript 值中反映表达式的数学结构，将ax + b表示为list("+", list("*", "a", "x"), "b")会更方便。将二元运算符放在其操作数之前称为前缀表示，与第 1.1.1 节介绍的中缀表示相反。使用前缀表示，微分问题的数据表示如下：

变量只是字符串。它们由原始谓词is_string识别：

    function is_variable(x) { return is_string(x); }

如果表示它们的字符串相等，两个变量是相同的：

    function is_same_variable(v1, v2) {
        return is_variable(v1) && is_variable(v2) && v1 === v2;
    }

和积是作为列表构造的：

    function make_sum(a1, a2) { return list("+", a1, a2); }
    function make_product(m1, m2) { return list("*", m1, m2); }

和是一个列表，其第一个元素是字符串"+"：

    function is_sum(x) {
        return is_pair(x) && head(x) === "+";
    }

被加数是和列表的第二项：

    function addend(s) { return head(tail(s)); }

被加数是和列表的第三项：

    function augend(s) { return head(tail(tail(s))); }

乘积是一个列表，其第一个元素是字符串"*"：

    function is_product(x) {
        return is_pair(x) && head(x) === "*";
    }

乘数是产品列表的第二项：

    function multiplier(s) { return head(tail(s)); }

被乘数是产品列表的第三项：

    function multiplicand(s) { return head(tail(tail(s))); }

因此，我们只需要将这些与由deriv体现的算法结合起来，就可以拥有一个可工作的符号微分程序。让我们看一些其行为的例子：

deriv(list("+", "x", 3), "x");
list("+", 1, 0)

deriv(list("*", "x", "y"), "x");
list("+", list("*", "x", 0), list("*", 1, "y"))

deriv(list("*", list("*", "x", "y"), list("+", "x", 3)), "x");
list("+", list("*", list("*", "x", "y"), list("+", 1, 0)),
          list("*", list("+", list("*", "x", 0), list("*", 1, "y")),
                    list("+", "x", 3)))

该程序生成的答案是正确的；但是，它们是未简化的。事实上

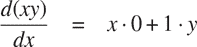
但我们希望程序知道x· 0 = 0，1 · y = y，0 + y = y。第二个例子的答案应该只是y。正如第三个例子所示，当表达式变得复杂时，这将成为一个严重的问题。

我们的困难很像我们在实现有理数时遇到的困难：我们没有将答案简化为最简形式。为了完成有理数的简化，我们只需要改变实现的构造函数和选择器。我们可以在这里采用类似的策略。我们不会改变deriv。相反，我们将改变make_sum，以便如果两个加数都是数字，make_sum将把它们相加并返回它们的和。此外，如果其中一个加数是 0，那么make_sum将返回另一个加数。

function make_sum(a1, a2) {
    return number_equal(a1, 0)
           ? a2
           : number_equal(a2, 0)
           ? a1
           : is_number(a1) && is_number(a2)
           ? a1 + a2
           : list("+", a1, a2);
}

这使用了函数number_equal，它检查表达式是否等于给定的数字：

function number_equal(exp, num) {
    return is_number(exp) && exp === num;
}

同样，我们将改变make_product以内置规则，即 0 乘以任何数都是 0，1 乘以任何数都是它本身：

function make_product(m1, m2) {
    return number_equal(m1, 0) || number_equal(m2, 0)
           ? 0
           : number_equal(m1, 1)
           ? m2
           : number_equal(m2, 1)
           ? m1
           : is_number(m1) && is_number(m2)
           ? m1 * m2
           : list("*", m1, m2);
}

这是这个版本在我们的三个例子上的工作方式：

deriv(list("+", "x", 3), "x");
`1`

deriv(list("*", "x", "y"), "x");
"y"

deriv(list("*", list("*", "x", "y"), list("+", "x", 3)), "x");
list("+", list("*", "x", "y"), list("*", "y", list("+", "x", 3)))

尽管这是一个很大的改进，但第三个例子表明，在我们得到一个将表达式放入我们可能同意的“最简形式”的程序之前，我们还有很长的路要走。代数简化的问题很复杂，因为，除其他原因外，对于一个目的来说可能是最简单的形式对于另一个目的来说可能不是。

练习 2.56

展示如何扩展基本的差异化器以处理更多种类的表达式。例如，实现差异化规则

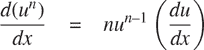
通过向deriv程序添加一个新子句并定义适当的函数is_exp、base、exponent和make_exp来实现这个表示法。（你可以使用字符串**来表示指数。）内置规则，任何数的 0 次方都是 1，任何数的 1 次方都是它本身。

练习 2.57

将差异化程序扩展到处理任意数量（两个或更多）项的和与积。然后上面的最后一个例子可以表示为

deriv(list("*", "x", "y", list("+", "x", 3)), "x");

尝试只通过改变和积的表示形式，而不改变deriv函数来实现这一点。例如，和的addend将是第一项，augend将是其余项的和。

练习 2.58

假设我们想修改差异化程序，使其适用于普通的数学表示法，其中+和*是中缀而不是前缀运算符。由于差异化程序是根据抽象数据定义的，我们可以通过仅改变定义差异化器要操作的代数表达式的表示的谓词、选择器和构造函数来修改它，以便它适用于不同的表达式表示。

a. 展示如何以中缀形式来区分代数表达式，就像这个例子一样：
```
list("x", "+", list(3, "*", list("x", "+", list("y", "+", 2))))
```
为了简化任务，假设+和*总是带有两个参数，并且表达式是完全括号化的。
b. 如果我们允许更接*普通中缀表示法的符号，即省略不必要的括号并假定乘法比加法优先级高，那么问题就会变得更加困难，就像这个例子一样：
```
list("x", "+", "3", "*", list("x", "+", "y", "+", 2))
```
你能设计适当的谓词、选择器和构造函数，使我们的导数程序仍然有效吗？

2.3.3 例子：表示集合

在前面的例子中，我们为两种复合数据对象构建了表示：有理数和代数表达式。在这些例子中，我们可以选择在构建时间或选择时间简化（减少）表达式，但除此之外，在列表方面选择这些结构的表示是直接的。当我们转向集合的表示时，表示的选择就不那么明显了。实际上，有许多可能的表示，它们在几个方面彼此之间有显著的不同。

非正式地，集合只是不同对象的集合。为了给出更精确的定义，我们可以采用数据抽象的方法。也就是说，我们通过指定在集合上使用的操作来定义“集合”。这些操作包括union_set，intersection_set，is_element_of_set和adjoin_set。函数is_element_of_set是一个谓词，用于确定给定元素是否是集合的成员。函数adjoin_set接受一个对象和一个集合作为参数，并返回一个包含原始集合元素和附加元素的集合。函数union_set计算两个集合的并集，即包含在任一参数中出现的每个元素的集合。函数intersection_set计算两个集合的交集，即仅包含同时出现在两个参数中的元素的集合。从数据抽象的角度来看，我们可以自由设计任何实现这些操作的表示，以与上述解释一致的方式实现。³³

无序列表的集合

一种表示集合的方法是将其元素列表化，其中没有元素出现超过一次。空集由空列表表示。在这种表示中，is_element_of_set类似于第 2.3.1 节的member函数。它使用equal而不是===，因此集合元素不必仅仅是数字或字符串：

function is_element_of_set(x, set) {
    return is_null(set)
           ? false
           : equal(x, head(set))
           ? true
           : is_element_of_set(x, tail(set));
}

使用这个，我们可以编写adjoin_set。如果要添加的对象已经在集合中，我们只需返回集合。否则，我们使用pair将对象添加到表示集合的列表中：

function adjoin_set(x, set) {
    return is_element_of_set(x, set)
           ? set
           : pair(x, set);
}

对于intersection_set，我们可以使用递归策略。如果我们知道如何形成set2和set1的tail的交集，我们只需要决定是否在其中包含set1的head。但这取决于head(set1)是否也在set2中。以下是得到的函数：

function intersection_set(set1, set2) {
    return is_null(set1) || is_null(set2)
           ? null
           : is_element_of_set(head(set1), set2)
           ? pair(head(set1), intersection_set(tail(set1), set2))
           : intersection_set(tail(set1), set2);
}

在设计表示时，我们应该关注的一个问题是效率。考虑我们的集合操作所需的步骤数。由于它们都使用is_element_of_set，因此此操作的速度对整个集合实现的效率有重大影响。现在，为了检查对象是否是集合的成员，is_element_of_set可能需要扫描整个集合。（在最坏的情况下，对象可能不在集合中。）因此，如果集合有n个元素，is_element_of_set可能需要最多n步。因此，所需的步骤数随着Θ(n)增长。使用此操作的adjoin_set所需的步骤数也随着Θ(n)增长。对于intersection_set，它对set1的每个元素进行is_element_of_set检查，所需的步骤数随着涉及的集合大小的乘积增长，或者对于大小为n的两个集合，为Θ(n²)。union_set也是如此。

练习 2.59

为无序列表表示的集合实现union_set操作。

练习 2.60

我们规定集合将被表示为一个没有重复的列表。现在假设我们允许重复。例如，集合{1, 2, 3}可以表示为列表list(2, 3, 2, 1, 3, 2, 2)。设计函数is_element_of_set、adjoin_set、union_set和intersection_set，这些函数操作这种表示。每个函数的效率与非重复表示的相应函数相比如何？是否有应用程序会优先使用这种表示而不是非重复表示？

有序列表的集合

加速我们的集合操作的一种方法是更改表示，使得集合元素按升序列出。为此，我们需要某种方法来比较两个对象，以便我们可以说哪个更大。例如，我们可以按字典顺序比较字符串，或者我们可以同意一些方法来为对象分配唯一的数字，然后通过比较相应的数字来比较元素。为了保持我们的讨论简单，我们只考虑集合元素是数字的情况，这样我们可以使用>和<来比较元素。我们将通过按升序列出其元素来表示一组数字。而我们上面的第一种表示允许我们以任何顺序列出集合{1, 3, 6, 10}的元素，我们的新表示只允许列表list(1, 3, 6, 10)。

有序的一个优点在于is_element_of_set中显示出来：在检查项目是否存在时，我们不再需要扫描整个集合。如果我们到达一个大于我们要查找的项目的集合元素，那么我们就知道该项目不在集合中。

function is_element_of_set(x, set) {
    return is_null(set)
           ? false
           : x === head(set)
           ? true
           : x < head(set)
           ? false
           : // x > head(set)
             is_element_of_set(x, tail(set));
}

这节省了多少步？在最坏的情况下，我们要找的项目可能是集合中最大的项目，因此步数与无序表示的步数相同。另一方面，如果我们搜索许多不同大小的项目，有时我们可以期望能够在列表开头附*停止搜索，而其他时候我们仍然需要检查大部分列表。*均而言，我们应该期望需要检查集合中大约一半的项目。因此，所需的*均步数约为n/2。这仍然是Θ(n)的增长，但*均而言，与先前的实现相比，它可以节省我们约 2 倍的步数。

我们通过intersection_set获得了更令人印象深刻的加速。在无序表示中，这个操作需要Θ(n²)步，因为我们对set2的每个元素执行了完整的扫描。但是在有序表示中，我们可以使用更聪明的方法。首先比较两个集合的初始元素x1和x2。如果x1等于x2，那么这给出了交集的一个元素，其余的交集是两个集合的tail的交集。然而，假设x1小于x2。由于x2是set2中最小的元素，我们可以立即得出x1不可能出现在set2中，因此不在交集中。因此，交集等于set2与set1的tail的交集。同样，如果x2小于x1，那么交集由set1与set2的tail的交集给出。这是函数：

function intersection_set(set1, set2) {
    if (is_null(set1) || is_null(set2)) {
        return null;
    } else {
        const x1 = head(set1);
        const x2 = head(set2);
        return x1 === x2
               ? pair(x1, intersection_set(tail(set1), tail(set2)))
               : x1 < x2
               ? intersection_set(tail(set1), set2)
               : // x2 < x1
                 intersection_set(set1, tail(set2));
    }
}

要估计此过程所需的步数，观察到在每一步中，我们将交集问题减少到计算更小集合的交集——从set1或set2或两者中删除第一个元素。因此，所需的步数最多是set1和set2大小的总和，而不是无序表示的大小乘积。这是Θ(n)的增长，而不是Θ(n²)——即使对于中等大小的集合，这也是相当大的加速。

练习 2.61

使用有序表示法给出adjoin_set的实现。类似于is_element_of_set，展示如何利用排序来生成一个函数，*均需要的步骤数量大约是无序表示的一半。

练习 2.62

为作为有序列表表示的集合提供一个Θ(n)的union_set实现。

将集合表示为二叉树

我们可以通过以树的形式排列集合元素来比有序列表表示更好。树的每个节点都包含集合的一个元素，称为该节点的“条目”，以及指向两个其他（可能为空）节点的链接。 “左”链接指向小于节点处的元素，“右”链接指向大于节点处的元素。图 2.16 显示了表示集合{1, 3, 5, 7, 9, 11}的一些树。同一集合可以用多种不同的方式表示为树。我们对有效表示的唯一要求是左子树中的所有元素都小于节点条目，右子树中的所有元素都大于节点条目。

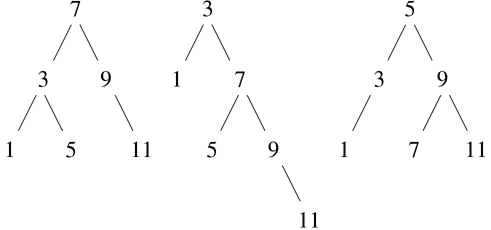
图 2.16 表示集合{1, 3, 5, 7, 9, 11}的各种二叉树。

树表示的优势在于：假设我们想要检查数字x是否包含在集合中。我们首先将x与顶部节点中的条目进行比较。如果x小于此条目，我们知道我们只需要搜索左子树；如果x大于此条目，我们只需要搜索右子树。现在，如果树是“*衡的”，这些子树的大小将约为原始大小的一半。因此，我们已经将搜索大小为n的树的问题减少到搜索大小为n/2的树。由于树的大小在每一步都减半，我们应该期望搜索大小为n的树所需的步骤数增长为Θ(log n)。对于大型集合，这将比以前的表示方式显著加快速度。

我们可以使用列表来表示树。每个节点将是一个包含三个项目的列表：节点处的条目，左子树和右子树。空列表的左子树或右子树表示那里没有连接的子树。我们可以通过以下函数描述这种表示法：

function entry(tree) { return head(tree); }
function left_branch(tree) { return head(tail(tree)); }
function right_branch(tree) { return head(tail(tail(tree))); }
function make_tree(entry, left, right) {
    return list(entry, left, right);
}

现在我们可以使用上述策略编写is_element_of_set：

function is_element_of_set(x, set) {
    return is_null(set)
           ? false
           : x === entry(set)
           ? true
           : x < entry(set)
           ? is_element_of_set(x, left_branch(set))
           : // x > entry(set)
             is_element_of_set(x, right_branch(set));
}

将项目添加到集合中的方法类似实现，并且需要Θ(log n)步骤。要添加项目x，我们将x与节点条目进行比较，以确定x应该添加到右侧还是左侧分支，并且在将x添加到适当的分支后，我们将这个新构造的分支与原始条目和另一个分支组合在一起。如果x等于条目，我们只需返回节点。如果我们被要求将x添加到空树中，我们生成一个具有x作为条目和空右侧和左侧分支的树。以下是函数：

function adjoin_set(x, set) {
    return is_null(set)
           ? make_tree(x, null, null)
           : x === entry(set)
           ? set
           : x < entry(set)
           ? make_tree(entry(set),
                       adjoin_set(x, left_branch(set)),
                       right_branch(set))
           : // x > entry(set)
             make_tree(entry(set),
                       left_branch(set),
                       adjoin_set(x, right_branch(set)));
}

上述声称搜索树可以在对数步骤中执行的假设是树是“*衡的”，即每棵树的左子树和右子树大致具有相同数量的元素，因此每个子树包含其父树元素的大约一半。但是我们如何确保我们构造的树是*衡的呢？即使我们从*衡树开始，使用adjoin_set添加元素可能会产生不*衡的结果。由于新添加元素的位置取决于元素与集合中已有项目的比较方式，我们可以预期，如果我们“随机”添加元素，树将*均*衡。但这并不是一个保证。例如，如果我们从空集开始，按顺序添加数字 1 到 7，我们最终得到图 2.17 中显示的高度不*衡的树。在这棵树中，所有左子树都是空的，因此它与简单的有序列表没有任何优势。解决这个问题的一种方法是定义一个操作，将任意树转换为具有相同元素的*衡树。然后我们可以在每隔几次adjoin_set操作之后执行此转换，以保持我们的集合*衡。还有其他解决这个问题的方法，其中大多数涉及设计新的数据结构，用于在Θ(log n)步骤中进行搜索和插入。³⁶

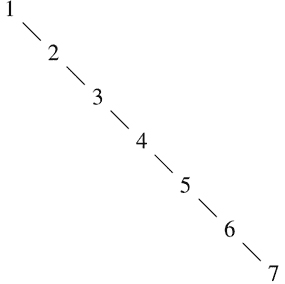
图 2.17 顺序添加 1 到 7 所产生的不*衡树。

练习 2.63

以下两个函数中的每一个都将二叉树转换为列表。

function tree_to_list_1(tree) {
    return is_null(tree)
           ? null
           : append(tree_to_list_1(left_branch(tree)),
                    pair(entry(tree),
                         tree_to_list_1(right_branch(tree))));
}

function tree_to_list_2(tree) {
    function copy_to_list(tree, result_list) {
        return is_null(tree)
               ? result_list
               : copy_to_list(left_branch(tree),
                              pair(entry(tree),
                                   copy_to_list(right_branch(tree),
                                                result_list)));
    }
    return copy_to_list(tree, null);
}

a. 这两个函数对每棵树都产生相同的结果吗？如果不是，结果有何不同？这两个函数为图 2.16 中的树产生了什么列表？
b. 这两个函数在将具有n个元素的*衡树转换为列表所需的步骤数量的增长顺序相同吗？如果不是，哪一个增长更慢？

练习 2.64

以下函数list_to_tree将有序列表转换为*衡二叉树。辅助函数partial_tree以整数n和至少n个元素的列表作为参数，并构造包含列表的前n个元素的*衡树。partial_tree返回的结果是一个由pair组成的对，其head是构造的树，tail是未包含在树中的元素列表。

function list_to_tree(elements) {
    return head(partial_tree(elements, length(elements)));
}
function partial_tree(elts, n) {
    if (n === 0) {
        return pair(null, elts);
    } else {
        const left_size = math_floor((n - 1) / 2);
        const left_result = partial_tree(elts, left_size);
        const left_tree = head(left_result);
        const non_left_elts = tail(left_result);
        const right_size = n - (left_size + 1);
        const this_entry = head(non_left_elts);
        const right_result = partial_tree(tail(non_left_elts), right_size);
        const right_tree = head(right_result);
        const remaining_elts = tail(right_result);
        return pair(make_tree(this_entry, left_tree, right_tree),
                    remaining_elts);
    }
}

a. 用尽可能清晰的方式写一段简短的段落，解释partial_tree是如何工作的。为列表list(1, 3, 5, 7, 9, 11)绘制list_to_tree生成的树。
b. list_to_tree将n个元素的列表转换为所需的步骤数量的增长顺序是多少？

练习 2.65

使用练习 2.63 和 2.64 的结果，为作为（*衡）二叉树实现的集合提供union_set和intersection_set的Θ(n)实现。³⁷

集合和信息检索

我们已经研究了使用列表表示集合的选项，并且已经看到数据对象的表示选择对使用数据的程序的性能有很大影响。专注于集合的另一个原因是，这里讨论的技术在涉及信息检索的应用中一再出现。

考虑一个包含大量个体记录的数据库，例如公司的人事档案或会计系统中的交易。典型的数据管理系统花费大量时间访问或修改记录中的数据，因此需要一种有效的访问记录的方法。这是通过识别每个记录的一部分作为标识键来完成的。键可以是任何唯一标识记录的东西。对于人事档案，它可能是员工的 ID 号。对于会计系统，它可能是交易号。无论键是什么，当我们将记录定义为数据结构时，我们应该包括一个key选择器函数，用于检索与给定记录关联的键。

现在我们将数据库表示为一组记录。要定位具有给定键的记录，我们使用一个名为lookup的函数，它以键和数据库作为参数，并返回具有该键的记录，如果没有这样的记录则返回false。函数lookup的实现方式几乎与is_element_of_set相同。例如，如果记录集被实现为无序列表，我们可以使用

function lookup(given_key, set_of_records) {
    return is_null(set_of_records)
           ? false
           : equal(given_key, key(head(set_of_records)))
           ? head(set_of_records)
           : lookup(given_key, tail(set_of_records));
}

当然，有更好的方法来表示大型集合，而不是作为无序列表。记录必须“随机访问”的信息检索系统通常通过基于树的方法实现，例如之前讨论过的二叉树表示。在设计这样的系统时，数据抽象的方法论可以提供很大的帮助。设计者可以使用简单直接的表示方法（例如无序列表）创建一个初始实现。这对于最终的系统来说是不合适的，但它可以用来提供一个“快速脏数据”数据库，用于测试系统的其余部分。稍后，数据表示可以修改为更复杂的形式。如果数据库是根据抽象选择器和构造器访问的，那么这种表示的更改不需要对系统的其余部分进行任何更改。

练习 2.66

为记录集结构化为按键的数值顺序排列的二叉树的情况实现lookup函数。

2.3.4 示例：霍夫曼编码树

本节提供了使用列表结构和数据抽象来操作集合和树的实践。应用于将数据表示为一系列一和零（位）的方法。例如，用于在计算机中表示文本的 ASCII 标准代码将每个字符编码为七位序列。使用七位可以区分2⁷，或 128 个可能的不同字符。一般来说，如果我们想区分n个不同的符号，我们将需要使用log₂n位每个符号。如果我们的所有消息由八个符号 A、B、C、D、E、F、G 和 H 组成，我们可以选择每个字符三位的代码，例如

A	000	C	010	E	100	G	110
B	001	D	011	F	101	H	111

使用这个代码，消息

BACADAEAFABBAAAGAH

被编码为 54 位的字符串

001000010000011000100000101000001001000000000110000111

诸如 ASCII 和上面的 A 到 H 代码之类的代码被称为固定长度代码，因为它们用相同数量的位表示消息中的每个符号。有时使用可变长度代码是有利的，其中不同的符号可以由不同数量的位表示。例如，莫尔斯电码不使用相同数量的点和破折号来表示字母表中的每个字母。特别是，最常见的字母 E 由一个单点表示。一般来说，如果我们的消息中有一些符号出现非常频繁，而另一些符号出现非常少，如果我们为频繁的符号分配较短的代码，我们可以更有效地编码数据（即每个消息使用更少的位）。考虑以下字母 A 到 H 的替代代码：

A	0	C	1010	E	1100	G	1110
B	100	D	1011	F	1101	H	1111

使用这个编码，与上面相同的消息被编码为

100010100101101100011010100100000111001111

这个字符串包含 42 位，因此与上面显示的固定长度编码相比，节省了超过 20%的空间。

使用可变长度编码的一个困难是在读取一系列零和一时，知道何时已经到达符号的结尾。摩尔斯电码通过在每个字母的点和划线序列之后使用特殊的分隔符编码（在这种情况下是暂停）来解决这个问题。另一个解决方案是设计编码，使得任何符号的完整编码都不是另一个符号的编码的开头（或前缀）。这样的编码称为前缀编码。在上面的例子中，A 由 0 编码，B 由 100 编码，因此没有其他符号可以以 0 或 100 开头的编码。

一般来说，如果我们使用可变长度的前缀编码，可以实现显著的节省，这些编码利用了消息中符号的相对频率。其中一种特定的方案称为哈夫曼编码方法，以其发现者大卫·哈夫曼命名。哈夫曼编码可以表示为一个二叉树，其叶子节点是被编码的符号。在树的每个非叶节点上，有一个包含所有位于节点下方的叶子中的符号的集合。此外，每个叶子上的符号被分配一个权重（即其相对频率），每个非叶节点包含一个权重，该权重是其下方所有叶子的权重之和。权重不用于编码或解码过程。我们将在下面看到它们如何用于帮助构建树。

图 2.18 显示了上面给出的 A 到 H 编码的哈夫曼树。叶子上的权重表明，该树是为了相对频率为 8 的 A、相对频率为 3 的 B 和其他每个字母的相对频率为 1 的消息而设计的。

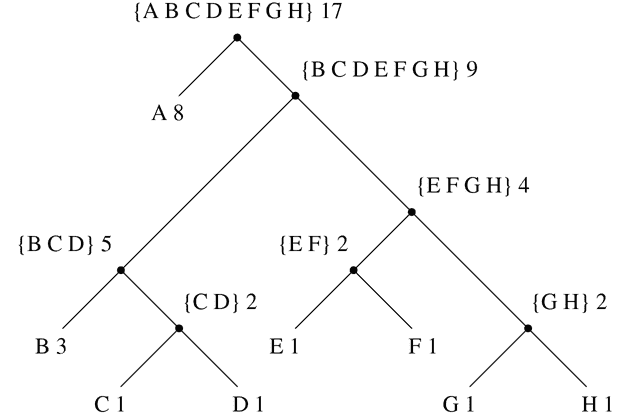
图 2.18 哈夫曼编码树。

给定一个哈夫曼树，我们可以通过从根开始并向下移动，直到到达包含符号的叶子为止，找到任何符号的编码。每次向下移动左分支时，我们将 0 添加到编码中，每次向下移动右分支时，我们将 1 添加到编码中。（我们决定要跟随哪个分支，通过测试看哪个分支是符号的叶节点或包含符号在其集合中。）例如，从图 2.18 的树的根开始，我们通过向右、向左、向右、向右移动到达 D 的叶子；因此，D 的编码是 1011。

使用哈夫曼树解码比特序列时，我们从根开始，使用比特序列的连续零和一来确定是向左还是向右移动。每次到达叶子时，我们在消息中生成一个新的符号，然后我们从树的根重新开始，找到下一个符号。例如，假设我们有上面的树和序列 10001010。从根开始，我们向右移动（因为字符串的第一个位是 1），然后向左移动（因为第二位是 0），然后向左移动（因为第三位也是 0）。这将带我们到 B 的叶子，因此解码消息的第一个符号是 B。现在我们再次从根开始，因为字符串的下一个位是 0，所以我们向左移动。这将带我们到 A 的叶子。然后我们从树的根重新开始，使用剩下的字符串 1010，所以我们向右、左、右、左移动，到达 C。因此，整个消息是 BAC。

生成哈夫曼树

给定一组符号和它们的相对频率的“字母表”，我们如何构建“最佳”编码？（换句话说，哪棵树会用最少的位来编码消息？）赫夫曼提出了一个算法来做到这一点，并证明了所得到的编码确实是相对频率与编码构造时频率匹配的消息的最佳可变长度编码。我们将不在这里证明赫夫曼编码的最优性，但我们将展示赫夫曼树是如何构建的。

生成赫夫曼树的算法非常简单。其思想是安排树，使得频率最低的符号出现在距离根最远的地方。从包含符号和它们的频率的叶子节点集开始，这些频率是根据构造编码的初始数据确定的。现在找到两个权重最低的叶子并合并它们，以产生一个节点，该节点具有这两个节点作为其左右分支。新节点的权重是两个权重的总和。从原始集合中删除这两个叶子，并用这个新节点替换它们。现在继续这个过程。在每一步中，合并两个权重最小的节点，将它们从集合中删除，并用一个节点替换它们，该节点具有这两个节点作为其左右分支。当只剩下一个节点时，即整个树的根节点时，该过程停止。以下是图 2.18 的赫夫曼树是如何生成的：

初始叶子	`{(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)}`
合并	`{(A 8) (B 3) ({C D} 2) (E 1) (F 1) (G 1) (H 1)}`
合并	`{(A 8) (B 3) ({C D} 2) ({E F} 2) (G 1) (H 1)}`
合并	`{(A 8) (B 3) ({C D} 2) ({E F} 2) ({G H} 2)}`
合并	`{(A 8) (B 3) ({C D} 2) ({E F G H} 4)}`
合并	`{(A 8) ({B C D} 5) ({E F G H} 4)}`
合并	`{(A 8) ({B C D E F G H} 9)}`
最终合并	`{({A B C D E F G H} 17)}`

该算法并不总是指定一个唯一的树，因为在每一步可能没有唯一的最小权重节点。此外，合并两个节点的顺序（即哪个将成为右分支，哪个将成为左分支）是任意的。

表示赫夫曼树

在下面的练习中，我们将使用一个使用赫夫曼树来编码和解码消息并根据上述算法生成赫夫曼树的系统。我们将首先讨论树是如何表示的。

树的叶子由包含字符串leaf，叶子上的符号和权重的列表表示：

function make_leaf(symbol, weight) {
    return list("leaf", symbol, weight);
}
function is_leaf(object) {
    return head(object) === "leaf";
}
function symbol_leaf(x) { return head(tail(x)); }
function weight_leaf(x) { return head(tail(tail(x))); }

一棵一般的树将是一个字符串code_tree的列表，一个左分支，一个右分支，一组符号和一个权重。符号集将只是符号的列表，而不是一些更复杂的集合表示。当我们通过合并两个节点来构造一棵树时，我们得到树的权重是节点权重的总和，符号集是节点的符号集的并集。由于我们的符号集被表示为列表，我们可以使用我们在 2.2.1 节中定义的append函数来形成并集：

function make_code_tree(left, right) {
    return list("code_tree", left, right,
                append(symbols(left), symbols(right)),
                weight(left) + weight(right));
}

如果我们以这种方式制作一棵树，我们将有以下选择器：

function left_branch(tree) { return head(tail(tree)); }
function right_branch(tree) { return head(tail(tail(tree))); }
function symbols(tree) {
    return is_leaf(tree)
           ? list(symbol_leaf(tree))
           : head(tail(tail(tail(tree))));
}
function weight(tree) {
    return is_leaf(tree)
           ? weight_leaf(tree)
           : head(tail(tail(tail(tail(tree)))));
}

函数symbols和weight必须根据它们是与叶子还是一般树一起调用而稍有不同。这些是通用函数（可以处理多种数据类型的函数）的简单示例，我们将在 2.4 和 2.5 节中有更多关于它们的话要说。

解码函数

以下函数实现了解码算法。它以零和一的列表以及赫夫曼树作为参数。

function decode(bits, tree) {
    function decode_1(bits, current_branch) {
        if (is_null(bits)) {
            return null;
        } else {
            const next_branch = choose_branch(head(bits),
                                              current_branch);
            return is_leaf(next_branch)
                   ? pair(symbol_leaf(next_branch),
                          decode_1(tail(bits), tree))
                   : decode_1(tail(bits), next_branch);
        }
    }
    return decode_1(bits, tree);
}
function choose_branch(bit, branch) {
    return bit === 0
           ? left_branch(branch)
           : bit === 1
           ? right_branch(branch)
           : error(bit, "bad bit – choose_branch");
}

函数decode_1接受两个参数：剩余位的列表和树中的当前位置。它不断地“向下”移动树，根据列表中的下一个位是零还是一选择左侧或右侧分支。（这是通过函数choose_branch完成的。）当它到达叶子时，它返回该叶子上的符号作为消息中的下一个符号，将其与解码消息的其余部分连接起来，从树的根开始。请注意choose_branch的最后一个子句中的错误检查，如果函数在输入数据中找到除零或一之外的其他内容，则会发出投诉。

加权元素的集合

在我们对树的表示中，每个非叶节点包含一组符号，我们已经将其表示为一个简单的列表。然而，上面讨论的生成树算法要求我们还要处理叶子和树的集合，依次合并两个最小的项目。由于我们需要重复地在集合中找到最小的项目，因此方便起见，我们使用有序表示来表示这种类型的集合。

我们将一个叶子和树的集合表示为一个元素列表，按权重递增排列。用于构建集合的adjoin_set函数与练习 2.61 中描述的类似；然而，项目是按其权重进行比较的，并且要添加到集合中的元素从未在其中。

function adjoin_set(x, set) {
    return is_null(set)
           ? list(x)
           : weight(x) < weight(head(set))
           ? pair(x, set)
           : pair(head(set), adjoin_set(x, tail(set)));
}

以下函数接受一个符号-频率对的列表，例如

list(list("A", 4), list("B", 2), list("C", 1), list("D", 1))

并构建一个初始的有序叶子集，准备根据 Huffman 算法合并：

function make_leaf_set(pairs) {
    if (is_null(pairs)) {
        return null;
    } else {
        const first_pair = head(pairs);
        return adjoin_set(
                   make_leaf(head(first_pair),        // symbol
                             head(tail(first_pair))), // frequency
                   make_leaf_set(tail(pairs)));
    }
}

练习 2.67

声明一个编码树和一个样本消息：

const sample_tree = make_code_tree(make_leaf("A", 4),
                                   make_code_tree(make_leaf("B", 2),
                                                  make_code_tree(
                                                      make_leaf("D", 1),
                                                      make_leaf("C", 1))));
const sample_message = list(0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0);

使用decode函数解码消息，并给出结果。

练习 2.68

encode函数以消息和树作为参数，并生成给定编码消息的位列表。

function encode(message, tree) {
    return is_null(message)
           ? null
           : append(encode_symbol(head(message), tree),
                    encode(tail(message), tree));
}

函数encode_symbol由你编写，返回根据给定树对给定符号进行编码的位列表。你应该设计encode_symbol，以便如果符号根本不在树中，则发出错误信号。通过使用样本树对你在练习 2.67 中获得的结果进行编码，并查看它是否与原始样本消息相同来测试你的函数。

练习 2.69

以下函数以其参数为一个符号-频率对的列表（其中没有一个符号出现在多个对中），并根据 Huffman 算法生成 Huffman 编码树。

function generate_huffman_tree(pairs) {
    return successive_merge(make_leaf_set(pairs));
}

将转换成一个有序叶子集的make_leaf_set函数如上所示。使用make_code_tree编写successive_merge函数，以便连续合并集合中最小权重的元素，直到只剩下一个元素，即所需的 Huffman 树。（这个函数有点棘手，但并不是真的复杂。如果你发现自己设计了一个复杂的函数，那么你几乎肯定做错了什么。你可以充分利用我们使用有序集合表示的事实。）

练习 2.70

以下带有相关相对频率的八个符号字母表被设计用来高效地编码 1950 年代摇滚歌曲的歌词。（注意，“字母表”的“符号”不一定是单个字母。）

A	2	NA	16
BOOM	1	SHA	3
GET	2	YIP	9
JOB	2	WAH	1

使用generate_huffman_tree（练习 2.69）生成相应的 Huffman 树，并使用encode（练习 2.68）对以下消息进行编码：

找一份工作

Sha na na na na na na na na

找一份工作

Sha na na na na na na na na

Wah yip yip yip yip yip yip yip yip yip

Sha boom

需要多少位来进行编码？如果我们对这个八个符号字母表使用固定长度编码，那么需要的最小位数是多少？

练习 2.71

假设我们有一个用于n个符号的赫夫曼树，并且符号的相对频率为1, 2, 4, ..., 2^(n–1)。为n=5绘制树；为n=10绘制树。在这样的树中（对于一般的n），编码最频繁的符号需要多少位？最不频繁的符号呢？

练习 2.72

考虑您在练习 2.68 中设计的编码函数。编码一个符号所需步骤的增长顺序是多少？确保包括在每个遇到的节点上搜索符号列表所需的步骤数。一般来说，回答这个问题是困难的。考虑相对频率如练习 2.71 中描述的n个符号的特殊情况，并给出编码字母表中最频繁和最不频繁的符号所需步骤数的增长顺序（作为n的函数）。

2.4 抽象数据的多重表示

我们引入了数据抽象，这是一种构建系统的方法，使得程序的大部分内容可以独立于实现程序操作的数据对象的选择而指定。例如，我们在 2.1.1 节中看到了如何将设计使用有理数的程序的任务与使用计算机语言的原始机制构造复合数据的任务分开。关键思想是建立一个抽象屏障——在这种情况下，有理数的选择器和构造器（make_rat、numer、denom）——它将有理数的使用方式与它们在列表结构方面的底层表示隔离开来。类似的抽象屏障将执行有理数算术的函数的细节（add_rat、sub_rat、mul_rat和div_rat）与使用有理数的“高级”函数隔离开来。生成的程序的结构如图 2.1 所示。

这些数据抽象屏障是控制复杂性的强大工具。通过隔离数据对象的底层表示，我们可以将设计大型程序的任务分解为可以分开执行的较小任务。但这种数据抽象还不够强大，因为对于数据对象来说，“底层表示”并不总是有意义的。

首先，一个数据对象可能有多个有用的表示方式，我们可能希望设计可以处理多个表示的系统。举个简单的例子，复数可以用两种几乎等效的方式表示：直角坐标形式（实部和虚部）和极坐标形式（幅度和角度）。有时直角坐标形式更合适，有时极坐标形式更合适。事实上，可以想象一个系统，其中复数以两种方式表示，并且用于操作复数的函数可以使用任一种表示。

更重要的是，编程系统通常是由许多人在较长时间内共同设计的，受到随时间变化的要求的影响。在这样的环境中，不可能让每个人事先就数据表示的选择达成一致。因此，除了将表示与使用隔离的数据抽象屏障之外，我们还需要将不同的设计选择与其他选择隔离开，并允许不同的选择在单个程序中共存。此外，由于大型程序通常是通过组合先前独立设计的模块创建的，我们需要一些约定，允许程序员将模块“增量”地合并到更大的系统中，即无需重新设计或重新实现这些模块。

在本节中，我们将学习如何处理可能由程序的不同部分以不同方式表示的数据。这需要构建通用函数——可以操作以多种方式表示的数据的函数。我们构建通用函数的主要技术是使用类型标签的数据对象，即包含有关如何处理它们的显式信息的数据对象。我们还将讨论数据导向编程，这是一种强大而方便的实现策略，用于通过加法组装具有通用操作的系统。

我们从简单的复数示例开始。我们将看到类型标签和数据导向风格如何使我们能够为复数设计独立的矩形和极坐标表示，同时保持抽象“复数”数据对象的概念。我们将通过定义复数的算术函数（add_complex、sub_complex、mul_complex和div_complex）来实现这一点，这些函数是基于通用选择器定义的，这些选择器可以访问复数的部分，而不考虑数字的表示方式。如图 2.19 所示，得到的复数系统包含两种不同的抽象屏障。 “水*”抽象屏障起到与图 2.1 中相同的作用。它们将“高级”操作与“低级”表示隔离开来。此外，还有一个“垂直”屏障，使我们能够分别设计和安装替代表示。

图 2.19 复数系统中的数据抽象屏障。

在第 2.5 节中，我们将展示如何使用类型标签和数据导向风格来开发通用算术包。这提供了函数（add、mul等），可以用于操作各种“数字”，并且在需要新类型的数字时可以轻松扩展。在第 2.5.3 节中，我们将展示如何在执行符号代数的系统中使用通用算术。

2.4.1 复数的表示

我们将开发一个系统，它可以对复数执行算术运算，这是一个简单但不切实际的示例，用于使用通用操作的程序。我们首先讨论复数的两种合理表示形式：有序对的矩形形式（实部和虚部）和极坐标形式（大小和角度）。第 2.4.2 节将展示如何通过使用类型标签和通用操作，使这两种表示可以在单个系统中共存。

与有理数一样，复数自然地表示为有序对。复数集可以被看作是一个二维空间，有两个正交轴，“实”轴和“虚”轴。（见图 2.20。）从这个角度来看，复数z = x + iy（其中i² = –1）可以被看作是*面上的点，其实部是x，虚部是y。复数的加法在这种表示中减少到坐标的加法：

Real-part(z[1] + z[2])  =  Real-part(z[1]) + Real-part(z[2]) 
Imaginary-part(z[1] + z[2])  =  Imaginary-part(z[1]) + Imaginary-part(z[2])

图 2.20 复数作为*面上的点。

当乘法复数时，更自然地考虑以极坐标形式表示复数，即大小和角度（图 2.20 中的r和A）。两个复数的乘积是通过拉伸一个复数的长度并通过另一个复数的角度旋转得到的向量：

Magnitude(z[1] · z[2])  =  Magnitude(z[1]) · Magnitude(z[2]) 

Angle(z[1] · z[2])  =  Angle(z[1]) + Angle(z[2])

因此，复数有两种不同的表示形式，适用于不同的操作。然而，从使用复数的程序编写者的角度来看，数据抽象原则表明，无论计算机使用哪种表示形式，都应该提供操纵复数的所有操作。例如，通常有用的是能够找到由矩形坐标指定的复数的幅值。同样，通常有用的是能够确定由极坐标指定的复数的实部。

为了设计这样一个系统，我们可以遵循与在 2.1.1 节中设计有理数包时相同的数据抽象策略。假设复数的操作是根据四个选择器实现的：real_part、imag_part、magnitude和angle。还假设我们有两个用于构造复数的函数：make_from_real_imag返回具有指定实部和虚部的复数，make_from_mag_ang返回具有指定幅值和角度的复数。这些函数具有这样的属性，对于任何复数z，都有

make_from_real_imag(real_part(z), imag_part(z));

和

make_from_mag_ang(magnitude(z), angle(z));

产生等于z的复数。

使用这些构造函数和选择器，我们可以使用构造函数和选择器指定的“抽象数据”来实现复数的算术运算，就像我们在 2.1.1 节中对有理数所做的那样。如上面的公式所示，我们可以根据实部和虚部相加和相减复数，而根据幅值和角度相乘和相除复数：

function add_complex(z1, z2) {
    return make_from_real_imag(real_part(z1) + real_part(z2),
                               imag_part(z1) + imag_part(z2));
}
function sub_complex(z1, z2) {
    return make_from_real_imag(real_part(z1) - real_part(z2),
                               imag_part(z1) - imag_part(z2));
}
function mul_complex(z1, z2) {
    return make_from_mag_ang(magnitude(z1) * magnitude(z2),
                             angle(z1) + angle(z2));
}
function div_complex(z1, z2) {
    return make_from_mag_ang(magnitude(z1) / magnitude(z2),
                             angle(z1) - angle(z2));
}

为了完成复数包，我们必须选择一种表示，并且必须根据原始数字和原始列表结构实现构造函数和选择器。有两种明显的方法可以做到这一点：我们可以将复数表示为“矩形形式”，即一对（实部，虚部），或者将其表示为“极坐标形式”，即一对（幅值，角度）。我们应该选择哪一种呢？

为了使不同的选择具体化，想象有两个程序员，Ben Bitdiddle 和 Alyssa P. Hacker，他们独立设计复数系统的表示。Ben 选择用矩形形式表示复数。通过这种选择，选择复数的实部和虚部是直接的，就像构造具有给定实部和虚部的复数一样。为了找到幅值和角度，或者构造具有给定幅值和角度的复数，他使用三角关系

 x = r cos A  
 r = √(x² + y²)

 y = r sin A  
 A = arctan(y, x)

这些关系将实部和虚部(x, y)与幅值和角度(r, A)联系起来。因此，Ben 的表示由以下选择器和构造函数给出：

function real_part(z) { return head(z); }
function imag_part(z) { return tail(z); }
function magnitude(z) {
    return math_sqrt(square(real_part(z)) + square(imag_part(z)));
}
function angle(z) {
    return math_atan2(imag_part(z), real_part(z));
}
function make_from_real_imag(x, y) { return pair(x, y); }

function make_from_mag_ang(r, a) {
    return pair(r * math_cos(a), r * math_sin(a));
}

相比之下，Alyssa 选择用极坐标形式表示复数。对她来说，选择幅值和角度是直接的，但她必须使用三角关系来获得实部和虚部。Alyssa 的表示是：

function real_part(z) {
    return magnitude(z) * math_cos(angle(z));
}
function imag_part(z) {
    return magnitude(z) * math_sin(angle(z));
}
function magnitude(z) { return head(z); }
function angle(z) { return tail(z); }
function make_from_real_imag(x, y) {
    return pair(math_sqrt(square(x) + square(y)),
                math_atan2(y, x));
}
function make_from_mag_ang(r, a) { return pair(r, a); }

数据抽象的学科确保add_complex、sub_complex、mul_complex和div_complex的相同实现将适用于 Ben 的表示或 Alyssa 的表示。

2.4.2 标记数据

将数据抽象视为“最小承诺原则”的应用之一。在 2.4.1 节中实现复数系统时，我们可以使用 Ben 的矩形表示或 Alyssa 的极坐标表示。由选择器和构造函数形成的抽象屏障使我们能够在最后可能的时刻推迟对数据对象的具体表示的选择，从而在系统设计中保留最大的灵活性。

最小承诺原则可以被推到更极端的程度。如果我们愿意，甚至可以在设计选择器和构造器之后保持表示的模糊性，并选择同时使用本的表示和 Alyssa 的表示。然而，如果两种表示都包含在一个系统中，我们将需要一些方法来区分极坐标形式的数据和矩形形式的数据。否则，例如，如果我们被要求找到一对（3，4）的“大小”，我们将不知道是回答 5（解释为矩形形式的数字）还是 3（解释为极坐标形式的数字）。实现这种区分的一种简单方法是在每个复数中包含一个类型标签——字符串“矩形”或“极坐标”。然后，当我们需要操作一个复数时，我们可以使用标签来决定应用哪个选择器。

为了操作带标签的数据，我们将假设我们有函数type_tag和contents，它们从数据对象中提取标签和实际内容（在复数的情况下是极坐标或矩形坐标）。我们还假设有一个函数attach_tag，它接受标签和内容，并产生一个带标签的数据对象。实现这一点的一种简单方法是使用普通的列表结构：

function attach_tag(type_tag, contents) {
    return pair(type_tag, contents);
}
function type_tag(datum) {
    return is_pair(datum)
           ? head(datum)
           : error(datum, "bad tagged datum – type_tag");
}
function contents(datum) {
    return is_pair(datum)
           ? tail(datum)
           : error(datum, "bad tagged datum – contents");
}

使用type_tag，我们可以定义谓词is_rectangular和is_polar，分别识别矩形和极坐标数：

function is_rectangular(z) {
    return type_tag(z) === "rectangular";
}
function is_polar(z) {
    return type_tag(z) === "polar";
}

有了类型标签，Ben 和 Alyssa 现在可以修改他们的代码，使得他们的两种不同表示可以在同一个系统中共存。每当 Ben 构造一个复数时，他将其标记为矩形。每当 Alyssa 构造一个复数时，她将其标记为极坐标。此外，Ben 和 Alyssa 必须确保他们的函数名称不冲突。一种方法是让 Ben 在他的每个表示函数的名称后附加后缀rectangular，让 Alyssa 在她的函数名称后附加polar。这是 Ben 修改后的矩形表示，来自第 2.4.1 节：

function real_part_rectangular(z) { return head(z); }
function imag_part_rectangular(z) { return tail(z); }
function magnitude_rectangular(z) {
    return math_sqrt(square(real_part_rectangular(z)) +
                     square(imag_part_rectangular(z)));
}
function angle_rectangular(z) {
    return math_atan(imag_part_rectangular(z),
                     real_part_rectangular(z));
}
function make_from_real_imag_rectangular(x, y) {
    return attach_tag("rectangular", pair(x, y));
}
function make_from_mag_ang_rectangular(r, a) {
    return attach_tag("rectangular",
                      pair(r * math_cos(a), r * math_sin(a)));
}

这是 Alyssa 修改后的极坐标表示：

function real_part_polar(z) {
    return magnitude_polar(z) * math_cos(angle_polar(z));
}
function imag_part_polar(z) {
    return magnitude_polar(z) * math_sin(angle_polar(z));
}
function magnitude_polar(z) { return head(z); }
function angle_polar(z) { return tail(z); }
function make_from_real_imag_polar(x, y) {
    return attach_tag("polar",
                      pair(math_sqrt(square(x) + square(y)),
                           math_atan(y, x)));
}
function make_from_mag_ang_polar(r, a) {
    return attach_tag("polar", pair(r, a));
}

每个通用选择器都被实现为一个函数，该函数检查其参数的标签，并调用处理该类型数据的适当函数。例如，要获得复数的实部，real_part检查标签以确定是使用 Ben 的real_part_rectangular还是 Alyssa 的real_part_polar。在任何一种情况下，我们使用contents来提取裸的、未标记的数据，并根据需要将其发送到矩形或极坐标函数：

function real_part(z) {
    return is_rectangular(z)
           ? real_part_rectangular(contents(z))
           : is_polar(z)
           ? real_part_polar(contents(z))
           : error(z, "unknown type – real_part");
}
function imag_part(z) {
    return is_rectangular(z)
           ? imag_part_rectangular(contents(z))
           : is_polar(z)
           ? imag_part_polar(contents(z))
           : error(z, "unknown type – imag_part");
}
function magnitude(z) {
    return is_rectangular(z)
           ? magnitude_rectangular(contents(z))
           : is_polar(z)
           ? magnitude_polar(contents(z))
           : error(z, "unknown type – magnitude");
}
function angle(z) {
    return is_rectangular(z)
           ? angle_rectangular(contents(z))
           : is_polar(z)
           ? angle_polar(contents(z))
           : error(z, "unknown type – angle");
}

为了实现复数算术运算，我们可以使用第 2.4.1 节中的相同函数add_complex、sub_complex、mul_complex和div_complex，因为它们调用的选择器是通用的，所以可以与任何表示一起使用。例如，函数add_complex仍然是

function add_complex(z1, z2) {
    return make_from_real_imag(real_part(z1) + real_part(z2),
                               imag_part(z1) + imag_part(z2));
}

最后，我们必须选择是使用本的表示法还是 Alyssa 的表示法来构造复数。一个合理的选择是，每当我们有实部和虚部时构造矩形数，每当我们有大小和角度时构造极坐标数：

function make_from_real_imag(x, y) {
    return make_from_real_imag_rectangular(x, y);
}
function make_from_mag_ang(r, a) {
    return make_from_mag_ang_polar(r, a);
}

生成的复数系统的结构如图 2.21 所示。该系统已被分解为三个相对独立的部分：复数算术运算、Alyssa 的极坐标实现和 Ben 的矩形实现。极坐标和矩形实现可以由本和 Alyssa 分别编写，并且这两者都可以作为第三个程序员在抽象构造器/选择器接口的基础表示来实现复数算术函数。

图 2.21 通用复数算术系统的结构。

由于每个数据对象都带有其类型标记，因此选择器以通用方式对数据进行操作。也就是说，每个选择器被定义为具有取决于其应用的特定数据类型的行为。注意将各个表示接口化的一般机制：在给定的表示实现中（比如，艾莉莎的极坐标包），复数是一个无类型的对（幅度，角度）。当通用选择器对polar类型的数字进行操作时，它会去掉标记并将内容传递给艾莉莎的代码。相反，当艾莉莎构造一个用于一般用途的数字时，她会给它打上一个类型标记，以便它可以被高级函数适当地识别。随着数据对象从一个级别传递到另一个级别时，去掉和附加标记的这种纪律可以成为一种重要的组织策略，我们将在第 2.5 节中看到。

2.4.3 数据导向编程和可加性

检查数据类型并调用适当的函数的一般策略称为类型分派。这是在系统设计中获得模块化的强大策略。另一方面，像在第 2.4.2 节中实现分派的方法有两个显著的弱点。一个弱点是通用接口函数（real_part、imag_part、magnitude和angle）必须了解所有不同的表示。例如，假设我们想将新的复数表示合并到我们的复数系统中。我们需要用类型标识这个新表示，然后在每个通用接口函数中添加一个子句，以检查新类型并应用该表示的适当选择器。

该技术的另一个弱点是，即使可以单独设计各个表示，我们必须保证整个系统中没有两个函数具有相同的名称。这就是为什么本和艾莉莎不得不更改他们在第 2.4.1 节中的原始函数的名称。

这两个弱点的根本问题是实现通用接口的技术不是可加的。实现通用选择器函数的人必须每次安装新表示时修改这些函数，而接口各个表示的人必须修改他们的代码以避免名称冲突。在这些情况下，必须对代码进行的更改是直截了当的，但仍然必须进行这些更改，这是一种不便和错误的来源。对于复数系统来说，这并不是什么大问题，但是假设复数有数百种不同的表示，而不是两种。假设抽象数据接口中有许多通用选择器需要维护。事实上，假设没有一个程序员知道所有接口函数或所有表示。这个问题是真实存在的，必须在大规模数据库管理系统等程序中加以解决。

我们需要的是进一步模块化系统设计的手段。这是由编程技术数据导向编程提供的。要理解数据导向编程的工作原理，首先观察一下，每当我们处理一组通用操作，这些操作对一组不同类型都是通用的时候，实际上，我们正在处理一个二维表，该表包含一个轴上可能的操作和另一个轴上可能的类型。表中的条目是为每种类型的参数实现每个操作的函数。在前一节中开发的复数系统中，操作名称、数据类型和实际函数之间的对应关系分散在通用接口函数的各种条件子句中。但是相同的信息可以组织在一个表中，如图 2.22 所示。

图 2.22 复数系统的操作表。

数据导向编程是一种直接设计程序与这样一个表一起工作的技术。以前，我们实现了将复数算术代码与两个表示包接口化的机制，作为一组函数，每个函数都对类型进行显式分派。在这里，我们将实现接口作为一个单一函数，该函数查找表中的操作名称和参数类型的组合，以找到正确的应用函数，然后将其应用于参数的内容。如果我们这样做，那么要向系统添加新的表示包，我们不需要更改任何现有的函数；我们只需要向表中添加新条目。

为了实现这个计划，假设我们有两个函数put和get，用于操作操作和类型表：

put(op, type, item)

将item安装在表中，由op和type索引。
get(op, type)

查找表中的op、type条目，并返回找到的项目。如果找不到项目，get返回一个唯一的原始值，该值由名称undefined引用，并由原始谓词is_undefined识别。

现在，我们可以假设put和get包含在我们的语言中。在第 3 章（第 3.3.3 节）中，我们将看到如何实现这些和其他操作来操作表。

以下是数据导向编程如何在复数系统中使用。开发了矩形表示的 Ben，实现他的代码就像他最初做的那样。他定义了一组函数或包，并通过向表中添加条目来将其接口化，告诉系统如何在矩形数上操作。这是通过调用以下函数完成的：

function install_rectangular_package() {
    // internal functions
    function real_part(z) { return head(z); }
    function imag_part(z) { return tail(z); }
    function make_from_real_imag(x, y) { return pair(x, y); }
    function magnitude(z) {
        return math_sqrt(square(real_part(z)) + square(imag_part(z)));
    }
    function angle(z) {
        return math_atan(imag_part(z), real_part(z));
    }
    function make_from_mag_ang(r, a) {
        return pair(r * math_cos(a), r * math_sin(a));
    }

    // interface to the rest of the system
    function tag(x) { return attach_tag("rectangular", x); }
    put("real_part", list("rectangular"), real_part);
    put("imag_part", list("rectangular"), imag_part);
    put("magnitude", list("rectangular"), magnitude);
    put("angle", list("rectangular"), angle);
    put("make_from_real_imag", "rectangular",
        (x, y) => tag(make_from_real_imag(x, y)));
    put("make_from_mag_ang", "rectangular",
        (r, a) => tag(make_from_mag_ang(r, a)));
    return "done";
}

请注意，这里的内部函数与第 2.4.1 节中 Ben 在孤立工作时编写的相同函数。为了将它们接口化到系统的其余部分，不需要进行任何更改。此外，由于这些函数声明是内部的安装函数，Ben 不必担心与矩形包外的其他函数名称冲突。为了将这些接口化到系统的其余部分，Ben 将他的real_part函数安装在操作名称real_part和类型list("rectangular")下，其他选择器也是如此。接口还定义了外部系统要使用的构造函数。这些与 Ben 内部定义的构造函数相同，只是它们附加了标签。

Alyssa 的极坐标包类似：

function install_polar_package() {
    // internal functions
    function magnitude(z) { return head(z); }
    function angle(z) { return tail(z); }
    function make_from_mag_ang(r, a) { return pair(r, a); }
    function real_part(z) {
        return magnitude(z) * math_cos(angle(z));
    }
    function imag_part(z) {
        return magnitude(z) * math_sin(angle(z));
    }
    function make_from_real_imag(x, y) {
        return pair(math_sqrt(square(x) + square(y)),
                    math_atan(y, x));
    }    

    // interface to the rest of the system
    function tag(x) { return attach_tag("polar", x); }
    put("real_part", list("polar"), real_part);
    put("imag_part", list("polar"), imag_part);
    put("magnitude", list("polar"), magnitude);
    put("angle", list("polar"), angle);
    put("make_from_real_imag", "polar",
        (x, y) => tag(make_from_real_imag(x, y)));
    put("make_from_mag_ang", "polar",
        (r, a) => tag(make_from_mag_ang(r, a)));
    return "done";
}

尽管 Ben 和 Alyssa 仍然使用彼此相同名称的原始函数（例如real_part），但这些声明现在是内部不同函数的（参见第 1.1.8 节），因此没有名称冲突。

复数算术选择器通过一个名为apply_generic的通用“操作”函数访问表，该函数将通用操作应用于一些参数。函数apply_generic在表中查找操作的名称和参数的类型，并在存在的情况下应用结果函数。

function apply_generic(op, args) {
    const type_tags = map(type_tag, args);
    const fun = get(op, type_tags);
    return ! is_undefined(fun)
           ? apply_in_underlying_javascript(fun, map(contents, args))
           : error(list(op, type_tags),
                   "no method for these types – apply_generic");
}

使用apply_generic，我们可以定义我们的通用选择器如下：

function real_part(z) { return apply_generic("real_part", list(z)); }
function imag_part(z) { return apply_generic("imag_part", list(z)); }
function magnitude(z) { return apply_generic("magnitude", list(z)); }
function angle(z)     { return apply_generic("angle", list(z));     }

注意，如果系统中添加了新的表示，这些都不会改变。

我们还可以从表中提取构造函数，供程序包外的程序使用，从实部和虚部以及从幅度和角度构造复数。与第 2.4.2 节一样，我们在有实部和虚部时构造矩形数，在有幅度和角度时构造极坐标数：

function make_from_real_imag(x, y) {
    return get("make_from_real_imag", "rectangular")(x, y);
}
function make_from_mag_ang(r, a) {
    return get("make_from_mag_ang", "polar")(r, a);
}

练习 2.73

第 2.3.2 节描述了一个执行符号微分的程序：

function deriv(exp, variable) {
    return is_number(exp)
           ? 0
           : is_variable(exp)
           ? is_same_variable(exp, variable) ? 1 : 0
           : is_sum(exp)
           ? make_sum(deriv(addend(exp), variable),
                      deriv(augend(exp), variable))
           : is_product(exp)
           ? make_sum(make_product(multiplier(exp),
                                   deriv(multiplicand(exp), variable)),
                      make_product(deriv(multiplier(exp), variable),
                                   multiplicand(exp)))
           // more rules can be added here
           : error(exp, "unknown expression type – deriv");
}
deriv(list("*", list("*", "x", "y"), list("+", "x", 4)), "x");
list("+", list("*", list("*", x, y), list("+", 1, 0)),
          list("*", list("+", list("*", x, 0), list("*", 1, y)),
                    list("+", x, 4)))

我们可以将这个程序视为对要进行区分的表达式类型进行调度。在这种情况下，数据的“类型标签”是代数运算符号（如+），正在执行的操作是deriv。我们可以通过将基本导数函数重写为数据导向风格来将这个程序转换为数据导向风格

function deriv(exp, variable) {
    return is_number(exp)
           ? 0
           : is_variable(exp)
           ? is_same_variable(exp, variable) ? 1 : 0
           : get("deriv", operator(exp))(operands(exp), variable);
}
function operator(exp) { return head(exp); }
function operands(exp) { return tail(exp); }

a. 解释上面做了什么。为什么我们不能将谓词is_number和is_variable合并到数据导向调度中？
b. 编写求和和乘积的导数函数，以及安装它们在上面程序使用的表中所需的辅助代码。
c. 选择任何你喜欢的额外区分规则，比如指数的规则（练习 2.56），并将其安装在这个数据导向系统中。
d. 在这个简单的代数操作程序中，表达式的类型是将其绑定在一起的代数运算符。然而，假设我们以相反的方式索引函数，使得deriv中的调度行看起来像
```
get(operator(exp), "deriv")(operands(exp), variable);
```
对导数系统的相应更改是什么？

练习 2.74

Insatiable Enterprises, Inc.是一个高度分散的企业集团公司，由遍布全球的大量独立部门组成。该公司的计算机设施刚刚通过一种巧妙的网络接口方案相互连接，使得整个网络对任何用户来说都像是一台单一的计算机。Insatiable 的总裁在首次尝试利用网络从部门档案中提取行政信息时，惊讶地发现，尽管所有部门的档案都以 JavaScript 中的数据结构实现，但使用的特定数据结构因部门而异。部门经理们匆忙召开会议，寻求一种整合档案的策略，既能满足总部的需求，又能保留部门的现有自治权。

展示如何使用数据导向编程实现这样的策略。例如，假设每个部门的人事档案都包含一个单一文件，其中包含以员工姓名为键的一组记录。集合的结构因部门而异。此外，每个员工的记录本身是一个集合（在不同部门结构不同），其中包含以address和salary为标识的信息。特别是：

a. 为总部实现一个get_record函数，该函数从指定的人事档案中检索指定员工的记录。该函数应适用于任何部门的档案。解释个别部门的档案应该如何结构化。特别是，必须提供什么类型的信息？
b. 为总部实现一个get_salary函数，该函数从任何部门的人事档案中返回给定员工的薪水信息。为了使此操作起作用，记录应该如何结构化？
c. 为总部实现一个find_employee_record函数。这个函数应该搜索所有部门的档案，找到给定员工的记录并返回记录。假设这个函数的参数是员工的姓名和所有部门档案的列表。
d. 当贪婪公司接管新公司时，必须进行哪些更改才能将新员工信息整合到中央系统中？

消息传递

数据导向编程的关键思想是通过显式处理操作和类型表来处理程序中的通用操作，比如图 2.22 中的表。我们在 2.4.2 节中使用的编程风格通过让每个操作负责自己的调度来组织所需的类型调度。实际上，这将操作和类型表分解为行，每个通用操作函数代表表的一行。

另一种实现策略是将表分解为列，而不是使用在数据类型上分派的“智能操作”，而是使用在操作名称上分派的“智能数据对象”。我们可以通过安排事物，使得数据对象，如矩形数，表示为一个函数，该函数以所需的操作名称作为输入，并执行指示的操作。在这样的学科中，make_from_real_imag可以被写成

function make_from_real_imag(x, y) {
    function dispatch(op) {
        return op === "real_part"
               ? x
               : op === "imag_part"
               ? y
               : op === "magnitude"
               ? math_sqrt(square(x) + square(y))
               : op === "angle"
               ? math_atan(y, x)
               : error(op, "unknown op – make_from_real_imag");
    }
    return dispatch;
}

相应的apply_generic函数，将通用操作应用于参数，现在只需将操作名称传递给数据对象，让对象完成工作：⁴⁵

function apply_generic(op, arg) { return head(arg)(op); }

请注意，make_from_real_imag返回的值是一个函数——内部的dispatch函数。这是在apply_generic请求执行操作时调用的函数。

这种编程风格称为消息传递。这个名字来自这样一个形象，即数据对象是一个接收所请求的操作名称作为“消息”的实体。我们已经在第 2.1.3 节中看到了消息传递的一个例子，在那里我们看到了如何定义pair，head和tail，而不是数据对象，而只是函数。在这里，我们看到消息传递不是一个数学技巧，而是一种组织具有通用操作的系统的有用技术。在本章的其余部分，我们将继续使用数据导向编程，而不是消息传递，来讨论通用算术操作。在第 3 章中，我们将回到消息传递，并且我们将看到它可以是一种构建仿真程序的强大工具。

练习 2.75

以消息传递方式实现构造函数make_from_mag_ang。这个函数应该类似于上面给出的make_from_real_imag函数。

练习 2.76

随着具有通用操作的大型系统的发展，可能需要新类型的数据对象或新操作。对于三种策略——具有显式分派的通用操作、数据导向风格和消息传递风格——描述必须对系统进行的更改，以添加新类型或新操作。对于经常需要添加新类型的系统，哪种组织方式最合适？对于经常需要添加新操作的系统，哪种组织方式最合适？

2.5 具有通用操作的系统

在前一节中，我们看到了如何设计系统，其中数据对象可以以多种方式表示。关键思想是通过通用接口函数将指定数据操作的代码与多种表示链接起来。现在我们将看到如何使用相同的思想，不仅定义可以适用于不同表示的操作，还可以定义可以适用于不同类型参数的操作。我们已经看到了几种不同的算术操作包：语言内置的原始算术（+，-，*，/），第 2.1.1 节中的有理数算术（add_rat，sub_rat，mul_rat，div_rat），以及我们在第 2.4.3 节中实现的复数算术。现在我们将使用数据导向技术来构建一个包含我们已经构建的所有算术包的算术操作包。

图 2.23 显示了我们将构建的系统的结构。注意抽象屏障。从使用“数字”的人的角度来看，有一个单一的函数add，它对提供的任何数字进行操作。函数add是通用接口的一部分，它允许使用数字的程序以统一的方式访问单独的普通算术、有理算术和复数算术包。任何单独的算术包（如复数包）本身可以通过通用函数（如add_complex）访问，这些函数结合了为不同表示设计的包（如矩形和极坐标）。此外，系统的结构是可加性的，因此可以单独设计各个算术包，并将它们组合以产生通用算术系统。

图 2.23 通用算术系统。

2.5.1 通用算术操作

设计通用算术操作的任务类似于设计通用复数操作。例如，我们希望有一个通用加法函数add，它在普通数字上的行为类似于普通原始加法+，在有理数上类似于add_rat，在复数上类似于add_complex。我们可以通过遵循与我们在 2.4.3 节中用于实现复数的通用选择器相同的策略来实现add和其他通用算术操作。我们将为每种数字类型附加一个类型标签，并使通用函数根据其参数的数据类型分派到适当的包。

通用算术函数定义如下：

function add(x, y) { return apply_generic("add", list(x, y)); }
function sub(x, y) { return apply_generic("sub", list(x, y)); }
function mul(x, y) { return apply_generic("mul", list(x, y)); }
function div(x, y) { return apply_generic("div", list(x, y)); }

我们首先安装一个用于处理普通数字的包，即我们语言的原始数字。我们用字符串javascript_number标记这些数字。此包中的算术操作是原始算术函数（因此无需定义额外的函数来处理未标记的数字）。由于这些操作每个都需要两个参数，它们被安装在由列表list("javascript_number", "javascript_number")键入的表中。

function install_javascript_number_package() {
    function tag(x) {
        return attach_tag("javascript_number", x);
    }
    put("add", list("javascript_number", "javascript_number"),
        (x, y) => tag(x + y));
    put("sub", list("javascript_number", "javascript_number"),
        (x, y) => tag(x - y));
    put("mul", list("javascript_number", "javascript_number"),
        (x, y) => tag(x * y));
    put("div", list("javascript_number", "javascript_number"),
        (x, y) => tag(x / y));
    put("make", "javascript_number",
        x => tag(x));
    return "done";
}

JavaScript-number 包的用户将通过函数创建（标记）普通数字：

function make_javascript_number(n) {
    return get("make", "javascript_number")(n);
}

现在通用算术系统的框架已经建立，我们可以轻松地包含新类型的数字。这是一个执行有理数算术的包。注意，由于可加性的好处，我们可以在包中使用 2.1.1 节中的有理数代码作为内部函数，而无需修改：

function install_rational_package() {
    // internal functions
    function numer(x) { return head(x); }
    function denom(x) { return tail(x); }
    function make_rat(n, d) {
        const g = gcd(n, d);
        return pair(n / g, d / g);
    }
    function add_rat(x, y) {
        return make_rat(numer(x) * denom(y) + numer(y) * denom(x),
                        denom(x) * denom(y));
    }
    function sub_rat(x, y) {
        return make_rat(numer(x) * denom(y) - numer(y) * denom(x),
                        denom(x) * denom(y));
    }
    function mul_rat(x, y) {
        return make_rat(numer(x) * numer(y),
                        denom(x) * denom(y));
    }
    function div_rat(x, y) {
        return make_rat(numer(x) * denom(y),
                        denom(x) * numer(y));
    }
    // interface to rest of the system
    function tag(x) {
        return attach_tag("rational", x);
    }
    put("add", list("rational", "rational"),
        (x, y) => tag(add_rat(x, y)));
    put("sub", list("rational", "rational"),
        (x, y) => tag(sub_rat(x, y)));
    put("mul", list("rational", "rational"),
        (x, y) => tag(mul_rat(x, y)));
    put("div", list("rational", "rational"),
        (x, y) => tag(div_rat(x, y)));
    put("make", "rational",
        (n, d) => tag(make_rat(n, d)));
    return "done";
}

function make_rational(n, d) {
    return get("make", "rational")(n, d);
}

我们可以安装一个类似的包来处理复数，使用标签complex。在创建包时，我们从表中提取了矩形和极坐标包定义的操作make_from_real_imag和make_from_mag_ang。可加性允许我们使用相同的add_complex、sub_complex、mul_complex和div_complex函数作为内部操作，这些函数来自 2.4.1 节。

function install_complex_package() {
    // imported functions from rectangular and polar packages
    function make_from_real_imag(x, y) {
        return get("make_from_real_imag", "rectangular")(x, y);
    }
    function make_from_mag_ang(r, a) {
        return get("make_from_mag_ang", "polar")(r, a);
    }
    // internal functions
    function add_complex(z1, z2) {
        return make_from_real_imag(real_part(z1) + real_part(z2),
                                   imag_part(z1) + imag_part(z2));
    }
    function sub_complex(z1, z2) {
        return make_from_real_imag(real_part(z1) - real_part(z2),
                                   imag_part(z1) - imag_part(z2));
    }
    function mul_complex(z1, z2) {
        return make_from_mag_ang(magnitude(z1) * magnitude(z2),
                                 angle(z1) + angle(z2));
    }
function div_complex(z1, z2) {
    return make_from_mag_ang(magnitude(z1) / magnitude(z2),
                                 angle(z1) - angle(z2));
    }
    // interface to rest of the system
    function tag(z) { return attach_tag("complex", z); }
    put("add", list("complex", "complex"),
        (z1, z2) => tag(add_complex(z1, z2)));
    put("sub", list("complex", "complex"),
        (z1, z2) => tag(sub_complex(z1, z2)));
    put("mul", list("complex", "complex"),
        (z1, z2) => tag(mul_complex(z1, z2)));
    put("div", list("complex", "complex"),
        (z1, z2) => tag(div_complex(z1, z2)));
    put("make_from_real_imag", "complex",
        (x, y) => tag(make_from_real_imag(x, y)));
    put("make_from_mag_ang", "complex",
        (r, a) => tag(make_from_mag_ang(r, a)));
    return "done";
}

复数包之外的程序可以通过实部和虚部或幅度和角度构造复数。注意，最初在矩形和极坐标包中定义的基础函数如何被导出到复数包，并从那里导出到外部世界。

function make_complex_from_real_imag(x, y){
    return get("make_from_real_imag", "complex")(x, y);
}
function make_complex_from_mag_ang(r, a){
    return get("make_from_mag_ang", "complex")(r, a);
}

我们这里有一个两级标签系统。一个典型的复数，比如矩形形式中的3 + 4i，如图 2.24 所示。外部标签("complex")用于将数字定向到复数包。一旦进入复数包，下一个标签("rectangular")用于将数字定向到矩形包。在一个庞大而复杂的系统中，可能会有许多级别，每个级别通过通用操作与下一个级别接口连接。当数据对象被“传递”时，用于将其定向到适当包的外部标签被剥离（通过应用contents），并且下一个级别的标签（如果有）变得可见，以便用于进一步的分派。

图 2.24 矩形形式中 3 + 4i 的表示。

在上述包中，我们使用了add_rat、add_complex和其他算术函数，其实就是原始写法。然而，一旦这些声明内部化到不同的安装函数中，它们就不再需要彼此不同的名称：我们可以在两个包中简单地将它们命名为add、sub、mul和div。

练习 2.77

路易斯·里森纳试图求值表达式magnitude(z)，其中z是图 2.24 中显示的对象。令他惊讶的是，他没有得到答案 5，而是从apply_generic得到了一个错误消息，说没有针对类型list("complex")的magnitude操作的方法。他把这个交互展示给了 Alyssa P. Hacker，后者说：“问题在于复数选择器从未为"complex"数字定义过，只为"polar"和"rectangular"数字定义过。要使其工作，你只需将以下内容添加到complex包中：”

put("real_part", list("complex"), real_part);
put("imag_part", list("complex"), imag_part);
put("magnitude", list("complex"), magnitude);
put("angle",      list("complex"), angle);

详细描述为什么这样可以工作。例如，跟踪在求值表达式magnitude(z)时调用的所有函数。特别是apply_generic被调用了多少次？在每种情况下分派给了哪个函数？

练习 2.78

javascript_number包中的内部函数本质上只是对原始函数+、-等的调用。由于我们的类型标签系统要求每个数据对象都附有类型，因此无法直接使用语言的原始函数。实际上，所有 JavaScript 实现都有一个类型系统，它们在内部使用。诸如is_string和is_number之类的原始谓词确定数据对象是否具有特定类型。修改第 2.4.2 节中的type_tag、contents和attach_tag的定义，以便我们的通用系统利用 JavaScript 的内部类型系统。也就是说，该系统应该像以前一样工作，只是普通数字应该简单地表示为 JavaScript 数字，而不是作为head为字符串"javascript_number"的对。

练习 2.79

定义一个通用相等谓词is_equal，用于测试两个数字的相等性，并将其安装在通用算术包中。此操作应适用于普通数字、有理数和复数。

练习 2.80

定义一个通用谓词is_equal_to_zero，用于测试其参数是否为零，并将其安装在通用算术包中。此操作应适用于普通数字、有理数和复数。

2.5.2 组合不同类型的数据

我们已经看到如何定义一个统一的算术系统，包括普通数、复数、有理数和我们可能决定发明的任何其他类型的数字，但我们忽略了一个重要问题。到目前为止，我们定义的操作将不同的数据类型视为完全独立。因此，有单独的包用于添加两个普通数或两个复数。我们还没有考虑的是，定义跨类型边界的操作是有意义的，比如将复数加到普通数上。我们已经非常费力地引入了程序的各个部分之间的障碍，以便它们可以分开开发和理解。我们希望以一种精心控制的方式引入跨类型操作，以便我们可以支持它们，而不严重违反我们的模块边界。

处理跨类型操作的一种方法是为每种可能的类型组合设计不同的函数，这些函数对于这些操作是有效的。例如，我们可以扩展复数包，以便它提供一个将复数加到普通数的函数，并使用标签list("complex", "javascript_number")将其安装在表中：⁴⁶

// to be included in the complex package
function add_complex_to_javascript_num(z, x) {
    return make_complex_from_real_imag(real_part(z) + x, imag_part(z));
}
put("add", list("complex", "javascript_number"),
    (z, x) => tag(add_complex_to_javascript_num(z, x)));

这种技术是行得通的，但它很繁琐。在这样的系统中，引入新类型的成本不仅仅是为该类型构建函数包，还包括实现跨类型操作的函数的构建和安装。这很容易比定义类型本身的操作所需的代码多得多。这种方法还破坏了我们将单独的包累加在一起的能力，或者至少限制了个别包的实现者需要考虑其他包的程度。例如，在上面的例子中，处理复数和普通数的混合操作应该是复数包的责任。然而，组合有理数和复数可能由复数包、有理数包或者使用这两个包中提取的操作的第三个包来完成。在设计具有许多包和许多跨类型操作的系统时，制定关于包之间责任分配的一致政策可能是一个艰巨的任务。

强制转换

在完全不相关的操作作用于完全不相关的类型的一般情况下，实现显式的跨类型操作，尽管繁琐，是人们所能期望的最好的。幸运的是，我们通常可以通过利用可能潜在于我们类型系统中的附加结构来做得更好。通常不同的数据类型并不是完全独立的，而且可能有一些方法，可以将一个类型的对象视为另一种类型的对象。这个过程称为强制转换。例如，如果我们被要求将一个普通数与一个复数进行算术运算，我们可以将普通数视为其虚部为零的复数。这将问题转化为两个复数的组合问题，可以通过复数算术包以普通方式处理。

一般来说，我们可以通过设计强制转换函数来实现这个想法，这些函数将一个类型的对象转换为另一个类型的等效对象。这是一个典型的强制转换函数，它将给定的普通数转换为具有该实部和零虚部的复数：

function javascript_number_to_complex(n) {
    return make_complex_from_real_imag(contents(n), 0);
}

我们将这些强制转换函数安装在一个特殊的强制转换表中，索引为两种类型的名称：

put_coercion("javascript_number", "complex",
             javascript_number_to_complex);

（我们假设有put_coercion和get_coercion函数可用于操作此表。）通常表中的某些槽位将是空的，因为通常无法将每种类型的任意数据对象强制转换为所有其他类型。例如，没有办法将任意复数强制转换为普通数字，因此在表中将不包括通用的complex_to_javascript_number函数。

一旦建立了强制转换表，我们可以通过修改第 2.4.3 节中的apply_generic函数以统一处理强制转换。当要求应用操作时，我们首先检查操作是否适用于参数的类型，就像以前一样。如果是，我们将分派到在操作和类型表中找到的函数。否则，我们尝试强制转换。为简单起见，我们只考虑有两个参数的情况。我们检查强制转换表，看看第一种类型的对象是否可以被强制转换为第二种类型。如果可以，我们强制转换第一个参数，然后再次尝试操作。如果第一种类型的对象通常无法被强制转换为第二种类型，我们尝试以另一种方式进行强制转换，看看是否有一种方法可以将第二个参数强制转换为第一个参数的类型。最后，如果没有已知的方法可以强制转换任一类型为另一类型，我们放弃。以下是该函数：

function apply_generic(op, args) {
    const type_tags = map(type_tag, args);
    const fun = get(op, type_tags);
    if (! is_undefined(fun)) {
        return apply(fun, map(contents, args));
    } else {
        if (length(args) === 2) {
            const type1 = head(type_tags);
            const type2 = head(tail(type_tags));
            const a1 = head(args);
            const a2 = head(tail(args));
            const t1_to_t2 = get_coercion(type1, type2);
            const t2_to_t1 = get_coercion(type2, type1);
            return ! is_undefined(t1_to_t2)
                   ? apply_generic(op, list(t1_to_t2(a1), a2))
                   : ! is_undefined(t2_to_t1)
                   ? apply_generic(op, list(a1, t2_to_t1(a2)))
                   : error(list(op, type_tags),
                           "no method for these types");
        } else {
            return error(list(op, type_tags),
                         "no method for these types");
        }
    }
}

与上述定义显式跨类型操作的方法相比，这种强制转换方案具有许多优点。虽然我们仍然需要编写强制转换函数来关联类型（对于具有n种类型的系统，可能需要n²个函数），但我们只需要为每对类型编写一个函数，而不是为每组类型和每个通用操作编写不同的函数。我们在这里所依赖的是这样一个事实，即类型之间的适当转换只取决于类型本身，而不取决于要应用的操作。

另一方面，可能有一些应用程序，我们的强制方案并不够通用。即使要合并的两个对象都无法转换为对方的类型，仍然可以通过将两个对象转换为第三种类型来执行操作。为了处理这种复杂性并仍然保持程序的模块化，通常需要构建利用类型之间关系中更进一步结构的系统，接下来我们将讨论这一点。

类型的层次结构

上述强制转换方案依赖于类型对之间存在自然关系的存在。通常，不同类型之间的关系具有更多的“全局”结构。例如，假设我们正在构建一个通用算术系统来处理整数、有理数、实数和复数。在这样的系统中，将整数视为有理数的一种特殊类型，而有理数又是实数的一种特殊类型，实数又是复数的一种特殊类型，这是非常自然的。实际上，我们拥有所谓的类型层次结构，例如，整数是有理数的子类型（即，可以应用于有理数的任何操作也可以自动应用于整数）。相反，我们说有理数是整数的超类型。我们这里拥有的特定层次结构是一种非常简单的结构，其中每种类型最多只有一个超类型和一个子类型。这样的结构，称为塔，在图 2.25 中有所说明。

图 2.25 类型的层次结构。

如果我们有一个塔结构，那么我们可以极大地简化将新类型添加到层次结构中的问题，因为我们只需要指定新类型如何嵌入到其上一级的超类型中，以及它如何成为其下一级类型的超类型。例如，如果我们想要将整数添加到复数中，我们不需要明确地定义一个特殊的强制转换函数integer_to_complex。相反，我们定义整数如何转换为有理数，有理数如何转换为实数，以及实数如何转换为复数。然后，我们允许系统通过这些步骤将整数转换为复数，然后将两个复数相加。

我们可以按照以下方式重新设计我们的apply_generic函数：对于每种类型，我们需要提供一个raise函数，它可以将该类型的对象在塔中提升一级。然后，当系统需要对不同类型的对象进行操作时，它可以依次提升较低的类型，直到所有对象在塔中处于相同的级别。（练习 2.83 和 2.84 涉及实现这种策略的细节。）

塔的另一个优点是，我们可以很容易地实现这样一个概念，即每种类型“继承”了在超类型上定义的所有操作。例如，如果我们没有为查找整数的实部提供一个特殊的函数，我们仍然应该期望整数的real_part是由于整数是复数的子类型而被定义的。在一个塔中，我们可以通过修改apply_generic以一种统一的方式安排这种情况发生。如果给定对象的类型没有直接定义所需的操作，我们将把对象提升到其超类型并重试。因此，我们沿着塔向上爬行，随着我们的参数的转换，直到我们找到可以执行所需操作的级别，或者达到顶部（在这种情况下我们放弃）。

塔相对于更一般的层次结构的另一个优点是，它为我们提供了一种简单的方法来将数据对象“降低”到最简单的表示。例如，如果我们将 2 + 3i加到4 - 3i，我们希望得到的答案是整数 6，而不是复数6 + 0i。练习 2.85 讨论了实现这种降低操作的方法。（诀窍在于我们需要一种通用的方法来区分那些可以被降低的对象，比如6 + 0i，和那些不能被降低的对象，比如6 + 2i。）

层次结构的不足之处

如果我们的系统中的数据类型可以自然地排列成一个塔，这将极大地简化处理不同类型的通用操作的问题，正如我们所见。不幸的是，这种情况通常并非如此。图 2.26 展示了一种更复杂的混合类型排列，其中显示了不同类型的几何图形之间的关系。我们看到，一般来说，一个类型可能有多个子类型。例如，三角形和四边形都是多边形的子类型。此外，一个类型可能有多个超类型。例如，等腰直角三角形可以被视为等腰三角形或直角三角形。这个多超类型的问题特别棘手，因为这意味着在层次结构中没有唯一的“提升”类型的方法。在对象上应用操作时，找到“正确”的超类型可能需要在整个类型网络中进行大量搜索，这是apply_generic等函数的一个问题。由于一般情况下一个类型有多个子类型，因此在将值“降低”到类型层次结构时也存在类似的问题。在设计大型系统的同时处理大量相互关联的类型是非常困难的，也是当前研究的一个重要领域。

图 2.26 几何图形类型之间的关系。

练习 2.81

路易斯·里森纳（Louis Reasoner）注意到apply_generic可能会尝试将参数强制转换为彼此的类型，即使它们已经具有相同的类型。因此，他推断，我们需要在强制转换表中放置函数以将每种类型的参数“强制”为其自己的类型。例如，除了上面显示的javascript_number_to_complex强制转换外，他还会这样做：

function javascript_number_to_javascript_number(n) { return n; }
function complex_to_complex(n) { return n; }
put_coercion("javascript_number", "javascript_number",
             javascript_number_to_javascript_number);
put_coercion("complex", "complex", complex_to_complex);

a. 如果安装了路易斯的强制转换函数，当apply_generic使用两个类型为complex的参数或两个类型为javascript_number的参数调用一个在这些类型的表中找不到的操作时会发生什么？例如，假设我们定义了一个通用的幂运算操作：
```
function exp(x, y) {
    return apply_generic("exp", list(x, y));
}
```
并且在 JavaScript-number 包中放置了一个幂运算函数，但在任何其他包中都没有：
```
// following added to JavaScript-number package
put("exp", list("javascript_number", "javascript_number"),
    (x, y) => tag(math_exp(x, y))); // using primitive math_exp
```
如果我们用两个复数作为参数调用exp会发生什么？
b. 路易斯是否正确，需要对相同类型的参数进行强制转换，或者apply_generic按原样工作？
c. 修改apply_generic，使其在两个参数具有相同类型时不尝试强制转换。

练习 2.82

展示如何将apply_generic泛化以处理多个参数的一般情况。一种策略是尝试将所有参数强制转换为第一个参数的类型，然后转换为第二个参数的类型，依此类推。给出一个情况的例子，该策略（以及上面给出的两参数版本）不够通用。（提示：考虑存在一些适当的混合类型操作的情况，这些操作将不会被尝试。）

练习 2.83

假设您正在设计一个用于处理类型塔的通用算术系统，如图 2.25 所示：整数，有理数，实数，复数。对于每种类型（复数除外），设计一个将该类型的对象提升一级的函数。展示如何安装一个通用的raise操作，该操作将适用于每种类型（复数除外）。

练习 2.84

使用练习 2.83 的raise操作，修改apply_generic函数，使其通过本节讨论的连续提升的方法强制其参数具有相同的类型。您需要设计一种方法来测试两种类型中哪种更高。以一种与系统的其余部分“兼容”的方式进行此操作，并且不会在向类型塔添加新级别时出现问题。

练习 2.85

本节提到了一种通过将数据对象尽可能降低到类型塔中的方法来“简化”数据对象。设计一个函数drop，以实现练习 2.83 中描述的类型塔的降低。关键是以一种一般的方式决定对象是否可以降低。例如，复数1.5 + 0i可以降低到real，复数1 + 0i可以降低到integer，而复数2 + 3i根本无法降低。以下是确定对象是否可以降低的计划：首先定义一个“推”对象下降到塔中的通用操作project。例如，投影复数将涉及丢弃虚部。然后，如果我们project它并将结果raise回到我们开始的类型，我们得到与我们开始的相等的东西，那么数字就可以被丢弃。展示如何通过编写一个drop函数来详细实现这个想法，该函数将对象尽可能地降低。您需要设计各种投影操作⁵⁰并在系统中安装project作为通用操作。您还需要使用通用相等谓词，例如练习 2.79 中描述的谓词。最后，使用drop重写练习 2.84 中的apply_generic，以便“简化”其答案。

练习 2.86

假设我们想处理复数，其实部、虚部、幅度和角度可以是普通数、有理数，或者我们可能希望添加到系统中的其他数。描述并实现系统需要的更改，以适应这一点。您将不得不定义诸如sine和cosine这样的操作，这些操作对普通数和有理数是通用的。

2.5.3 示例：符号代数

符号代数表达式的操作是一个复杂的过程，它展示了大规模系统设计中出现的许多最困难的问题。一般来说，代数表达式可以被看作是一个分层结构，即操作符应用于操作数的树。我们可以通过从一组原始对象（如常数和变量）开始，并通过代数运算符（如加法和乘法）组合这些对象来构造代数表达式。与其他语言一样，我们形成抽象，使我们能够用简单的术语引用复合对象。符号代数中的典型抽象是诸如线性组合、多项式、有理函数或三角函数等概念。我们可以将这些看作是复合的“类型”，它们经常有助于指导表达式的处理。例如，我们可以描述表达式

x² sin(y² + 1) + x cos 2y + cos(y³ – 2y²)

作为x的多项式，其系数是y的多项式的三角函数。

我们不打算在这里开发一个完整的代数运算系统。这样的系统是非常复杂的程序，包含深奥的代数知识和优雅的算法。我们要做的是看一看代数运算的一个简单但重要的部分：多项式的算术。我们将说明这样一个系统的设计者面临的决策类型，并且如何应用抽象数据和通用操作的思想来帮助组织这一努力。

多项式的算术

我们在设计一个用于多项式算术的系统时的第一个任务是决定多项式到底是什么。多项式通常是相对于某些变量（多项式的不定元）定义的。为简单起见，我们将限制自己只处理具有一个不定元的多项式（一元多项式）。我们将定义多项式为项的和，每个项可以是系数、不定元的幂，或者系数和不定元的乘积。系数被定义为不依赖于多项式的不定元的代数表达式。例如，

5x² + 3x + 7

是一个关于x的简单多项式，以及

(y² + 1)x³ + (2y)x + 1

是一个关于x的多项式，其系数是y的多项式。

我们已经在绕过一些棘手的问题。第一个多项式是否与多项式5y² + 3y + 7相同，还是不同？一个合理的答案可能是“如果我们把多项式纯粹看作是一个数学函数，那么是的，但如果我们把多项式看作是一种语法形式，那么不是”。第二个多项式在代数上等价于关于y的多项式，其系数是x的多项式。我们的系统应该认识到这一点吗？还是不应该？此外，还有其他表示多项式的方式，例如作为因子的乘积，或者（对于一元多项式）作为根的集合，或者作为在指定点集上的多项式值的列表。我们可以通过决定在我们的代数运算系统中，“多项式”将是一种特定的语法形式，而不是其潜在的数学含义来回避这些问题。

现在我们必须考虑如何进行多项式的算术。在这个简单的系统中，我们只考虑加法和乘法。此外，我们要求要组合的两个多项式必须具有相同的不定元。

我们将通过遵循数据抽象的熟悉原则来设计我们的系统。我们将使用一个称为poly的数据结构来表示多项式，它由一个变量和一组项组成。我们假设我们有选择器variable和term_list，它们从多项式中提取这些部分，以及一个构造函数make_poly，它从给定的变量和项列表组装一个多项式。一个变量将只是一个字符串，因此我们可以使用第 2.3.2 节中的is_same_variable函数来比较变量。以下函数定义了多项式的加法和乘法：

function add_poly(p1, p2) {
    return is_same_variable(variable(p1), variable(p2))
           ? make_poly(variable(p1),
                       add_terms(term_list(p1), term_list(p2)))
           : error(list(p1, p2), "polys not in same var – add_poly");
}
function mul_poly(p1, p2) {
    return is_same_variable(variable(p1), variable(p2))
           ? make_poly(variable(p1),
                       mul_terms(term_list(p1), term_list(p2)))
           : error(list(p1, p2), "polys not in same var – mul_poly");
}

为了将多项式纳入我们的通用算术系统，我们需要为它们提供类型标签。我们将使用标签"polynomial"，并在操作表中为带标签的多项式安装适当的操作。我们将把所有代码嵌入到多项式包的安装函数中，类似于第 2.5.1 节中的安装函数：

function install_polynomial_package() {
    // internal functions
    // representation of poly
    function make_poly(variable, term_list) {
        return pair(variable, term_list);
    }
    function variable(p) { return head(p); }
    function term_list(p) { return tail(p); }
    〈functions is_same_variable and is_variable from section 2.3.2〉    

    // representation of terms and term lists
    〈functions adjoin_term…coeff from text below〉

    function add_poly(p1, p2) { … }
    〈functions used by add_poly〉
    function mul_poly(p1, p2) { … }
    〈functions used by mul_poly〉    

    // interface to rest of the system
    function tag(p) { return attach_tag("polynomial", p); }
    put("add", list("polynomial", "polynomial"),
        (p1, p2) => tag(add_poly(p1, p2)));
    put("mul", list("polynomial", "polynomial"),
        (p1, p2) => tag(mul_poly(p1, p2)));
    put("make", "polynomial",
        (variable, terms) => tag(make_poly(variable, terms)));
    return "done";
}

多项式的加法是逐项进行的。必须合并同一次幂的项（即，具有相同未知数幂的项）。这是通过形成一个新的同一次幂的项来完成的，其系数是被加数的系数的和。一个加数中的项，如果在另一个加数中没有相同次幂的项，那么它们就简单地累积到正在构造的和多项式中。

为了操作项列表，我们将假定我们有一个构造函数the_empty_termlist，它返回一个空的项列表，以及一个构造函数adjoin_ term，它将一个新的项添加到项列表中。我们还将假定我们有一个谓词is_empty_termlist，它告诉我们给定的项列表是否为空，一个选择器first_term，它从项列表中提取最高次项，以及一个选择器rest_terms，它返回除了最高次项之外的所有项。为了操作项，我们将假设我们有一个构造函数make_term，它构造一个具有给定次序和系数的项，以及选择器order和coeff，它们分别返回项的次序和系数。这些操作使我们能够将项和项列表都视为数据抽象，我们可以分别担心它们的具体表示。

以下是构造两个多项式之和的项列表的函数;⁵³请注意，我们通过允许在**else**后面的块中添加另一个条件语句，略微扩展了第 1.3.2 节中描述的条件语句的语法：

function add_terms(L1, L2) {
    if (is_empty_termlist(L1)) {
        return L2;
    } else if (is_empty_termlist(L2)) {
        return L1;
    } else {
        const t1 = first_term(L1);
        const t2 = first_term(L2);
        return order(t1) > order(t2)
               ? adjoin_term(t1, add_terms(rest_terms(L1), L2))
               : order(t1) < order(t2)
               ? adjoin_term(t2, add_terms(L1, rest_terms(L2)))
               : adjoin_term(make_term(order(t1),
                                       add(coeff(t1), coeff(t2))),
                             add_terms(rest_terms(L1),
                                       rest_terms(L2)));
    }
}

这里最重要的一点是，我们使用了通用的加法函数add来将合并的项的系数相加。这具有强大的后果，我们将在下面看到。

为了将两个项列表相乘，我们将第一个列表的每个项与另一个列表的所有项相乘，重复使用mul_term_by_all_terms，它将给定的项与给定的项列表中的所有项相乘。结果项列表（对于第一个列表的每个项）被累积到一个和中。将两个项相乘形成一个次序是因子次序之和，系数是因子系数之积的项：

function mul_terms(L1, L2) {
    return is_empty_termlist(L1)
          ? the_empty_termlist
          : add_terms(mul_term_by_all_terms(
                                first_term(L1), L2),
                      mul_terms(rest_terms(L1), L2));
}
function mul_term_by_all_terms(t1, L) {
    if (is_empty_termlist(L)) {
        return the_empty_termlist;
    } else {
        const t2 = first_term(L);
        return adjoin_term(
                   make_term(order(t1) + order(t2),
                             mul(coeff(t1), coeff(t2))),
                   mul_term_by_all_terms(t1, rest_terms(L)));
    }
}

这确实就是多项式的加法和乘法。请注意，由于我们使用通用函数add和mul对项进行操作，我们的多项式包自动能够处理通用算术包已知的任何类型的系数。如果我们包括一个强制转换机制，例如在第 2.5.2 节中讨论的机制之一，那么我们也能够自动处理不同系数类型的多项式的操作，例如

因为我们在通用算术系统中安装了多项式加法和乘法函数add_ poly和mul_poly作为类型polynomial的add和mul操作，我们的系统也能够自动处理多项式操作，例如

(y + 1)x² + (y² + 1)x + (y – 1) · (y – 2)x + (y³ + 7)

原因是当系统尝试组合系数时，它将通过add和mul进行分派。由于系数本身是多项式（在y中），这些将使用add_poly和mul_poly进行组合。结果是一种“数据导向递归”，例如，对mul_poly的调用将导致递归调用mul_poly以便乘以系数。如果系数的系数本身是多项式（可能用于表示三个变量的多项式），数据方向将确保系统将遵循另一级递归调用，以及数据结构所决定的任意级别。

表示项列表

最后，我们必须面对实现一个良好的项列表表示的工作。项列表实际上是一组由项的顺序作为键的系数集合。因此，可以将第 2.3.3 节中讨论的任何表示集合的方法应用于此任务。另一方面，我们的函数add_terms和mul_terms总是按顺序从最高到最低的顺序访问项列表。因此，我们将使用某种有序列表表示。

我们应该如何构造表示项列表的列表？一个考虑因素是我们打算操作的多项式的“密度”。如果多项式在大多数阶的系数中都是非零的，则称为密集多项式。如果它有许多零项，则称为稀疏。例如，

A：x⁵ + 2x⁴ + 3x² – 2x – 5

是一个密集多项式，而

B：x¹⁰⁰ + 2x² + 1

是稀疏的。

密集多项式的项列表最有效地表示为系数的列表。例如，上面的多项式A可以很好地表示为list(1, 2, 0, 3, -2, -5)。在这种表示中，项的顺序是以该项系数开头的子列表的长度，减 1。这对于稀疏多项式B来说是一个糟糕的表示：会有一个巨大的零项列表，中间夹杂着一些孤独的非零项。项列表的更合理的表示是作为非零项的列表，其中每个项都是包含该项顺序和该顺序系数的列表。在这样的方案中，多项式B可以有效地表示为list(list(100, 1), list(2, 2), list(0, 1))。由于大多数多项式操作是在稀疏多项式上执行的，我们将使用这种方法。我们将假设项列表被表示为项的列表，从最高阶到最低阶的项。一旦我们做出了这个决定，实现项和项列表的选择器和构造器就很简单了。

function adjoin_term(term, term_list) {
    return is_equal_to_zero(coeff(term))
           ? term_list
           : pair(term, term_list);
}

const the_empty_termlist = null;
function first_term(term_list) { return head(term_list); }
function rest_terms(term_list) { return tail(term_list); }
function is_empty_termlist(term_list) { return is_null(term_list); }

function make_term(order, coeff) { return list(order, coeff); }
function order(term) { return head(term); }
function coeff(term) { return head(tail(term)); }

其中is_equal_to_zero如练习 2.80 中所定义。（另见下面的练习 2.87。）

多项式包的用户将通过以下函数创建（标记的）多项式：

function make_polynomial(variable, terms) {
    return get("make", "polynomial")(variable, terms);
}

练习 2.87

为通用算术包中的多项式安装is_equal_to_zero。这将允许adjoin_term用于系数本身是多项式的多项式。

练习 2.88

扩展多项式系统以包括多项式的减法。（提示：您可能会发现定义一个通用的否定操作很有帮助。）

练习 2.89

声明实现上述项列表表示的函数，适用于密集多项式。

练习 2.90

假设我们希望拥有一个对稀疏和密集多项式都有效的多项式系统。实现这一点的一种方法是在我们的系统中允许两种类型的项列表表示。这种情况类似于第 2.4 节中的复数示例，我们在那里允许了矩形和极坐标表示。为了做到这一点，我们必须区分不同类型的项列表，并使项列表上的操作成为通用的。重新设计多项式系统以实现这种泛化。这是一项重大工作，而不是一个局部变化。

练习 2.91

一个一元多项式可以被另一个一元多项式除以，得到一个多项式商和一个多项式余数。例如，

(x⁵ - 1) / (x² - 1) = x³ + x, 余数x – 1

可以通过长除法进行除法。也就是说，将被除数的最高次项除以除数的最高次项。结果是商的第一项。接下来，将结果乘以除数，从被除数中减去，通过递归地将差除以除数来得出答案的其余部分。当除数的次序超过被除数的次序时停止，并声明被除数为余数。此外，如果被除数变为零，返回零作为商和余数。

我们可以设计一个div_poly函数，模仿add_poly和mul_poly的模式。该函数检查两个多项式是否具有相同的变量。如果是这样，div_poly会剥离变量并将问题传递给div_terms，后者在项列表上执行除法操作。div_poly函数最终会将div_terms提供的结果重新附加到变量上。设计div_terms计算除法的商和余数是方便的。div_terms函数可以接受两个项列表作为参数，并返回商项列表和余数项列表的列表。

通过填写缺失的部分来完成div_terms的以下定义。使用这个来实现div_poly，它接受两个多项式作为参数，并返回商和余数多项式的列表。

function div_terms(L1, L2) {
    if (is_empty_termlist(L1)) {
        return list(the_empty_termlist, the_empty_termlist);
    } else {
        const t1 = first_term(L1);
        const t2 = first_term(L2);
        if (order(t2) > order(t1)) {
            return list(the_empty_termlist, L1);
        } else {
            const new_c = div(coeff(t1), coeff(t2));
            const new_o = order(t1) - order(t2);
            const rest_of_result = 〈compute rest of result recursively〉;
            〈form and return complete result〉
        }
    }
}

符号代数中的类型层次结构

我们的多项式系统说明了一个类型的对象（多项式）实际上可能是复杂对象，其中包含许多不同类型的对象作为部分。这在定义通用操作时并不困难。我们只需要为执行复合类型的部分必要操作安装适当的通用操作。事实上，我们看到多项式形成一种“递归数据抽象”，因为多项式的部分本身可能是多项式。我们的通用操作和数据导向的编程风格可以轻松处理这种复杂性。

另一方面，多项式代数是一个数据类型不能自然排列成塔形的系统。例如，可能存在多项式x，其系数是y的多项式。也可能存在多项式y，其系数是x的多项式。这两种类型都没有自然的“上下”关系，然而通常需要将每个集合中的元素相加。有几种方法可以做到这一点。一种可能性是通过扩展和重新排列项，将一个多项式转换为另一个多项式的类型，使得两个多项式具有相同的主要变量。通过对变量进行排序，可以在这个上建立一个类似塔的结构，从而总是将任何多项式转换为一个“规范形式”，其中优先级最高的变量占主导地位，较低优先级的变量被埋在系数中。这种策略效果相当不错，只是转换可能会不必要地扩展多项式，使其难以阅读，也许效率更低。这种塔形策略对于这个领域或者用户可以使用各种组合形式动态地发明新类型的任何领域都不是自然的。例如，三角函数、幂级数和积分。

控制强制转换在大规模代数操作系统的设计中是一个严重的问题并不奇怪。这样的系统的复杂性很大程度上涉及到各种类型之间的关系。事实上，可以说我们还没有完全理解强制转换。事实上，我们甚至还没有完全理解数据类型的概念。然而，我们所知道的为我们提供了强大的结构化和模块化原则，以支持大型系统的设计。

练习 2.92

通过对变量进行排序，扩展多项式包，使得多项式在不同变量中的加法和乘法可以工作。（这并不容易！）

扩展练习：有理函数

我们可以将我们的通用算术系统扩展到包括有理函数。这些是“分数”，其分子和分母都是多项式，例如

该系统应该能够对有理函数进行加法、减法、乘法和除法，并执行诸如

（这里的和已经通过去除公因子来简化。普通的“交叉乘法”会产生一个五次多项式的四次多项式。）

如果我们修改我们的有理算术包，使其使用通用操作，那么它将做我们想要的事情，除了将分数化简为最低项的问题。

练习 2.93

修改有理算术包以使用通用操作，但更改make_rat，使其不尝试将分数化简为最低项。通过调用make_rational在两个多项式上测试您的系统，以生成一个有理函数

const p1 = make_polynomial("x", list(make_term(2, 1), make_term(0, 1)));
const p2 = make_polynomial("x", list(make_term(3, 1), make_term(0, 1)));
const rf = make_rational(p2, p1);

现在使用add将rf加到自身。您会观察到这个加法函数不会将分数化简为最低项。

我们可以使用与整数相同的思想将多项式分数化简为最低项：修改make_rat，将分子和分母都除以它们的最大公约数。对于多项式来说，“最大公约数”的概念是有意义的。事实上，我们可以使用基本上与整数相同的欧几里得算法来计算两个多项式的最大公约数。 ⁵⁷整数版本是

function gcd(a, b) {
    return b === 0
           ? a
           : gcd(b, a % b);
}

使用这个，我们可以做一个明显的修改来定义一个在项列表上工作的 GCD 操作：

function gcd_terms(a, b) {
    return is_empty_termlist(b)
           ? a
           : gcd_terms(b, remainder_terms(a, b));
}

其中remainder_terms选出了由练习 2.91 中实现的项列表除法操作div_terms返回的列表的余项部分。

练习 2.94

使用div_terms，实现函数remainder_terms并使用它来定义gcd_terms。现在编写一个函数gcd_poly来计算两个多项式的多项式 GCD。（如果两个多项式不是在相同的变量上，则该函数应发出错误信号。）在系统中安装一个通用操作greatest_common_divisor，对于多项式，它将简化为gcd_poly，对于普通数字，它将简化为普通的gcd。作为测试，尝试

const p1 = make_polynomial("x", list(make_term(4, 1), make_term(3, -1),
                                     make_term(2, -2), make_term(1, 2)));
const p2 = make_polynomial("x", list(make_term(3, 1), make_term(1, -1)));
greatest_common_divisor(p1, p2);

并通过手动检查您的结果。

练习 2.95

定义P[1]，P[2]和P[3]为多项式

P[1]: x² – 2x + 1

P[2]: 11x² + 7

P[3]: 13x + 5

现在定义Q[1]为P[1]和P[2]的乘积，Q[2]为P[1]和P[3]的乘积，并使用greatest_common_divisor（练习 2.94）来计算Q[1]和Q[2]的 GCD。请注意，答案与P[1]不同。这个例子引入了非整数运算到计算中，导致 GCD 算法出现困难。要理解发生了什么，请尝试在计算 GCD 时跟踪gcd_terms，或者尝试手动进行除法。

如果我们使用以下修改的 GCD 算法（实际上只适用于具有整数系数的多项式），我们可以解决练习 2.95 中展示的问题。在 GCD 计算中进行任何多项式除法之前，我们将被除数乘以一个整数常数因子，选择保证在除法过程中不会出现任何分数。因此，我们的答案将与实际 GCD 相差一个整数常数因子，但在将有理函数化简为最低项时并不重要；GCD 将用于同时除以分子和分母，因此整数常数因子将被抵消。

更准确地说，如果P和Q是多项式，让O[1]是P的阶（即P的最高项的阶），O[2]是Q的阶。让c是Q的首项系数。然后可以证明，如果我们将P乘以整数化因子c^(1+)^O^(1–)^O^(2,)，则所得多项式可以使用div_terms算法除以Q，而不会引入任何分数。将被除数乘以这个常数然后再除以它，有时被称为P除以Q的伪除法。除法的余数称为伪余数。

练习 2.96

a. 实现函数pseudoremainder_terms，它与remainder_terms类似，只是在调用div_terms之前，它会将被除数乘以上面描述的整数化因子。修改gcd_terms以使用pseudoremainder_terms，并验证greatest_common_divisor现在在练习 2.95 中产生具有整数系数的答案。
b. GCD 现在具有整数系数，但它们比P[1]的系数大。修改gcd_terms，以便通过将所有系数除以它们的（整数）最大公约数来删除答案的系数的公共因子。

因此，这是将有理函数化简为最低项的方法：

使用练习 2.96 中的gcd_terms版本计算分子和分母的 GCD。
当获得 GCD 时，在通过 GCD 除以分子和分母之前，将分子和分母都乘以相同的整数化因子，以便通过 GCD 除法不会引入任何非整数系数。作为因子，您可以使用 GCD 的首项系数提高到 1 + O[1] – O[2]的幂，其中O[2]是 GCD 的阶，O[1]是分子和分母的阶的最大值。这将确保通过 GCD 除以分子和分母不会引入任何分数。
这个操作的结果将是一个分子和一个分母，它们都有整数系数。系数通常会非常大，因为所有的整数化因素，所以最后一步是通过计算分子和分母的所有系数的（整数）最大公约数，并通过这个因子除以它来去除冗余因子。

练习 2.97

a. 实现这个算法作为一个函数reduce_terms，它接受两个项列表n和d作为参数，并返回一个列表nn，dd，它们是通过上面给出的算法将n和d化简为最低项。还要编写一个函数reduce_poly，类似于add_poly，它检查两个多项式是否具有相同的变量。如果是这样，reduce_poly会剥离变量并将问题传递给reduce_terms，然后重新将变量附加到reduce_terms提供的两个项列表上。
b. 定义一个类似于reduce_terms的函数，它可以为整数做原始的make_rat所做的事情：
```
function reduce_integers(n, d) {
    const g = gcd(n, d);
    return list(n / g, d / g);
}
```
并定义reduce作为一个通用操作，它调用apply_generic来分派到reduce_poly（对于polynomial参数）或reduce_integers（对于javascript_ number参数）。现在，通过在组合给定的分子和分母形成有理数之前调用reduce，可以轻松地使有理算术包将分数化简为最低项。系统现在可以处理整数或多项式的有理表达式。要测试你的程序，请尝试在这个扩展练习的开头的例子：
```
const p1 = make_polynomial("x", list(make_term(1, 1), make_term(0, 1)));
const p2 = make_polynomial("x", list(make_term(3, 1), make_term(0, -1)));
const p3 = make_polynomial("x", list(make_term(1, 1)));
const p4 = make_polynomial("x", list(make_term(2, 1), make_term(0, -1)));

const rf1 = make_rational(p1, p2);
const rf2 = make_rational(p3, p4);

add(rf1, rf2);
```
看看你是否得到了正确的答案，正确地化简为最低项。

GCD 计算是任何对有理函数进行操作的系统的核心。上面使用的算法，虽然在数学上很直接，但非常慢。这种慢是部分由于大量的除法运算，部分是由于伪除法生成的中间系数的巨大大小。代数操作系统开发中的一个活跃领域是设计更好的算法来计算多项式的最大公约数。

三、模块化、对象和状态

原文：3 Modularity, Objects, and State

译者：飞龙

协议：CC BY-NC-SA 4.0

变化中安宁

（即使它在变化，它仍然保持不变。）

——赫拉克利特

变化越大，越是相同。

——阿方斯·卡尔

前面的章节介绍了构成程序的基本元素。我们看到了原始函数和原始数据是如何组合成复合实体的，我们也了解到抽象对于帮助我们应对大型系统的复杂性是至关重要的。但是这些工具并不足以用于设计程序。有效的程序合成还需要组织原则，可以指导我们制定程序的整体设计。特别是，我们需要策略来帮助我们结构大型系统，使它们成为模块化，也就是说，它们可以被“自然地”划分为可以单独开发和维护的连贯部分。

一种强大的设计策略，特别适用于构建用于建模物理系统的程序，是基于被建模系统的结构来构建程序的结构。对于系统中的每个对象，我们构建一个相应的计算对象。对于每个系统动作，我们在计算模型中定义一个符号操作。我们使用这种策略的希望是，扩展模型以适应新对象或新动作将不需要对程序进行战略性的更改，只需要添加这些对象或动作的新符号模拟。如果我们在系统组织上取得了成功，那么要添加新功能或调试旧功能，我们只需要在系统的局部部分工作。

在很大程度上，我们组织大型程序的方式是由我们对待建模系统的看法所决定的。在本章中，我们将研究两种突出的组织策略，这些策略源自对系统结构的两种相当不同的“世界观”。第一种组织策略集中在对象上，将一个大型系统视为一组随时间可能发生变化的不同对象。另一种组织策略集中在系统中流动的信息流上，就像电气工程师看待信号处理系统一样。

对象为基础的方法和流处理方法都在编程中引发了重大的语言问题。对于对象，我们必须关注计算对象如何改变，但又保持其身份不变。这将迫使我们放弃我们旧的替换计算模型（第 1.1.5 节），转而采用更机械但理论上不太可解的环境模型计算。处理对象、改变和身份的困难是需要在计算模型中处理时间的一个基本结果。当我们允许程序并发执行的可能性时，这些困难变得更加严重。当我们在模型中将模拟时间与计算机在求值过程中发生的事件顺序分离时，流方法可以得到最充分的利用。我们将使用一种称为延迟求值的技术来实现这一点。

3.1 分配和本地状态

我们通常将世界看作由独立的对象组成，每个对象都有随时间变化的状态。如果一个对象的行为受其历史影响，那么就说这个对象“有状态”。例如，银行账户有状态，因为对于问题“我可以取 100 美元吗？”的答案取决于存款和取款交易的历史。我们可以通过一个或多个状态变量来描述对象的状态，这些变量中包含了足够的关于历史的信息，以确定对象的当前行为。在一个简单的银行系统中，我们可以通过当前余额来描述账户的状态，而不是通过记住整个账户交易历史。

在由许多对象组成的系统中，这些对象很少是完全独立的。每个对象可能通过相互作用影响其他对象的状态，这些相互作用将一个对象的状态变量与其他对象的状态变量耦合在一起。事实上，当系统的状态变量可以被分成紧密耦合的子系统，并且这些子系统只与其他子系统松散耦合时，系统由独立对象组成的观点是最有用的。

这种对系统的观点可以是组织系统的计算模型的强大框架。为了使这样的模型具有模块化，它应该被分解成模拟系统中实际对象的计算对象。每个计算对象必须有其自己的本地状态变量来描述实际对象的状态。由于被建模系统中的对象的状态随时间变化，相应计算对象的状态变量也必须改变。如果我们选择通过编程语言中的普通符号名称来模拟系统中的时间流逝，那么语言必须提供赋值操作来使我们能够改变与名称关联的值。

3.1.1 本地状态变量

为了说明我们所说的具有时间变化状态的计算对象，让我们模拟从银行账户中取钱的情况。我们将使用一个名为withdraw的函数来实现这一点，该函数以要提取的amount作为参数。如果账户中有足够的钱来容纳提款，那么withdraw应该返回提款后剩余的余额。否则，withdraw应该返回消息资金不足。例如，如果我们开始

在账户中有 100 美元的情况下，我们应该使用withdraw获得以下响应序列：

withdraw(25);
75

withdraw(25);
50

withdraw(60);
"Insufficient funds"

withdraw(15);
35

注意，表达式withdraw(25)被求值两次，产生不同的值。这是函数的一种新行为。到目前为止，我们所有的 JavaScript 函数都可以被视为计算数学函数的规范。对函数的调用计算了应用于给定参数的函数的值，并且对具有相同参数的同一函数的两次调用总是产生相同的结果。¹

到目前为止，我们所有的名称都是不可变的。当应用函数时，其参数引用的值从不改变，一旦声明被求值，声明的名称就不会改变其值。为了实现像withdraw这样的函数，我们引入了变量声明，它使用关键字let，除了使用关键字const的常量声明。我们可以声明一个变量balance来表示账户中的余额，并将withdraw定义为一个访问balance的函数。withdraw函数检查balance是否至少与请求的amount一样大。如果是，withdraw将balance减去amount并返回balance的新值。否则，withdraw返回资金不足的消息。这是balance和withdraw的声明：

let balance = 100;

function withdraw(amount) {
    if (balance >= amount) {
        balance = balance - amount;
        return balance;
    } else {
        return "Insufficient funds";
    }
}

通过表达式语句来减少balance

balance = balance - amount;

赋值表达式的语法是

name = new-value

这里的name已经用let声明或作为函数参数，并且new-value是任何表达式。赋值改变了name，使得其值是通过求值new-value得到的结果。在这种情况下，我们正在改变balance，使其新值是从先前的balance值中减去amount得到的结果。²

withdraw函数还使用语句序列来导致两个语句在if测试为真的情况下被求值：首先减少balance，然后返回balance的值。一般来说，执行一个序列

stmt[1] stmt[2] ...stmt[n]

导致语句stmt[1]到stmt[n]按顺序进行求值。

尽管withdraw的功能符合预期，但变量balance存在问题。如上所述，balance是程序环境中定义的一个名称，并且可以自由访问和修改。如果我们可以将balance作为withdraw的内部变量，那将会更好，这样withdraw将是唯一可以直接访问balance的函数，任何其他函数只能间接访问balance（通过调用withdraw）。这将更准确地模拟balance是withdraw用来跟踪账户状态的本地状态变量的概念。

我们可以通过以下方式将balance作为withdraw的内部变量来重写定义：

function make_withdraw_balance_100() {
    let balance = 100;
    return amount => {
               if (balance >= amount) {
                   balance = balance - amount;
                   return balance;
               } else {
                   return "Insufficient funds";
               }
           };
}
const new_withdraw = make_withdraw_balance_100();

我们在这里所做的是使用let建立一个具有本地变量balance的环境，绑定到初始值 100。在这个本地环境中，我们使用 lambda 表达式创建一个函数，该函数以amount作为参数，并且像我们之前的withdraw函数一样行为。这个函数——作为make_withdraw_balance_100函数的主体求值的结果返回——行为与withdraw完全相同，但它的变量balance不可被任何其他函数访问。

将赋值与变量声明结合起来是我们用于构建具有本地状态的计算对象的一般编程技术。不幸的是，使用这种技术会引发一个严重的问题：当我们首次引入函数时，我们还引入了求值的替换模型（第 1.1.5 节）来解释函数应用的含义。我们说，应用一个函数，其主体是一个返回语句，应该被解释为用参数的值替换后求值函数的返回表达式。对于主体更复杂的函数，我们需要用参数的值替换来求值整个主体。问题在于，一旦我们在语言中引入赋值，替换就不再是函数应用的充分模型。（我们将在第 3.1.3 节看到为什么会这样。）因此，从技术上讲，我们目前无法理解new_withdraw函数的行为方式。为了真正理解new_withdraw这样的函数，我们需要开发一个新的函数应用模型。在第 3.2 节中，我们将介绍这样一个模型，以及对赋值和变量声明的解释。然而，首先，我们将检查new_withdraw所建立的主题的一些变化。

函数的参数以及使用let声明的名称都是变量。以下函数make_withdraw创建“取款处理器”。make_withdraw中的参数balance指定了账户中的初始金额。

function make_withdraw(balance) {
    return amount => {
               if (balance >= amount) {
                   balance = balance - amount;
                   return balance;
               } else {
                   return "Insufficient funds";
               }
           };
}

函数make_withdraw可以如下使用来创建两个对象W1和W2：

const W1 = make_withdraw(100);
const W2 = make_withdraw(100);

W1(50);
50

W2(70);
30

W2(40);
"Insufficient funds"

W1(40);
10

观察到W1和W2是完全独立的对象，每个对象都有自己的本地状态变量balance。从一个对象中提取不会影响另一个对象。

我们还可以创建处理存款和取款的对象，因此我们可以表示简单的银行账户。以下是一个返回具有指定初始余额的“银行账户对象”的函数：

function make_account(balance) {
    function withdraw(amount) {
        if (balance >= amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    function dispatch(m) {
        return m === "withdraw"
               ? withdraw
               : m === "deposit"
               ? deposit
               : error(m, "unknown request – make_account");
    }
    return dispatch;
}

每次调用make_account都会设置一个具有本地状态变量balance的环境。在此环境中，make_account定义了访问balance的函数deposit和withdraw，以及一个接受“消息”作为输入并返回两个本地函数之一的附加函数dispatch。dispatch函数本身作为代表银行账户对象的值返回。这正是我们在 2.4.3 节中看到的消息传递编程风格，尽管在这里我们将其与修改本地变量的能力结合使用。

函数make_account可以如下使用：

const acc = make_account(100);

acc("withdraw")(50);
50

acc("withdraw")(60);
"Insufficient funds"

acc("deposit")(40);
90

acc("withdraw")(60);
30

每次调用acc都会返回本地定义的deposit或withdraw函数，然后将其应用于指定的amount。与make_withdraw一样，对make_account的另一个调用

const acc2 = make_account(100);

将产生一个完全独立的账户对象，该对象维护其自己的本地balance。

练习 3.1

累加器是一个反复调用的函数，每次只接受一个数字参数并将其累积到总和中。每次调用它时，它都会返回当前累积的总和。编写一个函数make_accumulator，它生成累加器，每个累加器都维护一个独立的总和。make_accumulator的输入应该指定总和的初始值；例如

const a = make_accumulator(5); 

a(10);
15

a(10);
25

练习 3.2

在软件测试应用程序中，能够计算在计算过程中调用给定函数的次数是很有用的。编写一个函数make_monitored，该函数以一个函数f作为输入，该函数本身接受一个输入。make_monitored返回的结果是第三个函数，称为mf，它通过维护内部计数器来跟踪其被调用的次数。如果mf的输入是字符串"how many calls"，那么mf将返回计数器的值。如果输入是字符串"reset count"，那么mf将计数器重置为零。对于任何其他输入，mf返回调用f对该输入的结果并增加计数器。例如，我们可以制作sqrt函数的监视版本：

const s = make_monitored(math_sqrt);

s(100);
10

s("how many calls");
`1`

练习 3.3

修改make_account函数，使其创建受密码保护的账户。也就是说，make_account应该接受一个字符串作为额外的参数，如下所示

const acc = make_account(100, "secret password");

生成的账户对象应该只处理在创建账户时附带的密码，并且否则应该返回投诉：

acc("secret password", "withdraw")(40);
60

acc("some other password", "deposit")(40);
"Incorrect password"

练习 3.4

通过添加另一个本地状态变量修改练习 3.3 的make_account函数，以便如果一个账户连续访问超过七次并且密码不正确，它会调用函数call_the_cops。

3.1.2 引入赋值的好处

正如我们将看到的，将赋值引入我们的编程语言会导致一系列困难的概念问题。然而，将系统视为具有本地状态的对象集合是一种维护模块化设计的强大技术。举一个简单的例子，考虑设计一个函数rand，每次调用该函数时，它都会返回一个随机选择的整数。

“随机选择”是什么意思并不清楚。我们想要的是连续调用rand产生具有均匀分布统计特性的数字序列。我们不会在这里讨论生成适当序列的方法。相反，让我们假设我们有一个函数rand_update，如果我们从给定的数字x[1]开始并形成

`x[2]` = rand_update(`x[1]`);
`x[3]` = rand_update(`x[2]`);

然后值序列x[1], x[2], x[3], ...，将具有所需的统计特性。⁷

我们可以将rand实现为一个带有本地状态变量x的函数，该变量初始化为某个固定值random_init。每次调用rand都会计算x的当前值的rand_update，将其作为随机数返回，并将其存储为x的新值。

function make_rand() {
    let x = random_init;
    return () => {
              x = rand_update(x);
              return x;
           };
}
const rand = make_rand();

当然，我们可以通过直接调用rand_update来生成相同的随机数序列，而不使用赋值。然而，这意味着我们程序的任何部分使用随机数都必须明确记住x的当前值，以便作为rand_update的参数传递。要意识到这将是多么烦人，考虑使用随机数来实现一种称为蒙特卡罗模拟的技术。

蒙特卡罗方法包括从一个大集合中随机选择样本实验，然后根据从这些实验结果制表估计的概率进行推断。例如，我们可以利用6/π²是两个随机选择的整数没有公共因子的概率来*似π；也就是说，它们的最大公约数为 1 的概率。为了获得对π的*似值，我们进行大量实验。在每次实验中，我们随机选择两个整数并进行测试，以查看它们的最大公约数是否为 1。测试通过的次数所占的比例给出了我们对6/π²的估计，从中我们获得了对π的*似值。

我们程序的核心是一个名为monte_carlo的函数，它以尝试实验的次数和实验作为参数，实验表示为每次运行时返回真或假的无参数函数。函数monte_carlo对指定次数的试验运行实验，并返回一个数字，告诉我们实验被发现为真的试验的比例。

function estimate_pi(trials) {
    return math_sqrt(6 / monte_carlo(trials, dirichlet_test));
}
function dirichlet_test() {
    return gcd(rand(), rand()) === 1;
}
function monte_carlo(trials, experiment) {
    function iter(trials_remaining, trials_passed) {
        return trials_remaining === 0
               ? trials_passed / trials
               : experiment()
               ? iter(trials_remaining - 1, trials_passed + 1)
               : iter(trials_remaining - 1, trials_passed);
    }
    return iter(trials, 0);
}

现在让我们尝试使用rand_update直接进行相同的计算，而不是使用rand，这是我们不得不采取的方式，如果我们不使用赋值来模拟局部状态：

function estimate_pi(trials) {
    return math_sqrt(6 / random_gcd_test(trials, random_init));
}
function random_gcd_test(trials, initial_x) {
    function iter(trials_remaining, trials_passed, x) {
        const x1 = rand_update(x);
        const x2 = rand_update(x1);
        return trials_remaining === 0
               ? trials_passed / trials
               : gcd(x1, x2) === 1
               ? iter(trials_remaining - 1, trials_passed + 1, x2)
               : iter(trials_remaining - 1, trials_passed, x2);
    }
    return iter(trials, 0, initial_x);
}

虽然程序仍然很简单，但它暴露了一些痛苦的模块性漏洞。在我们程序的第一个版本中，使用rand，我们可以直接将蒙特卡罗方法表达为一个通用的monte_carlo函数，该函数以任意的experiment函数作为参数。在我们程序的第二个版本中，随机数生成器没有局部状态，random_gcd_test必须明确操作随机数x1和x2，并通过迭代循环将x2重新输入到rand_update中。随机数的显式处理将累积测试结果的结构与我们特定实验使用两个随机数的事实交织在一起，而其他蒙特卡罗实验可能使用一个随机数或三个随机数。甚至顶层函数estimate_pi也必须关注提供初始随机数。随机数生成器的内部泄漏到程序的其他部分，使我们难以将蒙特卡罗思想隔离出来，以便将其应用于其他任务。在程序的第一个版本中，赋值封装了随机数生成器的状态在rand函数内部，使得随机数生成的细节保持独立于程序的其他部分。

蒙特卡洛示例所展示的一般现象是：从复杂过程的某一部分的角度来看，其他部分似乎随时间变化。它们具有隐藏的随时间变化的局部状态。如果我们希望编写的计算机程序的结构反映了这种分解，我们将创建计算对象（例如银行账户和随机数生成器），其行为随时间变化。我们用局部状态变量模拟状态，并用对这些变量的赋值来模拟状态的变化。

通过引入赋值和将状态隐藏在局部变量中的技术，我们可以以比必须通过传递额外参数显式操作所有状态更模块化的方式来构建系统。然而，不幸的是，正如我们将看到的那样，事情并不那么简单。

练习 3.5

蒙特卡洛积分是一种通过蒙特卡洛模拟来估计定积分的方法。考虑计算由谓词P(x, y)描述的空间区域的面积，该谓词对于区域中的点(x, y)为真，对于不在区域中的点为假。例如，以(5, 7)为中心的半径为 3 的圆内的区域由测试(x – 5)² + (y – 7)² = 3²的谓词描述。为了估计由这样一个谓词描述的区域的面积，首先选择一个包含该区域的矩形。例如，对角线在(2, 4)和(8, 10)的矩形包含上述圆。所需的积分是矩形中位于该区域内的部分的面积。我们可以通过随机选择位于矩形中的点(x, y)，并对每个点测试P(x, y)来估计积分。如果我们尝试这样做很多次，那么落在该区域内的点的比例应该给出矩形中位于该区域内的比例的估计。因此，将这个比例乘以整个矩形的面积应该产生积分的估计。

实现蒙特卡洛积分作为一个名为estimate_integral的函数，该函数以谓词P、矩形的上下界x1、x2、y1和y2以及进行估计所需的试验次数作为参数。您的函数应该使用与上面用于估计π的相同的monte_carlo函数。使用您的estimate_integral通过测量单位圆的面积来估计π。

您会发现有一个从给定范围中随机选择一个数字的函数是很有用的。以下的random_in_range函数实现了这一点，它是基于 1.2.6 节中使用的math_random函数实现的，该函数返回小于 1 的非负数。

function random_in_range(low, high) {
    const range = high - low;
    return low + math_random() * range;
}

练习 3.6

能够重置随机数生成器以产生从给定值开始的序列是很有用的。设计一个新的rand函数，它被调用时带有一个参数，该参数是字符串"generate"或字符串"reset"，并且行为如下：rand("generate")产生一个新的随机数；rand("reset")(new-value)将内部状态变量重置为指定的new-value。因此，通过重置状态，可以生成可重复的序列。在测试和调试使用随机数的程序时，这些是非常方便的。

3.1.3 引入赋值的成本

正如我们所看到的，赋值使我们能够模拟具有局部状态的对象。然而，这种优势是有代价的。我们的编程语言不再能够根据我们在 1.1.5 节中介绍的函数应用替换模型来解释。此外，在处理对象和编程语言中的赋值时，没有简单的具有“良好”数学属性的模型可以成为一个足够的框架。

只要我们不使用赋值，对相同参数的同一函数的两次求值将产生相同的结果，因此函数可以被视为计算数学函数。因此，没有使用任何赋值的编程，就像我们在本书的前两章中所做的那样，因此被称为函数式编程。

要理解赋值如何使事情复杂化，考虑 3.1.1 节中make_withdraw函数的简化版本，它不需要检查金额是否不足：

function make_simplified_withdraw(balance) {
    return amount => {
               balance = balance - amount;
               return balance;
           };
}

const W = make_simplified_withdraw(25);

W(20);
5

W(10);
-5

将此函数与不使用赋值的以下make_decrementer函数进行比较：

function make_decrementer(balance) {
   return amount => balance - amount;
}

函数make_decrementer返回一个从指定金额balance中减去其输入的函数，但是在连续调用中没有累积效果，就像make_simplified_withdraw一样：

const D = make_decrementer(25);

D(20);
`5`

D(10);
15

我们可以使用替换模型来解释make_decrementer的工作原理。例如，让我们分析表达式的求值

make_decrementer(25)(20)

我们首先通过在make_decrementer的主体中用 25 替换balance来简化应用的函数表达式。这将表达式简化为

(amount => 25 - amount)(20)

现在我们通过在 lambda 表达式的主体中用 20 替换amount来应用函数：

25 - 20

最终答案是 5。

然而，观察一下，如果我们尝试用make_simplified_withdraw进行类似的替换分析会发生什么：

make_simplified_withdraw(25)(20)

我们首先通过在make_simplified_withdraw的主体中用 25 替换balance来简化函数表达式。这将表达式简化为⁹

(amount => {
    balance = 25 - amount;
    return 25;
})(20)

现在我们通过在 lambda 表达式的主体中用 20 替换amount来应用函数：

balance = 25 - 20;
return 25;

如果我们坚持替换模型，我们将不得不说函数应用的含义是首先将balance设置为 5，然后返回 25 作为表达式的值。这得到了错误的答案。为了得到正确的答案，我们必须以某种方式区分balance的第一次出现（在赋值的效果之前）和balance的第二次出现（在赋值的效果之后），而替换模型无法做到这一点。

这里的问题是，替换基本上是基于这样一个概念，即我们语言中的名称本质上是值的符号。这对常量效果很好。但是，一个变量的值可以随着赋值而改变，不能简单地成为一个值的名称。变量在某种程度上指的是一个值可以被存储的地方，而存储在这个地方的值可以改变。在 3.2 节中，我们将看到环境如何在我们的计算模型中扮演“位置”的角色。

相同和变化

这里出现的问题比计算模型的简单崩溃更加深刻。一旦我们在计算模型中引入变化，许多以前简单明了的概念就变得棘手。考虑两个事物“相同”的概念。

假设我们用相同的参数两次调用make_decrementer来创建两个函数：

const D1 = make_decrementer(25);
const D2 = make_decrementer(25);

D1和D2是相同的吗？一个可以接受的答案是是，因为D1和D2具有相同的计算行为——每个都是从 25 中减去其输入的函数。实际上，D1可以在任何计算中替换为D2而不改变结果。

与此形成对比的是两次调用make_simplified_withdraw：

const W1 = make_simplified_withdraw(25);
const W2 = make_simplified_withdraw(25);

W1和W2是相同的吗？当然不是，因为对W1和W2的调用具有不同的效果，如下交互序列所示：

W1(20);
5

W1(20);
-15

W2(20);
5

即使W1和W2在某种意义上是“相等”的，因为它们都是通过求值相同的表达式make_simplified_withdraw(25)创建的，但并不是说W1可以在任何表达式中替换为W2而不改变表达式的结果。

一个支持“等号可以替换为等号”概念的语言在不改变表达式的值的情况下被称为引用透明。当我们在计算机语言中包含赋值时，引用透明性就会被违反。这使得确定何时可以通过替换等价表达式来简化表达式变得非常棘手。因此，对使用赋值的程序进行推理变得极其困难。

一旦我们放弃了引用透明性，计算对象“相同”的概念就变得难以以正式的方式捕捉。事实上，我们的程序模拟的现实世界中“相同”的含义本身就不太清晰。通常情况下，我们只能通过修改一个对象，然后观察另一个对象是否以相同的方式发生了变化，来确定两个看似相同的对象是否确实是“同一个”。但是，我们如何判断一个对象是否“改变”，除了观察“相同”的对象两次并查看对象的某些属性是否从一次观察到下一次观察发生了变化？因此，我们无法在没有某种先验的“相同”概念的情况下确定“改变”，也无法在没有观察到改变的效果的情况下确定相同。

举个编程中出现这个问题的例子，考虑一下彼得和保罗各自有 100 美元的银行账户的情况。将这种情况建模为

const peter_acc = make_account(100);
const paul_acc = make_account(100);

和将其建模为

const peter_acc = make_account(100);
const paul_acc = peter_acc;

在第一种情况下，两个银行账户是不同的。彼得的交易不会影响保罗的账户，反之亦然。然而，在第二种情况下，我们已经定义paul_acc与peter_acc是同一件事。实际上，彼得和保罗现在有一个联合银行账户，如果彼得从peter_acc中取款，保罗会发现paul_acc中的钱变少。这两种相似但不同的情况可能会在构建计算模型时造成混淆。特别是对于共享账户，令人困惑的是有一个对象（银行账户）有两个不同的名称（peter_acc和paul_acc）；如果我们正在寻找程序中所有可能改变paul_acc的地方，我们必须记得也要查看那些改变peter_acc的地方。¹⁰

关于“相同”和“改变”的上述评论，可以观察到，如果彼得和保罗只能查看他们的银行余额，并且不能执行改变余额的操作，那么两个账户是否不同的问题就没有意义了。一般来说，只要我们不修改数据对象，我们就可以认为复合数据对象恰好是其各部分的总和。例如，有理数是通过给出其分子和分母来确定的。但是，在存在改变的情况下，复合数据对象具有一个与其组成部分不同的“身份”。即使我们通过取款改变了银行账户的余额，银行账户仍然是“相同的”银行账户；反之，我们可以有两个具有相同状态信息的不同银行账户。这种复杂性是我们对银行账户作为一个对象的感知的结果，而不是我们的编程语言的结果。例如，我们通常不将有理数视为具有身份的可变对象，这样我们就可以改变分子但仍然拥有“相同”的有理数。

命令式编程的陷阱

与函数式编程相比，大量使用赋值的编程被称为命令式编程。除了引发关于计算模型的复杂性之外，以命令式风格编写的程序容易出现在函数式程序中不会出现的错误。例如，回想一下 1.2.1 节中的迭代阶乘程序（这里使用条件语句而不是条件表达式）：

function factorial(n) {
    function iter(product, counter) {
        if (counter > n) {
            return product;
        } else {
            return iter(counter * product,
                        counter + 1);
        }
    }
    return iter(1, 1);
}

与在内部迭代循环中传递参数不同，我们可以采用更加命令式的风格，通过显式赋值来更新变量product和counter的值：

function factorial(n) { 
    let product = 1;
    let counter = 1;
    function iter() {
        if (counter > n) {
            return product;
        } else {
            product = counter * product;
            counter = counter + 1;
            return iter();
        }
    }
    return iter();
}

这并不会改变程序产生的结果，但它确实引入了一个微妙的陷阱。我们如何决定赋值的顺序？事实上，程序按照原样编写是正确的。但是，如果将赋值的顺序写反

counter = counter + 1;
product = counter * product;

一般来说，使用赋值进行编程会迫使我们仔细考虑赋值的相对顺序，以确保每个语句都使用了已更改的变量的正确版本。这个问题在函数式程序中根本不会出现。

如果考虑到多个进程同时执行的应用程序，那么命令式程序的复杂性将变得更加糟糕。我们将在第 3.4 节中回到这一点。然而，首先，我们将解决涉及赋值的表达式的计算模型，并探讨在设计模拟中使用具有局部状态的对象的用途。

练习 3.7

考虑make_account创建的银行账户对象，其中包括练习 3.3 中描述的密码修改。假设我们的银行系统需要能够创建联合账户。定义一个名为make_joint的函数来实现这一点。函数make_joint应该有三个参数。第一个是受密码保护的账户。第二个参数必须与账户定义时的密码匹配，才能进行make_joint操作。第三个参数是一个新密码。函数make_joint将使用新密码创建对原始账户的额外访问。例如，如果peter_acc是一个密码为"open sesame"的银行账户，则

const paul_acc = make_joint(peter_acc, "open sesame", "rosebud");

将允许使用名称paul_acc和密码"rosebud"在peter_acc上进行交易。您可能希望修改您对练习 3.3 的解决方案，以适应这一新功能。

练习 3.8

当我们在第 1.1.3 节中定义了求值模型时，我们说求值表达式的第一步是求值其子表达式。但我们从未指定子表达式应该以何种顺序进行求值（例如，从左到右还是从右到左）。当我们引入赋值时，操作符组合的操作数的求值顺序可能会影响结果。定义一个简单的函数f，使得求值f(0) + f(1)将返回 0，如果+的操作数从左到右进行求值，但如果操作数从右到左进行求值，则返回 1。

3.2 求值的环境模型

当我们在第 1 章介绍了复合函数时，我们使用了求值的替换模型（第 1.1.5 节）来定义应用函数到参数的含义：

要将复合函数应用到参数上，用相应的参数替换每个参数后，求值函数的返回表达式（更一般地说，是主体）。

一旦我们允许在我们的编程语言中进行赋值，这样的定义就不再合适。特别是，第 3.1.3 节认为，在存在赋值的情况下，一个名称不能仅仅被认为是代表一个值。相反，一个名称必须以某种方式指定一个“位置”，在这个位置中值可以被存储。在我们的新的求值模型中，这些位置将被维护在称为环境的结构中。

环境是一个帧的序列。每个帧都是一个绑定（可能为空）的表，它将名称与相应的值关联起来。（单个帧最多可以包含一个名称的绑定。）每个帧还有一个指向其封闭环境的指针，除非出于讨论的目的，该帧被认为是全局的。与环境相关的名称的值是由环境中包含该名称的第一个帧中的绑定给出的值。如果序列中的任何帧都没有为名称指定绑定，则称该名称在环境中是未绑定的。

图 3.1 显示了一个简单的环境结构，由三个标记为 I、II 和 III 的框架组成。在图中，A、B、C 和 D 是指向环境的指针。C 和 D 指向相同的环境。名称z和x在框架 II 中绑定，而y和x在框架 I 中绑定。环境 D 中x的值为 3。相对于环境 B，x的值也是 3。这是这样确定的：我们检查序列中的第一个框架（框架 III），并没有找到x的绑定，所以我们继续到封闭的环境 D，并在框架 I 中找到了绑定。另一方面，相对于环境 A，x的值为 7，因为序列中的第一个框架（框架 II）包含了x绑定到 7。相对于环境 A，框架 II 中x绑定到 7 被称为屏蔽了框架 I 中x绑定到 3。

图 3.1 一个简单的环境结构。

环境对于求值过程至关重要，因为它决定了表达式应该在其中环境中进行求值的上下文。事实上，可以说编程语言中的表达式本身并没有任何意义。相反，表达式只有在某个环境中进行求值时才会获得意义。甚至对于像display(1)这样直接的表达式的解释也取决于理解在其中名称display指的是显示值的原始函数的上下文。因此，在我们的求值模型中，我们将始终讨论相对于某个环境求值表达式。为了描述与解释器的交互，我们假设存在一个全局环境，由一个单一框架（没有封闭环境）组成，其中包括与原始函数相关联的名称的值。例如，display是原始显示函数的名称的想法被捕捉为名称display在全局环境中绑定到原始显示函数。

在求值程序之前，我们在全局环境中添加一个新框架，即程序框架，得到程序环境。我们将程序顶层声明的名称添加到这个框架中，这些名称在任何块之外声明。然后，给定的程序将相对于程序环境进行求值。

3.2.1 求值规则

解释器求值函数应用的整体规范与我们在第 1.1.4 节首次介绍时保持一致：

要求值一个应用：
1. 1. 求值应用的子表达式。¹²
2. 2. 将函数子表达式的值应用于参数子表达式的值。

求值环境模型取代了替换模型，以指定将复合函数应用于参数的含义。

在求值环境模型中，函数始终是一个由一些代码和指向环境的指针组成的对。函数只能通过求值 lambda 表达式来创建。这会产生一个函数，其代码是从 lambda 表达式的文本中获取的，其环境是求值 lambda 表达式以产生函数的环境。例如，考虑函数声明

function square(x) {
    return x * x;
}

在程序环境中求值。函数声明语法等同于底层的隐式 lambda 表达式。使用¹³也是等效的

const square = x => x * x;

这将求值x => x * x并将square绑定到结果值，都在程序环境中。

图 3.2 显示了求值此声明语句的结果。全局环境包含程序环境。为了减少混乱，在此图之后，我们将不显示全局环境（因为它总是相同的），但是通过从程序环境向上的指针来提醒我们它的存在。函数对象是一个对，其代码指定函数有一个参数，即x，和一个函数体return x * x;。函数的环境部分是指向程序环境的指针，因为这是求值 lambda 表达式以生成函数的环境。一个新的绑定，将函数对象与名称square关联起来，已添加到程序帧中。

图 3.2 在程序环境中求值function square(x) { return x * x; }所产生的环境结构。

一般来说，const，function和let会向帧中添加绑定。常量不允许赋值，因此我们的环境模型需要区分指向常量的名称和指向变量的名称。我们通过在名称后面的冒号后写一个等号来表示名称是常量。我们认为函数声明等同于常量声明；请参见图 3.2 中冒号后的等号。

现在我们已经看到了函数是如何创建的，我们可以描述函数是如何应用的。环境模型指定：要将函数应用于参数，创建一个新的环境，其中包含一个将参数绑定到参数值的帧。此帧的封闭环境是函数指定的环境。现在，在这个新环境中，求值函数体。

为了展示这条规则是如何遵循的，图 3.3 说明了在程序环境中求值表达式square(5)所创建的环境结构，其中square是在图 3.2 中生成的函数。应用函数会导致创建一个新的环境，图中标记为 E1，它以一个帧开始，其中函数的参数x绑定到参数 5。请注意，环境 E1 中的名称x后面跟着一个冒号，没有等号，这表明参数x被视为变量。从这个帧向上指的指针显示了帧的封闭环境是程序环境。这里选择程序环境，因为这是square函数对象的一部分所指示的环境。在 E1 中，我们求值函数体，return x * x;。由于 E1 中x的值是 5，结果是5 * 5，即 25。

图 3.3 在程序环境中求值square(5)所创建的环境。

函数应用的环境模型可以总结为两条规则：

通过构建一个帧，将函数的参数绑定到调用的参数，然后在构建的新环境的上下文中求值函数体，将函数对象应用于一组参数。新帧的封闭环境是被应用的函数对象的环境部分。应用的结果是在求值函数体时遇到的第一个return语句的返回表达式的结果。
通过在给定环境中求值 lambda 表达式来创建函数。生成的函数对象是一个对，包括 lambda 表达式的文本和指向创建函数的环境的指针。

最后，我们指定了赋值的行为，这个操作迫使我们首先引入环境模型。在某个环境中求值表达式name = value会找到环境中名称的绑定。也就是说，找到环境中包含名称绑定的第一个框架。如果绑定是变量绑定——在框架中名称后面只有:表示——那么该绑定将被更改以反映变量的新值。否则，如果框架中的绑定是常量绑定——在名称后面由:=表示——赋值会发出“对常量赋值”的错误。如果环境中的名称未绑定，则赋值会发出“变量未声明”的错误。

这些求值规则虽然比替换模型复杂得多，但仍然相当简单。此外，求值模型虽然抽象，但提供了解释器如何求值表达式的正确描述。在第 4 章中，我们将看到这个模型如何作为实现工作解释器的蓝图。以下各节通过分析一些说明性程序详细阐述了该模型的细节。

3.2.2 应用简单函数

当我们在 1.1.5 节介绍了替换模型时，我们展示了应用f(5)的求值结果为 136，给定以下函数声明：

function square(x) {
    return x * x;
}
function sum_of_squares(x, y) {
    return square(x) + square(y);
}
function f(a) {
    return sum_of_squares(a + 1, a * 2);
}

我们可以使用环境模型分析相同的例子。图 3.4 显示了通过在程序环境中求值f，square和sum_of_squares的定义而创建的三个函数对象。每个函数对象由一些代码组成，以及指向程序环境的指针。

图 3.4 程序框架中的函数对象。

在图 3.5 中，我们看到通过求值表达式f(5)创建的环境结构。对f的调用创建了一个新的环境 E1，从一个框架开始，其中f的参数a绑定到参数 5。在 E1 中，我们求值f的主体：

return sum_of_squares(a + 1, a * 2);

图 3.5 通过使用图 3.4 中的函数求值f(5)而创建的环境。

为了求值返回语句，我们首先求值返回表达式的子表达式。第一个子表达式sum_of_squares的值是一个函数对象。（注意如何找到这个值：我们首先查找 E1 的第一个框架，其中不包含sum_of_squares的绑定。然后我们继续到封闭环境，即程序环境，并找到图 3.4 中显示的绑定。）其他两个子表达式通过应用原始操作+和*来求值两个组合a + 1和a * 2，分别获得 6 和 10。

现在我们将函数对象sum_of_squares应用于参数 6 和 10。这将导致一个新的环境 E2，其中参数x和y绑定到参数。在 E2 中，我们求值语句

return square(x) + square(y);

这导致我们求值square(x)，其中square在程序框架中找到，x为 6。再次，我们建立一个新的环境 E3，在其中x绑定到 6，并在其中求值square的主体，即return x * x;。同样作为应用sum_of_squares的一部分，我们必须求值子表达式square(y)，其中y为 10。对square的第二次调用创建了另一个环境 E4，在其中square的参数x绑定到 10。在 E4 中，我们必须求值return x * x;。

需要注意的重要一点是，每次调用square都会创建一个包含x绑定的新环境。我们可以在这里看到不同的帧是如何保持分开的不同的名为x的本地变量的。请注意，square创建的每个帧都指向程序环境，因为这是square函数对象指定的环境。

在子表达式被求值之后，结果被返回。square的两次调用生成的值被sum_of_squares相加，这个结果被f返回。由于我们这里的重点是环境结构，我们不会详细讨论这些返回值是如何从调用传递到调用的；然而，这也是求值过程的一个重要方面，我们将在第 5 章中详细讨论它。

练习 3.9

在 1.2.1 节中，我们使用替换模型来分析两个计算阶乘的函数，一个是递归版本

function factorial(n) {
    return n === 1
           ? 1
           : n * factorial(n - 1);
}

和迭代版本

function factorial(n) {
    return fact_iter(1, 1, n);
}
function fact_iter(product, counter, max_count) {
    return counter > max_count
           ? product
           : fact_iter(counter * product,
                       counter + 1,
                       max_count);
}

展示了使用factorial函数的每个版本来求值factorial(6)的环境结构。¹⁶

3.2.3 帧作为本地状态的存储库

我们可以转向环境模型，看看如何使用函数和赋值来表示具有本地状态的对象。例如，考虑通过调用函数创建的“取款处理器”（来自第 3.1.1 节）

function make_withdraw(balance) {
    return amount => {
               if (balance >= amount) {
                   balance = balance - amount;
                   return balance;
               } else {
                   return "insufficient funds";
               }
           };
}

让我们描述一下

const W1 = make_withdraw(100);

接着

W1(50);
50

图 3.6 显示了在程序环境中声明make_withdraw函数的结果。这产生了一个包含指向程序环境的指针的函数对象。到目前为止，这与我们已经看到的例子没有什么不同，只是函数主体中的返回表达式本身是一个 lambda 表达式。

图 3.6 在程序环境中定义make_withdraw的结果。

当我们将函数make_withdraw应用到一个参数时，计算的有趣部分发生了：

const W1 = make_withdraw(100);

我们通常是通过设置环境 E1 来开始的，在这个环境中，参数balance绑定到参数 100。在这个环境中，我们求值make_withdraw的主体，即返回语句，其返回表达式是一个 lambda 表达式。对这个 lambda 表达式的求值构造了一个新的函数对象，其代码由 lambda 表达式指定，其环境是 E1，lambda 表达式被求值以产生函数的环境。由对make_withdraw的调用返回的结果是这个函数对象。由于常量声明本身是在程序环境中被求值的，所以它在程序环境中绑定到W1。图 3.7 显示了生成的环境结构。

图 3.7 求值const W1 = make_withdraw(100);的结果。

现在我们可以分析当W1应用到一个参数时会发生什么：

W1(50);
50

我们首先构建一个帧，在这个帧中，W1的参数amount绑定到参数 50。需要注意的关键点是，这个帧的封闭环境不是程序环境，而是环境 E1，因为这是由W1函数对象指定的环境。在这个新环境中，我们求值函数的主体：

if (balance >= amount) {
    balance = balance - amount;
    return balance;
} else {
    return "insufficient funds";
}

生成的环境结构如图 3.8 所示。正在求值的表达式引用了amount和balance。变量amount将在环境中的第一个帧中找到，而balance将通过跟随封闭环境指针到 E1 中找到。

图 3.8 应用函数对象W1创建的环境。

当执行赋值时，E1 中balance的绑定被更改。在调用W1完成时，balance为 50，并且仍然由函数对象W1指向包含balance的帧。绑定amount的帧（我们执行了更改balance的代码）不再相关，因为构造它的函数调用已经终止，并且没有来自环境其他部分的指针指向该帧。下次调用W1时，这将构建一个绑定amount的新帧，其封闭环境为 E1。我们看到 E1 充当了为函数对象W1保存局部状态变量的“位置”。图 3.9 显示了调用W1后的情况。

图 3.9 调用W1后的环境。

观察当我们通过再次调用make_withdraw创建第二个withdraw对象时会发生什么：

const W2 = make_withdraw(100);

这产生了图 3.10 中的环境结构，显示W2是一个函数对象，即一个带有一些代码和一个环境的对。W2的环境 E2 是通过调用make_withdraw创建的。它包含一个带有自己的局部绑定balance的帧。另一方面，W1和W2具有相同的代码：make_withdraw主体中 lambda 表达式指定的代码。¹⁷我们在这里看到了为什么W1和W2表现为独立对象。对W1的调用引用存储在 E1 中的状态变量balance，而对W2的调用引用 E2 中存储的balance。因此，对一个对象的局部状态的更改不会影响另一个对象。

图 3.10 使用const W2 = make_withdraw(100);创建第二个对象。

练习 3.10

在make_withdraw函数中，局部变量balance作为make_withdraw的参数创建。我们还可以使用我们可以称之为立即调用的 lambda 表达式单独创建局部状态变量，如下所示：

function make_withdraw(initial_amount) {
    return (balance =>
              amount => {
                  if (balance >= amount) {
                      balance = balance - amount;
                      return balance;
                   } else {
                      return "insufficient funds";
                   }
              })(initial_amount);
}

外部 lambda 表达式在求值后立即被调用。它的唯一目的是创建一个名为balance的局部变量，并将其初始化为initial_amount。使用环境模型分析make_withdraw的这个替代版本，绘制类似上面的图形以说明交互。

const W1 = make_withdraw(100);

W1(50);

const W2 = make_withdraw(100);

展示make_withdraw的两个版本创建具有相同行为的对象。这两个版本的环境结构有何不同？

3.2.4 内部声明

在本节中，我们处理包含声明的函数体或其他块（例如条件语句的分支）。每个块为在块中声明的名称打开一个新的作用域。为了在给定环境中求值一个块，我们通过一个包含在块的主体中直接声明的所有名称的新帧来扩展该环境，然后在新构建的环境中求值主体。

1.1.8 节介绍了函数可以具有内部声明的概念，从而导致块结构，如下面的函数计算*方根：

function sqrt(x) {
   function is_good_enough(guess) {
      return abs(square(guess) - x) < 0.001;
   }
   function improve(guess) {
      return average(guess, x / guess);
   }
   function sqrt_iter(guess){
      return is_good_enough(guess)
             ? guess
             : sqrt_iter(improve(guess));
   }
   return sqrt_iter(1);
}

现在我们可以使用环境模型来看为什么这些内部声明的行为符合预期。图 3.11 显示了在求值表达式sqrt(2)时，内部函数is_good_enough首次被调用，其中guess等于 1。

图 3.11 带有内部声明的sqrt函数。

观察环境的结构。名称sqrt在程序环境中绑定到一个函数对象，其关联的环境是程序环境。当调用sqrt时，形成了一个新的环境 E1，它是程序环境的下属，在其中参数x绑定到 2。然后在 E1 中求值了sqrt的主体。该主体是一个带有本地函数声明的块，因此 E1 被扩展为这些声明的新框架，导致新的环境 E2。然后在 E2 中求值了该块的主体。由于主体中的第一条语句是...

function is_good_enough(guess) {
    return abs(square(guess) - x) < 0.001;
}

求值此声明在环境 E2 中创建了函数is_good_enough。更准确地说，E2 中的第一个框架中的名称is_good_enough绑定到一个函数对象，其关联的环境是 E2。类似地，improve和sqrt_iter在 E2 中被定义为函数。为简洁起见，图 3.11 仅显示了is_good_enough的函数对象。

在定义了本地函数之后，仍然在环境 E2 中求值了表达式sqrt_iter(1)。因此，在环境 E2 中绑定到sqrt_iter的函数对象被调用，并以 1 作为参数。这创建了一个环境 E3，在其中sqrt_iter的参数guess绑定到 1。然后sqrt_iter调用is_good_enough，并以guess的值（来自 E3）作为is_good_enough的参数。这建立了另一个环境 E4，在其中is_good_enough的参数guess绑定到 1。尽管sqrt_iter和is_good_enough都有一个名为guess的参数，但这些是位于不同框架中的两个不同的本地变量。此外，E3 和 E4 都将 E2 作为其封闭环境，因为sqrt_iter和is_good_enough函数都将 E2 作为其环境部分。这的一个结果是is_good_enough主体中出现的名称x将引用 E1 中出现的x的绑定，即调用原始sqrt函数时的x的值。

因此，环境模型解释了使本地函数声明成为模块化程序的两个关键属性。

本地函数的名称不会干扰封闭函数之外的名称，因为当块在求值时，本地函数名称将绑定在创建时的框架中，而不是绑定在程序环境中。
本地函数可以通过使用参数名称作为自由名称来访问封闭函数的参数。这是因为本地函数的主体在比封闭函数的求值环境低的环境中进行求值。

练习 3.11

在 3.2.3 节中，我们看到环境模型如何描述具有本地状态的函数的行为。现在我们已经看到了内部声明的工作原理。典型的消息传递函数包含了这两个方面。考虑 3.1.1 节中的银行账户函数：

function make_account(balance) {
    function withdraw(amount) {
        if (balance >= amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    function dispatch(m) {
        return m === "withdraw"
               ? withdraw
               : m === "deposit"
               ? deposit
               : "Unknown request: make_account";
    }
    return dispatch;
}

展示由交互序列生成的环境结构

const acc = make_account(50);

acc("deposit")(40);
90

acc("withdraw")(60);
30

acc的本地状态在哪里保存？假设我们定义另一个帐户。

const acc2 = make_account(100);

如何保持两个帐户的本地状态不同？acc和acc2之间共享环境结构的哪些部分？

3.3 用可变数据建模

第 2 章讨论了复合数据作为构建计算对象的手段，这些对象有几个部分，以模拟具有多个方面的现实世界对象。在该章中，我们介绍了数据抽象的学科，根据这一学科，数据结构是根据构造函数来指定的，构造函数创建数据对象，选择器访问复合数据对象的部分。但是现在我们知道第 2 章没有涉及的数据的另一个方面。希望模拟由具有不断变化状态的对象组成的系统，这导致我们需要修改复合数据对象，以及构造和从中选择。为了模拟具有不断变化状态的复合对象，我们将设计数据抽象，以包括除选择器和构造函数之外的操作，称为变异器，这些操作修改数据对象。例如，模拟银行系统需要我们改变账户余额。因此，用于表示银行账户的数据结构可能允许一个操作

set_balance(account, new-value)

更改指定帐户的余额为指定的新值的操作。定义了突变器的数据对象称为可变数据对象。

第 2 章介绍了对偶对作为合成复合数据的通用“粘合剂”。我们从定义对偶对的基本突变器开始这一部分，以便对偶对可以作为构造可变数据对象的构建块。这些突变器极大地增强了对偶对的表示能力，使我们能够构建除了我们在第 2.2 节中使用的序列和树之外的数据结构。我们还提供了一些模拟的示例，其中复杂系统被建模为具有局部状态的对象集合。

3.3.1 可变列表结构

对对的基本操作——pair、head和tail——可以用来构造列表结构和从列表结构中选择部分，但它们无法修改列表结构。到目前为止，我们使用的列表操作也是如此，比如append和list，因为这些可以用pair、head和tail来定义。要修改列表结构，我们需要新的操作。

对于对来说，原始的修改器是set_head和set_tail。函数set_head接受两个参数，第一个参数必须是对。它修改这个对，用set_head的第二个参数的指针替换head指针。¹⁹

例如，假设x绑定到list(list("a", "b"), "c", "d")，y绑定到list("e", "f")，如图 3.12 所示。求值表达式set_head(x, y)修改了x绑定的对，用y的值替换了它的head。操作的结果如图 3.13 所示。结构x已被修改，现在等价于list(list("e", "f"), "c", "d")。代表列表list("a", "b")的对，由被替换的指针标识，现在已从原始结构中分离。²⁰

图 3.12 列表x：list(list("a", "b"), "c", "d")和y：list("e", "f")。

图 3.13 set_head(x, y)对图 3.12 中的列表的影响。

将图 3.13 与图 3.14 进行比较，它说明了执行的结果

const z = pair(y, tail(x));

x和y绑定到图 3.12 中的原始列表。现在，名称z绑定到由pair操作创建的新对；x绑定的列表保持不变。set_tail操作类似于set_head。唯一的区别是用tail指针替换对的head指针。在图 3.12 中执行set_tail(x, y)的效果如图 3.15 所示。这里，x的tail指针已被替换为指向list("e", "f")。此外，曾经是x的tail的列表list("c", "d")现在已从结构中分离。

图 3.14 const z = pair(y, tail(x));对图 3.12 中的列表的影响。

图 3.15 set_tail(x, y)对图 3.12 中的列表的影响。

函数pair通过创建新的对来构建新的列表结构，而set_head和set_tail修改现有的对。事实上，我们可以使用这两个修改器来实现pair，再加上一个get_new_pair函数，它返回一个不属于任何现有列表结构的新对。我们获得新对，将其head和tail指针设置为指定的对象，并将新对作为pair的结果返回。²¹

function pair(x, y) {
    const fresh = get_new_pair();
    set_head(fresh, x);
    set_tail(fresh, y);
    return fresh;
}

练习 3.12

在 2.2.1 节中引入了以下用于追加列表的函数：

function append(x, y) {
    return is_null(x)
           ? y
           : pair(head(x), append(tail(x), y));
}

函数append通过将x的元素依次添加到y的前面来形成一个新的列表。函数append_mutator类似于append，但它是一个修改器而不是构造器。它通过将它们拼接在一起来追加列表，修改x的最后一个对，使其tail现在是y。（使用空的x调用append_mutator是一个错误。）

function append_mutator(x, y) {
    set_tail(last_pair(x), y);
    return x;
}

这里last_pair是一个返回其参数中的最后一个对的函数：

function last_pair(x) {
    return is_null(tail(x))
          ? x
          : last_pair(tail(x));
}

考虑交互

const x = list("a", "b");

const y = list("c", "d");

const z = append(x, y);

z;
["a", ["b", ["c", ["d, null]]]]

tail(x);
response

const w = append_mutator(x, y);

w;
["a", ["b", ["c", ["d", null]]]]

tail(x);
response

缺少的response是什么？绘制框和指针图来解释你的答案。

练习 3.13

考虑以下make_cycle函数，它使用了练习 3.12 中定义的last_pair函数：

function make_cycle(x) {
    set_tail(last_pair(x), x);
    return x;
}

绘制一个框和指针图，显示由z创建的结构

const z = make_cycle(list("a", "b", "c"));

如果我们尝试计算last_pair(z)会发生什么？

练习 3.14

以下功能非常有用，尽管有些晦涩：

function mystery(x) {
    function loop(x, y) {
        if (is_null(x)) {
            return y;
        } else {
            const temp = tail(x);
            set_tail(x, y);
            return loop(temp, x);
        }
    }
    return loop(x, null);
}

函数loop使用“临时”名称temp来保存x的tail的旧值，因为下一行的set_tail会破坏tail。解释mystery一般是做什么的。假设v由以下定义

const v = list("a", "b", "c", "d");

绘制代表v绑定的列表的框和指针图。假设我们现在求值

const w = mystery(v);

绘制框和指针图，显示在求值此程序后v和w的结构。v和w的值将打印为什么？

共享和身份

我们在 3.1.3 节中提到了由赋值引入的“相同”和“改变”的理论问题。当不同的数据对象之间共享个别成对时，这些问题在实践中会出现。例如，考虑以下结构形成的结构

const x = list("a", "b");
const z1 = pair(x, x);

如图 3.16 所示，z1是一个head和tail都指向同一个x的成对。z1的head和tail共享x是pair实现的直接方式的结果。一般来说，使用pair构造列表将导致成对的交织结构，其中许多单个成对被许多不同的结构共享。

图 3.16 由pair(x, x)形成的列表z1。

与图 3.16 相比，图 3.17 显示了由此创建的结构

const z2 = pair(list("a", "b"), list("a", "b"));

在这个结构中，两个list("a", "b")列表中的成对是不同的，尽管它们包含相同的字符串。²²

图 3.17 由pair(list("a", "b"), list("a", "b"))形成的列表z2。

当被视为列表时，z1和z2都代表“相同”的列表：

list(list("a", "b"), "a", "b")

一般来说，如果我们只使用pair，head和tail在列表上操作，共享是完全不可检测的。但是，如果我们允许在列表结构上使用变异器，共享就变得重要。作为共享可能产生的差异的一个例子，考虑以下函数，该函数修改了应用于它的结构的head：

function set_to_wow(x) {
    set_head(head(x), "wow");
    return x;
}

尽管z1和z2是“相同”的结构，但将set_to_wow应用于它们会产生不同的结果。对于z1，改变head也会改变tail，因为在z1中head和tail是相同的成对。对于z2，head和tail是不同的，因此set_to_wow只修改head：

z1;
[["a", ["b", null]], ["a", ["b", null]]]

set_to_wow(z1);
[["wow", ["b", null]], ["wow", ["b", null]]]

z2;
[["a", ["b", null]], ["a", ["b", null]]]

set_to_wow(z2);
[["wow", ["b", null]], ["a", ["b", null]]]

检测列表结构中的共享的一种方法是使用原始谓词===，我们在 1.1.6 节中引入了它来测试两个数字是否相等，并在 2.3.1 节中扩展了它来测试两个字符串是否相等。当应用于两个非原始值时，x === y测试x和y是否是相同的对象（即x和y是否作为指针相等）。因此，对于图 3.16 和 3.17 中定义的z1和z2，head(z1) === tail(z1)为真，head(z2) === tail(z2)为假。

如下一节所示，我们可以利用共享来大大扩展可以由成对表示的数据结构的范围。另一方面，共享也可能是危险的，因为对结构所做的修改也会影响其他恰好共享修改部分的结构。变异操作set_head和set_tail应该谨慎使用；除非我们对数据对象的共享有很好的理解，否则变异可能会产生意想不到的结果。²³

练习 3.15

绘制框和指针图，解释set_to_wow对上述z1和z2结构的影响。

练习 3.16

Ben Bitdiddle 决定编写一个函数来计算任何列表结构中的成对数。“很容易”，他推理道。“任何结构中的成对数是head中的数加上tail中的数再加一来计算当前的成对数。”于是 Ben 写下了以下函数

function count_pairs(x) {
    return ! is_pair(x)
           ? 0
           : count_pairs(head(x)) +
             count_pairs(tail(x)) + 1;
}

展示这个函数是不正确的。特别是，绘制盒和指针图，表示由恰好三对组成的列表结构，Ben 的函数将返回 3；返回 4；返回 7；根本不返回。

练习 3.17

设计练习 3.16 中count_pairs函数的正确版本，该函数返回任何结构中不同对的数量。（提示：遍历结构，维护一个辅助数据结构，用于跟踪已经计数的对。）

练习 3.18

编写一个函数，检查列表并确定它是否包含循环，也就是说，一个试图通过连续的tail找到列表末尾的程序会进入无限循环。练习 3.13 构建了这样的列表。

练习 3.19

使用仅占用恒定空间的算法重新执行练习 3.18。（这需要一个非常聪明的想法。）

突变只是赋值

当我们引入复合数据时，我们在 2.1.3 节中观察到，对可以纯粹用函数表示：

function pair(x, y) {
    function dispatch(m) {
    return m === "head"
           ? x
           : m === "tail"
           ? y
           : error(m, "undefined operation – pair");
    }
    return dispatch;
}
function head(z) { return z("head"); }
function tail(z) { return z("tail"); }

对于可变数据，同样的观察是正确的。我们可以使用赋值和本地状态将可变数据对象实现为函数。例如，我们可以扩展上面的对实现，以处理set_head和set_tail，类似于我们在 3.1.1 节中使用make_account实现银行账户的方式：

function pair(x, y) {
    function set_x(v) { x = v; }
    function set_y(v) { y = v; }
    return m => m === "head"
                ? x
                : m === "tail"
                ? y
                : m === "set_head"
                ? set_x
                : m === "set_tail"
                ? set_y
                : error(m, "undefined operation – pair");
}
function head(z) { return z("head"); }
function tail(z) { return z("tail"); }
function set_head(z, new_value) {
    z("set_head")(new_value);
    return z;
}
function set_tail(z, new_value) {
    z("set_tail")(new_value);
    return z;
}

理论上，只需要赋值就可以解释可变数据的行为。一旦我们承认在我们的语言中进行赋值，我们就提出了所有问题，不仅是赋值的问题，而且是可变数据的问题。²⁴

练习 3.20

绘制环境图来说明语句序列的求值

const x = pair(1, 2);
const z = pair(x, x);
set_head(tail(z), 17);

head(x);
17

使用上面给出的对的函数实现。（比较练习 3.11。）

3.3.2 表示队列

改变器set_head和set_tail使我们能够使用对来构建不能仅用pair、head和tail构建的数据结构。本节展示了如何使用对来表示称为队列的数据结构。3.3.3 节将展示如何表示称为表的数据结构。

队列是一个序列，其中项目被插入到一端（称为队列的后端），并从另一端（前端）删除。图 3.18 显示了一个最初为空的队列，其中插入了项目a和b。然后移除了a，插入了c和d，并移除了b。因为项目总是按照插入的顺序移除，所以队列有时被称为FIFO（先进先出）缓冲区。

图 3.18 队列操作。

在数据抽象方面，我们可以将队列视为以下一组操作定义：

一个构造器：

make_queue()

返回一个空队列（不包含任何项目的队列）。
一个谓词：

is_empty_queue(queue)

测试队列是否为空。
一个选择器：

front_queue(queue)

返回队列前端的对象，如果队列为空则发出错误信号；它不修改队列。
两个改变器：

insert_queue(queue, item)

在队列的后端插入项目，并将修改后的队列作为其值返回。

delete_queue(queue)

移除队列前端的项目，并返回修改后的队列作为其值，如果在删除前队列为空，则发出错误信号。

因为队列是一系列项目，我们当然可以将其表示为普通列表；队列的前端将是列表的head，在队列中插入项目将相当于在列表末尾添加一个新元素，从队列中删除项目只是取列表的tail。然而，这种表示是低效的，因为为了插入一个项目，我们必须扫描列表直到达到末尾。由于我们扫描列表的唯一方法是通过连续的tail操作，因此对于n个项目的列表，这种扫描需要Θ(n)步骤。通过对列表表示的简单修改，可以克服这个缺点，使得队列操作可以实现为需要Θ(1)步骤；也就是说，需要的步骤数与队列的长度无关。

列表表示的困难之处在于需要扫描以找到列表的末尾。我们需要扫描的原因是，尽管将列表表示为一对对的链表是标准的方法，它很容易为我们提供指向列表开头的指针，但它并没有为我们提供指向末尾的指针。避免这个缺点的修改是将队列表示为列表，以及一个额外的指针，指示列表中的最后一对。这样，当我们要插入一个项目时，我们可以查看后指针，从而避免扫描列表。

然后，队列表示为一对指针，front_ptr和rear_ptr，分别指示普通列表中的第一对和最后一对。由于我们希望队列是一个可识别的对象，我们可以使用pair来组合这两个指针。因此，队列本身将是这两个指针的pair。图 3.19 说明了这种表示。

图 3.19 将队列实现为具有前端和后端指针的列表。

为了定义队列操作，我们使用以下函数，这些函数使我们能够选择和修改队列的前端和后端指针：

function front_ptr(queue) { return head(queue); }
function rear_ptr(queue) { return tail(queue); }
function set_front_ptr(queue, item) { set_head(queue, item); }
function set_rear_ptr(queue, item) { set_tail(queue, item); }

现在我们可以实现实际的队列操作。如果队列的前端指针是空列表，我们将考虑队列为空：

function is_empty_queue(queue) { return is_null(front_ptr(queue)); }

make_queue构造函数返回一个最初为空的队列，其head和tail都是空列表：

function make_queue() { return pair(null, null); }

要选择队列前端的项目，我们返回由前端指针指示的对的head：

function front_queue(queue) {
    return is_empty_queue(queue)
           ? error(queue, "front_queue called with an empty queue")
           : head(front_ptr(queue));
}

要在队列中插入一个项目，我们遵循图 3.20 中指示的结果的方法。我们首先创建一个新的对，其head是要插入的项目，其tail是空列表。如果队列最初为空，我们将队列的前端和后端指针设置为这个新对。否则，我们修改队列中的最后一对，使其指向新对，并且将后端指针设置为新对。

function insert_queue(queue, item) {
    const new_pair = pair(item, null);
    if (is_empty_queue(queue)) {
        set_front_ptr(queue, new_pair);
        set_rear_ptr(queue, new_pair);
    } else {
        set_tail(rear_ptr(queue), new_pair);
        set_rear_ptr(queue, new_pair);
    }
    return queue;
}

图 3.20 在图 3.19 的队列上使用insert_queue(q, "d")的结果。

要删除队列前端的项目，我们只需修改前端指针，使其现在指向队列中的第二个项目，可以通过跟随第一个项目的tail指针找到（参见图 3.21）：²⁵

function delete_queue(queue) {
    if (is_empty_queue(queue)) {
        error(queue, "delete_queue called with an empty queue");
    } else {
        set_front_ptr(queue, tail(front_ptr(queue)));
        return queue;
    }
}

图 3.21 在图 3.20 的队列上使用delete_queue(q)的结果。

练习 3.21

Ben Bitdiddle 决定测试上述队列实现。他将函数输入 JavaScript 解释器，并开始尝试它们：

const q1 = make_queue();

insert_queue(q1, "a");
[["a", null], ["a", null]]

insert_queue(q1, "b");
[["a", ["b", null]], ["b", null]]

delete_queue(q1);
[["b", null], ["b", null]]

delete_queue(q1);
[null, ["b", null]]

“这全都错了！”他抱怨道。“解释器的响应显示最后一个项目被插入队列两次。当我删除两个项目时，第二个b仍然存在，所以队列不是空的，尽管它应该是。”Eva Lu Ator 建议 Ben 误解了发生了什么。“不是项目被插入队列两次，”她解释道。“只是标准的 JavaScript 打印机不知道如何理解队列表示。如果你想正确打印队列，你必须为队列定义自己的打印函数。”解释 Eva Lu 所说的。特别是，说明 Ben 的示例产生了它们所产生的打印结果。定义一个函数print_queue，该函数以队列作为输入并打印队列中的项目序列。

练习 3.22

我们可以将队列表示为具有本地状态的函数，而不是将队列表示为一对指针。本地状态将包括指向普通列表的开头和结尾的指针。因此，make_queue函数将具有以下形式

function make_queue() {
    let front_ptr = ...;
    let rear_ptr = ...;
    〈declarations of internal functions〉
    function dispatch(m) {...}
    return dispatch;
}

完成make_queue的定义，并使用此表示提供队列操作的实现。

练习 3.23

双端队列（“deque”）是一个序列，其中项目可以在前端或后端插入和删除。双端队列的操作包括构造函数make_deque，谓词is_empty_deque，选择器front_deque和rear_deque，以及变异器front_insert_deque，front_delete_deque，rear_insert_deque和rear_delete_ deque。展示如何使用对表示 deque，并给出操作的实现。²⁶所有操作应在Θ(1)步骤中完成。

3.3.3 表示表

当我们在第 2 章研究了各种表示集合的方式时，在第 2.3.3 节中提到了通过识别键索引的记录表的维护任务。在第 2.4.3 节中的数据导向编程的实现中，我们广泛使用了二维表，其中使用两个键存储和检索信息。在这里，我们看到如何将表构建为可变列表结构。

首先考虑一维表，其中每个值都存储在单个键下。我们将表实现为记录的列表，每个记录都实现为一个由键和相关值组成的对。这些记录通过将head指向连续记录的对粘合在一起形成列表。这些粘合对被称为表的支柱。为了在向表中添加新记录时有一个可以更改的位置，我们将表构建为头列表。头列表在开头有一个特殊的支柱对，其中包含一个虚拟的“记录”——在这种情况下是任意选择的字符串"table"。图 3.22 显示了表的盒子和指针图。

a: 1
b: 2
c: 3

图 3.22 以头列表形式表示的表。

为了从表中提取信息，我们使用lookup函数，该函数以键作为参数并返回相关值（如果在该键下没有存储值，则返回undefined）。lookup函数是根据assoc操作定义的，该操作期望键和记录列表作为参数。请注意，assoc从不看到虚拟记录。assoc函数返回具有给定键作为head的记录。²⁷然后lookup函数检查assoc返回的结果记录是否不是undefined，并返回记录的值（tail）。

function lookup(key, table) {
    const record = assoc(key, tail(table));
    return is_undefined(record)
           ? undefined
           : tail(record);
}
function assoc(key, records) {
    return is_null(records)
           ? undefined
           : equal(key, head(head(records)))
           ? head(records)
           : assoc(key, tail(records));
}

要在指定的键下向表中插入一个值，我们首先使用assoc来查看表中是否已经存在具有该键的记录。如果没有，我们通过将键与值进行pair形成一个新记录，并将其插入到表的记录列表的头部（在虚拟记录之后）。如果已经存在具有该键的记录，我们将该记录的tail设置为指定的新值。表的标题为我们提供了一个固定的位置，以便插入新记录。²⁸

function insert(key, value, table) {
    const record = assoc(key, tail(table));
    if (is_undefined(record)) {
        set_tail(table,
                 pair(pair(key, value), tail(table)));
    } else {
        set_tail(record, value);
    }
    return "ok";
}

要构造一个新表，我们只需创建一个包含字符串"table"的列表：

function make_table() {
    return list("table");
}

二维表

在二维表中，每个值都由两个键索引。我们可以将这样的表构造为一个一维表，其中每个键都标识一个子表。图 3.23 显示了该表的框和指针图。

"math":
    "+": 43
    "-": 45
    "*": 42
"letters":
    "a": 97
    "b": 98

该对象有两个子表。（子表不需要特殊的标题字符串，因为标识子表的键就起到了这个作用。）

图 3.23 二维表。

当我们查找一个项目时，我们使用第一个键来标识正确的子表。然后我们使用第二个键来标识子表中的记录。

function lookup(key_1, key_2, table) {
    const subtable = assoc(key_1, tail(table));
    if (is_undefined(subtable)) {
        return undefined;
    } else {
        const record = assoc(key_2, tail(subtable));
        return is_undefined(record)
               ? undefined
               : tail(record);
    }
}

要在一对键下插入一个新项目，我们使用assoc来查看是否已经存储了第一个键下的子表。如果没有，我们构建一个包含单个记录（key_2，value）的新子表，并将其插入到第一个键下的表中。如果有一个

如果第一个键的子表已经存在，我们将使用上面描述的一维表的插入方法将新记录插入到该子表中：

function insert(key_1, key_2, value, table) {
    const subtable = assoc(key_1, tail(table));
    if (is_undefined(subtable)) {
        set_tail(table,
                 pair(list(key_1, pair(key_2, value)), tail(table)));
    } else {
        const record = assoc(key_2, tail(table));
        if (is_undefined(record)) {
            set_tail(subtable,
                     pair(pair(key_2, value), tail(subtable)));
        } else {
            set_tail(record, value);
        }
    }
    return "ok";
}

创建本地表

上面定义的lookup和insert操作将表作为参数。这使我们能够使用访问多个表的程序。处理多个表的另一种方法是为每个表单独拥有lookup和insert函数。我们可以通过过程化地表示一个表来实现这一点，将其作为一个对象，该对象将内部表作为其本地状态的一部分。当发送适当的消息时，这个“表对象”提供用于在内部表上操作的函数。以下是以这种方式表示的二维表的生成器：

function make_table() {
    const local_table = list("table");
    function lookup(key_1, key_2) {
        const subtable = assoc(key_1, tail(local_table));
        if (is_undefined(subtable)) {
            return undefined;
        } else {
            const record = assoc(key_2, tail(subtable));
            return is_undefined(record)
                   ? undefined
                   : tail(record);
        }
    }
    function insert(key_1, key_2, value) {
        const subtable = assoc(key_1, tail(local_table));
        if (is_undefined(subtable)) {
            set_tail(local_table,
                     pair(list(key_1, pair(key_2, value)),
                          tail(local_table)));
        } else {
            const record = assoc(key_2, tail(subtable));
            if (is_undefined(record)) {
                set_tail(subtable,
                         pair(pair(key_2, value), tail(subtable)));
            } else {
                set_tail(record, value);
            }
        }
    }
    function dispatch(m) {
        return m === "lookup"
               ? lookup
               : m === "insert"
               ? insert
               : error(m, "unknown operation – table");
    }
    return dispatch;
}

使用make_table，我们可以实现第 2.4.3 节中用于数据导向编程的get和put操作，如下所示：

const operation_table = make_table();
const get = operation_table("lookup");
const put = operation_table("insert");

函数get以两个键作为参数，put以两个键和一个值作为参数。这两个操作都访问同一个本地表，该表封装在通过调用make_table创建的对象中。

练习 3.24

在上面的表实现中，使用equal（由assoc调用）来测试键的相等性。这并不总是适当的测试。例如，我们可能有一个具有数字键的表，在这种情况下，我们不需要与我们查找的数字完全匹配，而只需要在某个公差范围内的数字。设计一个表构造函数make_table，它以一个same_key函数作为参数，该函数将用于测试键的“相等性”。函数make_table应返回一个dispatch函数，该函数可用于访问本地表的适当lookup和insert函数。

练习 3.25

将一维和二维表泛化，展示如何实现一个表，其中值存储在任意数量的键下，并且不同数量的键下可能存储不同的值。lookup和insert函数应以用于访问表的键列表作为输入。

练习 3.26

上面实现的搜索表需要扫描记录列表。这基本上是第 2.3.3 节的无序列表表示。对于大表，可能更有效地以不同的方式构造表。描述一个表实现，其中（键，值）记录使用二叉树组织，假设键可以以某种方式排序（例如，按数字或字母顺序）。（比较第 2 章的练习 2.66。）

练习 3.27

记忆化（也称为制表法）是一种使函数能够记录先前计算过的值的技术。这种技术可以极大地改善程序的性能。记忆化函数维护一个表，其中存储了以产生值的参数为键的先前调用的值。当记忆化函数被要求计算一个值时，它首先检查表，看看值是否已经存在，如果是，就返回该值。否则，它以普通方式计算新值，并将其存储在表中。作为记忆化的一个例子，回想一下第 1.2.2 节中用于计算斐波那契数的指数过程：

function fib(n) {
    return n === 0
           ? 0
           : n === 1
           ? 1
           : fib(n - 1) + fib(n - 2);
}

相同函数的记忆化版本是

const memo_fib = memoize(n => n === 0
                              ? 0
                              : n === 1
                              ? 1
                              : memo_fib(n - 1) +
                                memo_fib(n - 2)
                        );

其中记忆器定义为

function memoize(f) {
    const table = make_table();
    return x => {
               const previously_computed_result =
                   lookup(x, table);
               if (is_undefined(previously_computed_result)) {
                   const result = f(x);
                   insert(x, result, table);
                   return result;
               } else {
                   return previously_computed_result;
               }
           };
}

绘制一个环境图来分析memo_fib(3)的计算。解释为什么memo_fib计算第 n 个斐波那契数的步骤数量与 n 成比例。如果我们简单地将memo_fib定义为memoize(fib)，这种方案是否仍然有效？

3.3.4 数字电路模拟器

设计复杂的数字系统，如计算机，是一项重要的工程活动。数字系统是通过连接简单元素构建的。尽管这些单独元素的行为很简单，但它们的网络可能具有非常复杂的行为。计算机模拟提议的电路设计是数字系统工程师使用的重要工具。在本节中，我们设计了一个用于执行数字逻辑模拟的系统。这个系统代表了一种称为事件驱动模拟的程序类型，其中动作（“事件”）触发以后发生的更多事件，这些事件又触发更多事件，依此类推。

我们的电路的计算模型将由与构成电路的基本组件对应的对象组成。有电线，它们携带数字信号。数字信号在任何时刻只能有两个可能值之一，0 和 1。还有各种类型的数字功能框，它们将携带输入信号的电线连接到其他输出电线。这些框从它们的输入信号计算输出信号。输出信号的延迟时间取决于功能框的类型。例如，反相器是一个原始功能框，它反转其输入。如果反相器的输入信号变为 0，则一个反相器延迟后，反相器将把其输出信号更改为 1。如果反相器的输入信号变为 1，则一个反相器延迟后，反相器将把其输出信号更改为 0。我们以图 3.24 中的符号来绘制反相器。与门也显示在图 3.24 中，它是一个具有两个输入和一个输出的原始功能框。它将其输出信号驱动到与输入的逻辑与值相同的值。也就是说，如果其两个输入信号都变为 1，则一个与门延迟时间后，与门将强制其输出信号为 1；否则输出将为 0。或门是一个类似的两输入原始功能框，它将其输出信号驱动到与输入的逻辑或值相同的值。也就是说，如果至少一个输入信号为 1，则输出将变为 1；否则输出将变为 0。

图 3.24 数字逻辑模拟器中的原始函数。

我们可以将原始函数连接在一起，以构建更复杂的函数。为了实现这一点，我们将一些功能框的输出连接到其他功能框的输入。例如，图 3.25 中显示的半加器电路由一个或门、两个与门和一个反相器组成。它接收两个输入信号A和B，并有两个输出信号S和C。当A和B中恰好有一个为 1 时，S将变为 1，当A和B都为 1 时，C将变为 1。从图中我们可以看到，由于涉及到的延迟，输出可能在不同的时间生成。数字电路设计中的许多困难都源于这一事实。

图 3.25 一个半加器电路。

我们现在将构建一个用于建模我们希望研究的数字逻辑电路的程序。该程序将构建计算对象，对信号进行建模。功能框将由强制执行信号之间正确关系的函数进行建模。

我们模拟的一个基本元素将是一个名为make_wire的函数，用于构建信号线。例如，我们可以按照以下方式构建六根信号线：

const a = make_wire();
const b = make_wire();
const c = make_wire();
const d = make_wire();
const e = make_wire();
const s = make_wire();

我们通过调用一个构造该类型框的函数将一个函数框连接到一组线上。构造函数的参数是要连接到框的线。例如，鉴于我们可以构建与门、或门和反相器，我们可以将图 3.25 中显示的半加器连接在一起：

or_gate(a, b, d);
"ok"

and_gate(a, b, c);
"ok"

inverter(c, e);
"ok"

and_gate(d, e, s);
"ok"

更好的是，我们可以通过定义一个名为half_ adder的函数来显式命名这个操作，该函数构建这个电路，给定要连接到半加器的四根外部线：

function half_adder(a, b, s, c) {
    const d = make_wire();
    const e = make_wire();
    or_gate(a, b, d);
    and_gate(a, b, c);
    inverter(c, e);
    and_gate(d, e, s);
    return "ok";
}

制定这个定义的优势在于，我们可以使用half_adder本身作为创建更复杂电路的构建块。例如，图 3.26 展示了由两个半加器和一个或门组成的全加器。我们可以按照以下方式构建一个全加器：

function full_adder(a, b, c_in, sum, c_out) {
    const s = make_wire();
    const c1 = make_wire();
    const c2 = make_wire();
    half_adder(b, c_in, s, c1);
    half_adder(a, s, sum, c2);
    or_gate(c1, c2, c_out);
    return "ok";
}

定义了full_adder作为一个函数后，我们现在可以将其用作创建更复杂电路的构建块。（例如，参见练习 3.30。）

图 3.26 一个全加器电路。

实质上，我们的模拟器为我们提供了构建电路语言的工具。如果我们采用了我们在第 1.1 节中研究 JavaScript 时所采用的关于语言的一般观点，我们可以说原始功能框构成了语言的原始元素，将框连接在一起提供了一种组合的手段，指定框作为函数的连线模式作为抽象的手段。

原始功能框

原始功能框实现了一根线上的信号变化如何影响其他线上的信号的“力量”。为了构建功能框，我们使用以下操作：

get_signal(wire)

返回信号线上的当前值。
set_signal(wire, new-value):

将信号线上的信号值更改为新值。
add_action(wire, function-of -no-arguments):

断言指定的函数应该在线上的信号值发生变化时运行。这些函数是信号值变化传递给其他线的工具。

此外，我们将使用一个名为after_delay的函数，该函数接受一个时间延迟和一个要运行的函数，并在给定延迟后执行给定的函数。

使用这些功能，我们可以定义原始的数字逻辑功能。要通过反相器将输入连接到输出，我们使用add_action将输入线与一个函数关联起来，每当输入线上的信号值发生变化时，该函数就会运行。该函数计算输入信号的logical_not，然后在一个inverter_delay之后，将输出信号设置为这个新值：

function inverter(input, output) {
    function invert_input() {
        const new_value = logical_not(get_signal(input));
        after_delay(inverter_delay,
                    () => set_signal(output, new_value));
    }
    add_action(input, invert_input);
    return "ok";
}
function logical_not(s) {
    return s === 0
           ? 1
           : s === 1
           ? 0
           : error(s, "invalid signal");
}

与门稍微复杂一些。如果门的任一输入发生变化，则必须运行动作函数。它计算输入电线上的信号值的logical_and（使用类似于logical_not的函数），并设置在and_gate_delay之后在输出电线上发生新值的变化。

function and_gate(a1, a2, output) {
    function and_action_function() {
        const new_value = logical_and(get_signal(a1),
                                      get_signal(a2));
        after_delay(and_gate_delay,
                    () => set_signal(output, new_value));
    }
    add_action(a1, and_action_function);
    add_action(a2, and_action_function);
    return "ok";
}

练习 3.28

将或门定义为原始函数框。您的or_gate构造函数应类似于and_gate。

练习 3.29

构建或门的另一种方法是作为一个复合数字逻辑设备，由与门和反相器构建而成。定义一个函数or_gate来实现这一点。或门的延迟时间是多少，用and_gate_delay和inverter_delay来表示？

练习 3.30

图 3.27 显示了由串联n个全加器形成的链式进位加法器。这是用于加法两个n位二进制数的最简单形式的并行加法器。输入A[1]、A[2]、A[3]，...，A[n]和B[1]、B[2]、B[3]，...，B[n]是要相加的两个二进制数（每个A[k]和B[k]都是 0 或 1）。电路生成 S[1], S [2], S [3], ..., S [n]，和C，加法的进位。编写一个函数ripple_carry_adder来生成这个电路。该函数应该接受三个n个电线的列表作为参数——A[k]、B[k]和S[k]，还有另一个电线C。链式进位加法器的主要缺点是需要等待进位信号传播。以与门、或门和反相器的延迟来表示，获得n位链式进位加法器的完整输出所需的延迟是多少？

图 3.27 一个用于n位数字的链式进位加法器。

代表电线

在我们的模拟中，电线将是一个计算对象，具有两个本地状态变量：signal_value（最初为 0）和要在信号变化时运行的action_functions集合。我们使用消息传递样式实现电线，作为一组本地函数以及选择适当的本地操作的dispatch函数，就像我们在第 3.1.1 节中的简单银行账户对象中所做的那样：

function make_wire() {
    let signal_value = 0;
    let action_functions = null;
    function set_my_signal(new_value) {
        if (signal_value !== new_value) {
            signal_value = new_value;
            return call_each(action_functions);
        } else {
            return "done";
        }
    }
    function accept_action_function(fun) {
        action_functions = pair(fun, action_functions);
        fun();
    }
    function dispatch(m) {
        return m === "get_signal"
               ? signal_value
               : m === "set_signal"
               ? set_my_signal
               : m === "add_action"
               ? accept_action_function
               : error(m, "unknown operation – wire");
    }
    return dispatch;
}

本地函数set_my_signal测试新的信号值是否改变了电线上的信号。如果是，它将运行每个动作函数，使用以下函数call_each，该函数调用无参数函数列表中的每个项目：

function call_each(functions) {
    if (is_null(functions)) {
        return "done";
    } else {
        head(functions)();
        return call_each(tail(functions));
    }
}

本地函数accept_action_function将给定的函数添加到要运行的函数列表中，然后运行新函数一次。（参见练习 3.31。）

设置本地dispatch函数后，我们可以提供以下函数来访问线上的本地操作：³⁰

function get_signal(wire) {
    return wire("get_signal");
}
function set_signal(wire, new_value) {
    return wire("set_signal")(new_value);
}
function add_action(wire, action_function) {
    return wire("add_action")(action_function);
}

电线具有时变信号，可以逐步连接到设备，这是可变对象的典型特征。我们将它们建模为具有本地状态变量的函数，这些状态变量通过赋值进行修改。创建新电线时，将分配一组新的状态变量（通过make_wire中的let语句），并构造并返回一个新的dispatch函数，捕获具有新状态变量的环境。

电线被各种设备共享，这些设备已连接到它们。因此，通过与一个设备的交互所做的更改将影响连接到电线的所有其他设备。电线通过在建立连接时提供的动作函数来将更改通知给其邻居。

议程

完成模拟器所需的唯一事情是after_delay。这里的想法是我们维护一个数据结构，称为agenda，其中包含要执行的计划。议程定义了以下操作：

make_agenda()：

返回一个新的空议程。
is_empty_agenda(agenda)

如果指定的议程为空，则为真。
first_agenda_item(agenda)

返回日程表上的第一项。
remove_first_agenda_item(agenda)

通过删除第一项来修改日程表。
add_to_agenda(time, action, agenda)

通过添加给定的动作函数来修改日程表，以便在指定时间运行。
current_time(agenda)

返回当前模拟时间。

我们使用的特定日程表由the_agenda表示。函数after_delay向the_agenda添加新元素：

function after_delay(delay, action) {
    add_to_agenda(delay + current_time(the_agenda),
                  action,
                  the_agenda);
}

模拟由propagate函数驱动，该函数按顺序执行the_agenda上的每个函数。一般来说，随着模拟的运行，新的项目将被添加到日程表中，只要日程表上还有项目，propagate就会继续模拟：

function propagate() {
    if (is_empty_agenda(the_agenda)) {
        return "done";
    } else {
        const first_item = first_agenda_item(the_agenda);
        first_item();
        remove_first_agenda_item(the_agenda);
        return propagate();
    }
}

一个示例模拟

以下函数在动作上放置一个“探针”，展示了模拟器的运行。探针告诉导线，每当其信号值发生变化时，它应该打印新的信号值，以及当前时间和标识导线的名称。

function probe(name, wire) {
    add_action(wire,
               () => display(name + " " +
                             stringify(current_time(the_agenda)) +
                             ", new value = " +
                             stringify(get_signal(wire))));
}

我们首先初始化日程表，并为原始函数框架指定延迟：

const the_agenda = make_agenda();
const inverter_delay = 2;
const and_gate_delay = 3;
const or_gate_delay = 5;

现在我们定义了四根导线，并在其中两根上放置了探针：

const input_1 = make_wire();
const input_2 = make_wire();
const sum = make_wire();
const carry = make_wire();

probe("sum", sum);
"sum 0, new value = 0"

probe("carry", carry);
"carry 0, new value = 0"

接下来，我们连接半加器电路中的导线（如图 3.25 所示），将input_1上的信号设置为 1，并运行模拟：

half_adder(input_1, input_2, sum, carry);
"ok"

set_signal(input_1, 1);
"done"

propagate();
"sum 8, new value = 1"
"done"

sum信号在时间 8 时变为 1。现在距离模拟开始已经过去了八个时间单位。此时，我们可以将input_2上的信号设置为 1，并允许值传播：

set_signal(input_2, 1);
"done"

propagate();
"carry 11, new value = 1"
"sum 16, new value = 0"
"done"

在时间 11 时，carry变为 1，而在时间 16 时，sum变为 0。

练习 3.31

在make_wire中定义的内部函数accept_action_function指定了当新的动作函数被添加到导线时，立即运行该函数。解释为什么这种初始化是必要的。特别是，通过上面段落中的半加器示例追踪，并说出如果我们将accept_action_function定义为何，系统的响应会有何不同

function accept_action_function(fun) {
    action_functions = pair(fun, action_functions);
}

实施日程表

最后，我们详细介绍了日程表数据结构，该结构保存了计划用于将来执行的函数。

日程表由时间段组成。每个时间段都是一个数字（时间）和一个队列（参见练习 3.32），该队列保存了计划在该时间段内运行的函数。

function make_time_segment(time, queue) {
    return pair(time, queue);
}
function segment_time(s) { return head(s); }
function segment_queue(s) { return tail(s); }

我们将使用 3.3.2 节中描述的队列操作来操作时间段队列。

日程表本身是一个时间段的一维表。它与 3.3.3 节中描述的表不同之处在于，时间段将按照时间递增的顺序进行排序。此外，我们在日程表的头部存储当前时间（即，上次处理的动作的时间）。新构建的日程表没有时间段，并且当前时间为 0：

function make_agenda() { return list(0); }
function current_time(agenda) { return head(agenda); }
function set_current_time(agenda, time) {
    set_head(agenda, time);
}
function segments(agenda) { return tail(agenda); }
function set_segments(agenda, segs) {
    set_tail(agenda, segs);
}
function first_segment(agenda) { return head(segments(agenda)); }
function rest_segments(agenda) { return tail(segments(agenda)); }

如果日程表没有时间段，则为空：

function is_empty_agenda(agenda) {
    return is_null(segments(agenda));
}

要向日程表添加一个动作，我们首先检查日程表是否为空。如果是，我们为该动作创建一个时间段，并将其安装在日程表中。否则，我们扫描日程表，检查每个时间段的时间。如果我们找到了一个与我们指定时间相符的时间段，我们就将该动作添加到相关队列中。如果我们到达了晚于我们指定时间的时间，我们就在它之前插入一个新的时间段到日程表中。如果我们到达了日程表的末尾，我们必须在末尾创建一个新的时间段。

function add_to_agenda(time, action, agenda) {
    function belongs_before(segs) {
        return is_null(segs) || time < segment_time(head(segs));
    }
    function make_new_time_segment(time, action) {
        const q = make_queue();
        insert_queue(q, action);
        return make_time_segment(time, q);
    }
    function add_to_segments(segs) {
        if (segment_time(head(segs)) === time) {
            insert_queue(segment_queue(head(segs)), action);
        } else {
            const rest = tail(segs);
            if (belongs_before(rest)) {
                set_tail(segs, pair(make_new_time_segment(time, action),
                                    tail(segs)));
            } else {
                add_to_segments(rest);
            }
        }
    }
    const segs = segments(agenda);
    if (belongs_before(segs)) {
        set_segments(agenda,
                    pair(make_new_time_segment(time, action), segs));
    } else {
        add_to_segments(segs);
    }
}

删除日程表中的第一项的函数会删除第一个时间段中的队列中的项目。如果这个删除使时间段为空，我们就把它从时间段列表中移除。

function remove_first_agenda_item(agenda) {
    const q = segment_queue(first_segment(agenda));
    delete_queue(q);
    if (is_empty_queue(q)) {
        set_segments(agenda, rest_segments(agenda));
    } else {}
}

第一个日程表项位于第一个时间段的队列的头部。每当我们提取一个项目时，我们也会更新当前时间：

function first_agenda_item(agenda) {
    if (is_empty_agenda(agenda)) {
        error("agenda is empty – first_agenda_item");
    } else {
        const first_seg = first_segment(agenda);
        set_current_time(agenda, segment_time(first_seg));
        return front_queue(segment_queue(first_seg));
    }
}

练习 3.32

待在议程的每个时间段内运行的函数被保存在一个队列中。因此，每个时间段的函数按照它们被添加到议程的顺序被调用（先进先出）。解释为什么必须使用这个顺序。特别是，追踪一个与门的行为，当它的输入在同一个时间段内从0,1变为1,0，并说出如果我们将一个时间段的函数存储在一个普通列表中，只在前面添加和删除函数时，行为会有何不同。

3.3.5 约束的传播

计算机程序通常以单向计算的方式组织，它们对预先指定的参数执行操作以产生期望的输出。另一方面，我们经常以量之间的关系来建模系统。例如，机械结构的数学模型可能包括这样的信息：金属杆的挠度d与杆上的力F、杆的长度L、横截面积A和弹性模量E之间通过方程

dAE = FL

这样的方程不是单向的。给定这些量中的任意四个，我们可以使用它来计算第五个。然而，将方程转化为传统的计算机语言会迫使我们选择其中一个量来根据其他四个计算。因此，一个用于计算面积A的函数不能用于计算挠度d，即使A和d的计算都来自同一个方程。³⁴

在本节中，我们概述了一种能够让我们直接使用关系本身的语言的设计。语言的原始元素是 原始约束，它们陈述了某些量之间的关系。例如，adder(a, b, c)指定了量a、b和c必须满足方程a + b = c，multiplier(x, y, z)表达了约束xy = z，constant(3.14, x)表示x的值必须是 3.14。

我们的语言提供了一种将原始约束组合以表达更复杂关系的方法。我们通过构建 约束网络 来组合约束，其中约束由 连接器 连接。连接器是一个“持有”一个值的对象，可以参与一个或多个约束。例如，我们知道华氏温度和摄氏温度之间的关系是

9C = 5(F – 32)

这样的约束可以被看作是一个由原始加法器、乘法器和常量约束构成的网络（图 3.28）。在图中，我们可以看到左边有一个带有三个端口的乘法器盒子，标有m[1]、m[2]和p。这些将乘法器与网络的其余部分连接起来：m[1]端口连接到一个连接器C，它将持有摄氏温度。m[2]端口连接到一个连接器w，它也连接到一个持有 9 的常量盒子。乘法器盒子约束的p端口连接到另一个乘法器盒子的p端口，后者的m[2]连接到一个常量 5，m[1]连接到一个求和中的一个项。

图 3.28 表达为约束网络的关系9C = 5(F – 32)。

这样的网络进行计算的过程如下：当连接器被赋予一个值（由用户或与其链接的约束框），它会唤醒其所有相关约束（除了刚刚唤醒它的约束），通知它们它有一个值。然后每个唤醒的约束框轮询其连接器，看是否有足够的信息来确定连接器的值。如果是，该框将设置该连接器，然后唤醒其所有相关约束，依此类推。例如，在摄氏度和华氏度之间的转换中，w、x和y立即由常量框设置为 9、5 和 32。连接器唤醒乘法器和加法器，确定没有足够的信息来继续。如果用户（或网络的其他部分）将C设置为一个值（比如 25），最左边的乘法器将被唤醒，它将把u设置为25*9=225。然后u唤醒第二个乘法器，将v设置为 45，v唤醒加法器，将F设置为 77。

使用约束系统

要使用约束系统执行上面概述的温度计算，我们首先调用构造函数make_connector来创建两个连接器C和F，然后将它们链接到一个适当的网络中：

const C = make_connector();
const F = make_connector();
celsius_fahrenheit_converter(C, F);
"ok"

定义创建网络的函数如下：

function celsius_fahrenheit_converter(c, f) {
    const u = make_connector();
    const v = make_connector();
    const w = make_connector();
    const x = make_connector();
    const y = make_connector();
    multiplier(c, w, u);
    multiplier(v, x, u);
    adder(v, y, f);
    constant(9, w);
    constant(5, x);
    constant(32, y);
    return "ok";
}

这个函数创建内部连接器u、v、w、x和y，并使用原始约束构造函数adder、multiplier和constant将它们链接如图 3.28 所示。就像 3.3.4 节中的数字电路模拟器一样，用函数表达这些原始元素的组合自动为我们的语言提供了复合对象的抽象手段。

观察网络的运行，我们可以在连接器C和F上放置探针，使用类似于我们在 3.3.4 节中用来监视电线的probe函数。在连接器上放置探针将导致在给连接器赋值时打印消息：

probe("Celsius temp", C);
probe("Fahrenheit temp", F);

接下来我们将C的值设置为 25。（set_value的第三个参数告诉C这个指令来自user。）

set_value(C, 25, "user");
"Probe: Celsius temp = 25"
"Probe: Fahrenheit temp = 77"
"done"

C上的探针醒来并报告值。C也通过网络传播其值，如上所述。这将F设置为 77，探针上报告了这一点。

现在我们可以尝试将F设置为一个新值，比如 212：

set_value(F, 212, "user");
"Error! Contradiction: (77, 212)"

连接器抱怨它已经感知到矛盾：它的值是 77，有人试图将其设置为 212。如果我们真的想要使用新的值重新使用网络，我们可以告诉C忘记它的旧值：

forget_value(C, "user");
"Probe: Celsius temp = ?"
"Probe: Fahrenheit temp = ?"
"done"

C发现"user"，最初设置其值的人，现在正在撤回该值，因此C同意失去其值，如探针所示，并通知网络的其余部分。这些信息最终传播到F，现在F发现没有理由继续相信自己的值是 77。因此，F也放弃了它的值，如探针所示。

现在F没有值，我们可以自由地将其设置为 212：

set_value(F, 212, "user");
"Probe: Fahrenheit temp = 212"
"Probe: Celsius temp = 100"
"done"?

这个新值在网络中传播，强制C的值为 100，并由C上的探针注册。请注意，同一个网络被用来计算C给定F和计算F给定C。这种计算的非定向性是约束系统的显著特征。

实现约束系统

约束系统是通过具有局部状态的过程对象实现的，与 3.3.4 节中的数字电路模拟器非常相似。尽管约束系统的原始对象有些复杂，但整个系统更简单，因为不必担心议程和逻辑延迟。

连接器的基本操作如下：

has_value(connector)

告诉连接器是否有值。
get_value(connector)

返回连接器的当前值。
set_value(connector, new-value, informant)

表示通知者正在请求连接器将其值设置为新值。
forget_value(connector, retractor)

告诉连接器，撤回者正在请求它忘记其值。
connect(connector, new-constraint)

告诉连接器参与新的约束。

连接器通过函数inform_ about_value与约束进行通信，该函数告诉给定约束连接器具有值，并且inform_about_no_value告诉约束连接器已经失去了它的值。

Adder在加数连接器a1和a2以及一个sum连接器之间构造一个加法器约束。加法器实现为具有本地状态的函数（下面的函数me）：

function adder(a1, a2, sum) {
    function process_new_value() {
        if (has_value(a1) && has_value(a2)) {
            set_value(sum, get_value(a1) + get_value(a2), me);
        } else if (has_value(a1) && has_value(sum)) {
            set_value(a2, get_value(sum) - get_value(a1), me);
        } else if (has_value(a2) && has_value(sum)) {
            set_value(a1, get_value(sum) - get_value(a2), me);
        } else {}
    }
    function process_forget_value() {
        forget_value(sum, me);
        forget_value(a1, me);
        forget_value(a2, me);
        process_new_value();
    }
    function me(request) {
        if (request === "I have a value.") {
            process_new_value();
        } else if (request === "I lost my value.") {
            process_forget_value();
        } else {
            error(request, "unknown request – adder");
        }
    }
    connect(a1, me);
    connect(a2, me);
    connect(sum, me);
    return me;
}

函数adder将新的加法器连接到指定的连接器并将其作为其值返回。代表加法器的函数me充当本地函数的分派。与分派一起使用以下“语法接口”（参见第 3.3.4 节中的脚注 30）：

function inform_about_value(constraint) {
    return constraint("I have a value.");
}
function inform_about_no_value(constraint) {
    return constraint("I lost my value.");
}

当加法器被告知其连接器之一具有值时，将调用加法器的本地函数process_new_value。加法器首先检查看看a1和a2是否都有值。如果是这样，它会告诉sum将其值设置为两个加数的和。set_value的informant参数是me，即加法器对象本身。如果a1和a2都没有值，那么加法器会检查看看也许a1和sum有值。如果是这样，它会将a2设置为这两者的差。最后，如果a2和sum有值，这就为加法器提供了足够的信息来设置a1。如果加法器被告知其连接器之一失去了值，它会要求所有连接器现在都失去它们的值。（实际上只有这些值是由此加法器设置的才会丢失。）然后运行process_new_value。这最后一步的原因是一个或多个连接器可能仍然具有值（即，连接器可能具有一个不是最初由加法器设置的值），并且这些值可能需要通过加法器传播回去。

乘法器与加法器非常相似。如果因子中的任何一个为 0，即使另一个因子未知，它也会将其product设置为 0。

function multiplier(m1, m2, product) {
    function process_new_value() {
        if ((has_value(m1) && get_value(m1) === 0)
         || (has_value(m2) && get_value(m2) === 0)) {
            set_value(product, 0, me);
        } else if (has_value(m1) && has_value(m2)) {
            set_value(product, get_value(m1) * get_value(m2), me);
        } else if (has_value(product) && has_value(m1)) {
            set_value(m2, get_value(product) / get_value(m1), me);
        } else if (has_value(product) && has_value(m2)) {
            set_value(m1, get_value(product) / get_value(m2), me);
        } else {}
    }
    function process_forget_value() {
        forget_value(product, me);
        forget_value(m1, me);
        forget_value(m2, me);
        process_new_value();
    }
    function me(request) {
        if (request === "I have a value.") {
            process_new_value();
        } else if (request === "I lost my value.") {
            process_forget_value();
        } else {
            error(request, "unknown request – multiplier");
        }
    }
    connect(m1, me);
    connect(m2, me);
    connect(product, me);
    return me;
}

“常量”构造函数只是设置指定连接器的值。发送到常量框的任何“我有一个值。”或“我失去了我的价值。”消息都会产生错误。

function constant(value, connector) {
    function me(request) {
        error(request, "unknown request – constant");
    }
    connect(connector, me);
    set_value(connector, value, me);
    return me;
}

最后，探针打印有关设置或取消指定连接器的消息：

function probe(name, connector) {
    function print_probe(value) {
        display("Probe: " + name + " = " + stringify(value));
    }
    function process_new_value() {
        print_probe(get_value(connector));
    }
    function process_forget_value() {
        print_probe("?");
    }
    function me(request) {
        return request === "I have a value."
               ? process_new_value()
               : request === "I lost my value."
               ? process_forget_value()
               : error(request, "unknown request – probe");
    }
    connect(connector, me);
    return me;
}

表示连接器

连接器表示为具有本地状态变量value的过程对象，即连接器的当前值；informant，设置连接器值的对象；和constraints，连接器参与的约束列表。

function make_connector() {
    let value = false;
    let informant = false;
    let constraints = null;
    function set_my_value(newval, setter) {
        if (!has_value(me)) {
            value = newval;
            informant = setter;
            return for_each_except(setter,
                                   inform_about_value,
                                   constraints);
        } else if (value !== newval) {
            error(list(value, newval), "contradiction");
        } else {
            return "ignored";
        }
    }
    function forget_my_value(retractor) {
        if (retractor === informant) {
            informant = false;
            return for_each_except(retractor,
                                   inform_about_no_value,
                                   constraints);
        } else {
            return "ignored";
        }
    }
    function connect(new_constraint) {
        if (is_null(member(new_constraint, constraints))) {
            constraints = pair(new_constraint, constraints);
        } else {}
        if (has_value(me)) {
            inform_about_value(new_constraint);
        } else {}
        return "done";
    }
    function me(request) {
        if (request === "has_value") {
            return informant !== false;
        } else if (request === "value") {
            return value;
        } else if (request === "set_value") {
            return set_my_value;
        } else if (request === "forget") {
            return forget_my_value;
        } else if (request === "connect") {
            return connect;
        } else {
            error(request, "unknown operation – connector");
        }
    }
    return me;
}

当有请求设置连接器的值时，将调用连接器的本地函数set_my_value。如果连接器当前没有值，它将设置其值并记住请求设置值的约束作为informant。然后，连接器将通知除了请求设置值的约束之外的所有参与约束。这是通过以下迭代器实现的，该迭代器将指定的函数应用于列表中除给定项之外的所有项：

function for_each_except(exception, fun, list) {
    function loop(items) {
        if (is_null(items)) {
            return "done";
        } else if (head(items) === exception) {
            return loop(tail(items));
        } else {
            fun(head(items));
            return loop(tail(items));
        }
    }
    return loop(list);
}

如果要求连接器忘记其值，则运行forget_my_value，这是一个本地函数，首先检查请求是否来自最初设置值的相同对象。如果是这样，连接器会通知其关联的约束丢失了值。

本地函数connect将指定的新约束添加到约束列表中，如果它尚未在该列表中。然后，如果连接器具有值，它会告知新约束这一事实。

连接器的函数me用作对其他内部函数的调度，并且也代表连接器作为一个对象。以下函数为调度提供了语法接口：

function has_value(connector) {
    return connector("has_value");
}
function get_value(connector) {
    return connector("value");
}
function set_value(connector, new_value, informant) {
    return connector("set_value")(new_value, informant);
}
function forget_value(connector, retractor) {
    return connector("forget")(retractor);
}
function connect(connector, new_constraint) {
   return connector("connect")(new_constraint);
}

练习 3.33

使用原始乘法器、加法器和常量约束，定义一个名为averager的函数，该函数以三个连接器a，b和c作为输入，并建立约束，使得c的值是a和b的*均值。

练习 3.34

Louis Reasoner 想要构建一个*方器，这是一个具有两个端子的约束设备，使得第二个端子上的连接器 b 的值始终是第一个端子上连接器 a 的值的*方。他提出了以下由乘法器制成的简单设备：

function squarer(a, b) {
    return multiplier(a, a, b);
}

这个想法存在一个严重的缺陷。请解释。

练习 3.35

Ben Bitdiddle 告诉 Louis，避免练习 3.34 中的麻烦的一种方法是将*方器定义为一个新的原始约束。填写 Ben 的轮廓中用于实现这种约束的函数的缺失部分：

function squarer(a, b) {
    function process_new_value() {
        if (has_value(b)) {
            if (get_value(b) < 0) {
                error(get_value(b), "square less than 0 – squarer");
            } else {
                alternative[1]
            }
        } else {
            alternative[2]
        }
    }
    function process_forget_value() {
        body[1]
    }
    function me(request) {
        body[2]
    }
    statements
    return me;
}

练习 3.36

假设我们在程序环境中求值以下语句序列：

const a = make_connector();
const b = make_connector();
set_value(a, 10, "user");

在set_value的求值过程中的某个时间，将求值连接器的本地函数中的以下表达式：

for_each_except(setter, inform_about_value, constraints);

绘制一个环境图，显示上述表达式的求值环境。

练习 3.37

与更注重表达式的定义风格相比，celsius_fahrenheit_converter函数显得很繁琐，例如

function celsius_fahrenheit_converter(x) {
   return cplus(cmul(cdiv(cv(9), cv(5)), x), cv(32));
}

const C = make_connector();
const F = celsius_fahrenheit_converter(C);

在这里，cplus，cmul等是算术操作的“约束”版本。例如，cplus接受两个连接器作为参数，并返回一个与这些连接器相关的连接器，通过加法器约束：

function cplus(x, y) {
    const z = make_connector();
    adder(x, y, z);
    return z;
}

定义类似的函数cminus，cmul，cdiv和cv（常量值），使我们能够像上面的转换器示例一样定义复合约束。³⁷

3.4 并发性：时间至关重要

我们已经看到了具有局部状态的计算对象作为建模工具的强大力量。然而，正如 3.1.3 节所警告的那样，这种力量是有代价的：失去了引用透明性，引发了关于相同性和变化的一系列问题，并且需要放弃替换模型的求值，转而采用更复杂的环境模型。

隐藏在状态、相同性和变化的复杂性下的核心问题是，通过引入赋值，我们被迫将时间引入我们的计算模型中。在引入赋值之前，我们所有的程序都是无时间的，即任何具有值的表达式始终具有相同的值。相比之下，回想一下在 3.1.1 节开头介绍的从银行账户中提取和返回结果余额的建模示例：

withdraw(25);
75

withdraw(25);
50

这里对同一表达式的连续求值产生了不同的值。这种行为是由于赋值语句（在本例中是对变量balance的赋值）的执行划定了值发生变化的时间点。求值表达式的结果不仅取决于表达式本身，还取决于求值是在这些时间点之前还是之后发生的。以计算对象的局部状态构建模型迫使我们面对时间作为编程中的一个基本概念。

我们可以进一步构建计算模型，使其与我们对物理世界的感知相匹配。世界中的对象不是按顺序一个接一个地变化。相反，我们将它们视为同时并发执行。因此，通常自然地将系统建模为同时执行的线程（计算步骤序列）的集合。正如我们可以通过以对象的方式组织模型来使程序更加模块化，将计算模型分成部分以便分别和同时演变也是合适的。即使程序将在顺序计算机上执行，将程序编写成并发执行的方式也会迫使程序员避免不必要的时间约束，从而使程序更加模块化。

除了使程序更加模块化外，并发计算还可以比顺序计算提供速度优势。顺序计算机一次只执行一个操作，因此执行任务所需的时间与执行的总操作数成正比。然而，如果可以将问题分解为相对独立并且只需要偶尔通信的部分，那么可能可以将这些部分分配给单独的计算处理器，从而产生与可用处理器数量成正比的速度优势。

不幸的是，赋值引入的复杂性在并发存在时变得更加棘手。并发执行的事实，无论是因为世界是并行运行的，还是因为我们的计算机是，并发执行都会增加我们对时间理解的复杂性。

3.4.1 并发系统中时间的本质

表面上，时间似乎很简单。它是对事件施加的一种排序。对于任何事件A和B，要么A发生在B之前，A和B同时发生，或者A发生在B之后。例如，回到银行账户的例子，假设彼得从一个初始含有 100 美元的联合账户中提取了 10 美元，而保罗从中提取了 25 美元，留下 65 美元在账户中。根据两次提取的顺序，账户中的余额序列要么是 100 90 65，要么是 100 75 65。在银行系统的计算机实现中，这种不断变化的余额序列可以通过对变量balance进行连续赋值来建模。

然而，在复杂情况下，这样的观点可能会有问题。假设彼得和保罗，以及其他人，通过遍布全球的银行机器网络访问同一个银行账户。账户中的实际余额序列将严重依赖于访问的详细时间和机器之间通信的细节。

事件顺序的不确定性可能会在并发系统的设计中带来严重问题。例如，假设彼得和保罗的提取是作为两个共享一个公共变量balance的独立线程实现的，每个线程由第 3.1.1 节中给出的函数指定：

function withdraw(amount) {
    if (balance >= amount) {
        balance = balance - amount;
        return balance;
    } else {
        return "Insufficient funds";
    }
}

如果两个线程独立操作，那么彼得可能会测试余额并尝试提取合法金额。然而，保罗可能会在彼得检查余额和彼得完成提取之间提取一些资金，从而使彼得的测试无效。

事情可能会变得更糟。考虑这个声明

balance = balance - amount;

作为每个提取过程的一部分执行。这包括三个步骤：(1) 访问balance变量的值；(2) 计算新的余额；(3) 将balance设置为这个新值。如果彼得和保罗的提取同时执行这个语句，那么两个提取可能会交错访问balance和将其设置为新值的顺序。

图 3.29 中的时序图描述了一系列事件的顺序，其中balance从 100 开始，Peter 取款 10，Paul 取款 25，最终balance的值却是 75。正如图中所示，这种异常的原因是 Paul 将 75 赋给balance的假设是要减少的balance的值为 100。然而，当 Peter 将balance改为 90 时，这个假设变得无效。这对银行系统来说是一个灾难性的失败，因为系统中的总金额没有得到守恒。交易之前，系统中的总金额是 100 美元。之后，Peter 有 10 美元，Paul 有 25 美元，银行有 75 美元。^41

图 3.29 时序图显示了两笔银行取款事件的交错顺序可能导致最终余额不正确。

这里展示的一般现象是，多个线程可以共享一个公共状态变量。使这变得复杂的是，可能有多个线程同时尝试操作共享状态。对于银行账户的例子，在每笔交易中，每个客户都应该能够假设其他客户不存在。当客户以依赖于余额的方式改变余额时，他们必须能够假设在改变的那一刻之前，余额仍然是他们认为的那样。

并发程序的正确行为

上面的例子典型地说明了可能潜入并发程序的微妙错误。这种复杂性的根源在于不同线程之间共享的变量的赋值。我们已经知道，在编写使用赋值的程序时必须小心，因为计算的结果取决于赋值发生的顺序。^42 在并发线程中，我们必须特别小心赋值，因为我们可能无法控制不同线程所做的赋值的顺序。如果可能同时进行几个这样的更改（例如两个存款人访问联合账户），我们需要某种方式来确保我们的系统行为正确。例如，在联合银行账户的取款情况下，我们必须确保金钱是守恒的。为了使并发程序行为正确，我们可能需要对并发执行施加一些限制。

对并发的一种可能限制是规定不能同时发生改变任何共享状态变量的两个操作。这是一个非常严格的要求。对于分布式银行业务，这将要求系统设计者确保只能一次进行一笔交易。这既低效又过于保守。图 3.30 展示了 Peter 和 Paul 共享一个银行账户，Paul 也有一个私人账户。该图说明了从共享账户中取款（Peter 和 Paul 各取一笔）以及向 Paul 的私人账户存款。^43 从共享账户中取款的两笔操作不能同时进行（因为两者都访问并更新同一个账户），Paul 的存款和取款也不能同时进行（因为两者都访问并更新 Paul 钱包中的金额）。但是允许 Paul 向他的私人账户存款与 Peter 从共享账户中取款同时进行应该没有问题。

图 3.30 在 Bank1 的联合账户和 Bank2 的私人账户中同时存款和取款。

对并发的限制较少会确保并发系统产生与线程按某种顺序顺序运行时相同的结果。这一要求有两个重要方面。首先，它不要求线程实际上按顺序运行，而只要求产生与它们按顺序运行时相同的结果。例如，在图 3.30 的例子中，银行账户系统的设计者可以安全地允许保罗的存款和彼得的取款同时发生，因为最终结果将与这两个操作按顺序发生时的结果相同。其次，一个并发程序可能产生多个可能的“正确”结果，因为我们只要求结果与某些顺序的结果相同。例如，假设彼得和保罗的联合账户一开始有 100 美元，彼得存入 40 美元，同时保罗取出账户中的一半。然后，顺序执行可能导致账户余额为 70 美元或 90 美元（见练习 3.38）⁴⁴。

对并发程序的正确执行还有更弱的要求。用于模拟扩散（比如物体中的热量流动）的程序可能由大量线程组成，每个线程代表一小块空间，它们同时更新自己的值。每个线程反复将自己的值更改为自己的值和邻居的值的*均值。这种算法收敛到正确的答案，不受操作顺序的影响；对共享值的并发使用没有任何限制的必要。

练习 3.38

假设彼得、保罗和玛丽共享一个最初包含 100 美元的联合银行账户。同时，彼得存入 10 美元，保罗取出 20 美元，玛丽取出账户中的一半，执行以下命令：

彼得：	`balance = balance + 10`
保罗：	`balance = balance - 20`
玛丽：	`balance = balance - (balance / 2)`

a. 假设银行系统强制这三个线程按某种顺序顺序运行，请列出这三个交易完成后balance的所有不同可能值。
b. 如果系统允许线程交错，还可能产生哪些其他值？画出类似图 3.29 中的时间图，解释这些值是如何产生的。

3.4.2 控制并发的机制

我们已经看到处理并发线程的困难根源在于需要考虑不同线程中事件顺序的交错。例如，假设我们有两个线程，一个有三个有序事件（a，b，c），另一个有三个有序事件（x，y，z）。如果两个线程同时运行，而不限制它们的执行交错方式，那么与两个线程的各自顺序一致的 20 种不同可能的事件顺序：

（`a`，`b`，`c`，`x`，`y`，`z`）	（`a`，`x`，`b`，`y`，`c`，`z`）	（`x`，`a`，`b`，`c`，`y`，`z`）	（`x`，`a`，`y`，`z`，`b`，`c`）
（`a`，`b`，`x`，`c`，`y`，`z`）	（`a`，`x`，`b`，`y`，`z`，`c`）	（`x`，`a`，`b`，`y`，`c`，`z`）	（`x`，`y`，`a`，`b`，`c`，`z`）
（`a`，`b`，`x`，`y`，`c`，`z`）	（`a`，`x`，`y`，`b`，`c`，`z`）	（`x`，`a`，`b`，`y`，`z`，`c`）	（`x`，`y`，`a`，`b`，`z`，`c`）
（`a`，`b`，`x`，`y`，`z`，`c`）	（`a`，`x`，`y`，`b`，`z`，`c`）	（`x`，`a`，`y`，`b`，`c`，`z`）	（`x`，`y`，`a`，`z`，`b`，`c`）
（`a`，`x`，`b`，`c`，`y`，`z`）	（`a`，`x`，`y`，`z`，`b`，`c`）	（`x`，`a`，`y`，`b`，`z`，`c`）	（`x`，`y`，`z`，`a`，`b`，`c`）

作为设计这个系统的程序员，我们必须考虑这 20 种顺序的影响，并检查每种行为是否可接受。随着线程和事件数量的增加，这种方法很快变得难以控制。

设计并发系统的更实际的方法是设计通用机制，允许我们限制并发线程的交错，以确保程序行为是正确的。为此目的已经开发了许多机制。在本节中，我们描述其中之一，即序列化程序。

对共享状态进行序列化访问

序列化实现了以下思想：线程将同时执行，但将有一定的函数集合不能同时执行。更确切地说，序列化创建了一组特殊的函数集，以便每次只允许在每个序列化集中执行一个函数。如果正在执行集合中的某个函数，则试图执行集合中任何函数的线程将被迫等待，直到第一次执行完成。

我们可以使用序列化来控制对共享变量的访问。例如，如果我们想要基于该变量的先前值更新共享变量，我们将变量的先前值的访问和对变量的新值的赋值放在同一个函数中。然后，我们通过使用相同的序列化程序对所有这些函数进行序列化，以确保没有其他分配给变量的函数可以与此函数同时运行。这保证了变量的值在访问和相应的赋值之间不能被更改。

序列化程序

为了使上述机制更具体，假设我们已经扩展了 JavaScript，包括一个名为concurrent_execute的函数：

concurrent_execute(f[1], f[2], ..., f[k])

每个f必须是一个没有参数的函数。函数concurrent_execute为每个f创建一个单独的线程，该线程将f（无参数）应用于f。这些线程都同时运行。[^45]

作为如何使用它的示例，考虑

let x = 10;
concurrent_execute(() => { x = x * x; },
                   () => { x = x + 1; });

这创建了两个并发线程——T[1]，将x设置为x乘以x，以及T[2]，增加x。执行完成后，x将保留五种可能的值之一，具体取决于T[1]和T[2]的事件交错：

101:	`T[1]`将`x`设置为 100，然后`T[2]`将`x`增加到 101。
121:	`T[2]`将`x`增加到 11，然后`T[1]`将`x`设置为`x`乘以`x`。
110:	`T[2]`在`T[1]`之间将`x`从 10 更改为 11
	在求值`x * x`期间访问`x`的值。
11:	`T[2]`访问`x`，然后`T[1]`将`x`设置为 100，然后`T[2]`设置`x`。
100:	`T[1]`访问`x`（两次），然后`T[2]`将`x`设置为 11，然后`T[1]`设置`x`。

我们可以通过使用序列化函数来限制并发，这些函数是由序列化程序创建的。序列化程序是由make_serializer构造的，其实现如下所示。序列化程序接受一个函数作为参数，并返回一个行为类似于原始函数的序列化函数。对给定序列化程序的所有调用都返回相同集合中的序列化函数。

因此，与上面的示例相比，执行

let x = 10;
const s = make_serializer();
concurrent_execute(s(() => { x = x * x; }),
                   s(() => { x = x + 1; }));

可以产生x的两个可能值，101 或 121。其他可能性被消除，因为T[1]和T[2]的执行不能交错。

这是从 3.1.1 节中的make_account函数的一个版本，其中存款和取款已经被序列化：

function make_account(balance) {
    function withdraw(amount) {
        if (balance > amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    const protect = make_serializer();
    function dispatch(m) {
        return m === "withdraw"
               ? protect(withdraw)
               : m === "deposit"
               ? protect(deposit)
               : m === "balance"
               ? balance
               : error(m, "unknown request – make_account");
    }
    return dispatch;
}

通过这种实现，两个线程不能同时从单个帐户中提取或存款。这消除了图 3.29 中所示错误的来源，即 Peter 在 Paul 访问余额以计算新值和 Paul 实际执行分配之间更改帐户余额的时间。另一方面，每个帐户都有自己的序列化程序，因此不同帐户的存款和取款可以同时进行。

练习 3.39

如果我们改为按照以下方式对执行进行序列化，上述并发执行中的五种可能性中哪些仍然存在：

let x = 10;
const s = make_serializer();
concurrent_execute( () => { x = s(() => x * x)(); },
                   s(() => { x = x + 1; }));

练习 3.40

给出执行后可能的所有x的值

let x = 10;
concurrent_execute(() => { x = x * x; },
                   () => { x = x * x * x; });

如果我们使用序列化函数，那么这些可能性中还剩下哪些呢：

let x = 10;
const s = make_serializer(); concurrent_execute(s(() => { x = x * x; }),
                   s(() => { x = x * x * x; }));

练习 3.41

Ben Bitdiddle 担心最好按照以下方式实现银行账户（已更改的部分已在注释行中）：

function make_account(balance) {
    function withdraw(amount) {
        if (balance > amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    const protect = make_serializer();
    function dispatch(m) {
        return m === "withdraw"
               ? protect(withdraw)
               : m === "deposit"
               ? protect(deposit)
               : m === "balance"
               ? protect(() => balance)(undefined) // serialized
               : error(m, "unknown request – make_account");
    }
    return dispatch;
}

因为允许对银行余额进行未序列化访问可能会导致异常行为。你同意吗？有没有任何情景可以证明 Ben 的担忧？

练习 3.42

Ben Bitdiddle 建议，针对每个withdraw和deposit消息创建一个新的序列化函数是浪费时间。他说make_account可以被改变，这样对protect的调用就在dispatch函数之外完成。也就是说，一个账户每次要求提取函数时都会返回相同的序列化函数（该函数是在创建账户时同时创建的）。

function make_account(balance) {
    function withdraw(amount) {
        if (balance > amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    const protect = make_serializer();
    const protect_withdraw = protect(withdraw);
    const protect_deposit = protect(deposit);
    function dispatch(m) {
        return m === "withdraw"
               ? protect_withdraw
               : m === "deposit"
               ? protect_deposit
               : m === "balance"
               ? balance
               : error(m, "unknown request – make_account");
    }
    return dispatch;
}

这样改变安全吗？特别是，这两个版本的make_account允许的并发性有什么区别吗？

使用多个共享资源的复杂性

序列化器提供了一个强大的抽象，有助于隔离并发程序的复杂性，以便可以小心地（希望）正确地处理。然而，当只有一个共享资源（如单个银行账户）时，使用序列化器相对来说是相对简单的，但是当存在多个共享资源时，并发编程可能会非常困难。

为了说明可能出现的困难之一，假设我们希望交换两个银行账户的余额。我们访问每个账户以查找余额，计算余额之间的差额，从一个账户中提取这个差额，并将其存入另一个账户。我们可以这样实现：

function exchange(account1, account2) {
    const difference = account1("balance") - account2("balance");
    account1("withdraw")(difference);
    account2("deposit")(difference);
}

当只有一个线程尝试进行交换时，这个函数运行良好。然而，假设 Peter 和 Paul 都可以访问账户a[1]、a[2]和a[3]，Peter 交换a[1]和a[2]，同时 Paul 并发地交换a[1]和a[3]。即使对于单个账户的存款和取款都是串行化的（就像本节中上面显示的make_account函数一样），exchange仍然可能产生不正确的结果。例如，Peter 可能计算a[1]和a[2]的余额差，但是 Paul 可能在 Peter 完成交换之前改变a[1]的余额。为了正确的行为，我们必须安排exchange函数在整个交换过程中锁定对账户的任何其他并发访问。

我们可以通过使用两个账户的序列化器来实现这一点，以序列化整个exchange函数。为此，我们将安排访问账户的序列化器。请注意，我们故意打破了银行账户对象的模块化，通过消息传递来暴露序列化器。下面的make_account版本与第 3.1.1 节中给出的原始版本相同，只是提供了一个序列化器来保护余额变量，并且通过消息传递导出了序列化器：

function make_account_and_serializer(balance) {
    function withdraw(amount) {
        if (balance > amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    const balance_serializer = make_serializer();
    return m => m === "withdraw"
                ? withdraw
                : m === "deposit"
                ? deposit
                : m === "balance"
                ? balance
                : m === "serializer"
                ? balance_serializer
                : error(m, "unknown request – make_account");
}

我们可以使用这个来进行序列化的存款和取款。然而，与我们之前的序列化账户不同，现在每个银行账户对象的用户都有责任显式地管理序列化，例如：

function deposit(account, amount) {
    const s = account("serializer");
    const d = account("deposit");
    s(d(amount));
}

以这种方式导出序列化器为我们提供了足够的灵活性来实现一个序列化的交换程序。我们只需使用两个账户的序列化器对原始的exchange函数进行序列化：

function serialized_exchange(account1, account2) {
    const serializer1 = account1("serializer");
    const serializer2 = account2("serializer");
    serializer1(serializer2(exchange))(account1, account2);
}

练习 3.43

假设三个账户的余额初始为 $10、$20 和 $30，并且多个线程运行，交换账户中的余额。论证如果线程按顺序运行，在任意数量的并发交换之后，账户余额应该以某种顺序为 $10、$20 和 $30。绘制一个类似于图 3.29 中的时间图，以展示如果使用本节中账户交换程序的第一个版本，这个条件如何被违反。另外，论证即使使用这个exchange程序，账户余额的总和也会被保留。绘制一个时间图，以展示如果我们没有对各个账户上的交易进行序列化，即使这个条件也会被违反。

练习 3.44

考虑从一个账户转账到另一个账户的问题。本·比特迪德尔声称，即使有多个人同时在多个账户之间转账，使用任何序列化存款和取款交易的账户机制，例如上文中的make_account版本，也可以通过以下函数实现。

function transfer(from_account, to_account, amount) {
    from_account("withdraw")(amount);
    to_account("deposit")(amount);
}

路易斯·里森纳声称这里存在问题，我们需要使用更复杂的方法，比如处理交换问题所需的方法。路易斯是对的吗？如果不是，转账问题和交换问题之间的本质区别是什么？（假设from_account中的余额至少为amount。）

练习 3.45

路易斯·里森纳认为我们的银行账户系统现在过于复杂和容易出错，因为存款和取款不再自动序列化。他建议make_account_and_serializer应该导出序列化器（供serialized_exchange等函数使用），而不是像make_account一样使用它来序列化账户和存款。他建议重新定义账户如下：

function make_account_and_serializer(balance) {
    function withdraw(amount) {
        if (balance > amount) {
            balance = balance - amount;
            return balance;
        } else {
            return "Insufficient funds";
        }
    }
    function deposit(amount) {
        balance = balance + amount;
        return balance;
    }
    const balance_serializer = make_serializer();
    return m => m === "withdraw"
                ? balance_serializer(withdraw)
                : m === "deposit"
                ? balance_serializer(deposit)
                : m === "balance"
                ? balance
                : m === "serializer"
                ? balance_serializer
                : error(m, "unknown request – make_account");
}

然后存款的处理方式与原始的make_account相同：

function deposit(account, amount) {
    account("deposit")(amount);
}

解释路易斯的推理有什么问题。特别是考虑serialized_exchange被调用时会发生什么。

实现序列化器

我们根据一种称为互斥体的更原始的同步机制来实现序列化器。互斥体是支持两种操作的对象——可以获取互斥体，也可以释放互斥体。一旦互斥体被获取，那么在互斥体被释放之前，该互斥体上的其他获取操作都无法进行。在我们的实现中，每个序列化器都有一个关联的互斥体。给定一个函数f，序列化器返回一个函数，该函数获取互斥体，运行f，然后释放互斥体。这确保了由序列化器产生的函数中只有一个可以同时运行，这正是我们需要保证的序列化属性。为了将序列化器应用于接受任意数量参数的函数，我们使用 JavaScript 的剩余参数和展开语法。参数args前面的…收集函数的任何调用中的所有参数（这里是全部参数）到一个向量数据结构中。在应用f(…args)中args前面的…将args的元素展开，使它们成为f的单独参数。

function make_serializer() {
    const mutex = make_mutex();
    return f => {
               function serialized_f(…args) {
                   mutex("acquire");
                   const val = f(…args);
                   mutex("release");
                   return val;
               }
               return serialized_f;
           };
}

互斥体是一个可变对象（这里我们将使用一个一元列表，称为单元格），它可以保存true或false的值。当值为false时，互斥体可用于获取。当值为true时，互斥体不可用，任何试图获取互斥体的线程都必须等待。

我们的互斥锁构造函数make_mutex首先将单元内容初始化为假。要获取互斥锁，我们测试单元。如果互斥锁可用，我们将单元内容设置为真并继续。否则，我们在一个循环中等待，一遍又一遍地尝试获取，直到我们发现互斥锁可用。⁵⁰ 要释放互斥锁，我们将单元内容设置为假。

function make_mutex() {
    const cell = list(false);
    function the_mutex(m) {
    return m === "acquire"
           ? test_and_set(cell)
             ? the_mutex("acquire") // retry
             : true
           : m === "release"
           ? clear(cell)
           : error(m, "unknown request – mutex");
    }
    return the_mutex;
}
function clear(cell) {
    set_head(cell, false);
}

函数test_and_set测试单元并返回测试结果。此外，如果测试结果为假，test_and_set在返回假之前将单元内容设置为真。我们可以将这种行为表达为以下函数：

function test_and_set(cell) {
    if (head(cell)) {
        return true;
    } else {
        set_head(cell, true);
        return false;
    }
}

然而，这种test_and_set的实现并不足以满足要求。这里有一个关键的微妙之处，这是并发控制进入系统的基本地方：test_and_set操作必须被原子化执行。也就是说，我们必须保证，一旦一个线程测试了单元并发现它为假，单元内容实际上会在任何其他线程测试单元之前被设置为真。如果我们不能做到这一点，那么互斥锁可能会以类似于图 3.29 中的银行账户失败的方式失败。（参见练习 3.46。）

test_and_set的实际实现取决于我们的系统如何运行并发线程的细节。例如，我们可能正在使用时间片轮转机制在顺序处理器上执行并发线程，该机制循环遍历线程，允许每个线程在中断之前运行一小段时间。在这种情况下，test_and_set可以通过在测试和设置期间禁用时间片轮转来工作。另外，多处理计算机提供了直接在硬件中支持原子操作的指令。⁵¹

练习 3.46

假设我们使用文本中所示的普通函数来实现test_and_set，而不尝试使操作原子化。绘制一个类似于图 3.29 中的时序图，以演示互斥锁实现如何通过允许两个线程同时获取互斥锁而失败。

练习 3.47

信号量（大小为n）是互斥锁的一种泛化。像互斥锁一样，信号量支持获取和释放操作，但它更一般，最多n个线程可以同时获取它。尝试获取信号量的其他线程必须等待释放操作。给出信号量的实现

a. 以互斥锁为条件
b. 以原子test_and_set操作为条件。

死锁

现在我们已经看到了如何实现串行化器，我们可以看到即使在上面的serialized_exchange函数中，账户交换仍然存在问题。假设 Peter 试图将a[1]与a[2]交换，同时 Paul 尝试将a[2]与a[1]交换。假设 Peter 的线程到达了进入保护a[1]的串行化函数的点，就在那之后，Paul 的线程进入了保护a[2]的串行化函数。现在 Peter 无法继续（进入保护a[2]的串行化函数）直到 Paul 退出保护a[2]的串行化函数。同样，Paul 在 Peter 退出保护a[1]的串行化函数之前也无法继续。每个线程都永远被阻塞，等待另一个线程。这种情况被称为死锁。在提供对多个共享资源的并发访问的系统中，死锁总是一个危险。

在这种情况下避免死锁的一种方法是给每个账户分配一个唯一的标识号，并重写serialized_exchange，使得一个线程总是尝试首先进入保护最低编号账户的函数。虽然这种方法对于交换问题效果很好，但还有其他需要更复杂的死锁避免技术的情况，或者根本无法避免死锁。（参见练习 3.48 和 3.49。）⁵²

练习 3.48

详细解释上述避免死锁的方法（即，账户编号，并且每个线程尝试先获取编号较小的账户）在交换问题中避免死锁的原因。重写serialized_exchange以纳入这个想法。（您还需要修改make_account，以便每个账户都带有一个可以通过发送适当消息访问的编号。）

练习 3.49

给出一个情景，说明上述避免死锁的机制不起作用的情况。（提示：在交换问题中，每个线程事先知道它将需要访问的账户。考虑一个情况，一个线程必须在知道它将需要访问哪些额外的共享资源之前获得对一些共享资源的访问。）

并发、时间和通信

我们已经看到，编写并发系统需要控制不同线程访问共享状态时事件的顺序，并且我们已经看到如何通过合理使用串行器来实现这种控制。但并发的问题并不仅仅如此，因为从根本上来看，“共享状态”并不总是清楚是什么意思。

诸如test_and_set之类的机制要求线程在任意时间检查全局共享标志。这在现代高速处理器中实现起来是有问题且低效的，因为由于流水线和缓存内存等优化技术，内存的内容可能不会在每一时刻处于一致状态。因此，在一些多处理系统中，串行器范式正在被其他并发控制方法所取代。

共享状态的问题也出现在大型分布式系统中。例如，想象一个分布式银行系统，其中各个分行维护银行余额的本地值，并定期将其与其他分行维护的值进行比较。在这样的系统中，“账户余额”的价值在同步之后才会确定。如果 Peter 向他与 Paul 共同持有的账户存钱，我们应该在何时说账户余额已经改变——当本地分行的余额改变时，还是直到同步之后？如果 Paul 从不同的分行访问账户，对于银行系统来说应该放置什么合理的约束条件，以使行为“正确”？对于正确性来说，唯一重要的可能是 Peter 和 Paul 个别观察到的行为以及同步后账户的“状态”。关于“真实”账户余额或同步之间事件顺序的问题可能是无关或无意义的。

这里的基本现象是，同步不同的线程，建立共享状态，或对事件进行排序都需要线程之间的通信。实质上，并发控制中的任何时间概念都必须与通信紧密联系在一起。引人入胜的是，在相对论中也存在时间和通信之间的类似联系，光速（可以用来同步事件的最快信号）是一个将时间和空间联系起来的基本常数。我们在处理计算模型中的时间和状态时遇到的复杂性，实际上可能反映了物理宇宙的基本复杂性。

3.5 流

我们已经对作为建模工具的赋值有了很好的理解，也对赋值引发的复杂问题有了认识。现在是时候问问我们是否可以以不同的方式进行事情，以避免其中一些问题。在本节中，我们将探讨一种基于称为“流”的数据结构的状态建模的替代方法。正如我们将看到的，流可以减轻一些状态建模的复杂性。

让我们退一步，回顾一下这种复杂性的根源。为了模拟现实世界的现象，我们做出了一些看似合理的决定：我们用具有局部变量的计算对象来模拟具有局部状态的现实世界对象。我们将现实世界中的时间变化与计算机中的时间变化相对应。我们用模型对象的局部变量的赋值来实现计算机中模型对象状态的时间变化。

还有其他方法吗？我们能否避免将计算机中的时间与模拟世界中的时间相对应？我们必须使模型随时间变化以模拟变化中的世界现象吗？从数学函数的角度来思考这个问题。我们可以将数量x的随时间变化描述为时间的函数x(t)。如果我们一瞬间地专注于x，我们会认为它是一个变化的数量。然而，如果我们专注于值的整个时间历史，我们并不强调变化——函数本身并不改变。⁵⁶

如果时间以离散步骤来衡量，那么我们可以将时间函数建模为（可能是无限的）序列。在本节中，我们将看到如何以代表被建模系统的时间历史的序列来建模变化。为了实现这一点，我们引入了称为流的新数据结构。从抽象的角度来看，流只是一个序列。然而，我们会发现，将流的直接实现作为列表（如 2.2.1 节中所示）并不能充分展现流处理的威力。作为替代，我们引入了延迟求值技术，这使我们能够将非常大（甚至是无限的）序列表示为流。

流处理让我们能够建模具有状态的系统，而无需使用赋值或可变数据。这对于理论和实践都有重要的影响，因为我们可以构建避免引入赋值固有缺点的模型。另一方面，流框架本身也带来了困难，以及哪种建模技术能够导致更模块化和更易维护的系统的问题仍然是开放的。

3.5.1 流是延迟列表

正如我们在 2.2.3 节中看到的，序列可以作为组合程序模块的标准接口。我们为操作序列制定了强大的抽象，如map、filter和accumulate，以简洁而优雅的方式捕捉了各种操作。

不幸的是，如果我们将序列表示为列表，这种优雅是以计算效率严重不足的代价换来的，无论是在时间还是空间上。当我们将对序列的操作表示为列表的转换时，我们的程序必须在过程的每一步构造和复制数据结构（可能非常庞大）。

为了理解这一点，让我们比较两个计算区间内所有质数之和的程序。第一个程序是用标准的迭代风格编写的：⁵⁷

function sum_primes(a, b) {
    function iter(count, accum) {
        return count > b
               ? accum
               : is_prime(count)
               ? iter(count + 1, count + accum)
               : iter(count + 1, accum);
    }
    return iter(a, 0);
}

第二个程序使用 2.2.3 节的序列操作执行相同的计算：

function sum_primes(a, b) {
    return accumulate((x, y) => x + y,
                      0,
                      filter(is_prime,
                             enumerate_interval(a, b)));
}

在进行计算时，第一个程序只需要存储正在累积的总和。相比之下，第二个程序中的过滤器在enumerate_interval构建完整的区间数字列表之前无法进行任何测试。过滤器生成另一个列表，然后传递给accumulate，然后被折叠以形成总和。第一个程序不需要这样大的中间存储，我们可以将其视为逐步枚举区间，将每个质数添加到生成的总和中。

如果我们使用序列范例来计算从 10,000 到 1,000,000 的区间中第二个质数，那么使用列表的低效性就会变得非常明显，通过求值表达式

head(tail(filter(is_prime,
                 enumerate_interval(10000, 1000000))));

这个表达式确实找到了第二个素数，但计算开销是过分的。我们构造了一个接*一百万的整数列表，通过测试每个元素的素性来过滤这个列表，然后忽略了几乎所有的结果。在更传统的编程风格中，我们会交错枚举和过滤，并在达到第二个素数时停止。

流是一个巧妙的想法，它允许我们使用序列操作而不会产生列表操作的成本。有了流，我们可以实现两全其美：我们可以优雅地将程序构建为序列操作，同时获得增量计算的效率。基本思想是只部分构造流，并将部分构造传递给消费流的程序。如果消费者尝试访问尚未构造的流的一部分，流将自动构造足够的自身来产生所需的部分，从而保持整个流存在的幻觉。换句话说，尽管我们将编写程序，就好像我们正在处理完整的序列，但我们的流实现被设计为自动透明地交错流的构造和使用。

为了实现这一点，我们将使用对构造流，流的第一项在对的头部。然而，我们不是将流的其余值放入对的尾部，而是在那里放置一个“承诺”，以计算其余部分（如果有的话）。如果我们有一个数据项h和一个流t，我们通过求值pair(h, () => t)来构造一个流，其头部是h，尾部是t—流的尾部t被包装在一个没有参数的函数中，因此其求值将被延迟。空流是null，与空列表相同。

要访问非空流的第一个数据项，我们只需选择一对的head，就像列表一样。但是要访问流的尾部，我们需要求值延迟的表达式。为了方便起见，我们定义

function stream_tail(stream) {
    return tail(stream)();
}

这选择了一对的尾部，并应用在那里找到的函数来获得流的下一对（或者如果流的尾部为空则为null）—实际上，强制了对尾部的函数来实现其承诺。

我们可以制作和使用流，就像我们可以制作和使用列表一样，来表示按顺序排列的聚合数据。特别是，我们可以构建章节 2 中的列表操作的流模拟，例如list_ref、map和for_each:⁵⁸

function stream_ref(s, n) {
    return n === 0
           ? head(s)
           : stream_ref(stream_tail(s), n - 1);
}
function stream_map(f, s) {
    return is_null(s)
           ? null
           : pair(f(head(s)),
                  () => stream_map(f, stream_tail(s)));
}
function stream_for_each(fun, s) {
    if (is_null(s)) {
        return true;
    } else {
        fun(head(s));
        return stream_for_each(fun, stream_tail(s));
    }
}

stream_for_each函数对于查看流是有用的。

function display_stream(s) {
    return stream_for_each(display, s);
}

为了使流的实现自动透明地交错流的构造和使用，我们安排了流的尾部在被stream_tail函数访问时进行求值，而不是在pair构造流时进行求值。这种实现选择让人想起了我们在 2.1.2 节中讨论有理数时所看到的情况，那里我们看到我们可以选择实现有理数，使得分子和分母的约分在构造时或选择时进行。这两种有理数实现产生相同的数据抽象，但选择对效率有影响。流和普通列表之间存在类似的关系。作为数据抽象，流和列表是相同的。不同之处在于元素的求值时间。对于普通列表，head和tail都在构造时进行求值。对于流，tail在选择时进行求值。

流的实际应用

为了看到这种数据结构的行为，让我们分析上面看到的“过分”的素数计算，以流的术语重新表述：

head(stream_tail(stream_filter(
                     is_prime,
                     stream_enumerate_interval(10000, 1000000))));

我们将看到它确实有效地工作。

我们首先使用参数 10,000 和 1,000,000 调用stream_enumerate_interval函数。函数stream_enumerate_interval是enumerate_interval（2.2.3 节）的流模拟：

function stream_enumerate_interval(low, high) {
    return low > high
           ? null
           : pair(low,
                  () => stream_enumerate_interval(low + 1, high));
}

因此，由stream_enumerate_interval返回的结果，由pair组成，是⁵⁹

pair(10000, () => stream_enumerate_interval(10001, 1000000));

也就是说，stream_enumerate_interval返回一个表示为pair的流，其head为 10,000，tail是一个承诺，如果需要的话会枚举更多的间隔。现在，使用filter函数的流模拟对素数进行过滤。

function stream_filter(pred, stream) {
    return is_null(stream)
           ? null
           : pred(head(stream))
           ? pair(head(stream),
                  () => stream_filter(pred, stream_tail(stream)))
           : stream_filter(pred, stream_tail(stream));
}

函数stream_filter测试流的head（即 10,000）。由于这不是素数，stream_filter检查其输入流的尾部。调用stream_tail迫使延迟的stream_enumerate_interval，现在返回

pair(10001, () => stream_enumerate_interval(10002, 1000000));

函数stream_filter现在查看这个流的head，10,001，看到这也不是素数，强制另一个stream_tail，依此类推，直到stream_enumerate_interval产生素数 10,007，然后根据其定义，stream_filter返回

pair(head(stream),
     stream_filter(pred, stream_tail(stream)));

在这种情况下是

pair(10007,
     () => stream_filter(
              is_prime,
              pair(10008,
                   () => stream_enumerate_interval(10009, 1000000))));

这个结果现在传递给了我们原始表达式中的stream_tail。这迫使延迟的stream_filter，进而不断迫使延迟的stream_enumerate_interval，直到找到下一个素数，即 10,009。最后，结果传递给了我们原始表达式中的head。

pair(10009,
     () => stream_filter(
              is_prime,
              pair(10010,
                   () => stream_enumerate_interval(10011, 1000000))));

函数head返回 10,009，计算完成。只有测试了必要数量的整数以确定素数，只有在必要时才枚举了间隔以提供素数过滤器。

一般来说，我们可以将延迟求值看作是“需求驱动”的编程，即流处理中的每个阶段只激活足够满足下一个阶段的部分。我们所做的是将计算中的实际事件顺序与函数的表面结构分离。我们编写函数，就好像流“一次性”存在一样，而实际上，计算是逐步进行的，就像传统的编程风格一样。

一个优化

当我们构造流对时，我们通过将这些表达式包装在函数中来延迟求值它们的尾部表达式。我们在需要时通过应用函数来强制执行它们的求值。

这个实现足以使流按照广告宣传的方式工作，但是在需要时我们将考虑一个重要的优化。在许多应用中，我们最终会多次强制执行相同的延迟对象。这可能导致涉及流的递归程序严重低效。（见练习 3.57。）解决方案是构建延迟对象，使得第一次强制执行时，它们存储计算的值。后续的强制执行将简单地返回存储的值，而不重复计算。换句话说，我们实现了流对的构造，作为类似于练习 3.27 中描述的记忆化函数的一种方式。实现这一点的一种方法是使用以下函数，它以一个函数（无参数）作为参数，并返回函数的记忆化版本。第一次运行记忆化函数时，它保存计算结果。在后续的求值中，它只是返回结果。⁶⁰

function memo(fun) {
    let already_run = false;
    let result = undefined;
    return () => {
               if (!already_run) {
                   result = fun();
                   already_run = true;
                   return result;
               } else {
                   return result;
               }
           };
}

我们可以在构造流对时使用memo。例如，而不是

function stream_map(f, s) {
    return is_null(s)
           ? null
           : pair(f(head(s)),
                  () => stream_map(f, stream_tail(s)));
}

我们可以定义一个优化的函数stream_map如下：

function stream_map_optimized(f, s) {
    return is_null(s)
           ? null
           : pair(f(head(s)),
                  memo(() =>
                         stream_map_optimized(f, stream_tail(s))));
}

练习 3.50

声明一个函数stream_map_2，它接受一个二元函数和两个流作为参数，并返回一个流，其元素是将函数成对应用于参数流的相应元素的结果。

function stream_map_2(f, s1, s2) {
    …
}

类似于stream_map_optimized，通过修改stream_map_2声明一个函数stream_map_2_optimized，使结果流使用记忆化。

练习 3.51

请注意，我们的原始函数display在显示后返回其参数。解释器在求值以下序列中的每个语句时打印什么？

let x = stream_map(display, stream_enumerate_interval(0, 10));
stream_ref(x, 5);
stream_ref(x, 7);

如果使用stream_map_optimized而不是stream_map，解释器会打印什么？

let x = stream_map_optimized(display, stream_enumerate_interval(0, 10));
stream_ref(x, 5);
stream_ref(x, 7);

练习 3.52

考虑以下语句序列

let sum = 0;
function accum(x) {
    sum = x + sum;
    return sum;
}
const seq = stream_map(accum, stream_enumerate_interval(1, 20));
const y = stream_filter(is_even, seq);
const z = stream_filter(x => x % 5 === 0, seq);
stream_ref(y, 7);
display_stream(z);

在上述每个语句被求值后，sum的值是多少？求值stream_ref和display_stream表达式的打印响应是什么？如果我们在每个构造的流对的每个尾部应用了函数memo，如上面的优化建议，这些响应会有所不同吗？请解释。

3.5.2 无限流

我们已经看到如何支持操作流的幻觉，即使在实际上，我们只计算我们需要访问的流的部分。我们可以利用这种技术来有效地表示序列作为流，即使序列非常长。更重要的是，我们可以使用流来表示无限长的序列。例如，考虑以下正整数流的定义：

function integers_starting_from(n) {
    return pair(n, () => integers_starting_from(n + 1));
}
const integers = integers_starting_from(1);

这是有道理的，因为integers将是一个对，其head是 1，tail是一个承诺去产生从 2 开始的整数。这是一个无限长的流，但在任何给定的时间，我们只能检查其中的有限部分。因此，我们的程序永远不会知道整个无限流不存在。

使用integers，我们可以定义其他无限流，例如不能被 7 整除的整数流：

function is_divisible(x, y) { return x % y === 0; }
const no_sevens = stream_filter(x => ! is_divisible(x, 7),
                                integers);

然后我们可以通过访问该流的元素来找到不能被 7 整除的整数：

stream_ref(no_sevens, 100);
117

类似于integers，我们可以定义斐波那契数的无限流：

function fibgen(a, b) {
    return pair(a, () => fibgen(b, a + b));
}
const fibs = fibgen(0, 1);

常量fibs是一个对的head是 0，tail是一个承诺去求值fibgen(1, 1)。当我们求值这个延迟的fibgen(1, 1)时，它将产生一个对，其head是 1，tail是一个承诺去求值fibgen(1, 2)，依此类推。

要查看更激动人心的无限流，我们可以将no_sevens示例推广到使用称为厄拉托斯特尼筛法的方法构造质数的无限流。我们从从 2 开始的整数开始，这是第一个质数。为了得到其余的质数，我们首先从其余的整数中过滤出 2 的倍数。这留下了一个以 3 开始的流，这是下一个质数。现在我们从这个流的其余部分中过滤出 3 的倍数。这留下了一个以 5 开始的流，这是下一个质数，依此类推。换句话说，我们通过筛选过程构造质数，描述如下：对流 S 进行筛选，形成一个流，其第一个元素是 S 的第一个元素，其余部分是通过从 S 的其余部分中过滤出 S 的第一个元素的所有倍数并进行筛选得到的。这个过程可以很容易地用流操作来描述：

function sieve(stream) {
    return pair(head(stream),
                () => sieve(stream_filter(
                                 x => ! is_divisible(x, head(stream)),
                                 stream_tail(stream))));
}
const primes = sieve(integers_starting_from(2));

现在，要找到特定的质数，我们只需要询问：

stream_ref(primes, 50);
233

思考一下由sieve建立的信号处理系统，如图 3.31 中的“亨德森图”所示。输入流馈入一个unpairer，将流的第一个元素与其余部分分开。第一个元素用于构造一个可被整除的过滤器，通过该过滤器传递其余部分，并将过滤器的输出馈送到另一个筛子箱中。然后将原始的第一个元素与内部筛子的输出相连，形成输出流。因此，流不仅是无限的，信号处理器也是无限的，因为筛子中包含一个筛子。

图 3.31 将素数筛视为信号处理系统。每条实线代表正在传输的值流。从head到pair和filter的虚线表示这是一个单个值，而不是一个流。

隐式定义流

上述integers和fibs流是通过指定显式计算流元素的“生成”函数来定义的。指定流的另一种方法是利用延迟求值来隐式定义流。例如，以下语句定义了流ones为无限流的 1：

const ones = pair(1, () => ones);

这与递归函数的声明非常相似：ones是一个head为 1 且tail是一个承诺来求值ones的对，求值tail再次给我们一个 1 和一个承诺来求值ones，依此类推。

我们可以通过使用add_streams等操作来操作流，从而做更有趣的事情，该操作产生两个给定流的逐元素和。⁶⁴

function add_streams(s1, s2) {
    return stream_map_2((x1, x2) => x1 + x2, s1, s2);
}

现在我们可以如下定义整数：

const integers = pair(1, () => add_streams(ones, integers));

这定义了integers为一个流，其第一个元素为 1，其余部分是ones和integers的和。因此，integers的第二个元素是integers的第一个元素加 1，或 2；integers的第三个元素是integers的第二个元素加 1，或 3；依此类推。这个定义之所以有效，是因为在任何时候，integers流的足够部分已经生成，以便我们可以将其反馈到定义中以产生下一个整数。

我们可以以相同的方式定义斐波那契数：

const fibs = pair(0,
                  () => pair(1,
                             () => add_streams(stream_tail(fibs),
                                               fibs)));

这个定义表示fibs是一个以 0 和 1 开头的流，这样流的其余部分可以通过将fibs加到自身移位一个位置来生成：

1  1  2  3  5  8  13  21  ...  =  stream_tail(fibs) 

0  1  1  2  3  5  8  13  ...  =  fibs 

0  1  1  2  3  5  8  13  21  34  ...  =  fibs

函数scale_stream在制定这种流定义时也很有用。这将流中的每个项目乘以给定的常数：

function scale_stream(stream, factor) {
    return stream_map(x => x * factor,
                      stream);
}

例如，

const double = pair(1, () => scale_stream(double, 2));

产生 2 的幂的流：1, 2, 4, 8, 16, 32, ....

可以通过从整数开始并通过测试素数性进行过滤来给出素数流的另一种定义。我们需要第一个素数 2 来开始：

const primes = pair(2,
                    () => stream_filter(is_prime,
                                        integers_starting_from(3)));

这个定义并不像看起来那么简单，因为我们将测试一个数n是否为素数，方法是检查是否可以被小于或等于的素数（而不是任意整数）整除：

function is_prime(n) {
    function iter(ps) {
        return square(head(ps)) > n
               ? true
               : is_divisible(n, head(ps))
               ? false
               : iter(stream_tail(ps));
    }
    return iter(primes);
}

这是一个递归定义，因为primes是根据is_prime谓词定义的，而is_prime谓词本身使用primes流。这个函数之所以有效，是因为在任何时候，primes流的足够部分已经生成，以便我们可以测试下一个需要检查的数的素数性。也就是说，对于每个n，我们测试其是否为素数，要么n不是素数（在这种情况下，已经生成了一个可以整除它的素数），要么n是素数（在这种情况下，已经生成了一个素数，即小于n的素数，大于的素数）。

练习 3.53

不运行程序的情况下，描述由以下定义的流的元素

const s = pair(1, () => add_streams(s, s));

练习 3.54

定义一个函数mul_streams，类似于add_streams，它产生其两个输入流的逐元素乘积。与integers流一起使用，完成以下流的定义，其第n个元素（从 0 开始计数）是n + 1的阶乘：

const factorials = pair(1, () => mul_streams(〈??〉, 〈??〉));

练习 3.55

定义一个名为partial_sums的函数，该函数以流S作为参数，并返回其元素为S[0]，S[0] + S[1]，S[0] + S[1] + S[2]，...的流。例如，partial_sums(integers)应该是流1, 3, 6, 10, 15, ...。

练习 3.56

一个著名的问题，首次由 R. Hamming 提出，是按升序枚举所有没有除了 2、3 或 5 之外的质因数的正整数，而且没有重复。一个明显的方法是简单地依次测试每个整数，看它是否有除 2、3 和 5 之外的因子。但这非常低效，因为随着整数变大，符合要求的整数越来越少。作为替代方案，让我们称所需的数字流为S，并注意关于它的以下事实。

S以 1 开始。
scale_stream(S, 2)的元素也是S的元素。
scale_stream(S, 3)和scale_stream(S, 5)也是如此。
这些都是S的元素。

现在我们只需要从这些来源中组合元素。为此，我们定义一个函数merge，它将两个有序流合并成一个有序结果流，消除重复项：

function merge(s1, s2) {
    if (is_null(s1)) {
        return s2;
    } else if (is_null(s2)) {
        return s1;
    } else {
        const s1head = head(s1);
        const s2head = head(s2);
        return s1head < s2head
               ? pair(s1head, () => merge(stream_tail(s1), s2))
               : s1head > s2head
               ? pair(s2head, () => merge(s1, stream_tail(s2)))
               : pair(s1head, () => merge(stream_tail(s1), stream_tail(s2)));
    }
}

然后，可以使用merge构造所需的流，如下所示：

const S = pair(1, () => merge((??), (??)));

在上面标有(??)的地方填写缺失的表达式。

练习 3.57

使用基于add_streams函数的 fibs 声明计算第 n 个斐波那契数时执行了多少次加法？证明如果add_streams使用练习 3.50 中描述的stream_map_2_optimized函数，这个数字呈指数增长。

练习 3.58

给出函数计算的流的解释

function expand(num, den, radix) {
    return pair(math_trunc((num * radix) / den),
                () => expand((num * radix) % den, den, radix));
}

其中math_trunc丢弃其参数的小数部分，即除法的余数。expand(1, 7, 10)产生的连续元素是什么？expand(3, 8, 10)产生什么？

练习 3.59

在 2.5.3 节中，我们看到如何实现多项式算术系统，将多项式表示为项的列表。类似地，我们可以处理幂级数，例如

表示为无限流。我们将级数a[0] + a[1]x + a[2]x² + a[3]x³ + ...表示为其元素为系数a[0]，a[1], a[2], a[3], ...的流。

a. 级数a[0] + a[1]x + a[2]x² + a[3]x³ + ...的积分是级数
```
c + a[0]x + 1/2 a[1]x² + 1/3 a[2]x³ +  1/4 a[3]x⁴ + ...
```
定义一个函数integrate_series，它以流a[0], a[1], a[2], ...作为输入，表示幂级数，并返回非常数项积分的系数流a[0], 1/2 a[1], 1/3 a[2], ...。（由于结果没有常数项，它不表示幂级数；当我们使用integrate_series时，我们将使用pair将适当的常数添加到流的开头。）
b. 函数x -> eˣ是它自己的导数。这意味着eˣ和eˣ的积分是相同的级数，除了常数项，它是e⁰= 1。因此，我们可以生成eˣ的级数为
```
const exp_series = pair(1, () => integrate_series(exp_series));
```
展示如何从正弦的导数是余弦和余弦的导数是负正弦这两个事实开始生成正弦和余弦的级数：
```
const cosine_series = pair(1, 〈??〉);
const sine_series = pair(0, 〈??〉);
```

练习 3.60

使用练习 3.59 中级数表示为系数流的方式，通过add-streams实现级数相加。完成以下函数的声明以实现级数相乘：

function mul_series(s1, s2) {
    pair(〈??〉, () => add_streams(〈??〉, 〈??〉));
}

您可以通过验证sin²x + cos²x = 1，使用练习 3.59 中的级数来测试您的函数。

练习 3.61

设S是一个幂级数（练习 3.59），其常数项为 1。假设我们想找到幂级数1/S，即级数X，使得S X = 1。将S写为1 + S[R]，其中S[R]是常数项之后的S的部分。然后我们可以按如下方式解出X：

 S · X  =  1 

 (1 + S[R]) · X  =  1 

 X + S[R] · X  =  1 

 X  =  1 – S[R] · X

换句话说，X是常数项为 1 的幂级数，其高阶项由S[R]的负数乘以X给出。使用这个想法编写一个名为invert_unit_series的函数，该函数计算常数项为 1 的幂级数S的1/S。您需要使用练习 3.60 中的mul_series。

练习 3.62

使用练习 3.60 和 3.61 的结果定义一个名为div_series的函数，该函数可以将两个幂级数相除。div_series函数应适用于任何两个级数，只要分母级数以非零常数项开头。（如果分母有零常数项，则div_series应发出错误信号。）展示如何使用div_series与练习 3.59 的结果一起生成正切的幂级数。

3.5.3 利用流范式

具有延迟求值的流可以是一个强大的建模工具，提供了许多局部状态和赋值的好处。此外，它们避免了引入赋值到编程语言中时伴随的一些理论上的纠缠。

流方法可以提供启发，因为它允许我们构建具有不同模块边界的系统，而不是围绕对状态变量的赋值组织的系统。例如，我们可以将整个时间序列（或信号）视为关注的焦点，而不是单个时刻的状态变量的值。这使得方便地组合和比较来自不同时刻的状态组件。

将迭代公式表述为流过程

在 1.2.1 节中，我们介绍了迭代过程，通过更新状态变量进行。我们现在知道，我们可以将状态表示为“无时间”的值流，而不是一组要更新的变量。让我们在重新访问 1.1.7 节中的求*方根函数时采用这种观点。回想一下，这个想法是通过反复应用改进猜测的函数来生成越来越好的x的*方根的序列：

function sqrt_improve(guess, x) {
    return average(guess, x / guess);
}

在我们原始的sqrt函数中，我们让这些猜测成为状态变量的连续值。相反，我们可以生成无限的猜测流，从初始猜测值 1 开始：

function sqrt_stream(x) {
    return pair(1, () => stream_map(guess => sqrt_improve(guess, x),
                                    sqrt_stream(x)));
}

display_stream(sqrt_stream(2));
`1`
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
...

我们可以生成越来越多的流项，以获得越来越好的猜测。如果愿意，我们可以编写一个函数，直到答案足够好为止一直生成项。（参见练习 3.64。）

我们可以以相同的方式处理的另一个迭代是基于我们在 1.3.1 节中看到的交替级数生成π的*似值：

首先生成级数的和项流（奇整数的倒数，交替符号）。然后我们取越来越多项的和的流（使用练习 3.55 的partial_sums函数）并将结果缩放 4 倍：

function pi_summands(n) {
    return pair(1 / n, () => stream_map(x => - x, pi_summands(n + 2)));
}
const pi_stream = scale_stream(partial_sums(pi_summands(1)), 4);

display_stream(pi_stream);
`4`
2.666666666666667
3.466666666666667
2.8952380952380956
3.3396825396825403
2.9760461760461765
3.2837384837384844
3.017071817071818
...

这给我们提供了一个越来越好的π的*似流，尽管这些*似值收敛得相当慢。序列的八个项将π的值限制在 3.284 和 3.017 之间。

到目前为止，我们对状态流方法的使用与更新状态变量并没有太大不同。但是流使我们有机会做一些有趣的技巧。例如，我们可以使用序列加速器转换流，将*似值序列转换为收敛到与原始值相同的新序列，只是更快。

其中一种加速器，由十八世纪瑞士数学家 Leonhard Euler 提出，对于偏和交错级数的序列效果很好（交错符号的项的级数）。在欧拉的技术中，如果S[n]是原始和序列的第n项，则加速的序列具有项

因此，如果原始序列表示为值的流，则变换后的序列由

function euler_transform(s) {
    const s0 = stream_ref(s, 0);     // S[n][–1]
    const s1 = stream_ref(s, 1);     // S[n]
    const s2 = stream_ref(s, 2);     // S[n][+1]
    return pair(s2 - square(s2 - s1) / (s0 + (-2) * s1 + s2),
                memo(() => euler_transform(stream_tail(s))));
}

请注意，我们利用了第 3.5.1 节的记忆化优化，因为在接下来的内容中，我们将依赖于对生成的流的重复求值。

我们可以用我们对π的逼*序列来演示欧拉加速：

display_stream(euler_transform(pi_stream));
3.166666666666667
3.1333333333333337
3.1452380952380956
3.13968253968254
3.1427128427128435
3.1408813408813416
3.142071817071818
3.1412548236077655
...

更好的是，我们可以加速加速的序列，然后递归加速，依此类推。也就是说，我们创建了一个流的流（我们将其称为表格的结构），其中每个流都是前一个流的变换：

function make_tableau(transform, s) {
    return pair(s, () => make_tableau(transform, transform(s)));
}

表格的形式

 s[00]  s[01]  s[02]  s[03]  s[04]  ...

   s[10]  s[11]  s[12]  s[13]  ...

     s[20]  s[21]  s[22]  ...

         ...

最后，我们通过取表格的每一行的第一个项来形成一个序列：

function accelerated_sequence(transform, s) {
    return stream_map(head, make_tableau(transform, s));
}

我们可以演示这种“超加速”π序列：

display_stream(accelerated_sequence(euler_transform, pi_stream));
`4`
3.166666666666667
3.142105263157895
3.141599357319005
3.1415927140337785
3.1415926539752927
3.1415926535911765
3.141592653589778
...

结果令人印象深刻。取序列的八个项可以得到π的正确值，精确到小数点后 14 位。如果我们只使用原始的π序列，我们需要计算大约10¹³个项（即，扩展系列直到单个项小于10^(–13)）才能获得这么高的精度！

我们本可以在不使用流的情况下实现这些加速技术。但是流的表述特别优雅和方便，因为整个状态序列作为数据结构对我们可用，并且可以使用统一的一组操作进行操作。

练习 3.63

Louis Reasoner 对sqrt_stream函数生成的流的性能不满意，并尝试使用记忆化来优化它：

function sqrt_stream_optimized(x) {
    return pair(1,
                memo(() => stream_map(guess =>
                                        sqrt_improve(guess, x),
                                      sqrt_stream_optimized(x))));
}

Alyssa P. Hacker 提出

function sqrt_stream_optimized_2(x) {
    const guesses = pair(1,
                         memo(() => stream_map(guess =>
                                                 sqrt_improve(guess, x),
                                               guesses)));
    return guesses;
}

并声称 Louis 的版本比她的要低效得多，因为它执行了冗余计算。解释 Alyssa 的答案。Alyssa 的方法如果没有记忆化，是否比原始的sqrt_stream更有效？

练习 3.64

编写一个名为stream_limit的函数，它接受一个流和一个数字（容差）作为参数。它应该检查流，直到找到两个连续的元素，它们的绝对值之差小于容差，并返回这两个元素中的第二个。使用这个函数，我们可以通过

function sqrt(x, tolerance) {
    return stream_limit(sqrt_stream(x), tolerance);
}

练习 3.65

使用级数

计算三个逼*自然对数 2 的序列，方式与我们上面对π所做的方式相同。这些序列收敛得有多快？

无限流的对

在第 2.2.3 节中，我们看到序列范式如何处理传统的嵌套循环，作为对成对序列定义的过程。如果我们将这种技术推广到无限流，那么我们可以编写不容易表示为循环的程序，因为“循环”必须在无限集合上进行。

例如，假设我们想要将第 2.2.3 节的prime_sum_pairs函数推广为生成所有整数(i, j)对的流，其中i ≤ j，使得i + j是素数。如果int_pairs是所有整数(i, j)对的序列，其中i ≤ j，那么我们所需的流就是简单的⁶⁷

stream_filter(pair => is_prime(head(pair) + head(tail(pair))),
              int_pairs);

因此，我们的问题是生成int_pairs流。更一般地说，假设我们有两个流S = (S[i])和T = (T[j])，并想象一个无限的矩形数组

 (S[0], T[0])  (S[0], T[1])  (S[0], T[2])  ...

 (S[1], T[0])  (S[1], T[1])  (S[1], T[2])  ...

 (S[2], T[0])  (S[2], T[1])  (S[2], T[2])  ...

 ...

我们希望生成一个包含数组中所有位于对角线上方或对角线上的成对的流，即成对

 (S[0], T[0])  (S[0], T[1])  (S[0], T[2])  ...

   (S[1], T[1])  (S[1], T[2])  ...

     (S[2], T[2])  ...

       ...

（如果我们将S和T都作为整数流，那么这将是我们期望的流int_pairs。）

将成对的一般流称为pairs(S, T)，并将其视为由三部分组成：对(S[0], T[0])，第一行中其余的对，以及剩余的对。

 (S[0], T[0])  (S[0], T[1])  (S[0], T[2])  ... 

   (S[1], T[1])  (S[1], T[2])  ... 

     (S[2], T[2])  ... 

       ...

观察到这种分解中的第三部分（不在第一行中的对）是（递归地）由stream_tail(S)和stream_tail(T)形成的对。还要注意第二部分（第一行的其余部分）是

stream_map(x => list(head(s), x),
stream_tail(t));

因此，我们可以按以下方式形成我们的成对流：

function pairs(s, t) {
    return pair(list(head(s), head(t)),
                () => combine-in-some-way(
                          stream_map(x => list(head(s), x),
                                     stream_tail(t)),
                          pairs(stream_tail(s), stream_tail(t))));
}

为了完成函数，我们必须选择一种组合两个内部流的方法。一个想法是使用第 2.2.1 节中的append函数的流模拟：

function stream_append(s1, s2) {
    return is_null(s1)
           ? s2
           : pair(head(s1),
                  () => stream_append(stream_tail(s1), s2));
}

然而，这对于无限流来说是不合适的，因为它在合并第二个流之前从第一个流中取出所有元素。特别是，如果我们尝试使用以下方式生成所有正整数的成对：

pairs(integers, integers);

我们的结果流将首先尝试运行所有第一个整数等于 1 的对，因此永远不会产生任何其他第一个整数值的对。

为了处理无限流，我们需要设计一种组合顺序，以确保如果我们让程序运行足够长的时间，每个元素最终都会被访问到。实现这一点的一种优雅方法是使用以下interleave函数：

function interleave(s1, s2) {
    return is_null(s1)
           ? s2
           : pair(head(s1),
                  () => interleave(s2, stream_tail(s1)));
}

由于interleave从两个流中交替获取元素，因此第二个流的每个元素最终都会进入交错流中，即使第一个流是无限的。

因此，我们可以生成所需的成对流如下：

function pairs(s, t) {
    return pair(list(head(s), head(t)),
                () => interleave(stream_map(x => list(head(s), x),
                                            stream_tail(t)),
                                 pairs(stream_tail(s),
                                       stream_tail(t))));
}

练习 3.66

检查流pairs(integers, integers)。您能对成对放入流中的顺序做出一般性评论吗？例如，大约有多少对在(1,100)之前？对(99,100)之前？对(100,100)之前？（如果您能在这里做出精确的数学陈述，那就更好了。但是，如果您发现自己陷入困境，请随时给出更多的定性答案。）

练习 3.67

修改pairs函数，使得pairs(integers, integers)将生成所有整数对(i, j)的流（不带条件i ≤ j）。提示：您需要混合另一个流。

练习 3.68

Louis Reasoner 认为从三个部分构建成对流是不必要复杂的。他建议不将对(S[0], T[0])与第一行中其余的对分开，而是建议使用整个第一行，如下所示：

function pairs(s, t) {
    return interleave(stream_map(x => list(head(s), x),
                                 t),
                      pair(stream_tail(s), stream_tail(t)));
}

这样行得通吗？考虑一下，如果我们使用 Louis 对pairs的定义来求值pairs(integers, integers)会发生什么。

练习 3.69

编写一个名为triples的函数，该函数接受三个无限流S、T和U，并生成三元组(S[i], T[j], U[k])的流，其中i ≤ j ≤ k。使用triples生成所有正整数的勾股三元组的流，即三元组(i, j, k)，使得i ≤ j且i² + j² = k²。

练习 3.70

生成流时，以某种有用的顺序出现的整数对会更好，而不是通过特设的交错过程得到的顺序。如果我们定义一种方法来表明一个整数对“小于”另一个整数对，我们可以使用类似于练习 3.56 的merge函数的技术。这样做的一种方法是定义一个“加权函数”W(i, j)，并规定如果W(i[1], j[1]) < W(i[2], j[2])，则(i[1], j[1])小于(i[2], j[2])。编写一个名为merge_weighted的函数，它类似于merge，但merge_weighted接受一个额外的参数weight，这是一个计算一对整数的权重的函数，并用于确定结果合并流中元素应该出现的顺序。使用这个方法，将pairs推广为一个名为weighted_pairs的函数，它接受两个流，以及一个计算加权函数的函数，并生成整数对的流，根据权重排序。使用你的函数生成

a. 所有正整数对(i, j)的流，其中i ≤ j，根据和i + j进行排序
b. 所有正整数对(i, j)的流，其中i ≤ j，i和j都不能被 2、3 或 5 整除，并且这些对根据和2i + 3j + 5ij进行排序。

练习 3.71

有时称为拉马努金数的数字可以用两种以上的方式表示为两个立方数的和，以纪念数学家斯里尼瓦萨·拉马努金。有序的整数对流为计算这些数字提供了一种优雅的解决方案。要找到一个可以用两种不同方式写成两个立方数的和的数字，我们只需要生成根据和i³ + j³（参见练习 3.70）加权的整数对流，然后在流中搜索具有相同权重的两个连续整数对。编写一个函数来生成拉马努金数。第一个这样的数字是 1,729。接下来的五个是什么？

练习 3.72

类似于练习 3.71，生成一个流，其中包含所有可以用三种不同方式写成两个*方和的数字（显示它们可以这样写成的方式）。

流作为信号

我们通过将流描述为信号处理系统中的“信号”的计算模拟来开始我们对流的讨论。实际上，我们可以直接使用流来模拟信号处理系统，将信号在连续时间间隔的值表示为流的连续元素。例如，我们可以实现一个积分器或求和器，对于输入流x = (x[i])，初始值C和小增量dt，累积和。

并返回值流S = (S[i])。以下的integral函数类似于整数流的“隐式样式”定义（第 3.5.2 节）：

function integral(integrand, initial_value, dt) {
    const integ = pair(initial_value,
                       () => add_streams(scale_stream(integrand, dt),
                                         integ));
    return integ;
}

图 3.32 是一个与integral函数对应的信号处理系统的图片。输入流通过dt进行缩放，并通过加法器，其输出再次通过相同的加法器传递。integ的定义中的自引用在图中通过将加法器的输出连接到其中一个输入的反馈环中得到反映。

图 3.32 integral函数视为信号处理系统。

练习 3.73

我们可以使用流来模拟电路，以表示一系列时间点上的电流或电压值。例如，假设我们有一个由电阻R和电容C串联组成的 RC 电路。电路对注入电流i的电压响应v由图 3.33 中的公式确定，其结构由附带的信号流图所示。

图 3.33 一个 RC 电路和相关的信号流图。

编写一个模拟这个电路的函数RC。RC应该以R、C和dt的值作为输入，并应该返回一个函数，该函数以表示当前i的流和电容器电压v[0]的初始值作为输入，并产生电压v的流作为输出。例如，您应该能够通过求值const RC1 = RC(5, 1, 0.5)来使用RC来模拟一个R=5欧姆、C=1法拉和 0.5 秒时间步长的 RC 电路。这将定义RC1作为一个函数，它接受表示电流时间序列的流和初始电容器电压，并产生电压的输出流。

练习 3.74

艾莉莎·P·黑客正在设计一个系统，用于处理来自物理传感器的信号。她希望产生的一个重要特性是描述输入信号的零交叉的信号。也就是说，结果信号应该在输入信号从负变为正时为+1，在输入信号从正变为负时为-1，否则为 0。（假设 0 输入的符号为正。）例如，具有其相关零交叉信号的典型输入信号可能是

在艾莉莎的系统中，传感器的信号表示为一个流sense_data，而流zero_crossings是相应的零交叉流。艾莉莎首先编写了一个名为sign_change_detector的函数，该函数将两个值作为参数并比较这些值的符号以产生适当的 0、1 或-1。然后她按照以下方式构造了她的零交叉流：

function make_zero_crossings(input_stream, last_value) {
    return pair(sign_change_detector(head(input_stream), last_value),
                () => make_zero_crossings(stream_tail(input_stream),
                                          head(input_stream)));
}
const zero_crossings = make_zero_crossings(sense_data, 0);

艾莉莎的老板伊娃·卢·阿特走过来，建议这个程序大致等同于以下使用练习 3.50 中的stream_map_2函数的程序：

const zero_crossings = stream_map_2(sign_change_detector,
                                    sense_data,
                                    expression);

通过提供指定的expression来完成程序。

练习 3.75

很遗憾，艾莉莎在练习 3.74 中的零交叉检测器证明是不够的，因为传感器的嘈杂信号导致了虚假的零交叉。硬件专家莱姆·E·特维基建议艾莉莎在提取零交叉之前*滑信号以滤除噪音。艾莉莎接受了他的建议，并决定从通过将感应数据的每个值与前一个值进行*均构造的信号中提取零交叉。她向助手路易斯·里森纳解释了问题，后者试图实施这个想法，修改了艾莉莎的程序如下：

function make_zero_crossings(input_stream, last_value) {
    const avpt = (head(input_stream) + last_value) / 2;
    return pair(sign_change_detector(avpt, last_value),
                () => make_zero_crossings(stream_tail(input_stream),
                                          avpt));
}

这并没有正确实现艾莉莎的计划。找到路易斯安装的错误并修复它，而不改变程序的结构。（提示：您需要增加make_zero_crossings的参数数量。）

练习 3.76

伊娃·卢·阿特对路易斯在练习 3.75 中的方法提出了批评。他写的程序不是模块化的，因为它混合了*滑操作和零交叉提取。例如，如果艾莉莎找到了更好的方法来调节她的输入信号，提取器就不应该被改变。通过编写一个名为smooth的函数来帮助路易斯，该函数以流作为输入并产生一个流，其中每个元素都是两个连续输入流元素的*均值。然后使用smooth作为组件以更模块化的方式实现零交叉检测器。

3.5.4 流和延迟求值

在前一节的最后，integral函数展示了我们如何使用流来模拟包含反馈环的信号处理系统。图 3.32 中所示的加法器的反馈环是通过integral的内部流integ是根据自身定义的事实来建模的：

const integ = pair(initial_value,
                   () => add_streams(scale_stream(integrand, dt),
                                     integ));

解释器处理这种隐式定义的能力取决于将对add_streams的调用包装在 lambda 表达式中所产生的延迟。没有这种延迟，解释器无法在求值对add_streams的调用之前构造integ，这将要求integ已经被定义。一般来说，这种延迟对于使用流来模拟包含循环的信号处理系统至关重要。没有延迟，我们的模型必须被制定为信号处理组件的任何输入在输出产生之前必须被完全求值。这将禁止循环。

很不幸，带有循环的系统的流模型可能需要超出迄今为止所见的流编程模式的延迟。例如，图 3.34 显示了一个信号处理系统，用于解决微分方程dy/dt = f(y)，其中f是一个给定的函数。图中显示了一个映射组件，它将f应用于其输入信号，并以一种非常类似于实际用于解决这类方程的模拟计算机电路的反馈环路连接到积分器。

图 3.34 一个解方程dy/dt = f(y)的“模拟计算机电路”。

假设我们对y有一个初始值y[0]，我们可以尝试使用以下函数来模拟这个系统

function solve(f, y0, dt) {
    const y = integral(dy, y0, dt);
    const dy = stream_map(f, y);
    return y;
}

这个函数不起作用，因为在solve的第一行中，对integral的调用要求定义输入dy，而这直到solve的第二行才发生。

另一方面，我们的定义意图是有意义的，因为原则上我们可以开始生成y流而不知道dy。实际上，integral和许多其他流操作可以在只有关于参数的部分信息时生成部分答案。对于integral，输出流的第一个元素是指定的initial_value。因此，我们可以在不求值被积函数dy的情况下生成输出流的第一个元素。一旦我们知道y的第一个元素，solve的第二行中的stream_map就可以开始工作来生成dy的第一个元素，这将产生y的下一个元素，依此类推。

为了利用这个想法，我们将重新定义integral，以期望积分流作为延迟参数。函数integral将强制积分在需要生成输出流的第一个元素时才被求值：

function integral(delayed_integrand, initial_value, dt) {
    const integ =
        pair(initial_value, 
             () => {
                 const integrand = delayed_integrand();
                 return add_streams(scale_stream(integrand, dt),
                                    integ);
             });
    return integ;
}

现在我们可以通过延迟y的声明中dy的求值来实现我们的solve函数：

function solve(f, y0, dt) {
    const y = integral(() => dy, y0, dt);
    const dy = stream_map(f, y);
    return y;
}

一般来说，integral的每个调用者现在都必须延迟被积函数的参数。我们可以通过计算微分方程dy/dt = y的解在y = 1处的值来证明solve函数的工作：

stream_ref(solve(y => y, 1, 0.001), 1000);
2.716923932235896

练习 3.77

上面使用的integral函数类似于第 3.5.2 节中整数无限流的“隐式”定义。或者，我们可以给出更像integers-starting-from（也在第 3.5.2 节中）的integral的定义：

function integral(integrand, initial_value, dt) {
    return pair(initial_value,
                is_null(integrand)
                ? null
                : integral(stream_tail(integrand),
                           dt * head(integrand) + initial_value,
                           dt));
}

在带有循环的系统中使用时，这个函数与我们原始版本的integral一样存在问题。修改函数，以便它期望integrand作为延迟参数，因此可以在上面显示的solve函数中使用。

练习 3.78

考虑设计一个信号处理系统来研究齐次二阶线性微分方程

输出流，对y进行建模，是由一个包含循环的网络生成的。这是因为d²y/dt²的值取决于y和dy/dt的值，而这两者都是通过对d²y/dt²进行积分来确定的。我们想要编码的图表如图 3.35 所示。编写一个名为solve_2nd的函数，该函数以常数a、b和dt以及y和dy/dt的初始值y[0]和dy[0]作为参数，并生成y的连续值流。

图 3.35 用于解决二阶线性微分方程的信号流图。

练习 3.79

将练习 3.78 的solve_2nd函数泛化，以便用于解决一般的二阶微分方程d²y/dt² = f (dy/dt, y)。

练习 3.80

串联 RLC 电路由一个电阻、一个电容和一个电感器串联而成，如图 3.36 所示。如果R、L和C分别是电阻、电感和电容，那么这三个元件的电压（v）和电流（i）之间的关系由以下方程描述

电路连接规定了关系

i[R] = i[L] = –i[C]

v[C] = v[L] + v[R]

结合这些方程表明电路的状态（由电容器两端的电压v[C]和电感器中的电流i[L]总结）由一对微分方程描述

表示这个微分方程系统的信号流图如图 3.37 所示。

图 3.36 一个串联 RLC 电路。

图 3.37 一个用于解决串联 RLC 电路的信号流图。

编写一个名为RLC的函数，该函数以电路的参数R、L和C以及时间增量dt作为参数。类似于练习 3.73 中的RC函数，RLC应该生成一个函数，该函数接受状态变量的初始值，5v[C0]和i[L0]，并生成状态v[C]和i[L]的流的一对（使用pair）。使用RLC，生成一对流，模拟具有R = 1欧姆、C = 0.2法拉、L = 1亨利、dt = 0.1秒和初始值i[L0] = 0安培和v[C0] = 10伏特的串联 RLC 电路的行为。

正常顺序求值

本节中的示例说明了延迟求值如何提供很大的编程灵活性，但这些示例也表明了这如何使我们的程序变得更加复杂。例如，我们的新integral函数赋予我们建模具有循环的系统的能力，但现在我们必须记住应该使用延迟的被积函数来调用integral，并且使用integral的每个函数都必须意识到这一点。实际上，我们创建了两类函数：普通函数和接受延迟参数的函数。通常情况下，创建不同类别的函数会迫使我们创建不同类别的高阶函数。⁷³

避免需要两种不同类别的函数的一种方法是使所有函数都采用延迟参数。我们可以采用一种求值模型，其中所有函数的参数都自动延迟，并且只有在实际需要时才强制参数（例如，当原始操作需要时）。这将使我们的语言转换为使用正则序求值，我们在 1.1.5 节介绍求值替换模型时首次描述了这一点。转换为正则序求值提供了一种统一而优雅的方式来简化延迟求值的使用，如果我们只关注流处理，这将是一种自然的策略。在 4.2 节中，我们在研究了求值器之后，将看到如何以这种方式转换我们的语言。不幸的是，在函数调用中包含延迟会破坏我们设计依赖事件顺序的程序的能力，例如使用赋值、改变数据或执行输入或输出的程序。即使在一对的尾部延迟也会造成很大的混乱，正如练习 3.51 和 3.52 所示。据人所知，可变性和延迟求值在编程语言中并不相容。

3.5.5 函数式程序的模块化和对象的模块化

正如我们在 3.1.2 节中看到的，引入赋值的主要好处之一是，我们可以通过将大系统的部分状态封装或“隐藏”在局部变量中来增加系统的模块化。流模型可以在不使用赋值的情况下提供等效的模块化。举例来说，我们可以从流处理的角度重新实现我们在 3.1.2 节中研究的π的蒙特卡洛估计。

关键的模块化问题是，我们希望隐藏随机数生成器的内部状态，不让使用随机数的程序知道。我们从一个名为rand_update的函数开始，它的连续值提供了我们的随机数供应，并用它来生成一个随机数生成器：

function make_rand() {
    let x = random_init;
    return () => {
               x = rand_update(x);
               return x;
           };
}
const rand = make_rand();

在流的表述中，没有随机数生成器per se，只是通过连续调用rand_update产生的随机数流：

const random_numbers =
    pair(random_init,
         () => stream_map(rand_update, random_numbers));

我们用这个来构建在random_numbers流中对连续对执行的 Cesàro 实验结果的流：

function map_successive_pairs(f, s) {
    return pair(f(head(s), head(stream_tail(s))),
                () => map_successive_pairs(
                          f,
                          stream_tail(stream_tail(s))));
}
const dirichlet_stream =
    map_successive_pairs((r1, r2) => gcd(r1, r2) === 1,
                         random_numbers);

现在dirichlet_stream被输入到monte_carlo函数中，它产生一个概率估计的流。然后将结果转换为π的估计流。这个程序的版本不需要一个告诉要执行多少次试验的参数。通过查看pi流的更远处，可以获得更好的π估计（通过进行更多的实验）：

function monte_carlo(experiment_stream, passed, failed) {
    function next(passed, failed) {
        return pair(passed / (passed + failed),
                    () => monte_carlo(stream_tail(experiment_stream),
                                      passed, failed));
    }
    return head(experiment_stream)
           ? next(passed + 1, failed)
           : next(passed, failed + 1);
}
const pi = stream_map(p => math_sqrt(6 / p),
                      monte_carlo(dirichlet_stream, 0, 0));

这种方法具有相当的模块化，因为我们仍然可以制定一个通用的monte_carlo函数，可以处理任意的实验。但是没有赋值或局部状态。

练习 3.81

练习 3.6 讨论了将随机数生成器泛化，以允许重新设置随机数序列，从而产生可重复的“随机”数列。以此相同生成器的流形式进行一个流的表述，它在一个请求输入流上操作，请求是"generate"一个新的随机数或"reset"序列到指定值，并产生所需的随机数流。在你的解决方案中不要使用赋值。

练习 3.82

重新进行练习 3.5，使用流的术语进行蒙特卡洛积分。estimate_integral的流版本不会有一个告诉要执行多少次试验的参数。相反，它将产生基于越来越多试验的估计流。

时间的函数式编程视图

现在让我们回到本章开头提出的对象和状态问题，并从一个新的角度来审视它们。我们引入了赋值和可变对象，以提供一种模块化构建具有状态的系统的程序的机制。我们使用本地状态变量构建了计算对象，并使用赋值来修改这些变量。我们通过相应的计算对象的时间行为来模拟对象在世界中的时间行为。

现在我们已经看到，流提供了一种用本地状态模拟对象的替代方式。我们可以使用表示连续状态的时间历史的流来模拟变化的数量，例如某个对象的本地状态。实质上，我们使用流明确表示时间，这样我们就可以将模拟世界中的时间与求值过程中发生的事件序列分离开来。实际上，由于延迟求值的存在，模型中模拟的时间与求值过程中事件的顺序可能几乎没有关系。

为了对比这两种建模方法，让我们重新考虑一下监视银行账户余额的“取款处理器”的实现。在 3.1.3 节中，我们实现了一个简化版本的这样一个处理器：

function make_simplified_withdraw(balance) {
    return amount => {
               balance = balance - amount;
               return balance;
           };
}

对make_simplified_withdraw的调用会产生计算对象，每个对象都有一个名为balance的本地状态变量，该变量会随着对对象的连续调用而递减。该对象接受一个amount作为参数，并返回新的余额。我们可以想象银行账户的用户输入一系列输入到该对象中，并观察显示屏上显示的返回值序列。

或者，我们可以将取款处理器建模为一个函数，该函数以余额和要取款的金额流作为输入，并产生账户中连续余额的流：

function stream_withdraw(balance, amount_stream) {
    return pair(balance,
                () => stream_withdraw(balance - head(amount_stream),
                                      stream_tail(amount_stream)));
}

函数stream_withdraw实现了一个明确定义的数学函数，其输出完全由其输入确定。然而，假设输入amount_stream是用户输入的连续值的流，而结果余额的流被显示。那么，从输入值和观察结果的用户的角度来看，流程过程与make_simplified_withdraw创建的对象具有相同的行为。然而，使用流版本，没有赋值，没有本地状态变量，因此也没有我们在 3.1.3 节中遇到的理论困难。然而，系统具有状态！

这真是非常了不起。即使stream_withdraw实现了一个行为不会改变的明确定义的数学函数，用户在这里的感知是在与一个具有变化状态的系统进行交互。解决这个悖论的一种方法是意识到是用户的时间存在给系统带来了状态。如果用户能够从交互中退出，并考虑余额流而不是单独的交易，系统将显得没有状态。⁷⁴

从复杂过程的某一部分的角度来看，其他部分似乎随时间变化。它们具有隐藏的时间变化的本地状态。如果我们希望编写模拟我们世界中这种自然分解的程序（从我们作为该世界一部分的视角来看），并在我们的计算机中使用结构，我们将创建不是功能性的计算对象——它们必须随时间变化。我们使用本地状态变量来模拟状态，并使用对这些变量的赋值来模拟状态的变化。通过这样做，我们使计算模型的执行时间成为我们所在世界的时间，因此我们在计算机中得到了“对象”。

用对象建模是强大且直观的，主要是因为这与我们与之交互的世界的感知相匹配。然而，正如我们在本章中反复看到的那样，这些模型引发了关于约束事件顺序和同步多个进程的棘手问题。避免这些问题的可能性刺激了函数式编程语言的发展，这些语言不包括任何关于赋值或可变数据的规定。在这样的语言中，所有函数都实现其参数的明确定义的数学函数，其行为不会改变。函数式方法对处理并发系统非常有吸引力。

另一方面，如果我们仔细观察，我们也可以看到与时间相关的问题潜入了函数式模型。当我们希望设计交互式系统，特别是模拟独立实体之间的交互时，一个特别棘手的领域就会出现。例如，再次考虑允许联合银行账户的银行系统的实现。在使用赋值和对象的传统系统中，我们将彼得和保罗共享一个账户的事实建模为彼得和保罗都将其交易请求发送到同一个银行账户对象，正如我们在 3.1.3 节中所看到的。从流的角度来看，本质上没有“对象”，我们已经指出银行账户可以被建模为一个处理交易请求流以产生响应流的过程。因此，我们可以通过合并彼得的交易请求流和保罗的请求流，并将结果馈送到银行账户流程，来建模彼得和保罗共有一个联合银行账户，如图 3.38 所示。

图 3.38 一个联合银行账户，通过合并两个交易请求流来建模。

这种表述的问题在于合并的概念。不能简单地通过交替从彼得和保罗那里获取交易请求来合并这两个流。假设保罗很少访问账户。我们几乎无法强迫彼得等待保罗访问账户，然后才能发出第二笔交易。无论如何实现这样的合并，它都必须以某种方式交错这两个交易流，这种方式受到“彼得和保罗感知的”真实时间的约束，即如果彼得和保罗相遇，他们可以同意某些交易在会面之前被处理，而其他交易在会面之后被处理。这正是我们在 3.4.1 节中需要处理的约束，我们发现需要引入显式同步来确保并发处理具有状态对象的事件的“正确”顺序。因此，在支持函数式风格的尝试中，合并来自不同代理的输入重新引入了函数式风格旨在消除的相同问题。

我们开始本章的目标是构建计算模型，其结构与我们试图建模的真实世界的感知相匹配。我们可以将世界建模为一组独立的、有时间限制的、相互作用的具有状态的对象，或者我们可以将世界建模为一个单一的、无时间的、无状态的统一体。每种观点都有强大的优势，但单独的观点都不完全令人满意。一个宏伟的统一尚未出现。

四、元语言抽象

原文：4 Metalinguistic Abstraction

译者：飞龙

协议：CC BY-NC-SA 4.0

...魔法就在于文字——Abracadabra，开门，以及其他——但一个故事中的魔法词在另一个故事中并不神奇。真正的魔法是理解哪些词起作用，何时起作用，以及为什么起作用；诀窍就是学会这个诀窍。

...而这些词是由我们字母表的字母组成的：我们可以用笔画出的几十个波浪线。这就是关键！如果我们能得到这个关键，也是宝藏！就好像——好像宝藏的关键就是宝藏！

——约翰·巴斯，《奇美拉》

在我们对程序设计的研究中，我们已经看到，专业程序员使用与所有复杂系统设计者使用的相同的一般技术来控制设计的复杂性。他们将原始元素组合成复合对象，将复合对象抽象成更高级的构建块，并通过采用适当的系统结构的大规模视图来保持模块化。在说明这些技术时，我们使用 JavaScript 作为描述过程和构建计算数据对象和过程的语言，以模拟现实世界中复杂现象。然而，随着我们面对越来越复杂的问题，我们会发现 JavaScript，或者任何固定的编程语言，都无法满足我们的需求。为了更有效地表达我们的想法，我们必须不断转向新的语言。建立新语言是控制工程设计复杂性的强大策略；通过采用新语言，我们经常可以增强处理复杂问题的能力，使我们能够以不同的方式描述（因此思考）问题，使用特别适合手头问题的原语、组合手段和抽象手段。¹

编程赋予了多种语言。有物理语言，比如特定计算机的机器语言。这些语言涉及数据和控制的表示，以存储的个别位和原始机器指令。机器语言程序员关心如何利用给定的硬件来建立系统和实用程序，以有效地实现资源有限的计算。高级语言建立在机器语言基础上，隐藏了关于数据表示和程序表示的担忧，这些语言具有组合和抽象的手段，比如函数声明，适用于系统的大规模组织。

元语言抽象——建立新语言——在所有工程设计领域都起着重要作用。对于计算机编程来说尤为重要，因为在编程中，我们不仅可以制定新语言，还可以通过构建求值器来实现这些语言。编程语言的求值器（或解释器）是一个函数，当应用于语言的语句或表达式时，执行求值该语句或表达式所需的操作。把这看作编程中最基本的想法绝非夸大：

确定编程语言中语句和表达式的含义的求值器只是另一个程序。

要理解这一点就是改变我们作为程序员的形象。我们开始把自己看作语言的设计者，而不仅仅是他人设计的语言的使用者。

事实上，我们几乎可以将任何程序视为某种语言的求值器。例如，第 2.5.3 节的多项式处理系统体现了多项式算术规则，并将其实现为对列表结构数据的操作。如果我们增加这个系统的函数来读取和打印多项式表达式，我们就有了一个处理符号数学问题的特定目的语言的核心。第 3.3.4 节的数字逻辑模拟器和第 3.3.5 节的约束传播器本身就是合法的语言，每种语言都有自己的原语、组合手段和抽象手段。从这个角度来看，应对大规模计算机系统的技术与构建新计算机语言的技术融为一体，计算机科学本身不再（也不会更少）只是构建适当描述性语言的学科。

我们现在开始了解语言建立在其他语言基础上的技术之旅。在本章中，我们将以 JavaScript 为基础，将求值器实现为 JavaScript 函数。我们将通过为 JavaScript 本身构建一个求值器来迈出理解语言如何实现的第一步。我们的求值器实现的语言将是 JavaScript 的一个子集。尽管本章描述的求值器是针对 JavaScript 的特定子集编写的，但它包含了为顺序机器编写程序设计语言的求值器的基本结构。（事实上，大多数语言处理器深藏其中一个小型求值器。）为了说明和讨论的目的，求值器已经简化，并且一些重要的特性被省略了，这些特性对于生产质量的 JavaScript 系统来说是重要的。然而，这个简单的求值器足以执行本书中大部分的程序。

将求值器作为 JavaScript 程序可访问的一个重要优势是，我们可以通过将其描述为对求值器程序的修改来实现替代求值规则。我们可以利用这种能力的一个地方是，以更好的效果获得对计算模型体现时间概念的额外控制，这在第 3 章的讨论中是如此核心。在那里，我们通过使用流来解耦世界中的时间表示与计算机中的时间，来减轻一些状态和赋值的复杂性。然而，我们的流程序有时会很笨重，因为它们受到 JavaScript 的应用顺序求值的限制。在 4.2 节中，我们将改变基础语言，以提供更优雅的方法，通过修改求值器来提供正则顺序求值。

第 4.3 节实现了一个更有雄心的语言变化，即语句和表达式具有多个值，而不仅仅是一个单一值。在这种非确定性计算语言中，自然地表达生成所有可能值的过程，然后搜索满足某些约束的值。就计算模型和时间而言，这就像时间分支成一组“可能的未来”，然后搜索适当的时间线。通过我们的非确定性求值器，跟踪多个值和执行搜索都由语言的基础机制自动处理。

在第 4.4 节中，我们实现了一种逻辑编程语言，其中知识是以关系的形式表达，而不是以输入和输出的计算形式。尽管这使得语言与 JavaScript 或任何传统语言都大不相同，但我们将看到逻辑编程求值器与 JavaScript 求值器共享基本结构。

4.1 元循环求值器

我们的 JavaScript 求值器将作为 JavaScript 程序实现。用 JavaScript 实现 JavaScript 程序的求值似乎是循环的。然而，求值是一个过程，因此用 JavaScript 描述求值过程是合适的，毕竟，这是我们描述过程的工具。³ 用相同语言编写的求值器被称为元循环求值器。

元循环求值器本质上是对 3.2 节中描述的求值环境模型的 JavaScript 表述。回想一下，该模型指定了函数应用的求值有两个基本步骤：

1. 求值函数应用时，首先求值子表达式，然后将函数子表达式的值应用于参数子表达式的值。
2. 将复合函数应用于一组参数时，求值函数体在新环境中。为构造此环境，通过将函数对象的环境部分扩展为函数的参数绑定到应用函数的参数的帧。

这两条规则描述了求值过程的本质，即在环境中要求值的语句和表达式被简化为要应用于参数的函数，然后再简化为在新环境中要求值的新语句和表达式，依此类推，直到我们到达名称，其值在环境中查找，以及运算符和原始函数，这些直接应用（见图 4.1）。⁴ 这种求值循环将由求值器中两个关键函数evaluate和apply之间的相互作用体现出来，这些函数在 4.1.1 节中描述（见图 4.1）。

图 4.1 evaluate-apply循环揭示了计算机语言的本质。

求值器的实现将依赖于定义要求值的语句和表达式的语法的函数。我们将使用数据抽象使求值器独立于语言的表示。例如，我们不会选择将赋值表示为以名称开头后跟=的字符串，而是使用抽象谓词is_assignment来测试赋值，并使用抽象选择器assignment_symbol和assignment_value_expression来访问赋值的部分。4.1.2 节中提出的数据抽象层将使求值器保持独立于具体的语法问题，例如解释语言的关键字，以及表示程序组件的数据结构的选择。还有在 4.1.3 节中描述的操作，用于指定函数和环境的表示。例如，make_function构造复合函数，lookup_symbol_value访问名称的值，apply_primitive_function将原始函数应用于给定的参数列表。

4.1.1 求值器的核心

求值过程可以描述为evaluate和apply两个函数之间的相互作用。

函数`evaluate`

函数evaluate以程序组件（语句或表达式）和环境作为参数。它对组件进行分类并指导其求值。函数evaluate被构造为对要求值的组件的句法类型进行案例分析。为了保持函数的一般性，我们抽象地表达了组件类型的确定，不对各种组件类型的具体表示做出承诺。每种组件类型都有一个语法谓词来测试它，并选择其部分的抽象手段。这种抽象语法使我们可以通过使用相同的求值器，但使用不同的语法函数集合来轻松地看到如何改变语言的语法。

原始表达式

对于文字表达式，比如数字，evaluate返回它们的值。
函数evaluate必须在环境中查找名称以找到它们的值。

组合

对于函数应用，evaluate必须递归求值应用的函数表达式和参数表达式。得到的函数和参数被传递给apply，后者处理实际的函数应用。
操作符组合被转换为函数应用，然后进行求值。

句法形式

条件表达式或语句需要对其部分进行特殊处理，以便在谓词为真时求值结果，否则求值替代方案。
λ表达式必须通过将λ表达式指定的参数和主体与求值的环境一起打包，转换为可应用的函数。
一系列语句需要按照它们出现的顺序求值其组件。
一个块需要在反映块内声明的所有名称的新环境中求值其主体。
返回语句必须产生一个值，该值成为导致返回语句求值的函数调用的结果。
函数声明被转换为常量声明，然后进行求值。
常量或变量声明或赋值必须调用evaluate进行递归计算，以计算与正在声明或分配的名称关联的新值。必须修改环境以反映名称的新值。

这是evaluate的声明：

function evaluate(component, env) {
    return is_literal(component)
           ? literal_value(component)
           : is_name(component)
           ? lookup_symbol_value(symbol_of_name(component), env)
           : is_application(component)
           ? apply(evaluate(function_expression(component), env),
                   list_of_values(arg_expressions(component), env))
           : is_operator_combination(component)
           ? evaluate(operator_combination_to_application(component), env)
           : is_conditional(component)
           ? eval_conditional(component, env)
           : is_lambda_expression(component)
           ? make_function(lambda_parameter_symbols(component),
                           lambda_body(component), env)
           : is_sequence(component)
           ? eval_sequence(sequence_statements(component), env)
           : is_block(component)
           ? eval_block(component, env)
           : is_return_statement(component)
           ? eval_return_statement(component, env)
           : is_function_declaration(component)
           ? evaluate(function_decl_to_constant_decl(component), env)
           : is_declaration(component)
           ? eval_declaration(component, env)
           : is_assignment(component)
           ? eval_assignment(component, env)
           : error(component, "unknown syntax – evaluate");
}

为了清晰起见，evaluate已经被实现为使用条件表达式的案例分析。这样做的缺点是，我们的函数只处理了一些可区分的语句和表达式类型，而且没有新的类型可以在不编辑evaluate的声明的情况下定义。在大多数解释器实现中，根据组件的类型进行分派是以数据导向的方式进行的。这允许用户添加evaluate可以区分的新类型的组件，而无需修改evaluate本身的声明。（见练习 4.3。）

名称的表示由语法抽象处理。在内部，求值器使用字符串来表示名称，我们将这样的字符串称为符号。函数evaluate中使用的symbol_of_name从名称中提取其表示的符号。

应用

函数apply接受两个参数，一个函数和一个应用该函数的参数列表。函数apply将函数分类为两种：它调用apply_primitive_function来应用原始函数；它通过求值组成函数主体的块来应用复合函数。复合函数的主体的求值环境是通过扩展函数携带的基本环境来构建的，以包括将函数的参数绑定到要应用函数的参数的帧。这是apply的声明：

function apply(fun, args) {
    if (is_primitive_function(fun)) {
        return apply_primitive_function(fun, args);
    } else if (is_compound_function(fun)) {
        const result = evaluate(function_body(fun),
                               extend_environment(
                                   function_parameters(fun),
                                   args,
                                   function_environment(fun)));
        return is_return_value(result)
               ? return_value_content(result)
               : undefined;
    } else {
        error(fun, "unknown function type – apply");
    }
}

为了返回一个值，JavaScript 函数需要求值一个返回语句。如果一个函数在不求值返回语句的情况下终止，将返回值undefined。为了区分这两种情况，返回语句的求值将返回表达式的结果包装成一个返回值。如果函数体的求值产生了这样一个返回值，就会检索返回值的内容；否则将返回值undefined。⁶

函数参数

当evaluate处理函数应用时，它使用list_of_values来生成要应用函数的参数列表。函数list_of_values以应用的参数表达式作为参数。它求值每个参数表达式并返回相应值的列表：⁷

function list_of_values(exps, env) {
    return map(arg => evaluate(arg, env), exps);
}

条件语句

函数eval_conditional求值给定环境中条件组件的谓词部分。如果结果为真，则求值结果，否则求值替代结果：

function eval_conditional(component, env) {
    return is_truthy(evaluate(conditional_predicate(component), env))
           ? evaluate(conditional_consequent(component), env)
           : evaluate(conditional_alternative(component), env);
}

请注意，求值器不需要区分条件表达式和条件语句。

在eval_conditional中使用is_truthy突出了实现语言和实现语言之间的连接问题。conditional_predicate在正在实现的语言中进行求值，因此产生该语言中的一个值。解释器谓词is_truthy将该值转换为可以由实现语言中的条件表达式测试的值：真实的元循环表示可能与底层 JavaScript 的表示不同。⁸

序列

函数eval_sequence由evaluate用于求值顶层或块中的语句序列。它以语句序列和环境作为参数，并按照它们出现的顺序求值这些语句。返回的值是最终语句的值，但如果序列中任何语句的求值产生了返回值，那么将返回该值，并且忽略后续的语句。⁹

function eval_sequence(stmts, env) {
    if (is_empty_sequence(stmts)) {
        return undefined;
    } else if (is_last_statement(stmts)) {
        return evaluate(first_statement(stmts), env);
    } else {
        const first_stmt_value =
            evaluate(first_statement(stmts), env);
        if (is_return_value(first_stmt_value)) {
            return first_stmt_value;
        } else {
            return eval_sequence(rest_statements(stmts), env);
        }
    }
}

块

函数eval_block处理块。在块中声明的变量和常量（包括函数）具有整个块作为它们的作用域，因此在求值块的主体之前会“扫描出”它们。块的主体是根据通过将每个本地名称绑定到特殊值"unassigned"来扩展当前环境的环境进行求值。这个字符串作为一个占位符，在声明求值之前，访问名称的值会导致运行时错误（见第 1 章脚注 56 中的练习 4.12）。

function eval_block(component, env) {
    const body = block_body(component);
    const locals = scan_out_declarations(body);
    const unassigneds = list_of_unassigned(locals);
    return evaluate(body, extend_environment(locals,
                                             unassigneds,
                                             env));
}
function list_of_unassigned(symbols) {
    return map(symbol => "unassigned", symbols);
}

函数scan_out_declarations收集在函数体中声明的所有符号名称的列表。它使用declaration_symbol从找到的声明语句中检索表示名称的符号。

function scan_out_declarations(component) {
    return is_sequence(component)
           ? accumulate(append,
                        null,
                        map(scan_out_declarations,
                            sequence_statements(component)))
           : is_declaration(component)
           ? list(declaration_symbol(component))
           : null;
}

我们忽略嵌套在另一个块中的声明，因为该块的求值会处理它们。函数scan_out_declarations只在序列中查找声明，因为条件语句、函数声明和 lambda 表达式中的声明总是在嵌套块中。

返回语句

函数eval_return_statement用于求值返回语句。正如在apply和序列的求值中所看到的，返回语句的求值结果需要是可识别的，以便函数体的求值可以立即返回，即使在返回语句之后还有语句。为此，返回语句的求值将返回表达式的求值结果包装在一个返回值对象中。¹⁰

function eval_return_statement(component, env) {
    return make_return_value(evaluate(return_expression(component),
                                      env));
}

赋值和声明

函数eval_assignment处理对名称的赋值。（为了简化我们的求值器的表示，我们不仅允许对变量进行赋值，还允许对常量进行错误的赋值。练习 4.11 解释了我们如何区分常量和变量，并防止对常量进行赋值。）函数eval_assignment调用值表达式上的evaluate来找到要赋值的值，并调用assignment_symbol来检索表示名称的符号。函数eval_assignment将符号和值传递给assign_symbol_value，以安装在指定环境中。赋值的求值返回被赋的值。

function eval_assignment(component, env) {
    const value = evaluate(assignment_value_expression(component),
                           env);
    assign_symbol_value(assignment_symbol(component), value, env);
    return value;
}

常量和变量声明都由is_declaration语法谓词识别。它们的处理方式类似于赋值，因为eval_block已经将它们的符号绑定到当前环境中的"unassigned"。它们的求值将"unassigned"替换为值表达式的求值结果。

function eval_declaration(component, env) {
    assign_symbol_value(
        declaration_symbol(component),
        evaluate(declaration_value_expression(component), env), env);
    return undefined;
}

函数的返回值由return语句确定，因此eval_declaration中的返回值undefined只在声明发生在顶层，即在任何函数体之外时才重要。在这里，我们使用返回值undefined来简化表示；练习 4.8 描述了在 JavaScript 中求值顶层组件的真实结果。

练习 4.1

请注意，我们无法确定元循环求值器是从左到右还是从右到左求值参数表达式。它的求值顺序是从底层 JavaScript 继承的：如果map中pair的参数是从左到右求值的，那么list_of_values将从左到右求值参数表达式；如果pair的参数是从右到左求值的，那么list_of_values将从右到左求值参数表达式。

编写一个list_of_values的版本，无论底层 JavaScript 的求值顺序如何，都从左到右求值参数表达式。还要编写一个list_of_values的版本，从右到左求值参数表达式。

4.1.2 表示组件

程序员将程序编写为文本，即一系列以编程环境或文本编辑器输入的字符。要运行我们的求值器，我们需要从 JavaScript 值开始表示这个程序文本。在 2.3.1 节中，我们介绍了字符串来表示文本。我们希望求值诸如 1.1.2 节中的"const size = 2; 5 * size;"之类的程序。不幸的是，这样的程序文本并不能为求值器提供足够的结构。在这个例子中，程序部分"size = 2"和"5 * size"看起来相似，但含义完全不同。通过检查程序文本来实现抽象语法函数，如declaration_value_expression，将会很困难且容易出错。因此，在本节中，我们引入了一个名为parse的函数，将程序文本转换为标记列表表示，类似于 2.4.2 节的标记数据。例如，对上面的程序字符串应用parse会产生一个反映程序结构的数据结构：一个序列，其中包含一个将名称size与值 2 关联起来的常量声明和一个乘法。

parse("const size = 2; 5 * size;");
list("sequence",
     list(list("constant_declaration",
               list("name", "size"), list("literal", 2)),
          list("binary_operator_combination", "*",
               list("literal", 5), list("name", "size"))))

求值器使用的语法函数访问parse产生的标记列表表示。

求值器类似于第 2.3.2 节讨论的符号微分程序。这两个程序都操作符号数据。在这两个程序中，对对象进行操作的结果是通过递归地对对象的部分进行操作，并以一种取决于对象类型的方式将结果组合起来。在这两个程序中，我们使用数据抽象来将操作的一般规则与对象的表示方式分离开来。在微分程序中，这意味着相同的微分函数可以处理前缀形式的代数表达式，中缀形式的代数表达式，或者其他形式的代数表达式。对于求值器，这意味着被求值的语言的语法完全由parse和分类和提取parse产生的标记列表的部分的函数确定。

图 4.2 描述了由语法谓词和选择器形成的抽象屏障，这些语法谓词和选择器将求值器与程序的标记列表表示接口，这又与字符串表示由parse分隔开。下面我们描述程序组件的解析，并列出相应的语法谓词和选择器，以及如果需要的话的构造函数。

图 4.2 求值器中的语法抽象。

文字表达式

文字表达式被解析为带有标签"literal"和实际值的标记列表。

《literal-expression 》 = list("literal", value)

其中value是由literal-expression字符串表示的 JavaScript 值。这里《literal-expression》表示解析字符串literal-expression的结果。

parse("1;");
list("literal", 1)

parse("'hello world';");
list("literal", "hello world")

parse("null;");
list("literal", null)

文字表达式的语法谓词是is_literal。

function is_literal(component) {
   return is_tagged_list(component, "literal");
}

它是根据函数is_tagged_list定义的，该函数标识以指定字符串开头的列表：

function is_tagged_list(component, the_tag) {
   return is_pair(component) && head(component) === the_tag;
}

解析文字表达式产生的列表的第二个元素是其实际的 JavaScript 值。用于检索值的选择器是literal_value。

function literal_value(component) {
   return head(tail(component));
}

literal_value(parse("null;"));
null

在本节的其余部分，我们只列出语法谓词和选择器，并省略它们的声明，如果它们只是访问明显的列表元素。

我们为文字提供了一个构造函数，这将很方便：

function make_literal(value) {
   return list("literal", value);
}

名称

名称的标记列表表示包括标签"name"作为第一个元素和表示名称的字符串作为第二个元素。

《 name 》 = list("name", symbol)

其中symbol是一个包含构成程序中name的字符的字符串。名称的语法谓词是is_name。可以使用选择器symbol_of_name访问符号。我们为名称提供了一个构造函数，供operator_combination_to_application使用：

function make_name(symbol) {
   return list("name", symbol);
}

表达式语句

我们不需要区分表达式和表达式语句。因此，parse可以忽略这两种组件之间的区别：

《 expression; 》 = 《 expression 》

函数应用

函数应用的解析如下：

《 fun-expr(arg-expr[1], ..., arg-expr[n]) 》=
     list("application",
          《 fun-expr 》,
          list(《 arg-expr[1] 》, ..., 《 arg-expr[n] 》))

我们将is_application声明为语法谓词，function_expression和arg_expressions作为选择器。我们添加了一个函数应用的构造函数，供operator_combination_to_application使用：

function make_application(function_expression, argument_expressions) {
    return list("application",
                function_expression, argument_expressions);
}

条件

条件表达式的解析如下：

《 predicate ? consequent-expression : alternative-expression 》=
         list("conditional_expression",
              《 predicate 》,
              《 consequent-expression 》,
              《 alternative-expression 》)

类似地，条件语句的解析如下：

《 if (predicate) consequent-block else alternative-block 》=
         list("conditional_statement",
              《 predicate 》,
              《 consequent-block 》,
              《 alternative-block 》)

语法谓词is_conditional对两种条件都返回true，选择器conditional_predicate，conditional_consequent和conditional_alternative可以应用于两种条件。

Lambda 表达式

解析主体为表达式的 lambda 表达式，就好像主体由包含单个返回语句的块解析，返回表达式是 lambda 表达式的主体。

《 (name[1], ..., name[n]) => expression 》 =
    《 (name[1], ..., name[n]) => { return expression ; } 》

解析主体为块的 lambda 表达式如下：

《 (name[1], ..., name[n]) => block 》=
    list("lambda_expression",
     list(《 name[1] 》, ..., 《 name[n] 》),
     《 block 》)

语法谓词是is_lambda_expression，lambda 表达式的主体选择器是lambda_body。称为lambda_parameter_symbols的参数选择器还从名称中提取符号。

function lambda_parameter_symbols(component) {
    return map(symbol_of_name, head(tail(component)));
}

函数function_decl_to_constant_decl需要一个 lambda 表达式的构造函数：

function make_lambda_expression(parameters, body) {
    return list("lambda_expression", parameters, body);
}

序列

序列语句将一系列语句打包成一个单独的语句。语句序列的解析如下：

《 statement[1] ... statement[n] 》 =
      list("sequence", list(《 statement[1] 》, ..., 《 statement[n] 》))

语法谓词是is_sequence，选择器是sequence_statements。我们使用first_statement检索语句列表的第一个语句，使用rest_statements检索剩余的语句。我们使用谓词is_empty_sequence测试列表是否为空，并使用谓词is_last_statement测试列表是否只包含一个元素。¹¹

function first_statement(stmts) { return head(stmts); }
function rest_statements(stmts) { return tail(stmts); }
function is_empty_sequence(stmts) { return is_null(stmts); }
function is_last_statement(stmts) { return is_null(tail(stmts)); }

块

块的解析如下：¹²

《 { statements } 》 = list("block", 《 statements 》 )

这里statements指的是一系列语句，如上所示。语法谓词是is_block，选择器是block_body。

返回语句

返回语句的解析如下：

《 return expression; 》 = list("return_statement", 《 expression 》 )

语法谓词和选择器分别是is_return_statement和return_expression。

赋值

赋值的解析如下：

《 name = expression 》 = list("assignment", 《 name 》 , 《 expression 》 )

语法谓词是is_assignment，选择器是assignment_symbol和assignment_value_expression。符号包装在表示名称的标记列表中，因此assignment_symbol需要将其解包。

function assignment_symbol(component) {
    return symbol_of_name(head(tail(component))));
}

常量、变量和函数声明

常量和变量声明的解析如下：

《 const name = expression; 》 =
    list("constant_declaration", 《 name 》, 《 expression 》)
《 let name = expression; 》 =
    list("variable_declaration", 《 name 》, 《 expression 》)

选择器declaration_symbol和declaration_value_expression适用于两种情况。

function declaration_symbol(component) {
    return symbol_of_name(head(tail(component)));
}
function declaration_value_expression(component) {
    return head(tail(tail(component)));
}

函数function_decl_to_constant_decl需要一个常量声明的构造函数：

function make_constant_declaration(name, value_expression) {
    return list("constant_declaration", name, value_expression);
}

函数声明的解析如下：

function name(name[1], ... name[n]) block 》=
    list("function_declaration",
     《 name 》,
     list(《 name[1] 》, ..., 《 name[n] 》),
     《 block 》)

语法谓词is_function_declaration识别这些。选择器是function_declaration_name，function_declaration_parameters和function_declaration_body。

语法谓词is_declaration对所有三种声明返回true。

function is_declaration(component) {
    return is_tagged_list(component, "constant_declaration") ||
           is_tagged_list(component, "variable_declaration") ||
           is_tagged_list(component, "function_declaration");
}

派生组件

我们语言中的一些语法形式可以根据涉及其他语法形式的组件来定义，而不是直接实现。一个例子是函数声明，evaluate将其转换为值表达式为 lambda 表达式的常量声明。¹³

function function_decl_to_constant_decl(component) {
    return make_constant_declaration(
               function_declaration_name(component),
               make_lambda_expression(
                   function_declaration_parameters(component),
                   function_declaration_body(component)));
}

以这种方式实现函数声明的求值简化了求值器，因为它减少了必须明确指定求值过程的语法形式的数量。

同样，我们定义操作符组合以函数应用的形式。操作符组合是一元或二元的，并且在标记列表表示中携带其操作符符号作为第二个元素：

《 unary-operator expression 》=
    list("unary_operator_combination",
         "unary-operator",
         list(《 expression 》))

其中*是!（逻辑否定）或-unary（数值否定），并且

《 expression[1] binary-operator expression[2] 》=
    list("binary_operator_combination",
         "binary-operator",
         list(《 expression[1] 》, 《 expression[2] 》))

其中binary-operator是+，-，*，/，%，===，!==，>，<，>=或<=。语法谓词是is_operator_combination，is_unary_operator_combination和is_binary_operator_combination，选择器是operator_symbol，first_operand和second_operand。

求值器使用operator_combination_to_application将操作符组合转换为一个函数应用，其函数表达式是操作符的名称：

function operator_combination_to_application(component) {
    const operator = operator_symbol(component);
    return is_unary_operator_combination(component)
           ? make_application(make_name(operator),
                              list(first_operand(component)))
           : make_application(make_name(operator),
                              list(first_operand(component),
                                   second_operand(component)));
}

我们选择将组件（如函数声明和操作符组合）实现为语法转换的派生组件。逻辑组合操作也是派生组件（参见练习 4.4）。

练习 4.2

parse的逆操作称为unparse。它以parse生成的标记列表作为参数，并返回一个符合 JavaScript 表示的字符串。

a. 按照evaluate的结构（不包括环境参数），编写一个名为unparse的函数，但是产生一个表示给定组件的字符串，而不是对其进行求值。回想一下，从第 3.3.4 节中得知，操作符+可以应用于两个字符串以将它们连接起来，原始函数stringify将值（如 1.5、true、null和undefined）转换为字符串。请注意，通过使用括号（总是或在必要时）括起来，以保持操作符的优先级。
b. 在解决本节中的后续练习时，您的unparse函数会派上用场。通过向结果字符串添加" "（空格）和"\n"（换行）字符，以遵循本书中 JavaScript 程序中使用的缩进样式，改进unparse。为了使文本更易于阅读，向程序文本中添加（或删除）此类空白字符称为美化打印。

练习 4.3

重写evaluate，以便以数据导向的方式进行分派。将此与练习 2.73 中的数据导向微分函数进行比较。（您可以使用标记列表表示的标记作为组件类型。）

练习 4.4

回想一下，从第 1.1.6 节中得知，逻辑组合操作&&和||是条件表达式的语法糖：逻辑连接expression[1] && expression[2]是expression[1] ? expression[2] : false的语法糖，逻辑析取expression[1] || expression[2]是expression[1] ? true : expression[2]的语法糖。它们的解析如下：

《 expression[1] logical-operation expression[2] 》=
    list("logical_composition",
         "logical-operation",
         list(《 expression[1]  》, 《 expression[2]  》))

其中logical-operation是&&或||。通过声明适当的语法函数和求值函数eval_and和eval_or，将&&和||作为求值器的新语法形式。或者，展示如何将&&和||实现为派生组件。

练习 4.5

a. 在 JavaScript 中，lambda 表达式不能具有重复参数。第 4.1.1 节中的求值器没有检查这一点。
- 修改求值器，以便任何尝试应用具有重复参数的函数都会发出错误信号。
- 实现一个verify函数，检查给定程序中的任何 lambda 表达式是否包含重复参数。有了这样一个函数，我们可以在将其传递给evaluate之前检查整个程序。
为了在 JavaScript 的求值器中实现此检查，您更喜欢这两种方法中的哪一种？为什么？
b. 在 JavaScript 中，lambda 表达式的参数必须与 lambda 表达式的主体块中直接声明的名称不同（而不是在内部块中）。使用上面的首选方法来检查这一点。

练习 4.6

Scheme 语言包括一个名为let的变体。我们可以通过规定let声明隐式引入一个新的块，该块的主体包括声明和声明出现的语句序列中的所有后续语句，来*似 JavaScript 中let的行为。例如，程序

let* x = 3;
let* y = x + 2;
let* z = x + y + 5;
display(x * z);

显示 39 并且可以被视为一种简写

{
  let x = 3;
  {
    let y = x + 2;
    {
      let z = x + y + 5;
      display(x * z);
    }
  }
}

a. 在这样一个扩展的 JavaScript 语言中编写一个程序，当一些关键字let的出现被替换为let*时，其行为会有所不同。
b. 通过设计合适的标记列表表示并编写解析规则，将let*引入为一个新的语法形式。声明标记列表表示的语法谓词和选择器。
c. 假设parse实现了您的新规则，请编写一个let_star_to_nested_let函数，以转换给定程序中的任何let*的出现，如上所述。然后，通过运行evaluate(let_star_to_nested_let(p))来求值扩展语言中的程序p。
d. 作为一种替代方案，考虑通过向evaluate添加一个子句来实现let*，该子句识别新的语法形式并调用一个名为eval_let_star_declaration的函数。为什么这种方法行不通？

练习 4.7

JavaScript 支持重复执行给定语句的*while循环*。具体来说，

while (predicate) { body }

求值predicate，如果结果为true，则求值body，然后再次求值整个while循环。一旦predicate求值为false，while循环终止。

例如，回想一下第 3.1.3 节中迭代阶乘函数的命令式版本：

function factorial(n) {
    let product = 1;
    let counter = 1;
    function iter() {
        if (counter > n) {
            return product;
        } else {
            product = counter * product;
            counter = counter + 1;
            return iter();
        }
    }
    return iter();
}

我们可以使用while循环来制定相同的算法，如下所示：

function factorial(n) {
    let product = 1;
    let counter = 1;
    while (counter <= n) {
        product = counter * product;
        counter = counter + 1;
    }
    return product;
}

当循环被解析如下：

《 while (predicate) block 》 =
        list("while_loop", 《 predicate 》, 《 block 》)

a. 声明一个语法谓词和选择器来处理while循环。

b. 声明一个名为while_loop的函数，该函数接受谓词和主体作为参数，每个参数由一个没有参数的函数表示，并模拟while循环的行为。然后factorial函数如下所示：

function factorial(n) {
    let product = 1;
    let counter = 1;
    while_loop(() => counter <= n,
               () => {
                   product = counter * product;
                   counter = counter + 1;
               });
    return product;
}

你的while_loop函数应该生成一个迭代过程（参见第 1.2.1 节）。

c. 通过定义一个转换函数while_to_application，将while循环安装为一个派生组件，利用你的while_loop函数。
d. 当程序员在循环的主体内决定从包含循环的函数返回时，使用这种方法实现while循环会出现什么问题？
e. 改变你的方法来解决这个问题。直接为求值器安装while循环，使用一个名为eval_while的函数如何？
f. 遵循这种直接的方法，实现一个break;语句，它立即终止它所在的循环。
g. 实现一个predicate;语句，它只终止它所在的循环迭代，并继续求值while循环的谓词。

练习 4.8

函数主体的求值结果由其返回语句确定。继续参考脚注 9 和第 4.1.1 节中声明的求值，这个练习解决了一个问题，即由一系列语句（声明、块、表达式语句和条件语句）组成的 JavaScript 程序在任何函数主体之外的情况下应该是什么结果。

对于这样的程序，JavaScript 在产生值和不产生值的语句之间进行静态区分。（这里的“静态”意味着我们可以通过检查程序而不是运行它来进行区分。）所有声明都不产生值，所有表达式语句和条件语句都产生值。表达式语句的值是表达式的值。条件语句的值是执行的分支的值，如果该分支不产生值，则值为undefined。如果块的主体（语句序列）是产生值的，则块是产生值的，然后它的值是其主体的值。如果序列的任何组成语句是产生值的，则序列是产生值的，然后它的值是其最后产生值的组成语句的值。最后，如果整个程序不产生值，则其值为undefined。

a. 根据这个规范，以下四个程序的值是什么？

1; 2; 3;

1; { if (true) {} else { 2; } }

1; const x = 2;

1; { let x = 2; { x = x + 3; } }

b. 修改求值器以符合这个规范。

4.1.3 求值器数据结构

除了定义组件的表示形式之外，求值器实现还必须定义求值器在程序执行过程中内部操作的数据结构，例如函数和环境的表示以及true和false的表示。

谓词的测试

为了将条件语句的谓词限制为适当的谓词（求值为布尔值的表达式），我们坚持要求is_truthy函数只应用于布尔值，并且我们只接受布尔值true为真值。is_truthy的相反称为is_falsy。

function is_truthy(x) {
    return is_boolean(x)
           ? x
           : error(x, "boolean expected, received");
}
function is_falsy(x) { return ! is_truthy(x); }

表示函数

为了处理原始数据，我们假设有以下函数可用：

apply_primitive_function(fun, args)

将给定的原始函数应用于列表args中的参数值，并返回应用的结果。
is_primitive_function(fun)

测试fun是否为原始函数。

这些处理原始数据的机制在 4.1.4 节中进一步描述。

使用构造函数make_function构建复合函数，由参数、函数体和环境组成：

function make_function(parameters, body, env) {
    return list("compound_function", parameters, body, env);
}
function is_compound_function(f) {
    return is_tagged_list(f, "compound_function");
}
function function_parameters(f) { return list_ref(f, 1); }
function function_body(f) { return list_ref(f, 2); }
function function_environment(f) { return list_ref(f, 3); }

表示返回值

我们在 4.1.1 节中看到，当遇到return语句时，序列的求值终止，如果函数体的求值没有遇到return语句，则函数应用的求值需要返回值undefined。为了识别返回语句导致的值，我们引入返回值作为求值器数据结构。

function make_return_value(content) {
    return list("return_value", content);
}
function is_return_value(value) {
    return is_tagged_list(value, "return_value");
}
function return_value_content(value) {
    return head(tail(value));
}

环境操作

求值器需要操作来操作环境。如 3.2 节所述，环境是帧的序列，其中每个帧都是将符号与其对应值关联的绑定表。我们使用以下操作来操作环境：

lookup_symbol_value(symbol, env)

返回在环境env中绑定到symbol的值，如果symbol未绑定，则发出错误。
extend_environment(symbols, values, base-env)

返回一个新环境，由一个新帧组成，其中列表symbols中的符号绑定到列表values中的相应元素，封闭环境是环境base-env。
assign_symbol_value(symbol, value, env)

找到env中symbol绑定的最内层帧，并更改该帧，使symbol现在绑定到value，如果symbol未绑定，则发出错误。

为了实现这些操作，我们将环境表示为帧的列表。环境的封闭环境是列表的tail。空环境就是空列表。

function enclosing_environment(env) { return tail(env); }
function first_frame(env) { return head(env); }
const the_empty_environment = null;

每个环境的帧都表示为两个列表的对：一个是该帧中绑定的名称列表，另一个是相关值的列表。

function make_frame(symbols, values) { return pair(symbols, values); }
function frame_symbols(frame) { return head(frame); }
function frame_values(frame) { return tail(frame); }

通过将符号与值关联的新帧扩展环境，我们将一个由符号列表和值列表组成的帧添加到环境中。如果符号的数量与值的数量不匹配，则发出错误。

function extend_environment(symbols, vals, base_env) {
    return length(symbols) === length(vals)
           ? pair(make_frame(symbols, vals), base_env)
           : error(pair(symbols, vals),
                   length(symbols) < length(vals)
                   ? "too many arguments supplied"
                   : "too few arguments supplied");
}

这是在 4.1.1 节中由apply使用的，将函数的参数绑定到其参数。

要在环境中查找符号，我们扫描第一个帧中的符号列表。如果找到所需的符号，我们返回值列表中的相应元素。如果在当前帧中找不到符号，则搜索封闭环境，依此类推。如果达到空环境，则发出"未绑定的名称"错误。

function lookup_symbol_value(symbol, env) {
    function env_loop(env) {
        function scan(symbols, vals) {
            return is_null(symbols)
                   ? env_loop(enclosing_environment(env))
                   : symbol === head(symbols)
                   ? head(vals)
                   : scan(tail(symbols), tail(vals));
        }
        if (env === the_empty_environment) {
            error(symbol, "unbound name");
        } else {
            const frame = first_frame(env);
            return scan(frame_symbols(frame), frame_values(frame));
        }
    }
    return env_loop(env);
}

要在指定的环境中为符号分配新值，我们扫描符号，就像在lookup_symbol_value中一样，并在找到时更改相应的值。

function assign_symbol_value(symbol, val, env) {
    function env_loop(env) {
        function scan(symbols, vals) {
            return is_null(symbols)
                   ? env_loop(enclosing_environment(env))
                   : symbol === head(symbols)
                   ? set_head(vals, val)
                   : scan(tail(symbols), tail(vals));
        }
        if (env === the_empty_environment) {
            error(symbol, "unbound name – assignment");
        } else {
            const frame = first_frame(env);
            return scan(frame_symbols(frame), frame_values(frame));
        }
    }
    return env_loop(env);
}

这里描述的方法只是表示环境的许多合理方法中的一种。由于我们使用数据抽象来将求值器的其余部分与表示的详细选择隔离开来，如果需要，我们可以更改环境表示。（见练习 4.9。）在生产质量的 JavaScript 系统中，求值器环境操作的速度，特别是符号查找的速度，对系统的性能有重大影响。这里描述的表示虽然在概念上很简单，但并不高效，通常不会在生产系统中使用。¹⁶

练习 4.9

我们可以将框架表示为绑定的列表，其中每个绑定都是一个符号-值对，而不是将框架表示为列表对。重写环境操作以使用这种替代表示。

练习 4.10

函数lookup_symbol_value和assign_symbol_value可以用更抽象的函数来表达环境结构的遍历。定义一个捕获常见模式的抽象，并根据这个抽象重新定义这两个函数。

练习 4.11

我们的语言通过使用不同的关键字const和let区分常量和变量，并阻止对常量进行赋值。然而，我们的解释器并没有利用这种区别；函数assign_symbol_value将愉快地为给定的符号分配一个新值，而不管它是作为常量还是变量声明的。通过在尝试在赋值的左侧使用常量时调用函数error来纠正这个缺陷。您可以按照以下步骤进行：

引入谓词is_constant_declaration和is_variable_declaration，允许您区分这两种类型。如 4.1.2 节所示，parse通过使用标签"constant_declaration"和"variable_declaration"来区分它们。
更改scan_out_declarations和（如果必要）extend_environment，使常量在绑定它们的框架中与变量区分开来。
更改assign_symbol_value，使其检查给定的符号是作为变量还是常量声明的，并在后一种情况下发出错误信号，不允许对常量进行赋值操作。
更改eval_declaration，使其在遇到常量声明时调用一个新函数assign_constant_value，该函数不执行您在assign_symbol_value中引入的检查。
如果需要，更改apply以确保仍然可以对函数参数进行赋值。

练习 4.12

a. JavaScript 的规范要求实现在尝试访问名称的值之前对其声明进行求值时发出运行时错误（请参见 3.2.4 节的末尾）。为了在求值器中实现这种行为，更改lookup_symbol_value，如果它找到的值是"unassigned"，则发出错误信号。
b.同样，如果我们尚未求值其let声明，我们就不应该为变量分配新值。更改赋值的求值，以便在这种情况下，对使用let声明的变量进行赋值会发出错误信号。

练习 4.13

在我们在本书中使用的 ECMAScript 2015 的严格模式之前，JavaScript 变量的工作方式与 Scheme 变量有很大不同，这将使得将 Scheme 适应到 JavaScript 的工作变得不那么引人注目。

a.在 ECMAScript 2015 之前，JavaScript 中声明局部变量的唯一方法是使用关键字var而不是关键字let。使用var声明的变量的作用域是立即周围的函数声明或 lambda 表达式的整个主体，而不仅仅是立即封闭的块。修改scan_out_declarations和eval_block，使得使用const和let声明的名称遵循var的作用域规则。
b. 在非严格模式下，JavaScript 允许未声明的名称出现在赋值语句的=左侧。这样的赋值会将新的绑定添加到全局环境中。修改函数assign_symbol_value使赋值行为如此。严格模式禁止这样的赋值，旨在使程序更安全。通过阻止赋值向全局环境添加绑定来解决了什么安全问题？

4.1.4 作为程序运行求值器

有了求值器，我们手头上有了一个描述（用 JavaScript 表达）JavaScript 语句和表达式如何被求值的过程。将求值器表达为程序的一个优点是我们可以运行这个程序。这使我们在 JavaScript 中运行时，得到了 JavaScript 本身如何求值表达式的工作模型。这可以作为实验求值规则的框架，正如我们将在本章后面所做的那样。

我们的求值器程序最终将表达式简化为原始函数的应用。因此，我们运行求值器所需要的就是创建一个机制，调用底层 JavaScript 系统来模拟原始函数的应用。

每个原始函数名称和运算符都必须有一个绑定，这样当evaluate求值原始应用的函数表达式时，它将找到一个对象传递给apply。因此，我们建立了一个全局环境，将唯一对象与原始函数和运算符的名称相关联，这些名称可以出现在我们将要求值的表达式中。全局环境还包括undefined和其他名称的绑定，以便它们可以在要求值的表达式中用作常量。

function setup_environment() {
    return extend_environment(append(primitive_function_symbols,
                                     primitive_constant_symbols),
                              append(primitive_function_objects,
                                     primitive_constant_values),
                              the_empty_environment);
}
const the_global_environment = setup_environment();

我们如何表示原始函数对象并不重要，只要apply能够使用is_primitive_function和apply_primitive_function函数识别和应用它们。我们选择将原始函数表示为以字符串"primitive"开头并包含在底层 JavaScript 中实现该原始函数的函数的列表。

function is_primitive_function(fun) {
    return is_tagged_list(fun, "primitive");
}
function primitive_implementation(fun) { return head(tail(fun)); }

函数setup_environment将从列表中获取原始名称和实现函数：¹⁷

const primitive_functions = list(list("head", head ),
                                 list("tail", tail ),
                                 list("pair", pair ),
                                 list("is_null", is_null ),
                                 list("+", (x, y) => x + y ),
                                 〈more primitive functions〉
                                );
const primitive_function_symbols =
    map(f => head(f), primitive_functions);
const primitive_function_objects =
    map(f => list("primitive", head(tail(f))),
        primitive_functions);

与原始函数类似，我们通过函数setup_environment在全局环境中定义其他原始常量。

const primitive_constants = list(list("undefined", undefined),
                                 list("math_PI", math_PI)
                                 〈more primitive constants〉
                                );
const primitive_constant_symbols =
    map(c => head(c), primitive_constants);
const primitive_constant_values =
    map(c => head(tail(c)), primitive_constants);

要应用原始函数，我们只需使用底层 JavaScript 系统将实现函数应用于参数：¹⁸

function apply_primitive_function(fun, arglist) {
    return apply_in_underlying_javascript(
               primitive_implementation(fun), arglist);
}

为了方便运行元循环求值器，我们提供了一个驱动循环，模拟了底层 JavaScript 系统的读取-求值-打印循环。它打印一个提示符并将输入程序读取为一个字符串。它将程序字符串转换为标记列表表示的语句，如 4.1.2 节所述的过程，称为解析，由原始函数parse完成。我们在每个打印的结果之前加上一个输出提示，以区分程序的值和可能打印的其他输出。驱动循环获取前一个程序的程序环境作为参数。如 3.2.4 节末尾所述，驱动循环将程序视为在一个块中：它扫描出声明，通过包含每个名称绑定到"unassigned"的框架扩展给定的环境，并根据扩展的环境求值程序，然后将其作为参数传递给驱动循环的下一次迭代。

const input_prompt = "M-evaluate input: ";
const output_prompt = "M-evaluate value: ";
function driver_loop(env) {
    const input = user_read(input_prompt);
    if (is_null(input)) {
       display("evaluator terminated");
    } else {
       const program = parse(input);
       const locals = scan_out_declarations(program);
       const unassigneds = list_of_unassigned(locals);
       const program_env = extend_environment(locals, unassigneds, env);
       const output = evaluate(program, program_env);
       user_print(output_prompt, output);
       return driver_loop(program_env);
    }
}

我们使用 JavaScript 的prompt函数从用户那里请求并读取输入字符串：

function user_read(prompt_string) {
    return prompt(prompt_string);
}

当用户取消输入时，函数prompt返回null。我们使用一个特殊的打印函数user_print，以避免打印复合函数的环境部分，这可能是一个非常长的列表（甚至可能包含循环）。

function user_print(string, object) {
    function prepare(object) {
        return is_compound_function(object)
               ? "< compound-function >"
               : is_primitive_function(object)
               ? "< primitive-function >"
               : is_pair(object)
               ? pair(prepare(head(object)),
                      prepare(tail(object)))
               : object;
    }
    display(string + " " + stringify(prepare(object)));
}

现在我们需要做的就是初始化全局环境并启动驱动程序循环来运行求值器。以下是一个示例交互：

const the_global_environment = setup_environment();
driver_loop(the_global_environment);

M-求值输入：

function append(xs, ys) {
    return is_null(xs)
           ? ys
           : pair(head(xs), append(tail(xs), ys));
}

M-求值值：

undefined

M-求值输入：

append(list("a", "b", "c"), list("d", "e", "f"));

M-求值值：

["a", ["b", ["c", ["d", ["e", ["f", null]]]]]]

练习 4.14

Eva Lu Ator 和 Louis Reasoner 各自对元循环求值器进行实验。Eva 输入了map的定义，并运行了一些使用它的测试程序。它们都很好。相比之下，Louis 安装了map的系统版本作为元循环求值器的原语。当他尝试时，事情变得非常糟糕。解释为什么 Louis 的map失败，即使 Eva 的工作正常。

4.1.5 数据作为程序

在考虑一个求值 JavaScript 语句和表达式的 JavaScript 程序时，类比可能会有所帮助。程序含义的一个操作视图是，程序是对一个抽象（也许是无限大的）机器的描述。例如，考虑计算阶乘的熟悉程序：

function factorial(n) {
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}

我们可以将这个程序看作是一个包含递减、乘法和相等测试部分的机器的描述，还有一个两位置开关和另一个阶乘机器。（阶乘机器是无限的，因为它包含另一个阶乘机器。）图 4.3 是阶乘机器的流程图，显示了部件如何连接在一起。

图 4.3 阶乘程序，视为一个抽象机器。

以类似的方式，我们可以将求值器视为一个非常特殊的机器，它以描述一个机器作为输入。根据这个输入，求值器配置自身以模拟所描述的机器。例如，如果我们向求值器提供factorial的定义，如图 4.4 所示，求值器将能够计算阶乘。

图 4.4 求值器模拟阶乘机器。

从这个角度来看，我们的求值器被视为通用机器。当这些机器被描述为 JavaScript 程序时，它模仿其他机器。¹⁹这是令人震惊的。试着想象一个类似的电路求值器。这将是一个电路，它以编码其他电路计划的信号作为输入，比如一个滤波器。给定这个输入，电路求值器将表现得像一个具有相同描述的滤波器。这样一个通用电路几乎是难以想象的复杂。值得注意的是，程序求值器是一个相当简单的程序。²⁰

求值器的另一个引人注目的方面是，它充当了我们编程语言中操作的数据对象和编程语言本身之间的桥梁。想象一下，求值器程序（用 JavaScript 实现）正在运行，用户正在向求值器输入程序并观察结果。从用户的角度来看，输入程序如x * x;是编程语言中的一个程序，求值器应该执行它。然而，从求值器的角度来看，程序只是一个字符串，或者在解析后是一个标记列表表示，根据一套明确定义的规则进行操作。

用户的程序是求值器的数据并不一定会引起混淆。事实上，有时忽略这种区别并给用户明确地将一个字符串作为 JavaScript 语句进行求值的能力是很方便的，使用 JavaScript 的原始函数eval，它以字符串作为参数。它解析字符串，并且——只要它在语法上是正确的——在eval应用的环境中求值所得到的表示。因此，

eval("5 * 5;");

和

evaluate(parse("5 * 5;"), the_global_environment);

都将返回 25。²¹

练习 4.15

给定一个一参数函数f和一个对象a，如果求值表达式f(a)返回一个值（而不是以错误消息终止或永远运行），则称f在a上“停止”。证明不可能编写一个函数halts，它可以正确地确定对于任何函数f和对象a，f是否在a上停止。使用以下推理：如果你有这样一个函数halts，你可以实现以下程序：

function run_forever() { return run_forever(); }
function strange(f) {
    return halts(f, f)
           ? run_forever();
           : "halted";
}

现在考虑求值表达式strange(strange)并展示任何可能的结果（无论是停止还是永远运行）都违反了halts的预期行为。

4.1.6 内部声明

在 JavaScript 中，声明的作用域是紧邻声明的整个块，而不仅仅是从声明发生的地方开始的块的部分。本节将更详细地讨论这个设计选择。

让我们重新审视第 3.2.4 节中在函数f的主体中本地声明的相互递归函数is_even和is_odd。

function f(x) {
    function is_even(n) {
        return n === 0
               ? true
               : is_odd(n - 1);
    }
    function is_odd(n) {
        return n === 0
               ? false
               : is_even(n - 1);
    }
    return is_even(x);
}

我们的意图是，函数is_even主体中的名称is_odd应该指的是在is_even之后声明的函数is_odd。名称is_odd的作用域是f的整个主体块，而不仅仅是从is_odd的声明发生的地方开始的f主体的部分。事实上，当我们考虑is_odd本身是根据is_even定义的时候——所以is_even和is_odd是相互递归的函数——我们看到这两个声明的唯一令人满意的解释是将它们视为is_even和is_odd同时添加到环境中。更一般地，在块结构中，局部名称的作用域是在求值声明的整个块中。

在第 4.1.1 节的元循环求值器中，块的求值通过扫描块中的声明并使用包含所有声明名称绑定的帧扩展当前环境来实现局部名称的同时作用域。因此，在求值块体的新环境中已经包含了is_even和is_odd的绑定，任何一个这些名称的出现都指向正确的绑定。一旦它们的声明被求值，这些名称就绑定到它们声明的值，即具有扩展环境作为环境部分的函数对象。因此，例如，当is_even在f的主体中被应用时，它的环境已经包含了符号is_odd的正确绑定，而在is_even的主体中求值名称is_odd会检索到正确的值。

练习 4.16

考虑第 1.3.2 节中的函数f_3：

function f_3(x, y) {
    const a = 1 + x * y;
    const b = 1 - y;
    return x * square(a) + y * b + a * b;
}

a. 绘制在求值f_3的返回表达式期间生效的环境的图表。
b. 在求值函数应用时，求值器创建两个帧：一个用于参数，一个用于在函数的主体块中直接声明的名称，而不是在内部块中声明的名称。由于所有这些名称具有相同的作用域，一个实现可以合并这两个帧。更改求值器，使得对主体块的求值不会创建新的帧。您可以假设这不会导致帧中出现重复的名称（练习 4.5 证明了这一点）。

练习 4.17

Eva Lu Ator 正在编写程序，其中函数声明和其他语句是交错的。她需要确保在应用函数之前对声明进行求值。她抱怨道：“为什么求值器不能处理这个琐事，并且将所有函数声明提升到它们出现的块的开头？块外的函数声明应该提升到程序的开头。”

a. 修改求值器以遵循 Eva 的建议。
b. JavaScript 的设计者决定遵循 Eva 的方法。讨论这个决定。
c. 此外，JavaScript 的设计者决定允许使用赋值重新分配函数声明的名称。相应地修改您的解决方案并讨论这一决定。

练习 4.18

在我们的解释器中，递归函数是通过一种迂回的方式获得的：首先声明将引用递归函数的名称，并将其分配给特殊值"unassigned"；然后在该名称的范围内定义递归函数；最后将定义的函数分配给名称。当递归函数被应用时，主体中名称的任何出现都会正确地引用递归函数。令人惊讶的是，可以在不使用声明或赋值的情况下指定递归函数。以下程序通过应用递归阶乘函数计算 10 的阶乘：²³

(n => (fact => fact(fact, n))
      ((ft, k) => k === 1
                  ? 1
                  : k * ft(ft, k - 1)))(10);

a. 通过求值表达式来检查这确实计算了阶乘。为计算斐波那契数设计一个类似的表达式。

b. 考虑上面给出的函数f：

function f(x) {
    function is_even(n) {
        return n === 0
               ? true
               : is_odd(n - 1);
    }
    function is_odd(n) {
        return n === 0
               ? false
               : is_even(n - 1);
    }
    return is_even(x);
}

填写缺失的表达式以完成对f的替代声明，该声明没有内部函数声明：

function f(x) {
    return ((is_even, is_odd) => is_even(is_even, is_odd, x))
           ((is_ev, is_od, n) => n === 0 ? true : is_od(〈??〉, 〈??〉, 〈??〉),
            (is_ev, is_od, n) => n === 0 ? false : is_ev( 〈??〉, 〈??〉, 〈??〉));
}

顺序声明处理

我们 4.1.1 节的求值器设计对块的求值施加了运行时负担：它需要扫描块的主体以查找本地声明的名称，使用绑定这些名称的新框架扩展当前环境，并在此扩展环境中求值块主体。或者，块的求值可以使用空框架扩展当前环境。然后，块主体中每个声明的求值将向该框架添加一个新的绑定。为了实现这一设计，我们首先简化eval_block：

function eval_block(component, env) {
    const body = block_body(component);
    return evaluate(body, extend_environment(null, null, env);
}

函数eval_declaration不再能假定环境已经为该名称绑定。它不再使用assign_symbol_value来更改现有绑定，而是调用一个新函数add_binding_to_frame，将名称绑定到值表达式的值的第一个框架中的环境中。

function eval_declaration(component, env) {
    add_binding_to_frame(
        declaration_symbol(component),
        evaluate(declaration_value_expression(component), env),
        first_frame(env));
    return undefined;
}
function add_binding_to_frame(symbol, value, frame) {
    set_head(frame, pair(symbol, head(frame)));
    set_tail(frame, pair(value, tail(frame)));
}

顺序声明处理后，声明的范围不再是直接包围声明的整个块，而只是从声明发生的地方开始的块的一部分。尽管我们不再具有同时的范围，但顺序声明处理将正确地求值本节开头的函数f的调用，但出于“意外”的原因：由于内部函数的声明首先出现，直到所有这些函数都声明完毕之前，不会求值对这些函数的任何调用。因此，is_odd在执行is_even时已经被声明。实际上，对于任何内部声明首先出现在主体中且声明的值表达式的求值实际上不使用任何声明的名称的函数，顺序声明处理将给出与我们在 4.1.1 节中的扫描名称求值器相同的结果。练习 4.19 展示了一个不遵守这些限制的函数的示例，因此替代求值器与我们的扫描名称求值器并不等价。

顺序声明处理比扫描名称更高效且更易于实现。但是，使用顺序处理时，名称引用的声明可能取决于求值块中语句的顺序。在练习 4.19 中，我们看到对于是否希望这样做的观点可能会有不同。

练习 4.19

Ben Bitdiddle，Alyssa P. Hacker 和 Eva Lu Ator 正在就求值程序的期望结果进行争论

const a = 1;
function f(x) {
    const b = a + x;
    const a = 5;
    return a + b;
}
f(10);

Ben 断言应该使用声明的顺序处理结果：b被声明为 11，然后a被声明为 5，因此结果是 16。Alyssa 反对相互递归需要内部函数声明的同时作用规则，并且认为将函数名称与其他名称区别对待是不合理的。因此，她主张在第 4.1.1 节中实现的机制。这将导致在计算b的值时，a尚未被赋值。因此，在 Alyssa 看来，该函数应该产生错误。Eva 有第三种观点。她说，如果a和b的声明确实是同时的，那么在计算b时应该使用a的值 5。因此，在 Eva 看来，a应该是 5，b应该是 15，结果应该是 20。你支持这些观点中的哪一个（如果有的话）？你能想出一种实现内部声明的方法，使其符合 Eva 的期望吗？

4.1.7 将语法分析与执行分离

上面实现的求值器很简单，但非常低效，因为组件的语法分析与其执行交织在一起。因此，如果一个程序被执行多次，它的语法将被分析多次。例如，考虑使用以下factorial定义来求值factorial(4)：

function factorial(n) {
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}

每次调用factorial时，求值器必须确定函数体是条件表达式并提取谓词。只有这样才能求值谓词并根据其值进行分派。每次求值表达式factorial(n - 1) * n或子表达式factorial(n - 1)和n - 1时，求值器必须执行evaluate中的情况分析，以确定表达式是一个应用程序，并必须提取其函数表达式和参数表达式。这种分析是昂贵的。重复执行它是浪费的。

我们可以通过安排事物，使得语法分析只执行一次，从而使求值器变得更加高效。我们将evaluate分成两部分，analyze函数只接受组件。它执行语法分析并返回一个新函数，执行函数，它封装了执行分析组件所需的工作。执行函数以环境作为参数并完成求值。这样做可以节省工作，因为analyze只会在组件上调用一次，而执行函数可能会被多次调用。

通过将分析和执行分开，evaluate现在变成了

function evaluate(component, env) {
    return analyze(component)(env);
}

调用analyze的结果是要应用于环境的执行函数。analyze函数与第 4.1.1 节中的原始evaluate执行的情况分析相同，只是我们分派的函数只执行分析，而不是完全求值。

function analyze(component) {
    return is_literal(component)
           ? analyze_literal(component)
           : is_name(component)
           ? analyze_name(component)
           : is_application(component)
           ? analyze_application(component)
           : is_operator_combination(component)
           ? analyze(operator_combination_to_application(component))
           : is_conditional(component)
           ? analyze_conditional(component)
           : is_lambda_expression(component)
           ? analyze_lambda_expression(component)
           : is_sequence(component)
           ? analyze_sequence(sequence_statements(component))
           : is_block(component)
           ? analyze_block(component)
           : is_return_statement(component)
           ? analyze_return_statement(component)
           : is_function_declaration(component)
           ? analyze(function_decl_to_constant_decl(component))
           : is_declaration(component)
           ? analyze_declaration(component)
           : is_assignment(component)
           ? analyze_assignment(component)
           : error(component, "unknown syntax – analyze");
}

这是最简单的语法分析函数，处理文字表达式。它返回一个执行函数，忽略其环境参数，只返回文字的值。

function analyze_literal(component) {
    return env => literal_value(component);
}

查找名称的值仍然必须在执行阶段完成，因为这取决于知道环境。

function analyze_name(component) {
    return env => lookup_symbol_value(symbol_of_name(component), env);
}

分析一个应用程序，我们分析函数表达式和参数表达式，并构造一个执行函数，该函数调用函数表达式的执行函数（以获取要应用的实际函数）和参数表达式的执行函数（以获取实际参数）。然后我们将这些传递给execute_application，这类似于第 4.1.1 节中的apply。execute_application函数与apply不同之处在于，复合函数的函数体已经被分析过，因此不需要进行进一步的分析。相反，我们只需在扩展环境上调用函数体的执行函数。

function analyze_application(component) {
    const ffun = analyze(function_expression(component));
    const afuns = map(analyze, arg_expressions(component));
    return env => execute_application(ffun(env),
                                      map(afun => afun(env), afuns));
}
function execute_application(fun, args) {
    if (is_primitive_function(fun)) {
        return apply_primitive_function(fun, args);
    } else if (is_compound_function(fun)) {
        const result = function_body(fun)
                       (extend_environment(function_parameters(fun),
                                           args,
                                           function_environment(fun)));
        return is_return_value(result)
               ? return_value_content(result)
               : undefined;
    } else {
        error(fun, "unknown function type – execute_application");
    }
}

对于条件语句，我们在分析时提取并分析谓词、结果和替代。

function analyze_conditional(component) {
    const pfun = analyze(conditional_predicate(component));
    const cfun = analyze(conditional_consequent(component));
    const afun = analyze(conditional_alternative(component));
    return env => is_truthy(pfun(env)) ? cfun(env) : afun(env);
}

分析 lambda 表达式也实现了效率的主要提升：我们只对 lambda 主体进行一次分析，即使由 lambda 表达式的求值产生的函数可能被多次应用。

function analyze_lambda_expression(component) {
    const params = lambda_parameter_symbols(component);
    const bfun = analyze(lambda_body(component));
    return env => make_function(params, bfun, env);
}

对一系列语句的分析更为复杂。序列中的每个语句都经过分析，产生一个执行函数。这些执行函数组合在一起，产生一个接受环境作为参数并按顺序调用每个单独执行函数的执行函数。

function analyze_sequence(stmts) {
    function sequentially(fun1, fun2) {
        return env => {
                   const fun1_val = fun1(env);
                   return is_return_value(fun1_val)
                          ? fun1_val
                          : fun2(env);
               };
    }
    function loop(first_fun, rest_funs) {
        return is_null(rest_funs)
               ? first_fun
               : loop(sequentially(first_fun, head(rest_funs)),
                      tail(rest_funs));
    }
    const funs = map(analyze, stmts);
    return is_null(funs)
           ? env => undefined
           : loop(head(funs), tail(funs));
}

块的主体只被扫描一次以获取局部声明。当调用块的执行函数时，这些绑定将被安装在环境中。

function analyze_block(component) {
    const body = block_body(component);
    const bfun = analyze(body);
    const locals = scan_out_declarations(body);
    const unassigneds = list_of_unassigned(locals);
    return env => bfun(extend_environment(locals, unassigneds, env));
}

对于返回语句，我们分析返回表达式。返回语句的执行函数只是调用返回表达式的执行函数，并将结果包装在返回值中。

function analyze_return_statement(component) {
    const rfun = analyze(return_expression(component));
    return env => make_return_value(rfun(env));
}

函数analyze_assignment必须推迟实际设置变量，直到执行时才会提供环境。然而，分析赋值值表达式（递归地）在分析期间是效率的主要提升，因为赋值值表达式现在只会被分析一次。对于常量和变量声明也是如此。

function analyze_assignment(component) {
    const symbol = assignment_symbol(component);
    const vfun = analyze(assignment_value_expression(component));
    return env => {
               const value = vfun(env);
               assign_symbol_value(symbol, value, env);
               return value;
           };
}
function analyze_declaration(component) {
    const symbol = declaration_symbol(component);
    const vfun = analyze(declaration_value_expression(component));
    return env => {
               assign_symbol_value(symbol, vfun(env), env);
               return undefined;
           };
}

我们的新求值器使用与 4.1.2、4.1.3 和 4.1.4 节中相同的数据结构、语法函数和运行时支持函数。

练习 4.20

扩展本节中的求值器以支持while循环。（见练习 4.7。）

练习 4.21

Alyssa P. Hacker 不明白为什么analyze_sequence需要这么复杂。所有其他分析函数都是相应求值函数（或 4.1.1 节中的evaluate子句）的直接转换。她期望analyze_sequence看起来像这样：

function analyze_sequence(stmts) {
    function execute_sequence(funs, env) {
        if (is_null(funs)) {
            return undefined;
        } else if (is_null(tail(funs))) {
            return head(funs)(env);
        } else {
            const head_val = head(funs)(env);
            return is_return_value(head_val)
                   ? head_val
                   : execute_sequence(tail(funs), env);
        }
    }
    const funs = map(analyze, stmts);
    return env => execute_sequence(funs, env);
}

Eva Lu Ator 向 Alyssa 解释，文本中的版本在分析时更多地求值了序列的工作。Alyssa 的序列执行函数不是内置调用各个执行函数，而是按顺序循环调用这些函数：实际上，尽管序列中的各个语句已经被分析，但序列本身还没有被分析。

比较analyze_sequence的两个版本。例如，考虑常见情况（函数体的典型情况），即序列只有一个语句。Alyssa 程序生成的执行函数会做什么工作？上述文本中程序生成的执行函数又会做什么工作？这两个版本在包含两个表达式的序列中如何比较？

练习 4.22

设计并进行一些实验，比较原始的元循环求值器与本节中的版本的速度。使用你的结果来估计在各种函数中分析与执行所花费的时间比例。

4.2 惰性求值

现在我们有了一个表达为 JavaScript 程序的求值器，我们可以通过修改求值器来实验语言设计的替代选择。事实上，新语言通常是通过首先编写一个将新语言嵌入到现有高级语言中的求值器来发明的。例如，如果我们希望与 JavaScript 社区的其他成员讨论对 JavaScript 的某个修改方面，我们可以提供一个体现了这种改变的求值器。接收者可以使用新的求值器进行实验，并发送评论作为进一步的修改。高级实现基础不仅使得测试和调试求值器更容易；此外，嵌入使得设计者能够从基础语言中吸取特性，就像我们嵌入的 JavaScript 求值器使用了基础 JavaScript 的原语和控制结构一样。设计者只有在以后（如果有必要）才需要费力地在低级语言或硬件中构建完整的实现。在本节和下一节中，我们将探讨一些提供显著额外表达能力的 JavaScript 变体。

4.2.1 正常顺序和应用顺序

在第 1.1 节，我们开始讨论求值模型时，我们注意到 JavaScript 是一种 应用顺序 语言，也就是说，当函数被应用时，JavaScript 函数的所有参数都会被求值。相反，正常顺序 语言会延迟求值函数参数，直到实际参数值被需要为止。延迟求值函数参数直到最后可能的时刻（例如，直到它们被原始操作所需）被称为延迟求值。²⁹ 考虑函数

function try_me(a, b) {
    return a === 0 ? 1 : b;
}

在 JavaScript 中求值try_me(0, head(null));会导致错误。使用延迟求值，就不会出现错误。求值该语句将返回 1，因为参数head(null)永远不会被求值。

利用延迟求值的一个例子是声明一个函数unless

function unless(condition, usual_value, exceptional_value) {
    return condition ? exceptional_value : usual_value;
}

可以在诸如下面的语句中使用

unless(is_null(xs), head(xs), display("error: xs should not be null"));

这在应用顺序语言中不起作用，因为在调用unless之前通常值和异常值都会被求值（参见练习 1.6）。延迟求值的一个优点是，一些函数，比如unless，即使求值它们的一些参数会产生错误或不会终止，也可以进行有用的计算。

如果在求值参数之前进入函数体，则我们说该函数对该参数是 非严格 的。如果在进入函数体之前求值参数，则我们说该函数对该参数是严格的。³⁰ 在纯粹的应用顺序语言中，所有函数对每个参数都是严格的。在纯粹的正常顺序语言中，所有复合函数对每个参数都是非严格的，原始函数可以是严格的也可以是非严格的。还有一些语言（参见练习 4.29）允许程序员对他们定义的函数的严格性进行详细控制。

一个引人注目的例子是一个可以有用地变为非严格的函数pair（或者一般来说，几乎任何数据结构的构造函数）。即使元素的值未知，也可以进行有用的计算，将元素组合成数据结构并对生成的数据结构进行操作。例如，计算列表的长度而不知道列表中各个元素的值是完全有意义的。我们将在第 4.2.3 节中利用这个想法，将第 3 章的流实现为由非严格对组成的列表。

练习 4.23

假设（在普通的应用顺序 JavaScript 中）我们按上面所示定义unless，然后根据unless定义factorial如下

function factorial(n) {
    return unless(n === 1,
                  n * factorial(n - 1),
                  1);
}

如果我们尝试求值factorial(5)会发生什么？我们的函数在正常顺序语言中会工作吗？

练习 4.24

Ben Bitdiddle 和 Alyssa P. Hacker 对于实现诸如unless之类的惰性求值的重要性存在分歧。Ben 指出可以在应用序中实现unless作为一个语法形式。Alyssa 反驳说，如果这样做，unless将只是语法，而不是可以与高阶函数一起使用的函数。在这个论点的双方填写细节。展示如何将unless实现为一个派生组件（类似于操作符组合），通过在evaluate中捕获函数表达式为unless的应用。给出一个可能有用的情况的例子，其中unless作为函数而不是语法形式可用。

4.2.2 惰性求值的解释器

而不仅仅是evaluate，我们使用

基本思想是，在应用函数时，解释器必须确定哪些参数需要求值，哪些需要延迟。延迟的参数不会被求值；相反，它们会被转换为称为thunk的对象。thunk 必须包含在需要时产生参数值所需的信息，就好像它在应用时已经被求值一样。因此，thunk 必须包含参数表达式和函数应用被求值的环境。

在 thunk 中求值表达式的过程称为forcing。通常情况下，只有在需要其值时才会强制执行 thunk：当它被传递给将使用 thunk 值的原始函数时；当它是条件语句的谓词的值时；当它是即将被应用为函数的函数表达式的值时。我们可以选择是否对 thunk 进行记忆化，类似于第 3.5.1 节中对流的优化。使用记忆化时，第一次强制执行 thunk 时，它会存储计算出的值。后续的强制执行只需返回存储的值，而不重复计算。我们将使我们的解释器进行记忆化，因为这对许多应用来说更有效率。然而，这里有一些棘手的考虑。

修改求值器

惰性求值和第 4.1 节中的求值器在evaluate和apply中对函数应用的处理上的主要区别。

evaluate的is_application子句变成

: is_application(component)
? apply(actual_value(function_expression(component), env),
        arg_expressions(component), env)

这几乎与第 4.1.1 节中evaluate的is_application子句相同。然而，对于惰性求值，我们调用apply并传入参数表达式，而不是对它们进行求值后产生的参数。由于如果参数需要延迟，我们将需要环境来构造 thunk，因此我们也必须传递环境。我们仍然求值函数表达式，因为apply需要实际的函数来进行分派（原始函数与复合函数）并应用它。

在这一节中，我们将实现一个与 JavaScript 相同的正常顺序语言，只是每个参数中的复合函数是非严格的。原始函数仍然是严格的。修改第 4.1.1 节的求值器，使其解释的语言以这种方式运行并不困难。几乎所有所需的更改都集中在函数应用周围。

function actual_value(exp, env) {
   return force_it(evaluate(exp, env));
}

来代替，这样如果表达式的值是 thunk，它将被强制执行。

我们的新版本的apply也几乎与第 4.1.1 节中的版本相同。不同之处在于evaluate传入了未求值的参数表达式：对于原始函数（严格的），我们在应用原始函数之前求值所有参数；对于复合函数（非严格的），我们在应用函数之前延迟所有参数。

function apply(fun, args, env) {
    if (is_primitive_function(fun)) {
        return apply_primitive_function(
                   fun,
                   list_of_arg_values(args, env));              // changed
    } else if (is_compound_function(fun)) {
        const result = evaluate(
                           function_body(fun),
                           extend_environment(
                               function_parameters(fun),
                               list_of_delayed_args(args, env), // changed
                               function_environment(fun)));
        return is_return_value(result)
               ? return_value_content(result)
               : undefined;
    } else {
        error(fun, "unknown function type – apply");
    }
}

处理参数的函数与 4.1.1 节中的list_of_values几乎相同，只是list_of_delayed_args延迟参数而不是求值它们，而list_of_arg_values使用actual_value而不是evaluate：

function list_of_arg_values(exps, env) {
    return map(exp => actual_value(exp, env), exps);
}
function list_of_delayed_args(exps, env) {
    return map(exp => delay_it(exp, env), exps);
}

我们必须更改求值器的另一个地方是在处理条件语句时，我们必须使用actual_value而不是evaluate来获取谓词表达式的值，然后再测试它是真还是假：

function eval_conditional(component, env) {
    return is_truthy(actual_value(conditional_predicate(component), env))
           ? evaluate(conditional_consequent(component), env)
           : evaluate(conditional_alternative(component), env);
}

最后，我们必须更改driver_loop函数（来自 4.1.4 节），以使用actual_value而不是evaluate，这样如果延迟的值传播回读取-求值-打印循环，它将在打印之前被强制。我们还更改提示，指示这是惰性求值器：

const input_prompt = "L-evaluate input: ";
const output_prompt = "L-evaluate value: ";

function driver_loop(env) {
    const input = user_read(input_prompt);
    if (is_null(input)) {
        display("evaluator terminated");
    } else {
        const program = parse(input);
        const locals = scan_out_declarations(program);
        const unassigneds = list_of_unassigned(locals);
        const program_env = extend_environment(locals, unassigneds, env);
        const output = actual_value(program, program_env);
        user_print(output_prompt, output);
        return driver_loop(program_env);
    }
}

做出这些更改后，我们可以启动求值器并对其进行测试。成功求值 4.2.1 节中讨论的try_me表达式表明解释器正在执行惰性求值：

const the_global_environment = setup_environment(); driver_loop(the_global_environment);

左求值输入：

function try_me(a, b) {
    return a === 0 ? 1 : b;
}

左求值值：

undefined

左求值输入：

try_me(0, head(null));

左求值值：

`1`

表示 thunk

我们的求值器必须安排在将函数应用于参数时创建 thunk，并稍后强制这些 thunk。一个 thunk 必须将表达式与环境打包在一起，以便稍后可以生成参数。为了强制 thunk，我们只需从 thunk 中提取表达式和环境，并在环境中求值表达式。我们使用actual_value而不是evaluate，以便在表达式的值本身是 thunk 的情况下，我们将强制执行，依此类推，直到达到不是 thunk 的东西：

function force_it(obj) {
    return is_thunk(obj)
           ? actual_value(thunk_exp(obj), thunk_env(obj))
           : obj;
}

打包表达式与环境的一种简单方法是创建一个包含表达式和环境的列表。因此，我们可以按照以下方式创建 thunk：

function delay_it(exp, env) {
    return list("thunk", exp, env);
}
function is_thunk(obj) {
    return is_tagged_list(obj, "thunk");
}
function thunk_exp(thunk) { return head(tail(thunk)); }
function thunk_env(thunk) { return head(tail(tail(thunk))); }

实际上，我们为解释器想要的不完全是这样，而是已经被记忆的 thunk。当强制 thunk 时，我们将通过用其值替换存储的表达式并更改thunk标记来将其转换为已求值的 thunk，以便可以识别它已经被求值。³⁴

function is_evaluated_thunk(obj) {
    return is_tagged_list(obj, "evaluated_thunk");
}
function thunk_value(evaluated_thunk) {
    return head(tail(evaluated_thunk));
}
function force_it(obj) {
    if (is_thunk(obj)) {
        const result = actual_value(thunk_exp(obj), thunk_env(obj));
        set_head(obj, "evaluated_thunk");
        set_head(tail(obj), result); // replace exp with its value
        set_tail(tail(obj), null); // forget unneeded env
        return result;
    } else if (is_evaluated_thunk(obj)) {
        return thunk_value(obj);
    } else {
        return obj;
    }
}

注意，相同的delay_it函数在有记忆和无记忆的情况下都有效。

练习 4.25

假设我们向惰性求值器输入以下声明：

let count = 0;
function id(x) {
    count = count + 1;
    return x;
}

给出以下交互序列中的缺失值，并解释你的答案。

const w = id(id(10));

左求值输入：

count;

左求值值：

〈response〉

左求值输入：

w;

左求值值：

〈response〉

左求值输入：

count;

左求值值：

〈response〉

练习 4.26

函数evaluate在将函数表达式传递给apply之前使用actual_value而不是evaluate来求值函数表达式，以强制函数表达式的值。给出一个演示这种强制需求的示例。

练习 4.27

展示一个程序，你期望它在没有记忆的情况下运行得比有记忆的情况慢得多。另外，考虑以下交互，其中id函数的定义如练习 4.25 中所述，count从 0 开始：

function square(x) {
    return x * x;
}

左求值输入：

square(id(10));

左求值值：

〈response〉

左求值输入：

count;

左求值值：

〈response〉

给出求值器记忆和不记忆时的响应。

练习 4.28

改过自新的 C 程序员赛·D·费克特担心一些副作用可能永远不会发生，因为惰性求值器不会强制序列中的语句。由于序列中语句的值可能不会被使用（语句可能只是为了其效果而存在，例如赋值给变量或打印），因此可能没有后续使用这个值的情况（例如作为原始函数的参数），这将导致它被强制。因此，赛认为在求值序列时，我们必须强制序列中的所有语句。他建议修改 4.1.1 节中的evaluate_sequence，以使用actual_value而不是evaluate：

function eval_sequence(stmts, env) {
    if (is_empty_sequence(stmts)) {
        return undefined;
    } else if (is_last_statement(stmts)) {
        return actual_value(first_statement(stmts), env);
    } else {
        const first_stmt_value =
            actual_value(first_statement(stmts), env);
        if (is_return_value(first_stmt_value)) {
            return first_stmt_value;
        } else {
            return eval_sequence(rest_statements(stmts), env);
        }
    }
}

本·比特迪德尔认为赛伊是错误的。他向赛伊展示了练习 2.23 中描述的for_each函数，这给出了一个具有副作用的序列的重要示例：

function for_each(fun, items) {
    if (is_null(items)){
        return "done";
    } else {
        fun(head(items));
        for_each(fun, tail(items));
    }
}

他声称文本中的求值者（具有原始的eval_sequence）正确处理了这一点：

L-evaluate input:
for_each(display, list(57, 321, 88));

57
321
88
L-evaluate value:
"done"

解释为什么 Ben 对for_each的行为是正确的。

b. Cy 同意 Ben 关于for_each示例的观点，但说这不是他在提出对eval_sequence的更改时考虑的程序类型。他在惰性求值器中声明了以下两个函数：
```
function f1(x) {
    x = pair(x, list(2));
    return x;
}
function f2(x) {
    function f(e) { 
        e;
        return x;
    }
    return f(x = pair(x, list(2)));
}
```
原始eval_sequence的f1(1)和f2(1)的值是多少？Cy 对eval_sequence的建议更改后的值会是多少？
c. Cy 还指出，按照他的建议更改eval_sequence不会影响部分 a 中示例的行为。解释为什么这是真的。
d. 你认为序列在惰性求值器中应该如何处理？你喜欢 Cy 的方法，文本中的方法，还是其他方法？

练习 4.29

本节中采用的方法有些不愉快，因为它对 JavaScript 进行了不兼容的更改。实现惰性求值作为向上兼容的扩展可能更好，即普通 JavaScript 程序将像以前一样工作。我们可以通过在函数声明内部引入可选参数声明作为新的语法形式来实现这一点，以让用户控制参数是否延迟。顺便说一句，我们可能也可以让用户选择是否延迟记忆。例如，声明

function f(a, b, c, d) {
    parameters("strict", "lazy", "strict", "lazy_memo");
    ...
}

将f定义为一个四个参数的函数，其中在调用函数时会求值第一个和第三个参数，第二个参数会延迟，第四个参数既延迟又被记忆。您可以假设参数声明始终是函数声明体中的第一条语句，如果省略了参数声明，则所有参数都是严格的。因此，普通函数声明将产生与普通 JavaScript 相同的行为，而在每个复合函数的每个参数上添加"lazy_memo"声明将产生本节中定义的惰性求值器的行为。设计并实现所需的更改以产生 JavaScript 的这种扩展。parse函数将参数声明视为函数应用程序，因此您需要修改apply以分派到新的语法形式的实现。您还必须安排evaluate或apply确定何时延迟参数，并相应地强制或延迟参数，并且必须安排强制记忆或不适当。

4.2.3 流作为惰性列表

在 3.5.1 节中，我们展示了如何将流实现为延迟列表。我们使用 lambda 表达式构造了一个“承诺”来计算流的尾部，而不是在以后实际实现该承诺。我们被迫创建流作为一种新的数据对象，类似但不完全相同于列表，这要求我们重新实现许多用于流的普通列表操作（map，append等）。

使用惰性求值，流和列表可以是相同的，因此不需要单独的列表和流操作。我们需要做的就是安排pair是非严格的。实现这一点的一种方法是将惰性求值器扩展为允许非严格的原语，并将pair实现为其中之一。一个更简单的方法是回想一下（第 2.1.3 节）根本没有必要将pair实现为原语。相反，我们可以将对偶表示为函数：³⁶

function pair(x, y) {
    return m => m(x, y);
}
function head(z) {
    return z((p, q) => p);
}
function tail(z) {
    return z((p, q) => q);
}

根据这些基本操作，列表操作的标准定义将适用于无限列表（流）以及有限列表，并且流操作可以实现为列表操作。以下是一些示例：

function list_ref(items, n) {
    return n === 0
           ? head(items)
           : list_ref(tail(items), n - 1);
}
function map(fun, items) {
    return is_null(items)
           ? null
           : pair(fun(head(items)),
                  map(fun, tail(items)));
}
function scale_list(items, factor) {
    return map(x => x * factor, items);
}
function add_lists(list1, list2) {
    return is_null(list1)
           ? list2
           : is_null(list2)
           ? list1
           : pair(head(list1) + head(list2),
                  add_lists(tail(list1), tail(list2)));
}
const ones = pair(1, ones);
const integers = pair(1, add_lists(ones, integers));

左求值输入：

list_ref(integers, 17);

左求值值：

请注意，这些懒惰列表甚至比第 3 章的流更懒惰：列表的头部和尾部都被延迟。事实上，甚至访问懒惰对的head或tail也不需要强制列表元素的值。只有在真正需要时才会强制该值，例如用作原语的参数，或者作为答案打印时。

懒惰的对也有助于在第 3.5.4 节中出现的流的问题，我们发现，构建具有循环的系统的流模型可能需要我们在程序中添加额外的 lambda 表达式来延迟，除了构造流对所需的 lambda 表达式。通过惰性求值，所有函数的参数都被统一延迟。例如，我们可以按照我们在第 3.5.4 节最初打算的方式实现函数来集成列表和解决微分方程：

function integral(integrand, initial_value, dt) {
    const int = pair(initial_value,
                     add_lists(scale_list(integrand, dt),
                               int));
    return int;
}
function solve(f, y0, dt) {
    const y = integral(dy, y0, dt);
    const dy = map(f, y);
    return y;
}

左求值输入：

list_ref(solve(x => x, 1, 0.001), 1000);

左求值值：

2.716924

练习 4.30

给出一些例子，说明第 3 章的流和本节中描述的“更懒惰”的惰性列表之间的区别。你如何利用这种额外的懒惰？

练习 4.31

Ben Bitdiddle 通过求值表达式来测试上述懒惰列表的实现

head(list("a", "b", "c"));

令他惊讶的是，这产生了一个错误。经过一番思考，他意识到从原始list函数获得的“列表”与新定义的pair、head和tail操作的列表是不同的。修改求值器，使得在驱动循环中键入原始list函数的应用程序将产生真正的惰性列表。

练习 4.32

修改求值器的驱动循环，以便懒惰的对和列表以某种合理的方式打印出来。（你打算如何处理无限列表？）你可能还需要修改懒惰对的表示，以便求值器能够识别它们以便打印它们。

4.3 非确定性计算

在本节中，我们通过将支持自动搜索的功能内置到求值器中，扩展 JavaScript 求值器以支持一种称为非确定性计算的编程范式。这对于语言的改变比第 4.2 节中引入的惰性求值更为深刻。

非确定性计算，如流处理，对于“生成和测试”应用程序非常有用。考虑从两个正整数列表开始，并找到一对整数，一个来自第一个列表，一个来自第二个列表，它们的和是素数的任务。我们在第 2.2.3 节中看到了如何处理这个问题，并在第 3.5.3 节中使用无限流。我们的方法是生成所有可能的对的序列，并过滤这些对以选择其和为素数的对。无论我们是否像在第 2 章中那样实际生成整个对序列，还是像在第 3 章中那样交替生成和过滤，对于计算组织的基本形象来说都是无关紧要的。

非确定性方法唤起了不同的形象。想象一下，我们简单地选择（以某种方式）从第一个列表中选择一个数字，从第二个列表中选择一个数字，并要求（使用某种机制）它们的和是素数。这由以下函数表示：

function prime_sum_pair(list1, list2) {
    const a = an_element_of(list1);
    const b = an_element_of(list2);
    require(is_prime(a + b));
    return list(a, b);
}

这个函数似乎只是重新陈述了问题，而不是指定了解决问题的方法。尽管如此，这是一个合法的非确定性程序。

关键思想在于非确定性语言中的组件可以有多个可能的值。例如，an_element_of可能返回给定列表的任何元素。我们的非确定性程序求值器将通过自动选择一个可能的值并跟踪选择来工作。如果后续要求不满足，求值器将尝试不同的选择，并将不断尝试新的选择，直到求值成功，或者直到我们用尽了选择。就像惰性求值器使程序员摆脱了值如何延迟和强制的细节一样，非确定性程序求值器将使程序员摆脱选择如何进行的细节。

对比非确定性求值和流处理所唤起的不同时间形象是有启发性的。流处理使用惰性求值来解耦可能答案流被组装的时间和实际流元素产生的时间。求值器支持这样一个错觉，即所有可能的答案都以一个无时间的序列摆在我们面前。而非确定性求值中，一个组件代表了一组可能世界的探索，每个世界由一组选择确定。一些可能的世界导致了死胡同，而另一些则有有用的值。非确定性程序求值器支持这样一个错觉，即时间分支，我们的程序有不同的可能执行历史。当我们遇到死胡同时，我们可以重新访问之前的选择点，并沿着不同的分支继续。

下面实现的非确定性程序求值器称为amb求值器，因为它基于一个称为amb的新的语法形式。我们可以在amb求值器驱动循环中键入prime_sum_pair的上述声明（以及is_prime、an_element_of和require的声明），并按如下方式运行该函数：

amb-求值输入：

prime_sum_pair(list(1, 3, 5, 8), list(20, 35, 110));

开始一个新问题

amb-求值值：

[3, [20, null]]

返回的值是在求值器重复选择每个列表中的元素，直到成功选择之后获得的。

第 4.3.1 节介绍了amb并解释了它如何通过求值器的自动搜索机制支持非确定性。第 4.3.2 节介绍了非确定性程序的示例，第 4.3.3 节详细介绍了如何通过修改普通 JavaScript 求值器来实现amb求值器。

4.3.1 搜索和`amb`

为了支持非确定性，我们引入了一个称为amb的新的语法形式。表达式amb(``e[1], e[2], ... , e[n]``)以“模棱两可”的方式返回n个表达式e[i]中的一个值。例如，表达式

list(amb(1, 2, 3), amb("a", "b"));

可以有六个可能的值：

list(1, "a") list(1, "b") list(2, "a")
list(2, "b") list(3, "a") list(3, "b")

一个带有单个选择的amb表达式会产生一个普通（单个）值。

没有选择的amb表达式——表达式amb()——是一个没有可接受值的表达式。在操作上，我们可以将amb()看作是一个导致计算“失败”的表达式：计算中止，不产生值。利用这个想法，我们可以表达一个特定的谓词表达式p必须为真的要求如下：

function require(p) {
    if (! p) {
        amb();
    } else {}
}

使用amb和require，我们可以实现上面使用的an_element_of函数：

function an_element_of(items) {
    require(! is_null(items));
    return amb(head(items), an_element_of(tail(items)));
}

如果列表为空，则an_element_of的应用将失败。否则，它会模棱两可地返回列表的第一个元素或从列表的其余部分中选择的一个元素。

我们还可以表示无限范围的选择。以下函数可能返回大于或等于给定n的任何整数：

function an_integer_starting_from(n) {
    return amb(n, an_integer_starting_from(n + 1));
}

这类似于第 3.5.2 节中描述的integers_starting_from流函数，但有一个重要的区别：流函数返回一个表示以n开头的所有整数序列的对象，而amb函数返回一个单个整数。

抽象地说，我们可以想象求值amb表达式会导致时间分成分支，其中计算在每个分支上继续，使用表达式的可能值之一。我们说amb代表一个非确定性选择点。如果我们有一台具有足够多动态分配的处理器的机器，我们可以以直接的方式实现搜索。执行将继续进行，就像在顺序机器中一样，直到遇到amb表达式。在这一点上，将分配更多的处理器，并初始化以继续选择所暗示的所有并行执行。每个处理器将按顺序进行，就好像它是唯一的选择，直到它通过遇到失败而终止，或者进一步细分，或者完成。⁴¹

另一方面，如果我们有一台只能执行一个进程（或几个并发进程）的机器，我们必须按顺序考虑各种选择。人们可以想象修改求值器，在遇到选择点时随机选择一个分支进行跟踪。然而，随机选择很容易导致失败的值。我们可以尝试一遍又一遍地运行求值器，做出随机选择，并希望找到一个非失败的值，但更好的方法是系统地搜索所有可能的执行路径。我们将在本节中开发和使用的amb求值器实现了以下系统搜索：当求值器遇到amb的应用时，它最初选择第一个备选方案。这个选择本身可能导致进一步的选择。求值器总是在每个选择点最初选择第一个备选方案。如果一个选择导致失败，那么求值器会自动地⁴² 回溯到最*的选择点，并尝试下一个备选方案。如果在任何选择点用完备选方案，求值器将回到上一个选择点并从那里继续。这个过程导致了一种被称为深度优先搜索或按时间顺序回溯的搜索策略。⁴³

驱动循环

amb求值器的驱动循环具有一些不寻常的特性。它读取一个程序，并打印第一个非失败执行的值，就像上面显示的prime_sum_pair示例一样。如果我们想要看到下一个成功执行的值，我们可以要求解释器回溯并尝试生成第二个非失败执行。这是通过输入retry来表示的。如果给出除retry之外的任何其他输入，解释器将开始一个新问题，丢弃上一个问题中未探索的备选方案。以下是一个示例交互：

amb-求值输入：

prime_sum_pair(list(1, 3, 5, 8), list(20, 35, 110));

开始一个新问题

amb-求值值：

[3, [20, null]]

amb-求值输入：

retry

amb-求值值：

[3, [110, null]]

amb-求值输入：

retry

amb-求值值：

[8, [35, null]]

amb-求值输入：

retry

没有更多的值

prime_sum_pair([1, [3, [5, [8, null]]]], [20, [35, [110, null]]])

amb-求值输入：

prime_sum_pair(list(19, 27, 30), list(11, 36, 58));

开始一个新问题

amb-求值值：

[30, [11, null]]

练习 4.33

编写一个名为an_integer_between的函数，该函数返回给定边界之间的整数。这可以用来实现一个函数，找到勾股数三元组，即在给定边界之间的整数三元组（i，j，k），使得i ≤ j和i² + j² = k²，如下所示：

function a_pythogorean_triple_between(low, high) {
    const i = an_integer_between(low, high);
    const j = an_integer_between(i, high);
    const k = an_integer_between(j, high);
    require(i * i + j * j === k * k);
    return list(i, j, k);
}

练习 4.34

练习 3.69 讨论了如何生成所有勾股数三元组的流，对要搜索的整数大小没有上限。解释为什么在练习 4.33 中的函数中简单地将an_integer_between替换为an_integer_starting_from不是生成任意勾股数三元组的充分方式。编写一个实际可以实现这一点的函数。（也就是说，编写一个函数，重复输入retry理论上最终会生成所有的勾股数三元组。）

练习 4.35

Ben Bitdiddle 声称生成勾股数的以下方法比练习 4.33 中的方法更有效。他正确吗？（提示：考虑必须探索的可能性数量。）

function a_pythagorean_triple_between(low, high) {
    const i = an_integer_between(low, high);
    const hsq = high * high;
    const j = an_integer_between(i, high);
    const ksq = i * i + j * j;
    require(hsq >= ksq);
    const k = math_sqrt(ksq);
    require(is_integer(k));
    return list(i, j, k);
}

4.3.2 非确定性程序的示例

第 4.3.3 节描述了amb求值器的实现。然而，我们首先给出一些它的使用示例。非确定性编程的优势在于我们可以抑制搜索是如何进行的细节，从而以更高的抽象级别表达我们的程序。

逻辑谜题

以下谜题（改编自 Dinesman 1968）是一个典型的简单逻辑谜题：

软件公司 Gargle 正在扩张，Alyssa、Ben、Cy、Lem 和 Louis 将搬进新大楼的一排五个私人办公室。Alyssa 不会搬进最后一个办公室。Ben 不会搬进第一个办公室。Cy 既不搬进第一个办公室，也不搬进最后一个办公室。Lem 搬进比 Ben 晚的一个办公室。Louis 的办公室不会在 Cy 的旁边。Cy 的办公室也不会在 Ben 的旁边。谁搬进哪个办公室？

我们可以通过列举所有可能性并施加给定的限制来直接确定谁搬进哪个办公室：⁴⁴

function office_move() {
    const alyssa = amb(1, 2, 3, 4, 5);
    const ben = amb(1, 2, 3, 4, 5);
    const cy = amb(1, 2, 3, 4, 5);
    const lem = amb(1, 2, 3, 4, 5);
    const louis = amb(1, 2, 3, 4, 5);
    require(distinct(list(alyssa, ben, cy, lem, louis)));
    require(alyssa !== 5);
    require(ben !== 1);
    require(cy !== 5);
    require(cy !== 1);
    require(lem > ben);
    require(math_abs(louis - cy) !== 1);
    require(math_abs(cy - ben) !== 1);
    return list(list("alyssa", alyssa),
                list("ben", ben),
                list("cy", cy),
                list("lem", lem),
                list("louis", louis));
}

求值表达式office_move()的结果是

list(list("alyssa", 3), list("ben", 2), list("cy", 4),
     list("lem", 5), list("louis", 1))

尽管这个简单的函数有效，但速度非常慢。练习 4.37 和 4.38 讨论了一些可能的改进。

练习 4.36

修改办公室搬迁函数，省略 Louis 的办公室不会在 Cy 的旁边的要求。对于这个修改后的谜题有多少解？

练习 4.37

办公室搬迁函数中限制的顺序是否影响答案？它是否影响找到答案的时间？如果你认为它很重要，通过重新排列限制从给定的函数中获得更快的程序。如果你认为它不重要，请阐述你的观点。

练习 4.38

在办公室搬迁问题中，人们搬进办公室的分配集合有多少个，在办公室分配必须不同的要求之前和之后？生成所有可能的人员到办公室的分配，然后依靠回溯来消除它们是非常低效的。例如，大多数限制只依赖于一个或两个人员-办公室名称，因此可以在为所有人员选择办公室之前施加。编写并演示一个更有效的非确定性函数，它基于生成仅仅是之前的限制已经排除的那些可能性来解决这个问题。

练习 4.39

编写一个普通的 JavaScript 程序来解决办公室搬迁谜题。

练习 4.40

解决以下“说谎者”谜题（改编自 Phillips 1934）：

Alyssa、Cy、Eva、Lem 和 Louis 在 SoSoService 商务午餐。他们的餐点一个接一个地到达，比他们下订单的时间晚了很多。为了取悦 Ben，他们决定每个人都说一句真话和一句假话关于他们的订单：

Alyssa：“Lem 的餐第二个到了。我的第三个到了。”

Cy：“我的先到了。Eva 的第二个到了。”

Eva：“我的第三个到了，可怜的 Cy 的最后一个到了。”

Lem：“我的第二个到了。Louis 的第四个到了。”

Louis：“我的第四个到了。Alyssa 的第一个到了。”

五个用餐者的真实用餐顺序是什么？

练习 4.41

使用amb求值器来解决以下谜题（改编自 Phillips 1961）：

Alyssa、Ben、Cy、Eva 和 Louis 分别选择 SICP JS 的不同章节，并解决该章节中的所有练习。Louis 解决了“函数”章节中的练习，Alyssa 解决了“数据”章节中的练习，Cy 解决了“状态”章节中的练习。他们决定相互检查对方的工作，Alyssa 自愿检查“元”章节中的练习。由 Ben 解决“寄存器机器”章节中的练习，并由 Louis 检查。检查“函数”章节中的练习的人解决了 Eva 检查的练习。谁检查“数据”章节中的练习？

尝试编写程序，使其运行效率高（参见练习 4.38）。还要确定如果我们不知道 Alyssa 检查“Meta”章节中的练习，有多少解决方案。

练习 4.42

练习 2.42 描述了在国际象棋棋盘上放置皇后，使得没有两个皇后互相攻击的“八皇后谜题”。编写一个非确定性程序来解决这个谜题。

解析自然语言

设计为接受自然语言作为输入的程序通常从尝试解析输入开始，即将输入与某种语法结构匹配。例如，我们可以尝试识别由冠词后跟名词后跟动词组成的简单句子，如“The cat eats”。为了完成这样的分析，我们必须能够识别单词的词性。我们可以从一些分类各种单词的列表开始：

const nouns = list("noun", "student", "professor", "cat", "class");

const verbs = list("verb", "studies", "lectures", "eats", "sleeps");

const articles = list("article", "the", "a");

我们还需要一个语法，即一组描述语法元素如何由更简单的元素组成的规则。一个非常简单的语法可能规定一个句子总是由两部分组成——一个名词短语后跟一个动词——而一个名词短语由一个冠词后跟一个名词组成。有了这个语法，句子“The cat eats”被解析如下：

list("sentence",
     list("noun-phrase", list("article", "the"), list("noun", "cat"),
     list("verb", "eats"))

我们可以用一个简单的程序生成这样的解析，该程序为每个语法规则分别定义了函数。为了解析一个句子，我们识别它的两个组成部分，并返回带有符号sentence的这两个元素的列表：

function parse_sentence() {
    return list("sentence",
                parse_noun_phrase(),
                parse_word(verbs));
}

类似地，名词短语通过找到一个冠词后跟一个名词来解析：

function parse_noun_phrase() {
    return list("noun-phrase",
                parse_word(articles),
                parse_word(nouns));
}

在最低级别，解析归结为反复检查下一个尚未解析的单词是否属于所需词性的单词列表。为了实现这一点，我们维护一个全局变量not_yet_parsed，它是尚未解析的输入。每次检查一个单词时，我们要求not_yet_parsed必须非空，并且它应该以指定列表中的一个单词开头。如果是这样，我们就从not_yet_parsed中删除该单词，并返回该单词以及它的词性（该词性位于列表的开头）：

function parse_word(word_list) {
    require(! is_null(not_yet_parsed));
    require(! is_null(member(head(not_yet_parsed), tail(word_list))));
    const found_word = head(not_yet_parsed);
    not_yet_parsed = tail(not_yet_parsed);
    return list(head(word_list), found_word);
}

要开始解析，我们所需要做的就是将not_yet_parsed设置为整个输入，尝试解析一个句子，并检查是否有剩余的内容：

let not_yet_parsed = null;

function parse_input(input) {
    not_yet_parsed = input;
    const sent = parse_sentence();
    require(is_null(not_yet_parsed));
    return sent;
}

现在我们可以尝试解析器，并验证它是否适用于我们的简单测试句子：

amb-求值输入：

parse_input(list("the",  "cat",  "eats"));

开始一个新问题

amb-求值值：

list("sentence",
      list("noun-phrase", list("article", "the"), list("noun", "cat")),
      list("verb", "eats"))

amb求值器在这里很有用，因为使用require来表达解析约束非常方便。然而，当我们考虑更复杂的语法，其中有关于单元如何分解的选择时，自动搜索和回溯确实很有回报。

让我们在我们的语法中添加一个介词列表：

const prepositions = list("prep", "for", "to", "in", "by", "with");

并定义介词短语（例如，“为猫”）为介词后跟一个名词短语：

function parse_prepositional_phrase() {
    return list("prep-phrase",
                parse_word(prepositions),
                parse_noun_phrase());
}

现在我们可以定义一个句子为一个名词短语后跟一个动词短语，其中动词短语可以是一个动词，也可以是一个由介词短语扩展的动词短语：

function parse_sentence() {
    return list("sentence",
                parse_noun_phrase(),
                parse_verb_phrase());
}
function parse_verb_phrase() {
    function maybe_extend(verb_phrase) {
        return amb(verb_phrase,
                   maybe_extend(list("verb-phrase",
                                     verb_phrase,
                                     parse_prepositional_phrase())));
    }
    return maybe_extend(parse_word(verbs));
}

顺便说一下，我们还可以详细说明名词短语的定义，以允许“a cat in the class”这样的内容。我们过去称之为名词短语的东西，现在称之为简单名词短语，名词短语现在可以是一个简单名词短语，也可以是由介词短语扩展的名词短语：

function parse_simple_noun_phrase() {
    return list("simple-noun-phrase",
                parse_word(articles),
                parse_word(nouns));
}
function parse_noun_phrase() {
    function maybe_extend(noun_phrase) {
        return amb(noun_phrase,
                   maybe_extend(list("noun-phrase",
                                     noun_phrase,
                                     parse_prepositional_phrase())));
    }
    return maybe_extend(parse_simple_noun_phrase());
}

我们的新语法让我们能够解析更复杂的句子。例如

parse_input(list("the", "student", "with", "the", "cat",
                 "sleeps", "in", "the", "class"));

产生

list("sentence",
     list("noun-phrase",
          list("simple-noun-phrase",
               list("article", "the"), list("noun", "student")),
          list("prep-phrase", list("prep", "with"),
               list("simple-noun-phrase",
                    list("article", "the"),
                    list("noun", "cat")))),
     list("verb-phrase",
          list("verb", "sleeps"),
          list("prep-phrase", list("prep", "in"),
               list("simple-noun-phrase",
                    list("article", "the"),
                    list("noun", "class")))))

注意，给定的输入可能有多个合法的解析。在句子“The professor lectures to the student with the cat.”中，可能是教授正在和猫一起讲课，也可能是学生有这只猫。我们的非确定性程序找到了这两种可能性：

parse_input(list("the", "professor", "lectures",
                 "to", "the", "student", "with", "the", "cat"));

产生

list("sentence",
     list("simple-noun-phrase",
          list("article", "the"), list("noun", "professor")),
     list("verb-phrase",
          list("verb-phrase",
               list("verb", "lectures"),
               list("prep-phrase", list("prep", "to"),
                    list("simple-noun-phrase",
                    list("article", "the"),
                    list("noun", "student")))),
          list("prep-phrase", list("prep", "with"),
               list("simple-noun-phrase",
                    list("article", "the"),
                    list("noun", "cat")))))

要求求值器重试会产生

list("sentence",
     list("simple-noun-phrase",
          list("article", "the"), list("noun", "professor")),
     list("verb-phrase",
          list("verb", "lectures"),
          list("prep-phrase", list("prep", "to"),
               list("noun-phrase",
                    list("simple-noun-phrase",
                         list("article", "the"),
                         list("noun", "student")),
                    list("prep-phrase", list("prep", "with"),
                         list("simple-noun-phrase",
                         list("article", "the"),
                         list("noun", "cat")))))))

练习 4.43

使用上面给出的语法，以下句子可以有五种不同的解析方式：“The professor lectures to the student in the class with the cat.” 给出这五种解析并解释它们之间的意义差异。

练习 4.44

第 4.1 和 4.2 节的求值器不确定参数表达式的求值顺序。我们将看到amb求值器会从左到右对它们进行求值。解释为什么如果参数表达式以其他顺序进行求值，我们的解析程序将无法工作。

练习 4.45

Louis Reasoner 建议，由于动词短语要么是一个动词，要么是一个动词短语后跟一个介词短语，因此将函数parse_verb_phrase声明为以下方式（名词短语也是如此）会更加直接：

function parse_verb_phrase() {
    return amb(parse_word(verbs),
               list("verb-phrase",
                   parse_verb_phrase(),
                   parse_prepositional_phrase()));
}

这样行得通吗？如果我们交换amb中表达式的顺序，程序的行为会改变吗？

练习 4.46

扩展上面给出的语法以处理更复杂的句子。例如，您可以扩展名词短语和动词短语以包括形容词和副词，或者您可以处理并列句。

练习 4.47

Alyssa P. Hacker 对生成有趣的句子更感兴趣，而不是解析它们。她认为，通过简单地更改函数parse_word，使其忽略“输入句子”，而总是成功并生成一个合适的单词，我们可以使用我们为解析构建的程序来进行生成。实现 Alyssa 的想法，并展示生成的前六个或更多句子。

4.3.3 实现`amb`求值器

普通 JavaScript 程序的求值可能返回一个值，可能永远不会终止，也可能会发出错误。在非确定性 JavaScript 中，程序的求值可能会导致发现死胡同，此时求值必须回溯到先前的选择点。这种额外情况使得非确定性 JavaScript 的解释变得复杂。

我们将通过修改第 4.1.7 节的分析求值器来构建非确定性 JavaScript 的amb求值器。与分析求值器一样，组件的求值是通过调用分析该组件的执行函数来完成的。普通 JavaScript 的解释和非确定性 JavaScript 的解释之间的区别将完全体现在执行函数中。

执行函数和延续

请记住，普通求值器的执行函数接受一个参数：执行环境。相比之下，amb求值器中的执行函数接受三个参数：环境和两个称为延续函数的函数。组件的求值将通过调用这两个延续函数之一来完成：如果求值得到一个值，将调用成功延续并传递该值；如果求值导致发现死胡同，则调用失败延续。构造和调用适当的延续是非确定性求值器实现回溯的机制。

成功延续的工作是接收一个值并继续计算。除了该值之外，成功延续还传递另一个失败延续，如果使用该值导致死胡同，随后将调用该失败延续。

失败延续的工作是尝试非确定性过程的另一个分支。非确定性语言的本质在于组件可以代表在选择之间进行选择。这样的组件的求值必须继续进行所指示的备选选择之一，即使事先不知道哪些选择将导致可接受的结果。为了处理这个问题，求值器选择其中一个备选方案，并将该值传递给成功延续。除了该值之外，求值器还构造并传递一个失败延续，以便稍后调用以选择不同的备选方案。

在求值过程中触发失败（即调用失败延续）当用户程序明确拒绝当前攻击线路时（例如，调用require可能导致执行amb()，一个总是失败的表达式-见第 4.3.1 节）。此时手头的失败延续将导致最*的选择点选择另一个替代方案。如果在该选择点没有更多的替代方案需要考虑，将触发较早选择点的失败，依此类推。失败延续还会在驱动循环响应retry请求时调用，以找到程序的另一个值。

此外，如果在选择的过程中发生了副作用操作（例如对变量的赋值），当过程找到死胡同时，可能需要在进行新的选择之前撤消副作用。这是通过使副作用操作产生一个失败延续来实现的，该失败延续撤消副作用并传播失败。

总之，失败延续是由构建的

amb表达式-提供一种机制，如果amb表达式的当前选择导致死胡同，则进行替代选择。
顶层驱动程序-提供一种机制，在选择耗尽时报告失败；
分配-拦截失败并在回溯期间撤消分配。

只有在遇到死胡同时才会启动失败。这发生在

如果用户程序执行amb()；
如果用户在顶层驱动程序处键入retry。

在处理失败时也称为失败延续：

当由分配创建的失败延续完成撤消副作用时，它调用它拦截的失败延续，以将失败传播回导致此分配的选择点或顶层。
当amb的失败延续用尽选择时，它调用最初给amb的失败延续，以将失败传播回先前的选择点或顶层。

求值器的结构

amb求值器的语法和数据表示函数，以及基本的analyze函数，与第 4.1.7 节的求值器相同，只是我们需要额外的语法函数来识别amb语法形式：

function is_amb(component) {
    return is_tagged_list(component, "application") &&
           is_name(function_expression(component)) &&
           symbol_of_name(function_expression(component)) === "amb";
}
function amb_choices(component) {
    return arg_expressions(component);
}

我们继续使用第 4.1.2 节的解析函数，该函数不支持amb作为语法形式，而是将amb(``...``)视为函数应用。函数is_amb确保每当名称amb出现为应用的函数表达式时，求值器将“应用”视为不确定性选择点。

我们还必须在analyze的分发中添加一个子句，以识别这样的表达式并生成适当的执行函数：

...
: is_amb(component)
? analyze_amb(component)
: is_application(component)
...

顶层函数ambeval（类似于第 4.1.7 节中给出的evaluate版本）分析给定的组件，并将生成的执行函数应用于给定的环境，以及两个给定的延续：

function ambeval(component, env, succeed, fail) {
    return analyze(component)(env, succeed, fail);
}

成功延续是一个带有两个参数的函数：刚刚获得的值和另一个失败延续，如果该值导致后续失败，则使用该失败延续。失败延续是一个没有参数的函数。因此，执行函数的一般形式是

(env, succeed, fail) => {
    // succeed is (value, fail) => ...
    // fail is () => ...
    ...
}

例如，执行

ambeval(component,
        the_global_environment,
        (value, fail) => value,
        () => "failed");

将尝试求值给定的组件，并将返回组件的值（如果求值成功）或字符串"failed"（如果求值失败）。下面显示的驱动循环中对ambeval的调用使用了更复杂的延续函数，这些函数继续循环并支持retry请求。

amb求值器的大部分复杂性都来自于在执行函数相互调用时传递延续的机制。在阅读以下代码时，您应该将每个执行函数与第 4.1.7 节中给出的普通求值器的相应函数进行比较。

简单表达式

最简单类型表达式的执行函数基本上与普通求值器的执行函数相同，除了需要管理延续。执行函数只是成功地返回表达式的值，并传递给它们的失败延续。

function analyze_literal(component) {
    return (env, succeed, fail) =>
             succeed(literal_value(component), fail);
}

function analyze_name(component) {
    return (env, succeed, fail) =>
             succeed(lookup_symbol_value(symbol_of_name(component),
                                         env),
                    fail);
}

function analyze_lambda_expression(component) {
    const params = lambda_parameter_symbols(component);
    const bfun = analyze(lambda_body(component));
    return (env, succeed, fail) =>
             succeed(make_function(params, bfun, env),
                     fail);
}

请注意，查找名称总是“成功”的。如果lookup_symbol_value未能找到名称，它会像往常一样发出错误信号。这样的“失败”表示程序错误 - 引用未绑定的名称；这不是表明我们应该尝试另一个非确定性选择，而不是当前正在尝试的选择。

条件和序列

条件也以与普通求值器相似的方式处理。由analyze_conditional生成的执行函数调用谓词执行函数pfun，并使用一个成功延续来检查谓词值是否为真，并继续执行条件的结果或替代方案。如果pfun的执行失败，将调用条件表达式的原始失败延续。

function analyze_conditional(component) {
    const pfun = analyze(conditional_predicate(component));
    const cfun = analyze(conditional_consequent(component));
    const afun = analyze(conditional_alternative(component));
    return (env, succeed, fail) =>
             pfun(env,
                  // success continuation for evaluating the predicate
                  // to obtain pred_value (pred_value, fail2) =>
                    is_truthy(pred_value)
                    ? cfun(env, succeed, fail2)
                    : afun(env, succeed, fail2),
                  // failure continuation for evaluating the predicate
                  fail);
}

序列也以与以前的求值器相同的方式处理，除了在子函数sequentially中进行的操作，这些操作对于传递延续是必需的。即，为了依次执行a和b，我们使用一个成功延续调用a，该成功延续调用b。

function analyze_sequence(stmts) {
    function sequentially(a, b) {
        return (env, succeed, fail) =>
                 a(env,
                   // success continuation for calling a
                   (a_value, fail2) =>
                     is_return_value(a_value)
                     ? succeed(a_value, fail2)
                     : b(env, succeed, fail2),
                   // failure continuation for calling
                   a fail);
    }
    function loop(first_fun, rest_funs) {
        return is_null(rest_funs)
               ? first_fun
               : loop(sequentially(first_fun, head(rest_funs)),
                      tail(rest_funs));
    }
    const funs = map(analyze, stmts);
    return is_null(funs)
           ? env => undefined
           : loop(head(funs), tail(funs));
}

声明和赋值

声明是另一种情况，我们必须费力地管理延续，因为必须在实际声明新名称之前求值声明值表达式。为了实现这一点，使用环境、成功延续和失败延续调用声明值执行函数vfun。如果vfun的执行成功，获得了声明名称的值val，则声明名称并传播成功：

function analyze_declaration(component) {
    const symbol = declaration_symbol(component);
    const vfun = analyze(declaration_value_expression(component));
    return (env, succeed, fail) =>
             vfun(env,
                  (val, fail2) => {
                      assign_symbol_value(symbol, val, env);
                      return succeed(undefined, fail2);
                  },
                  fail);
}

赋值更有趣。这是我们真正使用延续的第一个地方，而不仅仅是传递它们。赋值的执行函数开始时与声明的执行函数类似。它首先尝试获取要分配给名称的新值。如果vfun的求值失败，赋值也失败。

然而，如果vfun成功，并且我们继续进行赋值，我们必须考虑这一计算分支可能以后会失败的可能性，这将需要我们回溯到赋值之外。因此，我们必须安排在回溯过程中撤消赋值。

这是通过给vfun一个成功继续（在下面标有注释1）来实现的，该成功继续在分配新值给变量并从分配中继续之前保存变量的旧值。与分配值一起传递的失败继续（在下面标有注释2）在继续失败之前恢复变量的旧值。也就是说，成功的分配提供了一个失败继续，该失败继续将拦截后续的失败；否则会调用fail2的任何失败都会调用此函数，以在实际调用fail2之前撤消分配。

function analyze_assignment(component) {
    const symbol = assignment_symbol(component);
    const vfun = analyze(assignment_value_expression(component));
    return (env, succeed, fail) =>
             vfun(env,
                  (val, fail2) => { // 1
                      const old_value = lookup_symbol_value(symbol,
                                                            env);
                      assign_symbol_value(symbol, val, env);
                      return succeed(val,
                                     () => { // 2
                                         assign_symbol_value(symbol,
                                                             old_value,
                                                             env);
                                         return fail2();
                                     });
                  },
                  fail);
}

返回语句和块

分析返回语句很简单。返回表达式被分析以产生执行函数。返回语句的执行函数调用具有成功继续的执行函数，该成功继续将返回值包装在返回值对象中并将其传递给原始成功继续。

function analyze_return_statement(component) {
    const rfun = analyze(return_expression(component));
    return (env, succeed, fail) =>
             rfun(env,
                  (val, fail2) =>
                    succeed(make_return_value(val), fail2),
                  fail);
}

块的执行函数在扩展环境上调用主体的执行函数，而不更改成功或失败继续。

function analyze_block(component) {
    const body = block_body(component);
    const locals = scan_out_declarations(body);
    const unassigneds = list_of_unassigned(locals);
    const bfun = analyze(body);
    return (env, succeed, fail) =>
             bfun(extend_environment(locals, unassigneds, env),
                  succeed,
                  fail);
}

函数应用

应用的执行函数中除了管理继续的技术复杂性外，没有新的想法。这种复杂性出现在analyze_ application中，因为我们在求值参数表达式时需要跟踪成功和失败继续。我们使用一个函数get_args来求值参数表达式的列表，而不是像普通求值器中那样简单地使用map。

function analyze_application(component) {
    const ffun = analyze(function_expression(component));
    const afuns = map(analyze, arg_expressions(component));
    return (env, succeed, fail) =>
             ffun(env,
                  (fun, fail2) =>
                    get_args(afuns,
                             env,
                             (args, fail3) =>
                               execute_application(fun,
                                                   args,
                                                   succeed,
                                                   fail3),
                             fail2),
                  fail);
}

在get_args中，注意如何通过使用一个递归调用get_args的成功继续来遍历afun执行函数列表并构造args的结果列表。每个对get_args的递归调用都有一个成功继续，其值是使用pair将新获得的参数添加到累积参数列表中得到的新列表：

function get_args(afuns, env, succeed, fail) {
    return is_null(afuns)
           ? succeed(null, fail)
           : head(afuns)(env,
                         // success continuation for this afun
                         (arg, fail2) =>
                           get_args(tail(afuns),
                                    env,
                                    // success continuation for
                                    // recursive call to get_args
                                    (args, fail3) =>
                                      succeed(pair(arg, args),
                                              fail3),
                                    fail2),
                         fail);
}

实际的函数应用是由execute_application执行的，与普通求值器一样，只是需要管理继续。

function execute_application(fun, args, succeed, fail) {
    return is_primitive_function(fun)
           ? succeed(apply_primitive_function(fun, args),
                     fail)
           : is_compound_function(fun)
           ? function_body(fun)(
                 extend_environment(function_parameters(fun),
                                    args,
                                    function_environment(fun)),
                 (body_result, fail2) =>
                   succeed(is_return_value(body_result)
                           ? return_value_content(body_result)
                           : undefined,
                           fail2),
                 fail)
           : error(fun, "unknown function type - execute_application");
}

求值`amb`表达式

amb语法形式是非确定性语言中的关键元素。在这里，我们看到了解释过程的本质以及跟踪继续的原因。amb的执行函数定义了一个循环try_next，该循环循环执行amb表达式的所有可能值的执行函数。每个执行函数都使用一个失败继续进行调用，该失败继续将尝试下一个值。当没有更多的替代方案可尝试时，整个amb表达式失败。

function analyze_amb(component) {
    const cfuns = map(analyze, amb_choices(component));
    return (env, succeed, fail) => {
               function try_next(choices) {
                   return is_null(choices)
                          ? fail()
                          : head(choices)(env,
                                          succeed,
                                          () =>
                                            try_next(tail(choices)));
               }
               return try_next(cfuns);
           };
}

驱动循环

由于允许用户重试求值程序的机制，amb求值器的驱动循环非常复杂。驱动程序使用一个名为internal_loop的函数，该函数以retry函数作为参数。意图是调用retry应该继续尝试非确定性求值中的下一个未尝试的替代方案。函数internal_loop要么在用户在驱动循环中键入retry时调用retry，要么通过调用ambeval开始新的求值。

对于对ambeval的此调用的失败继续通知用户没有更多的值，并重新调用驱动循环。

对于对ambeval的调用，成功的延续更加微妙。我们打印获得的值，然后使用retry函数重新调用内部循环，该函数将能够尝试下一个替代方案。这个next_alternative函数是传递给成功延续的第二个参数。通常，我们认为这第二个参数是一个失败延续，如果当前的求值分支后来失败了，就会使用它。然而，在这种情况下，我们已经完成了一个成功的求值，因此我们可以调用“失败”替代分支，以搜索额外的成功求值。

const input_prompt = "amb-求值输入：";
const output_prompt = "amb-求值值：";

function driver_loop(env) {
    function internal_loop(retry) {
        const input = user_read(input_prompt);
        if (is_null(input)) {
            display("evaluator terminated");
        } else if (input === "retry") {
            return retry();
        } else {
            display("Starting a new problem");
            const program = parse(input);
            const locals = scan_out_declarations(program);
            const unassigneds = list_of_unassigned(locals);
            const program_env = extend_environment(
                                     locals, unassigneds, env);
            return ambeval(
                       program,
                       program_env,
                       // ambeval success
                       (val, next_alternative) => {
                           user_print(output_prompt, val);
                           return internal_loop(next_alternative);
                       },
                       // ambeval failure
                       () => {
                           display("There are no more values of");
                           display(input);
                           return driver_loop(program_env);
                       });
        }
    }
    return internal_loop(() => {
                             display("There is no current problem");
                             return driver_loop(env);
                         });
}

对internal_loop的初始调用使用retry函数，该函数抱怨当前没有问题并重新启动驱动循环。如果用户在没有进行求值时输入retry，则会发生这种行为。

我们像往常一样启动驱动循环，通过设置全局环境并将其作为第一次迭代的封闭环境传递给driver_loop。

const the_global_environment = setup_environment();
driver_loop(the_global_environment);

练习 4.48

实现一个新的语法形式ramb，它类似于amb，但是以随机顺序搜索替代，而不是从左到右。展示这如何帮助艾丽莎在练习 4.47 中的问题。

练习 4.49

更改赋值的实现，使其在失败时不会被撤消。例如，我们可以从列表中选择两个不同的元素，并计算成功选择所需的尝试次数如下：

let count = 0;

let x = an_element_of("a", "b", "c");
let y = an_element_of("a", "b", "c"); count = count + 1;
require(x !== y); list(x, y, count);

开始新问题：

amb-求值值：

["a", ["b", [2, null]]]

amb-求值输入：

retry

amb-求值值：

["a", ["c", [3, null]]]

如果我们使用了赋值的原始含义而不是永久赋值，将显示哪些值？

练习 4.50

我们将可怕地滥用条件语句的语法，通过实现以下形式的结构：

if (evaluation_succeeds_take) { statement } else { alternative }

该结构允许用户捕获语句的失败。它像往常一样求值语句，如果求值成功，则像往常一样返回。但是，如果求值失败，将求值给定的替代语句，如下例所示：

amb-求值输入：

if (evaluation_succeeds_take) {
    const x = an_element_of(list(1, 3, 5));
    require(is_even(x));
    x;
} else {
    "all odd";
}

开始一个新问题

amb-求值值：

"all odd"

amb-求值输入：

if (evaluation_succeeds_take) {
    const x = an_element_of(list(1, 3, 5, 8));
    require(is_even(x));
    x;
} else {
    "all odd";
}

开始一个新问题

amb-求值值：

`8`

通过扩展amb求值器来实现此结构。提示：函数is_amb显示了如何滥用现有的 JavaScript 语法以实现新的语法形式。

练习 4.51

使用练习 4.49 中描述的新类型的赋值和结构

if (evaluation_succeeds_take) { ... } else { ... }

就像在练习 4.50 中一样，求值的结果将是什么

let pairs = null;
if (evaluation_succeeds_take) {
    const p = prime_sum_pair(list(1, 3, 5, 8), list(20, 35, 110));
    pairs = pair(p, pairs); // using permanent assignment
    amb();
} else {
    pairs;
}

练习 4.52

如果我们没有意识到require可以作为一个普通函数来实现，该函数使用amb，由用户作为非确定性程序的一部分来定义，我们将不得不将其实现为一个语法形式。这将需要语法函数

function is_require(component) {
    return is_tagged_list(component, "require");
}
function require_predicate(component) { return head(tail(component)); }

以及在analyze的调度中的新子句

: is_require(component)
? analyze_require(component)

以及处理require表达式的analyze_require函数。完成analyze_require的以下定义。

function analyze_require(component) {
    const pfun = analyze(require_predicate(component));
    return (env, succeed, fail) =>
            pfun(env,
                 (pred_value, fail2) =>
                   〈??〉
                   ? 〈??〉
                   : succeed("ok", fail2),
                 fail);
}

4.4 逻辑编程

在第 1 章中，我们强调计算机科学涉及命令式（如何）知识，而数学涉及声明式（什么是）知识。事实上，编程语言要求程序员以一种形式表达知识，该形式指示解决特定问题的逐步方法。另一方面，高级语言作为语言实现的一部分，提供了大量的方法论知识，使用户不必关心特定计算的进展细节。

大多数编程语言，包括 JavaScript，都是围绕计算数学函数的值而组织的。面向表达式的语言（如 Lisp、C、Python 和 JavaScript）利用了一个“双关语”，即描述函数值的表达式也可以被解释为计算该值的手段。因此，大多数编程语言都倾向于单向计算（具有明确定义的输入和输出的计算）。然而，也有根本不同的编程语言放松了这种偏见。我们在 3.3.5 节中看到了一个这样的例子，其中计算的对象是算术约束。在约束系统中，计算的方向和顺序没有那么明确定义；因此，在进行计算时，系统必须提供比普通算术计算更详细的“如何”知识。然而，这并不意味着用户完全摆脱了提供命令性知识的责任。有许多约束网络实现了相同的约束集，用户必须从数学上等价的网络集合中选择一个合适的网络来指定特定的计算。

第 4.3 节的非确定性程序求值器也摆脱了编程是关于构建计算单向函数的观点。在非确定性语言中，表达式可以有多个值，因此计算处理的是关系而不是单值函数。逻辑编程通过将编程的关系视野与一种称为统一的强大的符号模式匹配相结合来扩展这一思想。

这种方法在起作用时可以是编写程序的一种非常强大的方式。部分原因在于一个“是什么”事实可以用来解决许多不同的问题，这些问题可能有不同的“如何”组成部分。例如，考虑append操作，它接受两个列表作为参数，并将它们的元素组合成一个单一的列表。在 JavaScript 等过程式语言中，我们可以根据基本的列表构造函数pair来定义append，就像我们在 2.2.1 节中所做的那样。

function append(x, y) {
    return is_null(x)
           ? y
           : pair(head(x), append(tail(x), y));
}

这个函数可以被看作是将以下两条规则翻译成 JavaScript，第一条规则涵盖了第一个列表为空的情况，第二条规则处理了非空列表的情况，即两个部分的pair：

对于任何列表y，空列表和y append形成y。
对于任何u、v、y和z，如果pair(u, v)和y append形成pair(u, z)，那么v和y append形成z。

使用append函数，我们可以回答诸如

找到list("a", "b")和list("c", "d")的append。

但是，同样的两条规则也足以回答以下类型的问题，而函数无法回答：

找到一个列表y，它与list("a", "b")一起append以产生

    list("a", "b", "c", "d").

找到所有x和y，它们append形成list("a", "b", "c", "d")。

在逻辑编程语言中，程序员通过陈述上述关于append的两条规则来编写append“函数”。解释器会自动提供“如何”知识，以便使用这一对规则来回答关于append的所有三种类型的问题。

当代逻辑编程语言（包括我们在这里实现的语言）存在重大缺陷，因为它们的一般“如何”方法可能会导致它们陷入虚假的无限循环或其他不良行为。逻辑编程是计算机科学中的一个活跃研究领域。

在本章的前面，我们探讨了实现解释器的技术，并描述了对于类似 JavaScript 的语言（实际上，对于任何传统语言）的解释器所必不可少的元素。现在我们将应用这些想法来讨论逻辑编程语言的解释器。我们将这种语言称为查询语言，因为它非常适用于通过用语言表达的查询或问题来从数据库中检索信息。尽管查询语言与 JavaScript 非常不同，但我们将发现用相同的一般框架来描述语言是方便的：作为原始元素的集合，以及使我们能够将简单元素组合成更复杂元素的组合手段和使我们能够将复杂元素视为单个概念单位的抽象手段。逻辑编程语言的解释器比像 JavaScript 这样的语言的解释器复杂得多。尽管如此，我们将看到我们的查询语言解释器包含了在第 4.1 节的解释器中找到的许多相同元素。特别是，将有一个“求值”部分，根据类型对表达式进行分类，以及一个“应用”部分，实现语言的抽象机制（JavaScript 的情况下是函数，逻辑编程的情况下是规则）。此外，实现中的一个核心作用是由框架数据结构发挥的，它确定了符号和它们关联值之间的对应关系。我们查询语言实现的另一个有趣方面是我们大量使用了流，这在第 3 章中介绍过。

4.4.1 推理信息检索

逻辑编程在提供接口以用于信息检索的数据库方面表现出色。我们将在本章实现的查询语言旨在以这种方式使用。

为了说明查询系统的功能，我们将展示如何使用它来管理波士顿地区蓬勃发展的高科技公司 Gargle 的人员记录数据库。该语言提供了对人员信息的模式导向访问，并且还可以利用一般规则进行逻辑推断。

一个样本数据库

Gargle 的人员数据库包含有关公司人员的断言。以下是有关 Ben Bitdiddle 的信息，他是公司的计算机专家：

address(list("Bitdiddle", "Ben"),
        list("Slumerville", list("Ridge", "Road"), 10))
job(list("Bitdiddle", "Ben"), list("computer", "wizard"))
salary(list("Bitdiddle", "Ben"), 122000)

断言看起来就像 JavaScript 中的函数应用，但实际上它们代表了数据库中的信息。第一个符号——这里是address、job和salary——描述了各自断言中包含的信息种类，而“参数”是列表或原始值，如字符串和数字。第一个符号不需要像 JavaScript 中的常量或变量那样被声明；它们的范围是全局的。

作为公司的专家，Ben 负责公司的计算机部门，并监督两名程序员和一名技术员。以下是关于他们的信息：

address(list("Hacker", "Alyssa", "P"),
        list("Cambridge", list("Mass", "Ave"), 78))
job(list("Hacker", "Alyssa", "P"), list("computer", "programmer"))
salary(list("Hacker", "Alyssa", "P"), 81000)
supervisor(list("Hacker", "Alyssa", "P"), list("Bitdiddle", "Ben"))

address(list("Fect", "Cy", "D"),
        list("Cambridge", list("Ames", "Street"), 3))
job(list("Fect", "Cy", "D"), list("computer", "programmer"))
salary(list("Fect", "Cy", "D"), 70000)
supervisor(list("Fect", "Cy", "D"), list("Bitdiddle", "Ben"))

address(list("Tweakit", "Lem", "E"),
        list("Boston", list("Bay", "State", "Road"), 22))
job(list("Tweakit", "Lem", "E"), list("computer", "technician"))
salary(list("Tweakit", "Lem", "E"), 51000)
supervisor(list("Tweakit", "Lem", "E"), list("Bitdiddle", "Ben"))

还有一名程序员实习生，由 Alyssa 监督：

address(list("Reasoner", "Louis"),
        list("Slumerville", list("Pine", "Tree", "Road"), 80))
job(list("Reasoner", "Louis"),
        list("computer", "programmer", "trainee"))
salary(list("Reasoner", "Louis"), 62000)
supervisor(list("Reasoner", "Louis"), list("Hacker", "Alyssa", "P"))

所有这些人都在计算机部门，这可以从他们的工作描述中的第一个项目为“计算机”这个词来看出。

Ben 是一名高级雇员。他的主管是公司的大佬本人：

supervisor(list("Bitdiddle", "Ben"), list("Warbucks", "Oliver"))

address(list("Warbucks", "Oliver"),
        list("Swellesley", list("Top", "Heap", "Road")))
job(list("Warbucks", "Oliver"), list("administration", "big", "wheel"))
salary(list("Warbucks", "Oliver"), 314159)

除了由 Ben 监督的计算机部门，公司还有一个会计部门，由一名总会计和他的助手组成：

address(list("Scrooge", "Eben"),
        list("Weston", list("Shady", "Lane"), 10))
job(list("Scrooge", "Eben"), list("accounting", "chief", "accountant"))
salary(list("Scrooge", "Eben"), 141421)
supervisor(list("Scrooge", "Eben"), list("Warbucks", "Oliver"))

address(list("Cratchit", "Robert"),
        list("Allston", list("N", "Harvard", "Street"), 16))
job(list("Cratchit", "Robert"), list("accounting", "scrivener"))
salary(list("Cratchit", "Robert"), 26100)
supervisor(list("Cratchit", "Robert"), list("Scrooge", "Eben"))

公司的大佬还有一名行政助理：

address(list("Aull", "DeWitt"),
        list("Slumerville", list("Onion", "Square"), 5))
job(list("Aull", "DeWitt"), list("administration", "assistant"))
salary(list("Aull", "DeWitt"), 42195)
supervisor(list("Aull", "DeWitt"), list("Warbucks", "Oliver"))

数据库还包含有关持有其他种类工作的人可以做哪种工作的断言。例如，计算机专家可以做计算机程序员和计算机技术员的工作：

can_do_job(list("computer", "wizard"),
           list("computer", "programmer"))
can_do_job(list("computer", "wizard"),
           list("computer", "technician"))

计算机程序员可以代替实习生：

can_do_job(list("computer", "programmer"),
           list("computer", "programmer", "trainee"))

此外，众所周知，

can_do_job(list("administration", "assistant"),
           list("administration", "big", "wheel"))

简单查询

查询语言允许用户通过对系统提示的查询来从数据库中检索信息。例如，要找到所有计算机程序员，可以说

查询输入：

job($x, list("computer", "programmer"))

系统将响应以下项目：

查询结果：

job(list("Hacker", "Alyssa", "P"), list("computer", "programmer"))

job(list("Fect", "Cy", "D"), list("computer", "programmer"))

输入查询指定我们正在寻找与数据中的某个模式匹配的条目。在这个例子中，模式指定job作为我们正在寻找的信息类型。第一项可以是任何东西，第二项是字面上的列表list("computer", "programmer")。匹配断言中可以作为第一项的“任何东西”由模式变量$x指定。作为模式变量，我们使用以美元符号开头的 JavaScript 名称。我们将在下面看到为什么指定模式变量的名称比只在模式中放入一个符号（比如$）来代表“任何东西”更有用。系统通过显示所有与指定模式匹配的数据中的条目来响应简单查询。

模式可以有多个变量。例如，查询

address($x, $y)

将列出所有员工的地址。

模式可以没有变量，这种情况下查询只是确定该模式是否是数据中的一个条目。如果是，将会有一个匹配；如果不是，将没有匹配。

相同的模式变量可以在查询中出现多次，指定相同的“任何东西”必须出现在每个位置。这就是为什么变量有名称。例如，

supervisor($x, $x)

查找所有监督自己的人（尽管在我们的样本数据库中没有这样的断言）。

查询

job($x, list("computer", $type))

匹配所有工作条目，其第二项是一个第一项为"computer"的两元素列表：

job(list("Bitdiddle", "Ben"), list("computer", "wizard"))
job(list("Hacker", "Alyssa", "P"), list("computer", "programmer"))
job(list("Fect", "Cy", "D"), list("computer", "programmer"))
job(list("Tweakit", "Lem", "E"), list("computer", "technician"))

这个模式不匹配

job(list("Reasoner", "Louis"),
    list("computer", "programmer", "trainee"))

因为断言中的第二项是一个三元素列表，而模式的第二项指定应该有两个元素。如果我们想要更改模式，使得第二项可以是以"computer"开头的任何列表，我们可以指定

job($x, pair("computer", $type))

例如，

pair("computer", $type)

匹配数据

list("computer", "programmer", "trainee")

以$type为list("programmer", "trainee")。它也匹配数据

list("computer", "programmer")

以$type为list("programmer")，并匹配数据

list("computer")

以$type为空列表，null。

我们可以描述查询语言对简单查询的处理如下：

系统找到查询模式中变量的所有赋值，这些赋值满足该模式——也就是说，所有变量的值集合，使得如果模式变量被实例化为（替换为）这些值，结果就在数据中。
系统通过列出满足查询模式的变量赋值来响应查询。

注意，如果模式没有变量，查询将简化为确定该模式是否在数据中。如果是，空赋值将满足该模式。

练习 4.53

给出从数据库中检索以下信息的简单查询：

a. 由 Ben Bitdiddle 监督的所有人；
b. 会计部门所有人的姓名和工作；
c. 居住在 Slumerville 的所有人的姓名和地址。

复合查询

简单查询形成了查询语言的原始操作。为了形成复合操作，查询语言提供了组合的手段。查询语言成为逻辑编程语言的一个原因是，组合的手段反映了形成逻辑表达式时使用的组合手段：and，or和not。

我们可以使用and如下来找到所有计算机程序员的地址：

and(job($person, list("computer", "programmer")),
    address($person, $where))

结果输出为

and(job(list("Hacker", "Alyssa", "P"), list("computer", "programmer")),
    address(list("Hacker", "Alyssa", "P"),
            list("Cambridge", list("Mass", "Ave"), 78)))
and(job(list("Fect", "Cy", "D"), list("computer", "programmer")),
    address(list("Fect", "Cy", "D"),
            list("Cambridge", list("Ames", "Street"), 3)))

一般来说，

and(query[1], query[2], ..., query[n])

由同时满足query[1]，...，query[n]的模式变量的值集合来满足模式。

对于简单查询，系统通过找到满足查询的模式变量的所有赋值，然后显示具有这些值的查询的实例化来处理复合查询。

构建复合查询的另一种方法是通过or。例如，

or(supervisor($x, list("Bitdiddle", "Ben")),
   supervisor($x, list("Hacker", "Alyssa", "P")))

将找到所有由 Ben Bitdiddle 或 Alyssa P. Hacker 监督的员工：

or(supervisor(list("Hacker", "Alyssa", "P"),
              list("Bitdiddle", "Ben")),
   supervisor(list("Hacker", "Alyssa", "P"),
              list("Hacker", "Alyssa", "P")))

or(supervisor(list("Fect", "Cy", "D"),
              list("Bitdiddle", "Ben")),
   supervisor(list("Fect", "Cy", "D"),
              list("Hacker", "Alyssa", "P")))

or(supervisor(list("Tweakit", "Lem", "E"),
              list("Bitdiddle", "Ben")),
   supervisor(list("Tweakit", "Lem", "E"),
              list("Hacker", "Alyssa", "P")))

or(supervisor(list("Reasoner", "Louis"),
              list("Bitdiddle", "Ben")),
   supervisor(list("Reasoner", "Louis"),
              list("Hacker", "Alyssa", "P")))

一般来说，

or(query[1], query[2], ..., query[n])

由满足至少一个query[1] ... query[n]的模式变量的值集合满足。

复合查询也可以用not形成。例如，

and(supervisor($x, list("Bitdiddle", "Ben")),
    not(job($x, list("computer", "programmer"))))

找到所有由 Ben Bitdiddle 监督的不是计算机程序员的人。一般来说，

not(query[1])

由不满足query[1]的模式变量的所有赋值满足。⁵⁷

最终的组合形式以javascript_predicate开头，包含一个 JavaScript 谓词。一般来说，

javascript_predicate(predicate)

将满足predicate中实例化的predicate为真的模式变量的赋值。例如，要找到所有工资大于 5 万美元的人，我们可以写⁵⁸

and(salary($person, $amount), javascript_predicate($amount > 50000))

练习 4.54

制定检索以下信息的复合查询：

a. 所有由 Ben Bitdiddle 监督的人的姓名，以及他们的地址；
b. 所有工资低于 Ben Bitdiddle 的人，以及他们的工资和 Ben Bitdiddle 的工资；
c. 所有由不在计算机部门的人监督的人，以及主管的姓名和工作。

规则

除了原始查询和复合查询，查询语言还提供了抽象查询的手段。这些由规则给出。规则

rule(lives_near($person_1, $person_2),
    and(address($person_1, pair($town, $rest_1)),
        address($person_2, pair($town, $rest_2)),
        not(same($person_1, $person_2))))

指定如果两个人住在同一个城镇，那么他们住在附*。最后的not子句防止规则说所有人都住在自己附*。same关系由一个非常简单的规则定义：⁵⁹

rule(same($x, $x))

以下规则声明，如果一个人监督一个人，而这个人又是一个主管，那么这个人在组织中是一个“轮子”：

rule(wheel($person),
     and(supervisor($middle_manager, $person),
         supervisor($x, $middle_manager)))

规则的一般形式是

rule(conclusion, body)

其中conclusion是一个模式，body是任何查询。⁶⁰我们可以认为规则代表一个大（甚至无限）的断言集，即满足规则体的变量赋值的规则结论的所有实例化。当我们描述简单查询（模式）时，我们说变量的赋值满足模式，如果实例化的模式在数据库中。但是模式不一定要作为断言明确地在数据库中。它可以是由规则暗示的隐式断言。例如，查询

lives_near($x, list("Bitdiddle", "Ben"))

导致

lives_near(list("Reasoner", "Louis"), list("Bitdiddle", "Ben"))

lives_near(list("Aull", "DeWitt"), list("Bitdiddle", "Ben"))

要找到所有住在 Ben Bitdiddle 附*的计算机程序员，我们可以问

and(job($x, list("computer", "programmer")),
    lives_near($x, list("Bitdiddle", "Ben")))

与复合函数一样，规则可以作为其他规则的一部分（就像我们上面看到的lives_near规则），甚至可以递归地定义。例如，规则

rule(outranked_by($staff_person, $boss),
     or(supervisor($staff_person, $boss),
        and(supervisor($staff_person, $middle_manager),
            outranked_by($middle_manager, $boss))))

说一个员工在组织中被老板超越，如果老板是这个人的主管，或者（递归地）如果这个人的主管被老板超越。

练习 4.55

定义一个规则，规定如果人 1 和人 2 做同样的工作，或者做人 1 的工作的人也可以做人 2 的工作，那么人 1 可以取代人 2，前提是人 1 和人 2 不是同一个人。使用你的规则，给出以下查询：

a. 所有可以取代 Cy D. Fect 的人；
b. 所有可以取代收入比他们高的人的人，以及两个人的工资。

练习 4.56

定义一个规则，如果一个人在部门中工作但没有一个在部门中工作的主管，那么这个人在部门中是一个“大人物”。

练习 4.57

Ben Bitdiddle 错过了太多次会议。担心他忘记会议的习惯可能会让他失去工作，Ben 决定采取一些行动。他通过断言将公司的所有周会议添加到 Gargle 数据库中，如下所示：

meeting("accounting", list("Monday", "9am"))
meeting("administration", list("Monday", "10am"))
meeting("computer", list("Wednesday", "3pm"))
meeting("administration", list("Friday", "1pm"))

上述每个断言都是整个部门的会议。Ben 还为跨越所有部门的全公司会议添加了一个条目。公司的所有员工都参加这次会议。

meeting("whole-company", list("Wednesday", "4pm"))

a. 在星期五早上，Ben 想要查询当天发生的所有会议。他应该使用什么查询？
b. Alyssa P. Hacker 并不感到满意。她认为，通过指定她的名字来询问她的会议将会更有用。因此，她设计了一个规则，规定一个人的会议包括所有“整公司”会议以及该人所在部门的所有会议。填写 Alyssa 的规则的主体。
```
rule(meeting_time($person, $day_and_time),
     rule-body)
```
c. Alyssa 在周三早上到达工作岗位，想知道当天她需要参加哪些会议。在定义了上述规则之后，她应该提出什么查询来找出这一点？

练习 4.58

通过给出查询

lives_near($person, list("Hacker", "Alyssa", "P"))

Alyssa P. Hacker 能够找到住在她附*的人，可以和他们一起上班。另一方面，当她尝试通过查询找到所有住在附*的人的对时

lives_near($person_1, $person_2)

她注意到每对住在附*的人都被列出了两次；例如，

lives_near(list("Hacker", "Alyssa", "P"), list("Fect", "Cy", "D"))
lives_near(list("Fect", "Cy", "D"), list("Hacker", "Alyssa", "P"))

为什么会发生这种情况？有没有办法找到住在附*的人的名单，其中每对只出现一次？请解释。

逻辑作为程序

我们可以将规则视为一种逻辑蕴涵：如果对模式变量的值的分配满足主体，那么它满足结论。因此，我们可以认为查询语言具有根据规则执行逻辑推导的能力。例如，考虑第 4.4 节开头描述的append操作。正如我们所说的，append可以由以下两个规则来描述：

对于任何列表y，空列表和y append成y。
对于任何u、v、y和z，如果v和y append成z，则pair(u, v)和y append成pair(u, z)。

为了在我们的查询语言中表达这一点，我们为一个关系定义了两个规则

append_to_form(x, y, z)

我们可以将其解释为“x和y append成z”：

rule(append_to_form(null, $y, $y))

rule(append_to_form(pair($u, $v), $y, pair($u, $z)),
     append_to_form($v, $y, $z))

第一个规则没有主体，这意味着结论对于任何$y的值都成立。请注意第二个规则如何利用pair来命名列表的头部和尾部。

在给定这两个规则的情况下，我们可以制定计算两个列表的append的查询：

查询输入：

append_to_form(list("a", "b"), list("c", "d"), $z)

查询结果：

append_to_form(list("a", "b"), list("c", "d"), list("a", "b", "c", "d"))

更令人惊讶的是，我们可以使用相同的规则来询问“哪个列表append到list("a", "b")会产生list("a", "b", "c", "d")？” 这样做如下：

查询输入：

append_to_form(list("a", "b"), $y, list("a", "b", "c", "d"))

查询结果：

append_to_form(list("a", "b"), list("c", "d"), list("a", "b", "c", "d"))

我们可以要求所有append成list("a", "b", "c", "d")的列表对：

查询输入：

append_to_form($x, $y, list("a", "b", "c", "d"))

查询结果：

append_to_form(null, list("a", "b", "c", "d"), list("a", "b", "c", "d"))

append_to_form(list("a"), list("b", "c", "d"), list("a", "b", "c", "d"))

append_to_form(list("a", "b"), list("c", "d"), list("a", "b", "c", "d"))

append_to_form(list("a", "b", "c"), list("d"), list("a", "b", "c", "d"))

append_to_form(list("a", "b", "c", "d"), null, list("a", "b", "c", "d"))

查询系统似乎在使用规则推断上述查询的答案时表现出相当多的智能。实际上，正如我们将在下一节中看到的那样，系统正在遵循一个明确定义的算法来解开规则。不幸的是，尽管系统在append情况下的工作令人印象深刻，但一般方法可能会在更复杂的情况下崩溃，正如我们将在第 4.4.3 节中看到的那样。

练习 4.59

以下规则实现了一个next_to_in关系，找到列表的相邻元素：

rule(next_to_in($x, $y, pair($x, pair($y, $u))))

rule(next_to_in($x, $y, pair($v, $z)),
     next_to_in($x, $y, $z))

对以下查询的响应将是什么？

next_to_in($x, $y, list(1, list(2, 3), 4))
next_to_in($x, 1, list(2, 1, 3, 1))

练习 4.60

定义规则来实现练习 2.17 的last_pair操作，该操作返回包含非空列表的最后一个元素的列表。在以下查询中检查您的规则：

last_pair(list(3), $x)
last_pair(list(1, 2, 3), $x)
last_pair(list(2, $x), list(3))

您的规则在诸如last_pair($x, list(3))的查询上是否正确工作？

练习 4.61

以下数据库（参见创世记 4）追溯了亚当的后裔的家谱，经由该隐：

son("Adam", "Cain")
son("Cain", "Enoch")
son("Enoch", "Irad")
son("Irad", "Mehujael") son("Mehujael", "Methushael") son("Methushael", "Lamech") wife("Lamech", "Ada")
son("Ada", "Jabal")
son("Ada", "Jubal")

制定规则，例如“如果S是F的儿子，F是G的儿子，那么S是G的孙子”，以及“如果W是M的妻子，S是W的儿子，那么S是M的儿子”（这在圣经时代比今天更真实），这将使查询系统能够找到该隐的孙子；拉麦的儿子；麦土撒的孙子。（参见练习 4.67，了解推断更复杂关系的一些规则。）

4.4.2 查询系统的工作原理

在第 4.4.4 节中，我们将介绍查询解释器的一组函数实现。在本节中，我们将概述解释器的一般结构，独立于低级实现细节。在描述解释器的实现之后，我们将能够理解查询语言的逻辑操作与数学逻辑操作的一些微妙差异以及一些限制。

显然，查询求值器必须执行某种搜索，以便将查询与数据库中的事实和规则匹配。一种方法是将查询系统实现为一个非确定性程序，使用第 4.3 节的amb求值器（参见练习 4.75）。另一种可能性是使用流来管理搜索。我们的实现遵循第二种方法。

查询系统围绕两个中心操作组织，称为模式匹配和统一。我们首先描述模式匹配，并解释这个操作，以及信息的组织方式，以流的形式的帧，使我们能够实现简单和复合查询。接下来我们讨论统一，这是模式匹配的一般化，需要实现规则。最后，我们展示整个查询解释器如何通过一个函数组合在一起，类似于第 4.1 节中描述的解释器对表达式进行分类的方式。

模式匹配

模式匹配器是一个测试某个数据是否符合指定模式的程序。例如，数据list(list("a", "b"), "c", list("a", "b"))与模式list($x, "c", $x)匹配，其中模式变量$x绑定到list("a", "b")。相同的数据列表与模式list($x, $y, $z)匹配，其中$x和$z都绑定到list("a", "b")，$y绑定到"c"。它还与模式list(list($x, $y), "c", list($x, $y))匹配，其中$x绑定到"a"，$y绑定到"b"。但是，它不与模式list($x, "a", $y)匹配，因为该模式指定了第二个元素为字符串"a"的列表。

查询系统使用的模式匹配器将模式、数据和指定各种模式变量绑定的帧作为输入。它检查数据是否与模式匹配，并且与帧中已有的绑定一致。如果是，它返回给定的帧，其中可能包含由匹配确定的任何绑定。否则，它指示匹配失败。

使用模式list($x, $y, $x)来匹配list("a", "b", "a")，给定一个空帧，例如，将返回一个指定$x绑定为"a"和$y绑定为"b"的帧。尝试使用相同的模式、相同的数据和指定$y绑定为"a"的帧进行匹配将失败。尝试使用相同的模式、相同的数据和一个帧，其中$y绑定为"b"和$x未绑定，将返回给定的帧，增加了$x绑定为"a"。

模式匹配器是处理不涉及规则的简单查询所需的全部机制。例如，处理查询

job($x, list("computer", "programmer"))

我们扫描数据库中的所有断言，并选择与最初空帧相匹配的断言。对于我们找到的每个匹配，我们使用匹配返回的帧来实例化具有$x值的模式。

帧流

通过使用流，模式对帧的测试是有组织的。给定一个单个帧，匹配过程逐个运行数据库条目。对于每个数据库条目，匹配器生成一个特殊符号，指示匹配失败，或者是帧的扩展。所有数据库条目的结果被收集到一个流中，通过过滤器传递以清除失败。结果是所有通过与数据库中某个断言的匹配扩展给定帧的所有帧的流。⁶¹

在我们的系统中，查询接受帧的输入流，并对流中的每个帧执行上述匹配操作，如图 4.5 所示。也就是说，对于输入流中的每个帧，查询生成一个新的流，其中包含通过与数据库中的断言匹配的该帧的所有扩展。然后将所有这些流组合成一个巨大的流，其中包含输入流中每个帧的所有可能扩展。这个流是查询的输出。

图 4.5 查询处理帧流。

为了回答一个简单的查询，我们使用一个输入流，其中包含一个单个的空帧的查询。生成的输出流包含对空帧的所有扩展（即，对我们查询的所有答案）。然后使用这些帧的流来生成原始查询模式的副本流，其中变量由每个帧中的值实例化，这是最终打印的流。

复合查询

当我们处理复合查询时，流式帧实现的真正优雅之处就显而易见了。复合查询的处理利用了我们的匹配器要求匹配与指定帧一致的能力。例如，处理两个查询的and，如

and(can_do_job($x, list("computer", "programmer", "trainee")),
    job($person, $x))

（非正式地，“找到所有能够做计算机程序员实习生工作的人”），我们首先找到所有与模式匹配的条目

can_do_job($x, list("computer", "programmer", "trainee"))

这产生了一系列帧，每个帧都包含$x的绑定。然后对于流中的每个帧，我们找到所有与之匹配的条目

job($person, $x)

以与$x的给定绑定一致的方式。每个这样的匹配都将产生一个包含$x和$person绑定的帧。两个查询的and可以被视为两个组成查询的串联组合，如图 4.6 所示。通过第一个查询过滤的帧将通过第二个查询进行进一步的过滤和扩展。

图 4.6 两个查询的and组合是通过对帧流进行串联操作而产生的。

图 4.7 显示了计算两个查询的or的类似方法，作为两个组成查询的并联组合。输入的帧流分别由每个查询单独扩展。然后合并两个结果流以产生最终的输出流。

图 4.7 两个查询的or组合是通过并行操作帧流并合并结果来产生的。

即使从这个高层描述中，处理复合查询的过程可能会很慢。例如，由于查询可能会为每个输入帧产生多个输出帧，并且and中的每个查询都从前一个查询中获取其输入帧，因此and查询在最坏的情况下可能需要执行指数数量的匹配（参见练习 4.73）。⁶² 尽管处理简单查询的系统非常实用，但处理复杂查询非常困难。⁶³

从帧流的观点来看，某些查询的not作为一个过滤器，删除所有可以满足查询的帧。例如，给定模式

not(job($x, list("computer", "programmer")))

我们尝试，对于输入流中的每个帧，产生满足job($x, list("computer", "programmer"))的扩展帧。我们从输入流中删除所有存在这样的扩展的帧。结果是一个仅由那些绑定$x不满足job($x, list("computer", "programmer"))的帧组成的流。例如，在处理查询时

and(supervisor($x, $y),
    not(job($x, list("computer", "programmer"))))

第一个子句将生成具有$x和$y绑定的帧。然后，not子句将通过删除所有绑定$x满足$x是计算机程序员的限制的帧来过滤这些帧。⁶⁴

javascript_predicate语法形式被实现为帧流上的类似过滤器。我们使用流中的每个帧来实例化模式中的任何变量，然后应用 JavaScript 谓词。我们从输入流中删除所有谓词失败的帧。

统一

为了处理查询语言中的规则，我们必须能够找到结论与给定查询模式匹配的规则。规则结论类似于断言，只是它们可以包含变量，因此我们需要一种称为统一的模式匹配的泛化，其中“模式”和“数据”都可以包含变量。

统一器接受两个包含常量和变量的模式，并确定是否可能为变量分配值，使得两个模式相等。如果可以，它返回一个包含这些绑定的帧。例如，统一list($x, "a", $y)和list($y, $z, "a")将指定一个帧，其中$x，$y和$z都必须绑定到"a"。另一方面，统一list($x, $y, "a")和list($x, "b", $y)将失败，因为没有值可以使两个模式相等。（为了使模式的第二个元素相等，$y必须是"b"；然而，为了使第三个元素相等，$y必须是"a"。）查询系统中使用的统一器，就像模式匹配器一样，接受一个帧作为输入，并执行与该帧一致的统一。

统一算法是查询系统中最技术上困难的部分。对于复杂的模式，执行统一可能需要推理。要统一

list($x, $x)

和

list(list("a", $y, "c"), list("a", "b", $z))

例如，算法必须推断出$x应该是list("a", "b", "c")，$y应该是"b"，$z应该是"c"。我们可以将这个过程看作是在模式组件之间解方程组。一般来说，这些是同时方程，可能需要大量的操作来解决。⁶⁵ 例如，统一list($x, $x)和list(list("a", $y, "c"), list("a", "b", $z))可以被认为是指定同时方程

$x = list("a", $y, "c")

$x = list("a", "b", $z)

这些方程意味着

list("a", $y, "c") = list("a", "b", $z)

这反过来意味着

"a" = "a", $y = "b", "c" = $z

因此

$x = list("a", "b", "c")

在成功的模式匹配中，所有模式变量都被绑定，它们被绑定的值只包含常量。到目前为止，我们所见到的所有统一的例子也是如此。然而，一般来说，成功的统一可能并不完全确定变量的值；一些变量可能保持未绑定，而其他变量可能绑定到包含变量的值。

考虑list($x, "a")和list(list("b", $y), $z)的统一。我们可以推断$x=list("b", $y)和"a"=$z，但我们无法进一步解决$x或$y。统一不会失败，因为通过为$x和$y分配值，可以使这两个模式相等。由于这种匹配无论如何都不会限制$y可以取的值，所以不会将$y的绑定放入结果帧中。但是，这种匹配确实限制了$x的值。无论$y有什么值，$x必须是list("b", $y)。因此，将$x绑定到模式list("b", $y)放入帧中。如果以后确定了$y的值并将其添加到帧中（通过需要与此帧一致的模式匹配或统一），则先前绑定的$x将引用此值。

应用规则

统一是查询系统的组成部分，用于从规则中进行推理。要了解如何实现这一点，可以考虑处理涉及应用规则的查询，例如

lives_near($x, list("Hacker", "Alyssa", "P"))

为了处理这个查询，我们首先使用上面描述的普通模式匹配函数来查看数据库中是否有任何与这个模式匹配的断言。（在这种情况下不会有任何匹配，因为我们的数据库中没有关于谁住在附*的直接断言。）下一步是尝试将查询模式与每条规则的结论统一。我们发现模式与规则的结论统一。

rule(lives_near($person_1, $person_2),
     and(address($person_1, pair($town, $rest_1)),
         address($person_2, list($town, $rest_2)),
         not(same($person_1, $person_2))))

导致一个指定$x应该绑定到（具有与）$person_1相同的值，并且$person_2绑定到list("Hacker", "Alyssa", "P")的帧。现在，相对于这个帧，我们求值规则体给出的复合查询。成功的匹配将通过为$person_1提供绑定来扩展此帧，因此也会提供$x的值，我们可以用它来实例化原始查询模式。

一般来说，查询求值器在尝试在指定了一些模式变量绑定的帧中建立查询模式时，使用以下方法应用规则：

将查询与规则的结论统一，如果成功，形成原始帧的扩展。
相对于扩展帧，求值规则体形成的查询。

注意这与 JavaScript 中evaluate/apply求值器中应用函数的方法有多么相似：

将函数的参数绑定到其参数以形成扩展原始函数环境的帧。
相对于扩展环境，求值函数体形成的表达式。

这两个求值器之间的相似之处应该不足为奇。正如函数定义是 JavaScript 中的抽象手段一样，规则定义是查询语言中的抽象手段。在每种情况下，我们通过创建适当的绑定来解开抽象，并相对于这些绑定来求值规则或函数体。

简单查询

我们在本节前面看到了如何在没有规则的情况下求值简单查询。现在我们已经看到了如何应用规则，我们可以描述如何通过使用规则和断言来求值简单查询。

给定查询模式和帧流，我们为输入流中的每个帧生成两个流：

通过将模式与数据库中的所有断言进行匹配获得的扩展帧的流（使用模式匹配器），
通过应用所有可能的规则（使用统一器）获得的扩展帧的流。

将这两个流附加起来，产生的流包含了满足原始帧一致的给定模式的所有方式。这些流（每个输入流中的每个帧一个）现在都被组合成一个大流，因此包含了原始输入流中的任何帧扩展以产生与给定模式匹配的所有方式。

查询求值器和驱动循环

尽管底层匹配操作复杂，但系统的组织方式与任何语言的求值器类似。协调匹配操作的函数称为evaluate_query，它的作用类似于 JavaScript 的evaluate函数。函数evaluate_query的输入是一个查询和一个帧流。它的输出是一个帧流，对应于成功匹配查询模式的情况，这些帧扩展了输入流中的某个帧，如图 4.5 所示。与evaluate类似，evaluate_query对不同类型的表达式（查询）进行分类，并为每个类型的表达式调用适当的函数。对于每种句法形式（and、or、not和javascript_predicate）以及简单查询，都有一个函数。

驱动循环类似于本章其他求值器中的driver_loop函数，它读取用户键入的查询。对于每个查询，它调用evaluate_query，并提供查询和由单个空帧组成的流。这将产生所有可能匹配的流（所有可能的扩展到空帧的情况）。对于结果流中的每个帧，它使用帧中找到的变量的值来实例化原始查询。然后打印这些实例化的查询流。

驱动程序还检查特殊命令assert，该命令表示输入不是查询，而是要添加到数据库的断言或规则。例如，

assert(job(list("Bitdiddle", "Ben"), list("computer", "wizard")))

assert(rule(wheel($person),
            and(supervisor($middle_manager, $person),
                supervisor($x, $middle_manager))))

4.4.3 逻辑编程是数理逻辑吗？

查询语言中使用的组合方式乍看起来与数理逻辑中的“与”、“或”和“非”操作相同，事实上，查询语言规则的应用是通过一种合法的推理方法完成的。尽管如此，将查询语言与数理逻辑等同起来并不是真正有效的，因为查询语言提供了一个控制结构，以过程化方式解释逻辑语句。我们经常可以利用这种控制结构。例如，要找到所有程序员的主管，我们可以用两种逻辑上等价的形式来制定查询：

and(job($x, list("computer", "programmer")),
    supervisor($x, $y))

或

and(supervisor($x, $y),
    job($x, list("computer", "programmer")))

如果一个公司的主管比程序员多得多，最好使用第一种形式而不是第二种形式，因为数据库必须为第一个and子句产生的每个中间结果（帧）扫描。

逻辑编程的目的是为程序员提供将计算问题分解为两个独立问题的技术：“要计算什么”和“如何计算”。这是通过选择数理逻辑陈述的子集来实现的，该子集足够强大，可以描述任何想要计算的内容，但又足够弱，可以有可控的过程性解释。这里的意图是，一种逻辑编程语言中指定的程序应该是一个可以由计算机执行的有效程序。控制（“如何”计算）是通过使用语言的求值顺序来实现的。我们应该能够安排子句的顺序和每个子句内部子目标的顺序，以便以被认为是有效和高效的顺序进行计算。同时，我们应该能够将计算结果（“要计算什么”）视为逻辑法则的简单结果。

我们的查询语言可以被视为数学逻辑的一个过程可解释子集。一个断言代表一个简单的事实（一个原子命题）。规则代表规则结论成立的推论。规则有一个自然的过程解释：要建立规则的结论，要建立规则的主体。因此，规则指定了计算。然而，因为规则也可以被看作是数学逻辑的陈述，我们可以通过断言，即通过完全在数学逻辑中工作，来证明逻辑程序所完成的任何“推理”都是可以被证明的。⁷⁰

无限循环

逻辑程序的过程性解释的一个结果是，可以构建解决某些问题的无望低效程序。当系统陷入无限循环时，效率低下的极端情况发生。举个简单的例子，假设我们正在建立一个包括著名婚姻的数据库，包括

assert(married("Minnie", "Mickey"))

如果我们现在问

married("Mickey", $who)

我们将得不到任何回应，因为系统不知道如果A与B结婚，那么B也与A结婚。因此，我们断言规则

assert(rule(married($x, $y),
            married($y, $x)))

再次查询

married("Mickey", $who)

不幸的是，这将使系统陷入无限循环，如下所示：

系统发现married规则适用；也就是说，规则结论married($x, $y)与查询模式married("Mickey", $who)统一，产生一个帧，其中$x绑定为"Mickey"，$y绑定为$who。因此，解释器继续在这个帧中求值规则主体married($y, $x)，实际上是处理查询married($who, "Mickey")。
一个答案，married("Minnie", "Mickey")，直接出现在数据库中作为一个断言。
married规则也适用，因此解释器再次求值规则主体，这次等同于married("Mickey", $who)。

系统现在陷入了无限循环。实际上，系统是否会在陷入循环之前找到简单的答案married("Minnie", "Mickey")取决于关于系统检查数据库中项目顺序的实现细节。这是可以发生的循环的一种非常简单的例子。相关规则的集合可能导致更难以预料的循环，并且循环的出现可能取决于and中子句的顺序（参见练习 4.62）或关于系统处理查询的顺序的低级细节。⁷¹

`not`的问题

查询系统中的另一个怪癖涉及not。给定第 4.4.1 节的数据库，考虑以下两个查询：

and(supervisor($x, $y),
    not(job($x, list("computer", "programmer"))))

and(not(job($x, list("computer", "programmer"))),
    supervisor($x, $y))

这两个查询不会产生相同的结果。第一个查询首先查找与supervisor($x, $y)匹配的数据库中的所有条目，然后通过删除满足job($x, list("computer", "programmer"))的值的结果帧来过滤结果。第二个查询首先通过过滤传入的帧来删除可以满足job($x, list("computer", "programmer"))的帧。由于唯一的传入帧是空的，它检查满足job($x, list("computer", "programmer"))的模式的数据库。由于通常存在这种形式的条目，not子句会过滤掉空帧并返回一个空的帧流。因此，整个复合查询返回一个空的帧流。

问题在于我们的not实现实际上是作为变量值的过滤器。如果在处理not子句时，一些变量保持未绑定（如上面的示例中的$x），系统将产生意外的结果。类似的问题也会出现在使用javascript_predicate时——如果其中一些变量未绑定，JavaScript 谓词将无法工作。参见练习 4.74。

查询语言的not与数学逻辑中的not有一种更为严重的不同之处。在逻辑中，我们解释语句“not P”表示P不是真的。然而，在查询系统中，“not P”表示P不能从数据库中的知识中推导出来。例如，给定第 4.4.1 节的人事数据，系统会愉快地推断出各种not语句，比如本·比迪德尔不是棒球迷，外面不下雨，2+2 不等于 4。换句话说，逻辑编程语言中的not反映了所谓的封闭世界假设，即所有相关信息都已包含在数据库中。

练习 4.62

路易斯·里森纳错误地从数据库中删除了outranked_by规则（第 4.4.1 节）。当他意识到这一点时，他迅速重新安装了它。不幸的是，他对规则进行了轻微更改，并将其输入为

rule(outranked_by($staff_person, $boss),
     or(supervisor($staff_person, $boss),
        and(outranked_by($middle_manager, $boss),
            supervisor($staff_person, $middle_manager))))

就在路易斯将这些信息输入系统后，德维特·奥尔过来询问谁的地位高于本·比迪德尔。他发出了查询

outanked_by(list("Bitdiddle", "Ben"), $who)

回答后，系统陷入无限循环。解释原因。

练习 4.63

赛伊·D·费克特期待着有一天能在组织中崛起，他提出了一个查询，以找到所有的车轮（使用第 4.4.1 节的wheel规则）：

wheel($who)

令他惊讶的是，系统的回应是

查询结果：

wheel(list("Warbucks", "Oliver"))

wheel(list("Bitdiddle", "Ben"))

wheel(list("Warbucks", "Oliver"))

wheel(list("Warbucks", "Oliver"))

wheel(list("Warbucks", "Oliver"))

为什么奥利弗·沃巴克斯被列出了四次？

练习 4.64

本一直在将查询系统概括为提供有关公司的统计信息。例如，要找到所有计算机程序员的总薪水，可以说

sum($amount,
    and(job($x, list("computer", "programmer")),
        salary($x, $amount)))

一般来说，本的新系统允许形式的表达

accumulation_function(variable,
                      query-pattern)

其中accumulation_function可以是sum、average或maximum之类的东西。本推断实现这应该很容易。他只需将查询模式提供给evaluate_query。这将产生一系列框架。然后，他将通过一个映射函数将这个流传递给累积函数，从而提取流中每个框架的指定变量的值，并将结果流传递给累积函数。就在本完成实现并准备尝试时，赛伊路过，仍在思考练习 4.63 中wheel查询结果。当赛伊向本展示系统的回应时，本叹息道：“哦，不，我的简单累积方案行不通！”

本刚刚意识到了什么？概述他可以用来挽救情况的方法。

练习 4.65

设计一种方法，在查询系统中安装一个循环检测器，以避免文本和练习 4.62 中所示的简单循环。一般的想法是，系统应该维护其当前推断链的某种历史，并且不应该开始处理它已经在处理的查询。描述这个历史中包含的信息（模式和框架），以及应该如何进行检查。（在你研究第 4.4.4 节中的查询系统实现的细节之后，你可能想修改系统以包括你的循环检测器。）

练习 4.66

定义规则来实现练习 2.18 的reverse操作，该操作以相反的顺序返回包含与给定列表相同元素的列表。（提示：使用append_to_form。）你的规则能回答查询reverse(list(1, 2, 3), $x)和查询reverse($x, list(1, 2, 3))吗？

练习 4.67

让我们修改练习 4.61 的数据库和规则，将great添加到孙子关系中。这应该使系统能够推断出伊拉德是亚当的曾孙，或者贾伯尔和尤巴尔是亚当的曾曾曾曾曾孙。

a.更改数据库中的断言，使得只有一种关系信息，即related。第一项描述了关系。因此，不是son("Adam", "Cain")，而是related("son", "Adam", "Cain")。例如，表示关于 Irad 的事实为

related(list("great", "grandson"), "Adam", "Irad")
b.编写规则，确定列表是否以单词"grandson"结尾。
c.使用这个来表达一个允许推导关系的规则

list(pair("great", $rel), $x, $y)

其中$rel是以"grandson"结尾的列表。
d.检查你的规则在查询related(list("great", "grandson"), $g, $ggs)和related($relationship, "Adam", "Irad")上的表现。

4.4.4 实现查询系统

4.4.2 节描述了查询系统的工作原理。现在我们通过提供系统的完整实现来填写细节。

4.4.4.1 驱动循环

查询系统的驱动循环反复读取输入表达式。如果表达式是要添加到数据库中的规则或断言，那么信息就会被添加。否则，假定表达式是一个查询。驱动程序将此查询传递给evaluate_query，并与一个由单个空帧组成的初始帧流一起传递。求值的结果是通过满足在数据库中找到的变量值来生成的帧流。这些帧用于形成一个新的流，其中包含原始查询的副本，其中变量被帧流提供的值实例化，最终的流被显示：

const input_prompt = "Query input:";
const output_prompt = "Query results:";

function query_driver_loop() {
    const input = user_read(input_prompt) + ";";
    if (is_null(input)) {
        display("evaluator terminated");
    } else {
        const expression = parse(input);
        const query = convert_to_query_syntax(expression);
        if (is_assertion(query)) {
            add_rule_or_assertion(assertion_body(query));
            display("Assertion added to data base.");
        } else {
            display(output_prompt);
            display_stream(
              stream_map(
                 frame =>
                   unparse(instantiate_expression(expression, frame)),
                 evaluate_query(query, singleton_stream(null))));
        }
        return query_driver_loop();
    }
}

在这里，与本章中的其他求值器一样，我们使用parse将作为字符串给出的查询语言的组件转换为 JavaScript 语法表示。（我们在输入表达式字符串后附加了一个分号，因为parse期望一个语句。）然后我们进一步将语法表示转换为适合查询系统的概念级别，使用convert_to_query_syntax，它在 4.4.4.7 节中声明，以及谓词is_assertion和选择器assertion_body。函数add_rule_or_assertion在 4.4.4.5 节中声明。查询求值产生的帧用于实例化语法表示，结果被解析成字符串进行显示。函数instantiate_expression和unparse在 4.4.4.7 节中声明。

4.4.4.2 求值器

evaluate_query函数由query_driver_loop调用，是查询系统的基本求值器。它以查询和帧流作为输入，并返回扩展帧的流。它通过使用get和put进行数据导向分派来识别句法形式，就像我们在第 2 章中实现通用操作一样。任何未被识别为句法形式的查询都被假定为简单查询，由simple_query处理。

function evaluate_query(query, frame_stream) {
    const qfun = get(type(query), "evaluate_query");
    return is_undefined(qfun)
           ? simple_query(query, frame_stream)
           : qfun(contents(query), frame_stream);
}

函数type和contents在 4.4.4.7 节中定义，实现了句法形式的抽象语法。

简单查询

simple_query函数处理简单查询。它以简单查询（模式）和帧流作为参数，并返回通过扩展每个帧的所有数据库匹配项形成的流。

function simple_query(query_pattern, frame_stream) {
    return stream_flatmap(
               frame =>
                 stream_append_delayed(
                     find_assertions(query_pattern, frame),
                     () => apply_rules(query_pattern, frame)),
               frame_stream);
}

对于输入流中的每个框架，我们使用find_assertions（第 4.4.4.3 节）来匹配数据库中所有断言与模式，产生一个扩展框架的流，并使用apply_rules（第 4.4.4.4 节）来应用所有可能的规则，产生另一个扩展框架的流。这两个流被合并（使用stream_append_delayed，第 4.4.4.6 节）以生成给定模式可以满足的所有方式的流，与原始框架一致（参见练习 4.68）。输入框架的流使用stream_flatmap（第 4.4.4.6 节）组合，形成一个大的流，列出原始输入流中任何框架可以扩展以与给定模式匹配的所有方式。

复合查询

我们处理and查询，如图 4.6 所示，使用conjoin函数，它以连接词和框架流作为输入，并返回扩展框架的流。首先，conjoin处理框架流以找到满足连接词中第一个查询的所有可能框架扩展的流。然后，使用这个新的框架流，它递归地将conjoin应用于其余的查询。

function conjoin(conjuncts, frame_stream) {
    return is_empty_conjunction(conjuncts)
           ? frame_stream
           : conjoin(rest_conjuncts(conjuncts),
                     evaluate_query(first_conjunct(conjuncts),
                                    frame_stream));
}

陈述

put("and", "evaluate_query", conjoin);

设置evaluate_query以在遇到and时分派到conjoin。

我们类似地处理or查询，如图 4.7 所示。or的各个分离词的输出流分别计算，并使用第 4.4.4.6 节中的interleave_delayed函数合并。（参见练习 4.68 和 4.69。）

function disjoin(disjuncts, frame_stream) {
    return is_empty_disjunction(disjuncts)
           ? null
           : interleave_delayed(
                evaluate_query(first_disjunct(disjuncts), frame_stream),
                () => disjoin(rest_disjuncts(disjuncts), frame_stream));
}
put("or", "evaluate_query", disjoin);

在第 4.4.4.7 节中给出了表示连接词和分离词的谓词和选择器。

过滤器

not语法形式由第 4.4.2 节中概述的方法处理。我们尝试扩展输入流中的每个框架以满足被否定的查询，并且只有在不能扩展时才将给定框架包含在输出流中。

function negate(exps, frame_stream) {
    return stream_flatmap(
               frame =>
                 is_null(evaluate_query(negated_query(exps),
                                        singleton_stream(frame)))
                 ? singleton_stream(frame)
                 : null, frame_stream);
}
put("not", "evaluate_query", negate);

javascript_predicate语法形式类似于not的过滤器。流中的每个框架用于实例化谓词中的变量，实例化的谓词被求值，谓词求值为false的框架被过滤出输入流。使用evaluate（第 4.1 节）从the_global_environment求值实例化的谓词，因此可以处理任何 JavaScript 表达式，只要在求值之前实例化所有模式变量。

function javascript_predicate(exps, frame_stream) {
    return stream_flatmap(
               frame =>
                 evaluate(instantiate_expression(
                              javascript_predicate_expression(exps),
                              frame),
                          the_global_environment)
                 ? singleton_stream(frame)
                 : null,
               frame_stream);
}
put("javascript_predicate", "evaluate_query", javascript_predicate);

always_true语法形式提供了一个始终满足的查询。它忽略其内容（通常为空），并简单地通过输入流中的所有框架。rule_body选择器（第 4.4.4.7 节）使用always_true为没有定义体的规则提供体（即，始终满足的规则）。

function always_true(ignore, frame_stream) {
    return frame_stream;
}
put("always_true", "evaluate_query", always_true);

定义not和javascript_predicate的选择器在第 4.4.4.7 节中给出。

4.4.4.3 通过模式匹配查找断言

函数find_assertions由simple_query（第 4.4.4.2 节）调用，以模式和框架作为输入。它返回一个框架流，每个框架都通过给定模式的数据库匹配扩展给定框架。它使用fetch_assertions（第 4.4.4.5 节）获取数据库中所有断言的流，应该检查这些断言是否与模式和框架匹配。这里使用fetch_assertions的原因是我们通常可以应用简单的测试来消除数据库中的许多条目，使其不再是成功匹配的候选项。如果我们消除了fetch_assertions并简单地检查数据库中所有断言的流，系统仍然可以工作，但计算效率会降低，因为我们需要对匹配器进行更多的调用。

function find_assertions(pattern, frame) {
    return stream_flatmap(
                datum => check_an_assertion(datum, pattern, frame),
                fetch_assertions(pattern, frame));
}

函数check_an_assertion以数据对象（断言）、模式和框架作为参数，并返回一个包含扩展框架的单元素流，或者如果匹配失败则返回null。

function check_an_assertion(assertion, query_pat, query_frame) {
    const match_result = pattern_match(query_pat, assertion,
                                       query_frame);
    return match_result === "failed"
           ? null
           : singleton_stream(match_result);
}

基本模式匹配器返回字符串failed或给定框架的扩展。匹配器的基本思想是逐个元素地检查模式与数据，累积模式变量的绑定。如果模式和数据对象相同，则匹配成功，我们返回迄今为止累积的绑定框架。否则，如果模式是一个变量（由 4.4.4.7 节中声明的is_variable函数检查），我们通过将变量绑定到数据来扩展当前框架，只要这与框架中已有的绑定一致。如果模式和数据都是对，我们（递归地）将模式的头与数据的头进行匹配以产生一个框架；然后在这个框架中，我们将模式的尾与数据的尾进行匹配。如果这些情况都不适用，则匹配失败，我们返回字符串failed。

function pattern_match(pattern, data, frame) {
    return frame === "failed"
           ? "failed"
           : equal(pattern, data)
           ? frame
           : is_variable(pattern)
           ? extend_if_consistent(pattern, data, frame)
           : is_pair(pattern) && is_pair(data)
           ? pattern_match(tail(pattern),
                           tail(data),
                           pattern_match(head(pattern),
                                         head(data),
                                         frame))
           : "failed";
}

这是一个通过添加新绑定来扩展框架的函数，如果这与框架中已有的绑定一致的话：

function extend_if_consistent(variable, data, frame) {
    const binding = binding_in_frame(variable, frame);
    return is_undefined(binding)
           ? extend(variable, data, frame)
           : pattern_match(binding_value(binding), data, frame);
}

如果框架中没有变量的绑定，我们只需将变量的绑定添加到数据中。否则，我们在框架中将数据与框架中变量的值进行匹配。如果存储的值只包含常量，那么它必须在模式匹配期间由extend_if_consistent存储，匹配只是简单地测试存储的值和新值是否相同。如果是，则返回未修改的框架；如果不是，则返回失败指示。然而，存储的值可能包含模式变量，如果它是在统一期间存储的（见 4.4.4.4 节）。存储的模式与新数据的递归匹配将为这个模式中的变量添加或检查绑定。例如，假设我们有一个框架，其中$x绑定到list("f", $y)，而$y未绑定，我们希望通过将$x绑定到list("f", "b")来扩充这个框架。我们查找$x并发现它绑定到list("f", $y)。这导致我们在同一个框架中将list("f", $y)与建议的新值list("f", "b")进行匹配。最终，这个匹配通过添加$y绑定到"b"来扩展框架。变量$x仍然绑定到list("f", $y)。我们从不修改存储的绑定，也不会为给定变量存储多个绑定。

extend_if_consistent使用的函数来操作绑定在 4.4.4.8 节中定义。

4.4.4.4 规则和统一

函数apply_rules是find_assertions（4.4.4.3 节）的规则类比。它以模式和框架作为输入，并通过应用来自数据库的规则形成一个扩展框架流。函数stream_flatmap将apply_a_rule映射到可能适用的规则流（由fetch_rules选择，4.4.4.5 节），并组合结果框架的流。

function apply_rules(pattern, frame) {
    return stream_flatmap(rule => apply_a_rule(rule, pattern, frame),
                          fetch_rules(pattern, frame));
}

函数apply_a_rule使用 4.4.2 节中概述的方法应用规则。它首先通过将规则结论与给定框架中的模式统一来扩充其参数框架。如果成功，它就在这个新框架中求值规则主体。

然而，在发生这些情况之前，程序会将规则中的所有变量重命名为唯一的新名称。这样做的原因是为了防止不同规则应用的变量相互混淆。例如，如果两个规则都使用名为$x的变量，那么每个规则在应用时可能都会向框架中添加一个$x的绑定。这两个$x互不相关，我们不应该被误导以为这两个绑定必须一致。我们可以设计一个更聪明的环境结构来代替重命名变量；然而，我们选择的重命名方法是最直接的，即使不是最有效的（见练习 4.76）。这里是apply_a_rule函数：

function apply_a_rule(rule, query_pattern, query_frame) {
    const clean_rule = rename_variables_in(rule);
    const unify_result = unify_match(query_pattern,
                                     conclusion(clean_rule),
                                     query_frame);
    return unify_result === "failed"
           ? null
           : evaluate_query(rule_body(clean_rule),
                            singleton_stream(unify_result));
}

提取规则的部分的选择器rule_body和conclusion在 4.4.4.7 节中定义。

我们通过将唯一标识符（如数字）与每个规则应用关联，并将此标识符与原始变量名结合起来来生成唯一的变量名。例如，如果规则应用标识符为 7，我们可能会将规则中的每个$x更改为$x_7，将规则中的每个$y更改为$y_7。（函数make_new_variable和new_rule_application_id包含在第 4.4.4.7 节的语法函数中。）

function rename_variables_in(rule) {
    const rule_application_id = new_rule_application_id();
    function tree_walk(exp) {
        return is_variable(exp)
               ? make_new_variable(exp, rule_application_id)
               : is_pair(exp)
               ? pair(tree_walk(head(exp)),
                      tree_walk(tail(exp)))
               : exp;
    }
    return tree_walk(rule);
}

统一算法被实现为一个函数，它以两个模式和一个框架作为输入，并返回扩展的框架或字符串"failed"。统一器类似于模式匹配器，只是它是对称的 - 变量允许在匹配的两侧。函数unify_match基本上与pattern_match相同，只是下面有一个额外的子句（标记为***），用于处理右侧对象为变量的情况。

function unify_match(p1, p2, frame) {
    return frame === "failed"
           ? "failed"
           : equal(p1, p2)
           ? frame
           : is_variable(p1)
           ? extend_if_possible(p1, p2, frame)
           : is_variable(p2) // *
           ? extend_if_possible(p2, p1, frame) // *
           : is_pair(p1) && is_pair(p2)
           ? unify_match(tail(p1),
                         tail(p2),
                         unify_match(head(p1),
                                     head(p2),
                                     frame))
           : "failed";
}

在统一中，就像单向模式匹配一样，我们只希望接受框架的提议扩展，只有当它与现有绑定一致时才会这样。在统一中使用的函数extend_if_possible与模式匹配中使用的函数extend_if_consistent相同，只是在程序中有两个特殊检查，标记为***。在第一种情况下，如果我们尝试匹配的变量未绑定，但我们尝试匹配的值本身是（不同的）变量，则有必要检查该值是否已绑定，并且如果是，则匹配其值。如果匹配的双方都未绑定，我们可以将其中一个绑定到另一个。

第二个检查处理尝试将变量绑定到包含该变量的模式的情况。只要在两个模式中重复一个变量，这种情况就会发生。例如，考虑在两个模式list($x, $x)和list($y, 包含 $y 的表达式)中统一，在其中$x和$y都未绑定的框架中。首先，将$x与$y匹配，将$x绑定到$y。接下来，将相同的$x与包含$y的给定表达式匹配。由于$x已绑定到$y，这导致将$y与表达式匹配。如果我们认为统一器是在找到一组使模式相同的模式变量的值，那么这些模式暗示了查找一个$y，使得$y等于包含$y的表达式。我们拒绝这样的绑定；这些情况由谓词depends_on识别。另一方面，我们不希望拒绝将变量绑定到自身的尝试。例如，考虑统一list($x, $x)和list($y, $y)。将$x绑定到$y的第二次尝试将$y（$x的存储值）与$y（$x的新值）匹配。这由unify_match的equal子句处理。

function extend_if_possible(variable, value, frame) {
    const binding = binding_in_frame(variable, frame);
    if (! is_undefined(binding)) {
        return unify_match(binding_value(binding),
                            value, frame);
    } else if (is_variable(value)) { // *
         const binding = binding_in_frame(value, frame);
        return ! is_undefined(binding)
               ? unify_match(variable,
                             binding_value(binding),
                             frame)
               : extend(variable, value, frame);
    } else if (depends_on(value, variable, frame)) { // *
        return "failed";
    } else {
        return extend(variable, value, frame);
    }
}

函数depends_on是一个谓词，用于测试提议作为模式变量值的表达式是否依赖于该变量。这必须相对于当前框架来完成，因为表达式可能包含已经依赖于我们测试变量的值的变量的出现。depends_on的结构是一个简单的递归树遍历，我们在必要时替换变量的值。

function depends_on(expression, variable, frame) {
    function tree_walk(e) {
        if (is_variable(e)) {
            if (equal(variable, e)) {
                return true;
            } else {
                const b = binding_in_frame(e, frame);
                return is_undefined(b)
                       ? false
                       : tree_walk(binding_value(b));
            }
        } else {
            return is_pair(e)
                   ? tree_walk(head(e)) || tree_walk(tail(e))
                   : false;
        }
    }
    return tree_walk(expression);
}

4.4.4.5 维护数据库

设计逻辑编程语言的一个重要问题是安排事物，以便在检查给定模式时尽可能少地检查不相关的数据库条目。为此，我们将断言表示为一个列表，其头部是表示断言信息类型的字符串。我们将断言存储在单独的流中，每种信息类型一个流，在一个由信息类型索引的表中。要获取可能匹配模式的断言，我们返回（以便使用匹配器进行测试）所有具有相同头部（相同信息类型）的存储断言。更聪明的方法也可以利用帧中的信息。我们避免构建用于索引程序的标准；相反，我们调用体现我们标准的谓词和选择器。

function fetch_assertions(pattern, frame) {
    return get_indexed_assertions(pattern);
}
function get_indexed_assertions(pattern) {
    return get_stream(index_key_of(pattern), "assertion-stream");
}

get_stream函数在表中查找流，并在没有存储内容时返回一个空的流。

function get_stream(key1, key2) {
    const s = get(key1, key2);
    return is_undefined(s) ? null : s;
}

规则也是类似地存储，使用规则结论的头部。一个模式可以匹配具有相同头部的规则结论的规则。因此，当获取可能匹配模式的规则时，我们获取所有结论具有与模式相同头部的规则。

function fetch_rules(pattern, frame) {
    return get_indexed_rules(pattern);
}
function get_indexed_rules(pattern) {
    return get_stream(index_key_of(pattern), "rule-stream");
}

add_rule_or_assertion函数由query_driver_loop用于向数据库添加断言和规则。每个项目都存储在索引中。

function add_rule_or_assertion(assertion) {
    return is_rule(assertion)
           ? add_rule(assertion)
           : add_assertion(assertion);
}
function add_assertion(assertion) {
    store_assertion_in_index(assertion);
    return "ok";
}
function add_rule(rule) {
    store_rule_in_index(rule);
    return "ok";
}

要实际存储断言或规则，我们将其存储在适当的流中。

function store_assertion_in_index(assertion) {
    const key = index_key_of(assertion);
    const current_assertion_stream =
                get_stream(key, "assertion-stream");
    put(key, "assertion-stream",
        pair(assertion, () => current_assertion_stream));
}
function store_rule_in_index(rule) {
    const pattern = conclusion(rule);
    const key = index_key_of(pattern);
    const current_rule_stream =
                get_stream(key, "rule-stream");
    put(key, "rule-stream",
        pair(rule, () => current_rule_stream));
}

模式（断言或规则结论）存储在表中的键是它以字符串开头的字符串。

function index_key_of(pattern) { return head(pattern); }

4.4.4.6 流操作

查询系统使用了一些流操作，这些操作在第 3 章中没有介绍。stream_append_delayed和interleave_delayed函数与stream_append和interleave（第 3.5.3 节）类似，只是它们接受了一个延迟参数（就像第 3.5.4 节中的integral函数）。这在某些情况下会推迟循环（参见练习 4.68）。

function stream_append_delayed(s1, delayed_s2) {
    return is_null(s1)
           ? delayed_s2()
           : pair(head(s1),
                  () => stream_append_delayed(stream_tail(s1),
                                              delayed_s2));
}
function interleave_delayed(s1, delayed_s2) {
    return is_null(s1)
           ? delayed_s2()
           : pair(head(s1),
                  () => interleave_delayed(delayed_s2(),
                                           () => stream_tail(s1)));
}

stream_flatmap函数在查询求值器中用于在帧流上映射函数并组合结果帧流，它是第 2.2.3 节中为普通列表引入的flatmap函数的流模拟。然而，与普通的flatmap不同，我们使用交错过程累积流，而不是简单地追加它们（参见练习 4.69 和 4.70）。

function stream_flatmap(fun, s) {
    return flatten_stream(stream_map(fun, s));
}
function flatten_stream(stream) {
    return is_null(stream)
           ? null
           : interleave_delayed(
                  head(stream),
                  () => flatten_stream(stream_tail(stream)));
}

求值器还使用以下简单函数生成由单个元素组成的流：

function singleton_stream(x) {
    return pair(x, () => null);
}

4.4.4.7 查询语法函数和实例化

我们在第 4.4.4.1 节中看到，驱动循环首先将输入字符串转换为 JavaScript 语法表示。输入被设计成看起来像 JavaScript 表达式，以便我们可以使用第 4.1.2 节中的parse函数，并且还支持javascript_predicate中的 JavaScript 表示。例如，

parse('job($x, list("computer", "wizard"));');

产生

list("application",
     list("name", "job"),
     list(list("name", "$x"),
          list("application",
               list("name", "list"),
               list(list("literal", "computer"),
                    list("literal", "wizard")))))

标签"application"表示，从语法上讲，查询将被视为 JavaScript 中的函数应用。函数unparse将语法转换回字符串：

unparse(parse('job($x, list("computer", "wizard"));'));
'job($x, list("computer", "wizard"))'

在查询处理器中，我们假设了断言、规则和查询的查询语言特定表示。函数convert_to_query_syntax将语法表示转换为该表示。使用相同的示例，

convert_to_query_syntax(parse('job($x, list("computer", "wizard"));'));

产生

list("job", list("name", "$x"), list("computer", "wizard"))

查询系统函数，如第 4.4.4.5 节中的add_rule_or_assertion和第 4.4.4.2 节中的evaluate_query，使用下面声明的选择器和谓词，如type、contents、is_rule和first_conjunct，对查询语言特定表示进行操作。图 4.8 描述了查询系统使用的三个抽象屏障以及转换函数parse、unparse和convert_to_query_syntax如何连接它们。

图 4.8 查询系统中的语法抽象。

处理模式变量

在查询处理过程中，谓词is_variable用于查询语言特定表示，并在实例化过程中用于 JavaScript 语法表示，以识别以美元符号开头的名称。我们假设有一个char_at函数，它返回一个字符串，该字符串仅包含给定位置的给定字符串的字符。⁷⁵

function is_variable(exp) {
    return is_name(exp) && char_at(symbol_of_name(exp), 0) === "$";
}

唯一变量是通过规则应用（在 4.4.4.4 节）中的以下函数构建的。规则应用的唯一标识符是一个数字，每次应用规则时都会递增。⁷⁶

let rule_counter = 0;

function new_rule_application_id() { 
    rule_counter = rule_counter + 1;
    return rule_counter;
}
function make_new_variable(variable, rule_application_id) {
    return make_name(symbol_of_name(variable) + "_" +
                     stringify(rule_application_id));
}

函数`convert_to_query_syntax`

函数convert_to_query_syntax通过简化断言、规则和查询，将 JavaScript 语法表示递归转换为查询语言特定表示，使得应用程序的函数表达式中的名称的符号成为标记，除非该符号是"pair"或"list"，则构建一个（未标记的）JavaScript 对或列表。这意味着convert_to_query_syntax在转换过程中解释构造函数pair和list的应用，并且处理函数（如 4.4.4.3 节的pattern_match和 4.4.4.4 节的unify_match）可以直接操作预期的对和列表，而不是在解析器生成的语法表示上进行操作。javascript_predicate的（单元素）“参数”列表保持未处理，如下所述。变量保持不变，文字简化为其包含的原始值。

function convert_to_query_syntax(exp) {
   if (is_application(exp)) {
     const function_symbol = symbol_of_name(function_expression(exp));
     if (function_symbol === "javascript_predicate") {
       return pair(function_symbol, arg_expressions(exp));
     } else {
       const processed_args = map(convert_to_query_syntax,
                                  arg_expressions(exp));
       return function_symbol === "pair"
              ? pair(head(processed_args), head(tail(processed_args)))
              : function_symbol === "list"
              ? processed_args
              : pair(function_symbol, processed_args);
     }
   } else if (is_variable(exp)) {
     return exp;
   } else { // exp is literal
     return literal_value(exp);
   }
}

对此处理的一个例外是javascript_predicate。由于其谓词表达式的实例化 JavaScript 语法表示被传递给 4.1.1 节的evaluate，来自parse的原始语法表示需要保持在表达式的查询语言特定表示中。在 4.4.1 节的这个例子中

and(salary($person, $amount), javascript_predicate($amount > 50000))

convert_to_query_syntax生成一个数据结构，其中 JavaScript 语法表示嵌入在查询语言特定表示中：

list("and",
     list("salary", list("name", "$person"), list("name", "$amount")),
     list("javascript_predicate",
          list("binary_operator_combination",
               ">",
               list("name", "$amount"),
               list("literal", 50000))))

为了求值已处理查询的javascript_predicate子表达式，4.4.4.2 节的函数javascript_predicate调用嵌入的 JavaScript 语法表示的$amount > 50000的instantiate_expression（下文）来替换变量list("name", "$amount")为一个文字，例如list("literal", 70000)，表示$amount绑定的原始值，这里是 70000。JavaScript 求值器可以求值实例化的谓词，现在表示为70000 > 50000。

表达式的实例化

4.4.4.2 节的函数javascript_predicate和 4.4.4.1 节的驱动循环在表达式上调用instantiate_expression，以获得一个副本，其中表达式中的任何变量都被给定帧中的值替换。输入和结果表达式使用 JavaScript 语法表示，因此从实例化变量中得到的任何值都需要从其在绑定中的形式转换为 JavaScript 语法表示。

function instantiate_expression(expression, frame) {
   return is_variable(expression)
          ? convert(instantiate_term(expression, frame))
          : is_pair(expression)
          ? pair(instantiate_expression(head(expression), frame),
                 instantiate_expression(tail(expression), frame))
          : expression;
}

函数instantiate_term以变量、对或原始值作为第一个参数，并以帧作为第二个参数，并递归地将第一个参数中的变量替换为帧中的值，直到达到原始值或未绑定变量。当过程遇到对时，将构造一个新的对，其部分是原始部分的实例化版本。例如，如果在帧f中将$x绑定到对[$y, 5]，并且$y又绑定到 3，那么将instantiate_term应用于list("name", "$x")和f的结果是对[3, 5]。

function instantiate_term(term, frame) {
    if (is_variable(term)) {
        const binding = binding_in_frame(term, frame);
        return is_undefined(binding)
              ? term // leave unbound variable as is
           : instantiate_term(binding_value(binding), frame);
    } else if (is_pair(term)) {
        return pair(instantiate_term(head(term), frame),
                    instantiate_term(tail(term), frame));
    } else { // term is a primitive value
        return term;
    }
}

函数convert构造了一个 JavaScript 语法表示，用于instantiate_term返回的变量、对或原始值。原始中的一对变成了 JavaScript 的对构造函数的应用，原始值变成了文字。

function convert(term) {
    return is_variable(term)
           ? term
           : is_pair(term)
           ? make_application(make_name("pair"),
                              list(convert(head(term)),
                                   convert(tail(term))))
           : // term is a primitive value
             make_literal(term);
}

为了说明这三个函数，考虑查询时发生的情况

job($x, list("computer", "wizard"))

其 JavaScript 语法表示在第 4.4.4.7 节开头给出，由驱动循环处理。假设结果流的帧g将变量$x绑定到["Bitdiddle", $y]，变量$y绑定到["Ben", null]。

instantiate_term(list("name", "$x"), g)

返回列表

list("Bitdiddle", "Ben")

将convert转换为

list("application",
     list("name", "pair"),
     list(list("literal", "Bitdiddle"),
          list("application",
               list("name", "pair"),
               list(list("literal", "Ben"),
                    list("literal", null)))))

应用于查询的 JavaScript 语法表示和帧g的instantiate_expression的结果是：

list("application",
     list("name", "job"),
     list(list("application",
               list("name", "pair"),
               list(list("literal", "Bitdiddle"),
                    list("application",
                         list("name", "pair"),
                         list(list("literal", "Ben"),
                              list("literal", null))))),
          list("application",
               list("name", "list"),
               list(list("literal", "computer"),
                    list("literal", "wizard")))))

驱动循环取消解析此表示并将其显示为：

'job(list("Bitdiddle", "Ben"), list("computer", "wizard"))'

函数`unparse`

函数unparse通过应用第 4.1.2 节的语法规则将给定的 JavaScript 语法表示转换为字符串。我们仅描述了unparse用于第 4.4.1 节示例中出现的那些表达式的类型，将语句和其余类型的表达式留给练习 4.2。通过stringifying其值来转换文字，将名称转换为其符号。应用通过取消解析函数表达式格式化，我们可以假定这里是一个名称，后面跟着用括号括起来的逗号分隔的参数表达式字符串。二元运算符组合使用中缀表示法格式化。

function unparse(exp) {
    return is_literal(exp)
           ? stringify(literal_value(exp))
           : is_name(exp)
           ? symbol_of_name(exp)
           : is_list_construction(exp)
           ? unparse(make_application(make_name("list"),
                                      element_expressions(exp)))
           : is_application(exp) && is_name(function_expression(exp))
           ? symbol_of_name(function_expression(exp)) +
                 "(" +
                 comma_separated(map(unparse, arg_expressions(exp))) +
                 ")"
           : is_binary_operator_combination(exp)
           ? "(" + unparse(first_operand(exp)) +
             " " + operator_symbol(exp) +
             " " + unparse(second_operand(exp)) +
             ")"
           〈unparsing other kinds of JavaScript components〉
           : error(exp, "unknown syntax – unparse");
}
function comma_separated(strings) {
    return accumulate((s, acc) => s + (acc === "" ? "" : ", " + acc),
                      "",
                      strings);
}

函数unparse可以在没有子句的情况下正常工作

: is_list_construction(exp)
? unparse(make_application(make_name("list"),
                           element_expressions(exp)))

但在模式变量由列表实例化的情况下，输出字符串将是不必要冗长的。在上面的例子中，处理查询

job($x, list("computer", "wizard"))

产生将$x绑定到["Bitdiddle", ["Ben", null]]的帧，unparse产生

'job(list("Bitdiddle", "Ben"), list("computer", "wizard"))'

但是，如果没有子句，它将产生

'job(pair("Bitdiddle", pair("Ben", null)), list("computer", "wizard"))'

明确构造了构成第一个列表的两个对。为了实现第 4.4.1 节中使用的更简洁的格式，我们插入了一个子句来检查表达式是否构造了一个列表，如果是的话，我们将其格式化为list的单个应用，该应用是我们从表达式中提取的元素表达式的列表。列表构造是文字null或pair的应用，其第二个参数本身是列表构造。

function is_list_construction(exp) {
    return (is_literal(exp) && is_null(literal_value(exp))) ||
           (is_application(exp) && is_name(function_expression(exp)) &&
            symbol_of_name(function_expression(exp)) === "pair" &&
            is_list_construction(head(tail(arg_expressions(exp)))));
}

从给定的列表构造中提取元素表达式相当于收集pair的应用的第一个参数，直到达到文字null。

function element_expressions(list_constr) {
    return is_literal(list_constr)
           ? null // list_constr is literal null
           :      // list_constr is application of pair
             pair(head(arg_expressions(list_constr)),
                  element_expressions(
                      head(tail(arg_expressions(list_constr)))));
}

查询语言特定表示的谓词和选择器

函数type和contents，由evaluate_query（第 4.4.4.2 节）使用，指定了查询语言特定表示的句法形式由其头部的字符串标识。它们与第 2.4.2 节中的type_tag和contents函数相同，只是错误消息不同。

function type(exp) {
    return is_pair(exp)
           ? head(exp)
           : error(exp, "unknown expression type");
}
function contents(exp) {
    return is_pair(exp)
           ? tail(exp)
           : error(exp, "unknown expression contents");
}

以下函数由query_driver_loop（第 4.4.4.1 节）使用，指定规则和断言通过assert命令添加到数据库中，函数convert_to_query_syntax将其转换为形式的一对["assert", rule-or-assertion]：

function is_assertion(exp) {
    return type(exp) === "assert";
}
function assertion_body(exp) { return head(contents(exp)); }

以下是and、or、not和javascript_predicate语法形式（第 4.4.4.2 节）的谓词和选择器的声明：

function is_empty_conjunction(exps) { return is_null(exps); }
function first_conjunct(exps) { return head(exps); }
function rest_conjuncts(exps) { return tail(exps); }

function is_empty_disjunction(exps) { return is_null(exps); }
function first_disjunct(exps) { return head(exps); }
function rest_disjuncts(exps) { return tail(exps); }

function negated_query(exps) { return head(exps); }

function javascript_predicate_expression(exps) { return head(exps); }

以下三个函数定义了查询语言特定规则的表示：

function is_rule(assertion) {
    return is_tagged_list(assertion, "rule");
}
function conclusion(rule) { return head(tail(rule)); }
function rule_body(rule) {
    return is_null(tail(tail(rule)))
           ? list("always_true")
           : head(tail(tail(rule)));
}

4.4.4.8 帧和绑定

帧被表示为绑定的列表，绑定是变量-值对：

function make_binding(variable, value) {
    return pair(variable, value);
}
function binding_variable(binding) {
    return head(binding);
}
function binding_value(binding) {
    return tail(binding);
}
function binding_in_frame(variable, frame) {
    return assoc(variable, frame);
}
function extend(variable, value, frame) {
    return pair(make_binding(variable, value), frame);
}

练习 4.68

路易斯·里森纳想知道为什么simple_query和disjoin函数（第 4.4.4.2 节）是使用延迟表达式实现的，而不是定义如下：

function simple_query(query_pattern, frame_stream) {
    return stream_flatmap(
               frame =>
                 stream_append(find_assertions(query_pattern, frame),
                               apply_rules(query_pattern, frame)),
               frame_stream);
}
function disjoin(disjuncts, frame_stream) {
    return is_empty_disjunction(disjuncts)
           ? null
           : interleave(
                  evaluate_query(first_disjunct(disjuncts), frame_stream),
                  disjoin(rest_disjuncts(disjuncts), frame_stream));
}

您能举例说明这些更简单的定义会导致不良行为的查询吗？

练习 4.69

为什么disjoin和stream_flatmap交错流而不是简单地附加它们？给出说明交错效果更好的例子。（提示：为什么我们在 3.5.3 节中使用interleave？）

练习 4.70

flatten_stream为什么在其主体中使用延迟表达式？以下定义它会有什么问题：

function flatten_stream(stream) {
    return is_null(stream)
           ? null
           : interleave(head(stream),
                        flatten_stream(stream_tail(stream)));
}

练习 4.71

Alyssa P. Hacker 建议在negate，javascript_predicate和find_assertions中使用stream_flatmap的简化版本。她观察到在这些情况下映射到帧流中的函数总是产生空流或单例流，因此在组合这些流时不需要交错。

a. 填写 Alyssa 程序中的缺失表达式。

function simple_stream_flatmap(fun, s) {
    return simple_flatten(stream_map(fun, s));
}
function simple_flatten(stream) {
    return stream_map(〈??〉,
                      stream_filter(〈??〉, stream));
}

b. 如果我们以这种方式改变它，查询系统的行为会改变吗？

练习 4.72

为查询语言实现一个名为unique的语法形式。unique的应用应该成功，如果数据库中满足指定查询的项目恰好有一个。例如，

unique(job($x, list("computer", "wizard")))

应该打印一个项目流

unique(job(list("Bitdiddle", "Ben"), list("computer", "wizard")))

由于 Ben 是唯一的计算机巫师，而

unique(job($x, list("computer", "programmer")))

应该打印空流，因为有不止一个计算机程序员。此外，

and(job($x, $j), unique(job($anyone, $j)))

应列出所有只由一个人填写的工作以及填写它们的人。

实现unique有两个部分。第一部分是编写处理这种语法形式的函数，第二部分是使evaluate_query分派到该函数。第二部分是微不足道的，因为evaluate_query以数据导向的方式进行分派。如果您的函数被称为uniquely_asserted，您只需要

put("unique", "evaluate_query", uniquely_asserted);

和evaluate_query将为每个type（头）为字符串"unique"的查询分派到此函数。

真正的问题是编写函数uniquely_asserted。这应该将unique查询的contents（尾部）作为输入，以及一系列帧的流。对于流中的每个帧，它应该使用evaluate_query来查找满足给定查询的所有扩展帧的流。任何流中不恰好有一个项目的流都应该被消除。剩下的流应该被传回来累积成一个大流，这是unique查询的结果。这类似于not语法形式的实现。

通过形成一个列出监督恰好一个人的所有人的查询来测试您的实现。

练习 4.73

我们将and的实现作为查询的系列组合（图 4.6）是优雅的，但效率低下，因为在处理and的第二个查询时，我们必须为第一个查询产生的每个帧扫描数据库。如果数据库有N个元素，并且典型查询产生的输出帧数量与N成比例（比如N / k），那么为了处理第一个查询产生的每个帧，需要N²/k次模式匹配器调用。另一种方法是分别处理and的两个子句，然后寻找所有兼容的输出帧对。如果每个查询产生N / k个输出帧，那么这意味着我们必须执行N²/k²个兼容性检查——比我们当前方法所需的匹配次数少k倍。

设计一个使用这种策略的and的实现。您必须实现一个函数，该函数以两个帧作为输入，检查帧中的绑定是否兼容，如果是，则生成一个合并两组绑定的帧。此操作类似于统一。

练习 4.74

在第 4.4.3 节中，我们看到not和javascript_predicate可能会导致查询语言在应用到变量未绑定的帧时给出“错误”的答案。想出一种修复这个缺点的方法。一个想法是通过向帧附加一个“承诺”来进行“延迟”过滤，只有当足够的变量被绑定时才能实现过滤操作。我们可以等到执行所有其他操作之后再执行过滤。然而，出于效率的考虑，我们希望尽快进行过滤，以减少生成的中间帧的数量。

练习 4.75

将查询语言重新设计为一个非确定性程序，以使用第 4.3 节的求值器来实现，而不是作为一个流程过程。在这种方法中，每个查询将产生一个单一的答案（而不是所有答案的流），用户可以输入retry来查看更多答案。你会发现，我们在本节构建的许多机制都被非确定性搜索和回溯所包含。然而，你可能也会发现，你的新查询语言在行为上有微妙的差异。你能找到一些例子来说明这种差异吗？

练习 4.76

当我们在第 4.1 节实现 JavaScript 求值器时，我们看到了如何使用局部环境来避免函数参数之间的名称冲突。例如，在求值中

function square(x) {
    return x * x;
}
function sum_of_squares(x, y) {
    return square(x) + square(y);
}
sum_of_squares(3, 4);

在square和sum_of_squares中的x之间没有混淆，因为我们在一个特别构造的环境中求值每个函数的主体，该环境包含局部名称的绑定。在查询系统中，我们使用了一种不同的策略来避免在应用规则时出现名称冲突。每次应用规则时，我们都会使用新的名称对变量进行重命名，这些名称保证是唯一的。对于 JavaScript 求值器的类似策略将是放弃局部环境，而是在应用函数时每次重命名函数的主体中的变量。

为查询语言实现一个使用环境而不是重命名的规则应用方法。看看你是否可以在你的环境结构上构建，以创建处理大型系统的查询语言构造，比如块结构函数的规则类比。你能把这些与在特定上下文中进行推理（例如，“如果我假设P是真的，那么我就能推断出A和B。”）作为解决问题的方法联系起来吗？（这个问题是开放式的。）

五、使用寄存器机进行计算

原文：5 Computing with Register Machines

译者：飞龙

协议：CC BY-NC-SA 4.0

我的目标是表明天堂机器不是一种神圣的生命体，而是一种钟表（相信钟表有灵魂属性的人将制造者的荣耀归功于作品），因为几乎所有多种运动都是由一种最简单和物质力量引起的，就像钟表的所有运动都是由单一重力引起的。

——约翰内斯·开普勒（致赫尔瓦特·冯·霍恩堡的信，1605 年）

我们开始这本书是通过研究过程，并通过用 JavaScript 编写的函数来描述过程。为了解释这些函数的含义，我们使用了一系列的求值模型：第 1 章的替换模型，第 3 章的环境模型，以及第 4 章的元循环求值器。我们对元循环求值器的研究，特别是消除了 JavaScript 类似语言如何解释的许多神秘。但是，即使元循环求值器也留下了一些重要的问题没有解答，因为它未能阐明 JavaScript 系统中的控制机制。例如，求值器没有解释子表达式的求值如何返回一个值给使用这个值的表达式。此外，求值器也没有解释一些递归函数如何生成迭代过程（即使用恒定空间进行求值），而其他递归函数将生成递归过程。本章将解决这两个问题。

我们将描述过程，以传统计算机的逐步操作为基础。这样的计算机，或者寄存器机，顺序执行操作指令，这些指令操作固定一组称为寄存器的存储元素的内容。典型的寄存器机指令将原始操作应用于一些寄存器的内容，并将结果分配给另一个寄存器。我们对寄存器机执行的过程的描述看起来非常像传统计算机的“机器语言”程序。但是，我们不会专注于任何特定计算机的机器语言，而是会检查几个 JavaScript 函数，并设计一个特定的寄存器机来执行每个函数。因此，我们将从硬件架构师的角度而不是机器语言计算机程序员的角度来处理我们的任务。在设计寄存器机时，我们将开发用于实现重要编程构造（如递归）的机制。我们还将提供一种描述寄存器机设计的语言。在第 5.2 节中，我们将实现一个使用这些描述来模拟我们设计的机器的 JavaScript 程序。

我们的寄存器机的大多数原始操作都非常简单。例如，一个操作可能会将从两个寄存器中获取的数字相加，产生一个结果存储到第三个寄存器中。这样的操作可以通过简单描述的硬件来执行。然而，为了处理列表结构，我们还将使用head、tail和pair的内存操作，这需要一个复杂的存储分配机制。在第 5.3 节中，我们将研究它们的实现，以更基本的操作为基础。

在第 5.4 节中，当我们积累了将简单函数表述为寄存器机的经验后，我们将设计一台机器，执行第 4.1 节中元循环求值器描述的算法。这将填补我们对 JavaScript 程序如何解释的理解中的空白，通过为求值器中的控制机制提供一个明确的模型。在第 5.5 节中，我们将研究一个简单的编译器，将 JavaScript 程序转换为可以直接使用求值器寄存器机的寄存器和操作执行的指令序列。

5.1 设计寄存器机

设计一个寄存器机器，我们必须设计它的数据路径（寄存器和操作）和控制器，以便对这些操作进行排序。为了说明一个简单寄存器机器的设计，让我们来看一下欧几里得算法，它用于计算两个整数的最大公约数（GCD）。正如我们在 1.2.5 节中看到的，欧几里得算法可以通过迭代过程来执行，如下函数所示：

function gcd(a, b) {
    return b === 0 ? a : gcd(b, a % b);
}

执行此算法的机器必须跟踪两个数字a和b，因此让我们假设这些数字存储在两个具有这些名称的寄存器中。所需的基本操作是测试寄存器b的内容是否为零，并计算寄存器a的内容除以寄存器b的余数。余数操作是一个复杂的过程，但暂时假设我们有一个计算余数的原始设备。在 GCD 算法的每个周期中，寄存器a的内容必须被寄存器b的内容替换，b的内容必须被a的旧内容除以b的旧内容的余数替换。如果这些替换可以同时进行将会很方便，但在我们的寄存器机器模型中，我们假设每次只能为一个寄存器分配一个新值。为了完成这些替换，我们的机器将使用第三个“临时”寄存器，我们称之为t。（首先余数将被放置在t中，然后b的内容将被放置在a中，最后存储在t中的余数将被放置在b中。）

我们可以通过使用图 5.1 中显示的数据路径图来说明此机器所需的寄存器和操作。在此图中，寄存器（a、b和t）由矩形表示。将值分配给寄存器的每种方法都由一个带有按钮的箭头表示——绘制为——在箭头头部后面，从数据源指向寄存器。按下按钮时，允许数据源的值“流”入指定的寄存器。每个按钮旁边的标签是我们将用来引用按钮的名称。这些名称是任意的，可以选择具有助记值（例如，a<-b表示按下将寄存器b的内容分配给寄存器a的按钮）。寄存器的数据源可以是另一个寄存器（如a<-b分配中），操作结果（如t<-r分配中），或者是一个常数（一个无法更改的内置值，在数据路径图中由包含常数的三角形表示）。

图 5.1 GCD 机器的数据路径。

计算常数和寄存器内容的值的操作在数据路径图中由一个梯形表示，其中包含操作的名称。例如，图 5.1 中标记为rem的框表示一个计算所附寄存器a和b的内容的余数的操作。箭头（没有按钮）从输入寄存器和常数指向框，箭头将操作的输出值连接到寄存器。测试由包含测试名称的圆圈表示。例如，我们的 GCD 机器有一个测试操作，用于测试寄存器b的内容是否为零。测试也有从其输入寄存器和常数的箭头，但它没有输出箭头；它的值由控制器而不是数据路径使用。总的来说，数据路径图显示了机器所需的寄存器和操作，以及它们之间的连接方式。如果我们将箭头视为电线，按钮视为开关，数据路径图就非常像可以由电子元件构建的机器的接线图。

为了使数据路径实际计算 GCD，必须按正确的顺序按下按钮。我们将根据控制器图表描述这个顺序，如图 5.2 所示。控制器图表的元素指示应如何操作数据路径组件。控制器图表中的矩形框标识要按下的数据路径按钮，并且箭头描述从一步到下一步的顺序。图表中的菱形代表一个决定。根据菱形中指定的数据路径测试的值，将遵循两个顺序箭头中的一个。我们可以根据物理类比来解释控制器：将图表视为一个迷宫，弹珠在其中滚动。当弹珠滚入一个框中时，它会按照框的名称按下数据路径按钮。当弹珠滚入决策节点（例如b = 0的测试）时，它会根据指定测试的结果离开节点。

图 5.2 GCD 机器的控制器。

将数据路径和控制器结合起来，完全描述了一个计算 GCD 的机器。我们将控制器（滚动的弹珠）放在标有start的地方，然后在寄存器a和b中放入数字。当控制器到达done时，我们将在寄存器a中找到 GCD 的值。

练习 5.1

设计一个寄存器机器，使用以下函数指定的迭代算法计算阶乘。为这台机器绘制数据路径和控制器图表。

function factorial(n) {
    function iter(product, counter) {
    return counter > n
           ? product
           : iter(counter * product,
                  counter + 1);
    }
    return iter(1, 1);
}

5.1.1 描述寄存器机器的语言

数据路径和控制器图表足以表示诸如 GCD 之类的简单机器，但对于描述 JavaScript 解释器之类的大型机器来说，它们是笨重的。为了能够处理复杂的机器，我们将创建一种以文本形式呈现数据路径和控制器图表中提供的所有信息的语言。我们将从直接反映图表的符号开始。

我们通过描述寄存器和操作来定义机器的数据路径。为了描述一个寄存器，我们给它一个名称，并指定控制分配给它的按钮。我们给每个按钮一个名称，并指定进入由按钮控制的寄存器的数据的来源（来源可以是寄存器、常量或操作）。为了描述一个操作，我们给它一个名称，并指定它的输入（寄存器或常量）。

我们将机器的控制器定义为一系列指令，以及标识序列中入口点的标签。指令可以是以下之一：

按下数据路径按钮的名称，以将值分配给寄存器。（这对应于控制器图表中的一个框。）
一个test指令，执行指定的测试。
一个条件分支（branch指令）到控制器标签指示的位置，基于先前测试的结果。（测试和分支一起对应于控制器图表中的菱形。）如果测试为假，则控制器应继续执行序列中的下一条指令。否则，控制器应继续执行标签后的指令。
一个无条件分支（go_to指令），命名控制器标签，以便继续执行。

机器从控制器指令序列的开头开始，并在执行到达序列末尾时停止。除非分支改变了控制流，否则指令将按照它们列出的顺序执行。

图 5.3 显示了以这种方式描述的 GCD 机器。这个例子只是暗示了这些描述的一般性，因为 GCD 机器是一个非常简单的情况：每个寄存器只有一个按钮，并且每个按钮和测试在控制器中只使用一次。

图 5.3 GCD 机器的规范。

不幸的是，阅读这样的描述是困难的。为了理解控制器指令，我们必须不断地参考按钮名称和操作名称的定义，为了理解按钮的功能，我们可能必须参考操作名称的定义。因此，我们将转换我们的符号，将数据路径和控制器描述的信息合并在一起，以便我们可以一起看到。

为了获得这种描述形式，我们将用它们的行为定义替换任意按钮和操作名称。也就是说，我们将说（在控制器中）“按下分配给寄存器t的按钮”并分别说（在数据路径中）“按钮t<-r将rem操作的值分配给寄存器t”和“rem操作的输入是寄存器a和b的内容”，我们将说（在控制器中）“按下将rem操作的值分配给寄存器t的按钮”。类似地，我们将说（在控制器中）“执行=测试”并分别说（在数据路径中）“=测试作用于寄存器b的内容和常量 0”，我们将说“对寄存器b的内容和常量 0 执行=测试”。我们将省略数据路径描述，只保留控制器序列。因此，GCD 机器的描述如下：

controller(
  list(
    "test_b",
      test(list(op("="), reg("b"), constant(0))),
      branch(label("gcd_done")),
      assign("t", list(op("rem"), reg("a"), reg("b"))),
      assign("a", reg("b")),
      assign("b", reg("t")),
      go_to(label("test_b")),
    "gcd_done"))

这种描述形式比图 5.3 中所示的形式更容易阅读，但它也有缺点：

对于大型机器来说，它更冗长，因为每当在控制器指令序列中提到元素时，就会重复数据路径元素的完整描述。（这在 GCD 示例中不是问题，因为每个操作和按钮只使用一次。）此外，重复数据路径描述会使机器的实际数据路径结构变得模糊；对于大型机器来说，有多少寄存器、操作和按钮以及它们如何相互连接并不明显。
因为机器定义中的控制器指令看起来像 JavaScript 表达式，很容易忘记它们不是任意的 JavaScript 表达式。它们只能表示合法的机器操作。例如，操作只能直接作用于常量和寄存器的内容，而不能作用于其他操作的结果。

尽管存在这些缺点，但在本章中我们将使用这种寄存器机器语言，因为我们更关心理解控制器，而不是理解数据路径中的元素和连接。然而，我们应该记住，数据路径设计在设计真实机器时至关重要。

练习 5.2

使用寄存器机器语言描述练习 5.1 中的迭代阶乘机器。

行动

让我们修改 GCD 机器，以便我们可以输入我们想要的最大公约数的数字并打印答案。我们不会讨论如何制作一个可以读取和打印的机器，而是假设（就像我们在 JavaScript 中使用prompt和display时一样）它们作为原始操作是可用的。

prompt操作类似于我们一直在使用的操作，因为它产生一个可以存储在寄存器中的值。但prompt不从任何寄存器中获取输入；它的值取决于我们设计的机器之外发生的事情。

我们将允许我们机器的操作具有这样的行为，并且将绘制和标注prompt的使用，就像我们对任何计算值的其他操作一样。

另一方面，display操作在根本上与我们一直在使用的操作不同：它不会产生要存储在寄存器中的输出值。尽管它有一个效果，但这个效果不是在我们设计的机器的一部分上。我们将这种操作称为动作。我们将在数据路径图中表示动作，就像我们表示计算值的操作一样 - 作为一个包含动作名称的梯形。箭头从任何输入（寄存器或常数）指向动作框。我们还将一个按钮与动作关联起来。按下按钮会使动作发生。为了使控制器按下动作按钮，我们使用一种称为perform的新类型指令。因此，打印寄存器a的内容的动作在控制器序列中表示为指令

perform(list(op("display"), reg("a")))

图 5.4 显示了新 GCD 机器的数据路径和控制器。与其在打印答案后停止，我们让它重新开始，以便它反复读取一对数字，计算它们的 GCD，并打印结果。这种结构类似于我们在第 4 章解释器中使用的驱动循环。

图 5.4 一个读取输入并打印结果的 GCD 机器。

5.1.2 机器设计中的抽象

我们经常定义一个机器包括实际上非常复杂的“原始”操作。例如，在第 5.4 节和 5.5 节中，我们将把 JavaScript 的环境操作视为原始操作。这种抽象是有价值的，因为它使我们能够忽略机器的某些部分的细节，以便我们可以集中精力处理设计的其他方面。然而，我们将大量复杂性隐藏起来，并不意味着机器设计是不切实际的。我们总是可以用更简单的原始操作来替换复杂的“原始”。

考虑 GCD 机器。该机器具有一个指令，计算寄存器a和b的内容的余数，并将结果赋给寄存器t。如果我们想要构建 GCD 机器而不使用原始的余数运算，我们必须指定如何通过更简单的操作（如减法）来计算余数。实际上，我们可以编写一个 JavaScript 函数以这种方式找到余数：

function remainder(n, d) {
    return n < d
           ? n
           : remainder(n - d, d);
}

因此，我们可以用减法和比较测试来替换 GCD 机器数据路径中的余数运算。图 5.5 显示了详细机器的数据路径和控制器。指令

assign("t", list(op("rem"), reg("a"), reg("b")))

在 GCD 控制器定义中被替换为包含循环的一系列指令，如图 5.6 所示。

图 5.5 详细 GCD 机器的数据路径和控制器。

图 5.6 GCD 机器的控制器指令序列，如图 5.5 所示。

练习 5.3

设计一个使用牛顿法计算*方根的机器，如第 1.1.7 节中描述的，并在第 1.1.8 节中用以下代码实现：

function sqrt(x) {
    function is_good_enough(guess) {
        return math_abs(square(guess) - x) < 0.001;
    }
    function improve(guess) {
        return average(guess, x / guess);
    }
    function sqrt_iter(guess) {
        return is_good_enough(guess)
               ? guess
           : sqrt_iter(improve(guess));
    }
    return sqrt_iter(1);
}

首先假设is_good_enough和improve操作作为原始操作可用。然后展示如何通过算术操作来扩展这些操作。通过绘制数据路径图和用寄存器机器语言编写控制器定义，描述每个sqrt机器设计的版本。

5.1.3 子程序

设计执行计算的机器时，我们通常希望安排组件被不同部分的计算共享，而不是复制组件。考虑一个包括两个 GCD 计算的机器——一个是寻找寄存器a和b中内容的 GCD，另一个是寻找寄存器c和d中内容的 GCD。我们可能首先假设有一个原始的gcd操作，然后用更原始的操作来扩展两个gcd的实例。图 5.7 仅显示了结果机器数据路径的 GCD 部分，而没有显示它们如何连接到机器的其余部分。该图还显示了机器控制器序列的相应部分。

图 5.7 具有两个 GCD 计算的机器的数据路径和控制器序列的部分。

这台机器有两个余数运算框和两个用于测试相等性的框。如果复制的组件很复杂，比如余数框，这将不是一种经济的建造机器的方式。我们可以通过使用相同的组件来避免复制数据路径组件进行两个 GCD 计算，只要这样做不会影响较大机器的其余计算。如果寄存器a和b中的值在控制器到达gcd_2时不再需要（或者这些值可以移动到其他寄存器以供安全保管），我们可以更改机器，使其在计算第二个 GCD 时使用寄存器a和b，而不是寄存器c和d。如果这样做，我们将获得图 5.8 所示的控制器序列。

图 5.8 使用相同的数据路径组件进行两个不同的 GCD 计算的机器的控制器序列的部分。

我们已经删除了重复的数据路径组件（使数据路径再次如图 5.1 所示），但是控制器现在有两个仅在它们的入口点标签上不同的 GCD 序列。最好用单个序列的分支替换这两个序列——一个gcd子程序——在该子程序的末尾我们再次分支到主指令序列中的正确位置。我们可以通过以下方式实现这一点：在分支到gcd之前，我们将一个区分值（如 0 或 1）放入特殊寄存器continue。在gcd子程序结束时，根据continue寄存器的值，我们返回到after_gcd_1或after_gcd_2。图 5.9 显示了结果控制器序列的相关部分，其中仅包括gcd指令的单个副本。

图 5.9 使用continue寄存器避免图 5.8 中重复的控制器序列。

这是处理小问题的合理方法，但如果控制器序列中有许多 GCD 计算的实例，这将是很笨拙的。为了决定在gcd子程序之后继续执行的位置，我们需要在数据路径中进行测试，并在控制器中为所有使用gcd的地方添加分支指令。实现子程序的更强大方法是使continue寄存器保存控制器序列中执行完成后应继续执行的入口点的标签。实现这种策略需要寄存器机器的数据路径和控制器之间的一种新连接：必须有一种方法将标签分配给寄存器，以便可以从寄存器中获取此值，并用于在指定的入口点继续执行。

为了反映这种能力，我们将扩展寄存器机器语言的assign指令，允许将寄存器分配为控制器序列中标签的值（作为一种特殊类型的常量）。我们还将扩展go_to指令，允许执行继续在寄存器的内容描述的入口点处继续，而不仅仅是在常量标签描述的入口点处。使用这些新构造，我们可以通过分支到continue寄存器中存储的位置来终止gcd子程序。这导致了图 5.10 中显示的控制器序列。

图 5.10 将标签分配给continue寄存器简化并概括了图 5.9 中显示的策略。

具有多个子例程的机器可以使用多个继续寄存器（例如gcd_continue，factorial_continue），或者我们可以让所有子例程共享一个continue寄存器。共享更经济，但是如果我们有一个子例程（sub1）调用另一个子例程（sub2），我们必须小心。除非sub1在设置continue以调用sub2之前将continue的内容保存在其他寄存器中，否则sub1完成时将不知道要去哪里。下一节中开发的处理递归的机制也提供了解决嵌套子例程调用问题的更好解决方案。

5.1.4 使用堆栈实现递归

到目前为止，我们所展示的思想可以通过指定具有与过程的每个状态变量对应的寄存器的寄存器机器来实现任何迭代过程。该机器重复执行控制器循环，改变寄存器的内容，直到满足某个终止条件。在控制器序列的每一点上，机器的状态（表示迭代过程的状态）完全由寄存器的内容（状态变量的值）确定。

然而，实现递归过程需要额外的机制。考虑以下用于计算阶乘的递归方法，我们在 1.2.1 节中首次研究了这个方法：

function factorial(n) {
    return n === 1
           ? 1
           : n * factorial(n - 1);
}

从函数中我们可以看到，计算n!需要计算(n – 1)!. 我们的 GCD 机器，模拟了函数

function gcd(a, b) {
    return b === 0 ? a : gcd(b, a % b);
}

同样需要计算另一个 GCD。但是gcd函数和factorial之间有一个重要的区别，gcd函数将原始计算减少为新的 GCD 计算，而factorial需要计算另一个阶乘作为子问题。在 GCD 中，新 GCD 计算的答案是原始问题的答案。要计算下一个 GCD，我们只需将新参数放入 GCD 机器的输入寄存器中，并通过执行相同的控制器序列重用机器的数据路径。当机器完成解决最终的 GCD 问题时，它已经完成了整个计算。

在阶乘（或任何递归过程）的情况下，新阶乘子问题的答案不是原始问题的答案。必须将(n – 1)!的值乘以n才能得到最终答案。如果我们试图模仿 GCD 设计，并通过减少n寄存器并重新运行阶乘机器来解决阶乘子问题，我们将不再拥有旧值n以便将结果相乘。因此，我们需要第二个阶乘机器来处理

子问题。这第二个阶乘计算本身有一个阶乘子问题，需要第三个阶乘机器，依此类推。由于每个阶乘机器中包含另一个阶乘机器，因此总机器包含无限数量的类似机器的嵌套，因此无法从固定的有限数量的部分构建。

然而，如果我们能够安排在机器的每个嵌套实例中使用相同的组件，我们就可以将阶乘过程实现为一个寄存器机。具体来说，计算n!的机器应该使用相同的组件来处理计算(n – 1)!的子问题，以及(n – 2)!的子问题，依此类推。这是合理的，因为阶乘过程规定需要无限数量的相同机器的副本来执行计算，但在任何给定时间只有一个副本需要处于活动状态。当机器遇到递归子问题时，它可以暂停主问题的工作，重复使用相同的物理部件来处理子问题，然后继续暂停的计算。

在子问题中，寄存器的内容将与主问题中的内容不同。（在这种情况下，n寄存器被递减。）为了能够继续暂停的计算，机器必须保存任何在解决子问题后将需要的寄存器的内容，以便在解决子问题后恢复这些内容以继续暂停的计算。在阶乘的情况下，我们将保存n的旧值，在完成对递减的n寄存器的阶乘计算后将其恢复。

由于嵌套递归调用的深度没有先验限制，我们可能需要保存任意数量的寄存器值。这些值必须以它们被保存的相反顺序进行恢复，因为在递归的嵌套中，最后进入的子问题是第一个完成的。这决定了使用“栈”或“后进先出”数据结构来保存寄存器值。我们可以通过添加两种指令来扩展寄存器机器语言以包括一个栈：使用save指令将值放入栈中，并使用restore指令从栈中恢复值。在一系列值被保存到栈上后，一系列restore将以相反的顺序检索这些值。

借助栈的帮助，我们可以为每个阶乘子问题重复使用阶乘机器的数据路径的单个副本。在重用操作数据路径的控制器序列方面存在类似的设计问题。为了重新执行阶乘计算，控制器不能简单地回到开始，因为在解决(n – 1)!子问题后，机器仍然必须将结果乘以n。控制器必须暂停计算n!，解决(n – 1)!子问题，然后继续计算n!。阶乘计算的这种观点表明了在 5.1.3 节中描述的子程序机制的使用，其中控制器使用continue寄存器来转移到解决子问题的序列的部分，然后继续在主问题上离开的地方。因此，我们可以制作一个返回到存储在continue寄存器中的入口点的阶乘子程序。在每个子程序调用周围，我们保存和恢复continue，就像我们对n寄存器做的那样，因为阶乘计算的每个“级别”将使用相同的continue寄存器。也就是说，阶乘子程序在调用自身解决子问题时必须在continue中放入一个新值，但为了返回到调用它解决子问题的地方，它将需要旧值。

图 5.11 显示了实现递归factorial函数的机器的数据路径和控制器。该机器有一个堆栈和三个寄存器，称为n，val和continue。为了简化数据路径图，我们没有命名寄存器分配按钮，只有堆栈操作按钮（sc和sn用于保存寄存器，rc和rn用于恢复寄存器）。要操作这台机器，我们将要计算阶乘的数放入寄存器n中并启动机器。当机器到达fact_done时，计算完成，答案将在val寄存器中找到。在控制器序列中，每次递归调用之前都会保存n和continue，并在调用返回时恢复。从调用返回是通过跳转到continue中存储的位置来实现的。机器启动时会初始化continue寄存器，以便最后的返回将到达fact_done。val寄存器保存了阶乘计算的结果，不会在递归调用之前保存，因为在子程序返回后，旧的val内容是没有用的。只有新值，也就是子计算产生的值，是需要的。

图 5.11 递归阶乘机器。

尽管原则上阶乘计算需要一个无限的机器，但是图 5.11 中的机器实际上是有限的，除了堆栈，堆栈可能是无限的。然而，任何特定的堆栈物理实现都将是有限大小的，这将限制机器可以处理的递归调用的深度。阶乘的这种实现说明了将递归算法实现为普通寄存器机器加上堆栈的一般策略。当遇到递归子问题时，我们在堆栈上保存当前值将在解决子问题后需要的寄存器，解决递归子问题，然后恢复保存的寄存器并继续在主问题上执行。continue寄存器必须始终保存。是否需要保存其他寄存器取决于特定的机器，因为并非所有递归计算都需要在解决子问题时修改的寄存器的原始值（参见练习 5.4）。

双重递归

让我们来看一个更复杂的递归过程，即我们在 1.2.2 节中介绍的树递归计算斐波那契数：

function fib(n) {
    return n === 0
           ? 0
           : n === 1
           ? 1
           : fib(n - 1) + fib(n - 2);
}

就像阶乘一样，我们可以使用寄存器机器来实现递归斐波那契计算，其中有寄存器n，val和continue。这台机器比阶乘的机器更复杂，因为在控制器序列中有两个地方需要进行递归调用——一次是计算Fib(n – 1)，一次是计算Fib(n – 2)。为了为每个调用设置准备，我们保存将来需要的寄存器的值，将n寄存器设置为需要递归计算的数（n – 1或n – 2），并将continue分配给主序列中的入口点以便返回（分别是afterfib_n_1或afterfib_n_2）。然后我们进入fib_loop。当我们从递归调用返回时，答案在val中。图 5.12 显示了这台机器的控制器序列。

图 5.12 计算斐波那契数的机器的控制器。

练习 5.4

指定实现以下每个函数的寄存器机器。对于每台机器，编写一个控制器指令序列，并绘制一个显示数据路径的图。

a. 递归指数运算：

function expt(b, n) {
    return n === 0
           ? 1
           : b * expt(b, n - 1);
}

b. 迭代指数运算：

function expt(b, n) {
    function expt_iter(counter, product) {
        return counter === 0
               ? product
               : expt_iter(counter - 1, b * product);
    }
    return expt_iter(n, 1);
}

练习 5.5

手动模拟阶乘和斐波那契机器，使用一些复杂的输入（需要执行至少一个递归调用）。显示执行中每个重要点的堆栈内容。

练习 5.6

Ben Bitdiddle 观察到斐波那契机器的控制器序列有额外的save和额外的restore，可以删除以使机器更快。这些指令在哪里？

5.1.5 指令摘要

我们的寄存器机器语言中的控制器指令具有以下形式之一，其中每个input[i]是reg(register-name)或constant(constant-value)。

这些指令是在 5.1.1 节中引入的：

assign(register-name, reg(register-name))

assign(register-name, constant(constant-value))

assign(register-name, list(op(operation-name), input[1], ..., input[n]))

perform(list(op(operation-name), input[1], ..., input[n]))

test(list(op(operation-name), input[1], ..., input[n]))

branch(label(label-name))

go_to(label(label-name))

使用寄存器保存标签是在 5.1.3 节中引入的：

assign(register-name, label(label-name))

go_to(reg(register-name))

使用堆栈的指令是在 5.1.4 节中引入的：

save(register-name)

restore(register-name)

到目前为止，我们看到的唯一类型的constant-value是一个数字，但稍后我们还将使用字符串和列表。例如，constant("abc")是字符串"abc"，constant(null)是空列表，constant(list("a", "b", "c"))是列表list("a", "b", "c")。

5.2 寄存器机器模拟器

为了更好地理解寄存器机器的设计，我们必须测试我们设计的机器，以查看它们是否按预期运行。测试设计的一种方法是手动模拟控制器的操作，就像练习 5.5 中那样。但是，除了最简单的机器外，这种方法非常乏味。在本节中，我们构建了一个模拟器，用于模拟寄存器机器语言描述的机器。该模拟器是一个 JavaScript 程序，具有四个接口函数。第一个使用寄存器机器的描述来构建机器的模型（一个数据结构，其部分对应于要模拟的机器的部分），另外三个允许我们通过操作模型来模拟机器：

make_machine(register-names, operations, controller)

构建并返回具有给定寄存器、操作和控制器的机器模型。
set_register_contents(machine-model, register-name, value)

在给定机器中的模拟寄存器中存储一个值。
get_register_contents(machine-model, register-name)

返回给定机器中模拟寄存器的内容。
start(machine-model)

模拟给定机器的执行，从控制器序列的开头开始，直到到达序列的末尾。

作为这些函数如何使用的示例，我们可以定义gcd_machine为 5.1.1 节中 GCD 机器的模型，如下所示：

const gcd_machine =
    make_machine(
        list("a", "b", "t"),
        list(list("rem", (a, b) => a % b),
         list("=", (a, b) => a === b)),
        list(
          "test_b",
            test(list(op("="), reg("b"), constant(0))),
            branch(label("gcd_done")),
            assign("t", list(op("rem"), reg("a"), reg("b"))),
            assign("a", reg("b")),
            assign("b", reg("t")),
            go_to(label("test_b")),
      "gcd_done"));

make_machine的第一个参数是一个寄存器名称列表。下一个参数是一个表（包含两个元素列表的列表），将每个操作名称与实现该操作的 JavaScript 函数配对（即，给定相同的输入值产生相同的输出值）。最后一个参数指定控制器，格式为标签和机器指令的列表，就像 5.1 节中的格式。

要使用这台机器计算 GCD，我们设置输入寄存器，启动机器，并在模拟终止时检查结果：

set_register_contents(gcd_machine, "a", 206);
"done"

set_register_contents(gcd_machine, "b", 40);
"done"

start(gcd_machine);
"done"

get_register_contents(gcd_machine, "a");
`2`

这个计算将比用 JavaScript 编写的gcd函数运行得慢得多，因为我们将模拟低级机器指令，比如assign，通过更复杂的操作。

练习 5.7

使用模拟器测试您在练习 5.4 中设计的机器。

5.2.1 机器模型

make_machine生成的机器模型表示为使用消息传递技术在第 3 章中开发的本地状态的函数。为了构建这个模型，make_machine首先调用函数make_new_machine来构造所有寄存器机器共有的部分。由make_new_machine构建的基本机器模型本质上是一种包含一些寄存器和堆栈的容器，以及一个执行机制，逐个处理控制器指令。

然后函数make_machine扩展了这个基本模型（通过向其发送消息）以包括所定义的特定机器的寄存器、操作和控制器。首先，它为新机器中提供的每个寄存器名称分配一个寄存器，并在机器中安装指定的操作。然后，它使用一个汇编器（在第 5.2.2 节中描述）将控制器列表转换为新机器的指令，并将其安装为机器的指令序列。函数make_machine返回修改后的机器模型作为其值。

function make_machine(register_names, ops, controller) {
    const machine = make_new_machine();
    for_each(register_name =>
               machine("allocate_register")(register_name),
             register_names);
    machine("install_operations")(ops);
    machine("install_instruction_sequence")
           (assemble(controller, machine));
    return machine;
}

寄存器

我们将寄存器表示为具有局部状态的函数，就像第 3 章中一样。函数make_register创建一个可以访问或更改值的寄存器：

function make_register(name) {
    let contents = "unassigned";
    function dispatch(message) {
        return message === "get"
               ? contents
               : message === "set"
               ? value => { contents = value; }
               : error(message, "unknown request – make_register");
    }
    return dispatch;
}

以下函数用于访问寄存器：

function get_contents(register) {
    return register("get");
}
function set_contents(register, value) {
    return register("set")(value);
}

栈

我们也可以将栈表示为具有局部状态的函数。函数make_stack创建一个栈，其局部状态包括栈上项目的列表。栈接受请求将项目push到栈上，pop弹出栈顶项目并返回它，以及initialize将栈初始化为空。

function make_stack() {
    let stack = null;
    function push(x) {
        stack = pair(x, stack);
        return "done";
    }
    function pop() {
        if (is_null(stack)) {
            error("empty stack – pop");
        } else {
            const top = head(stack);
            stack = tail(stack);
            return top;
        }
    }
    function initialize() {
        stack = null;
        return "done";
    }
    function dispatch(message) {
        return message === "push"
               ? push
               : message === "pop"
               ? pop()
               : message === "initialize"
               ? initialize()
               : error(message, "unknown request – stack");
    }
    return dispatch;
}

以下函数用于访问栈：

function pop(stack) {
    return stack("pop");
}
function push(stack, value) {
    return stack("push")(value);
}

基本机器

make_new_machine函数，如图 5.13 所示，构造了一个对象，其局部状态包括一个栈、一个最初为空的指令序列、一个最初包含一个初始化栈操作的操作列表，以及一个寄存器表，最初包含两个寄存器，名为flag和pc（代表“程序计数器”）。内部函数allocate_register添加新条目到寄存器表中，内部函数lookup_register在表中查找寄存器。

图 5.13 make_new_machine函数实现了基本的机器模型。

flag寄存器用于控制模拟机器中的分支。我们的test指令将flag的内容设置为测试的结果（真或假）。我们的branch指令通过检查flag的内容来决定是否进行分支。

pc寄存器确定指令在机器运行时的顺序。这种顺序由内部函数execute实现。在模拟模型中，每条机器指令都是一个数据结构，其中包括一个没有参数的函数，称为指令执行函数，调用这个函数模拟执行指令。随着模拟的运行，pc指向指令序列中下一条要执行的指令的位置。函数execute获取该指令，通过调用指令执行函数来执行它，并重复这个循环，直到没有更多的指令需要执行（即，直到pc指向指令序列的末尾）。

作为其操作的一部分，每个指令执行函数修改pc以指示下一个要执行的指令。branch和go_to指令将pc更改为指向新的目的地。所有其他指令只是推进pc，使其指向序列中的下一条指令。请注意，每次调用execute都会再次调用execute，但这不会产生无限循环，因为运行指令执行函数会改变pc的内容。

函数make_new_machine返回一个分发函数，实现对内部状态的消息传递访问。请注意，启动机器是通过将pc设置为指令序列的开头并调用execute来完成的。

为了方便起见，我们提供了一个机器的start操作的替代接口，以及用于设置和检查寄存器内容的函数，如第 5.2 节开头所述：

function start(machine) {
    return machine("start");
}
function get_register_contents(machine, register_name) {
    return get_contents(get_register(machine, register_name));
}
function set_register_contents(machine, register_name, value) {
    set_contents(get_register(machine, register_name), value);
    return "done";
}

这些函数（以及第 5.2.2 和 5.2.3 节中的许多函数）使用以下内容来查找给定机器中具有给定名称的寄存器：

function get_register(machine, reg_name) {
    return machine("get_register")(reg_name);
}

5.2.2 汇编器

汇编器将机器的控制器指令序列转换为相应的机器指令列表，每个指令都有其执行函数。总的来说，汇编器很像我们在第 4 章中学习的求值器——它有一个输入语言（在本例中是寄存器机器语言），我们必须对语言中的每种组件执行适当的操作。

为每条指令生成一个执行函数的技术正是我们在 4.1.7 节中用来通过将分析与运行时执行分离来加速求值器的技术。正如我们在第 4 章中看到的，可以在不知道名称的实际值的情况下执行对 JavaScript 表达式的有用分析。在这里，类似地，可以在不知道机器寄存器的实际内容的情况下执行对寄存器机器语言表达式的有用分析。例如，我们可以用指向寄存器对象的指针来替换对寄存器的引用，并且可以用指向标签在指令序列中指定位置的指针来替换对标签的引用。

在生成指令执行函数之前，汇编器必须知道所有标签的引用，因此它首先通过扫描控制器序列来将标签与指令分离。在扫描控制器时，它同时构造了指令列表和一个将每个标签与指向该列表中的指针关联起来的表。然后汇编器通过为每条指令插入执行函数来增强指令列表。

assemble函数是汇编器的主要入口。它接受控制器序列和机器模型作为参数，并返回要存储在模型中的指令序列。assemble函数调用extract_labels来从提供的控制器构建初始指令列表和标签表。extract_labels的第二个参数是一个函数，用于处理这些结果：该函数使用update_insts生成指令执行函数并将其插入指令列表，然后返回修改后的列表。

function assemble(controller, machine) {
    return extract_labels(controller,
                          (insts, labels) => {
                              update_insts(insts, labels, machine);
                              return insts;
                          });
}

extract_labels函数接受一个名为controller的列表和一个名为receive的函数作为参数。函数receive将被调用并传入两个值：（1）一个名为insts的指令数据结构列表，其中包含来自controller的指令；和（2）一个名为labels的表，它将controller中的每个标签与其指定的insts列表中的位置关联起来。

function extract_labels(controller, receive) {
    return is_null(controller)
           ? receive(null, null)
           : extract_labels(
                 tail(controller),
                 (insts, labels) => {
                   const next_element = head(controller);
                   return is_string(next_element)
                          ? receive(insts,
                                    pair(make_label_entry(next_element,
                                                          insts),
                                         labels))
                          : receive(pair(make_inst(next_element),
                                         insts),
                                    labels);
                 });
}

extract_labels函数通过顺序扫描controller的元素并累积insts和labels来工作。如果一个元素是字符串（因此是标签），则将适当的条目添加到labels表中。否则，该元素将被累积到insts列表中。

update_insts函数修改了指令列表，该列表最初只包含控制器指令，以包括相应的执行函数：

function update_insts(insts, labels, machine) {
    const pc = get_register(machine, "pc");
    const flag = get_register(machine, "flag");
    const stack = machine("stack");
    const ops = machine("operations");
    return for_each(inst => set_inst_execution_fun(
                                inst,
                                make_execution_function(
                                    inst_controller_instruction(inst),
                                    labels, machine, pc,
                                    flag, stack, ops)),
                    insts);
}

机器指令数据结构简单地将控制器指令与相应的执行函数配对。当extract_labels构造指令时，执行函数尚不可用，而是稍后由update_insts插入。

function make_inst(inst_controller_instruction) {
    return pair(inst_controller_instruction, null);
}
function inst_controller_instruction(inst) {
    return head(inst);
}
function inst_execution_fun(inst) {
    return tail(inst);
}
function set_inst_execution_fun(inst, fun) {
    set_tail(inst, fun);
}

我们的模拟器不使用控制器指令，但保留它以便进行调试（参见练习 5.15）。

标签表的元素是成对出现的：

function make_label_entry(label_name, insts) {
    return pair(label_name, insts);
}

表中的条目将使用查找。

function lookup_label(labels, label_name) {
    const val = assoc(label_name, labels);
    return is_undefined(val)
           ? error(label_name, "undefined label – assemble")
           : tail(val);
}

练习 5.8

以下寄存器机器代码是模棱两可的，因为标签here被定义了多次：

"start",
  go_to(label("here")),
"here",
  assign("a", constant(3)),
  go_to(label("there")),
"here",
  assign("a", constant(4)),
  go_to(label("there")),
"there",

按照目前的模拟器，当控制到达there时，寄存器a的内容将是什么？修改extract_labels函数，使得汇编器在使用相同的标签名称指示两个不同位置时会发出错误信号。

5.2.3 指令及其执行函数

汇编器调用make_execution_function为控制器指令生成执行函数。就像第 4.1.7 节的求值器中的analyze函数一样，这根据指令类型分发以生成适当的执行函数。这些执行函数的细节决定了寄存器机器语言中各个指令的含义。

function make_execution_function(inst, labels, machine,
                                 pc, flag, stack, ops) {
    const inst_type = type(inst);
    return inst_type === "assign"
           ? make_assign_ef(inst, machine, labels, ops, pc)
           : inst_type === "test"
           ? make_test_ef(inst, machine, labels, ops, flag, pc)
           : inst_type === "branch"
           ? make_branch_ef(inst, machine, labels, flag, pc)
           : inst_type === "go_to"
           ? make_go_to_ef(inst, machine, labels, pc)
           : inst_type === "save"
           ? make_save_ef(inst, machine, stack, pc)
           : inst_type === "restore"
           ? make_restore_ef(inst, machine, stack, pc)
           : inst_type === "perform"
           ? make_perform_ef(inst, machine, labels, ops, pc)
           : error(inst, "unknown instruction type – assemble");
}

controller序列的元素由make_machine接收并传递给assemble，它们是字符串（用于标签）和带有标签的列表（用于指令）。指令中的标签是一个字符串，用于标识指令类型，比如"go_to"，列表的其余元素包含参数，比如go_to的目的地。make_execution_function中的分发使用

function type(instruction) { return head(instruction); }

当求值作为make_machine的第三个参数的list表达式时，带有标签的列表被构造。list的每个参数都是一个字符串（求值为其自身）或者是一个带有指令标签列表构造函数的调用。例如，assign("b", reg("t"))调用构造函数assign，参数为"b"和调用构造函数reg的结果，参数为"t"。构造函数及其参数确定了寄存器机器语言中各个指令的语法。指令构造函数和选择器如下所示，以及使用选择器的执行函数生成器。

指令`assign`

make_assign_ef函数为assign指令生成执行函数：

function make_assign_ef(inst, machine, labels, operations, pc) {
    const target = get_register(machine, assign_reg_name(inst));
    const value_exp = assign_value_exp(inst);
    const value_fun =
        is_operation_exp(value_exp)
        ? make_operation_exp_ef(value_exp, machine, labels, operations)
        : make_primitive_exp_ef(value_exp, machine, labels);
    return () => {
               set_contents(target, value_fun());
               advance_pc(pc);
           };
}

assign函数构造assign指令。选择器assign_reg_ name和assign_value_exp从assign指令中提取寄存器名称和值表达式。

function assign(register_name, source) {
    return list("assign", register_name, source);
}
function assign_reg_name(assign_instruction) {
    return head(tail(assign_instruction));
}
function assign_value_exp(assign_instruction) {
    return head(tail(tail(assign_instruction)));
}

make_assign_ef函数使用get_register查找寄存器名称以生成目标寄存器对象。如果值是操作的结果，则将值表达式传递给make_ operation_exp_ef，否则将其传递给make_primitive_exp_ef。这些函数（如下所示）分析值表达式并为该值生成执行函数。这是一个没有参数的函数，称为value_fun，在模拟期间将被求值以产生要分配给寄存器的实际值。请注意，查找寄存器名称和分析值表达式的工作只在汇编时执行一次，而不是每次模拟指令时执行。这种工作的节省是我们使用执行函数的原因，并直接对应于我们在第 4.1.7 节的求值器中将程序分析与执行分开获得的工作节省。

make_assign_ef返回的结果是assign指令的执行函数。当这个函数被调用（由机器模型的execute函数调用），它将目标寄存器的内容设置为执行value_fun得到的结果。然后通过运行函数将pc前进到下一条指令

function advance_pc(pc) {
    set_contents(pc, tail(get_contents(pc)));
}

advance_pc函数是除branch和go_to之外的所有指令的正常终止。

指令`test`，`branch`和`go_to`

make_test_ef函数以类似的方式处理test指令。它提取指定要测试的条件的表达式，并为其生成执行函数。在模拟时，调用条件的函数，将结果赋给flag寄存器，并将pc前进：

function make_test_ef(inst, machine, labels, operations, flag, pc) {
    const condition = test_condition(inst);
    if (is_operation_exp(condition)) {
        const condition_fun = make_operation_exp_ef(
                                  condition, machine,
                                  labels, operations);
        return () => {
                   set_contents(flag, condition_fun());
                   advance_pc(pc);
               };
    } else {
        error(inst, "bad test instruction – assemble");
    }
}

test函数构造test指令。选择器test_condition从测试中提取条件。

function test(condition) { return list("test", condition); }
function test_condition(test_instruction) {
    return head(tail(test_instruction));
}

branch指令的执行函数检查flag寄存器的内容，然后将pc的内容设置为分支目的地（如果分支被执行），或者只是推进pc（如果分支未被执行）。请注意，branch指令中指定的目的地必须是一个标签，make_branch_ef函数强制执行此条件。还要注意，标签是在汇编时查找的，而不是每次模拟branch指令时查找。

function make_branch_ef(inst, machine, labels, flag, pc) {
    const dest = branch_dest(inst);
    if (is_label_exp(dest)) {
        const insts = lookup_label(labels, label_exp_label(dest));
        return () => {
                   if (get_contents(flag)) {
                       set_contents(pc, insts);
                   } else {
                       advance_pc(pc);
                   }
               };
    } else {
        error(inst, "bad branch instruction – assemble");
    }
}

branch函数构造branch指令。选择器branch_dest从分支中提取目的地。

function branch(label) { return list("branch", label); }
function branch_dest(branch_instruction) {
    return head(tail(branch_instruction));
}

go_to指令类似于分支，不同之处在于目的地可以指定为标签或寄存器，并且没有条件需要检查——pc总是设置为新的目的地。

function make_go_to_ef(inst, machine, labels, pc) {
    const dest = go_to_dest(inst);
    if (is_label_exp(dest)) {
        const insts = lookup_label(labels, label_exp_label(dest));
        return () => set_contents(pc, insts);
    } else if (is_register_exp(dest)) {
        const reg = get_register(machine, register_exp_reg(dest));
        return () => set_contents(pc, get_contents(reg));
    } else {
        error(inst, "bad go_to instruction – assemble");
    }
}

go_to函数构造go_to指令。选择器go_to_dest从go_to指令中提取目的地。

function go_to(label) { return list("go_to", label); }
function go_to_dest(go_to_instruction) {
    return head(tail(go_to_instruction));
}

其他指令

堆栈指令save和restore只是使用指定寄存器的堆栈并推进pc：

function make_save_ef(inst, machine, stack, pc) {
    const reg = get_register(machine, stack_inst_reg_name(inst));
    return () => {
               push(stack, get_contents(reg));
               advance_pc(pc);
           };
}
function make_restore_ef(inst, machine, stack, pc) {
    const reg = get_register(machine, stack_inst_reg_name(inst));
    return () => {
               set_contents(reg, pop(stack));
               advance_pc(pc);
           };
}

save和restore函数构造save和restore指令。选择器stack_inst_reg_name从这些指令中提取寄存器名称。

function save(reg) { return list("save", reg); }
function restore(reg) { return list("restore", reg); }
function stack_inst_reg_name(stack_instruction) {
    return head(tail(stack_instruction));
}

由make_perform_ef处理的最终指令类型生成要执行的动作的执行函数。在模拟时，执行动作函数并推进pc。

function make_perform_ef(inst, machine, labels, operations, pc) {
    const action = perform_action(inst);
    if (is_operation_exp(action)) {
        const action_fun = make_operation_exp_ef(action, machine,
                                                 labels, operations);
        return () => {
                   action_fun();
                   advance_pc(pc);
               };
    } else {
        error(inst, "bad perform instruction – assemble");
    }
}

perform函数构造perform指令。选择器perform_action从perform指令中提取动作。

function perform(action) { return list("perform", action); }
function perform_action(perform_instruction) {
    return head(tail(perform_instruction));
}

子表达式的执行函数

可能需要对reg、label或constant表达式的值进行赋值给寄存器（如上面的make_assign_ef）或输入到操作中（如下面的make_operation_exp_ef）。以下函数生成执行函数，以在模拟期间为这些表达式生成值：

function make_primitive_exp_ef(exp, machine, labels) {
    if (is_constant_exp(exp)) {
        const c = constant_exp_value(exp);
        return () => c;
    } else if (is_label_exp(exp)) {
        const insts = lookup_label(labels, label_exp_label(exp));
        return () => insts;
    } else if (is_register_exp(exp)) {
        const r = get_register(machine, register_exp_reg(exp));
        return () => get_contents(r);
    } else {
        error(exp, "unknown expression type – assemble");
    }
}

reg、label和constant表达式的语法由以下构造函数确定，以及相应的谓词和选择器。

function reg(name) { return list("reg", name); }
function is_register_exp(exp) { return is_tagged_list(exp, "reg"); }
function register_exp_reg(exp) { return head(tail(exp)); }

function constant(value) { return list("constant", value); }
function is_constant_exp(exp) {
    return is_tagged_list(exp, "constant");
}
function constant_exp_value(exp) { return head(tail(exp)); }

function label(name) { return list("label", name); }
function is_label_exp(exp) { return is_tagged_list(exp, "label"); }
function label_exp_label(exp) { return head(tail(exp)); }

assign、perform和test指令可能包括对机器操作（由op表达式指定）对一些操作数（由reg和constant表达式指定）的应用。以下函数为“操作表达式”（包含指令中的操作和操作数表达式的列表）生成执行函数：

function make_operation_exp_ef(exp, machine, labels, operations) {
    const op = lookup_prim(operation_exp_op(exp), operations);
    const afuns = map(e => make_primitive_exp_ef(e, machine, labels),
                      operation_exp_operands(exp));
    return () => apply_in_underlying_javascript(
                     op, map(f => f(), afuns));
}

操作表达式的语法由

function op(name) { return list("op", name); }
function is_operation_exp(exp) {
    return is_pair(exp) && is_tagged_list(head(exp), "op");
}
function operation_exp_op(op_exp) { return head(tail(head(op_exp))); }
function operation_exp_operands(op_exp) { return tail(op_exp); }

注意，操作表达式的处理非常类似于求值器中analyze_application函数对函数应用的处理，我们为每个操作数生成一个执行函数。在模拟时，我们调用操作数函数并将模拟操作的 JavaScript 函数应用于生成的值。我们使用apply_in_underlying_javascript函数，就像在 4.1.4 节中的apply_primitive_function中所做的那样。这是为了将op应用于第一个map生成的参数列表afuns的所有元素，就好像它们是op的单独参数一样。如果没有这样做，op将被限制为一元函数。

通过在机器的操作表中查找操作名称来找到模拟函数：

function lookup_prim(symbol, operations) {
    const val = assoc(symbol, operations);
    return is_undefined(val)
           ? error(symbol, "unknown operation – assemble")
           : head(tail(val));
}

练习 5.9

上面对机器操作的处理允许它们对标签以及寄存器的内容和常量进行操作。修改表达式处理函数以强制执行操作只能与寄存器和常量一起使用的条件。

练习 5.10

当我们在 5.1.4 节中介绍save和restore时，我们没有指定如果尝试恢复不是最后一个保存的寄存器会发生什么，例如在以下序列中

save(y);
save(x);
restore(y);

对于restore的含义有几种合理的可能性：

a. restore(y)将最后一个保存在堆栈上的值放入y中，无论该值来自哪个寄存器。这是我们模拟器的行为方式。展示如何利用这种行为来消除 5.1.4 节（图 5.12）中 Fibonacci 机器的一条指令。
b. restore(y)将最后一个保存在堆栈上的值放入y中，但前提是该值是从y保存的；否则，它会发出错误信号。修改模拟器以使其行为如此。您将不得不更改save以将寄存器名称与值一起放入堆栈。
c. restore(y)将最后一个保存在y中的值放入y中，而不管在y之后保存的其他寄存器是什么。修改模拟器以使其行为如此。您将不得不为每个寄存器关联一个单独的堆栈。您应该使initialize_stack操作初始化所有寄存器堆栈。

练习 5.11

模拟器可用于帮助确定实现具有给定控制器的机器所需的数据路径。扩展汇编程序以在机器模型中存储以下信息：

所有指令的列表，去除重复项，按指令类型（assign，go_to等）排序；
一个（无重复）的寄存器列表，用于保存入口点（这些是由go_to指令引用的寄存器）；
一个（无重复）的寄存器列表，这些寄存器被“保存”或“恢复”；
对于每个寄存器，列出（无重复）分配给它的源（例如，图 5.11 中的阶乘机器中val寄存器的源是constant(1)和list(op("*"), reg("n"), reg("val"))）。

扩展与机器的消息传递接口，以提供对这些新信息的访问。为了测试您的分析器，定义来自图 5.12 的 Fibonacci 机器，并检查您构建的列表。

练习 5.12

修改模拟器，使其使用控制器序列来确定机器具有哪些寄存器，而不是要求在make_machine的参数中预分配寄存器的列表。不要在make_machine中预分配寄存器，而是在汇编指令装配时首次看到它们时逐个分配它们。

5.2.4 监控机器性能

模拟不仅用于验证提议的机器设计的正确性，还用于测量机器的性能。例如，我们可以在模拟程序中安装一个“计量器”，用于测量计算中使用的堆栈操作次数。为此，我们修改我们的模拟堆栈以跟踪寄存器保存在堆栈上的次数和堆栈达到的最大深度，并在堆栈的接口中添加一个打印统计信息的消息，如下所示。我们还在基本机器模型中添加一个操作来打印堆栈统计信息，通过在make_new_machine中初始化the_ops来实现

list(list("initialize_stack",
          () => stack("initialize")),
     list("print_stack_statistics",
          () => stack("print_statistics")));

这是make_stack的新版本：

function make_stack() {
    let stack = null;
    let number_pushes = 0;
    let max_depth = 0;
    let current_depth = 0;
    function push(x) {
        stack = pair(x, stack);
        number_pushes = number_pushes + 1;
        current_depth = current_depth + 1;
        max_depth = math_max(current_depth, max_depth);
        return "done";
    }
    function pop() {
        if (is_null(stack)) {
            error("empty stack – pop");
        } else {
            const top = head(stack);
            stack = tail(stack);
            current_depth = current_depth - 1;
            return top;
        }
    }
    function initialize() {
        stack = null;
        number_pushes = 0;
        max_depth = 0;
        current_depth = 0;
        return "done";
    }
    function print_statistics() {
        display("total pushes = " + stringify(number_pushes));
        display("maximum depth = " + stringify(max_depth));
    }
    function dispatch(message) {
        return message === "push"
               ? push
               : message === "pop"
               ? pop()
               : message === "initialize"
               ? initialize()
               : message === "print_statistics"
               ? print_statistics()
               : error(message, "unknown request – stack");
    }
    return dispatch;
}

练习 5.14 到 5.18 描述了可以添加到寄存器机模拟器的其他有用的监控和调试功能。

练习 5.13

测量计算n！所需的推送次数和最大堆栈深度，对于各个小值的n，使用图 5.11 中显示的阶乘机器。从您的数据中确定关于n的总推送操作次数和计算n！所需的最大堆栈深度的公式。请注意，这两者都是n的线性函数，因此由两个常数确定。为了打印统计信息，您将需要增加阶乘机器的指令来初始化堆栈并打印统计信息。您可能还希望修改机器，使其重复读取n的值，计算阶乘，并打印结果（就像我们在图 5.4 中对 GCD 机器所做的那样），这样您就不必反复调用get_register_contents，set_register_contents和start。

练习 5.14

将指令计数添加到寄存器机器模拟中。也就是说，让机器模型跟踪执行的指令数量。扩展机器模型的接口，接受一个新的消息，打印指令计数的值并将计数重置为零。

练习 5.15

增强模拟器以提供指令跟踪。也就是说，在执行每条指令之前，模拟器应该打印该指令。使机器模型接受trace_on和trace_off消息以打开和关闭跟踪。

练习 5.16

扩展练习 5.15 的指令跟踪，以便在打印指令之前，模拟器打印出控制器序列中紧接着该指令的任何标签。要小心以不干扰指令计数（练习 5.14）的方式进行此操作。您将需要使模拟器保留必要的标签信息。

练习 5.17

修改 5.2.1 节的make_register函数，以便可以跟踪寄存器。寄存器应该接受打开和关闭跟踪的消息。当寄存器被跟踪时，将值分配给寄存器应该打印寄存器的名称，寄存器的旧内容以及正在分配的新内容。扩展机器模型的接口，允许您为指定的机器寄存器打开和关闭跟踪。

练习 5.18

Alyssa P. Hacker 希望模拟器中有一个断点功能，以帮助她调试她的机器设计。您已被聘请为她安装此功能。她希望能够指定控制器序列中的一个位置，模拟器将在那里停止，并允许她检查机器的状态。您要实现一个函数

set_breakpoint(machine, label, n)

在给定标签后的第n条指令之前设置一个断点。例如， `

set_breakpoint(gcd_machine, "test_b", 4)

在gcd_machine中的寄存器a分配之前设置断点。当模拟器到达断点时，它应该打印标签和断点的偏移量，并停止执行指令。然后 Alyssa 可以使用get_register_contents和set_register_contents来操纵模拟机的状态。然后她应该能够通过说

proceed_machine(machine)

她还应该能够通过以下方式删除特定的断点

cancel_breakpoint(machine, label, n)

或通过以下方式删除所有断点

cancel_all_breakpoints(machine)

5.3 存储分配和垃圾收集

在第 5.4 节中，我们将展示如何将 JavaScript 求值器实现为寄存器机器。为了简化讨论，我们将假设我们的寄存器机器可以配备列表结构内存，其中用于操作列表结构数据的基本操作是原始的。假设这样的内存存在是一个有用的抽象，当一个解释器专注于控制机制时，但这并不反映当代计算机的实际原始数据操作的真实视图。为了更全面地了解系统如何有效支持列表结构内存，我们必须调查如何表示列表结构，以使其与传统计算机内存兼容。

在实现列表结构时有两个考虑因素。第一个纯粹是一个表示问题：如何仅使用典型计算机内存的存储和寻址能力来表示对，使用“盒子和指针”结构。第二个问题涉及内存管理随着计算的进行。JavaScript 系统的操作至关重要的依赖于不断创建新的数据对象的能力。这些包括由 JavaScript 函数明确创建的对象，以及由解释器本身创建的结构，例如环境和参数列表。尽管在具有无限量快速可寻址内存的计算机上不断创建新的数据对象不会造成问题，但计算机内存只有有限的大小（更可惜）。因此，JavaScript 提供了自动存储分配设施，以支持无限内存的幻觉。当不再需要数据对象时，分配给它的内存会自动回收并用于构造新的数据对象。提供这种自动存储分配的各种技术。我们将在本节中讨论的方法称为垃圾收集。

5.3.1 记忆作为向量

传统计算机内存可以被认为是一个包含信息的小隔间数组。每个小隔间都有一个唯一的名称，称为其地址或位置。典型的内存系统提供两种原始操作：一种是获取存储在指定位置的数据，另一种是将新数据分配给指定位置。内存地址可以递增以支持对一些小隔间的顺序访问。更一般地，许多重要的数据操作要求将内存地址视为数据，可以存储在内存位置中，并在机器寄存器中进行操作。列表结构的表示是这种地址算术的一个应用。

为了模拟计算机内存，我们使用一种称为向量的新数据结构。抽象地说，向量是一个复合数据对象，其各个元素可以通过整数索引来访问，而访问的时间与索引无关。为了描述内存操作，我们使用两个用于操作向量的函数。

vector_ref(vector, n)返回向量的第n个元素。
vector_set(vector, n, value)将向量的第n个元素设置为指定的值。

例如，如果v是一个向量，那么vector_ref(v, 5)会得到向量v中的第五个条目，vector_set(v, 5, 7)会将向量v的第五个条目的值更改为 7。对于计算机内存，这种访问可以通过地址算术来实现，将指定向量在内存中的基地址与指定向量特定元素的索引相结合。

表示数据

我们可以使用向量来实现列表结构内存所需的基本对结构。让我们想象计算机内存被分成两个向量：the_heads和the_tails。我们将表示列表结构如下：对于一对的指针是两个向量中的索引。一对的head是指定索引的the_heads中的条目，一对的tail是指定索引的the_tails中的条目。我们还需要一种表示除对之外的对象（如数字和字符串）的方法，以及一种区分一种数据类型与另一种的方法。有许多方法可以实现这一点，但它们都可以归结为使用类型化指针，即将“指针”的概念扩展到包括有关数据类型的信息。数据类型使系统能够区分指向一对的指针（它由“对”数据类型和内存向量中的索引组成）和指向其他类型数据的指针（它由其他数据类型和用于表示该类型数据的任何内容组成）。如果它们的指针相同，两个数据对象被认为是相同的（===）。图 5.14 说明了使用这种方法表示list(list(1, 2), 3, 4)，其盒式图也显示在图中。我们使用字母前缀来表示数据类型信息。因此，指向索引 5 的对的指针表示为p5，空列表由指针e0表示，指向数字 4 的指针表示为n4。在盒式图中，我们在每对的左下方指示了指定head和tail存储位置的向量索引。the_heads和the_tails中的空白位置可能包含其他列表结构的部分（这里不感兴趣）。

图 5.14 列表list(list(1, 2), 3, 4)的盒式图和内存向量表示。

例如，指向数字的指针，比如n4，可能由一个指示数字数据的类型和数字 4 的实际表示组成。为了处理无法在单个指针分配的固定空间中表示的太大的数字，我们可以使用一个不同的bignum数据类型，其中指针指定一个列表，其中存储了数字的各个部分。

一个字符串可以被表示为一个类型化的指针，该指针指定了形成字符串打印表示的字符序列。当解析器遇到字符串文字时，它构造这样一个序列，字符串连接运算符+和诸如stringify之类的字符串生成原始函数也构造这样一个序列。由于我们希望两个字符串实例被===识别为“相同”的字符串，并且我们希望===是指针相等的简单测试，我们必须确保如果系统两次看到相同的字符串，它将使用相同的指针（指向相同的字符序列）来表示这两个实例。为了实现这一点，系统维护一个称为字符串池的表，其中包含它曾经遇到的所有字符串。当系统即将构造一个字符串时，它会检查字符串池，看看它以前是否见过相同的字符串。如果没有，它会构造一个新的字符串（指向新的字符序列的类型化指针）并将这个指针输入字符串池。如果系统以前见过这个字符串，它会返回字符串池中存储的字符串指针。这个用唯一指针替换字符串的过程称为字符串国际化。

实现原始列表操作

根据上述表示方案，我们可以用一个或多个原始向量操作替换寄存器机器的每个“原始”列表操作。我们将使用两个寄存器the_heads和the_tails来标识内存向量，并假设vector_ref和vector_set可用作原始操作。我们还假设指针的数值操作（例如递增指针，使用对指针索引向量，或者将两个数字相加）仅使用类型指针的索引部分。

例如，我们可以使一个寄存器机器支持以下指令

assign(reg[1], list(op("head"), reg(reg[2])))

assign(reg[1], list(op("tail"), reg(reg[2])))

如果我们分别实现这些，作为

assign(reg[1], list(op("vector_ref"), reg("the_heads"), reg(reg[2])))

assign(reg[1], list(op("vector_ref"), reg("the_tails"), reg(reg[2])))

指令

perform(list(op("set_head"), reg(reg[1]), reg(reg[2])))

perform(list(op("set_tail"), reg(reg[1]), reg(reg[2])))

被实现为

perform(list(op("vector_set"), reg("the_heads"), reg(reg[1]), reg(reg[2])))

perform(list(op("vector_set"), reg("the_tails"), reg(reg[1]), reg(reg[2])))

pair操作通过分配一个未使用的索引并将pair的参数存储在该索引向量位置的the_heads和the_tails中来执行。我们假设有一个特殊的寄存器free，它始终保存一个包含下一个可用索引的对指针，并且我们可以递增该指针的索引部分以找到下一个空闲位置。¹² 例如，指令

assign(reg[1], list(op("pair"), reg(reg[2]), reg(reg[3])))

被实现为以下向量操作的序列：¹³

perform(list(op("vector_set"),
             reg("the_heads"), reg("free"), reg(reg[2]))),
perform(list(op("vector_set"),
             reg("the_tails"), reg("free"), reg(reg[3]))),
assign(reg[1], reg("free")),
assign("free", list(op("+"), reg("free"), constant(1)))

===操作

list(op("==="), reg(reg[1]), reg(reg[2]))

简单地测试寄存器中所有字段的相等性，而诸如is_pair、is_null、is_string和is_number之类的谓词只需要检查类型字段。

实现堆栈

尽管我们的寄存器机器使用堆栈，但在这里我们不需要做任何特殊处理，因为堆栈可以用列表来建模。堆栈可以是由特殊寄存器the_stack指向的保存值的列表。因此，save(reg)可以被实现为

assign("the_stack", list(op("pair"), reg(reg), reg("the_stack")))

同样，restore(reg)可以被实现为

assign(reg, list(op("head"), reg("the_stack")))
assign("the_stack", list(op("tail"), reg("the_stack")))

和perform(list(op("initialize_stack")))可以被实现为

assign("the_stack", constant(null))

这些操作可以进一步扩展为上述的向量操作。然而，在传统的计算机体系结构中，通常有利于将堆栈分配为单独的向量。然后，通过增加或减少对该向量的索引来推送和弹出堆栈。

练习 5.19

绘制盒子和指针表示以及由以下列表结构产生的内存向量表示（如图 5.14 中所示）。

const x = pair(1, 2);
const y = list(x, x);

初始情况下，free指针为p1。free的最终值是多少？哪些指针代表了x和y的值？

练习 5.20

为以下函数实现寄存器机器。假设列表结构内存操作可用作机器原语。

a. 递归count_leaves：

function count_leaves(tree) {
    return is_null(tree)
           ? 0
           : ! is_pair(tree)
           ? 1
           : count_leaves(head(tree)) +
             count_leaves(tail(tree));
}

b. 递归count_leaves并带有显式计数器：

function count_leaves(tree) {
    function count_iter(tree, n) {
    return is_null(tree)
               ? n
               : ! is_pair(tree)
               ? n + 1
               : count_iter(tail(tree),
                            count_iter(head(tree), n));
    }
    return count_iter(tree, 0);
}

练习 5.21

3.3.1 节的练习 3.12 提出了一个append函数，它将两个列表连接起来形成一个新列表，以及一个append_mutator函数，它将两个列表拼接在一起。设计一个寄存器机器来实现这些函数。假设列表结构内存操作可用作原始操作。

5.3.2 维持内存无限的幻觉

5.3.1 节中概述的表示方法解决了实现列表结构的问题，前提是我们有无限的内存。在真实的计算机中，我们最终会耗尽用于构造新对的空间。¹⁴ 然而，在典型计算中生成的大多数对仅用于保存中间结果。在访问这些结果之后，这些对将不再需要——它们是垃圾。例如，计算

accumulate((x, y) => x + y,
           0,
           filter(is_odd, enumerate_interval(0, n)))

构造两个列表：枚举和过滤枚举的结果。当累积完成时，这些列表将不再需要，并且分配的内存可以被回收。如果我们可以安排定期收集所有的垃圾，并且如果这样做以大约与我们构造新对的速度相同的速度回收内存，我们将保留内存无限的幻觉。

为了回收对，我们必须有一种方法来确定哪些分配的对不再需要（即它们的内容不再能影响计算的未来）。我们将研究用于实现这一点的方法称为垃圾收集。垃圾收集基于这样的观察：在基于列表结构的内存的解释中的任何时刻，只有可以通过从当前机器寄存器中的指针开始的一系列head和tail操作到达的对象才能影响计算的未来。任何不可访问的内存单元都可以被回收。 ¹⁵

执行垃圾收集有许多方法。我们将在这里研究的方法称为停止-复制。基本思想是将内存分为两半：“工作内存”和“空闲内存”。当pair构造成对时，它们被分配在工作内存中。当工作内存满时，我们通过定位工作内存中所有有用的对并将其复制到空闲内存中来执行垃圾收集。（通过跟踪所有head和tail指针来定位有用的对，从机器寄存器开始。）由于我们不复制垃圾，所以可能会有额外的空闲内存，我们可以用来分配新的对。此外，工作内存中的任何内容都不再需要，因为其中的所有有用对都已经被复制。因此，如果我们交换工作内存和空闲内存的角色，我们可以继续处理；新的对将在新的工作内存中（原来的空闲内存）分配。当这个满了，我们可以将有用的对复制到新的空闲内存中（原来的工作内存）。

实现停止-复制垃圾收集器

现在我们使用寄存器机器语言更详细地描述停止-复制算法。我们假设有一个名为root的寄存器，其中包含一个指向最终指向所有可访问数据的结构的指针。这可以通过在开始垃圾收集之前将所有机器寄存器的内容存储在由root指向的预分配列表中来安排。我们还假设，除了当前的工作内存之外，还有可用的空闲内存，我们可以将有用的数据复制到其中。当前的工作内存由基地址在名为the_heads和the_tails的寄存器中的向量组成，而空闲内存在名为new_heads和new_tails的寄存器中。

当我们耗尽当前工作内存中的空闲单元时，也就是说，当pair操作尝试将free指针增加到内存向量的末尾之外时，垃圾收集就会被触发。当垃圾收集过程完成时，root指针将指向新的内存，从root可访问的所有对象都将被移动到新的内存中，free指针将指示新内存中可以分配新对的下一个位置。此外，工作内存和新内存的角色将被交换-新的对将在新的内存中构造，从free指示的位置开始，而（之前的）工作内存将作为下一次垃圾收集的新内存可用。图 5.15 显示了垃圾收集前后内存的布局。

图 5.15 垃圾收集过程中内存的重新配置。

垃圾收集过程的状态由维护两个指针来控制：free和scan。它们被初始化为指向新内存的开始。算法从将root指向的一对重新定位到新内存的开始。复制这对，调整root指针指向新位置，并递增free指针。此外，标记这对的旧位置以显示其内容已被移动。标记的方法如下：在“头”位置，我们放置一个特殊标记，表示这是一个已经移动的对象（这样的对象传统上被称为破碎的心）。在“尾”位置，我们放置一个转发地址，指向对象已被移动的位置。

搬迁根节点后，垃圾收集器进入基本循环。算法的每一步中，“扫描”指针（最初指向已搬迁的根节点）指向一个已移动到新内存中的一对，但其“头”和“尾”指针仍指向旧内存中的对象。这些对象都被重新定位，然后“扫描”指针递增。要重新定位一个对象（例如，我们正在扫描的一对中由“头”指针指示的对象），我们检查对象是否已经被移动（由对象的“头”位置上的破碎心标记表示）。如果对象尚未被移动，我们将其复制到free指示的位置，更新free，在对象的旧位置设置一个破碎的心，并更新指向对象的指针（在这个例子中，我们正在扫描的一对的“头”指针）指向新位置。如果对象已经被移动，其转发地址（在破碎心的“尾”位置找到）将替换正在扫描的一对中的指针。最终，所有可访问的对象都将被移动和扫描，此时“扫描”指针将超过free指针，进程将终止。

我们可以将停止-复制算法指定为寄存器机器的一系列指令。重新定位对象的基本步骤是通过一个名为relocate_old_result_in_new的子例程来完成的。这个子例程从一个名为old的寄存器中获取其参数，即要重新定位的对象的指针。它重新定位指定的对象（在此过程中递增free），将指向重新定位对象的指针放入一个名为new的寄存器中，并通过跳转到存储在寄存器relocate_continue中的入口点返回。要开始垃圾收集，我们调用这个子例程来重新定位root指针，然后初始化free和scan。当root的重新定位完成后，我们将新指针安装为新的root，并进入垃圾收集器的主循环。

"begin_garbage_collection",
  assign("free", constant(0)),
  assign("scan", constant(0)),
  assign("old", reg("root")),
  assign("relocate_continue", label("reassign_root")),
  go_to(label("relocate_old_result_in_new")),
"reassign_root",
  assign("root", reg("new")),
  go_to(label("gc_loop")),

在垃圾收集器的主循环中，我们必须确定是否还有更多的对象需要扫描。我们通过测试scan指针是否与free指针重合来做到这一点。如果指针相等，则所有可访问的对象都已经被重新定位，我们将跳转到gc_flip，清理一切，以便我们可以继续中断的计算。如果仍有要扫描的一对，我们调用重新定位子例程来重新定位下一对的“头”（将“头”指针放入old中）。设置relocate_continue寄存器，以便子例程将返回更新“头”指针。

"gc_loop",
  test(list(op("==="), reg("scan"), reg("free"))),
  branch(label("gc_flip")),
  assign("old", list(op("vector_ref"), reg("new_heads"), reg("scan"))),
  assign("relocate_continue", label("update_head")),
  go_to(label("relocate_old_result_in_new")),

在update_head中，我们修改正在扫描的一对的“头”指针，然后继续重新定位“尾”。当重新定位和更新“尾”完成后，我们完成了扫描该对，因此我们继续进行主循环。

"update_head",
  perform(list(op("vector_set"),
               reg("new_heads"), reg("scan"), reg("new"))),
  assign("old", list(op("vector_ref"),
                     reg("new_tails"), reg("scan"))),
  assign("relocate_continue", label("update_tail")),
  go_to(label("relocate_old_result_in_new")),
"update_tail",
  perform(list(op("vector_set"),
               reg("new_tails"), reg("scan"), reg("new"))),
  assign("scan", list(op("+"), reg("scan"), constant(1))),
  go_to(label("gc_loop")),

子例程relocate_old_result_in_new的重定位对象如下：如果要重定位的对象（由old指向）不是一对，那么我们将返回指向对象的相同指针（在new中不变）。（例如，我们可能正在扫描一个head为数字 4 的对。如果我们按照第 5.3.1 节中描述的方式将head表示为n4，那么我们希望“重定位”的head指针仍然是n4。）否则，我们必须执行重定位。如果要重定位的对的head位置包含一个破碎心标记，那么该对实际上已经被移动，因此我们从破碎心的tail位置检索转发地址，并将其返回到new中。如果old中的指针指向尚未移动的对，则我们将该对移动到新内存中的第一个空闲单元（由free指向），并通过在旧位置存储破碎心标记和转发地址来设置破碎心。子例程relocate_old_result_in_new使用寄存器oldht来保存由old指向的对象的head或tail。¹⁹

"relocate_old_result_in_new",
  test(list(op("is_pointer_to_pair"), reg("old"))),
  branch(label("pair")),
  assign("new", reg("old")),
  go_to(reg("relocate_continue")),
"pair",
  assign("oldht", list(op("vector_ref"),
                       reg("the_heads"), reg("old"))),
  test(list(op("is_broken_heart"), reg("oldht"))),
  branch(label("already_moved")),
  assign("new", reg("free")),     // new location for pair
  // Update free pointer
  assign("free", list(op("+"), reg("free"), constant(1))),
  // Copy the head and tail to new memory
  perform(list(op("vector_set"),
               reg("new_heads"), reg("new"),
               reg("oldht"))),
  assign("oldht", list(op("vector_ref"),
                      reg("the_tails"), reg("old"))),
  perform(list(op("vector_set"),
               reg("new_tails"), reg("new"),
               reg("oldht"))),
  // Construct the broken heart
  perform(list(op("vector_set"),
               reg("the_heads"), reg("old"),
               constant("broken_heart"))),
  perform(list(op("vector_set"),
               reg("the_tails"), reg("old"),
               reg("new"))),
  go_to(reg("relocate_continue")),
"already_moved",
  assign("new", list(op("vector_ref"),
                     reg("the_tails"), reg("old"))),
  go_to(reg("relocate_continue")),

在垃圾收集过程的最后，我们通过交换指针来交换旧内存和新内存的角色：交换the_heads和new_heads，以及the_tails和new_tails。然后，我们将准备好在内存耗尽时执行另一次垃圾收集。

"gc_flip",
  assign("temp", reg("the_tails")),
  assign("the_tails", reg("new_tails")),
  assign("new_tails", reg("temp")),
  assign("temp", reg("the_heads")),
  assign("the_heads", reg("new_heads")),
  assign("new_heads", reg("temp"))

5.4 显式控制求值器

在第 5.1 节中，我们看到如何将简单的 JavaScript 程序转换为寄存器机器的描述。我们现在将对更复杂的程序执行此转换，即第 4.1.1–4.1.4 节中的元循环求值器，该程序展示了如何用evaluate和apply函数描述 JavaScript 解释器的行为。本节中开发的显式控制求值器展示了在求值过程中使用的基础函数调用和参数传递机制如何可以用寄存器和堆栈上的操作来描述。此外，显式控制求值器可以作为 JavaScript 解释器的实现，用一种非常类似于传统计算机的本机机器语言编写。求值器可以由第 5.2 节的寄存器机器模拟器执行。或者，它可以用作构建 JavaScript 求值器的机器语言实现的起点，甚至是用于求值 JavaScript 程序的专用机器的起点。图 5.16 展示了这样一个硬件实现：一个硅片作为 Scheme 的求值器，该语言在本书的原版中代替了 JavaScript。芯片设计者从与本节描述的求值器类似的寄存器机器的数据路径和控制器规格开始，并使用设计自动化程序构建集成电路布局。²⁰

图 5.16 Scheme 求值器的硅片实现。

寄存器和操作

在设计显式控制求值器时，我们必须指定在我们的寄存器机器中使用的操作。我们描述了元循环求值器，使用诸如is_literal和make_function之类的函数来描述抽象语法。在实现寄存器机器时，我们可以将这些函数扩展为基本的列表结构内存操作的序列，并在我们的寄存器机器上实现这些操作。然而，这将使我们的求值器非常冗长，使基本结构被细节所遮盖。为了阐明表述，我们将在寄存器机器的原始操作中包括第 4.1.2 节中给出的语法函数和第 4.1.3 和 4.1.4 节中给出的表示环境和其他运行时数据的函数。为了完全指定一个可以在低级机器语言中编程或在硬件中实现的求值器，我们将用更基本的操作替换这些操作，使用我们在第 5.3 节中描述的列表结构实现。

我们的 JavaScript 求值器寄存器机器包括一个堆栈和七个寄存器：comp、env、val、continue、fun、argl和unev。comp寄存器用于保存要求值的组件，env包含要执行求值的环境。在求值结束时，val包含在指定环境中求值组件获得的值。continue寄存器用于实现递归，如第 5.1.4 节中所述。（求值器需要递归调用自身，因为求值一个组件需要求值其子组件。）fun、argl和unev寄存器用于求值函数应用。

我们不会提供数据路径图来显示求值器的寄存器和操作如何连接，也不会提供完整的机器操作列表。这些都隐含在求值器的控制器中，将会详细介绍。

5.4.1 调度程序和基本求值

求值器中的中心元素是从eval_dispatch开始的指令序列。这对应于第 4.1.1 节中描述的元循环求值器的evaluate函数。当控制器从eval_dispatch开始时，它在由env指定的环境中求值由comp指定的组件。求值完成后，控制器将转到存储在continue中的入口点，而val寄存器将保存组件的值。与元循环的evaluate一样，eval_dispatch的结构是对待求值组件的语法类型的情况分析。

"eval_dispatch",
  test(list(op("is_literal"), reg("comp"))),
  branch(label("ev_literal")),
  test(list(op("is_name"), reg("comp"))),
  branch(label("ev_name")),
  test(list(op("is_application"), reg("comp"))),
  branch(label("ev_application")),
  test(list(op("is_operator_combination"), reg("comp"))),
  branch(label("ev_operator_combination")),
  test(list(op("is_conditional"), reg("comp"))),
  branch(label("ev_conditional")),
  test(list(op("is_lambda_expression"), reg("comp"))),
  branch(label("ev_lambda")),
  test(list(op("is_sequence"), reg("comp"))),
  branch(label("ev_sequence")),
  test(list(op("is_block"), reg("comp"))),
  branch(label("ev_block")),
  test(list(op("is_return_statement"), reg("comp"))),
  branch(label("ev_return")),
  test(list(op("is_function_declaration"), reg("comp"))),
  branch(label("ev_function_declaration")),
  test(list(op("is_declaration"), reg("comp"))),
  branch(label("ev_declaration")),
  test(list(op("is_assignment"), reg("comp"))),
  branch(label("ev_assignment")),
  go_to(label("unknown_component_type")),

求值简单表达式

数字和字符串、名称和 lambda 表达式没有要求值的子表达式。对于这些情况，求值器只需将正确的值放入val寄存器中，并在continue指定的入口点继续执行。简单表达式的求值由以下控制器代码执行：

"ev_literal",
  assign("val", list(op("literal_value"), reg("comp"))),
  go_to(reg("continue")),
"ev_name",
  assign("val", list(op("symbol_of_name"), reg("comp"), reg("env"))),
  assign("val", list(op("lookup_symbol_value"),
                     reg("val"), reg("env"))),
  go_to(reg("continue")),
"ev_lambda",
  assign("unev", list(op("lambda_parameter_symbols"), reg("comp"))),
  assign("comp", list(op("lambda_body"), reg("comp"))),
  assign("val", list(op("make_function"),
                     reg("unev"), reg("comp"), reg("env"))),
  go_to(reg("continue")),

观察ev_lambda如何使用unev和comp寄存器来保存 lambda 表达式的参数和主体，以便它们可以与env中的环境一起传递给make_function操作。

条件句

与元循环求值器一样，语法形式通过选择性地求值组件的片段来处理。对于条件句，我们必须求值谓词，并根据谓词的值决定是求值结果还是替代方案。

在求值谓词之前，我们保存条件本身，即在comp中，以便稍后提取结果或替代项。为了求值谓词表达式，我们将其移动到comp寄存器中并转到eval_dispatch。env寄存器中的环境已经是正确的环境，用于求值谓词。但是，我们保存env，因为稍后我们将需要它来求值结果或替代项。我们设置continue，以便在求值完谓词后在ev_conditional_decide处恢复求值。然而，首先我们保存continue的旧值，因为稍后我们需要它来返回到等待条件值的语句的求值。

"ev_conditional",
  save("comp"), // save conditional for later
save("env"),
save("continue"),
assign("continue", label("ev_conditional_decide")),
assign("comp", list(op("conditional_predicate"), reg("comp"))),
  go_to(label("eval_dispatch")), // evaluate the predicate

在求值谓词后，在ev_conditional_decide处恢复时，我们测试它是真还是假，并根据结果在转到eval_dispatch之前将结果或替代项放在comp中。请注意，这里恢复env和continue设置了eval_dispatch具有正确的环境，并在正确的位置继续接收条件的值。

"ev_conditional_decide",
  restore("continue"),
  restore("env"),
  restore("comp"),
  test(list(op("is_falsy"), reg("val"))),
  branch(label("ev_conditional_alternative")),
"ev_conditional_consequent",
  assign("comp", list(op("conditional_consequent"), reg("comp"))),
  go_to(label("eval_dispatch")),
"ev_conditional_alternative",
  assign("comp", list(op("conditional_alternative"), reg("comp"))),
  go_to(label("eval_dispatch")),

序列求值

显式控制求值器中从ev_sequence开始处理语句序列的部分类似于元循环求值器的eval_ sequence函数。

ev_sequence_next和ev_sequence_continue处的条目形成一个循环，依次求值序列中的每个语句。未求值语句的列表保存在unev中。在ev_sequence处，我们将要求值的语句序列放在unev中。如果序列为空，我们将val设置为undefined，并通过ev_sequence_empty跳转到continue。否则，我们开始序列求值循环，首先在堆栈上保存continue的值，因为continue寄存器将用于循环中的局部控制流，原始值在语句序列之后继续时是需要的。在求值每个语句之前，我们检查序列中是否有其他语句需要求值。如果有，我们保存未求值语句的其余部分（保存在unev中）和必须求值这些语句的环境（保存在env中），并调用eval_dispatch来求值已放置在comp中的语句。在此求值后，这两个保存的寄存器在ev_sequence_continue处被恢复。

该序列中的最终语句在入口点ev_sequence_last_statement处以不同的方式处理。由于在此之后没有更多的语句需要求值，因此在转到eval_dispatch之前，我们不需要保存unev或env。整个序列的值是最后一个语句的值，因此在求值最后一个语句之后，除了继续保存在ev_sequence处保存的入口点外，没有其他事情要做。我们不是设置continue以安排eval_dispatch返回到这里，然后从堆栈中恢复continue并在该入口点继续，而是在转到eval_dispatch之前从堆栈中恢复continue，以便eval_dispatch在求值语句后继续在该入口点继续。

"ev_sequence",
  assign("unev", list(op("sequence_statements"), reg("comp"))),
  test(list(op("is_empty_sequence"), reg("unev"))),
  branch(label("ev_sequence_empty")),
  save("continue"),
"ev_sequence_next",
  assign("comp", list(op("first_statement"), reg("unev"))),
  test(list(op("is_last_statement"), reg("unev"))),
  branch(label("ev_sequence_last_statement")),
  save("unev"),
  save("env"),
  assign("continue", label("ev_sequence_continue")),
  go_to(label("eval_dispatch")),
"ev_sequence_continue",
  restore("env"),
  restore("unev"),
  assign("unev", list(op("rest_statements"), reg("unev"))),
  go_to(label("ev_sequence_next")),
"ev_sequence_last_statement",
  restore("continue"),
  go_to(label("eval_dispatch")),

"ev_sequence_empty",
  assign("val", constant(undefined)),
  go_to(reg("continue")),

与元循环求值器中的eval_sequence不同，ev_sequence不需要检查是否求值了返回语句以终止序列求值。这个求值器中的“显式控制”允许返回语句直接跳转到当前函数应用的继续部分，而不是恢复序列求值。因此，序列求值不需要关心返回，甚至不需要知道语言中返回语句的存在。因为返回语句跳出了序列求值代码，所以在ev_sequence_continue处保存的寄存器的恢复不会被执行。稍后我们将看到返回语句如何从堆栈中移除这些值。

5.4.2 求值函数应用

函数应用由包含函数表达式和参数表达式的组合指定。函数表达式是一个值为函数的子表达式，参数表达式是值为应用函数的参数的子表达式。元循环evaluate通过递归调用自身来处理应用，以求值组合的每个元素，然后将结果传递给apply，执行实际的函数应用。显式控制求值器也是这样做的；这些递归调用是通过go_to指令实现的，同时使用堆栈保存寄存器，在递归调用返回后将被恢复。在每次调用之前，我们将小心地确定哪些寄存器必须被保存（因为它们的值稍后将被需要）²³

与元循环求值器一样，操作符组合被转换为对应于操作符的原始函数的应用。这发生在ev_operator_combination中，在这里在comp中进行了转换，并且通过到ev_application的下降。²⁴

我们通过求值函数表达式开始应用的求值，以产生一个函数，稍后将应用于求值的参数表达式。为了求值函数表达式，我们将其移动到comp寄存器中，并转到eval_dispatch。env寄存器中的环境已经是正确的环境，用于求值函数表达式。但是，我们保存env，因为稍后我们将需要它来求值参数表达式。我们还将参数表达式提取到unev中，并将其保存在堆栈上。我们设置continue，以便eval_dispatch在函数表达式求值后将在ev_appl_did_function_expression处恢复。但首先，我们保存continue的旧值，告诉控制器在应用后继续的位置。

"ev_operator_combination",
  assign("comp", list(op("operator_combination_to_application"),
                      reg("comp"), reg("env"))),
"ev_application",
  save("continue"),
  save("env"),
  assign("unev", list(op("arg_expressions"), reg("comp"))),
  save("unev"),
  assign("comp", list(op("function_expression"), reg("comp"))),
  assign("continue", label("ev_appl_did_function_expression")),
  go_to(label("eval_dispatch")),

从求值函数表达式返回后，我们继续求值应用的参数表达式，并将结果参数累积到argl中的列表中。（这类似于求值一系列语句，只是我们收集值。）首先，我们恢复未求值的参数表达式和环境。我们将argl初始化为空列表。然后，我们将由求值函数表达式产生的函数分配给fun寄存器。如果没有参数表达式，我们直接转到apply_dispatch。否则，我们在堆栈上保存fun并开始参数求值循环：²⁵

"ev_appl_did_function_expression",
  restore("unev"), // the argument expressions
  restore("env"),
  assign("argl", list(op("empty_arglist"))),
  assign("fun", reg("val")), // the function
  test(list(op("is_null"), reg("unev"))),
  branch(label("apply_dispatch")),
  save("fun"),

参数求值循环的每个周期从unev中的列表中求值一个参数表达式，并将结果累积到argl中。为了求值参数表达式，我们将其放入comp寄存器中，并转到eval_dispatch，然后设置continue，以便执行将在参数累积阶段恢复。但首先，我们保存到目前为止累积的参数（保存在argl中），环境（保存在env中），以及要求值的剩余参数表达式（保存在unev中）。对于最后一个参数表达式的求值，特殊情况在ev_appl_last_arg中处理。

"ev_appl_argument_expression_loop",
  save("argl"),
  assign("comp", list(op("head"), reg("unev"))),
  test(list(op("is_last_argument_expression"), reg("unev"))),
  branch(label("ev_appl_last_arg")),
  save("env"),
  save("unev"),
  assign("continue", label("ev_appl_accumulate_arg")),
  go_to(label("eval_dispatch")),

当参数表达式被求值后，值被累积到argl中的列表中。然后，参数表达式从unev中的未求值参数表达式列表中移除，并且参数求值循环继续。

"ev_appl_accumulate_arg",
  restore("unev"),
  restore("env"),
  restore("argl"),
  assign("argl", list(op("adjoin_arg"), reg("val"), reg("argl"))),
  assign("unev", list(op("tail"), reg("unev"))),
  go_to(label("ev_appl_argument_expression_loop")),

最后一个参数表达式的求值处理方式不同，序列中的最后一个语句也是如此。在去往eval_dispatch之前，没有必要保存环境或未求值的参数表达式列表，因为在求值最后一个参数表达式后将不再需要它们。因此，我们从求值返回到一个特殊的入口点ev_appl_accum_last_arg，它恢复参数列表，累积新的参数，恢复保存的函数，并进行应用。

"ev_appl_last_arg",
  assign("continue", label("ev_appl_accum_last_arg")),
  go_to(label("eval_dispatch")),
"ev_appl_accum_last_arg",
  restore("argl"),
  assign("argl", list(op("adjoin_arg"), reg("val"), reg("argl"))),
  restore("fun"),
  go_to(label("apply_dispatch")),

参数求值循环的细节决定了解释器求值组合的参数表达式的顺序（例如，从左到右或从右到左—参见练习 3.8）。这个顺序不是由元循环求值器确定的，元循环求值器从其实现的底层 JavaScript 继承其控制结构。因为我们在ev_appl_argument_expression_loop中使用head来从unev中提取连续的参数表达式，并在ev_appl_accumulate_arg中使用tail来提取其余的参数表达式，显式控制求值器将按照 ECMAScript 规范要求，按照从左到右的顺序求值组合的参数表达式。

函数应用

入口点apply_dispatch对应于元循环求值器的apply函数。当我们到达apply_dispatch时，fun寄存器包含要应用的函数，argl包含要应用的已求值参数的列表。保存的continue值（最初传递给eval_dispatch并保存在ev_application处），告诉在函数应用的结果返回到哪里，存储在堆栈上。应用完成后，控制器转移到由保存的continue指定的入口点，带有应用的结果在val中。与元循环的apply一样，有两种情况需要考虑。要么要应用的函数是原始的，要么是复合函数。

"apply_dispatch",
  test(list(op("is_primitive_function"), reg("fun"))),
  branch(label("primitive_apply")),
  test(list(op("is_compound_function"), reg("fun"))),
  branch(label("compound_apply")),
  go_to(label("unknown_function_type")),

我们假设每个原始函数都是这样实现的，以便从argl中获取其参数并将其结果放入val中。要指定机器如何处理原始函数，我们需要提供一系列控制器指令来实现每个原始函数，并安排primitive_apply分派到由fun的内容标识的原始函数的指令。由于我们对求值过程的结构感兴趣，而不是原始函数的细节，因此我们将使用一个apply_primitive_function操作，将fun中的函数应用于argl中的参数。为了模拟 5.2 节中的模拟器的求值器，我们使用apply_primitive_function函数，它调用底层的 JavaScript 系统来执行应用，就像我们在 4.1.1 节中对元循环求值器所做的那样。计算出原始应用的值后，我们恢复continue并转到指定的入口点。

"primitive_apply",
  assign("val", list(op("apply_primitive_function"),
                     reg("fun"), reg("argl"))),
  restore("continue"),
  go_to(reg("continue")),

标记为compound_apply的指令序列指定了复合函数的应用。要应用复合函数，我们以类似于元循环求值器的方式进行。我们构造一个框架，将函数的参数绑定到参数，使用这个框架来扩展函数携带的环境，并在这个扩展的环境中求值函数的主体。

此时，复合函数在寄存器fun中，其参数在argl中。我们将函数的参数提取到unev中，将其环境提取到env中。然后我们用扩展参数绑定的环境构造的环境替换env中的环境。然后我们将函数的主体提取到comp中。自然的下一步将是恢复保存的continue并继续到eval_dispatch来求值主体，并在val中使用结果继续到恢复的延续，就像对序列的最后一个语句所做的那样。但是有一个复杂性！

这个复杂性有两个方面。一方面，在函数体的求值过程中的任何时刻，返回语句可能需要函数返回返回表达式的值作为函数体的值。但是，返回语句可能在函数体中嵌套任意深，因此在遇到返回语句的时刻的堆栈不一定是从函数返回所需的堆栈。调整堆栈以进行返回的一种方法是在堆栈上放置一个标记，可以被返回代码找到。这是通过push_marker_to_stack指令实现的。然后返回代码可以使用revert_stack_to_marker指令将堆栈恢复到标记指示的位置，然后求值返回表达式。

复杂性的另一个方面是，如果函数体的求值在不执行返回语句的情况下终止，函数体的值必须是undefined。为了处理这个问题，我们设置continue寄存器指向return_undefined的入口点，然后去eval_dispatch求值函数体。如果在函数体的求值过程中没有遇到返回语句，函数体的求值将继续在return_undefined处。

"compound_apply",
  assign("unev", list(op("function_parameters"), reg("fun"))),
  assign("env", list(op("function_environment"), reg("fun"))),
  assign("env", list(op("extend_environment"),
                     reg("unev"), reg("argl"), reg("env"))),
  assign("comp", list(op("function_body"), reg("fun"))),
  push_marker_to_stack(),
  assign("continue", label("return_undefined")),
  go_to(label("eval_dispatch")),

解释器中env寄存器被赋予新值的唯一地方是compound_apply和ev_block（5.4.3 节）。就像在元循环求值器中一样，用于求值函数体的新环境是从函数携带的环境中构建的，以及参数列表和相应的名称绑定列表。

当在ev_return处求值返回语句时，我们使用revert_stack_ to_marker指令将堆栈恢复到函数调用开始时的状态，通过从堆栈中删除所有值直到包括标记。因此，restore("continue")将恢复函数调用的延续，这是在ev_application处保存的。然后我们继续求值返回表达式，其结果将放入val中，因此在继续求值返回表达式后返回函数时的值。

"ev_return",
  revert_stack_to_marker(),
  restore("continue"),
  assign("comp", list(op("return_expression"), reg("comp"))),
  go_to(label("eval_dispatch")),

如果在函数体的求值过程中没有遇到返回语句，求值将继续在return_undefined处，这是在compound_apply中设置的延续。为了从函数中返回undefined，我们将undefined放入val中，并转到在ev_application中放入堆栈的入口点。然而，在我们可以从堆栈中恢复该延续之前，我们必须删除在compound_apply保存的标记。

"return_undefined",
  revert_stack_to_marker(),
  restore("continue"),
  assign("val", constant(undefined)),
  go_to(reg("continue")),

返回语句和尾递归

在第 1 章中，我们说过，由函数描述的过程如下

function sqrt_iter(guess, x) {
    return is_good_enough(guess, x)
           ? guess
           : sqrt_iter(improve(guess, x), x);
}

这是一个迭代过程。即使函数在语法上是递归的（以自身定义），但从一个调用sqrt_iter到下一个调用时，逻辑上并不需要求值器保存信息。一个求值器可以执行sqrt_iter这样的函数，而不需要在函数继续调用自身时增加存储空间，这被称为尾递归求值器。

第 4 章中求值器的元循环实现不是尾递归的。它将返回语句实现为返回值对象的构造函数，该对象包含要返回的值，并检查函数调用的结果是否是这样的对象。如果函数体的求值产生一个返回值对象，则函数的返回值是该对象的内容；否则，返回值是undefined。返回值对象的构造和最终对函数调用结果的检查都是延迟操作，这导致堆栈上的信息积累。

我们的显式控制求值器是尾递归的，因为它不需要包装返回值以进行检查，从而避免了由延迟操作导致的堆栈积累。在ev_return中，为了求值计算函数返回值的表达式，我们直接转移到eval_dispatch，堆栈上除了函数调用之前的内容之外没有其他东西。我们通过使用revert_stack_to_marker来撤销函数对堆栈的任何保存（因为我们正在返回），从而实现这一点。然后，我们在转到eval_dispatch之前从堆栈中恢复continue，而不是安排eval_dispatch在这里返回，然后从堆栈中恢复continue并在该入口点继续。这样，eval_dispatch在求值表达式后将在该入口点继续。最后，我们转移到eval_dispatch而不在堆栈上保存任何信息。因此，当我们继续求值返回表达式时，堆栈与我们即将计算其返回值的函数调用之前的堆栈相同。因此，求值返回表达式——即使它是一个函数调用（如sqrt_iter中的情况，其中条件表达式简化为对sqrt_iter的调用）——都不会导致堆栈上积累任何信息。³⁰

如果我们没有考虑到不需要在求值返回表达式时保留堆栈上的无用信息，我们可能会采取直接的方法来求值返回表达式，然后回来恢复堆栈，并最终在等待函数调用结果的入口点继续：

"ev_return",  // alternative implementation: not tail-recursive
  assign("comp", list(op("return_expression"), reg("comp"))),
  assign("continue", label("ev_restore_stack")),
  go_to(label("eval_dispatch")),
"ev_restore_stack",
revert_stack_to_marker(),     // undo saves in current function
restore("continue"),          // undo save at ev_application
  go_to(reg("continue")),

这可能看起来像是对我们以前用于求值返回语句的代码的一个微小更改：唯一的区别是，我们延迟了对堆栈中任何寄存器保存的撤销，直到返回表达式的求值之后。解释器对于任何表达式仍然会给出相同的值。但是这个改变对于尾递归实现来说是致命的，因为现在我们必须在求值返回表达式之后回来撤销（无用的）寄存器保存。这些额外的保存将在一系列函数调用中累积。因此，像sqrt_iter这样的过程将需要与迭代次数成比例的空间，而不是需要常量空间。这种差异可能是显著的。例如，使用尾递归，可以仅使用函数调用和返回机制来表示无限循环：

function count(n) {
    display(n);
    return count(n + 1);
}

没有尾递归，这样的函数最终会耗尽堆栈空间，并且表达真正的迭代将需要除了函数调用之外的某种控制机制。

请注意，我们的 JavaScript 实现需要使用return才能实现尾递归。因为寄存器保存的撤销发生在ev_return，从count函数中删除return将导致最终耗尽堆栈空间。这解释了在第 4 章中无限驱动循环中使用return的原因。

练习 5.22

解释一下，如果从count中删除return，堆栈是如何构建起来的：

function count(n) {
    display(n);
    count(n + 1);
}

练习 5.23

通过在compound_apply处使用save来实现push_marker_to_stack的等效操作，以在堆栈上存储特殊的标记值。在ev_return和return_undefined处实现revert_stack_to_marker的等效操作，作为一个循环，重复执行restore直到遇到标记。请注意，这将需要将值恢复到与保存时不同的寄存器。这是必要的，因为从堆栈弹出的唯一方法是通过恢复到寄存器。提示：您需要创建一个唯一的常量作为标记，例如使用const marker = list("marker")。因为list创建一个新的对，它不能与堆栈上的其他任何东西===。

练习 5.24

按照 5.2.3 节中save和restore的实现，将push_marker_to_stack和revert_stack_to_marker实现为寄存器机器指令。添加push_marker和pop_marker函数来访问堆栈，与 5.2.1 节中push和pop的实现相呼应。请注意，您不需要实际将标记插入堆栈。相反，您可以向堆栈模型添加一个本地状态变量，以跟踪每次push_marker_to_stack之前的save的位置。如果选择将标记放在堆栈上，请参考练习 5.23 中的提示。

5.4.3 块、赋值和声明

块

块的主体是在当前环境的基础上进行求值的，该环境通过将所有本地名称绑定到值"unassigned"的帧进行扩展。我们暂时利用val寄存器来保存块中声明的所有变量的列表，该列表是通过第 4.1.1 节中的scan_out_declarations获得的。假定scan_out_declarations和list_of_unassigned函数作为机器操作可用。

"ev_block",
  assign("comp", list(op("block_body"), reg("comp"))),
  assign("val", list(op("scan_out_declarations"), reg("comp"))),

save("comp"), // so we can use it to temporarily hold unassigned values
  assign("comp", list(op("list_of_unassigned"), reg("val"))),
  assign("env", list(op("extend_environment"),
                     reg("val"), reg("comp"), reg("env"))),
  restore("comp"), // the block body
  go_to(label("eval_dispatch")),

赋值和声明

赋值由ev_assignment处理，通过eval_dispatch到达，其中包含在comp中的赋值表达式。ev_assignment中的代码首先求值表达式的值部分，然后将新值安装到环境中。假定assign_symbol_value函数作为机器操作可用。

"ev_assignment",
  assign("unev", list(op("assignment_symbol"), reg("comp"))),
  save("unev"), // save variable for later
  assign("comp", list(op("assignment_value_expression"), reg("comp"))),
  save("env"),
  save("continue"),
  assign("continue", label("ev_assignment_install")),
  go_to(label("eval_dispatch")), // evaluate assignment value
"ev_assignment_install",
  restore("continue"),
  restore("env"),
  restore("unev"),
  perform(list(op("assign_symbol_value"),
               reg("unev"), reg("val"), reg("env"))),
  go_to(reg("continue")),

变量和常量的声明都是以类似的方式处理的。请注意，赋值的值是被赋的值，声明的值是undefined。这是通过在继续之前将val设置为undefined来处理的。与元循环求值器一样，我们将函数声明转换为一个值表达式为 lambda 表达式的常量声明。这发生在ev_function_declaration，它在comp中进行转换并且继续到ev_declaration。

"ev_function_declaration",
  assign("comp",
         list(op("function_decl_to_constant_decl"), reg("comp"))),
"ev_declaration",
  assign("unev", list(op("declaration_symbol"), reg("comp"))),
  save("unev"), // save declared name
  assign("comp",
         list(op("declaration_value_expression"), reg("comp"))),
  save("env"),
  save("continue"),
  assign("continue", label("ev_declaration_assign")),
  go_to(label("eval_dispatch")), // evaluate declaration value
"ev_declaration_assign",
  restore("continue"),
  restore("env"),
  restore("unev"),
  perform(list(op("assign_symbol_value"),
               reg("unev"), reg("val"), reg("env"))),
  assign("val", constant(undefined)),
  go_to(reg("continue")),

练习 5.25

扩展求值器以处理while循环，将其转换为while_loop函数的应用，如练习 4.7 所示。您可以将while_loop函数的声明粘贴到用户程序的前面。您可以通过假设语法转换器while_to_application作为机器操作来“作弊”。参考练习 4.7，讨论如果允许在while循环中使用return、break和continue语句，这种方法是否有效。如果不行，您如何修改显式控制求值器以运行包含这些语句的while循环程序？

练习 5.26

修改求值器，使其使用基于第 4.2 节的惰性求值的正常顺序求值。

5.4.4 运行求值器

随着显式控制求值者的实施，我们完成了从第 1 章开始的一个发展，其中我们已经探索了逐渐更精确的求值过程模型。我们从相对不正式的替换模型开始，然后在第 3 章将其扩展为环境模型，这使我们能够处理状态和变化。在第 4 章的元循环求值者中，我们使用 JavaScript 本身作为一种语言，以使在求值组件期间构建的环境结构更加明确。现在，通过寄存器机器，我们仔细研究了求值者的存储管理、参数传递和控制机制。在每个新的描述级别上，我们都不得不提出问题并解决在以前不太精确的求值处理中不明显的模糊问题。要理解显式控制求值者的行为，我们可以模拟它并监视其性能。

我们将在我们的求值机器中安装一个驱动循环。这起到了第 4.1.4 节中driver_loop函数的作用。求值者将重复打印提示，读取程序，通过转到eval_dispatch来求值程序，并打印结果。如果在提示处没有输入任何内容，我们将跳转到标签evaluator_done，这是控制器中的最后一个入口点。以下说明构成了显式控制求值器的控制器序列的开头：³²

"read_evaluate_print_loop",
  perform(list(op("initialize_stack"))),
  assign("comp", list(op("user_read"),
                      constant("EC-evaluate input:"))),
  assign("comp", list(op("parse"), reg("comp"))),
  test(list(op("is_null"), reg("comp"))),
  branch(label("evaluator_done")),
  assign("env", list(op("get_current_environment"))),
  assign("val", list(op("scan_out_declarations"), reg("comp"))),
  save("comp"),    // so we can use it to temporarily hold unassigned values
  assign("comp", list(op("list_of_unassigned"), reg("val"))),
  assign("env", list(op("extend_environment"),
                     reg("val"), reg("comp"), reg("env"))),
  perform(list(op("set_current_environment"), reg("env"))),
  restore("comp"), // the program
  assign("continue", label("print_result")),
  go_to(label("eval_dispatch")),
"print_result",
  perform(list(op("user_print"),
               constant("EC-evaluate value:"), reg("val"))),
  go_to(label("read_evaluate_print_loop")),

我们将当前环境（最初是全局环境）存储在变量current_environment中，并在每次循环时更新它以记住过去的声明。操作get_current_environment和set_current_ environment只是获取和设置这个变量。

let current_environment = the_global_environment;
function get_current_environment() {
    return current_environment;
}
function set_current_environment(env) {
    current_environment = env;
}

当我们在函数中遇到错误（例如在apply_dispatch处指示的“未知函数类型”错误）时，我们会打印错误消息并返回到驱动循环。³³

"unknown_component_type",
  assign("val", constant("unknown syntax")),
  go_to(label("signal_error")),

"unknown_function_type",
  restore("continue"), // clean up stack (from apply_dispatch)
  assign("val", constant("unknown function type")),
  go_to(label("signal_error")),

"signal_error",
  perform(list(op("user_print"),
               constant("EC-evaluator error:"), reg("val"))),
  go_to(label("read_evaluate_print_loop")),

为了模拟的目的，我们在每次通过驱动循环时初始化堆栈，因为在求值中断后（例如未声明的名称）可能不为空。³⁴

如果我们将在第 5.4.1–5.4.4 节中呈现的所有代码片段组合起来，我们可以创建一个求值者机器模型，可以使用第 5.2 节的寄存器机器模拟器运行。

const eceval = make_machine(list("comp", "env", "val", "fun",
                                 "argl", "continue", "unev"),
                            eceval_operations,
                            list("read_evaluate_print_loop",
                                 〈entire machine controller as given above〉
                                 "evaluator_done"));

我们必须定义 JavaScript 函数来模拟求值者作为原语使用的操作。这些是我们在第 4.1 节中用于元循环求值者的相同函数，以及在第 5.4 节中的脚注中定义的少数额外函数。

const eceval_operations = list(list("is_literal", is_literal),
                               〈complete list of operations for eceval machine〉);

最后，我们可以初始化全局环境并运行求值者：

const the_global_environment = setup_environment();
start(eceval);

EC-求值输入：

function append(x, y) {
    return is_null(x)
           ? y
           : pair(head(x), append(tail(x), y));
}

EC-求值值：

undefined

EC-求值输入：

append(list("a", "b", "c"), list("d", "e", "f"));

EC-求值值：

["a", ["b", ["c", ["d", ["e", ["f", null]]]]]]

当然，以这种方式求值程序将比直接在 JavaScript 中输入它们要花费更长的时间，因为涉及多个级别的模拟。我们的程序由显式控制求值者机器求值，该机器由 JavaScript 程序模拟，JavaScript 解释器本身也在求值。

监控求值者的性能

模拟可以是指导求值者实施的强大工具。模拟不仅使探索寄存器机器设计的变化变得容易，还可以监视模拟求值者的性能。例如，性能中的一个重要因素是求值者如何有效地使用堆栈。我们可以通过使用收集堆栈使用统计信息的模拟器版本（第 5.2.4 节）定义求值者寄存器机器，并在求值者的print_result入口点添加指令来打印统计信息，观察求值各种程序所需的堆栈操作数量：

"print_result",
  perform(list(op("print_stack_statistics"))), // added instruction
  // rest is same as before
  perform(list(op("user_print"),
               constant("EC-evaluate value:"), reg("val"))),
  go_to(label("read_evaluate_print_loop")),

现在与求值者的交互看起来像这样：

EC-求值输入：

function factorial (n) {
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}

总推送= 4

最大深度= 3

EC-求值值：

undefined

EC-求值输入：

factorial(5);

总推送次数 = 151

最大深度 = 28

EC-求值值：

120

请注意，求值器的驱动循环在每次交互开始时重新初始化堆栈，因此打印的统计数据将仅涉及用于求值上一个程序的堆栈操作。

练习 5.27

使用监控堆栈来探索求值器的尾递归属性（第 5.4.2 节）。启动求值器并定义迭代factorial函数，该函数来自第 1.2.1 节：

function factorial(n) {
    function iter(product, counter) {
    return counter > n
           ? product
           : iter(counter * product,
                  counter + 1);
    }
    return iter(1, 1);
}

运行该函数，使用一些小的n值。记录计算n!所需的最大堆栈深度和推送次数。

a. 您会发现求值n!所需的最大深度与n无关。那个深度是多少？
b. 根据您的数据，确定用于求值n!的总推送操作次数的n的公式，其中n >= 1。请注意，使用的操作次数是n的线性函数，因此由两个常数确定。

练习 5.28

与练习 5.27 进行比较，探索以下函数的行为，用于递归计算阶乘：

function factorial(n) {
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}

通过使用监控堆栈运行此函数，确定作为n的函数的堆栈的最大深度和用于求值n!的总推送次数。（同样，这些函数将是线性的。）通过使用适当的n表达式填写以下表格来总结您的实验：

	最大深度	推送次数
递归阶乘
迭代阶乘

最大深度是求值器在执行计算时使用的空间量的度量，推送次数与所需时间相关。

练习 5.29

修改求值器的定义，通过更改ev_return，如第 5.4.2 节所述，使求值器不再是尾递归。重新运行练习 5.27 和 5.28 中的实验，以证明factorial函数的两个版本现在都需要随着输入增长而线性增长的空间。

练习 5.30

监视树递归 Fibonacci 计算中的堆栈操作：

function fib(n) {
    return n < 2 ? n : fib(n - 1) + fib(n - 2);
}

a. 给出一个关于计算Fib(n)所需的堆栈的最大深度的n的公式，其中n ≥ 2。提示：在第 1.2.2 节中，我们认为该过程使用的空间随n呈线性增长。
b. 给出一个公式，用于计算Fib(n)的总推送次数，其中n ≥ 2。您应该发现推送次数（与使用的时间相关）随着n呈指数增长。提示：让S(n)表示计算Fib(n)时使用的推送次数。您应该能够证明存在一个公式，用S(n – 1)、S(n – 2)和一些固定的“开销”常数k来表示S(n)。给出公式，并说明k是多少。然后证明S(n)可以表示为aFib(n + 1) + b，并给出a和b的值。

练习 5.31

我们的求值器目前只捕获并信号两种错误——未知组件类型和未知函数类型。其他错误将使我们退出求值器读取-求值-打印循环。当我们使用寄存器机模拟器运行求值器时，这些错误会被底层 JavaScript 系统捕获。这类似于当用户程序出错时计算机崩溃。³⁵制作一个真正的错误系统是一个大项目，但值得努力去理解这里涉及的内容。

a. 在求值过程中发生的错误，例如尝试访问未绑定的名称，可以通过更改查找操作来捕获，使其返回一个不同的条件代码，这个代码不可能是任何用户名称的可能值。求值器可以测试这个条件代码，然后执行必要的操作转到signal_error。找到求值器中需要进行这种更改的所有地方并修复它们。这是很多工作。
b. 处理错误的问题更糟糕，这些错误是通过应用原始函数来发出的，比如尝试除以零或尝试提取字符串的head。在专业编写的高质量系统中，每个原始应用都会作为原始的一部分进行安全检查。例如，对head的每次调用都可以首先检查参数是否是一对。如果参数不是一对，应用将返回一个特殊的条件代码给求值器，然后报告失败。我们可以通过使每个原始函数检查适用性并在失败时返回适当的特殊条件代码来安排在我们的寄存器机器模拟器中。然后，求值器中的primitive_apply代码可以检查条件代码，并在必要时转到signal_error。构建这个结构并使其工作。这是一个重大项目。

5.5 编译

第 5.4 节的显式控制求值器是一个寄存器机器，其控制器解释 JavaScript 程序。在本节中，我们将看到如何在控制器不是 JavaScript 解释器的寄存器机器上运行 JavaScript 程序。

显式控制求值器机器是通用的——它可以执行任何可以用 JavaScript 描述的计算过程。求值器的控制器编排其数据路径的使用，以执行所需的计算。因此，求值器的数据路径是通用的：它们足以执行我们想要的任何计算，只要有适当的控制器。³⁶

商用通用计算机是围绕一组寄存器和操作组织的寄存器机器，构成了一组高效和方便的通用数据路径。通用机器的控制器是一个解释器，用于解释我们一直在使用的寄存器机器语言。这种语言被称为机器的本地语言，或者简称为机器语言。用机器语言编写的程序是使用机器的数据路径的指令序列。例如，显式控制求值器的指令序列可以被视为通用计算机的机器语言程序，而不是专用解释器机器的控制器。

在高级语言和寄存器机器语言之间弥合差距的常见策略有两种。显式控制求值器说明了解释的策略。用机器的本地语言编写的解释器配置机器以执行用于求值的语言（称为源语言）编写的程序。源语言的原始函数被实现为用给定机器的本地语言编写的子例程库。要解释的程序（称为源程序）表示为数据结构。解释器遍历这个数据结构，分析源程序。在这样做的同时，它通过从库中调用适当的原始子例程来模拟源程序的预期行为。

在这一部分，我们探讨了编译的替代策略。给定源语言和机器的编译器将源程序翻译成等效的程序（称为目标程序），用机器的本地语言编写。我们在这一部分实现的编译器将 JavaScript 编写的程序翻译成要使用显式控制求值器机器数据路径执行的指令序列。³⁷

与解释相比，编译可以大大提高程序执行的效率，我们将在编译器概述中解释。另一方面，解释器提供了一个更强大的交互式程序开发和调试环境，因为正在执行的源程序可以在运行时进行检查和修改。此外，由于整个原语库都存在，因此在调试期间可以构建新程序并将其添加到系统中。

考虑到编译和解释的互补优势，现代程序开发环境采用混合策略。这些系统通常组织得很好，以便解释函数和编译函数可以相互调用。这使程序员可以编译那些假定已经调试的程序部分，从而获得编译的效率优势，同时保留解释执行模式，用于程序中处于交互式开发和调试状态的部分。

编译器概述

我们的编译器在结构和功能上都与我们的解释器非常相似。因此，编译器用于分析组件的机制将类似于解释器使用的机制。此外，为了方便地接口编译和解释的代码，我们将设计编译器生成遵循与解释器相同的寄存器使用约定的代码：环境将保留在env寄存器中，参数列表将累积在argl中，要应用的函数将在fun中，函数将在val中返回它们的答案，并且函数应返回的位置将保留在continue中。通常，编译器将源程序转换为执行与解释器在求值相同源程序时执行的基本相同的寄存器操作的目标程序。

这种描述提出了实现一个基本编译器的策略：我们以与解释器相同的方式遍历组件。当我们遇到解释器在求值组件时执行的寄存器指令时，我们不执行该指令，而是将其累积到一个序列中。生成的指令序列将成为目标代码。观察编译相对于解释的效率优势。每次解释器求值一个组件时，例如f(96, 22)，它都会执行对组件进行分类的工作（发现这是一个函数应用），并测试参数表达式列表的结束（发现有两个参数表达式）。使用编译器，组件只在编译时分析一次。编译器生成的目标代码仅包含求值函数表达式和两个参数表达式、组装参数列表以及将函数（在fun中）应用于参数（在argl中）的指令。

这与我们在第 4.1.7 节的分析求值器中实现的优化相同。但是在编译代码中还有进一步提高效率的机会。解释器运行时，遵循一个必须适用于语言中的任何组件的过程。相比之下，编译代码的一个特定段意味着执行某个特定的组件。这可能会有很大的不同，例如在使用堆栈保存寄存器时。当解释器求值一个组件时，必须为任何可能发生的情况做好准备。在求值子组件之前，解释器保存所有以后可能需要的寄存器，因为子组件可能需要任意求值。另一方面，编译器可以利用它正在处理的特定组件的结构来生成避免不必要的堆栈操作的代码。

以应用程序f(96, 22)为例。在解释器求值应用程序的函数表达式之前，它通过保存包含参数表达式和环境的寄存器来为此求值做好准备，这些值稍后将被需要。然后解释器求值函数表达式以获取val中的结果，恢复保存的寄存器，最后将结果从val移动到fun。然而，在我们处理的特定表达式中，函数表达式是名称f，其求值是通过不改变任何寄存器的机器操作lookup_symbol_value完成的。我们在本节中实现的编译器将利用这一事实，并生成使用指令求值函数表达式的代码。

assign("fun",
       list(op("lookup_symbol_value"), constant("f"), reg("env")))

lookup_symbol_value的参数在编译时从解析器对f(96, 22)的表示中提取。这段代码不仅避免了不必要的保存和恢复，还直接将查找的值分配给fun，而解释器将在val中获取结果，然后将其移动到fun。

编译器还可以优化对环境的访问。在分析了代码之后，编译器可以知道特定名称的值将位于哪个帧中，并直接访问该帧，而不是执行lookup_symbol_value搜索。我们将在第 5.5.6 节讨论如何实现这样的词法寻址。然而，在那之前，我们将专注于上述寄存器和堆栈优化的类型。编译器还可以执行许多其他优化，例如将原始操作“内联”编码，而不是使用通用的apply机制（参见练习 5.41）；但我们在这里不会强调这些。本节的主要目标是在一个简化（但仍然有趣）的上下文中说明编译过程。

5.5.1 编译器的结构

在第 4.1.7 节中，我们修改了我们原始的元循环解释器，将分析与执行分开。我们分析每个组件以产生一个以环境为参数并执行所需操作的执行函数。在我们的编译器中，我们将基本上进行相同的分析。但是，我们不会生成执行函数，而是生成要由我们的寄存器机器运行的指令序列。

compile函数是编译器中的顶层调度。它对应于第 4.1.1 节的evaluate函数，第 4.1.7 节的analyze函数，以及第 5.4.1 节中显式控制求值器的eval_dispatch入口。编译器和解释器一样，使用了第 4.1.2 节中定义的组件语法函数。compile函数对要编译的组件的句法类型进行案例分析。对于每种类型的组件，它都会分派到一个专门的代码生成器。

function compile(component, target, linkage) {
    return is_literal(component)
           ? compile_literal(component, target, linkage)
           : is_name(component)
           ? compile_name(component, target, linkage)
           : is_application(component)
           ? compile_application(component, target, linkage)
           : is_operator_combination(component)
           ? compile(operator_combination_to_application(component),
                     target, linkage)
           : is_conditional(component)
           ? compile_conditional(component, target, linkage)
           : is_lambda_expression(component)
           ? compile_lambda_expression(component, target, linkage)
           : is_sequence(component)
           ? compile_sequence(sequence_statements(component),
                              target, linkage)
           : is_block(component)
           ? compile_block(component, target, linkage)
           : is_return_statement(component)
           ? compile_return_statement(component, target, linkage)
           : is_function_declaration(component)
           ? compile(function_decl_to_constant_decl(component),
                     target, linkage)
           : is_declaration(component)
           ? compile_declaration(component, target, linkage)
           : is_assignment(component)
           ? compile_assignment(component, target, linkage)
           : error(component, "unknown component type – compile");
}

目标和链接

函数compile和它调用的代码生成器除了要编译的组件外，还需要两个参数。一个是目标，它指定编译后的代码将返回组件的值的寄存器。还有一个链接描述符，它描述了组件编译后的代码在执行完毕后应该如何进行。链接描述符可以要求代码执行以下三种操作之一：

继续到下一个指令序列（这是由链接描述符"next"指定的），
跳转到continue寄存器的当前值，作为从函数调用返回的一部分（这由链接描述符"return"指定），或
跳转到命名的入口点（这是通过使用指定的标签作为链接描述符来指定的）。

例如，使用val寄存器作为目标和链接为"next"编译字面量5应该产生指令

assign("val", constant(5))

使用链接"return"编译相同的表达式应该产生指令

assign("val", constant(5)),
go_to(reg("continue"))

在第一种情况下，执行将继续进行下一个指令序列。在第二种情况下，我们将跳转到continue寄存器中存储的任何入口点。在这两种情况下，表达式的值将被放入目标val寄存器中。我们的编译器在编译返回语句的返回表达式时使用"return"链接。就像在显式控制求值器中一样，从函数调用返回发生在三个步骤中：

1. 将堆栈恢复到标记并恢复continue（它保存了在函数调用开始时设置的继续）
2. 计算返回值并将其放入val
3. 跳转到continue中的入口点

返回语句的编译显式生成了用于恢复堆栈和恢复continue的代码。返回表达式使用目标val和链接"return"进行编译，以便计算返回值的生成代码将返回值放入val，并以跳转到continue结束。

指令序列和堆栈使用

每个代码生成器返回一个包含它为组件生成的目标代码的指令序列。复合组件的代码生成是通过组合子组件的简单代码生成器的输出来完成的，就像复合组件的求值是通过求值子组件来完成的。

组合指令序列的最简单方法是一个名为append_instruction_sequences的函数，它接受两个要依次执行的指令序列作为参数。它将它们附加在一起并返回组合的序列。也就是说，如果seq[1]和seq[2]是指令序列，那么求值

append_instruction_sequences(seq[1], seq[2])

产生序列

seq[1]
seq[2]

每当需要保存寄存器时，编译器的代码生成器使用preserving，这是一种更微妙的组合指令序列的方法。函数preserving接受三个参数：一组寄存器和两个要依次执行的指令序列。它以这样的方式附加序列，以便在第一个序列的执行过程中保留集合中每个寄存器的内容，如果这对于执行第二个序列是必要的。也就是说，如果第一个序列修改了寄存器并且第二个序列实际上需要寄存器的原始内容，那么preserving在附加序列之前将寄存器的save和restore包装在第一个序列周围。否则，preserving简单地返回附加的指令序列。因此，例如，

preserving(list(reg[1], reg[2]), seq[1], seq[2])

根据seq[1]和seq[2]如何使用reg[1]和reg[2]，产生以下四种指令序列之一：

 seq[1]  save(reg[1]),  save(reg[2]),  save(reg[2]), 

 seq[2]  seq[1]  seq[1]  save(reg[1]), 

   restore(reg[1]),  restore(reg[2]),  seq[1] 

   seq[2]  seq[2]  restore(reg[1]), 

       restore(reg[2]), 

       seq[2]

通过使用preserving来组合指令序列，编译器避免了不必要的堆栈操作。这也隔离了是否在preserving函数内生成save和restore指令的细节，将它们与编写每个单独代码生成器时出现的问题分开。实际上，除了调用函数的代码保存continue和返回函数的代码恢复它之外，代码生成器并没有显式产生save或restore指令：这些对应的save和restore指令是由不同的compile调用显式生成的，而不是由preserving匹配生成的（我们将在 5.5.3 节中看到）。

原则上，我们可以简单地将指令序列表示为指令列表。然后，append_instruction_sequences函数可以通过执行普通的列表append来组合指令序列。然而，preserving将是一个复杂的操作，因为它必须分析每个指令序列以确定序列如何使用其寄存器。preserving也将是低效的，因为它必须分析其每个指令序列参数，即使这些序列本身可能已经通过对preserving的调用构造，这样它们的部分已经被分析。为了避免这种重复的分析，我们将与每个指令序列关联一些关于其寄存器使用的信息。当我们构造基本指令序列时，我们将明确提供这些信息，并且组合指令序列的函数将从与要组合的序列相关联的信息中推导出组合序列的寄存器使用信息。

指令序列将包含三个信息：

必须在序列中的指令执行之前初始化的寄存器集合（这些寄存器被称为序列需要的寄存器），
指令序列中被指令修改的寄存器集合，
序列中的实际指令。

我们将把指令序列表示为其三个部分的列表。因此，指令序列的构造函数是

function make_instruction_sequence(needs, modifies, instructions) {
    return list(needs, modifies, instructions);
}

例如，查找当前环境中符号x的值，将结果赋给val，然后继续执行的两条指令序列需要初始化寄存器env和continue，并修改寄存器val。因此，这个序列将被构造为

make_instruction_sequence
    list("env", "continue"), list("val"), list(assign("val",
                list(op("lookup_symbol_value"), constant("x"),
                     reg("env"))),
         go_to(reg("continue"))));

组合指令序列的函数在 5.5.4 节中显示。

练习 5.32

在求值函数应用时，显式控制求值器总是在函数表达式的求值周围保存和恢复env寄存器，在每个参数表达式的求值周围保存和恢复env（最后一个除外），在每个参数表达式的求值周围保存和恢复argl，并在参数表达式序列的求值周围保存和恢复fun。对于以下每个应用，说出这些save和restore操作中哪些是多余的，因此可以通过编译器的preserving机制消除：

f("x", "y")
f()("x", "y")
f(g("x"), y)
f(g("x"), "y")

练习 5.33

使用preserving机制，编译器将避免在应用的函数表达式的求值周围保存和恢复env，在函数表达式是名称的情况下。我们也可以将这样的优化构建到求值器中。事实上，5.4 节的显式控制求值器已经通过将没有参数的应用视为特殊情况来执行类似的优化。

a.将显式控制求值器扩展为识别函数表达式为名称的组件的一个单独类，并利用这一事实来求值这些组件。
b. Alyssa P. Hacker 建议通过扩展求值器以识别越来越多的特殊情况，我们可以合并所有编译器的优化，这将消除编译的优势。你对这个想法有什么看法？

5.5.2 编译组件

在本节和下一节中，我们实现了compile函数分派到的代码生成器。

编译链接代码

一般来说，每个代码生成器的输出都将以由函数compile_linkage生成的指令结尾，这些指令实现了所需的链接。如果链接是"return"，那么我们必须生成指令go_to(reg("continue"))。这需要continue寄存器，不修改任何寄存器。如果链接是"next"，那么我们不需要包括任何额外的指令。否则，链接是一个标签，我们会生成一个go_to到该标签，这是一个不需要或修改任何寄存器的指令。

function compile_linkage(linkage) {
    return linkage === "return"
           ? make_instruction_sequence(list("continue"), null,
                                       list(go_to(reg("continue"))))
           : linkage === "next"
           ? make_instruction_sequence(null, null, null)
           : make_instruction_sequence(null, null,
                                       list(go_to(label(linkage))));
}

链接代码通过保留 continue寄存器附加到指令序列，因为"return"链接将需要continue寄存器：如果给定的指令序列修改continue并且链接代码需要它，continue将被保存和恢复。

function end_with_linkage(linkage, instruction_sequence) {
    return preserving(list("continue"),
                      instruction_sequence,
                      compile_linkage(linkage));
}

编译简单组件

字面表达式和名称的代码生成器构造指令序列，将所需的值分配给目标寄存器，然后按链接描述符指定的方式继续。

字面值在编译时从被编译的组件中提取，并放入assign指令的常量部分。对于名称，当运行编译程序时，会生成一个指令来使用lookup_symbol_value操作，以查找当前环境中与符号关联的值。与字面值一样，符号在编译时从被编译的组件中提取。因此，symbol_of_name(component)只在编译程序时执行一次，并且该符号出现为assign指令中的常量。

function compile_literal(component, target, linkage) {
    const literal = literal_value(component);
    return end_with_linkage(linkage,
               make_instruction_sequence(null, list(target),
                   list(assign(target, constant(literal)))));
}
function compile_name(component, target, linkage) {
    const symbol = symbol_of_name(component);
    return end_with_linkage(linkage,
               make_instruction_sequence(list("env"), list(target),
                   list(assign(target,
                               list(op("lookup_symbol_value"),
                                    constant(symbol),
                                    reg("env"))))));
}

这些任务说明修改目标寄存器，查找符号的指令需要env寄存器。

赋值和声明的处理方式与解释器中的处理方式类似。函数compile_assignment_declaration递归生成代码，计算与符号关联的值，并将更新环境中与符号关联的值的两条指令序列附加到其中，并将整个组件的值（赋值的值或声明的undefined）分配给目标寄存器。递归编译的目标为val和链接为"next"，以便代码将其结果放入val并继续在其后附加的代码。附加的代码保留env，因为更新符号-值关联需要环境，并且计算值的代码可能是复杂表达式的编译，可能以任意方式修改寄存器。

function compile_assignment(component, target, linkage) {
    return compile_assignment_declaration(
               assignment_symbol(component),
               assignment_value_expression(component),
               reg("val"),
               target, linkage);
}
function compile_declaration(component, target, linkage) {
    return compile_assignment_declaration(
               declaration_symbol(component),
               declaration_value_expression(component),
               constant(undefined),
               target, linkage);
}
function compile_assignment_declaration(
             symbol, value_expression, final_value,
             target, linkage) {
    const get_value_code = compile(value_expression, "val", "next");
    return end_with_linkage(linkage,
               preserving(list("env"),
                   get_value_code,
                   make_instruction_sequence(list("env", "val"),
                                             list(target),
                        list(perform(list(op("assign_symbol_value"),
                                          constant(symbol),
                                          reg("val"),
                                          reg("env"))),
                             assign(target, final_value)))));
}

附加的两条指令序列需要env和val并修改目标。请注意，尽管我们为此序列保留了env，但我们没有保留val，因为get_value_code旨在将其结果明确放入val以供此序列使用。（实际上，如果我们保留了val，我们将会有一个错误，因为这将导致在运行get_value_code后恢复val的先前内容。）

编译条件

使用给定目标和链接编译的条件代码的形式为

〈compilation of predicate, target val, linkage "next"〉
  test(list(op("is_falsy"), reg("val"))),
  branch(label("false_branch")),
"true_branch",
  〈compilation of consequent with given target and given linkage or* after_cond〉
"false_branch",
  〈compilation of alternative with given target and linkage〉
"after_cond"

为了生成这段代码，我们编译谓词、结果和替代，并将生成的代码与用于测试谓词结果的指令以及用于标记真假分支和条件结束的新生成标签组合起来。在这种代码排列中，如果测试为假，我们必须绕过真分支。唯一的小复杂之处在于如何处理真分支的链接。如果条件的链接是"return"或者一个标签，那么真假分支都将使用相同的链接。如果链接是"next"，那么真分支将以跳过假分支代码到条件结束标签的跳转结束。

function compile_conditional(component, target, linkage) {
    const t_branch = make_label("true_branch");
    const f_branch = make_label("false_branch");
    const after_cond = make_label("after_cond");
    const consequent_linkage =
            linkage === "next" ? after_cond : linkage;
    const p_code = compile(conditional_predicate(component),
                           "val", "next");
    const c_code = compile(conditional_consequent(component),
                           target, consequent_linkage);
    const a_code = compile(conditional_alternative(component),
                           target, linkage);
    return preserving(list("env", "continue"),
             p_code,
             append_instruction_sequences(
               make_instruction_sequence(list("val"), null,
                 list(test(list(op("is_falsy"), reg("val"))),
                      branch(label(f_branch)))),
               append_instruction_sequences(
                 parallel_instruction_sequences(
                   append_instruction_sequences(t_branch, c_code),
                   append_instruction_sequences(f_branch, a_code)),
                 after_cond)));
}

在谓词代码周围保留env寄存器，因为它可能会被true和false分支所需要，continue也被保留，因为它可能会被这些分支中的链接代码所需要。真假分支的代码（它们不是顺序执行的）使用特殊的组合器parallel_instruction_sequences进行附加，该组合器在 5.5.4 节中描述。

编译序列

语句序列的编译与显式控制求值器中它们的求值并行进行，唯一的例外是：如果一个return语句出现在序列的任何位置，我们将其视为最后一条语句。序列的每个语句都会被编译——最后一条语句（或return语句）使用指定为序列的链接，其他语句使用"next"链接（执行序列的其余部分）。单个语句的指令序列被附加在一起，以便保留env（需要用于序列的其余部分）和continue（可能需要用于序列末尾的链接）。

function compile_sequence(seq, target, linkage) {
    return is_empty_sequence(seq)
           ? compile_literal(make_literal(undefined), target, linkage)
           : is_last_statement(seq) ||
                 is_return_statement(first_statement(seq))
           ? compile(first_statement(seq), target, linkage)
           : preserving(list("env", "continue"),
                 compile(first_statement(seq), target, "next"),
                 compile_sequence(rest_statements(seq),
                                  target, linkage));
}

将return语句视为序列中的最后一条语句，避免编译return语句之后永远不会执行的“死代码”。删除is_return_statement检查不会改变对象程序的行为；然而，有许多原因不编译死代码，这超出了本书的范围（安全性、编译时间、对象代码的大小等），许多编译器对死代码会发出警告。

编译块

通过在块的编译体之前添加一个assign指令来编译块。该赋值通过将在块中声明的名称绑定到值"unassigned"的帧扩展了当前环境。这个操作既需要又修改了env寄存器。

function compile_block(stmt, target, linkage) {
    const body = block_body(stmt);
    const locals = scan_out_declarations(body);
    const unassigneds = list_of_unassigned(locals);
    return append_instruction_sequences(
               make_instruction_sequence(list("env"), list("env"),
                   list(assign("env", list(op("extend_environment"),
                                           constant(locals),
                                           constant(unassigneds),
                                           reg("env"))))),
               compile(body, target, linkage));
}

编译 lambda 表达式

Lambda 表达式构造函数。lambda 表达式的对象代码必须具有以下形式

〈construct function object and assign it to target register〉
〈linkage〉

编译 lambda 表达式时，我们还会生成函数体的代码。虽然在函数构造时不会执行函数体，但是将其插入到对象代码中 lambda 表达式的代码之后是很方便的。如果 lambda 表达式的链接是一个标签或者"return"，那么这样做是可以的。但是如果链接是"next"，我们需要通过跳转到函数体之后插入的标签的链接来跳过函数体的代码。因此，对象代码的形式如下

〈construct function object and assign it to target register〉
〈code for given linkage〉 or go_to(label("after_lambda"))
〈compilation of function body〉
"after_lambda"

函数 compile_lambda_expression 生成构造函数对象的代码，然后是函数体的代码。函数对象将在运行时通过将当前环境（声明点的环境）与编译函数体的入口点（新生成的标签）组合来构造。

function compile_lambda_expression(exp, target, linkage) {
    const fun_entry = make_label("entry");
    const after_lambda = make_label("after_lambda");
    const lambda_linkage =
            linkage === "next" ? after_lambda : linkage;
    return append_instruction_sequences(
               tack_on_instruction_sequence(
                   end_with_linkage(lambda_linkage,
                       make_instruction_sequence(list("env"),
                                                 list(target),
                           list(assign(target,
                                    list(op("make_compiled_function"),
                                         label(fun_entry),
                                         reg("env")))))),
                   compile_lambda_body(exp, fun_entry)),
               after_lambda);
}

函数compile_lambda_expression使用特殊的组合器tack_on_ instruction_sequence（来自 5.5.4 节）而不是append_instruction_ sequences来将函数体附加到 lambda 表达式代码中，因为函数体不是将在进入组合序列时执行的指令序列的一部分；相反，它只是在序列中，因为那是一个方便的放置位置。

函数compile_lambda_body构造函数主体的代码。此代码以入口点的标签开头。接下来是指令，这些指令将导致运行时求值环境切换到正确的环境，以求值函数主体——即函数的环境，扩展为包括参数与调用函数时的参数的绑定。之后是函数主体的代码，增强以确保它以返回语句结束。增强的主体使用目标val进行编译，以便其返回值将被放置在val中。传递给此编译的链接描述符是无关紧要的，因为它将被忽略。⁴⁴由于需要链接参数，我们随意选择了"next"。

function compile_lambda_body(exp, fun_entry) {
    const params  = lambda_parameter_symbols(exp);
    return append_instruction_sequences(
        make_instruction_sequence(list("env", "fun", "argl"),
                                  list("env"),
            list(fun_entry,
                 assign("env",
                        list(op("compiled_function_env"),
                             reg("fun"))),
                 assign("env",
                        list(op("extend_environment"),
                             constant(params),
                             reg("argl"),
                             reg("env"))))),
        compile(append_return_undefined(lambda_body(exp)),
                "val", "next"));
}

为了确保所有函数最终都通过执行返回语句结束，compile_ lambda_body在 lambda 主体中附加了一个返回语句，其返回表达式是文字undefined。为此，它使用函数append_return_ undefined，该函数构造了解析器的标记列表表示（来自 4.1.2 节）的序列，其中包括主体和一个return undefined;语句。

function append_return_undefined(body) {
    return list("sequence", list(body,
                                 list("return_statement",
                                      list("literal", undefined))));
}

对 lambda 主体的这种简单转换是确保没有显式返回的函数具有返回值undefined的第三种方法。在元循环求值器中，我们使用了返回值对象，它还在停止序列求值中发挥了作用。在显式控制求值器中，没有显式返回的函数继续到一个入口点，该入口点将undefined存储在val中。参见练习 5.35，了解处理插入返回语句的更加优雅的方法。

练习 5.34

42 脚注指出编译器并未识别所有死代码的实例。编译器要检测所有死代码的实例需要什么？

提示：答案取决于我们如何定义死代码。一个可能的（也有用的）定义是“在序列中跟随返回语句的代码”——但是在if (false) ...的结果分支中的代码呢？或者在练习 4.15 中调用run_forever()之后的代码呢？

练习 5.35

append_return_undefined的当前设计有点粗糙：它总是将return undefined;附加到 lambda 主体，即使在主体的每个执行路径中已经有了返回语句。重写append_return_undefined，使其仅在不包含返回语句的路径末尾插入return undefined;。在下面的函数上测试您的解决方案，用任何表达式替换e[1]和e[2]，用任何（非返回）语句替换s[1]和s[2]。在t中，返回语句应该添加在两个(*)或仅在(**)中。在w和h中，返回语句应该添加在一个(*)中。在m中，不应添加返回语句。

5.5.3 编译应用程序和返回语句

编译过程的本质是编译函数应用程序。使用给定目标和链接的应用程序的代码具有以下形式

〈compilation of function expression, target fun, linkage "next"〉
〈evaluate argument expressions and construct argument list in* argl〉
〈compilation of function call with given target and linkage〉

寄存器env，fun和argl在函数和参数表达式的求值过程中可能需要保存和恢复。请注意，这是编译器中唯一指定目标不是val的地方。

所需的代码由compile_application生成。这将递归编译函数表达式，以生成将要应用的函数放入fun的代码，并编译参数表达式，以生成求值应用的各个参数表达式的代码。参数表达式的指令序列（由construct_arglist组合）与构造argl中的参数列表的代码组合在一起，生成的参数列表代码与函数代码和执行函数调用的代码（由compile_function_call生成）组合在一起。在附加代码序列时，必须在函数表达式的求值周围保留env寄存器（因为求值函数表达式可能会修改env，这将需要用于求值参数表达式），并且在构造参数列表时必须保留fun寄存器（因为求值参数表达式可能会修改fun，这将需要用于实际的函数应用）。continue寄存器在整个过程中也必须保留，因为它在函数调用中需要用于链接。

function compile_application(exp, target, linkage) {
    const fun_code = compile(function_expression(exp), "fun", "next");
    const argument_codes = map(arg => compile(arg, "val", "next"),
                               arg_expressions(exp));
    return preserving(list("env", "continue"),
                      fun_code,
                      preserving(list("fun", "continue"),
                          construct_arglist(argument_codes),
                          compile_function_call(target, linkage)));
}

构建参数列表的代码将求值每个参数表达式为val，然后使用pair将该值与在argl中累积的参数列表组合起来。由于我们按顺序将参数添加到argl的前面，所以我们必须从最后一个参数开始，以第一个结束，这样参数将按顺序出现在生成的列表中。我们不想浪费一条指令来将argl初始化为空列表以准备进行这一系列的求值，因此我们让第一个代码序列构造初始的argl。参数列表构造的一般形式如下：

〈compilation of last argument, targeted to val〉
〈assign("argl", list(op("list"), reg("val"))),
〈compilation of next argument, targeted to val〉
〈assign("argl", list(op("pair"), reg("val"), reg("argl"))),
...
〈compilation of first argument, targeted to val〉
assign("argl", list(op("pair"), reg("val"), reg("argl"))),

在每个参数求值周围必须保留argl寄存器，除了第一个（这样迄今为止累积的参数不会丢失），并且在每个参数求值周围必须保留env（供后续参数求值使用）。

编译这个参数代码有点棘手，因为第一个要求值的参数表达式的特殊处理以及在不同位置需要保留argl和env。construct_arglist函数以求值各个参数表达式的代码作为参数。如果根本没有参数表达式，它只是发出指令

assign(argl, constant(null))

否则，construct_arglist创建代码，用最后一个参数初始化argl，并附加代码来求值其余的参数，并依次将它们添加到argl中。为了从后到前处理参数，我们必须按照compile_application提供的顺序反转参数代码序列的列表。

function construct_arglist(arg_codes) {
    if (is_null(arg_codes)) {
        return make_instruction_sequence(null, list("argl"),
                   list(assign("argl", constant(null))));
    } else {
        const rev_arg_codes = reverse(arg_codes);
        const code_to_get_last_arg =
            append_instruction_sequences(
                head(rev_arg_codes),
                make_instruction_sequence(list("val"), list("argl"),
                    list(assign("argl",
                                list(op("list"), reg("val"))))));
        return is_null(tail(rev_arg_codes))
               ? code_to_get_last_arg
               : preserving(list("env"),
                     code_to_get_last_arg,
                     code_to_get_rest_args(tail(rev_arg_codes)));
    }
}
function code_to_get_rest_args(arg_codes) {
    const code_for_next_arg =
        preserving(list("argl"),
            head(arg_codes),
            make_instruction_sequence(list("val", "argl"), list("argl"),
                list(assign("argl", list(op("pair"),
                                         reg("val"), reg("argl"))))));
    return is_null(tail(arg_codes))
           ? code_for_next_arg
           : preserving(list("env"),
                        code_for_next_arg,
                        code_to_get_rest_args(tail(arg_codes)));
}

应用函数

在求值函数应用的元素之后，编译的代码必须将fun中的函数应用于argl中的参数。该代码执行的基本上与第 4.1.1 节中的元循环求值器中的apply函数或第 5.4.2 节中的显式控制求值器中的apply_dispatch入口相同的分发。它检查要应用的函数是原始函数还是编译函数。对于原始函数，它使用apply_primitive_function；我们很快将看到它如何处理编译函数。函数应用代码的形式如下：

  test(list(op("primitive_function"), reg("fun"))),
  branch(label("primitive_branch")),
"compiled_branch",
 〈code to apply compiled function with given target and appropriate linkage〉
"primitive_branch",
  assign(target,
         list(op("apply_primitive_function"), reg("fun"), reg("argl"))),
 〈linkage〉
"after_call"

注意，编译的分支必须跳过原始分支。因此，如果原始函数调用的链接是"next"，则复合分支必须使用跳转到原始分支之后插入的标签的链接。（这类似于compile_conditional中真分支使用的链接。）

function compile_function_call(target, linkage) {
    const primitive_branch = make_label("primitive_branch");
    const compiled_branch = make_label("compiled_branch");
    const after_call = make_label("after_call");
    const compiled_linkage = linkage === "next" ? after_call : linkage;
    return append_instruction_sequences(
        make_instruction_sequence(list("fun"), null,
            list(test(list(op("is_primitive_function"), reg("fun"))),
                 branch(label(primitive_branch)))),
            append_instruction_sequences(
                parallel_instruction_sequences(
                    append_instruction_sequences(
                        compiled_branch,
                        compile_fun_appl(target, compiled_linkage)),
                    append_instruction_sequences(
                        primitive_branch,
                        end_with_linkage(linkage,
                            make_instruction_sequence(list("fun", "argl"),
                                                      list(target),
                                list(assign(
                                       target,
                                       list(op("apply_primitive_function"),
                                            reg("fun"), reg("argl")))))))),
            after_call));
}

原始分支和复合分支（例如compile_ conditional中的真分支和假分支）使用parallel_instruction_sequences附加，而不是普通的append_instruction_sequences，因为它们不会按顺序执行。

应用编译函数

函数应用和返回的处理是编译器最微妙的部分。编译函数（由compile_lambda_expression构造）具有一个入口点，这是一个标签，指定函数代码的起始位置。在这个入口点的代码中，计算val中的结果，并通过执行编译返回语句的指令结束。

编译函数应用程序的代码与显式控制求值器（第 5.4.2 节）使用堆栈的方式相同：在跳转到编译函数的入口点之前，它将函数调用的继续保存到堆栈中，然后是一个标记，允许将堆栈恢复到调用之前的状态，并将继续保持在顶部。

  // set up for return from function
  save("continue"),
  push_marker_to_stack(),
  // jump to the function's entry point
  assign("val", list(op("compiled_function_entry"), reg("fun"))),
  go_to(reg("val")),

编译返回语句（使用compile_return_statement）会生成相应的代码来恢复堆栈并恢复并跳转到continue。

  revert_stack_to_marker(),
  restore("continue"),
  〈evaluate the return expression and store the result in val〉
  go_to(reg("continue")), // "return"-linkage code

除非函数进入无限循环，否则它将通过执行上述返回代码结束，该代码是由程序中的return语句或由compile_lambda_body插入的返回undefined生成的。

具有给定目标和链接的编译函数应用程序的直接代码将设置continue，使函数返回到本地标签而不是最终链接，以将函数值从val复制到目标寄存器（如果需要）。如果链接是标签，它将如下所示：

  assign("continue", label("fun_return")), // where function should return to
  save("continue"),       // will be restored by the function
  push_marker_to_stack(), // allows the function to revert stack to find fun_return
  assign("val", list(op("compiled_function_entry"), reg("fun"))),
  go_to(reg("val")),    // eventually reverts stack, restores and jumps to continue
"fun_return",             // the function returns to here
  assign(target, reg("val")), // included if target is not val
  go_to(label(linkage)),   // linkage code

或者像这样-在开始时保存调用者的继续，以便在结束时恢复并转到它-如果链接是return（也就是说，如果应用程序在return语句中并且其值是要返回的结果）：

  save("continue"), // save the caller's continuation
  assign("continue", label("fun_return")), // where function should return to
  save("continue"), // will be restored by the function
push_marker_to_stack(), // allows the function to revert stack to find fun_return
  assign("val", list(op("compiled_function_entry"), reg("fun"))),
  go_to(reg("val")), // eventually reverts stack, restores and jumps to continue
"fun_return", // the function returns to here
  assign(target, reg("val")), // included if target is not val
  restore("continue"), // restore the caller's continuation
  go_to(reg("continue")), // linkage code

这段代码设置continue，使函数返回到标签fun_return并跳转到函数的入口点。fun_return处的代码将函数的结果从val传输到目标寄存器（如果需要），然后跳转到链接指定的位置。（链接始终是return或标签，因为compile_function_call会将复合函数分支的next链接替换为after_call标签。）在跳转到函数的入口点之前，我们保存continue并执行push_marker_to_stack()以使函数能够返回到程序中预期的位置并具有预期的堆栈。revert_stack_to_marker()和restore("continue")指令由compile_return_statement为函数体中的每个return语句生成。

实际上，如果目标不是val，那么上面的代码就是我们的编译器将生成的代码。然而，通常情况下，目标是val（编译器指定不同寄存器的唯一时间是将函数表达式的求值目标指向fun），因此函数结果直接放入目标寄存器，无需跳转到复制它的特殊位置。相反，我们通过设置continue来简化代码，使被调用函数直接“返回”到调用者链接指定的位置：

〈set up continue for linkage and push the marker〉
assign("val", list(op("compiled_function_entry"), reg("fun"))),
go_to(reg("val")),

如果链接是一个标签，我们将设置continue，使函数继续在该标签处。（也就是说，被调用函数结束时的go_to(reg("continue"))相当于上面的fun_return处的go_to(label(linkage))。）

assign("continue", label(linkage)),
save("continue"),
push_marker_to_stack(),
assign("val", list(op("compiled_function_entry"), reg("fun"))),
go_to(reg("val")),

如果链接是return，我们不需要分配continue：它已经保存了所需的位置。（也就是说，被调用函数结束时的go_to(reg("continue"))会直接到达fun_return处的go_to(reg("continue"))所指定的位置。）

save("continue"),
push_marker_to_stack(),
assign("val", list(op("compiled_function_entry"), reg("fun"))),
go_to(reg("val")),

使用这种实现的return链接，编译器生成尾递归代码。在返回语句中的函数调用，其值是要返回的结果，进行直接转移，而不在堆栈上保存不必要的信息。

假设我们处理了链接为return且目标为val的函数调用的情况，方式与非val目标的情况相同。这将破坏尾递归。我们的系统仍然会为任何函数调用返回相同的值。但每次调用函数时，我们都会保存continue并在调用后返回以撤消（无用的）保存。这些额外的保存会在函数调用的嵌套中累积。⁴⁸

函数compile_fun_appl通过考虑四种情况生成上述函数应用代码，具体取决于调用的目标是否为val以及链接是否为return。请注意，指令序列被声明为修改所有寄存器，因为执行函数体可能以任意方式更改寄存器。⁴⁹

function compile_fun_appl(target, linkage) {
    const fun_return = make_label("fun_return");
    return target === "val" && linkage !== "return"
           ? make_instruction_sequence(list("fun"), all_regs,
                 list(assign("continue", label(linkage)),
                      save("continue"),
                      push_marker_to_stack(),
                      assign("val", list(op("compiled_function_entry"),
                                         reg("fun"))),
                      go_to(reg("val"))))
           : target !== "val" && linkage !== "return"
           ? make_instruction_sequence(list("fun"), all_regs,
                 list(assign("continue", label(fun_return)),
                      save("continue"),
                      push_marker_to_stack(),
                      assign("val", list(op("compiled_function_entry"),
                                         reg("fun"))),
                      go_to(reg("val")),
                      fun_return,
                      assign(target, reg("val")),
                      go_to(label(linkage))))
           : target === "val" && linkage === "return"
           ? make_instruction_sequence(list("fun", "continue"),
                                       all_regs,
                 list(save("continue"),
                      push_marker_to_stack(),
                      assign("val", list(op("compiled_function_entry"),
                                         reg("fun"))),
                      go_to(reg("val"))))
           : // target !== "val" && linkage === "return"
             error(target, "return linkage, target not val – compile");
}

我们已经展示了如何在链接是return时为函数应用生成尾递归链接代码，也就是说，当应用在返回语句中时，它的值是要返回的结果。同样，正如在 5.4.2 节中解释的那样，这里使用的堆栈标记机制（以及显式控制求值器）仅在这种情况下产生尾递归行为。为函数应用生成的代码的这两个方面结合在一起，确保当函数通过返回函数调用的值结束时，不会累积堆栈。

编译返回语句

无论给定的链接和目标如何，返回语句的代码都采用以下形式：

revert_stack_to_marker(),
restore("continue"),   // saved by compile_fun_appl
〈evaluate the return expression and store the result in val〉
go_to(reg("continue")) // "return"-linkage code

使用标记还原堆栈的指令，然后恢复continue对应于compile_fun_appl生成的指令，用于保存continue和标记堆栈。通过使用return链接编译返回表达式时生成最终跳转到continue。函数compile_return_statement与所有其他代码生成器不同，因为它忽略了目标和链接参数——它总是使用目标val和链接return编译返回表达式。

function compile_return_statement(stmt, target, linkage) {
    return append_instruction_sequences(
               make_instruction_sequence(null, list("continue"),
                   list(revert_stack_to_marker(),
                        restore("continue"))),
               compile(return_expression(stmt), "val", "return"));
}

5.5.4 组合指令序列

本节描述了指令序列的表示和组合的详细信息。回想一下 5.5.1 节，指令序列被表示为所需寄存器的列表，修改的寄存器和实际指令。我们还将标签（字符串）视为指令序列的退化情况，它不需要或修改任何寄存器。因此，为了确定指令序列所需和修改的寄存器，我们使用选择器。

function registers_needed(s) {
    return is_string(s) ? null : head(s);
}
function registers_modified(s) {
    return is_string(s) ? null : head(tail(s));
}
function instructions(s) {
    return is_string(s) ? list(s) : head(tail(tail(s)));
}

要确定给定序列是否需要或修改给定寄存器，我们使用谓词。

function needs_register(seq, reg) {
    return ! is_null(member(reg, registers_needed(seq)));
}
function modifies_register(seq, reg) {
    return ! is_null(member(reg, registers_modified(seq)));
}

通过这些谓词和选择器，我们可以实现编译器中使用的各种指令序列组合器。

基本组合器是append_instruction_sequences。它以两个将按顺序执行的指令序列作为参数，并返回一个指令序列，其语句是两个序列的语句附加在一起。微妙的一点是确定所需和修改的寄存器。它修改了任一序列修改的寄存器；它需要那些必须在第一个序列运行之前初始化的寄存器（第一个序列需要的寄存器），以及第二个序列需要但第一个序列未初始化（修改）的寄存器。

函数append_instruction_sequences给出了两个指令序列seq1和seq2，并返回指令序列，其指令是seq1的指令，后跟seq2的指令，其修改的寄存器是seq1或seq2修改的寄存器，并且所需的寄存器是seq1所需的寄存器以及seq2所需的寄存器，这些寄存器不被seq1修改。（在集合操作方面，所需寄存器的新集合是seq1所需的寄存器的并集，与seq2所需的寄存器和seq1修改的寄存器的差集。）因此，append_instruction_sequences的实现如下：

function append_instruction_sequences(seq1, seq2) {
    return make_instruction_sequence(
               list_union(registers_needed(seq1),
                          list_difference(registers_needed(seq2),
                                         registers_modified(seq1))),
               list_union(registers_modified(seq1),
                          registers_modified(seq2)),
               append(instructions(seq1), instructions(seq2)));
}

这个函数使用一些简单的操作来操作列表表示的集合，类似于第 2.3.3 节中描述的（无序）集合表示：

function list_union(s1, s2) {
    return is_null(s1)
           ? s2
           : is_null(member(head(s1), s2))
           ? pair(head(s1), list_union(tail(s1), s2))
           : list_union(tail(s1), s2);
}
function list_difference(s1, s2) {
    return is_null(s1)
           ? null
           : is_null(member(head(s1), s2))
           ? pair(head(s1), list_difference(tail(s1), s2))
           : list_difference(tail(s1), s2);
}

函数preserving，第二个主要的指令序列组合器，接受一个寄存器列表regs和两个要顺序执行的指令序列seq1和seq2。它返回一个指令序列，其指令是seq1的指令，后跟seq2的指令，seq1中被seq1修改但seq2所需的寄存器在seq1周围有适当的save和restore指令来保护。为了实现这一点，preserving首先创建一个具有所需的save，然后是seq1的指令，然后是所需的restore的序列。这个序列需要被保存和恢复的寄存器，以及seq1所需的寄存器，并修改了seq1修改的寄存器，但不包括被保存和恢复的寄存器。然后以通常的方式附加这个增强的序列和seq2。以下函数以递归方式实现了这种策略，遍历要保留的寄存器列表：

function preserving(regs, seq1, seq2) {
    if (is_null(regs)) {
        return append_instruction_sequences(seq1, seq2);
    } else {
        const first_reg = head(regs);
        return needs_register(seq2, first_reg) &&
               modifies_register(seq1, first_reg)
               ? preserving(tail(regs),
                     make_instruction_sequence(
                         list_union(list(first_reg),
                                    registers_needed(seq1)),
                         list_difference(registers_modified(seq1),
                                         list(first_reg)),
                         append(list(save(first_reg)),
                                append(instructions(seq1),
                                       list(restore(first_reg))))),
                     seq2)
               : preserving(tail(regs), seq1, seq2);
    }
}

另一个序列组合器tack_on_instruction_sequence由compile_lambda_expression使用，用于将函数体附加到另一个序列。因为函数体不是“内联”执行作为组合序列的一部分，所以它的寄存器使用对嵌入它的序列的寄存器使用没有影响。因此，当我们将其附加到其他序列时，我们忽略函数体的所需和修改的寄存器集。

function tack_on_instruction_sequence(seq, body_seq) {
    return make_instruction_sequence(
               registers_needed(seq),
               registers_modified(seq),
               append(instructions(seq), instructions(body_seq)));
}

函数compile_conditional和compile_function_call使用一个特殊的组合器parallel_instruction_sequences来附加跟随测试的两个替代分支。这两个分支永远不会按顺序执行；对于测试的任何特定求值，将进入其中一个分支。因此，第二个分支所需的寄存器仍然需要由组合序列，即使这些寄存器被第一个分支修改。

function parallel_instruction_sequences(seq1, seq2) {
    return make_instruction_sequence(
               list_union(registers_needed(seq1),
                          registers_needed(seq2)),
               list_union(registers_modified(seq1),
                          registers_modified(seq2)),
               append(instructions(seq1), instructions(seq2)));
}

5.5.5 编译代码的示例

现在我们已经看到了编译器的所有元素，让我们看一个编译代码的示例，看看这些元素如何组合在一起。我们将通过将parse应用于程序的字符串表示（这里使用反引号ˋ...ˋ）来编译递归factorial函数的声明作为compile的第一个参数，反引号可以像单引号和双引号一样工作，但允许字符串跨越多行。

compile(parse(ˋ
function factorial(n) {
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}
              ˋ),
        "val",
        "next");

我们已经指定声明的值应放在val寄存器中。我们不在乎编译后的代码在执行声明后做什么，因此我们选择"next"作为链接描述符是任意的。

函数compile确定它得到了一个函数声明，因此将其转换为常量声明，然后调用compile_declaration。这将编译代码来计算要分配的值（目标为val），然后是安装声明的代码，然后是将声明的值（即值undefined）放入目标寄存器的代码，最后是链接代码。在计算值时，env寄存器被保留，因为它需要用于安装声明。因为链接是"next"，所以在这种情况下没有链接代码。因此，编译代码的骨架如下

〈save env if modified by code to compute value〉
〈compilation of declaration value, target val, linkage "next"〉
〈restore env if saved above〉
perform(list(op("assign_symbol_value"),
             constant("factorial"),
             reg("val"),
             reg("env"))),
assign("val", constant(undefined))

编译生成名称factorial的值的表达式是一个 lambda 表达式，其值是计算阶乘的函数。函数compile通过调用compile_lambda_expression来处理这个问题，它编译函数体，将其标记为新的入口点，并生成将函数体与运行时环境组合并将结果分配给val的指令。然后，序列跳过编译的函数代码，该代码插入到此处。函数代码本身首先通过将参数n绑定到函数参数的帧来扩展函数的声明环境。然后是实际的函数体。由于名称的值的代码不修改env寄存器，因此不会生成上面显示的可选的save和restore。（此时不执行entry1处的函数代码，因此其对env的使用是无关紧要的。）因此，编译代码的骨架变为

  assign("val", list(op("make_compiled_function"),
                     label("entry1"),
                     reg("env"))),
  go_to(label("after_lambda2")),
"entry1",
  assign("env", list(op("compiled_function_env"), reg("fun"))),
  assign("env", list(op("extend_environment"),
                     constant(list("n")),
                     reg("argl"),
                     reg("env"))),
  〈compilation of function body〉
"after_lambda2",
  perform(list(op("assign_symbol_value"),
               constant("factorial"),
               reg("val"),
               reg("env"))),
  assign("val", constant(undefined))

函数体总是使用目标val和链接"next"编译（由compile_lambda_body）。在这种情况下，函数体由单个返回语句组成：⁵⁰

return n === 1
       ? 1
       : factorial(n - 1) * n;

函数compile_return_statement生成代码，使用标记还原堆栈并恢复continue寄存器，然后编译返回表达式，目标为val，链接为"return"，因为其值将从函数返回。返回表达式是一个条件表达式，compile_conditional生成代码，首先计算谓词（目标为val），然后检查结果并在谓词为假时绕过真分支。在谓词代码周围保留env和continue寄存器，因为它们可能需要用于条件表达式的其余部分。真分支和假分支都使用目标val和链接"return"进行编译。（也就是说，条件的值，即由其任一分支计算得到的值，是函数的值。）

  revert_stack_to_marker(),
  restore("continue"),
  〈save continue, env if modified by predicate and needed by branches〉
  〈compilation of predicate, target val, linkage "next"〉
  〈restore continue, env if saved above〉
  test(list(op("is_falsy"), reg("val"))),
  branch(label("false_branch4")),
"true_branch3",
  〈compilation of true branch, target val, linkage "return"〉
"false_branch4",
  〈compilation of false branch, target val, linkage "return"〉
"after_cond5",

谓词n === 1是一个函数应用（在转换运算符组合后）。这查找函数表达式（符号"==="）并将该值放入fun中。然后将参数1和n的值组合成argl。然后测试fun是否包含原始函数或复合函数，并相应地分派到原始分支或复合分支。两个分支都在after_call标签处恢复。复合分支必须设置continue以跳过原始分支，并将标记推送到堆栈以匹配函数的编译返回语句中的还原操作。在函数和参数表达式的求值周围保留寄存器的要求不会导致寄存器的保存，因为在这种情况下，这些求值不会修改相关寄存器。

  assign("fun", list(op("lookup_symbol_value"),
                     constant("==="), reg("env"))),
  assign("val", constant(1)),
  assign("argl", list(op("list"), reg("val"))),
  assign("val", list(op("lookup_symbol_value"),
                     constant("n"), reg("env"))),
  assign("argl", list(op("pair"), reg("val"), reg("argl"))),
  test(list(op("is_primitive_function"), reg("fun"))),
  branch(label("primitive_branch6")),
"compiled_branch7",
  assign("continue", label("after_call8")),
  save("continue"),
  push_marker_to_stack(),
  assign("val", list(op("compiled_function_entry"), reg("fun"))),
  go_to(reg("val")),
"primitive_branch6",
  assign("val", list(op("apply_primitive_function"),
                     reg("fun"),
                     reg("argl"))),
"after_call8",

真分支，即常量 1，编译（目标为val和链接return）为

  assign("val", constant(1)),
  go_to(reg("continue")),

假分支的代码是另一个函数调用，其中函数是符号"*"的值，参数是n和另一个函数调用的结果（对factorial的调用）。每个调用都设置了fun和argl以及自己的原始和复合分支。图 5.17 显示了factorial函数声明的完整编译。请注意，由于谓词中的函数调用修改了这些寄存器并且需要用于函数调用和分支中的“返回”链接，因此上面显示的continue和env的可能“保存”和“恢复”实际上是生成的。

图 5.17 factorial函数声明的编译。

练习 5.36

考虑以下阶乘函数的声明，它与上面给出的函数略有不同：

function factorial_alt(n) {
    return n === 1
           ? 1
           : n * factorial_alt(n - 1);
}

编译此函数并将生成的代码与factorial的代码进行比较。解释您发现的任何差异。这两个程序中哪一个执行效率更高？

练习 5.37

编译迭代阶乘函数

function factorial(n) {
    function iter(product, counter) {
        return counter > n
               ? product
               : iter(product * counter, counter + 1);
    }
    return iter(1, 1);
}

注释生成的代码，显示迭代和递归版本的factorial之间的基本差异，使一个进程构建堆栈空间，另一个在恒定堆栈空间中运行。

练习 5.38

编译了哪个程序以生成图 5.18 中显示的代码？

图 5.18 编译器输出的示例。参见练习 5.38。

练习 5.39

我们的编译器为应用程序的参数产生什么样的求值顺序？是从左到右（如 ECMAScript 规范所规定的）还是从右到左，还是其他顺序？编译器中的哪个部分确定了这个顺序？修改编译器，使其产生其他求值顺序。（参见 5.4.1 节中对显式控制求值器的求值顺序的讨论。）改变参数求值的顺序如何影响构造参数列表的代码的效率？

练习 5.40

理解编译器对优化堆栈使用的“保留”机制的一种方法是看看如果我们不使用这个想法会生成什么额外的操作。修改“保留”，使其总是生成“保存”和“恢复”操作。编译一些简单的表达式，并识别生成的不必要的堆栈操作。将代码与保留机制完整生成的代码进行比较。

练习 5.41

我们的编译器在避免不必要的堆栈操作方面很聪明，但在编译语言的原始函数调用方面一点也不聪明，这些原始函数调用是通过机器提供的原始操作来实现的。例如，考虑编译计算a + 1的代码量：代码在argl中设置参数列表，将原始加法函数（通过在环境中查找符号"+"找到）放入fun，并测试函数是原始的还是复合的。编译器总是生成代码来执行测试，以及原始和复合分支的代码（只有一个会被执行）。我们没有展示实现原始的控制器部分，但我们假设这些指令利用了机器数据路径中的原始算术操作。考虑如果编译器可以开放代码原始操作——也就是说，如果它可以生成代码直接使用这些原始机器操作，将会生成多少更少的代码。表达式a + 1可能被编译成如下简单的形式⁵¹

assign("val", list(op("lookup_symbol_value"), constant("a"), reg("env"))),
assign("val", list(op("+"), reg("val"), constant(1)))

在这个练习中，我们将扩展我们的编译器以支持对选定原语的开放编码。将为这些原语函数的调用生成专用代码，而不是一般的函数应用代码。为了支持这一点，我们将用特殊的参数寄存器arg1和arg2来扩展我们的机器。机器的原始算术操作将从arg1和arg2中获取它们的输入。结果可以放入val、arg1或arg2中。

编译器必须能够识别源程序中开放编码原语的应用。我们将扩展compile函数中的分派，以识别这些原语的名称，以及它当前识别的句法形式。对于我们编译器的每个句法形式，都有一个代码生成器。在这个练习中，我们将为开放编码的原语构建一组代码生成器。

a. 与句法形式不同，开放编码的原语都需要求值它们的参数表达式。编写一个名为spread_arguments的代码生成器，供所有开放编码代码生成器使用。函数spread_arguments应接受参数表达式列表，并将给定的参数表达式编译为连续的参数寄存器。注意，参数表达式可能包含对开放编码原语的调用，因此在参数表达式求值期间必须保留参数寄存器。
b. JavaScript 运算符===、*、-和+等在寄存器机器中作为原始函数实现，并在全局环境中用符号===、*、-和+引用。在 JavaScript 中，不可能重新声明这些名称，因为它们不符合名称的句法限制。这意味着可以安全地开放编码它们。对于每个原始函数===、*、-和+，编写一个代码生成器，该代码生成器接受一个带有命名该函数的函数表达式的应用，以及一个目标和链接描述符，并生成代码将参数传播到寄存器，然后执行针对给定目标和给定链接的操作。使compile分派到这些代码生成器。
c. 尝试在“阶乘”示例上使用你的新编译器。将生成的代码与不使用开放编码产生的结果进行比较。

5.5.6 词法寻址

编译器执行的最常见优化之一是名称查找的优化。到目前为止，我们实现的编译器生成使用求值器机器的lookup_symbol_value操作的代码。这通过将名称与当前绑定的每个名称进行比较来搜索名称，通过运行时环境逐帧向外工作。如果框架嵌套深或名称很多，这种搜索可能很昂贵。例如，考虑在返回的五个参数的函数的应用中，求解表达式x * y * z时查找x的值的问题。

((x, y) =>
   (a, b, c, d, e) =>
     ((y, z) => x * y * z)(a * b * x, c + d + x))(3, 4)

每次lookup_symbol_value搜索x时，它必须确定符号x不等于y或z（在第一个框架中），也不等于a、b、c、d或e（在第二个框架中）。因为我们的语言是词法作用域的，任何组件的运行时环境都将与组件所在的程序的词法结构相对应。因此，编译器在分析上述表达式时可以知道，每次应用函数时，x * y * z中的x的绑定将在当前框架的外部两个框架处找到，并且将是该框架中的第一个绑定。

我们可以利用这一事实，通过发明一种新的名称查找操作lexical_address_lookup，它接受环境和由两个数字组成的词法地址作为参数：帧编号，指定要跳过多少帧，和位移编号，指定在该帧中要跳过多少绑定。操作lexical_address_lookup将生成相对于当前环境存储在该词法地址的名称的值。如果我们将lexical_address_lookup操作添加到我们的机器中，我们可以让编译器生成使用这个操作引用名称的代码，而不是lookup_symbol_value。同样，我们的编译代码可以使用新的lexical_address_assign操作，而不是assign_symbol_value。使用词法寻址，对象代码中不需要包含任何名称的符号引用，帧在运行时也不需要包含符号。

为了生成这样的代码，编译器必须能够确定它即将编译引用的名称的词法地址。程序中名称的词法地址取决于代码中的位置。例如，在以下程序中，表达式e[1]中x的地址是(2,0)——向后两个帧，帧中的第一个名称。在那一点上，y的地址是(0,0)，c的地址是(1,2)。在表达式e[2]中，x在(1,0)，y在(1,1)，c在(0,2)。

((x, y) =>
   (a, b, c, d, e) =>
     ((y, z) => e1)(e2, c + d + x))(3, 4);

编译器产生使用词法寻址的代码的一种方法是维护一个称为编译时环境的数据结构。这个数据结构跟踪当执行特定的名称访问操作时，绑定将位于运行时环境的哪个帧的哪个位置。编译时环境是一个帧的列表，每个帧包含一个符号列表。与符号相关联的值将不会有，因为值不是在编译时计算的。（练习 5.47 将改变这一点，作为常量的优化。）编译时环境成为compile的一个额外参数，并传递给每个代码生成器。对compile的顶层调用使用包括所有原始函数和原始值名称的编译时环境。当编译 lambda 表达式的主体时，compile_lambda_body通过包含函数参数的帧扩展编译时环境，以便使用扩展的环境编译主体。同样，当编译块的主体时，compile_block通过包含主体的本地名称的帧扩展编译时环境。在编译的每个点上，compile_name和compile_assignment_declaration使用编译时环境以生成适当的词法地址。

练习 5.42 到 5.45 描述了如何完成词法寻址策略的草图，以便将词法查找纳入编译器。练习 5.46 和 5.47 描述了编译时环境的其他用途。

练习 5.42

编写一个实现新查找操作的函数lexical_address_lookup。它应该接受两个参数——词法地址和运行时环境，并返回存储在指定词法地址的名称的值。如果名称的值是字符串"unassigned"，函数lexical_address_lookup应该发出错误信号。还要编写一个实现改变指定词法地址处名称的值的操作的函数lexical_address_assign。

练习 5.43

修改编译器以维护上述编译时环境。也就是说，向compile和各种代码生成器添加一个编译时环境参数，并在compile_lambda_body和compile_block中扩展它。

练习 5.44

编写一个函数find_symbol，它以符号和编译时环境作为参数，并返回相对于该环境的符号的词法地址。例如，在上面显示的程序片段中，在编译表达式e[1]期间的编译时环境是

list(list("y", "z"),
     list("a", "b", "c", "d", "e"),
     list("x", "y"))

函数find_symbol应该产生

find_symbol("c", list(list("y", "z"),
                      list("a", "b", "c", "d", "e"),
                      list("x", "y")));
list(1, 2)

find_symbol("x", list(list("y", "z"),
                      list("a", "b", "c", "d", "e"),
                      list("x", "y")));
list(2, 0)

find_symbol("w", list(list("y", "z"),
                      list("a", "b", "c", "d", "e"),
                      list("x", "y")));
"not found"

练习 5.45

使用练习 5.44 中的find_symbol，重写compile_assignment_declaration和compile_name以输出词法地址指令。在find_symbol返回"not found"的情况下（即名称不在编译时环境中），应报告编译时错误。在一些简单情况下测试修改后的编译器，例如本节开头的嵌套 lambda 组合。

练习 5.46

在 JavaScript 中，试图为声明为常量的名称分配新值会导致错误。练习 4.11 展示了如何在运行时检测此类错误。通过本节中介绍的技术，我们可以在编译时检测尝试为常量分配新值的行为。为此，扩展函数compile_lambda_body和compile_block以记录在编译时环境中名称是声明为变量（使用let或作为参数）还是常量（使用const或function）。修改compile_assignment以在检测到对常量的赋值时报告适当的错误。

练习 5.47

编译时对常量的了解打开了许多优化的大门，使我们能够生成更高效的目标代码。除了在练习 5.46 中扩展编译时环境以指示声明为常量的名称外，如果在编译时知道常量的值或其他可以帮助我们优化代码的信息，我们可以存储常量的值。

a. 诸如const name = literal;的常量声明允许我们在声明的范围内用literal替换所有name的出现，这样就不必在运行时环境中查找name。这种优化称为常量传播。使用扩展的编译时环境存储字面常量，并修改compile_name以在生成的assign指令中使用存储的常量而不是lookup_symbol_value操作。
b. 函数声明是一个派生组件，它扩展为常量声明。让我们假设全局环境中原始函数的名称也被视为常量。如果我们进一步扩展我们的编译时环境以跟踪哪些名称指向编译函数，哪些指向原始函数，我们可以将检查函数是编译还是原始的测试从运行时移动到编译时。这使得目标代码更加高效，因为它通过编译器替换了在生成的代码中每个函数应用必须执行一次的测试。使用这样扩展的编译时环境，修改compile_function_call，以便在编译时确定所调用的函数是编译还是原始时，只生成compiled_branch或primitive_branch中的指令。
c. 像第(a)部分那样用字面值替换常量名称为另一种优化铺*了道路，即用编译时计算的结果替换对字面值的原始函数的应用。这种优化称为常量折叠，通过在编译器中执行加法，将诸如40 + 2之类的表达式替换为42。扩展编译器以对数字的算术运算和字符串连接执行常量折叠。

5.5.7 将编译代码与求值器进行接口

我们还没有解释如何将编译代码加载到求值器机器中，或者如何运行它。我们将假设明确控制求值器机器已经被定义，就像第 5.4.4 节中所述，其中还有脚注 43（第 5.5.2 节）中指定的其他操作。我们将实现一个名为compile_and_go的函数，该函数编译 JavaScript 程序，将生成的目标代码加载到求值器机器中，并使机器运行求值器全局环境中的代码，打印结果，并进入求值器的驱动循环。我们还将修改求值器，以便解释组件可以调用编译函数以及解释函数。然后，我们可以将编译函数放入机器中，并使用求值器调用它：

compile_and_go(parse(ˋ
function factorial(n) { 
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}
                     ˋ));

EC-求值值：

undefined

EC-求值输入：

factorial(5);

EC-求值值：

120

为了使求值器能够处理编译函数（例如，求值上面的factorial调用），我们需要更改apply_dispatch（第 5.4.2 节）处的代码，以便它识别编译函数（与复合函数或原始函数不同），并直接将控制转移到编译代码的入口点。⁵²

"apply_dispatch",
  test(list(op("is_primitive_function"), reg("fun"))),
  branch(label("primitive_apply")),
  test(list(op("is_compound_function"), reg("fun"))),
  branch(label("compound_apply")),
  test(list(op("is_compiled_function"), reg("fun"))),
  branch(label("compiled_apply")),
  go_to(label("unknown_function_type")),

"compiled_apply",
  push_marker_to_stack(),
  assign("val", list(op("compiled_function_entry"), reg("fun"))),
  go_to(reg("val")),

在compiled_apply处，与compound_apply一样，我们将一个标记推送到堆栈，以便编译函数中的返回语句可以将堆栈恢复到此状态。请注意，在标记堆栈之前，在compiled_apply处没有保存continue，因为求值器被安排在apply_dispatch处，继续将位于堆栈顶部。

为了使我们能够在启动求值器机器时运行一些编译代码，我们在求值器机器的开头添加了一个branch指令，如果flag寄存器被设置，该指令将使机器转到新的入口点。⁵³

  branch(label("external_entry")), // branches if flag is set
"read_evaluate_print_loop",
  perform(list(op("initialize_stack"))),
  ...

external_entry处的代码假定机器以val包含的指令序列的位置启动，该指令序列将结果放入val，并以go_to(reg("continue"))结束。从这个入口点开始跳转到由val指定的位置，但首先分配continue，以便执行将返回到print_result，该函数打印val中的值，然后转到求值器的读取-求值-打印循环的开头。⁵⁴

"external_entry",
  perform(list(op("initialize_stack"))),
  assign("env", list(op("get_current_environment"))),
  assign("continue", label("print_result")),
  go_to(reg("val")),

现在我们可以使用以下函数来编译函数声明，执行编译代码，并运行读取-求值-打印循环，以便尝试该函数。因为我们希望编译代码继续到continue的位置，并在val中返回结果，所以我们使用val作为目标编译程序，并使用"return"作为链接。为了将编译器生成的目标代码转换为求值器寄存器机器的可执行指令，我们使用寄存器机器模拟器（第 5.2.2 节）中的assemble函数。为了使解释程序引用编译程序中顶层声明的名称，我们扫描顶层名称，并通过将这些名称绑定到"unassigned"来扩展全局环境，知道编译代码将为它们分配正确的值。然后，我们将val寄存器初始化为指向指令列表，设置flag以便求值器将转到external_entry，然后启动求值器。

function compile_and_go(program) {
    const instrs = assemble(instructions(compile(program,
                                                 "val", "return")),
                            eceval);
    const toplevel_names = scan_out_declarations(program);
    const unassigneds = list_of_unassigned(toplevel_names);
    set_current_environment(extend_environment(
                               toplevel_names,
                               unassigneds,
                               the_global_environment));
    set_register_contents(eceval, "val", instrs);
    set_register_contents(eceval, "flag", true);
    return start(eceval);
}

如果我们已经设置了堆栈监视，就像在第 5.4.4 节的末尾一样，我们可以检查编译代码的堆栈使用情况：

compile_and_go(parse(ˋ
function factorial(n) { 
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}
                     ˋ));

总推送次数= 0

最大深度= 0

EC-求值值：

undefined

EC-求值输入：

factorial(5);

总推送次数= 36

最大深度= 14

EC-求值值：

120

将此示例与使用相同函数的解释版本求值factorial(5)进行比较，该函数显示在第 5.4.4 节的末尾。解释版本需要 151 次推送和最大堆栈深度为 28。这说明了我们编译策略带来的优化。

解释和编译

有了本节中的程序，我们现在可以尝试解释和编译的替代执行策略。解释器将机器提升到用户程序的级别；编译器将用户程序降低到机器语言的级别。我们可以将 JavaScript 语言（或任何编程语言）视为建立在机器语言上的一系列连贯的抽象。解释器适用于交互式程序开发和调试，因为程序执行步骤是根据这些抽象组织的，因此对程序员更易理解。编译代码可以更快地执行，因为程序执行步骤是根据机器语言组织的，并且编译器可以进行跨越更高级抽象的优化。

解释和编译的选择也导致将语言移植到新计算机的不同策略。假设我们希望为新机器实现 JavaScript。一种策略是从第 5.4 节的显式控制求值器开始，并将其指令转换为新机器的指令。另一种策略是从编译器开始，并更改代码生成器，以便为新机器生成代码。第二种策略允许我们首先使用运行在原始 JavaScript 系统上的编译器编译任何 JavaScript 程序，并将其与运行时库的编译版本链接起来，在新机器上运行任何 JavaScript 程序。更好的是，我们可以编译编译器本身，并在新机器上运行它来编译其他 JavaScript 程序。或者我们可以编译第 4.1 节中的解释器之一，以产生在新机器上运行的解释器。

练习 5.48

通过比较编译代码和求值器在相同计算中使用的堆栈操作，我们可以确定编译器优化堆栈使用的程度，无论是在速度上（减少总堆栈操作次数）还是在空间上（减少最大堆栈深度）。将这种优化的堆栈使用与相同计算的特定用途机器的性能进行比较，可以在一定程度上反映编译器的质量。

a. 练习 5.28 要求您确定作为n的函数，求值器计算n!所需的推送次数和最大堆栈深度。练习 5.13 要求您对图 5.11 中显示的特定用途阶乘机执行相同的测量。现在使用编译的factorial函数执行相同的分析。

取编译版本中推送次数与解释版本中推送次数的比率，并对最大堆栈深度做同样的操作。由于计算n!所需的操作次数和堆栈深度与n成线性关系，因此这些比率在n变大时应该接*常数。这些常数是多少？同样，找出特定用途机器的堆栈使用量与解释版本的使用量的比率。

比较特定用途与解释代码的比率与编译与解释代码的比率。您应该会发现，特定用途的机器比编译代码更有效，因为手工定制的控制器代码应该比我们的基本通用编译器生成的代码要好得多。
b. 您能否提出改进编译器的建议，以帮助它生成性能更接*手工定制版本的代码？

练习 5.49

进行类似于练习 5.48 中的分析，以确定编译树递归斐波那契函数的有效性

function fib(n) {
    return n < 2 ? n : fib(n - 1) + fib(n - 2);
}

与使用图 5.12 的专用斐波那契机器相比的效果。（有关解释性能的测量，请参见练习 5.30。）对于斐波那契，使用的时间资源与n不成线性关系；因此，堆栈操作的比值不会接*与n无关的极限值。

练习 5.50

本节描述了如何修改显式控制求值器，以便解释代码可以调用编译函数。展示如何修改编译器，以便编译函数不仅可以调用原始函数和编译函数，还可以调用解释函数。这需要修改compile_function_call来处理复合（解释）函数的情况。确保处理与compile_fun_appl中相同的所有target和linkage组合。要执行实际的函数应用，代码需要跳转到求值器的compound_apply入口点。这个标签不能在目标代码中直接引用（因为汇编器要求所有被汇编的代码引用的标签都在那里定义），所以我们将在求值器机器中添加一个名为compapp的寄存器来保存这个入口点，并添加一个指令来初始化它：

  assign("compapp", label("compound_apply")),
  branch(label("external_entry")),     // branches if flag is set
"read_evaluate_print_loop",
  ...

要测试您的代码，请先声明一个调用函数g的函数f。使用compile_and_go编译f的声明并启动求值器。现在，在求值器中输入，声明g并尝试调用f。

练习 5.51

本节实现的compile_and_go接口很笨拙，因为编译器只能被调用一次（在启动求值器机器时）。通过提供一个compile_and_run原语来增强编译器-解释器接口，可以从显式控制求值器中调用它，如下所示：

EC-求值输入：

compile_and_run(parse(ˋ
function factorial(n) {
    return n === 1
           ? 1
           : factorial(n - 1) * n;
}
                      ˋ));

EC-求值值：

undefined

EC-求值输入：

factorial(5)

EC-求值值：

120

posted @ 2024-02-12 12:52 lsgxeva 阅读(1) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

MyGitee - https://gitee.com/lsgx/ MyGithub - https://github.com/lsgxeva/ Download - https://d.serctl.com Proxy - tcp://frpgz1.idcfengye.com:10000

SICP JavaScript 描述

MyGitee - https://gitee.com/lsgx/
MyGithub - https://github.com/lsgxeva/
Download - https://d.serctl.com
Proxy - tcp://frpgz1.idcfengye.com:10000