Codeforces Round #740 (Div. 2, based on VK Cup 2021 - Final (Engine)) D2. Up the Strip (数学,DP)

• 题意：给你一个数\(x\),每次有两种操作可以选择，一是从\(x\)跳到\([1,x-1]\)的任意一个数，二是跳到\(\lfloor \frac{x}{z} \rfloor\ \ (z \in[2,x])\).问你从\(x\)到一有多少种方案.

• 题解：假设\(S(x)\)为\(x\)能到达的所有位置的贡献\(f(i)\)集合,考虑\(S(x+1)\)和\(S(x)\)的差别

  1.\(S(x+1)\)比\(S(x)\)多了一个\(f(1)\),因为\(\lfloor \frac{x+1}{x+1} \rfloor=1\).

  2.\(S(x+1)\)比\(S(x)\)多了一个\(f(x)\),因为\((x+1)-1=x\).

  3.观察\(\sum^{x+1}_{i=2} \lfloor \frac{x+1}{i} \rfloor\)和\(\sum^{x}_{i=2} \lfloor \frac{x}{i} \rfloor\)的区别，其实它们的区别很小，因为只差了\(1\)，手玩几个样例，发现，区别是：对于\(x+1\)，当\(i | x+1\)时，它的值为\(k+1\)，而此时的\(i\)对于\(x\)的值为\(k\)。所以对于\(S(x)\)我们要将所有\(i|x+1\)的\(f(k)\)换成\(f(k+1)\)，然后再进行上述1，2操作就能得到\(S(x+1)\)了。

  具体实现的方法为：对于每个\(f(i)\)，去找\(i\)的倍数，然后\(S(i)\)的贡献加上\(f(i)-f(i-1)\)这样就可以实现替换。根据调和级数，这一步的复杂度为\(O(\log n)\).

  

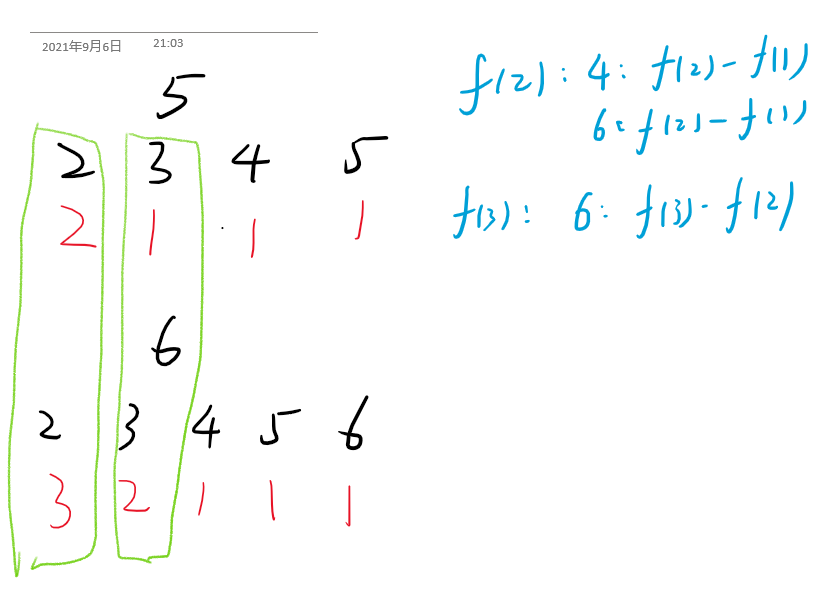
  如上图，\(i=2\)的时候，将\(i=6\)的原本的\(f(1)\)换成了\(f(2)\).\(i=3\)也是同理。

• 代码 ：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 4e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  ll f[N];
  
  int main() {
      int n;
      ll m;
      scanf("%d %lld",&n,&m);
      f[1]=1;
      for(int i=2;i<=n;++i){
          if(i==2) f[2]=2;
          else f[i]=(f[i]+f[i-1]+f[i-1]+1+m)%m;
          for(int j=i+i;j<=n;j+=i){
              f[j]=(f[j]+f[i]-f[i-1]+m)%m;
          }
      }
      printf("%lld\n",f[n]);
      return 0;
  }