2021-7-23 Number of Ways

难度 1700

题目 Codeforces:

C. Number of Ways

time limit per test

2 seconds

memory limit per test

256 megabytes

　　You've got array a[1], a[2], ..., a[n], consisting of n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.

More formally, you need to find the number of such pairs of indices i, j (2 ≤ i ≤ j ≤ n - 1), that .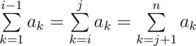

Input

　　The first line contains integer n (1 ≤ n ≤ 5·105), showing how many numbers are in the array. The second line contains n integers a[1], a[2], ..., a[n] (|a[i]| ≤  109) — the elements of array a.

Output

　　Print a single integer — the number of ways to split the array into three parts with the same sum.

Keyword

split 分开

contiguous 相邻的

 

题目解析

本题大意是对题目给出的数组进行切割，分成三部分，使得三部分分别的元素和相等，可能存在不止一种或者零种可能，所以题目要求输出有多少种切割的方式。切割不能改变数组的顺序。

这题题目很简短，也很容易理解，已知的数组所有元素，即已知当前数组的元素和，那么要使切割后的三个部分元素和相等，我们很轻易的就能知道三个部分的元素和等于原来数组的元素和除以3.

同时因为题目给出的切割不能改变顺序，所以我们这题用前缀和来做，创建一个范围上限的数组来存储每一个数字对应的前缀和。

同时可以先提前判断，如果原来的数组的元素和不能整除3，说明不可能出现三个部分的和相等，或者如果题目给出的数组元素数量小于三个也不可能，所以这样两种情况可以提前输出0.

剩余的情况我们进行判断，首先对前缀和数组进行遍历，我们必须明白，因为三部分和相等，所以只要前两个部分的元素和相等且等于原来数组的元素和除以三，那么就说明出现了一种情况。

解析完毕，以下是参考代码

#include<iostream>
using namespace std;
typedef long long ll;
ll a[500000];
int main()
{
    ll n, x, sum = 0, temp = 0;
    cin >> n >> a[0];
    for (int i = 1; i < n; i++)
    {
        cin >> x;
        a[i] = a[i - 1] + x;
    }
    if (n < 3 || a[n - 1] % 3)cout << 0 << "\n";
    else
    {
        for (int i = 0; i < n - 1; i++)
        {
            if (a[i] == a[n - 1] / 3 * 2)sum += temp;
            if (a[i] == a[n - 1] / 3)temp++;
        }
        cout << sum << "\n";
    }
    return 0;
}