题解：P2963 [USACO09NOV] Cow Rescue G

另类做法。

感谢 @chenly8128 提供的图片。

思路

首先我们对每个点坐标重新标号。即原来的 $(x,y)$ 变为 $(x,n-x+y)$。变更完后坐标如下图。

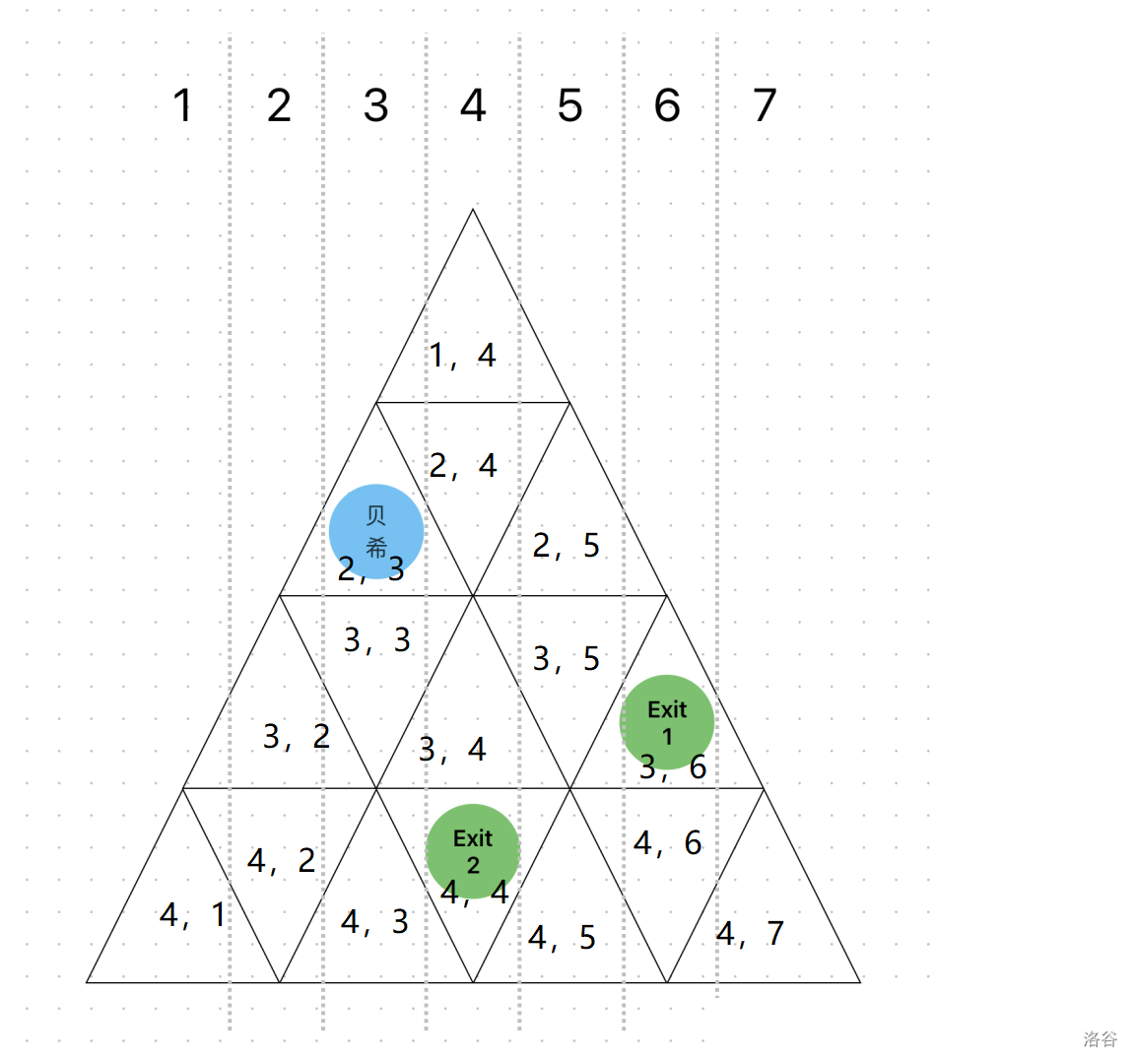
然后我们需要对于起点，画 $2$ 条线，即：

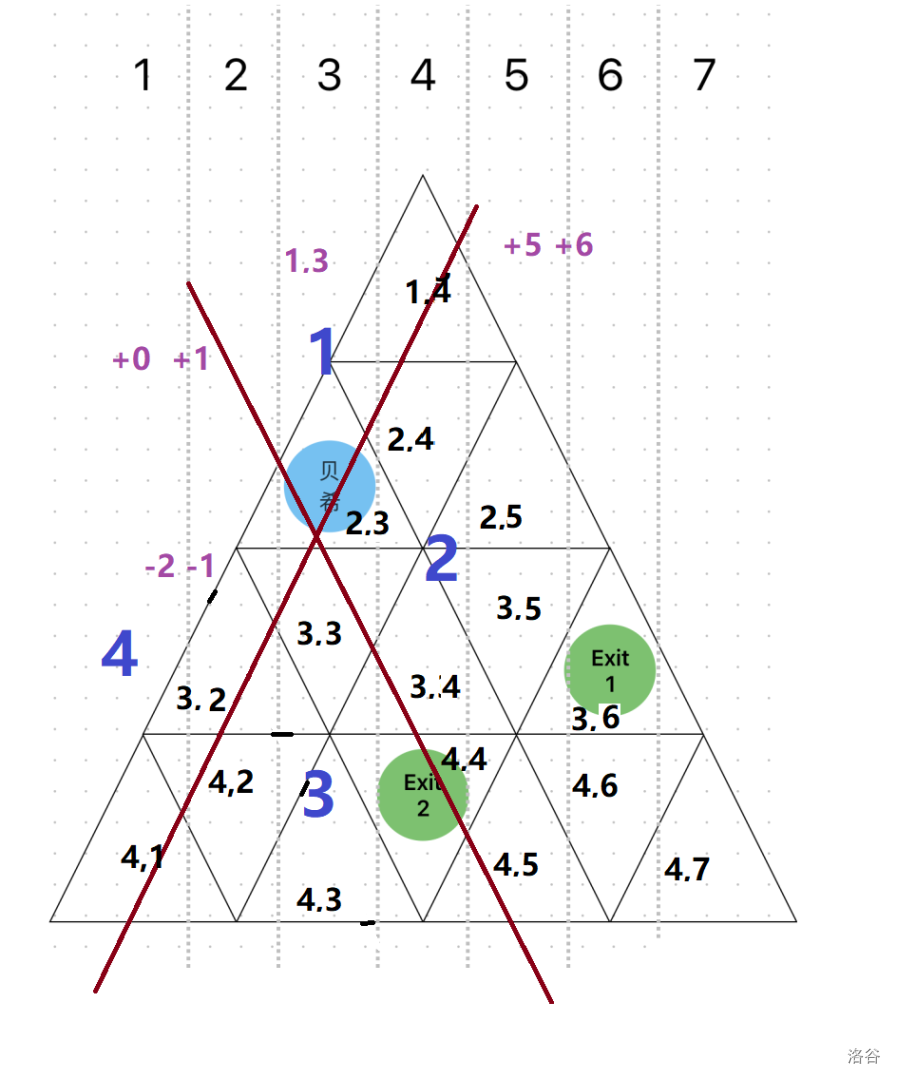
这两条线把整个平面分成了 $4$ 部分。

首先，在同一直线上的点 $(x_1,y_1)$ 与 $(x_2,y_2)$，它们的距离为 $|x_1-x_2|+|y_1-y_2|$。

同一纵坐标的点也有性质：对于点 $(x_1,y)$ 与 $(x_2,y)$，它们的距离为 $|x_1-x_2|$。

然后对于 $2$ 和 $4$ 两个区域的点，不难发现 $(x,y)$ 与 $(sx,sy)$ 的距离就是 $|sx-x|+|sy-y|$，这个手搓几组就能发现。

关键是对于另外两个区域的求解，以区域 $3$ 为例。

研究两条直线的性质，发现：从左下到右上的线途径的点横纵坐标之和只有两个值，这样我们就可以用 $(a,b)$（其中 $a<b$）表示一条直线。例如上图中的左下到右上的线，我们可以用 $(5,6)$ 表示。

从左上到右下线上的点也满足一个性质：横纵坐标差为定值（此处的横纵坐标差默认为 $x-y$）。可以用 $(c,d)$ 表示这种直线（$c>d$）。例如上图的直线，就是 $(0,-1)$。

手搓一下就会发现：$a$ 为奇数，$b$ 为偶数，$c$ 为偶数，$d$ 为奇数。

这样，我们可以 $\operatorname{O}(1)$ 地通过一个点求解一条直线的表示。

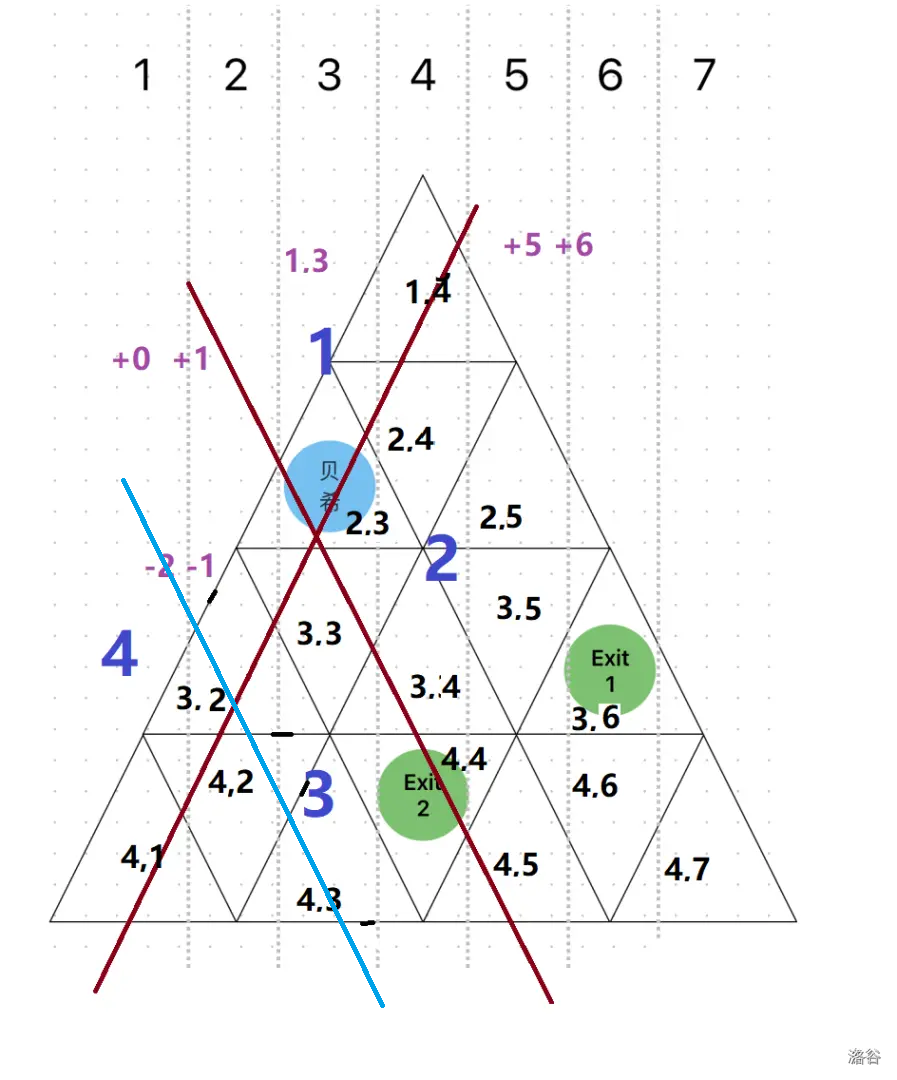
假如我们要求 $(4,3)$ 到 $(2,3)$ 的距离，如何求呢？

首先要明确一个事实：如果 $x$ 和 $y$ 都是整数，且 $x+y$ 为奇数，则 $x-y$ 是奇数。

不难发现交点有 $2$ 个，一个横纵坐标相加是奇数，一个是偶数。

我们选取奇数的求解交点坐标 $(x,y)$。

按照上面的性质：

$a$ 为奇数，$b$ 为偶数，$c$ 为偶数，$d$ 为奇数。

可以发现 $(x,y)$ 满足一个方程组：

$$\begin{cases} x+y=a\\ x-y=d \end{cases}$$

显然 $x=\dfrac{a+d}{2}$，$y=a-\dfrac{a+d}{2}$。

然后就可以用直线上点的坐标公式求距离了。假设起点是 $(sx,sy)$，终点是 $(tx,ty)$，那么经过 $(x,y)$ 由 $(sx,sy)$ 到 $(tx,ty)$ 的距离是 $|sx-x|+|sy-y|+|tx-x|+|ty-y|$。

到这里我们就做完了。证明在代码下面。

注意一个细节：Bessie 逃出迷宫还要再花 $1$ 秒。

另一个细节：我们在前面转化了横纵坐标，但是题目中要求输出的不是这个，所以要转回去。原来是 $y_0$，现在变成了 $y=n-x+y_0$，自然 $y_0=y-n+x$。

代码

#include<bits/stdc++.h>
using namespace std;
int n,m,x[10005],y[10005],ansx,ansy,ans=2147483647,sx,sy,nans;
int abss(int _){
	if(_>0)return _;
	return -_;
}
int main(){
	cin>>n>>m>>sx>>sy;
	sy=n-sx+sy;
	int a,b,c,d;
	if((sx+sy)%2==1){
		a=sx+sy;
		b=a+1;
	}
	else{
		b=sx+sy;
		a=b-1;
	}
	for(int i=1;i<=m;i++){
		cin>>x[i]>>y[i];
		y[i]=n-x[i]+y[i];
	}
	for(int i=1;i<=m;i++){
		int hc=abss(sx-x[i]),zc=abss(sy-y[i]);
		if(hc<=zc){
			nans=hc+zc;
		}
		else{
			if((x[i]-y[i])%2==0){
				c=y[i]-x[i];
				d=c+1;
			}
			else{
				d=y[i]-x[i];
				c=d-1;
			}
			int jx,jy;
			jx=(a-d)/2;
			jy=a-jx;
			nans=abss(jx-x[i])+abss(jx-sx)+abss(jy-y[i])+abss(jy-sy);
		}
		if(nans<ans){
			ansx=x[i];
			ansy=y[i];
			ans=nans;
		}
	}
	cout<<ansx<<' '<<(ansy-n+ansx)<<endl<<ans+1;
	return 0;
}

证明

如何证明上面的做法是正确的？

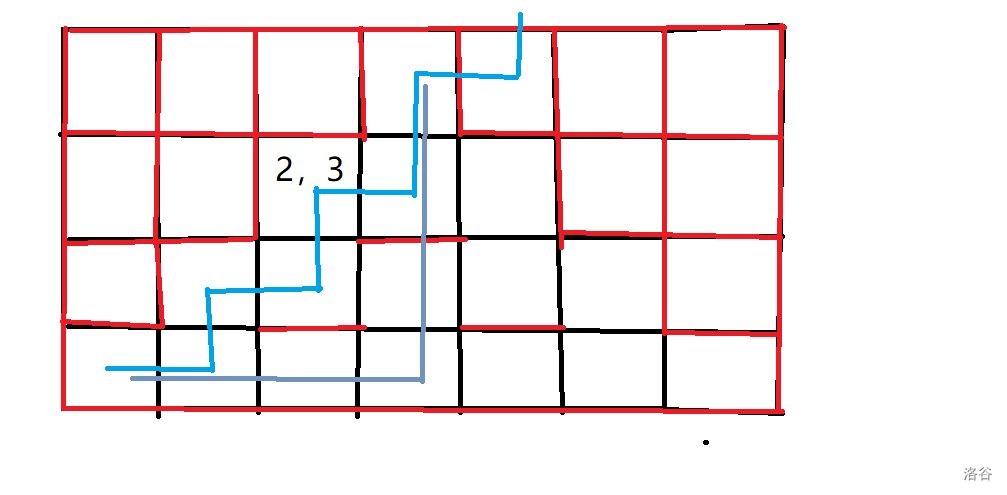
其实我们可以把这个三角形矩阵抽象成一个正方形矩阵：

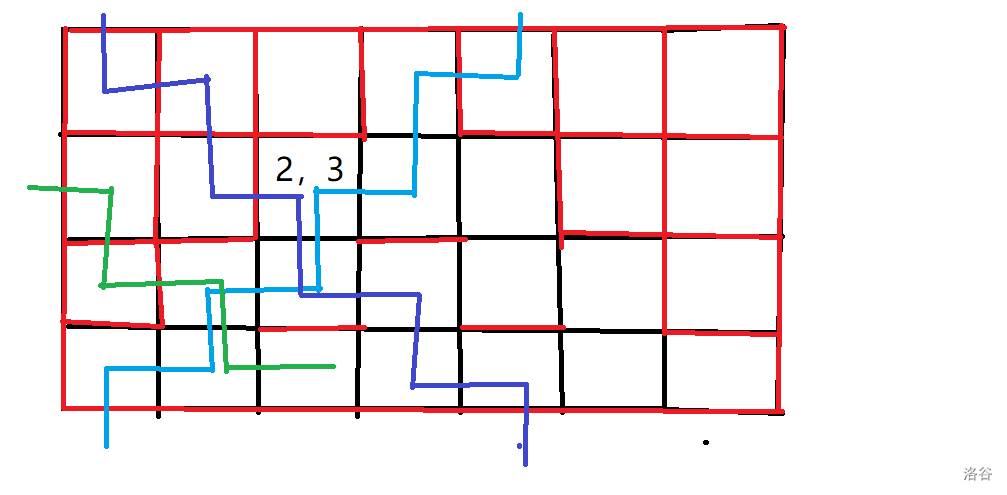
黑色代表可以走，红色则代表不能走。

不难发现我们在原图中画的每一条线（即两条蓝线和一条绿线）都是正好绕过了每一个不能走的边。

首先对于区域 $2$ 和区域 $4$（即线外面的区域），如果只能 $90^{\circ}$ 转弯，那么很显然我们可以把这条折线平移成只拐一次弯的折线，即：

再加上同一纵坐标上的移动，这一条线实质上是绕着长方形边框走了一圈，显然最优。

再看线内：

我们显然希望绕过的红边最少最优，因为每绕过一个红边就要多走两步。

而我们在前面提到我们在原图中画的每一条线（即两条蓝线和一条绿线）都是正好绕过了每一个不能走的边，也就是意味着它走了每一条可以走的边。

或者可以这么理解：我们如果沿着绿线从 $(4,3)$ 往上走，在不向右走的情况下，到达同一纵坐标的横坐标最大，也就是最靠右。如果这个点就是前文提到的交点，那么我们就可以沿着另一条线直接到达。

所以这样的路线一定是最优的。