一致性hash算法

　　数据库分库分表或者是分布式缓存时，不可避免的都会遇到一个问题：如何将数据均匀的分散到各个节点中，并且尽量的在加减节点时能使受影响的数据最少

　　hash取模

       将传入的 Key 按照 index = hash(key) % N 这样来计算出需要存放的节点。其中 hash 函数是一个将字符串转换为正整数的哈希映射方法，N 就是节点的数量。这样可以满足数据的均匀分配，但是这个算法的容错性和扩展性都较差。

        增加或删除了一个节点时，所有的 Key 都需要重新计算，显然这样成本较高，为此需要一个算法满足分布均匀同时也要有良好的容错性和拓展性。

　　一致性Hash算法

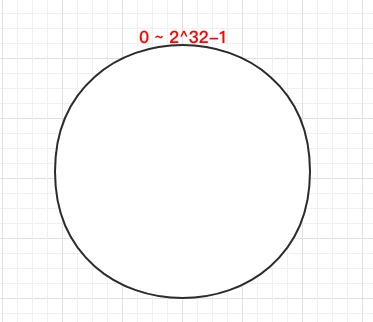
       一致 Hash 算法是将所有的哈希值构成了一个环，其范围在 0 ~ 2^32-1。如下图：

       

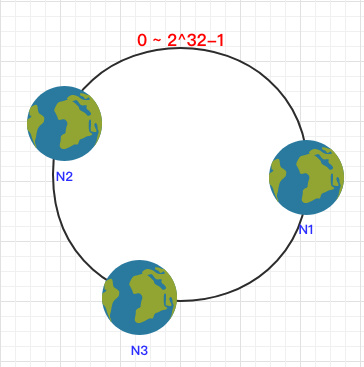
       之后将各个节点散列到这个环上，可以用节点的 IP、hostname 这样的唯一性字段作为 Key 进行 hash(key)，散列之后如下：

　　

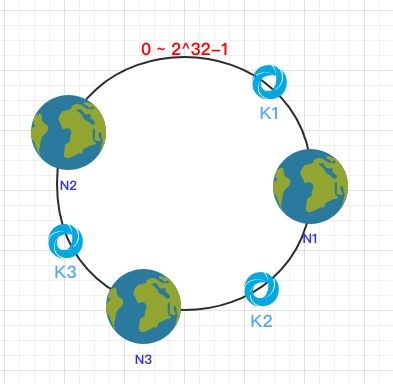
 　　之后需要将数据定位到对应的节点上，使用同样的 hash 函数 将 Key 也映射到这个环上，按照顺时针方向就可以把 k1 定位到 N1节点，k2 定位到 N3节点，k3 定位到 N2节点。

　　

 　　容错性

　　这时假设 N1 宕机：

　　

 

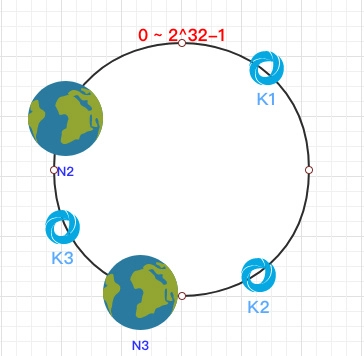
 　　根据顺时针方向，k2 和 k3 保持不变，只有 k1 被重新映射到了 N3。这样就很好的保证了容错性，当一个节点宕机时只会影响到少少部分的数据。

　　拓展性

　　当新增一个节点时:

　　

 　　在 N2 和 N3 之间新增了一个节点 N4 ，这时会发现受印象的数据只有 k3，其余数据也是保持不变，所以这样也很好的保证了拓展性。

        缺点：

　　加减节点 会造成 哈希环 中部分数据 无法命中。当使用 少量节点 时，节点变化 将大范围影响 哈希环 中 数据映射，不适合 少量数据节点 的分布式方案。普通 的 一致性哈希分区 在增减节点时，需要 增加一倍 或 减去一半 节点才能保证 数据 和 负载的均衡。

　　虚拟节点

　　虚拟槽分区 巧妙地使用了 哈希空间，使用 分散度良好 的 哈希函数 把所有数据 映射 到一个 固定范围 的 整数集合 中，整数定义为 槽（slot）。这个范围一般 远远大于 节点数，比如 Redis Cluster 槽范围是 0 ~ 16383。槽 是集群内 数据管理 和 迁移 的 基本单位。采用 大范围槽 的主要目的是为了方便 数据拆分 和 集群扩展。每个节点会负责 一定数量的槽，如图所示：

    

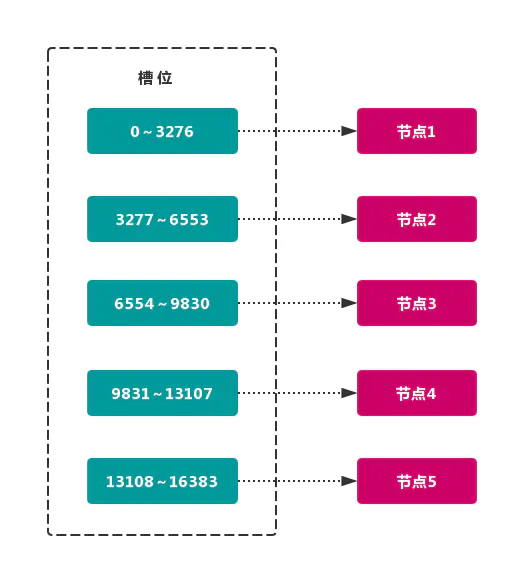
 　　结构很容易 添加 或者 删除 节点。如果 增加 一个节点 6，就需要从节点 1 ~ 5 获得部分 槽 分配到节点 6 上。如果想 移除 节点 1，需要将节点 1 中的 槽 移到节点 2 ~ 5 上，然后将 没有任何槽 的节点 1 从集群中 移除 即可。

　　Redis的数据分区

　　Redis Cluster 采用 虚拟槽分区，所有的 键 根据 哈希函数 映射到 0~16383 整数槽内，计算公式：slot = CRC16（key）& 16383。每个节点负责维护一部分槽以及槽所映射的 键值数据，如图所示：

　　

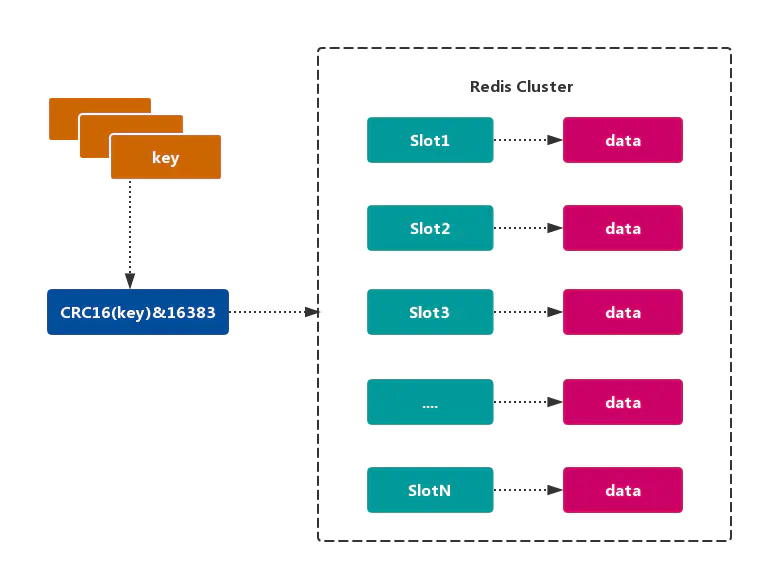
　　和一致性哈希相比

1. 它并不是闭合的，key的定位规则是根据CRC-16(key)%16384的值来判断属于哪个槽区，从而判断该key属于哪个节点，而一致性哈希是根据hash(key)的值来顺时针找第一个hash(ip)的节点，从而确定key存储在哪个节点。
2. 一致性哈希是创建虚拟节点来实现节点宕机后的数据转移并保证数据的安全性和集群的可用性的。redis cluster是采用master节点有多个slave节点机制来保证数据的完整性的,master节点写入数据，slave节点同步数据。当master节点挂机后，slave节点会通过选举机制选举出一个节点变成master节点，实现高可用。但是这里有一点需要考虑，如果master节点存在热点缓存，某一个时刻某个key的访问急剧增高，这时该mater节点可能操劳过度而死，随后从节点选举为主节点后，同样宕机，一次类推，造成缓存雪崩

 一致性hash实现：

初始化一个长度为 N 的数组。
将服务节点通过 hash 算法得到的正整数，同时将节点自身的数据（hashcode、ip、端口等）存放在这里。
完成节点存放后将整个数组进行排序（排序算法有多种）。
客户端获取路由节点时，将自身进行 hash 也得到一个正整数；
遍历这个数组直到找到一个数据大于等于当前客户端的 hash 值，就将当前节点作为该客户端所路由的节点。
如果没有发现比客户端大的数据就返回第一个节点（满足环的特性）

　     实现代码

@Slf4j
@Getter
@Setter
public class SortHashMap {
    private Node[] buckets;

    private static final int DEFAULT_SIZE = 10;

    private int size = 0;

    public SortHashMap() {
        buckets = new Node[DEFAULT_SIZE];
    }

    /**
     * 添加元素
     *
     * @param key
     * @param value
     */
    public void add(Long key, String value) {
        checkSize(size);
        Node node = new Node(key, value);
        buckets[size++] = node;
    }

    public void checkSize(int size) {
        if (size >= buckets.length) {
            int originLen = buckets.length;
            int newLen = originLen + originLen >> 1;
            buckets = Arrays.copyOf(buckets, newLen);
        }
    }

    public void sort() {
        Arrays.sort(buckets, 0, size, Comparator.comparing(Node::getKey));
    }

    public String getAdjoinNode(Long key) {
        if (size == 0) {
            return null;
        }
        for (Node node : buckets) {
            if (node == null) {
                continue;
            }
            if (node.getKey() >= key) {
                return node.getValue();
            }
        }
        return buckets[0].getValue();
    }

    @Override
    public String toString() {
        return "SortHashMap{" +
                "buckets=" + Arrays.toString(buckets) +
                '}';
    }
}

　　改进：不用对数据进行排序；而是在写入的时候就排好顺序，使用TreeMap

@Slf4j
public class TreeMapTest {

    public static void main(String[] args) {
        TreeMap<Long, String> sortMap = new TreeMap<>();
        sortMap.put(4L, "192.168.23.14");
        sortMap.put(64L, "192.168.23.64");
        sortMap.put(164L, "192.168.23.164");
        sortMap.put(200L, "192.168.23.200");

        SortedMap<Long, String> last = sortMap.tailMap(89L);
        if (!last.isEmpty()) {
            log.info("结果:{}", last.get(last.firstKey()));
        } else {
            log.info("结果:{}", sortMap.firstEntry().getValue());
        }
    }
}