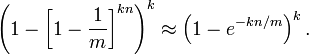Bloom Filter,即布隆过滤器,是一种空间效率很高的随机数据结构。
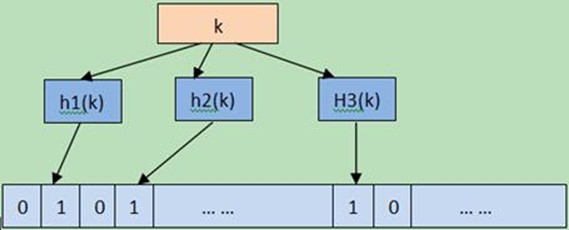
原理:开辟m个bit位数组的空间,并全部置零,使用k个哈希函数将元素映射到数组中,相应位置1.如下图,元素K通过哈希函数h1,h2,h3在数组上置1。
LevelDB中加入bloom filter的支持。目前针对一次查询,LevelDB可能需要在每个level上进行一次磁盘随机访问。通过使用bloom filter可以大大减少所需要的磁盘I/O操作。比如,假设调用者正在查找一个值为"Foo"的key,LevelDB会从每个level下选择相应的SSTable文件(那些range包含了该key的文件),之后会在这些SSTable文件上进行随机读。如果每个SSTable都有一个对应的bloom filter,那么查找时就可以很容易地通过检查bloom filter跳过那些不包含该key的SSTable文件。
在leveldb的实现中,Name()返回"leveldb.BuiltinBloomFilter",因此metaindex block 中的key就是"filter.leveldb.BuiltinBloomFilter"。Leveldb使用了double hashing来模拟多个hash函数,当然这里不是用来解决冲突的。
和线性再探测(linearprobing)一样,Double hashing从一个hash值开始,重复向前迭代,直到解决冲突或者搜索完hash表。不同的是,double hashing使用的是另外一个hash函数,而不是固定的步长。
给定两个独立的hash函数h1和h2,对于hash表T和值k,第i次迭代计算出的位置就是:h(i, k) = (h1(k) + i*h2(k)) mod |T|。
对此,Leveldb选择的hash函数是:
Gi(x)=H1(x)+iH2(x)
H2(x)=(H1(x)>>17) | (H1(x)<<15)
H1是一个基本的hash函数,H2是由H1循环右移得到的,Gi(x)就是第i次循环得到的hash值。【理论分析可参考论文Kirsch,Mitzenmacher2006】
说明bloomfliter 的原理之后来看下Leveldb是怎么来实现它的, 使用CreateFilter创建一个bloomfliter
virtual void CreateFilter(const Slice* keys, int n, std::string* dst) const { // Compute bloom filter size (in both bits and bytes) size_t bits = n * bits_per_key_; // For small n, we can see a very high false positive rate. Fix it // by enforcing a minimum bloom filter length. if (bits < 64) bits = 64; size_t bytes = (bits + 7) / 8; bits = bytes * 8; const size_t init_size = dst->size(); dst->resize(init_size + bytes, 0); dst->push_back(static_cast<char>(k_)); // Remember # of probes in filter char* array = &(*dst)[init_size]; for (size_t i = 0; i < n; i++) { // Use double-hashing to generate a sequence of hash values. // See analysis in [Kirsch,Mitzenmacher 2006]. uint32_t h = BloomHash(keys[i]); const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits for (size_t j = 0; j < k_; j++) { const uint32_t bitpos = h % bits; array[bitpos/8] |= (1 << (bitpos % 8)); h += delta; } } }
函数KeyMayMatch ()在读取数据的时候调用
virtual bool KeyMayMatch(const Slice& key, const Slice& bloom_filter) const { const size_t len = bloom_filter.size(); if (len < 2) return false; const char* array = bloom_filter.data(); const size_t bits = (len - 1) * 8; // Use the encoded k so that we can read filters generated by // bloom filters created using different parameters. const size_t k = array[len-1]; if (k > 30) { // Reserved for potentially new encodings for short bloom filters. // Consider it a match. return true; } uint32_t h = BloomHash(key); const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits for (size_t j = 0; j < k; j++) { const uint32_t bitpos = h % bits; if ((array[bitpos/8] & (1 << (bitpos % 8))) == 0) return false; h += delta; } return true; }
计算key的hash值,重复计算阶段的步骤,循环计算k个hash值,只要有一个结果对应的bit位为0,就认为不匹配,否则认为匹配。
错误率估计
但Bloom Filter的这种高效是有一定代价的:在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误认为属于这个集合(false positive)。因此,Bloom Filter不适合那些"零错误"的应用场合。而在能容忍低错误率的应用场合下,Bloom Filter通过极少的错误换取了存储空间的极大节省。
吴军的数学之美中对Bloom Filter的错误率有详细解释。
假设 Hash 函数以等概率条件选择并设置 Bit Array 中的某一位,m 是该位数组的大小,k 是 Hash 函数的个数,那么位数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位的概率是:
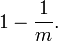
那么在所有 k 次 Hash 操作后该位都没有被置 "1" 的概率是:

如果我们插入了 n 个元素,那么某一位仍然为 "0" 的概率是:
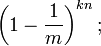
因而该位为 "1"的概率是:
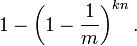
现在检测某一元素是否在该集合中。标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 "1",但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中(False Positives),该概率由以下公式确定: