DASCTF复盘 (二)、RE -> 奇怪的交易 & python逆向

奇怪的交易

一、查壳

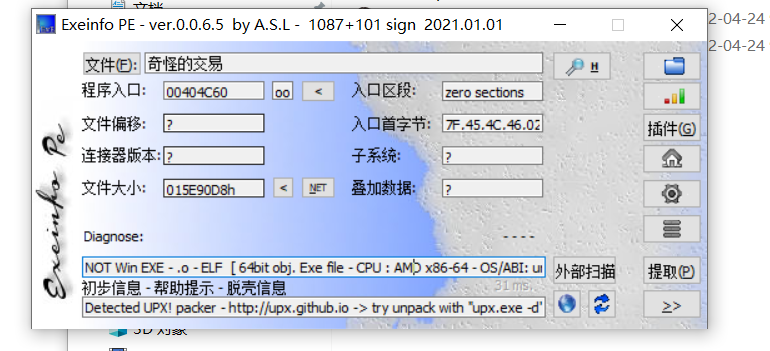
64位的upx壳，放到linux下直接upx -d脱掉

二、IDA静态分析

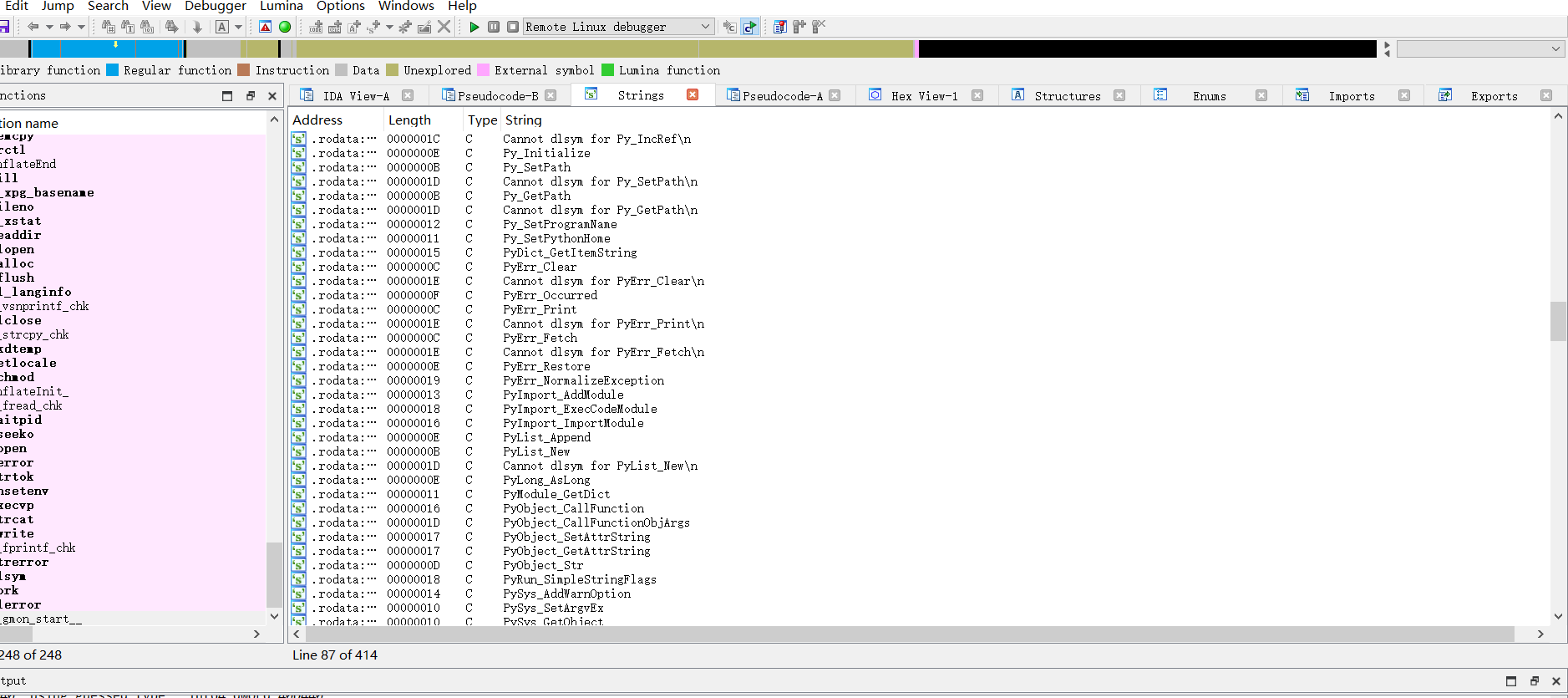
看这些字符串，大部分都有py前缀，猜测为python打包的elf文件

三、python解包

1、dump出pydata段

在Linux下直接dump出pydata段

objcopy --dump-section pydata=unwerid.dump qgdjy

得到.dump文件

2、解包dump文件

我们在相对应的python版本(需要是python3.10，不然有可能得不到.pyz文件)

python310.exe pyinstxtractor.py unwerid.dump

3、修改模数

奇怪的交易.pyc

根据struct.pyc修改前16个字节

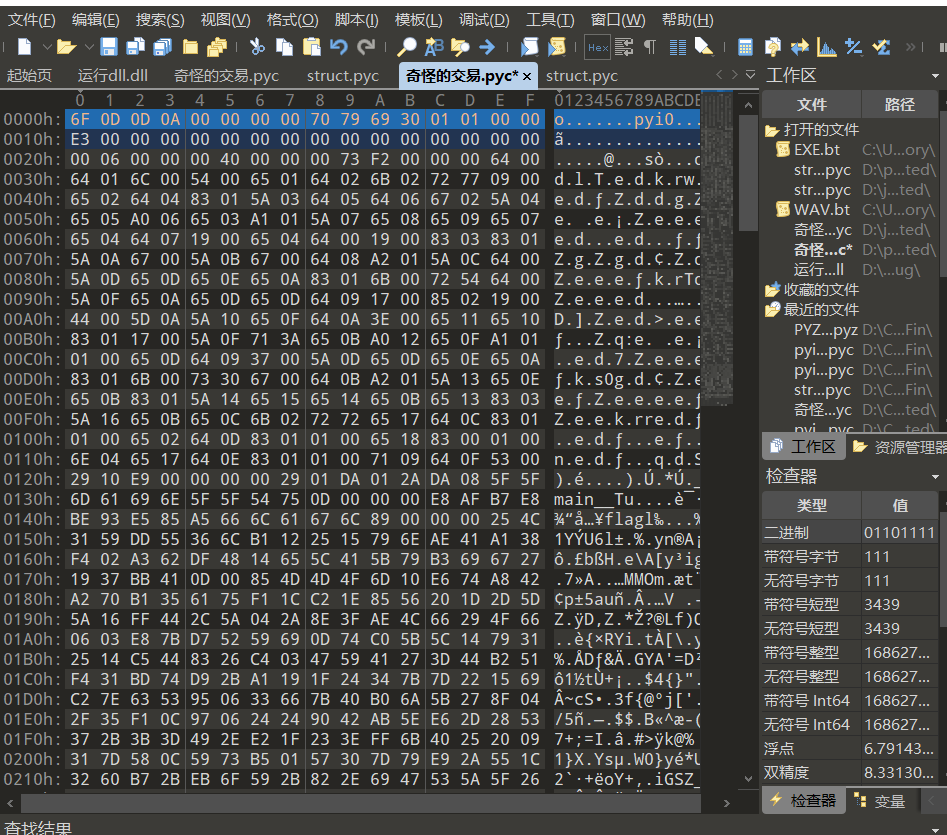
4、反编译奇怪的交易.pyc

pycdc '/home/tlsn/Desktop/Ctf/奇怪的交易.pyc' //需要下载pycdc工具

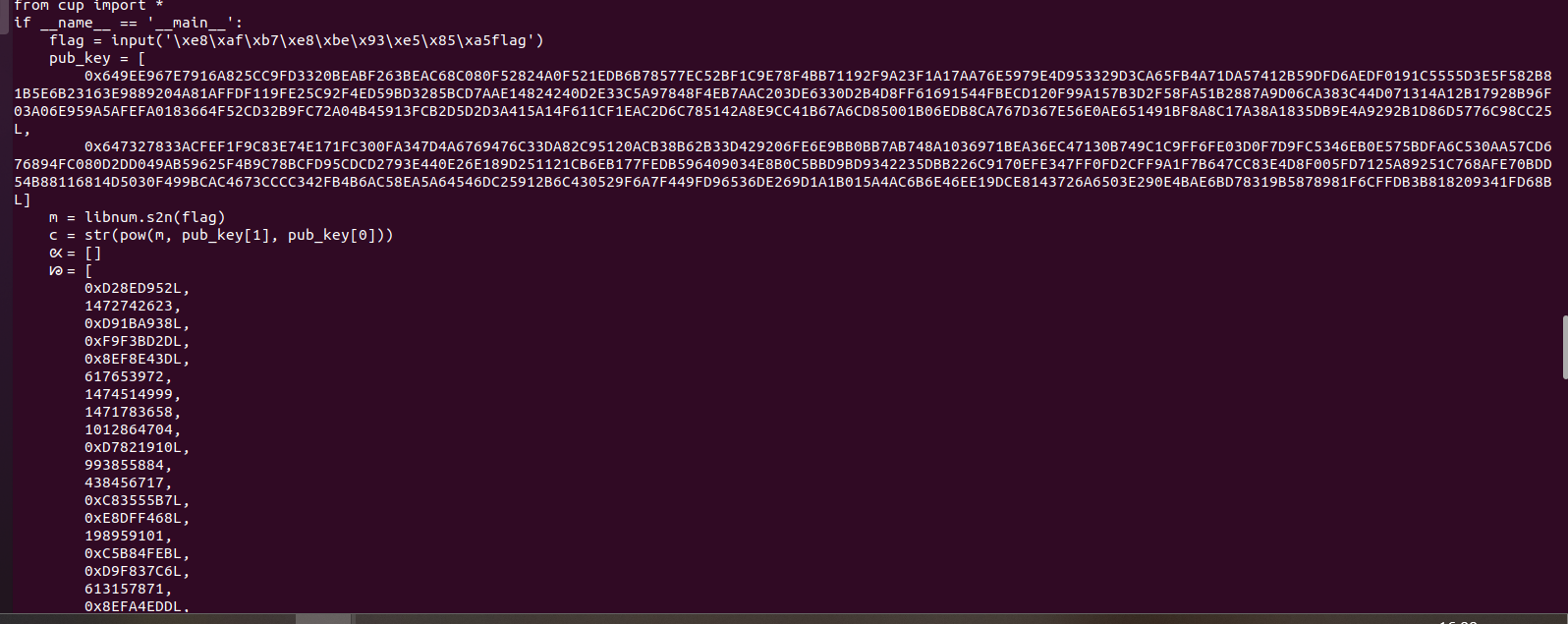
得到解密代码

# Source Generated with Decompyle++
# File: 奇怪的交易.pyc (Python 3.10)

from cup import *
if __name__ == '__main__':
    flag = input('\xe8\xaf\xb7\xe8\xbe\x93\xe5\x85\xa5flag')
    pub_key = [
        0x649EE967E7916A825CC9FD3320BEABF263BEAC68C080F52824A0F521EDB6B78577EC52BF1C9E78F4BB71192F9A23F1A17AA76E5979E4D953329D3CA65FB4A71DA57412B59DFD6AEDF0191C5555D3E5F582B81B5E6B23163E9889204A81AFFDF119FE25C92F4ED59BD3285BCD7AAE14824240D2E33C5A97848F4EB7AAC203DE6330D2B4D8FF61691544FBECD120F99A157B3D2F58FA51B2887A9D06CA383C44D071314A12B17928B96F03A06E959A5AFEFA0183664F52CD32B9FC72A04B45913FCB2D5D2D3A415A14F611CF1EAC2D6C785142A8E9CC41B67A6CD85001B06EDB8CA767D367E56E0AE651491BF8A8C17A38A1835DB9E4A9292B1D86D5776C98CC25L,
        0x647327833ACFEF1F9C83E74E171FC300FA347D4A6769476C33DA82C95120ACB38B62B33D429206FE6E9BB0BB7AB748A1036971BEA36EC47130B749C1C9FF6FE03D0F7D9FC5346EB0E575BDFA6C530AA57CD676894FC080D2DD049AB59625F4B9C78BCFD95CDCD2793E440E26E189D251121CB6EB177FEDB596409034E8B0C5BBD9BD9342235DBB226C9170EFE347FF0FD2CFF9A1F7B647CC83E4D8F005FD7125A89251C768AFE70BDD54B88116814D5030F499BCAC4673CCCC342FB4B6AC58EA5A64546DC25912B6C430529F6A7F449FD96536DE269D1A1B015A4AC6B6E46EE19DCE8143726A6503E290E4BAE6BD78319B5878981F6CFFDB3B818209341FD68BL]
    m = libnum.s2n(flag)
    c = str(pow(m, pub_key[1], pub_key[0]))
    ᘡ = []
    ᘙ = [
        0xD28ED952L,
        1472742623,
        0xD91BA938L,
        0xF9F3BD2DL,
        0x8EF8E43DL,
        617653972,
        1474514999,
        1471783658,
        1012864704,
        0xD7821910L,
        993855884,
        438456717,
        0xC83555B7L,
        0xE8DFF468L,
        198959101,
        0xC5B84FEBL,
        0xD9F837C6L,
        613157871,
        0x8EFA4EDDL,
        97286225,
        0x8B4B608CL,
        1471645170,
        0xC0B62792L,
        583597118,
        0xAAB1C22DL,
        0xBDB9C266L,
        1384330715,
        0xAE9F9816L,
        0xD1F40B3CL,
        0x8206DDC3L,
        0xC4E0BADCL,
        0xE407BD26L,
        145643141,
        0x8016C6A5L,
        0xAF4AB9D3L,
        506798154,
        994590281,
        0x85082A0BL,
        0xCA0BC95AL,
        0xA7BE567CL,
        1105937096,
        1789727804,
        0xDFEFB591L,
        0x93346B38L,
        1162286478,
        680814033,
        0xAEE1A7A2L,
        0x80E574AEL,
        0xF154F55FL,
        2121620700,
        0xFCBDA653L,
        0x8E902444L,
        0xCA742E12L,
        0xB8424071L,
        0xB4B15EC2L,
        0x943BFA09L,
        0xBC97CD93L,
        1285603712,
        798920280,
        0x8B58328FL,
        0xF9822360L,
        0xD1FD15EEL,
        1077514121,
        1436444106,
        0xA2D6C17EL,
        1507202797,
        500756149,
        198754565,
        0x8E014807L,
        880454148,
        1970517398,
        0xBFC6EE25L,
        1161840191,
        560498076,
        1782600856,
        0x9D93FEBEL,
        1285196205,
        788797746,
        1195724574,
        0xF2174A07L,
        103427523,
        0x952BFE83L,
        0xF730AC4CL,
        617564657,
        978211984,
        1781482121,
        0x8379D23AL,
        0xEAD737EEL,
        0xE41555FBL,
        659557668,
        0x99F3B244L,
        1561884856,
        0x842C31A4L,
        1189296962,
        169145316,
        0xA5CE044CL,
        1323893433,
        824667876,
        408202876,
        0xE0178482L,
        0xF412BBBCL,
        1508996065,
        162419237,
        0xDE740B00L,
        0xB7CB64FDL,
        0xEBCADB1FL,
        0x8EAE2326L,
        0x933C216CL,
        0xD7D1F649L,
        481927014,
        0xA448AC16L,
        0xBC082807L,
        1261069441,
        2063238535,
        0x8474A61DL,
        101459755,
        0xBC5654D1L,
        1721190841,
        1078395785,
        176506553,
        0xD3C5280FL,
        1566142515,
        1938949000,
        1499289517,
        0xC59872F8L,
        829714860,
        0xE51502A2L,
        952932374,
        1283577465,
        2045007203,
        0xEBE6A798L,
        0xE09575CDL,
        0xADDF4157L,
        0xC4770191L,
        482297421,
        1734231412,
        0xDAC71054L,
        0x99807E43L,
        0xA88D74B1L,
        0xCB77E028L,
        1533519803,
        0xEEEBC3B6L,
        0xE7E680E5L,
        272960248,
        317508587,
        0xC4B10CDCL,
        0x91776399L,
        27470488,
        1666674386,
        1737927609,
        750987808,
        0x8E364D8FL,
        0xA0985A77L,
        562925334,
        0x837D6DC3L]
    i = 0
    if i < len(c):
        ᘞ = 0
        ᘡ.append(ᘞ)
        i += 4
        if not i < len(c):
            ᘝ = [
                54,
                54,
                54,
                54]
            ᘠ = len(ᘡ)
            res = encrypt(ᘠ, ᘡ, ᘝ)
            if ᘡ == ᘙ:
                print('You are right!')
                input('')
                quit()
            else:
                print('Why not drink a cup of tea and have a rest?')
    continue

结合python的字节码，可以发现这个反编译不完整，为此，我们需要手撸字节码

import libnum
from cup import *

if __name__ == '__main__':
    flag = input('请输入flag')
    pub_key = [12702192797044914024075774649965354105344232304099465264316470282606351700311177624703682814557100043599414982439635470829841890299241342602374578366076034128412992290094164613120745611751102797279925764448133764246126488845600641524814194290745105708735258127757986238766868988676022258542038318776640732920027324986285887310132372524224961045858183153047991881042129131551711617627844146600513830709959185824512201669420128585170924683844128155435146399996585220865423125338735154727569986267948480523307784641442521735105741341230032585576300299944879647981670048377150556292280650846158185797588466680532743801893,12680615221091469696163926483122992106481999501435284497098601343706982733487916553201934931961274845294041438909951977672521864927961654544622905443692482152403380984734291652023321187458458985625147422841102922314725726207365632256563373977251725785357590588556314671253970422319546403985257810950046085994573229162322957630767327089195523762665081311711474689269184996318744510300057603532953644164998953897411177604349567514705039306693117602798453972917348902600111420473965929048876821563646206875034926505783009957256212261250539005023918242209009676914632796839852778318989278092929214021282438144809708279435]
    m = libnum.s2n(flag)        #字符串转化为整形
    c = str(pow(m,pub_key[1] ,pub_key[0]))
    aaa = []
    bbb = [3532577106, 1472742623, 3642468664, 4193500461, 2398676029, 617653972, 1474514999, 1471783658, 1012864704, 3615627536, 993855884, 438456717, 3358938551, 3906991208, 198959101, 3317190635, 3656923078, 613157871, 2398768861, 97286225, 2336972940, 1471645170, 3233163154, 583597118, 2863776301, 3183067750, 1384330715, 2929694742, 3522431804, 2181488067, 3303062236, 3825712422, 145643141, 2148976293, 2940910035, 506798154, 994590281, 2231904779, 3389770074, 2814269052, 1105937096, 1789727804, 3757028753, 2469686072, 1162286478, 680814033, 2934024098, 2162521262, 4048876895, 2121620700, 4240287315, 2391811140, 3396611602, 3091349617, 3031523010, 2486958601, 3164065171, 1285603712, 798920280, 2337813135, 4186055520, 3523024366, 1077514121, 1436444106, 2731983230, 1507202797, 500756149, 198754565, 2382448647, 880454148, 1970517398, 3217485349, 1161840191, 560498076, 1782600856, 2643721918, 1285196205, 788797746, 1195724574, 4061612551, 103427523, 2502688387, 4147162188, 617564657, 978211984, 1781482121, 2205798970, 3939973102, 3826603515, 659557668, 2582884932, 1561884856, 2217488804, 1189296962, 169145316, 2781742156, 1323893433, 824667876, 408202876, 3759637634, 4094868412, 1508996065, 162419237, 3732146944, 3083560189, 3955940127, 2393776934, 2470191468, 3620861513, 481927014, 2756226070, 3154651143, 1261069441, 2063238535, 2222237213, 101459755, 3159774417, 1721190841, 1078395785, 176506553, 3552913423, 1566142515, 1938949000, 1499289517, 3315102456, 829714860, 3843359394, 952932374, 1283577465, 2045007203, 3957761944, 3767891405, 2917089623, 3296133521, 482297421, 1734231412, 3670478932, 2575334979, 2827842737, 3413631016, 1533519803, 4008428470, 3890643173, 272960248, 317508587, 3299937500, 2440520601, 27470488, 1666674386, 1737927609, 750987808, 2385923471, 2694339191, 562925334, 2206035395]
    i= 0
    while i < len(c) :
        ccc = 0
        for ii in c[slice(i,i+4)]:       #slice函数！！！！！
            ccc = ord(ii) + (ccc<<8)   #调用函数后，堆栈恢复原来再加1的位置
        aaa.append(ccc)
        i = i + 4
        if i >= len(c):          #选择不跳
            ddd = [54, 54, 54, 54]
            eee = len(aaa)
            res = encrypt(eee,aaa,ddd)
    if aaa == bbb:
        print("You are right")
        input('')
        quit()
    else:
        print("Why not drink a cup of tea and have a rest?")

程序代码流程中flag作为明文经过了RSA加密，其密文到最后被用于了encrypt函数中

我们发现，encrypt函数未知，且程序使用了位置的cup包，猜测cencrypt函数来自cup包

而cup包中的文件就藏在.pyz文件夹中

下图就是存放cup包的文件夹

但cup.pyc文件被加密了

加密的方法与密钥在下图中

archive.pyc就是加密的过程，crypto_key是加密的密钥，而我们现在就需要解密.pyz文件

四、解密.pyz文件

1、获取密钥

https://tool.lu/pyc/

2、解密

这里我们直接引用别人的解密脚本...

import tinyaes
import zlib

CRYPT_BLOCK_SIZE = 16

# 从crypt_key.pyc获取key，也可自行反编译获取
key = bytes('0000000000000tea', 'utf-8')

inf = open('cup.pyc.encrypted', 'rb')  # 打开加密文件
outf = open('cup.pyc', 'wb')  # 输出文件

# 按加密块大小进行读取
iv = inf.read(CRYPT_BLOCK_SIZE)

cipher = tinyaes.AES(key, iv)

# 解密
plaintext = zlib.decompress(cipher.CTR_xcrypt_buffer(inf.read()))

# 补pyc头(最后自己补也行)
outf.write(b'\x6f\x0d\x0d\x0a\0\0\0\0\0\0\0\0\0\0\0\0')

# 写入解密数据
outf.write(plaintext)

inf.close()
outf.close()

最后得到cup.pyc文件

3、反编译cup.pyc

pycdc cup.pyc > cuppyc.txt

即得到cup的encrypt函数

# Source Generated with Decompyle++
# File: cup.pyc (Python 3.10)

import libnum
from ctypes import *

def MX(z, y, total, key, p, e):
    temp1 = (z.value >> 5 ^ y.value << 2) + (y.value >> 3 ^ z.value << 4)
    temp2 = (total.value ^ y.value) + (key[p & 3 ^ e.value] ^ z.value)
    return c_uint32(temp1 ^ temp2)


def encrypt(ᘗ, ᘖ, ᘘ):
    ᘜ = 0x9E3779B9L
    ᘛ = 6 + 52 // ᘗ
    total = c_uint32(0)
    ᘔ = c_uint32(ᘖ[ᘗ - 1])
    ᘕ = c_uint32(0)
    if ᘛ > 0:
        total.value += ᘜ
        ᘕ.value = total.value >> 2 & 3
        ᘚ = c_uint32(ᘖ[0])
        ᘖ[ᘗ - 1] = c_uint32(ᘖ[ᘗ - 1] + MX(ᘔ, ᘚ, total, ᘘ, ᘗ - 1, ᘕ).value).value
        ᘔ.value = ᘖ[ᘗ - 1]
        ᘛ -= 1
        if not ᘛ > 0:
            return ᘖ

很明显是xxTEA加密

五、解密

首先是xxTEA加密

1、xxTEA解密算法

#include <stdio.h>  
#include <stdint.h>  

#define DELTA 0x9e3779b9  
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))  
  
void btea(uint32_t *v, int n, uint32_t const key[4])  
{  
    uint32_t y, z, sum;  
    unsigned p, rounds, e;  
    if (n > 1)            /* Coding Part */  
    {  
        rounds = 6 + 52/n;  
        sum = 0;  
        z = v[n-1];  
        do  
        {  
            sum += DELTA;  
            e = (sum >> 2) & 3;  
            for (p=0; p<n-1; p++)  
            {  
                y = v[p+1];  
                z = v[p] += MX;  
            }  
            y = v[0];  
            z = v[n-1] += MX;  
        }  
        while (--rounds);  
    }  
    else if (n < -1)      /* Decoding Part */  
    {  
        n = -n;  
        rounds = 6 + 52/n;  
        sum = rounds*DELTA;  
        y = v[0];  
        do  
        {  
            e = (sum >> 2) & 3;  
            for (p=n-1; p>0; p--)  
            {  
                z = v[p-1];  
                y = v[p] -= MX;  
            }  
            z = v[n-1];  
            y = v[0] -= MX;  
            sum -= DELTA;  
        }  
        while (--rounds);  
    }  
}  
  
void xxTea()
{
    //密文// 168-14+1 = 155
    uint32_t v[155]= {3532577106, 1472742623, 3642468664, 4193500461, 2398676029, 617653972, 1474514999, 1471783658, 1012864704, 3615627536, 993855884, 438456717, 3358938551, 3906991208, 198959101, 3317190635, 3656923078, 613157871, 2398768861, 97286225, 2336972940, 1471645170, 3233163154, 583597118, 2863776301, 3183067750, 1384330715, 2929694742, 3522431804, 2181488067, 3303062236, 3825712422, 145643141, 2148976293, 2940910035, 506798154, 994590281, 2231904779, 3389770074, 2814269052, 1105937096, 1789727804, 3757028753, 2469686072, 1162286478, 680814033, 2934024098, 2162521262, 4048876895, 2121620700, 4240287315, 2391811140, 3396611602, 3091349617, 3031523010, 2486958601, 3164065171, 1285603712, 798920280, 2337813135, 4186055520, 3523024366, 1077514121, 1436444106, 2731983230, 1507202797, 500756149, 198754565, 2382448647, 880454148, 1970517398, 3217485349, 1161840191, 560498076, 1782600856, 2643721918, 1285196205, 788797746, 1195724574, 4061612551, 103427523, 2502688387, 4147162188, 617564657, 978211984, 1781482121, 2205798970, 3939973102, 3826603515, 659557668, 2582884932, 1561884856, 2217488804, 1189296962, 169145316, 2781742156, 1323893433, 824667876, 408202876, 3759637634, 4094868412, 1508996065, 162419237, 3732146944, 3083560189, 3955940127, 2393776934, 2470191468, 3620861513, 481927014, 2756226070, 3154651143, 1261069441, 2063238535, 2222237213, 101459755, 3159774417, 1721190841, 1078395785, 176506553, 3552913423, 1566142515, 1938949000, 1499289517, 3315102456, 829714860, 3843359394, 952932374, 1283577465, 2045007203, 3957761944, 3767891405, 2917089623, 3296133521, 482297421, 1734231412, 3670478932, 2575334979, 2827842737, 3413631016, 1533519803, 4008428470, 3890643173, 272960248, 317508587, 3299937500, 2440520601, 27470488, 1666674386, 1737927609, 750987808, 2385923471, 2694339191, 562925334, 2206035395};
    //密钥// 
    uint32_t const k[4]= {54,54,54,54};  
    int n= 2; 
    btea(v, -155, k);
    printf("解密后的数据为:\n");
    for(int i = 0;i<=154;i++){
         printf("%u",v[i]);
    }  
    
}
int main()  
{  

    //Tea();
    //xTea();
    xxTea();
    return 0;  
}  

//82524318580866181489254815189294161689287685790912952396004997084221752782570270782563666382550584887616363587603256787603307395952696890926034394307768289235256989254738489287659889280927394274821092623467680846546292629944880885816389267896690939192194320773190965356185899268887570667280892523389254865880853151280879314290945541690939141687564062987563960884254366892590699380872760880899077089281105880846571495998417895985464585886341285879608285879634585905899380866207380846571587563908887596882294320824987577016884202066087603281895998520580905425989261291695972382594281477494281400085925714487557458092636575380866258290938987889261394594268344592590674084208670590926008390912901582550532895946117394274898482537476994327300890912952394268446684241285482550482180872811484234782687616338380899102885906028192649605585879633995985387587590123795985362187603307884228152592597278680879416195965701082570091890971960995978808695985387484208440887557560890971756095965752784234885395985310584261074395946040189235231380866155380899000192590648795965778494287902587590149792610335095965727287590226390919556892610155590932511389274449884261048289241605380846494985879608980898949784215173682583224487557483985886315585925611787564088789254917394327275287603358992629995480899051684208670789294136690945541189254917785886239182550482087603205180866130585912376392610232984201886757

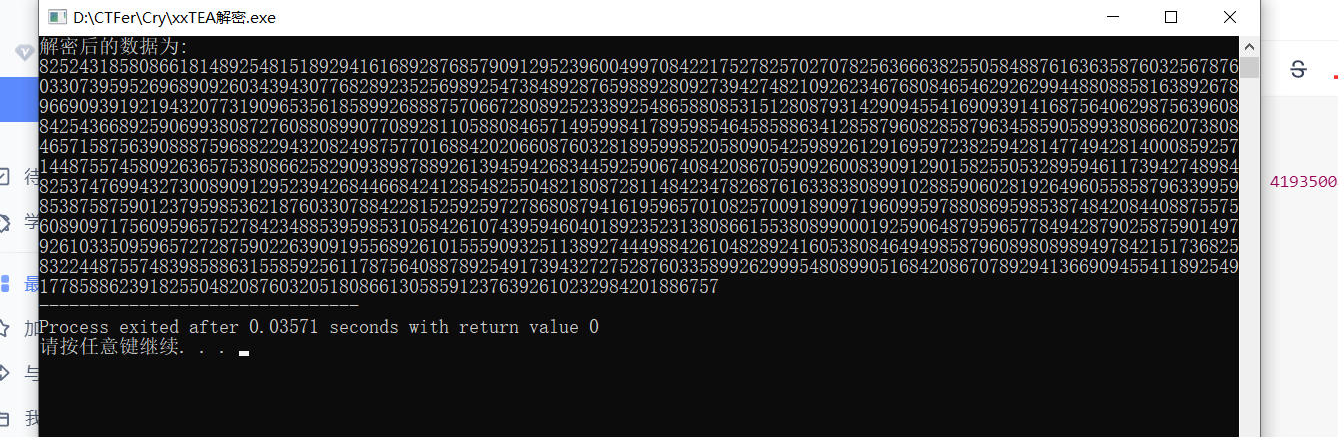
2、逆推密文

结合反编译的奇怪的交易.py文件，我们发现，RSA加密后得到的密文被加密了，我们需要逆推密文

逆推的方法我没有想到，我这里直接爆破得到密文

aaa=  "82524318580866181489254815189294161689287685790912952396004997084221752782570270782563666382550584887616363587603256787603307395952696890926034394307768289235256989254738489287659889280927394274821092623467680846546292629944880885816389267896690939192194320773190965356185899268887570667280892523389254865880853151280879314290945541690939141687564062987563960884254366892590699380872760880899077089281105880846571495998417895985464585886341285879608285879634585905899380866207380846571587563908887596882294320824987577016884202066087603281895998520580905425989261291695972382594281477494281400085925714487557458092636575380866258290938987889261394594268344592590674084208670590926008390912901582550532895946117394274898482537476994327300890912952394268446684241285482550482180872811484234782687616338380899102885906028192649605585879633995985387587590123795985362187603307884228152592597278680879416195965701082570091890971960995978808695985387484208440887557560890971756095965752784234885395985310584261074395946040189235231380866155380899000192590648795965778494287902587590149792610335095965727287590226390919556892610155590932511389274449884261048289241605380846494985879608980898949784215173682583224487557483985886315585925611787564088789254917394327275287603358992629995480899051684208670789294136690945541189254917785886239182550482087603205180866130585912376392610232984201886757"
cc = ""
print(len(aaa))#1512
arr = "1234567890"
num = 0
while num <= len(aaa) :
    index = aaa[num : num+9]
    num += 9
    IntIndex = int(index)
    if num == 1386+9:       #不是9的整数，最后多出两位,我们需要拿出来单独考虑
        cc += str(9)
        break
    #print(IntIndex)
    for a in arr:
        for b in arr:
            for c in arr:
                for d in arr:
                    guess = a+b+c+d
                    s = 0
                    for ii in guess:
                        s = (s << 8) + ord(ii)
                    if s == IntIndex:
                        cc += guess
print(cc)
#10610336534759505889607399322387179316771488492347274741918862678692508953185876570981227584004676580623553664818853686933004290078153620168054665086468417541382824708104480882577200529822968531743002301934310349005341104696887943182074473298650903541494918266823037984054778903666406545980557074219162536057146090758158128189406073809226361445046225524917089434897957301396534515964547462425719205819342172669899546965221084098690893672595962129879041507903210851706793788311452973769358455761907303633956322972510500253009083922781934406731633755418753858930476576720874219359466503538931371444470303193503733920039

自此，我们拥有密文，拥有指数e，拥有模N，只需要求出明文flag即可

3、RSA维纳攻击

我看了看维纳攻击算法，还没有看明白，不是很懂，先直接抄的别人的算法

import gmpy2


def transform(x, y):  # 使用辗转相处将分数 x/y 转为连分数的形式
    res = []
    while y:
        res.append(x // y)
        x, y = y, x % y
    return res


def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return denominator, numerator  # 得到渐进分数的分母和分子，并返回


# 求解每个渐进分数
def sub_fraction(x, y):
    res = transform(x, y)
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def get_pq(a, b, c):  # 由p+q和pq的值通过维达定理来求解p和q
    par = gmpy2.isqrt(b * b - 4 * a * c)  # 由上述可得，开根号一定是整数，因为有解
    x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
    return x1, x2


def wienerAttack(e, n):
    for (d, k) in sub_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        px, qy = get_pq(1, n - phi + 1, n)
        if px * qy == n:
            p, q = abs(int(px)), abs(int(qy))  # 可能会得到两个负数，负负得正未尝不会出现
            d = gmpy2.invert(e, (p - 1) * (q - 1))  # 求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元d
            return d
    print("该方法不适用")


e = 12680615221091469696163926483122992106481999501435284497098601343706982733487916553201934931961274845294041438909951977672521864927961654544622905443692482152403380984734291652023321187458458985625147422841102922314725726207365632256563373977251725785357590588556314671253970422319546403985257810950046085994573229162322957630767327089195523762665081311711474689269184996318744510300057603532953644164998953897411177604349567514705039306693117602798453972917348902600111420473965929048876821563646206875034926505783009957256212261250539005023918242209009676914632796839852778318989278092929214021282438144809708279435
n = 12702192797044914024075774649965354105344232304099465264316470282606351700311177624703682814557100043599414982439635470829841890299241342602374578366076034128412992290094164613120745611751102797279925764448133764246126488845600641524814194290745105708735258127757986238766868988676022258542038318776640732920027324986285887310132372524224961045858183153047991881042129131551711617627844146600513830709959185824512201669420128585170924683844128155435146399996585220865423125338735154727569986267948480523307784641442521735105741341230032585576300299944879647981670048377150556292280650846158185797588466680532743801893
d = wienerAttack(e, n)
print("d=", d)

#33571675128122591561306367006363497084111816786422461826474644084160755024963

这样可以求出来d

4、求得明文flag

有了d之后，我们就可以直接解出flag了:

import gmpy2


def transform(x, y):  # 使用辗转相处将分数 x/y 转为连分数的形式
    res = []
    while y:
        res.append(x // y)
        x, y = y, x % y
    return res


def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return denominator, numerator  # 得到渐进分数的分母和分子，并返回


# 求解每个渐进分数
def sub_fraction(x, y):
    res = transform(x, y)
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def get_pq(a, b, c):  # 由p+q和pq的值通过维达定理来求解p和q
    par = gmpy2.isqrt(b * b - 4 * a * c)  # 由上述可得，开根号一定是整数，因为有解
    x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
    return x1, x2


def wienerAttack(e, n):
    for (d, k) in sub_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        px, qy = get_pq(1, n - phi + 1, n)
        if px * qy == n:
            p, q = abs(int(px)), abs(int(qy))  # 可能会得到两个负数，负负得正未尝不会出现
            d = gmpy2.invert(e, (p - 1) * (q - 1))  # 求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元d
            return d
    print("该方法不适用")

from Crypto.Util.number import long_to_bytes
e = 12680615221091469696163926483122992106481999501435284497098601343706982733487916553201934931961274845294041438909951977672521864927961654544622905443692482152403380984734291652023321187458458985625147422841102922314725726207365632256563373977251725785357590588556314671253970422319546403985257810950046085994573229162322957630767327089195523762665081311711474689269184996318744510300057603532953644164998953897411177604349567514705039306693117602798453972917348902600111420473965929048876821563646206875034926505783009957256212261250539005023918242209009676914632796839852778318989278092929214021282438144809708279435
n = 12702192797044914024075774649965354105344232304099465264316470282606351700311177624703682814557100043599414982439635470829841890299241342602374578366076034128412992290094164613120745611751102797279925764448133764246126488845600641524814194290745105708735258127757986238766868988676022258542038318776640732920027324986285887310132372524224961045858183153047991881042129131551711617627844146600513830709959185824512201669420128585170924683844128155435146399996585220865423125338735154727569986267948480523307784641442521735105741341230032585576300299944879647981670048377150556292280650846158185797588466680532743801893
d = wienerAttack(e, n)
print("d=", d)

c= 10610336534759505889607399322387179316771488492347274741918862678692508953185876570981227584004676580623553664818853686933004290078153620168054665086468417541382824708104480882577200529822968531743002301934310349005341104696887943182074473298650903541494918266823037984054778903666406545980557074219162536057146090758158128189406073809226361445046225524917089434897957301396534515964547462425719205819342172669899546965221084098690893672595962129879041507903210851706793788311452973769358455761907303633956322972510500253009083922781934406731633755418753858930476576720874219359466503538931371444470303193503733920039

flag = pow(c,d,n)
print(flag)
print(long_to_bytes(flag))

#10610336534759505889607399322387179316771488492347274741918862678692508953185876570981227584004676580623553664818853686933004290078153620168054665086468417541382824708104480882577200529822968531743002301934310349005341104696887943182074473298650903541494918266823037984054778903666406545980557074219162536057146090758158128189406073809226361445046225524917089434897957301396534515964547462425719205819342172669899546965221084098690893672595962129879041507903210851706793788311452973769358455761907303633956322972510500253009083922781934406731633755418753858930476576720874219359466503538931371444470303193503733920039
#flag{You_Need_Some_Tea}

flag即为

flag{You_Need_Some_Tea}

posted @ 2022-04-29 22:44 TLSN 阅读(420) 评论(0) 收藏举报

刷新页面返回顶部

_TLSN

DASCTF复盘 (二)、RE -> 奇怪的交易 & python逆向

一、查壳

二、IDA静态分析

三、python解包

1、dump出pydata段

2、解包dump文件

3、修改模数

4、反编译奇怪的交易.pyc

四、解密.pyz文件

1、获取密钥

2、解密

3、反编译cup.pyc

五、解密

1、xxTEA解密算法

2、逆推密文

3、RSA维纳攻击

4、求得明文flag

公告

_TLSN

DASCTF复盘 (二)、RE -> 奇怪的交易 & python逆向

一、查壳

二、IDA静态分析

三、python解包

1、dump出pydata段

2、解包dump文件

3、修改模数

4、反编译 奇怪的交易.pyc

四、解密.pyz文件

1、获取密钥

2、解密

3、反编译cup.pyc

五、解密

1、xxTEA解密算法

2、逆推密文

3、RSA维纳攻击

4、求得明文flag

公告

4、反编译奇怪的交易.pyc