(二十一)、Cry->RSA_gcd & 拓展->共模攻击

 

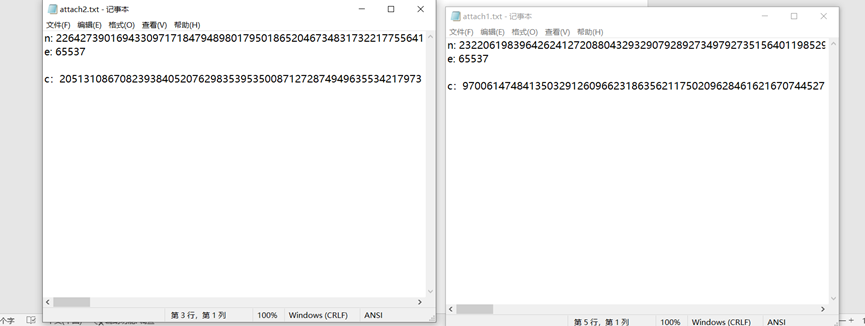
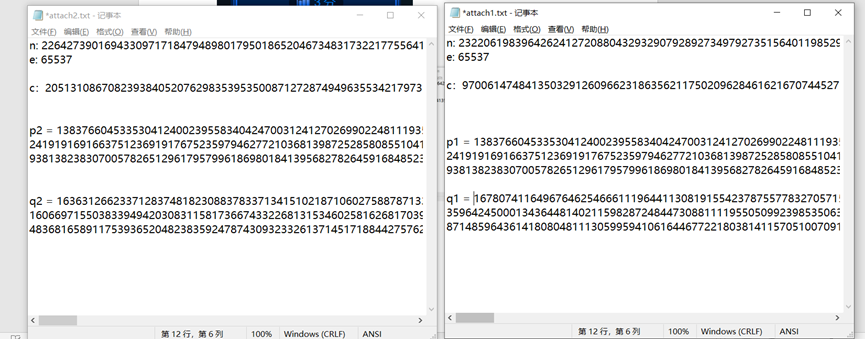
一、解出p和q

http://factordb.com/

 

 

二、解密脚本

import base64
n2 = 22642739016943309717184794898017950186520467348317322177556419830195164079827782890660385734113396507640392461790899249329899658620250506845740531699023854206947331021605746078358967885852989786535093914459120629747240179425838485974008209140597947135295304382318570454491064938082423309363452665886141604328435366646426917928023608108470382196753292656828513681562077468846105122812084765257799070754405638149508107463233633350462138751758913036373169668828888213323429656344812014480962916088695910177763839393954730732312224100718431146133548897031060554005592930347226526561939922660855047026581292571487960929911
n1 = 23220619839642624127208804329329079289273497927351564011985292026254914394833691542552890810511751239656361686073628273309390314881604580204429708461587512500636158161303419916259271078173864800267063540526943181173708108324471815782985626723198144643256432774984884880698594364583949485749575467318173034467846143380574145455195152793742611717169602237969286580028662721065495380192815175057945420182742366791661416822623915523868590710387635935179876275147056396018527260488459333051132720558953142984038635223793992651637708150494964785475065404568844039983381403909341302098773533325080910057845573898984314246089

c1 = 9700614748413503291260966231863562117502096284616216707445276355274869086619796527618473213422509996843430296526594113572675840559345077344419098900818709577642324900405582499683604786981144099878021784567540654040833912063141709913653416394888766281465200682852378794478801329251224801006820925858507273130504236563822120838520746270280731121442839412258397191963036040553539697846535038841541209050503061001070909725806574230090246041891486506980939294245537252610944799573920844235221096956391095716111629998594075762507345430945523492775915790828078000453705320783486744734994213028476446922815870053311973844961
c2 = 20513108670823938405207629835395350087127287494963553421797351726233221750526355985253069487753150978011340115173042210284965521215128799369083065796356395285905154260709263197195828765397189267866348946188652752076472172155755940282615212228370367042435203584159326078238921502151083768908742480756781277358357734545694917591921150127540286087770229112383605858821811640935475859936319249757754722093551370392083736485637225052738864742947137890363135709796410008845576985297696922681043649916650599349320818901512835007050425460872675857974069927846620905981374869166202896905600343223640296138423898703137236463508
e0 = 65537

p1 = 138376604533530412400239558340424700312412702699022481119357799054715877829291635290832719835033140580690053865677079316241919169166375123691917675235979462772103681398725285808551041924624882840901583892858174270714471366531758975241868470938138238307005782651296179579961869801841395682782645916848523771439
q1 = 167807411649676462546661119644113081915542378755778327057156191284453150887662343414908916953154897183613548083558919410359642450001343644814021159828724844730881111955050992398535063409828169462180970629537792676998647880110463527555034040871485964361418080481113059959410616446772218038141157051007091689351

p2 = 138376604533530412400239558340424700312412702699022481119357799054715877829291635290832719835033140580690053865677079316241919169166375123691917675235979462772103681398725285808551041924624882840901583892858174270714471366531758975241868470938138238307005782651296179579961869801841395682782645916848523771439
q2 = 163631266233712837481823088378337134151021871060275887871338250274359922218053543333532579728777813509956261662615493179160669715503833949420308311581736674332268131534602581626817039237393599222688271607325131529790640375765697832746614700483681658911753936520482383592478743093233261371451718844275762094649

def lcm (p,q):   #最小公倍数
    pxq = q * p
    if(p < q):
        ans = p
        p = q
        q = ans
    while p % q :
        bns = p % q
        p = q
        q = bns
    return pxq // q

def getd(e,l):
    k = 1
    while True:
        if(((l * k) + 1) % e) == 0:
            de = ((l * k)  + 1) // e
            if de > l:                  #d的值必须保证小于l
                return 0
            else:
                return de
        k +=1

l1 = lcm(p1-1,q1-1)
l2 = lcm(p2-1,q2-1)

d1 = getd(e0,l1)
d2 = getd(e0,l2)

fin1 = pow(c1,d1,n1)
fin2 = pow(c2,d2,n2)
hex_fin1 = hex(fin1)
hex_fin2 = hex(fin2)

hex=hex_fin1+hex_fin2[2:]

print(base64.b16decode(hex[2:].upper()))

 

三、总结

1、首先，p与q的解法不该这么解，应该求n1与n2的最大公因数q，再用n1，n2分别除以q，得到对应的p1，p2

 

2、base64.b16decode的使用

最后一步本来应该先把hex字符串转化成整形，再通过asc码表转化成字符串，但base16的解码刚好做的就是这一件事，我们直接使用base.b16decode函数即可

 

四、拓展->共模攻击

在看wp的时候，了解到了RSA的共模攻击，这里记录一下

1、共模攻击，就是知道RSA的公钥和两个密文，从而得知明文的攻击

 

2、比如说，我们有明文p，模数n，通过e1,e2产生了两个密文c1,c2。监听者如果知道了

 

密文c1，c2就能推导出明文，也就是说已知公钥(e1,n)与(e2,n)与密文c1,c2可以求得p

 

方法如下

3、如果e1与e2互质

那么gcd(e1,e2) = 1

设s1,s2 且皆为整数，一正一负

有e1*s1+e2*s2 = 1

通过扩展欧几里得算法，可求得s1与s2，方法如下

 

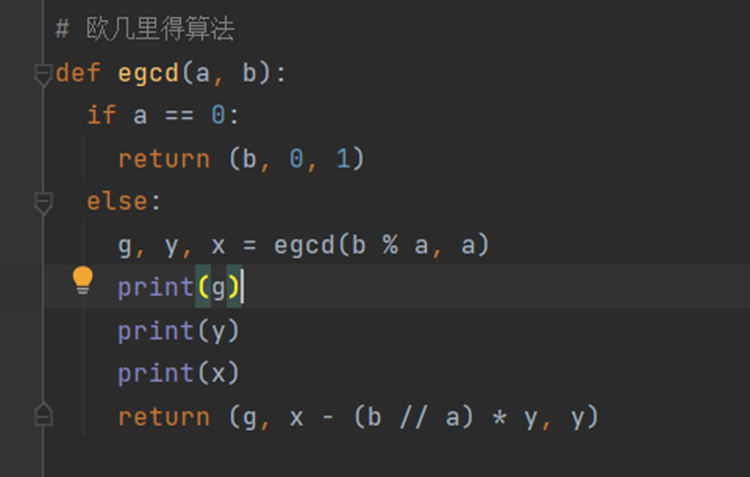
返回的结果是元组的形式，设为y,则y[1]与y[2] 就是要求的s1与s2

 

 

4、化简

由

C1 = m ^ e1 % n

C2 = m ^ e2 % n

可得

(c1^s1*c2^s2)%n = ((m^e1%n)^s1*(m^e2%n)^s2)%n

->

(c1^s1*c2^s2)%n = ((m^e1)^s1*(m^e2)^s2)%n

->

(c1^s1*c2^s2)%n = (m^(e1^s1+e2^s2))%n

 

又e1 * s1 + e2*s2 = 1

->

C1 ^ s1* c2 ^ s2 = m

 

然鹅要求一个数的负数次幂，与常规方法并不一样

 

我们需要先求得这个数的模反元素,然后求这个模反元素的 负次幂

 

5、就像这样

 

 

 

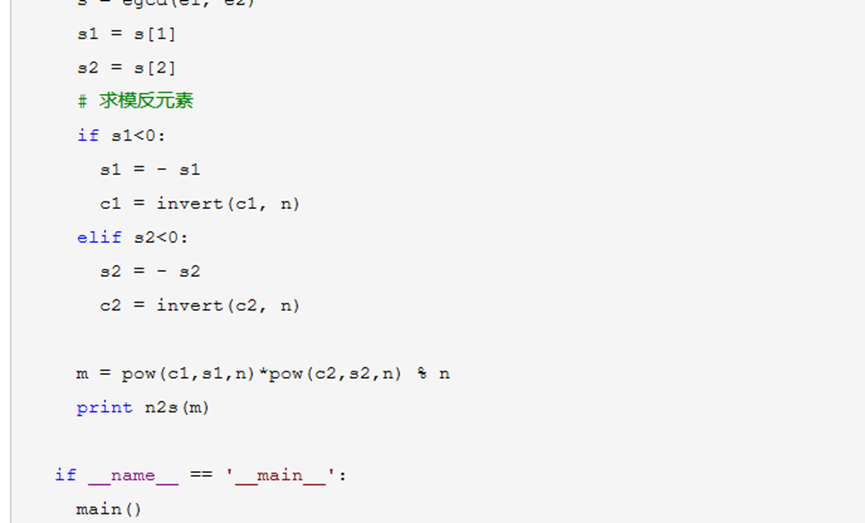
6、参考

https://www.cnblogs.com/gwind/p/8013154.html