(十四)、攻防世界cry新手村 & RSA & 椭圆曲线加密 & base64 &传统密码学
前言:在做逆向题的时候遇到了好多加密解密类型的题,有些大佬的wp一眼都能看出来题目的做法 ,我看到了差距,想学习一下密码学,同时提升一下 python 编程的能力
01 base64
一、得到文件
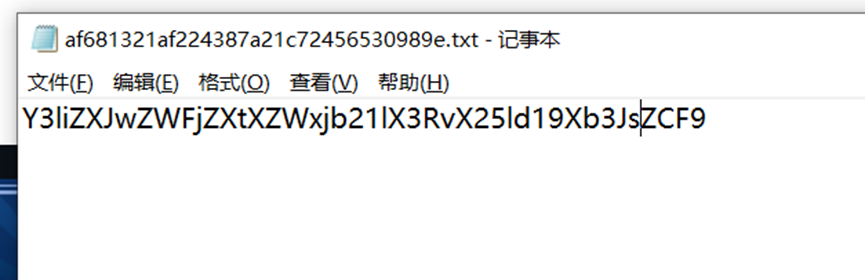
二、解密,拿到flag
使用工具解密
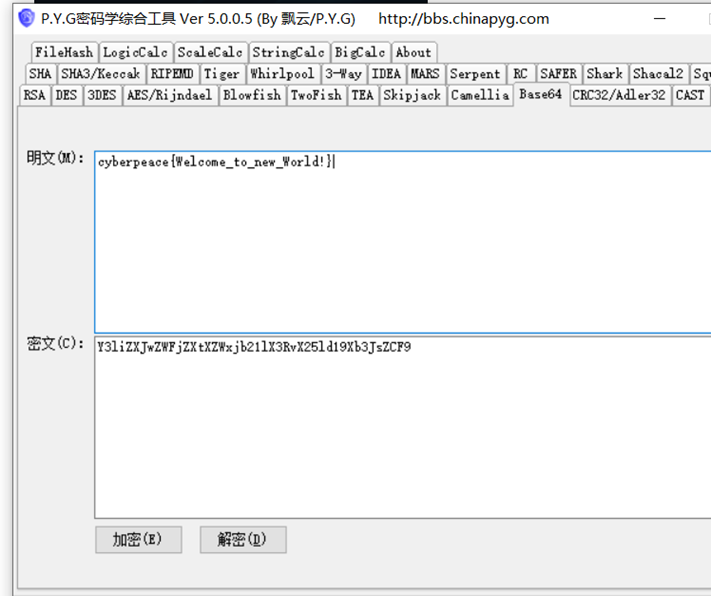
cyberpeace{Welcome_to_new_World!}
三、下面让我们了解一下base64加密吧
1、Base64标准索引表
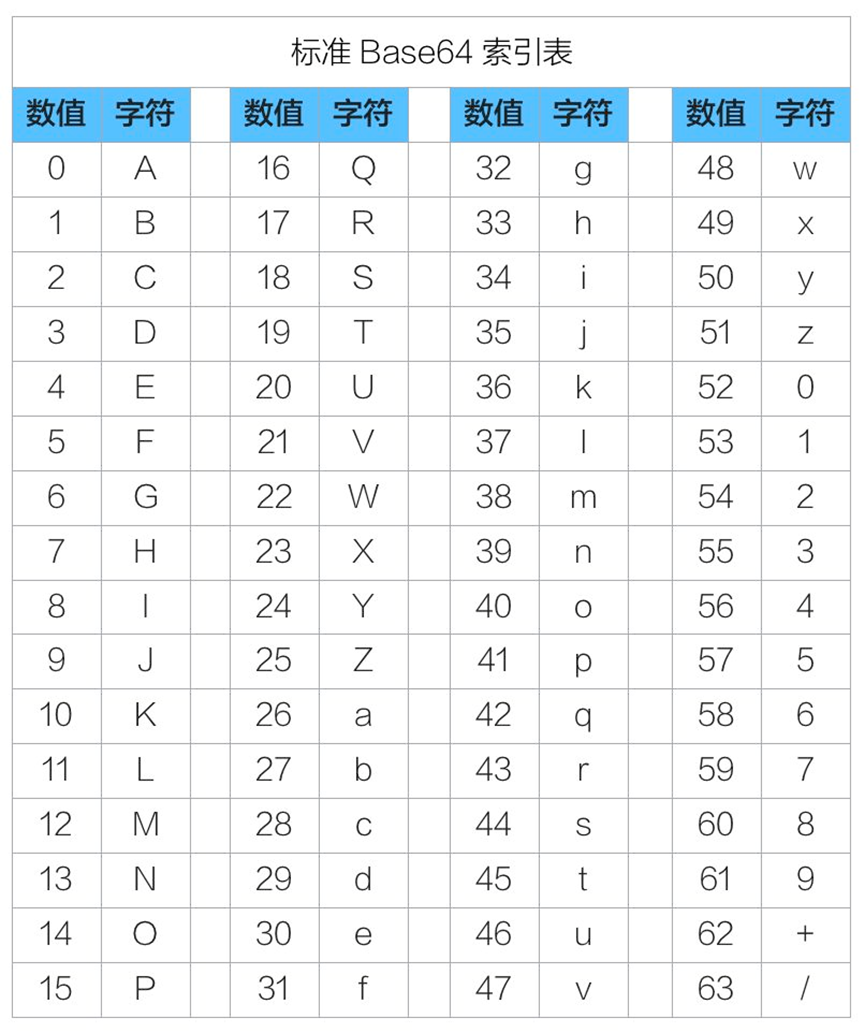
可以看到base64索引表 包含了26个英文字母大小写,10个数字,还有两个特殊符号 “+”,”/”
2、加密方法
第一步,将字符串每三个字节分成一组,一组就是24位。
第二步,将字符串转化成asc码再把asc码转化成二进制的形式
第三步,把二进制数每6位分成一组,每组前面补两个0,即构成8位
第四步,查密码表,替换每组对应的值
注意,由于是6位一组,末尾可能会出现为数不够的情况,不够补零,如果补了两个零,最后得到的base64编码后面需要加一个 = ,如果补了四个零,则需要加 ==
3、实际使用
在ctf中有的题目会变换索引表来进行考察base64 加解密
比如攻防世界RE 第52题 2ex1 ,就是通过变换索引表实现base64加密的。
4、base64加密的特点
(1)、标准的base64加密只有那64个字符
(2)、等号一定用作后缀!!!!!
(3)、base64编码后的字符串一定能被4整除(算上等号),因为base64编码三个字节一组,且位数除以4
5、拓展
Base64用6位表示字符,base32 就是用5位表示字符,同理base16就是用4位表示字符
附Base32索引表
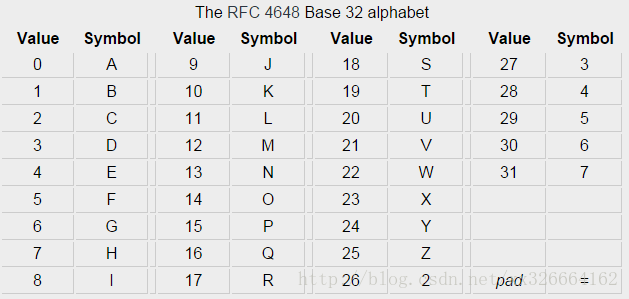
附Base16索引表

02 Casesar
凯撒加密
一、 取得文件

二、 凯撒解密
偏移挨着试试就能得到答案
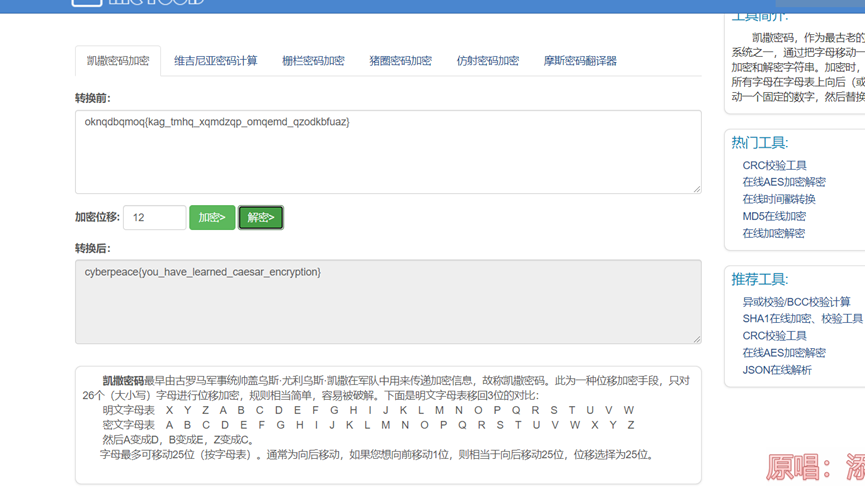
cyberpeace{you_have_learned_caesar_encryption}
三、下面我们了解一下凯撒加密原理
1、替换加密
凯撒加密采用的是替换加密技术,
比如 明文是 ABCDEF 密文是DEFGHI 那就说明偏移为3(解密时,密钥为3)
2、变种凯撒加密
有的凯撒加密算法会在字母偏移的基础上加上自己的下表偏移,比如明文为DEF,设置偏移为3,DEF在偏移的同时加上自己的下表。
比如E的下表是1,那就再加上大小为1的偏移,所以E变换为 A;F下表为2 ,变换后再加上大小为2的偏移,变为A。
通过这种加密,DEF最后变成 AAA
3、凯撒加密的局限性
凯撒加密只能对字母进行偏移
4、凯撒加密特点
一般来说凯撒加密的字母只有大写或小写
03 Morse
摩斯密码
一、取得文件
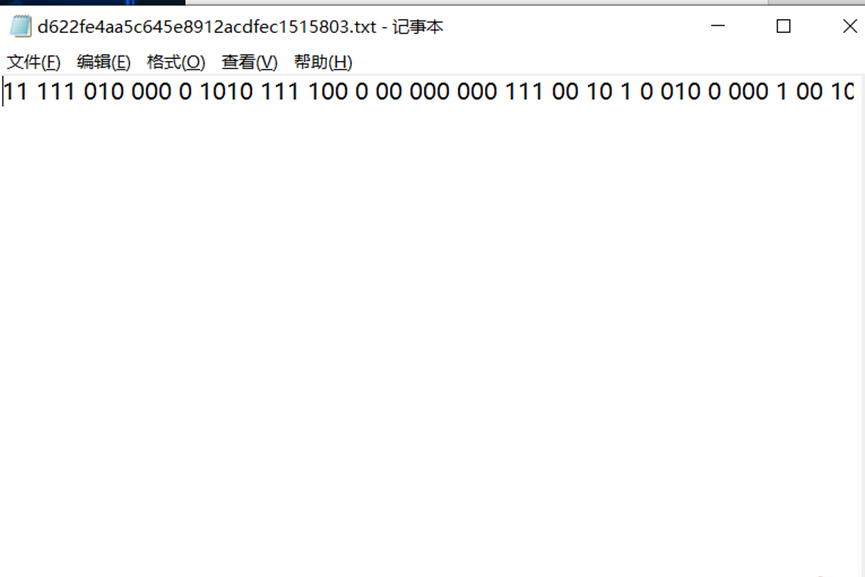
二、摩斯密码解密
注意先把0和1转化成 .与- ,把空格转化为/

注意转化格式

最后flag为 cyberpeace{morsecodeissointeresting}
三、 下面了解一下摩斯密码的原理
摩斯密码的原理是用特殊的符号代表具体的字母
摩斯密码对照表如下:
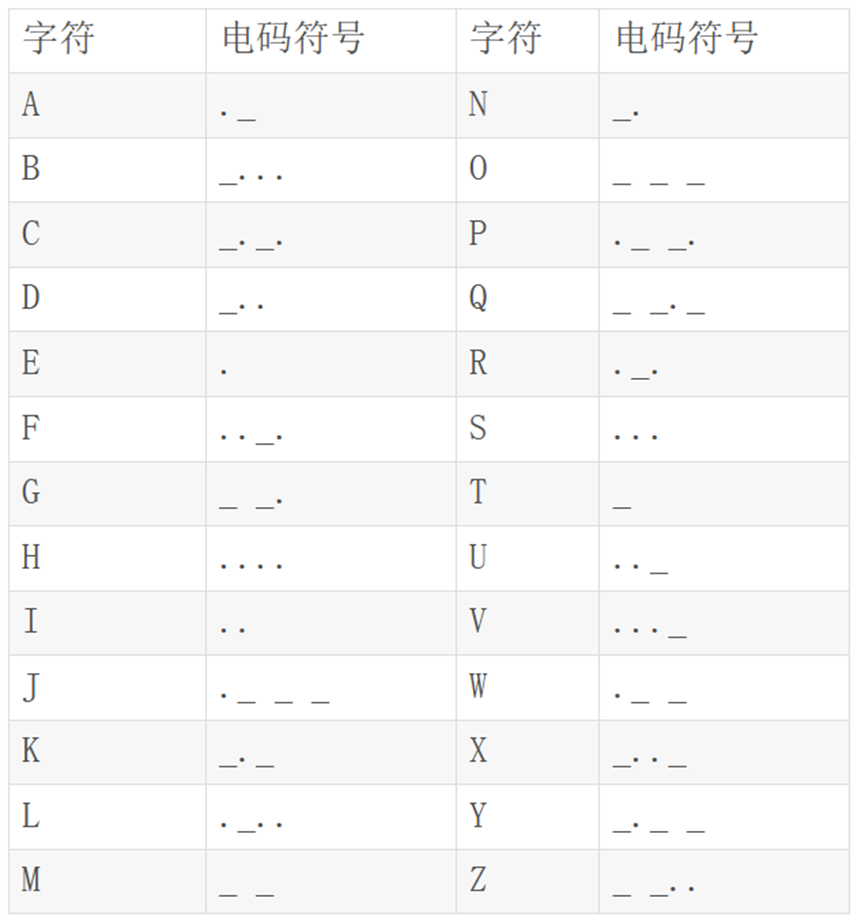
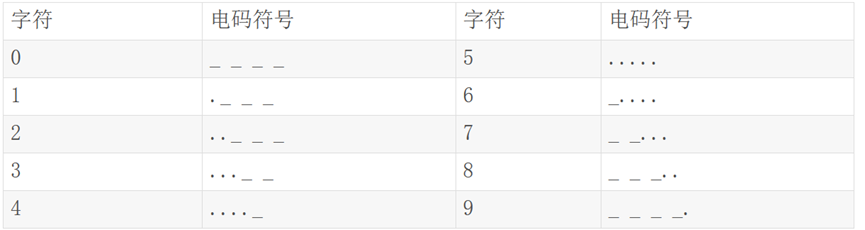
在一些网站上用的是-代替_加密 有的网站用 / 来分别不同字符之间的加密
四、 摩斯密码的特征
由. – 与 /组成,/ 为不同字符之间的分隔符
04 幂数加密
云影密码
一、拿到密文

二、解密
以0为字符的分解:
88421 122 48 2244 4 142242 248 122
23 5 12 12 4 15 14 5
对照ABCDEFG…字母下表
可得:WELLDONE
Flag即为: cyberpeace{WLLDONE}
三、下面我们研究一下二进制幂数加密原理
1、二进制幂数加密
幂数加密,即用数字表示英文字母
由于英文字母只有26个字母。只要2的0、1、2、3、4、5次幂就可以表示31个单元。通过用二进制幂数表示字母序号数来加密。
明文: d o n o t p u l l a l l y o u r e g g s i n o n e b a s k e t
字母序号:4 15 14 15 20 16 21 12 12 1 12 12 25 15 21 18 5 7 7 19 9 14 15 14 5 2 1 19 11 5 20
比如 4 = 2^2,所以4经过加密后就是2;15=2^0+2^1+2^2+2^3所以15加密后是0123
字母加密结果对照:

2、云影密码(01248密码)
一般的二进制幂数加密使用 01234来表示字母次序,而云影密码是用01248表示字母次序(0代表字母之间的分隔)
云影密码的优势就是好算,比如同样对下表为15的字母加密,普通的二进制幂数加密后是:0123 而云影加密后是:148 或者 142242 。即每位相加即是字母下表的序号
四、特征或局限性
特征就是只由01234 / 组成或01248组成
局限就是只加密字母
05 Railfence
www变种栅栏密码
一、 拿到密文
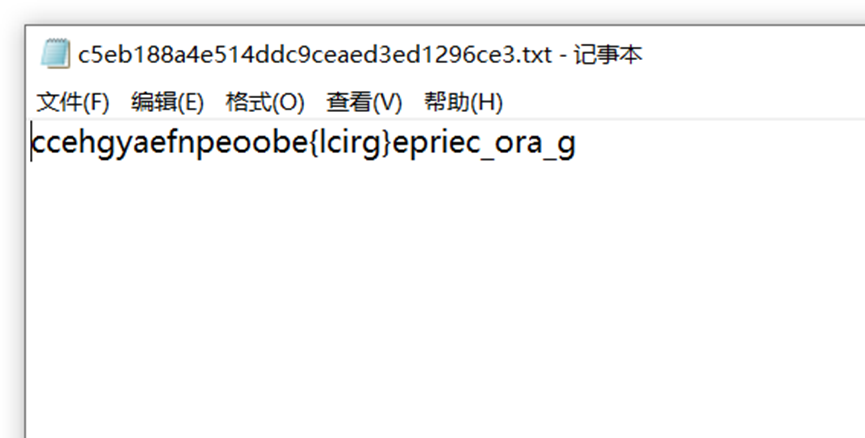
二、 解密
这是栅栏密码的变种形式,www栅栏密码

Flag : cyberpeace{railfence_cipher_gogogo}
三、下面我们研究一下栅栏密码的原理
1、理论
栅栏密码就是把要加密的明文分成N个一组,然后把每组的第1个字连起来,形成一段无规律的话。 不过栅栏密码本身有一个潜规则,就是组成栅栏的字母一般不会太多。(一般不超过30个,也就是一、两句话)
2、 加密原理

四、栅栏密码的变种---www型栅栏密码
就是让数字以W型的形式排列

06 不仅仅是Morse
一、 获取密文

二、 解密
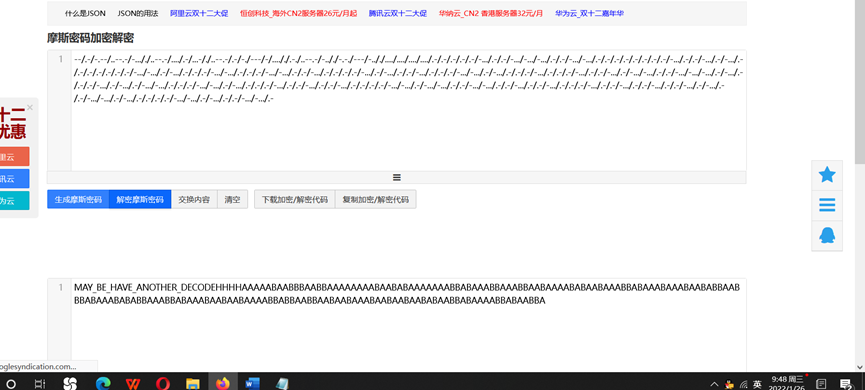
第一步是摩斯密码,第二步是培根密码
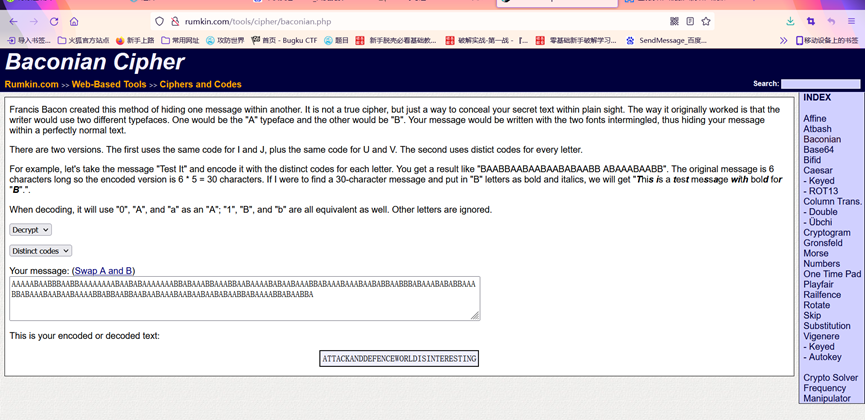
那么flag就是: cyberpeace{attackanddefenceworldisinteresting}
三、 下面我们来了解一下培根密码
1、由来
培根密码,又名倍康尼密码,是由法兰西斯·培根发明的一种隐写术。
2、原理
使用a和b来代替密文中的英文字母,培根密码其实是一种替换密码
3、 转化表
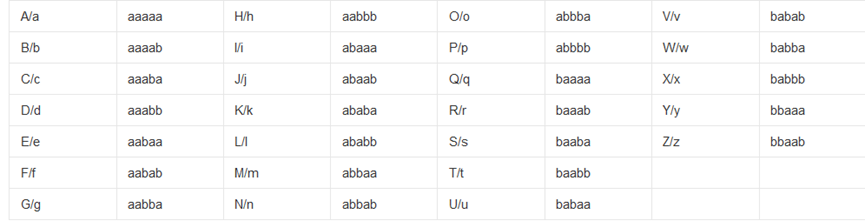
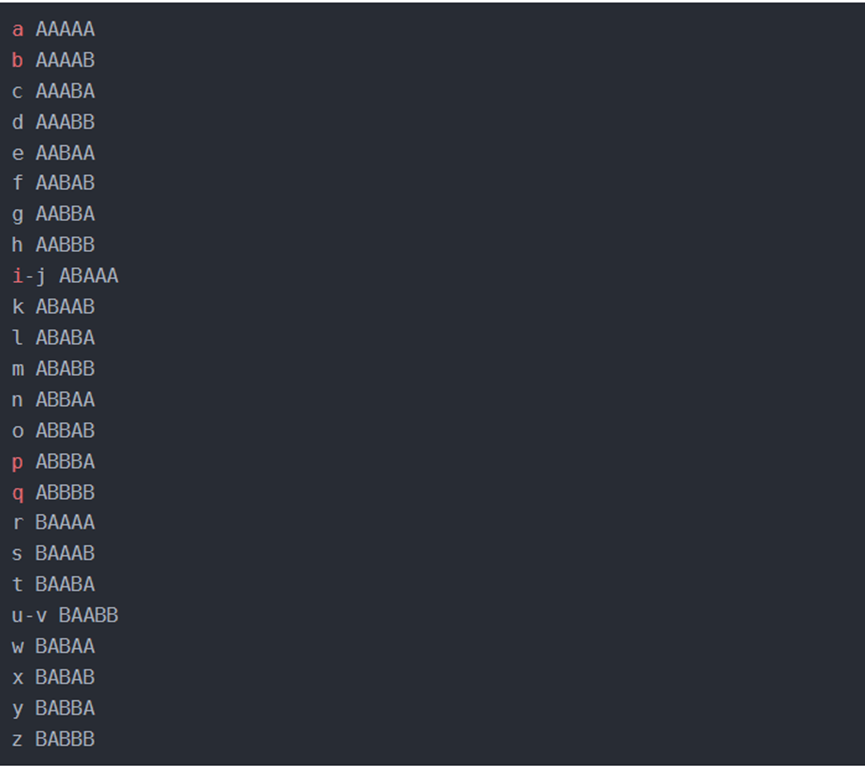
解密时倒序即可
四、拓展
我们甚至可以用两个不同的属性来实现培根密码的隐藏
比如:
以下一段包含了'steganography',正常字体是A,粗体是B:
To encodeamessage each letteroftheplaintextis replaced by a group of fiveofthe letters'A'or 'B'.
我们把正常字体的字母转化成A,把粗体字体的字母转化成B,得到结果后再次对照培根密码转化表就可以解密得到明文 steganography 了
这种方法能很好的影藏培根密码
五、特点
1、普通的培根根密码由大量的A,B或a,b组成,很好辨认
2、普通的培根密码只是加密字母
3、培根密码有比较强的可拓展性,使得它可以加密任何具有两种不同属性的明文
07 混合编码
一、 拿到密文

二、 解密
首先是Base64解密
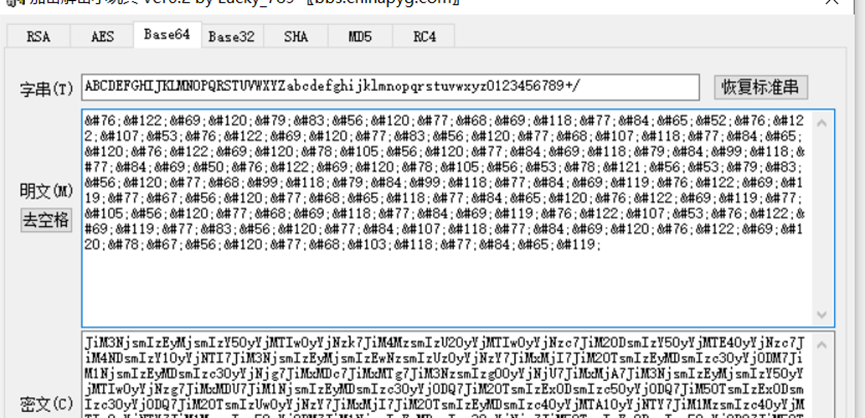
然后是unicode解密
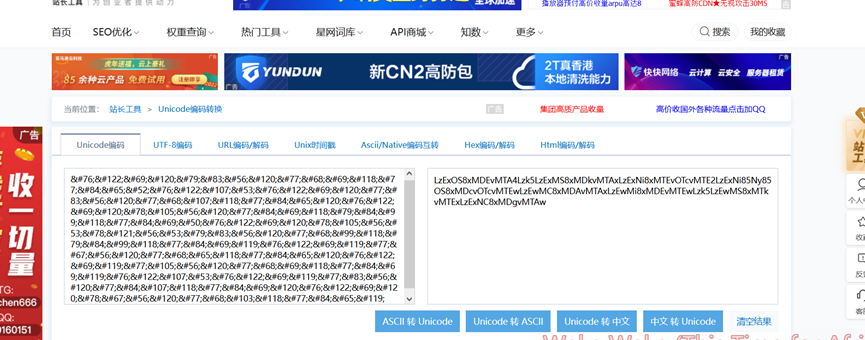
再然后是base64解密
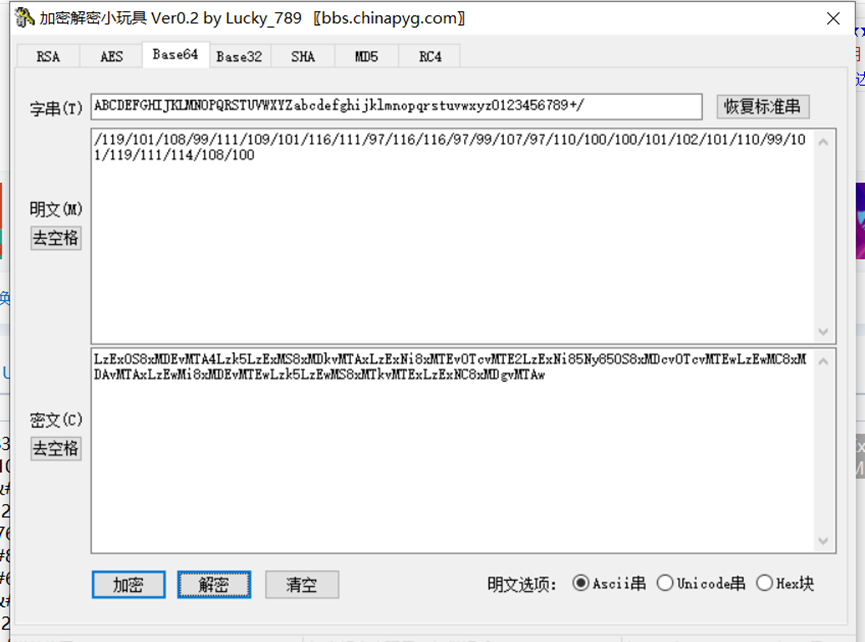
最后asc码解密
拿到flag:cyberpeace{welcometoattackanddefenceworld}
三、 记录一下编码的特点
1、unicode编码特点是 \u ; &# ;
2、base64 后面有等号,只由那64个字符组成
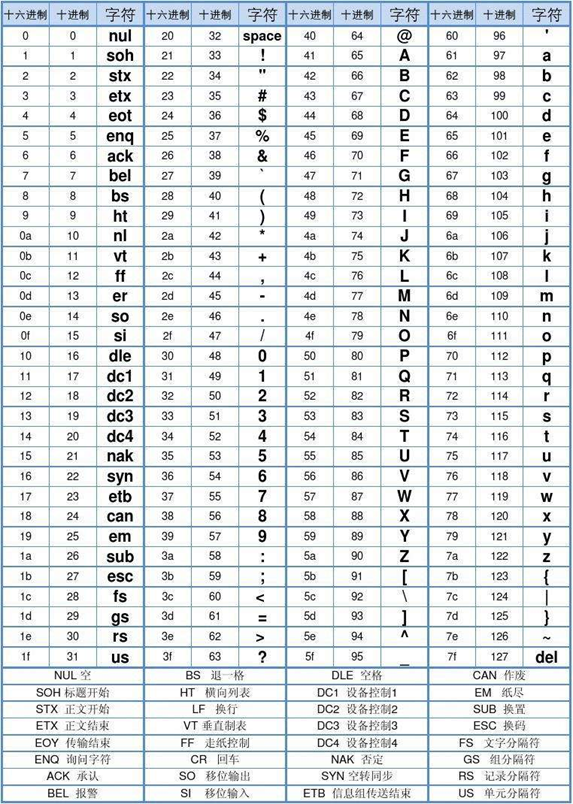
四、asc码表
08 easy_RSA
RSA加密
一、 拿到文件

二、解密
公钥是(E,N),私钥是(D,N),所以密钥对即为(E,D,N)
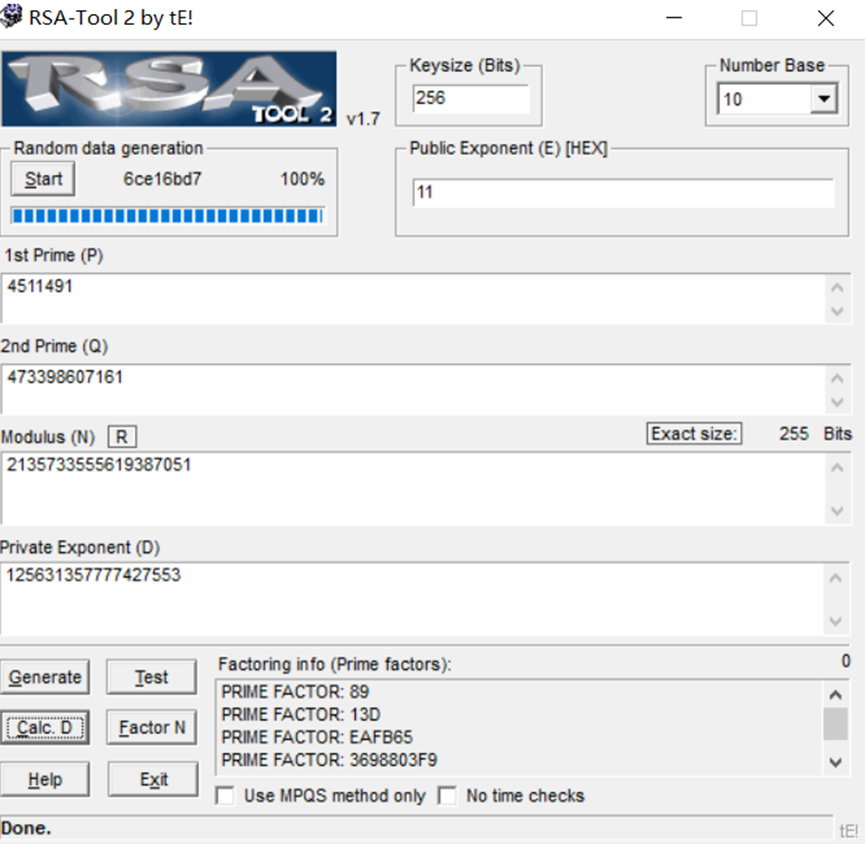
这里介绍一下工具的使用
右上方的NumberBase代表了进制
左下角的calc.D表示获取D的值,Factor N表示把N质数分解,分解的值显示在P,Q编辑框中
Flag: cyberpeace{125631357777427553}
三、我们研究下RSA加密算法
1、非对称加密
RSA加密算法是一种非对称加密算法,所谓非对称,就是指该算法加密和解密使用不同的密钥,即使用加密密钥进行加密、解密密钥进行解密。
2、RSA算法的一般使用
RSA算法通常是先生成一对RSA密钥,其中之一是保密密钥,由用户保存;另一个为公开密钥,可对外公开。为提高保密强度,RSA密钥至少为500位长,一般推荐使用1024位。
3、RSA加密过程

抄自 https://blog.csdn.net/a745233700/article/details/102341542
4、 RSA解密过程

抄自 https://blog.csdn.net/a745233700/article/details/102341542
5、 生成密钥对
公钥是(E,N),私钥是(D,N),所以密钥对即为(E,D,N)

抄自 https://blog.csdn.net/a745233700/article/details/102341542
09 easychallenge
一、拿到文件

二、反编译
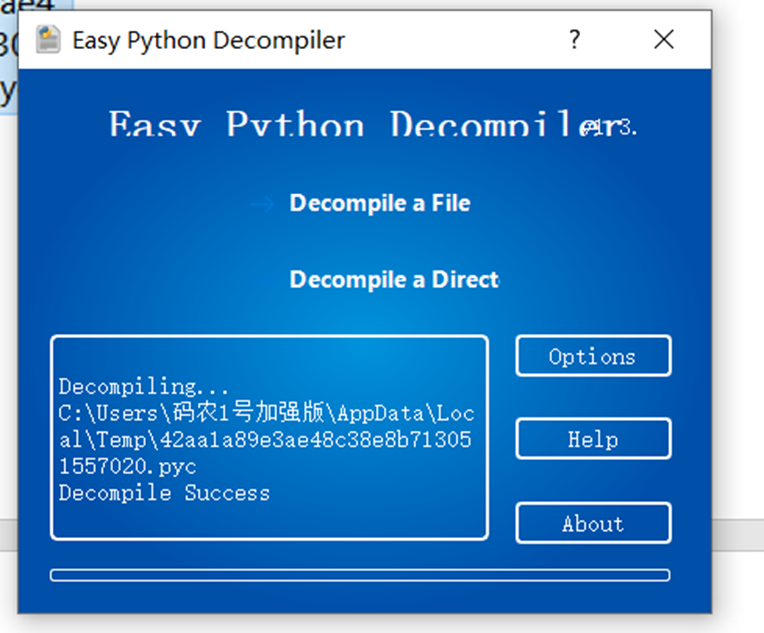
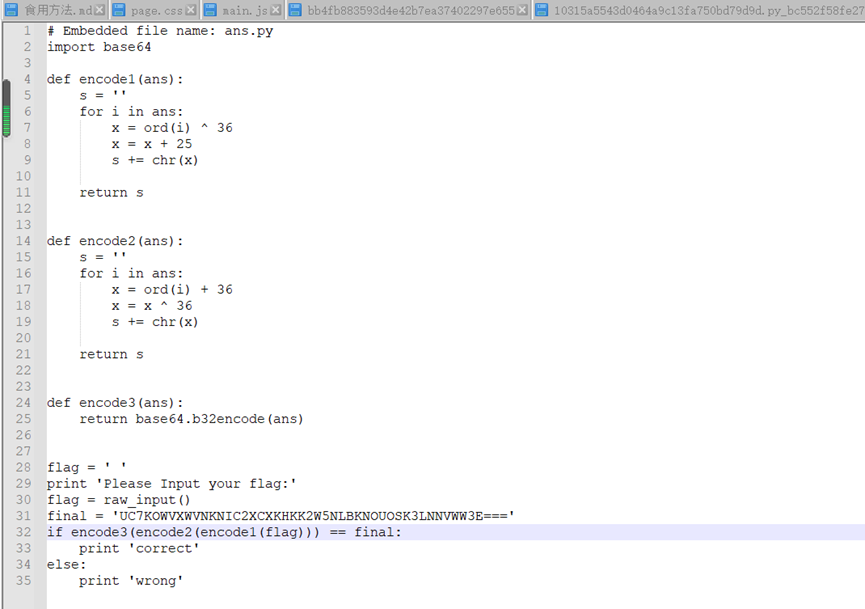
三、分析
将输入的字符经过三次加密后与final指向的字符串相等则拿到flag,逆向题
四、 解密
解密脚本如下:
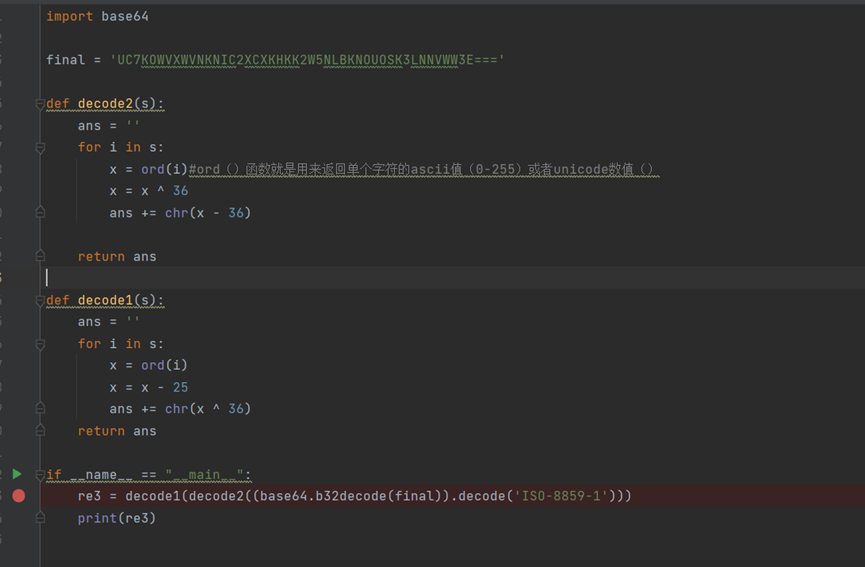
import base64 final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E===' def decode2(s): ans = '' for i in s: x = ord(i)#ord()函数就是用来返回单个字符的ascii值(0-255)或者unicode数值() x = x ^ 36 ans += chr(x - 36) return ans def decode1(s): ans = '' for i in s: x = ord(i) x = x - 25 ans += chr(x ^ 36) return ans if __name__ == "__main__": re3 = decode1(decode2((base64.b32decode(final)).decode('ISO-8859-1'))) print(re3)
拿到flag: cyberpeace{interestinghhhhh}

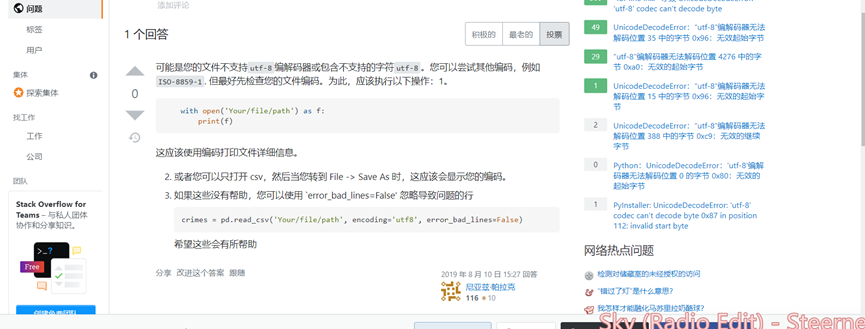
写脚本的时候出现了这个问题,不支持utf-8编码,记录一下,下次遇到不慌
五、 总结
一道简单的逆向题,没什么好说的
10 转轮机加密
转轮机加密(wheel cipher)
一、获取文件
二、 解密
猜想了很多格式都没有猜到,不装了,不会
参考 https://www.freesion.com/article/2890547950/
我们从加密的角度来理解这道题
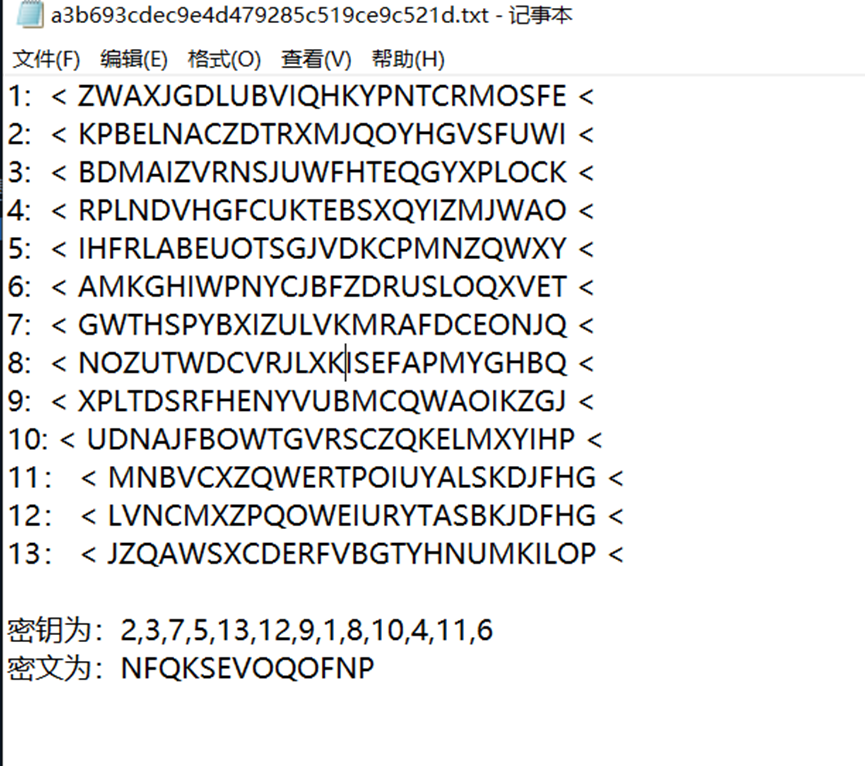
假设我们是加密的人,假设我们已知明文,我们的机器则是 13 转轮密码机
一开始我们的转轮机上不同转轮的值显示的是我们要加密的明文,然后我们转动这13个转轮来加密我们13位的明文,转动后转轮机显示的结果即是密文,密文即是
一般的转轮机工作到这里可能就结束了,但这个转轮机转动之后又改变了13个转轮位置,
改变的方法就相当于密钥,改变后的结果就是下图

这样一想,我们解密的思路就清晰了
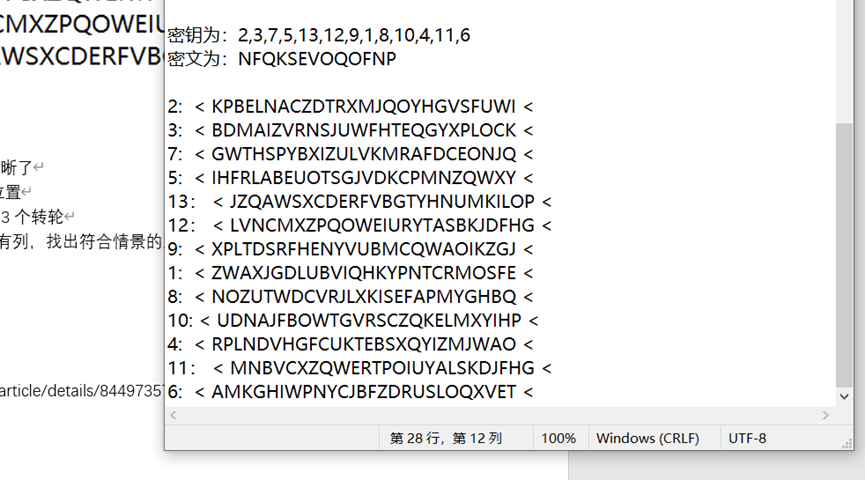
1、 先用密钥恢复13个转轮的位置
2、 再通过13位密文分别转动13个转轮
3、 我们不知道一开始明文是第几列,所以我们要判断,即看遍所有列,找出符合情景的那一个答案
调整转轮后:
转动转轮后
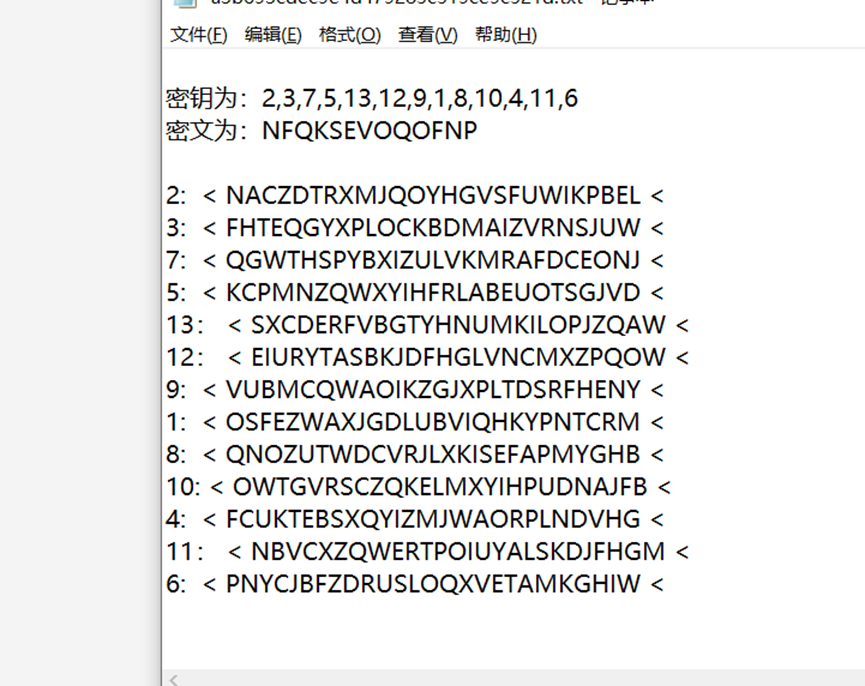

对比列找到 flag(注意到这个二战)

第18列拿到flag: fireinthehole

三、转轮机工作原理
资料好少,不过易懂,直接贴链接:
https://blog.csdn.net/zdh89786/article/details/84497357
11 Normal_RSA

一、 获取文件

一个enc文件和一个pem文件
.enc文件用wire’shark打不开
记事本打开:


猜测分别是加密后的文件与公钥
二、 思路展开
我们知道了公钥可以根据公钥求E和N。再根据N求p与q,进而得到L,最后得到D。这样我们就获得密钥对


三、 解密
这里介绍一个工具 openssl
Kail上自带
1、openssl
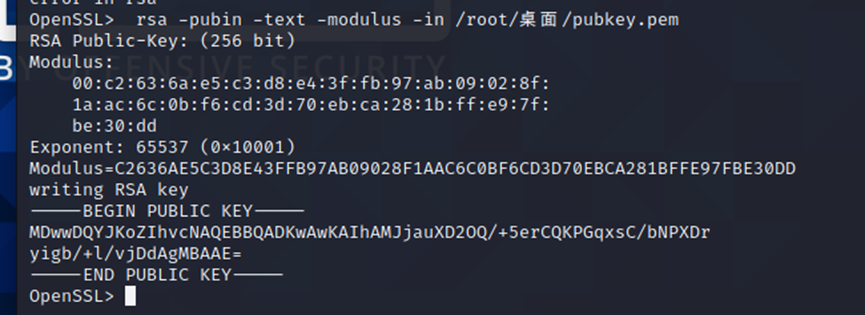
-pubin :指定输入文件是公钥
-text : 以明文的形式输出各个参数值
-modulus : 输出模数值
-in val :指定输入文件
这样我们就得到了模N(Modulus) =
C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
以及e = 65537
2、下面我们根据N(Modulus)获取 p 与 q
首先把modulus转化成10进制
网站: https://tool.lu/hexconvert/
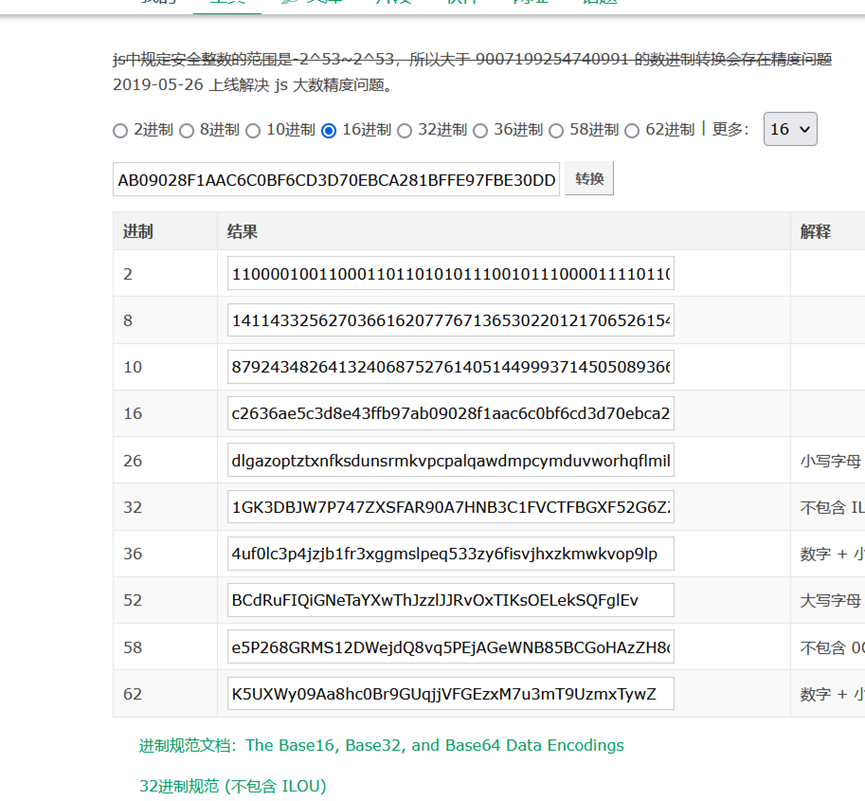
得到10进制:
87924348264132406875276140514499937145050893665602592992418171647042491658461
Modulus大数分解:
http://www.factordb.com/
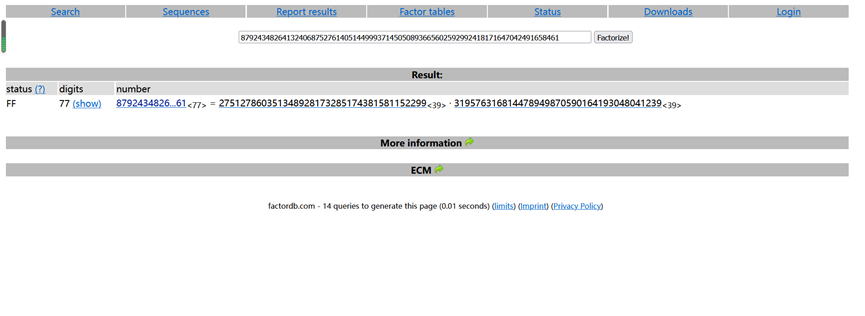
得到p:275127860351348928173285174381581152299
q: 319576316814478949870590164193048041239
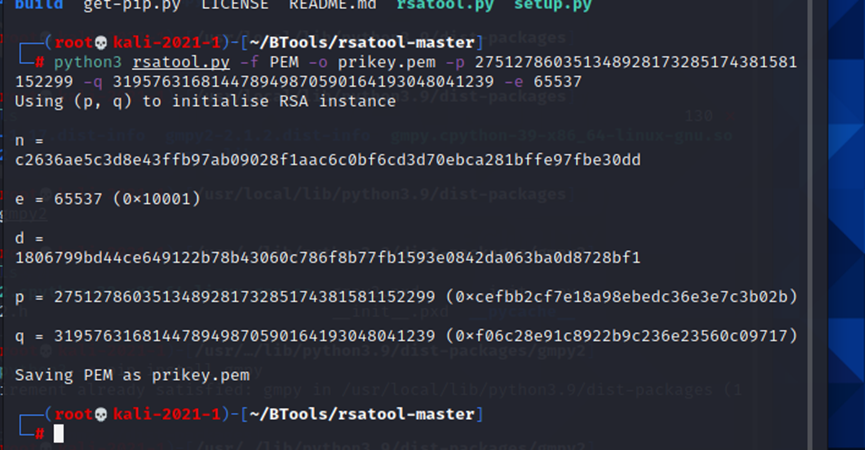
3、使用rsatools计算
python rsatool.py -f PEM -o private.pem -p 275127860351348928173285174381581152299 -q 319576316814478949870590164193048041239 -e 65537
4、 用私钥解密flag
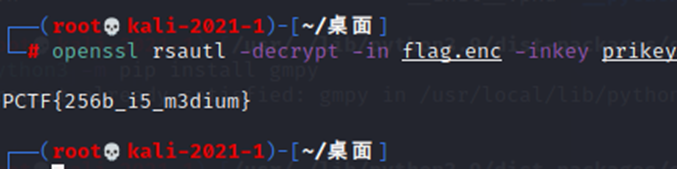
openssl rsautl -decrypt -in flag.enc -inkey prikey.pem

参考 https://segmentfault.com/a/1190000018084284
5、 拿到flag
RCTF{256b_i5_m3dium}
总结
这道题主要是对openssl工具与rsatools等常用工具的使用
12 Easy_ECC

一、 获取文件
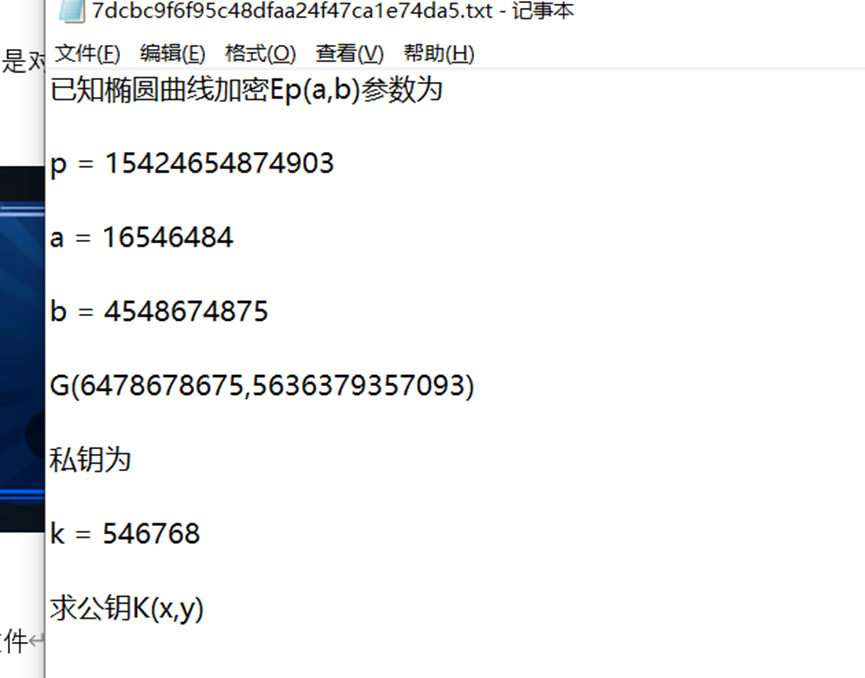
椭圆曲线加密(ECC)
二、 求公钥
没学过椭圆曲线加密,为此看了下面这个博客,感悟颇多
https://blog.csdn.net/qmickecs/article/details/76585303
椭圆曲线的一般式:
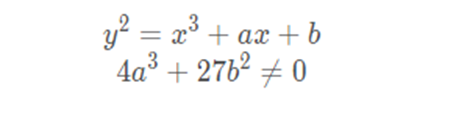
推测得到的文件上的a,b即为这个椭圆曲线的参数,G应该椭圆曲线上的基点
密钥k为所乘倍数
P为模
三、 ECCTOOL拿到flag
链接:https://bbs.pediy.com/thread-66683.htm
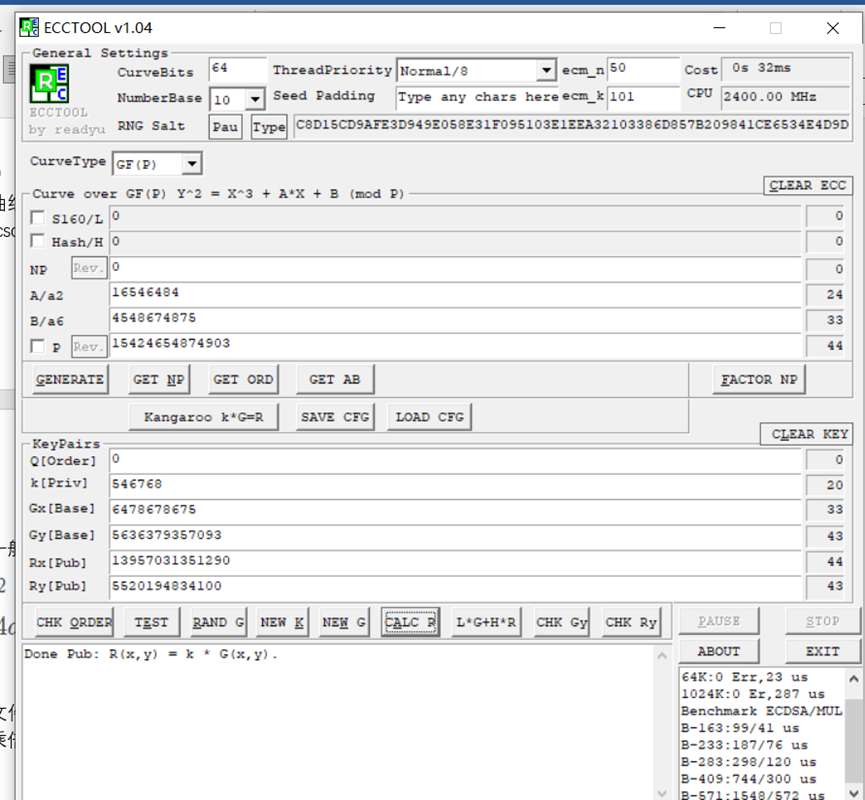
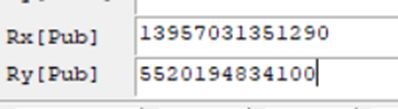

拿到flag
cyberpeace{19477226185390}
四、 我们了解一下椭圆曲线加密
下面所有内容皆来自下面这个博客
https://blog.csdn.net/qmickecs/article/details/76585303
为了方便我自己复习,我对此博客内容进行了摘抄,只是摘抄
1、 简介
椭圆曲线加密简称ecc ,全名:elliptic curve encryption
椭圆曲线安全性特别高,比特币,许多大型网站的身份认证机制便是以ECC为基础的
下面介绍椭圆曲线之前,先说说什么离散对数问题
2、离散对数问题
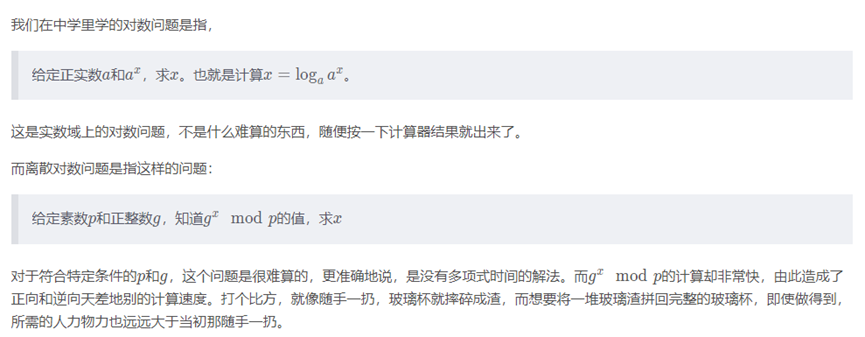
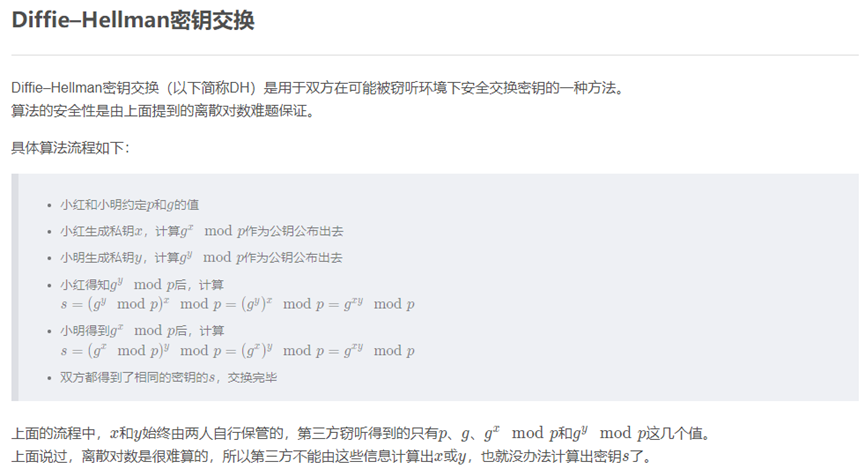
3、Diffie–Hellman密钥交换
4、椭圆曲线
椭圆曲线不同于我们学的圆锥曲线,因为椭圆曲线是三次方程描述的曲线
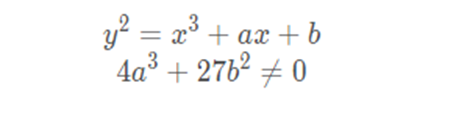


5、椭圆曲线上的运算
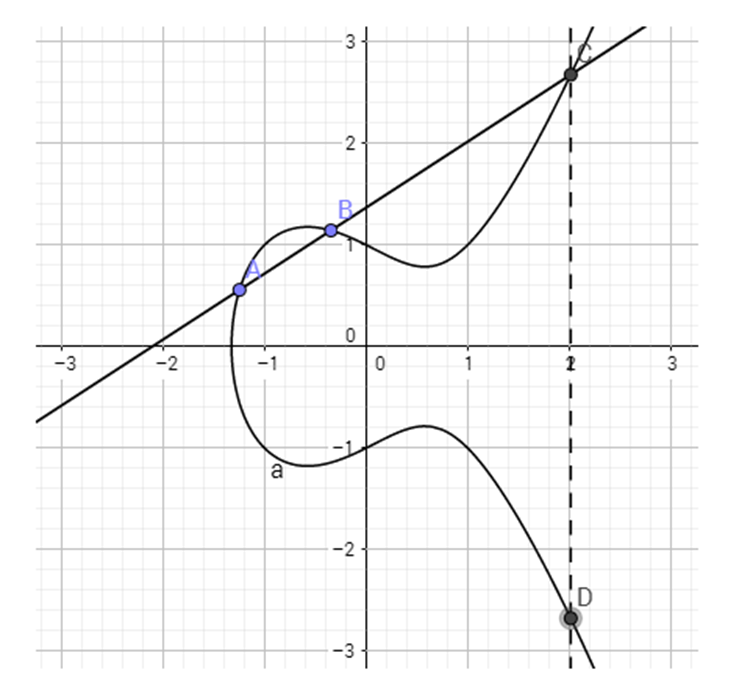
首先是加法
设椭圆曲线上有两点,A和B点,那么作过这两点的直线与该曲线相交于第三点(C点),然后关于X轴对称得到D点,则D为这两个点的和,记作D = A + B 。很明显,D点也在该曲线上。所以椭圆曲线上两点之和也是曲线上的点。
这样一来,可以证明交换律和结合律:

画图网站: https://www.geogebra.org/classic
当A,B两点形成的直线垂直于X轴时:
我们定义坐标系中距离X轴无穷远点为椭圆曲线上的一个特殊点,称为0点(零点)。 因为任意一条垂直于X轴的直线都会与椭圆曲线相交于0点。
对于这个0点,有以下结论:
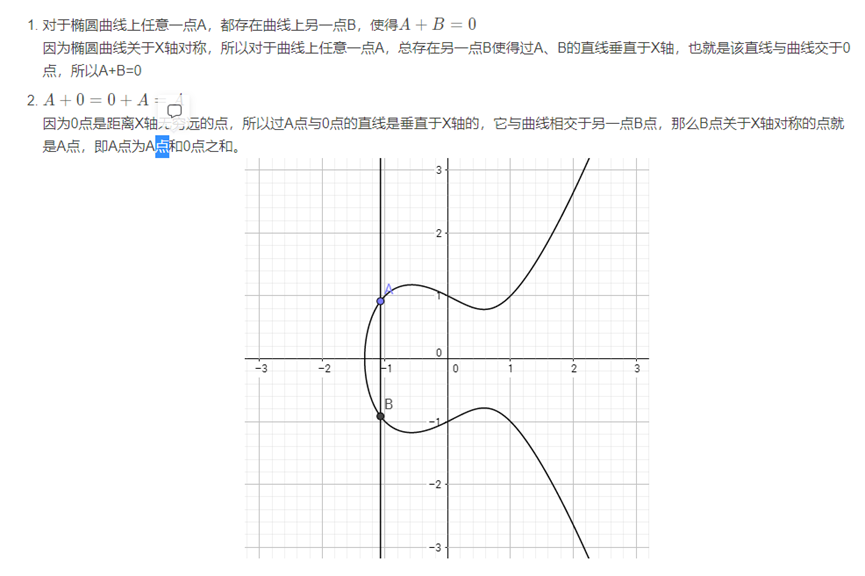
这样以来我们变相定义了椭圆曲线中的负数。若A + B = 0 ,那么B = − A 。椭圆曲线上点的减法也就自然而然地出现了,A − B = A + ( − B )
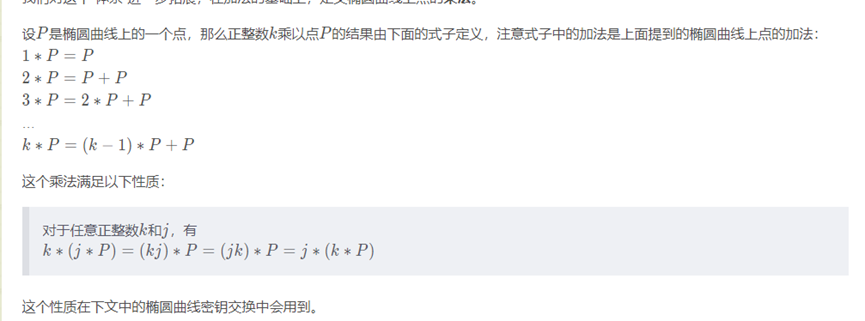
下面再定义乘法
6、椭圆曲线上的离散对数问题
设P为椭圆曲线上的一点,如果我们像计算k倍P的值,可以通过累计k-1次P的方法计算,但是显然,这种方法很笨,时间复杂度是线性的
我们可以用结合律:

这个方法被称为快速幂算法,原本常用于快速计算某个数的k次幂,这里将其推广到椭圆曲线点乘的快速计算中。
利用快速幂算法计算k ∗ P 的时间复杂度是对数级的,但是要在知道k ∗ P 和P的前提下,倒推出k的值,没有比挨个尝试k的值快太多的算法。于是椭圆曲线加密依赖的数学难题就这么诞生了。
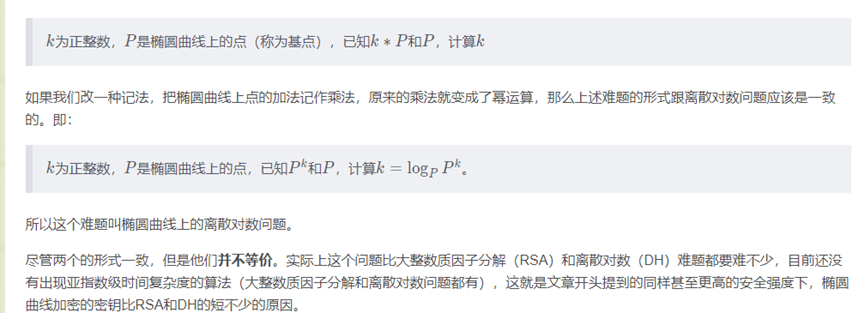
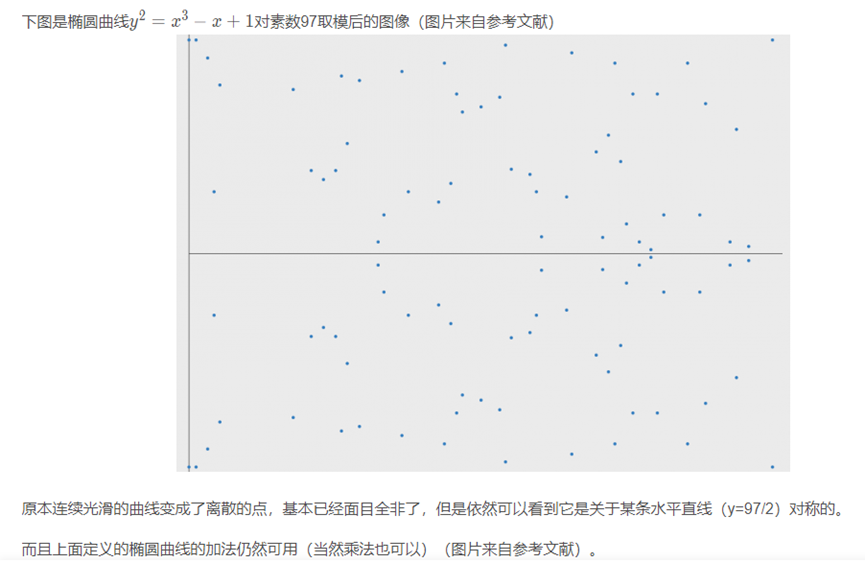
7、有限域上的椭圆曲线
实数域上的椭圆曲线是连续的,有无限个点,密码学要求有限点。
实数域上的椭圆曲线的运算有误差,不精确。密码学要求精确。
所以我们需要引入有限域上的椭圆曲线。

取模后的椭圆曲线仍然对称:
8、基于椭圆曲线的DH密钥交换(ECDH)
ECDH跟DH的流程基本是一致的。

由于计算椭圆曲线上的离散对数是很难的,所以第三方没办法在只知道x ∗ P和y ∗ P的情况下计算出x或y的值
椭圆曲线知识,均是摘抄下面这个博客的..
https://blog.csdn.net/qmickecs/article/details/76585303
五、 ECC vs RSA的优缺点

抄自 http://www.noobyard.com/article/p-ywxsfiik-dh.html
Cry新手题总结
至此,cry12道新手题已全部完成,后面几道题还是很难的
在这12道题中我学到了base64加密,凯撒加密,摩斯密码,幂数加密及其变种云影密码,栅栏加密极其变种www栅栏加密,RSA加密,转轮机加密,椭圆曲线加密
这几道题有的很有意思,有的需要脑洞,有的比较难。
未来的路才刚刚开始


 浙公网安备 33010602011771号
浙公网安备 33010602011771号