Manacher（马拉车）

概述

字符串算法。本来想跟 KMP 放一块说的，结果发现自己直到 HASC2025 才学会。这里单独拿出来简要记录一下。

Manacher 算法主要用于处理与回文子串相关的问题。对于给定字符串\(S\)的任意一个位置，这种算法可以处理出以该位置为中心的回文串的最长半径。据说这对许多询问回文子串相关的问题都有很大的帮助。

具体来看一个简单的问题：求出一个字符串\(S\)的最长回文子串。

算法流程

为了简便，以下所有提及的回文串都按奇数长度来考虑。

记\(p_i\)表示\(S\)中以\(i\)位置为中心的最长回文串的半径（半径包括自己，比如aba的半径为\(2\)）。按照字符串算法的常见思路，我们按照增量递推的方法来求\(p_i\)，假定\(p_{1...i-1}\)已经求得，同时维护一个\(r\)，表示到\(i\)之前右端点最靠右的回文子串的右端点。记\(mid\)表示该回文子串的中心。

如果当前\(i\leq r\)，显然有\(p_i\ge \min(p_{2\times mid-i},r-i)\)。来个图看看。

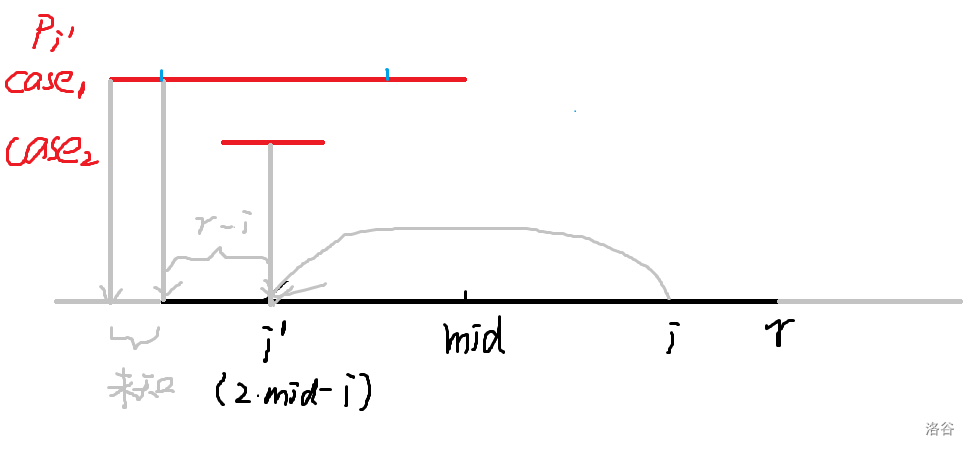
黑色段是我们维护的当前右端点最靠右的回文子串。

记\(i'\)为\(i\)关于\(mid\)对称过来的位置（如图，这个位置就是\(2\times mid-i\)），根据回文串的性质，如果以\(i'\)为中心的回文串仍在黑色段范围内（即图中\(case_2\)），那么\(p_i=p_{i'}\)，因为要是\(p_i\)还能扩展，\(p_{i'}\)早就扩展过了。如果不在（即图中\(case_1\)），那么\(i\)的答案最多取到上图蓝色框定范围的半径（长度为\(r-i\)），因为有个未知段，同时这种情况下我们还需在当前\(p_i\)基础上向两边暴力扩展判断。

如果当前\(i>r\)，我们啥都不知道，只能暴力扩展。

最后更新一下\(r\)和\(mid\)就可以了。

对于偶数长度回文串的情况怎么办？为了避免讨论，在原字符串首尾和每个字符之间插入一个特殊字符然后直接跑就可以了。

void pre(){
	t[++tt] = '&', t[++tt] = '#';//为了防止越界最前面多放一个不同的字符
	for(int i = 1; i <= n; i++){
		t[++tt] = s[i], t[++tt] = '#';
	}
	n = tt;
}

signed main(){
	cin >> s;
	n = s.size();
	s = " " + s;
	pre();
	for(int i = 1, r = 0, l = 1, mid = 1; i <= n; i++){
		if(i > r) p[i] = 1;
		else p[i] = min(p[2 * mid - i], r - i);
		while(t[i + p[i]] == t[i - p[i]]) p[i]++;
		if(i + p[i] - 1 > r){
			r = i + p[i] - 1;
			mid = i;
		}
	}
	int res = 0;
	for(int i = 1; i <= tt; i++) res = max(res, p[i] - 1);
	cout << res;
	return 0;
}

就复杂度来说，一眼望去瓶颈好像在 while 循环上，事实上一旦执行该循环\(r\)至少增大\(1\)，最多增到\(n\)，因此复杂度线性。