KMP与AC自动机

部分内容参考了 OI Wiki 和一些 blog ，对于一些时间复杂度的证明等细节去那里找。

KMP算法

引入

考虑一个问题，有一个字符串\(s\)和一个模式串\(t\)，如何求出\(t\)在\(s\)中的出现次数和每次出现的位置？

我们有一个简单的\(O(n^2)\)做法，但如果要求在\(O(n)\)的时间内求出答案呢？

kmp 算法就用来解决这类问题。

前置芝士之前缀函数

给定一个长度为\(n\)的字符串\(s\)，其前缀函数被定义为一个长度为\(n\)的数组\(nxt\)。其中\(nxt_i\)的定义是：

1. 如果子串\(s[0,i]\)有一对相等的真前缀与真后缀：\(s[0,k−1]\)和\(s[i−(k−1),i]\)，那么\(nxt_i\)就是这个相等的真前缀（或者真后缀，因为它们相等）的长度，也就是\(nxt_i=k\)；
2. 如果不止有一对相等的，那么\(nxt_i\)就是其中最长的那一对的长度；
3. 如果没有相等的，那么\(nxt_i=0\)。简单来说\(nxt_i\)就是，子串\(s[0,i]\)最长的相等的真前缀与真后缀的长度。

以上摘自 OI WiKi 。

举个栗子：对于 ABAB ，\(nxt=2\)，最长相等真前后缀为 AB 。

对于一个字符串\(s\)，要想求得\(nxt\)，我们目前仍只有一个\(O(n^3)\)算法。如何高效求出前缀函数？这是 KMP 算法的基础。

前缀函数的高效计算

首先考虑一个性质：对于任意\(nxt_i,0<i<n\)，都有\(nxt_i \leq nxt_{i-1}+1\)。这是因为对于当前字符串\(s[0,i]\)，必定有\(s[0,nxt_i-1]=s[i-nxt_i+1,i]\)。后面新来一个字符时，若\(s[nxt_i]=s[i+1]\)，显然\(nxt_{i+1}=nxt_i+1\)，若不相等，当然就会减小。

于是上述第一种情况\(O(1)\)即可。

n = strlen(s);
for(int i = 0; i < n; i++){
	int p = pi[i - 1];
	if(s[p] == s[i]) pi[i] = pi[i - 1] + 1;
	else for(int j = i; j; j--){
		if(check(0, j - 1, i - j + 1, i)){
			pi[i] = j;
			break;
		}
	}
}

这样一来，时间复杂度大致降到了\(O(n^2)\)，考虑进一步优化第二种情况。

对于那个新来的，如果最长的匹配不上，显然要优先考虑次长的。容易知道次长的是\(s[0,nxt_{nxt_i-1}-1]\)，原因见下图(图中\(π_i\)为\(nxt_i\))。

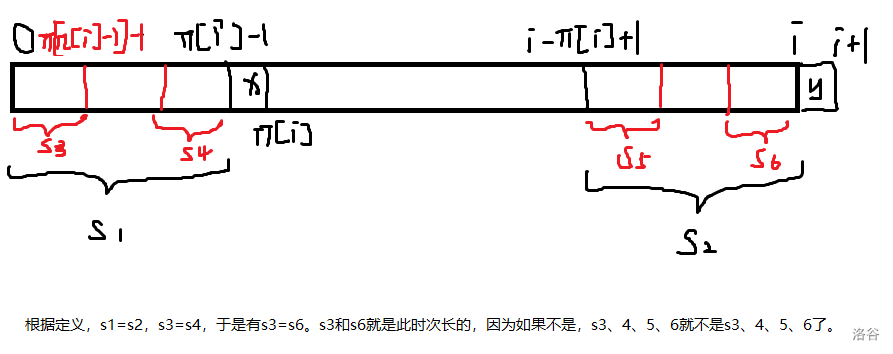
于是我们不用一个一个判断了，直接类似递归的去判断\(s[0,nxt_{nxt_i-1}-1]\)就可以了。

int n = s.size();
s = " " + s;
nxt[1] = 0;
for(int i = 2, j = 0; i <= n; i++){
    while(j > 0 && s[i] != s[j + 1]) j = nxt[j];
    if(s[i] == s[j + 1]) j++;
    nxt[i] = j;
}

现在我们成功的拥有了一个\(O(n)\)的前缀函数的计算方法。

真正的KMP

回到最开始的那个问题。

尝试构造一个字符串\(S=t+'\#'+s\)。也就是把\(t\)和\(s\)拼在一起，二者中间插入一个 # 号（或者任意一个在\(s\)和\(t\)中都没有出现过的字符）。然后对着这个新的字符串求一遍前缀函数即可。在求前缀函数过程中，只要出现\(nxt_i=|t|\)，就意味着\(t\)在\(s\)中出现了一次。原因显然。由于 # 号只有一个，限制了\(nxt_i\)不可能超过\(|t|\)。

这就是 KMP 算法。其他扩展应用等待\(update\)。

AC自动机

其实和AC没有一点关系，它叫 Aho-Corasick automaton 。

引入

上面我们探讨了字符串\(s\)和一个模式串\(t\)匹配的问题，利用 KMP 算法可以在\(O(|s|+|t|)\)的时间内求出答案。那如果是\(s\)和多个模式串\(t_i\)匹配，要求出有多少个模式串在\(s\)中出现过且仍希望在\(O(n)\)时间内解决呢？

前置芝士之自动机

OI 中所说的「自动机」一般都指「确定有限状态自动机」。自动机是一个对信号序列进行判定的数学模型。「信号序列」是指一连串有顺序的信号，例如字符串从前到后的每一个字符、数组从 1 到 n 的每一个数、数从高到低的每一位等。自动机的结构就是一张有向图，而自动机的工作方式和流程图类似，不同的是：自动机的每一个结点都是一个判定结点；自动机的结点只是一个单纯的状态而非任务；自动机的边可以接受多种字符（不局限于 T 或 F）。

以上摘自 OI WiKi 。

简单来说就是一个借助一堆转移关系和式子进行判断的东西。

AC自动机的构建

概述

AC自动机的结构基础是 Trie ，以 KMP 算法思想建立，用于解决类似上面提出的多模式匹配问题。AC自动机的构造分为 Trie 的建立和失配指针的构造两个主要步骤。

Trie 的建立

拿所有模式串\(t_i\)构建一棵 Trie 树，标记每个模式串的词尾。

void insert(char s[]){
	int n =  strlen(s), p = 0;
	for(int i = 0; i < n; i++){
		if(! tr[p][s[i] - 'a']) tr[p][s[i] - 'a'] = ++tot;
		p = tr[p][s[i] - 'a'];
	}
	cnt[p] += 1;//在词尾标记
}

失配指针的构建

既然叫失配指针 (fail) ，其实就是为了匹配不上时用的。在 KMP 算法中，我们用 nxt 数组解决了失配的问题。当面临多模式匹配时，情况就相对复杂一点。

fail 是干什么的？对于 Trie 上的一个节点\(i\)，如果它的 fail 指向\(j\)，则一定满足从根节点到\(j\)所连成的串是从根节点到\(i\)所连成的串的后缀。并且一定是能找到的最长后缀。如果找不到这样的后缀，就让 fail 指向根节点。所有根节点的儿子的 fail 都指向根节点。这样一旦匹配不上，就立马可以走向最有可能匹配上的位置去统计。

所以应当如何构建？

对于代表字符\(c\)的节点\(v\)，假设其父亲\(u\)的 fail 已经设置好了，那么\(fail(v)\)为\(w\)，\(w\)是\(fali(u)\)的代表字符\(c\)的儿子。这样一说有点绕，形式上就是令：\(fail(v)=w,t_{u,v}=t_{fail(u),w}=c\)。如果\(t_{fail(u),w}\)不存在，那么就跳到\(fail(u)\)上继续寻找，直到根节点。

为什么这样构建？

父亲\(u\)的 fail 已经建好了，它要么指向\(i\)满足根节点到\(i\)是与根节点到\(u\)匹配的最长后缀，要么指向根节点。\(v\)相当于是\(u\)后面新来一个\(c\)字符，如果\(i\)后面也有一个\(c\)字符的边指向\(j\)，\(v\)和\(j\)就可以在原来基础上进行下一步匹配。如果找不到，就只能换一个更短的后缀，也就是去\(fail(u)\)那儿找。

这样理论上差不多了，然而实现上还有一个问题：构建 fail 时，可能需要跳转很多次 fail 才能找到最终指向的点，时间复杂度或许无法保证。于是提前进行处理，如果任意一个节点\(u\)没有代表字符\(c\)的子节点，那么在原 Trie 上新加一条边，令其指向\(fail(u)\)的代表\(c\)的子节点（因为\(fail(u)\)已经提前这样处理好了，肯定有\(c\)子节点）。这样就不需要一直跳了。当然，如果一开始就没有\(c\)就只能指向根了。

事实上，上述过程是一个 BFS 的过程，因为是一层一层进行的。

void bfs(){
	for(int i = 0; i < 26; i++){
		int y = tr[0][i];
		if(! y) continue;
		fail[y] = 0;
		q.push(y);
	}
	while(q.size()){
		int x = q.front();
		q.pop();
		for(int i = 0; i < 26; i++){
			int y = tr[x][i];
			if(y){
				fail[y] = tr[fail[x]][i];
				q.push(y);
			}else tr[x][i] = tr[fail[x]][i];//连新边
		}
	}
}

查询

拿着模式串\(t_i\)已经把AC自动机构建好了，现在\(s\)来了，该查询答案了（见“引入”部分）。

按照\(s\)在自动机上走，在每个节点时都跳一跳 fail 。fail 本质上连成一个后缀集合，\(t_i\)在\(s\)中的任意一次出现都可以看成是\(s\)的以某一位置为结尾的前缀的后缀，因此每个都会被统计到。如果到某个节点是某个模式串词尾，把答案拿走后\(cnt\)赋为\(-1\)，这样不会多算，同时保证了 Trie 上每个点最多经过一遍，复杂度为\(O(Σ|t|)\)。

int ask(){
	int n = s.size(), p = 0, res = 0;
	for(int i = 0; i < n; i++){
		p = tr[p][s[i] - 'a'];
		int y = p;
		while(y && cnt[y] != -1){
			res += cnt[y];
			cnt[y] = -1;
			y = fail[y];
		}
	}
	return res;
}

AC自动机的优化

容易发现，上面的问题很有局限性。要是问你每个模式串在\(s\)中的出现次数，就不能拿过一个点的答案就把\(cnt\)赋为\(-1\)了，因为我们是拿着\(s\)在 Trie 上走，肯定需要一部分点被重复统计。这样的话不还得在询问时反复跳 fail ，你不寄了。

于是要进一步优化。先不写了，等待\(update\)