网络流系列

网络流的初步认识

所谓网络，就是一张有向图\(G=\{V,E\}\)，对于图中每条有向边\((x,y)\in E\)，都有一个容量\(c(x,y)\)，特别的，如果\((x,y)\notin E\)，那么\(c(x,y)=0\)。网络中还有两个特殊的节点，分别是源点\(S\)和汇点\(T\)。每条有向边可能会有一个流量\(f(x,y)\)，\(f(x,y)\)必须满足以下三条性质：

1.\(\forall(x,y)\in E,f(x,y)\leq c(x,y).\)

2.\(\forall(x,y)\in E,f(x,y)=-f(y,x).\)

3.\(\forall x\not =S,x\not =T,\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)\)

第一条性质显然，流量不能超过容量。第二条性质揭示了网络流具有对称性。第三条性质表明，没有节点会储存流，所有流入该节点的都会全部从该节点流出。

一条边的剩余容量为初始容量减去流量。

所有流都从\(S\)流出，最终都流到\(T\)，没有流流入\(S\)，也没有流从\(T\)流出。形象地来说，一张流网络就如同一片水网，\(S\)为水源，水渠中流过不超过流量限制的水流，最终都会于终点\(T\)。

整个流网络的流量为：\(\sum_{(S,v)\in E}f(S,v)\)。

在上面的流网络中，每条边上黑色数字表示容量，红色数字表示流量，图中任意一条流量路径都是一条可行流，即每条边的流量都满足限制。边\((1,2)\)和\((3,T)\)已经满流，不能再有更大的流量经过。当前这张网络的流量为\(10\)。

网络流之最大流

对于一张网络，其在满足流量限制下的最大流量称为最大流。最大流的应用比较广泛，在二分图系列中提到的不少二分图上的问题都可以用最大流来解决。

Edmonds-Karp(EK)算法

在当前网络中，如果存在一条从\(S\)到\(T\)的路径，满足路径上每一条边的剩余流量都\(>0\)，那么该路径称为一条增广路。注意和二分图中的增广路区分开。如果这条增广路径上所经边的剩余容量的最小值为\(minc\)，那么沿着这条增广路显然可以让整张网络的流量增加\(minc\)。（为什么是剩余容量的最小值？因为如果增加的流量大于它，剩余容量最小的那条边的流量就会不满足性质1，它会被撑爆）。反过来，如果当前网络找不到增广路，说明不能再进行扩展，最大流已被找到。

\(EK\)算法的主要过程就是不断进行 BFS 操作，每次寻找一条最短的从\(S\)到\(T\)的增广路，增流，更新路径上每条边的剩余流量，并把增加的流量累计到答案里。

这样似乎做完了，然而还有一个重要的问题：假如我们当前扩展的一条增广路不是最优选择怎么办？

下面是一个直观的例子：

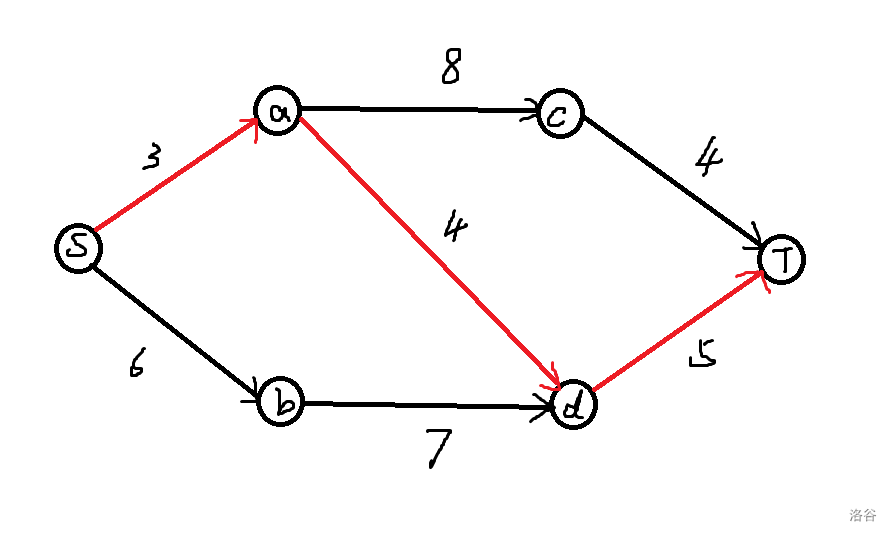
在最开始找增广路时，我们找到了\(S\to a\to d\to T\)这条路径，流量增加\(3\)；再找第二条增广路，找到\(S\to b\to d\to T\)，流量增加\(2\)；此时找不到第三条增广路，于是最大流为\(5\)。容易发现这个答案是错误的，我们可以有两条更优的流量路径，分别是\(S\to a\to c\to T\)和\(s\to b\to d\to T\)，这样正确的最大流是\(8\)。

为什么没有计算出正确的答案？因为我们路径找错了。在我们找出第一条增广路（标为红色）时，扩展了\((a,d)\)这条边，事实上这条边是不应该有流量的；同时，我们让\((S,a)\)满流了，于是后面\(a\to c\to T\)这条路径被堵住走不了了，因此最后无法找到最优答案。

于是我们需要一个类似反悔操作的东西来避免上述情况出现。我们称之为退流。对于每条边\((u,v)\)，我们构造一条不存在的反向边\((v,u)\)，如果在扩展一条增广路\(path1\)时，原边流量增加了\(k\)（即剩余容量减少\(k\)），我们令其反向边的剩余容量增加\(k\)，表示多了\(k\)的流量可以退流。如果在寻找一条新的增广路\(path2\)时从\((u,v)\)的反向边\((v,u)\)走过，并增大了\(k'\)的流量，就表示有\(k'\)的流量退流，即有\(k'\)的流量不再沿\(u\to v\)走，而是沿\(u\to x(x\not = v,(u,x)\in path2)\)走了，类似于抵消。通俗来讲，我们用边\((u,v)\)分别把\(path1\)和\(path2\)划分成前半部分和后半部分，在退流操作后，相当于令\(path1\)的前半部分接上\(path2\)的后半部分，令\(path2\)的前半部分接上\(path1\)的后半部分，构成两条新的流量路径。至于边\((u,v)\)中是否还有流量，取决于退流的流量大小。

事实上，退流操作恰好符合了流量性质的第二条，原边流量增加\(f\)，其反向边流量就要增加\(-f\)，也即反向边剩余容量增加\(f\)。所以退流操作的正确性可以保证，看起来也非常自然。对此，算阶上是这样叙述的：

当一条边的流量\(f(x,y)>0\)时，根据斜对称性质，它的反向边的流量\(f(y,x)<0\)，此时必定有\(f(y,x)<c(y,x)\)，因此每条边的反向边也要考虑。

那么在实现\(EK\)算法时，我们对原边建出反向边，在修改原边剩余流量时也对应修改其反向边剩余流量即可。在具体实现上可以采用邻接表成对储存的方法。

\(EK\)算法时间复杂度为\(O(nm^2)\)，实际效率更高，一般可处理\(10^3\)至\(10^4\)规模的网络。

下面给出代码以供复习时查看。此代码可以通过P3376 【模板】网络最大流。

void add(int x, int y, int z){
	ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
	ver[++tot]=x,edge[tot]=0,nxt[tot]=head[y],head[y]=tot;
}

bool bfs(){
	while(q.size()) q.pop();
	memset(vis,0,sizeof vis);
	memset(incf,0x3f,sizeof incf);
	q.push(s);
	vis[s]=1;
	while(q.size()){
		int x=q.front();
		q.pop();
		for(int i=head[x];i;i=nxt[i]){
			int y=ver[i];
			if(edge[i]&&!vis[y]){
				incf[y]=min(incf[x], edge[i]);
				vis[y]=1;
				pre[y]=i;
				q.push(y);
				if(y==t) return 1;
			}
		}
	}
	return 0;
}

void update(){
	int x=t;
	while(x!=s){
		int i = pre[x];
		edge[i]-=incf[t];
		edge[i^1]+=incf[t];
		x=ver[i^1];
	}
	ans+=incf[t];
}

void work(){
	cin>>n>>m>>s>>t;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
	}
	while(bfs()) update();
	cout<<ans;
}

Dinic算法

可以说是比较容易实现的效率最高的网络流算法之一。

网络中所有节点以及剩余容量\(>0\)的边组成的子图称为残量网络。在 EK 算法中，每次遍历整张残量网络，却只找到一条增广路，看起来还可以优化。

考虑我们通过 BFS 对原图进行分层。一个节点\(x\)的层次记为\(d_x\)，也就是从\(S\)到\(x\)需要最少经过的边数。在图\(G\)分好层后的子图\(G'\)中，满足\(\forall(x,y)\in G',d_y=d_x+1\)。

我们在\(G'\)中进行增广，对于每个节点\(x\)，向所有从\(x\)出发能够到达的层次深于\(x\)的节点进行增广。并不是找到一条增广路就走，而是把所有流入\(x\)的流量都给下面分配下去，并实时更新剩余容量，直到增广不了了，后面塞不下了，或者流进\(x\)的流量分配完了，要等下一次从别的边可能进来新流量可供分配时，才回去。

如果在增广过程中遇到边\((u,v)\)剩余容量为\(0\)或者\(v\)以后已经增广到极限不能再增广，那么下次在到达\(u\)时显然没必要再尝试走这条边进行增广。于是我们考虑记录\(now_u\)表示从\(u\)出发的第一条有必要尝试增广的边，这样避免了重复进行不必要的遍历。这称为当前弧优化，是 Dinic 算法时间复杂度正确的一部分。

还有一个常数优化：

多路增广是 Dinic 算法的一个常数优化——如果我们在层次图上找到了一条从\(s\)到\(t\)的增广路\(p\)，则接下来我们未必需要重新从\(s\)出发找下一条增广路，而可能从\(p\)上最后一个仍有剩余容量的位置出发寻找一条岔路进行增广。

接下来我们整理一下 Dinic 算法的基本流程：

1.不断对残量网络 BFS 分层，直到无法分到\(T\)，即不存在增广路。

2.在当前层次图上 DFS 增广，并实时更新剩余容量。注意上述优化。

Dnic 算法时间复杂度为\(O(n^2m)\)，实际上远远达不到这个上界。它一般可以处理\(10^4\)到\(10^5\)规模的网络，较为常用。给代码。

void add(int x,int y,int z){
	ver[++tot]=y,edge[tot]=z,nxt[tot]=head[x],head[x]=tot;
	ver[++tot]=x,edge[tot]=0,nxt[tot]=head[y],head[y]=tot;
}

bool bfs(){
	memset(d,0,sizeof(d));
	while(q.size()) q.pop();
	q.push(s);
	d[s]=1;
	now[s]=head[s];
	while(q.size()){
		int p=q.front();
		q.pop();
		for(int i=head[p];i;i=nxt[i]){
			if(edge[i]&&!d[ver[i]]){
				q.push(ver[i]);
				d[ver[i]]=d[p]+1;
				now[ver[i]]=head[ver[i]];
				if(ver[i]==t) return 1;
			}
		}
	}
	return 0;
}

ll dinic(int p,ll flow){
	if(p==t) return flow;
	int to=0;
	ll rest=flow,k,i;
	for(i=now[p];i&&rest;i=nxt[i]){
		now[p]=i;
		if(edge[i]&&d[ver[i]]==d[p]+1){
			k=dinic(ver[i],min(rest,(ll)edge[i]));
			if(!k) d[ver[i]]=0;
			edge[i]-=k;
			edge[i^1]+=k;
			rest-=k;
		}
	}
	return flow-rest;
}

void work(){
	cin>>n>>m>>s>>t;
	for(int i=1;i<=m;i++){
		int u,v,c;
		cin>>u>>v>>c;
		add(u,v,c);
	}
	ll flow=0;
	while(bfs()) while(flow=dinic(s,INF)) ans+=flow;
	cout<<ans;
}

最大流与二分图

在这里补一补二分图系列中的坑。

最大流求二分图最大匹配

先将原二分图连好边，容量均为\(1\)。设立一个源点\(S\)和汇点\(T\)。令所有左部点和\(S\)连边，所有右部点和\(T\)连边，这些边容量也为\(1\)。直接跑最大流即可。

最大流求二分图多重匹配

跟上面基本一样，只是把所有原图中的点与\(S\)或\(T\)连的边的容量改设为每个点的最大可连边数即可。

典例与建模分析(已停更)

网络流难得不是算法，而是建模，如何将题目与网络流模型建立联系，这个反而是最难的。

例题：POJ1149 PIGS

我们先来考虑最直接的建图方式。按照以下规则建图。

• 把每个猪圈\(i\)拆成\(N\)个节点。相当于每个顾客\(j\)，即每一轮购买\(j\)都对应第\(j\)层的\(i\)。
• 从源点向第一层每个猪圈连一条边，容量为该猪圈内猪的初始数量。也就是一开始从这个猪圈最多能买到这么多猪。
• 从每个顾客向汇点连一条边，容量为该顾客最多能买的猪的数量。
• 对于每个顾客\(j\)，从他能买的所有猪圈\(i\)向他连一条边（注意连第\(j\)层的\(i\)），容量为\(+\infty\)，原因是由于猪可以调换，每一轮购买过后一些猪圈内可购买猪的数量可能增加。具体增加多少我们并不知道，但猪圈上限和顾客上限都已经被前面两条连边规则限制好了，所以直接把容量设为\(+\infty\)即可。
• 对于每一轮购买\(j\)，如果顾客\(j\)能买猪圈\(i\)，那么从第\(j\)层的所有\(i\)向第\(j+1\)层的所有\(i\)连边，每条边的容量为\(+\infty\)，这表示在第\(j+1\)个顾客来之前，第\(j\)个顾客买过的猪圈的猪可以随意调换。

我们用\(1\)流量代表\(1\)头猪，源点向猪圈\(1\)流量代表初始分配一头猪可供购买，猪圈向猪圈\(1\)流量代表一头猪从原来的猪圈调换到另一个猪圈，顾客向汇点\(1\)流量代表买下了一头猪。如此跑最大流即可。这就是网络流方面基本的模型转化，在互相联系的东西之间连边，将具体的题目限制转化成容量的限制，抽象出来来考虑。

然而我们注意到这样建图最多有\(2+N+M\times N=1e5+\)个结点，跑起来会很慢。所以必须优化。

完结通知：不想写了