组合数

1、求组合数，从a中选b个数的方案：

#include <iostream>
using namespace std;
const int N = 2001, mod = 1e9 + 7;

int c[N][N];
void init()
{
    for(int i = 0;i < N;i++)
        for(int j = 0; j <= i; j++)
            if(!j) c[i][j] = 1;
            else c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod;
}

int main()
{
    init();
    int n;
    cin>>n;
    while(n--)
    {
        int a, b;
        cin>>a>>b;
        cout<<c[a][b]<<endl;
    }
}

从a中选b个的方案 = 假如先拿出一个，然后剩下的a-1个选b个的方案（不包含拿出的这个数，所以要选b个） + 剩下的a-1个选b-1个的方案（包含拿出的这一个数，所以要选b-1个）之和。

 首先预处理出所有的方案数，时间复杂度为2000 * 2000 = 4e6;

注意边界c[i][0] (0 <= i <= N) c[i][0] = 1;

1）n<=1e5,  1<=a,b<=2000 用的是递推c[a][b] = c[a-1][b] + c[a-1][b-1];

2）n<=1e4, 1<=a,b<=1e5, 预处理 Cab = a! / b! * (a - b)!, fact[i] = i! mod 1e9+7; a / b mod p != a mod p / b mod p, 用逆元来算，把除法变成乘法。

预处理初阶乘的逆元：infact[i] = i!^-1 mod 1e9 + 7;

 

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;

int fact[N], infact[N];
LL quickPow(int a, int k, int p)
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}
int main()
{
    fact[0] = infact[0] = 1;
    for(int i = 1; i < N;i++)
    {
        fact[i] = (LL) fact[i-1] * i % mod;
        infact[i] = (LL)infact[i-1] * quickPow(i, mod-2,mod) % mod;
    }
    int n;
    cin>>n;
    while(n--)
    {
        int a, b;
        cin>>a>>b;
        cout<<(LL)fact[a] * infact[a-b] % mod * infact[b] % mod<<endl;
    }
}

也就是说逆元就是把除法改成乘法了b /a ,那么1 / a就是a的逆元了。求逆元的方法费马定理：b * b^-1 ≡ 1 ( mod p) 那么逆元就是b^(p-2) 也就是说infact[i] = infact[i-1] * i^-1, 因为i^-1 * i ≡ 1 (mod p), 所以i^-1 = i^(p-2).

 3) 如果a,b<=10^18 那么就要用Lucas定理。

 

 

 

 

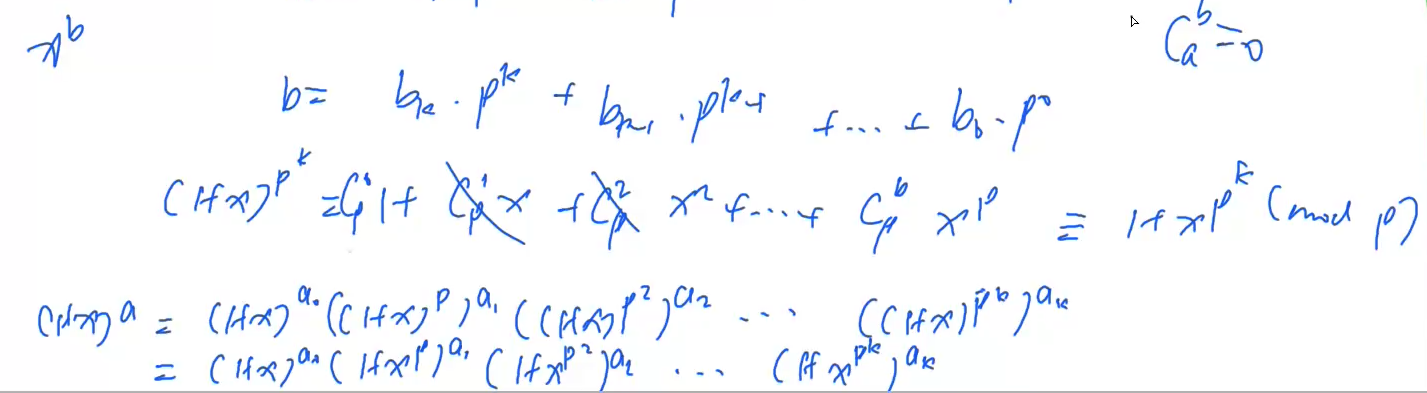
 lucas定理：

#include <iostream>
#include <algorithm>
using namespace std;
typedef unsigned long long LL;

int p;

int quickPow(int a, int k)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(LL a, LL b)
{
    LL res = 1;
    for(LL i = 1, j = a; i <= b; i++, j--)
    {
        res = (LL)res * j % p;
        res = (LL)res * quickPow(i, p - 2) % p;
    }
    return res;
}

int lucas(LL a, LL b)
{
    if(a < p && b < p) return C(a,b);
    return (LL) C(a % p, b % p) * lucas(a / p, b / p) % p;
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        LL a, b;
        cin>>a>>b>>p;
        cout<<lucas(a,b)<<endl;
    }
    
    return 0;
}

 

 最后用高精度求解完整组合数，没有取模。

#include <iostream>
#include <algorithm>
#include <vector>
const int N = 5010;
using namespace std;
int primes[N], cnt;
int sum[N];
bool st[N];
//线性筛质数
void get_primes(int n)
{
    for(int i = 2;i <= n; i++)
    {
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0; primes[j] <= n / i;j++)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
//n!包含质数p,p^2,p^3...p^k的个数
int get(int n, int p)
{
    int res = 0;
    while(n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}

vector<int> mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for(int i = 0; i < a.size(); i++)
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    
    while(t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}

int main()
{
    int a,b;
    cin>>a>>b;
    get_primes(a);
    
    for(int i = 0;i < cnt; i++)
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    
    vector<int> res;
    res.push_back(1);
    
    for(int i = 0; i < cnt; i++)
        for(int j = 0; j < sum[i]; j ++)
            res = mul(res, primes[i]);//高精度乘法的模板
            
    for(int i = res.size() - 1; i >= 0; i --)
        printf("%d",res[i]);
    puts("");
    
    return 0;
}

 高精度乘法这里比较妙：第一重循环：质数的个数，第二重循环：每个质数的个数，这样就把有的每个质数都乘进来。

for(int i = 0; i < a.size(); i++)
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    
    while(t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
还有一个是求a!中质数的个数方法也很是巧妙：

int res = 0;
    while(n)
    {
        res += n / p;
        n /= p;
    }

比如5！质数2的个数：res = 2 + 1 = 3, 5 * 4 * 3 * 2 * 1 = 2 ^ 3 * 30,质数2确实是是3个。
5！质数3的个数：  res = 5 / 3 + 1 / 3 = 1个。
再然后是非常好用的线性筛模板：

void get_primes(int n)
{
    for(int i = 2; i <= n;i++)
    {
        if(!st[i]) primes[cnt++] = i;
        for(int j = 0; j <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}

 

//卡特兰数：每种数列可以转化为一条路径，同样每个路径也可以转化为一种01排列。0：向右，1：向上，那么要使得前缀中0的个数大于等于1个
//就要使得路径都在所有的{(0,0),(6,6)}即 y = x这条对角线的下面，同时也要使得我们的路径不得经过 y = x - 1;
//总的方案数C12^6 - 经过y = x - 1的方案数 = 不经过的方案数。不合法的路径一定是（0,0)到（5,7)  C2n^n - C2n^n-1

 

 

 

 

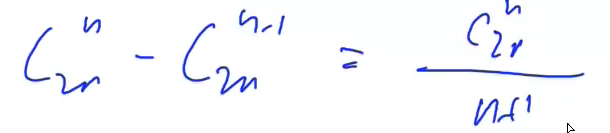
 如果取模的数是质数，那么就可以用快速幂来计算逆元，但是如果不是的话，那么只能用扩展欧几里得来求逆元

#include <iostream>
#include <algorithm>
using namespace std;
const int mod = 1e9 + 7;
typedef long long LL;

int quickPow(int a, int k)
{
    int res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res * a % mod;
        k >>= 1;
        a = (LL)a * a % mod;
    }
    return res;
}

int main()
{
    int n;
    cin>>n;
    int a = 2 * n, b = n;
    int res = 1;
    
    for(int i = a; i > a - b; i--) res = (LL) res * i % mod;  //(2n - n + 1)!
    for(int i = 1; i <= b; i++) res = (LL) res * quickPow(i, mod - 2) % mod;
    
    res = (LL) res * quickPow(n + 1, mod - 2) % mod;
    
    cout<<res<<endl;
    
    return 0;
}