hihocoder #1185 : 连通性·三 tarjan

#1185 : 连通性·三

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

暑假到了!!小Hi和小Ho为了体验生活，来到了住在大草原的约翰家。今天一大早，约翰因为有事要出去，就拜托小Hi和小Ho忙帮放牧。

约翰家一共有N个草场，每个草场有容量为W[i]的牧草，N个草场之间有M条单向的路径。

小Hi和小Ho需要将牛羊群赶到草场上，当他们吃完一个草场牧草后，继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后，小hi和小Ho就把牛羊群赶回家。

一开始小Hi和小Ho在1号草场，在回家之前，牛羊群最多能吃掉多少牧草？

举个例子：

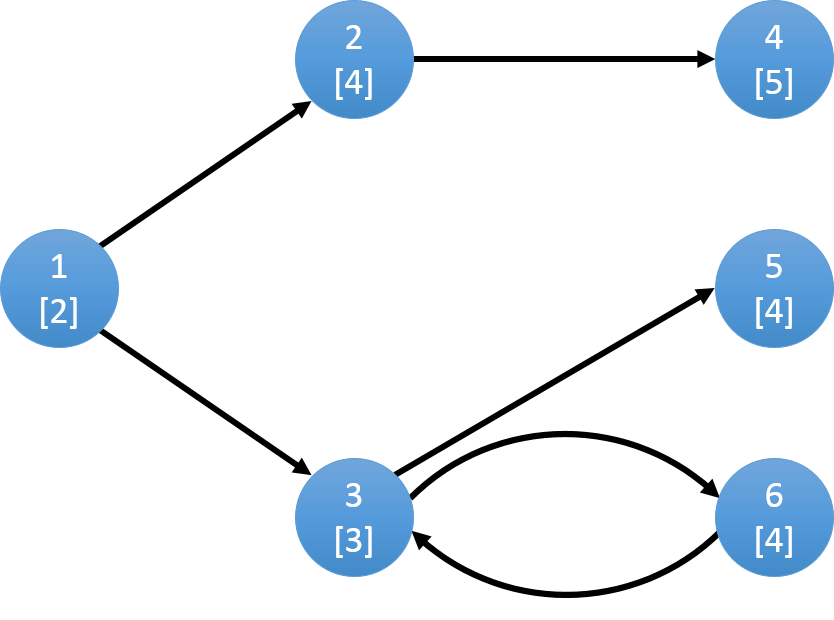
图中每个点表示一个草场，上部分数字表示编号，下部分表示草场的牧草数量w。

在1吃完草之后，小Hi和小Ho可以选择把牛羊群赶到2或者3，假设小Hi和小Ho把牛羊群赶到2：

吃完草场2之后，只能到草场4，当4吃完后没有可以到达的草场，所以小Hi和小Ho就把牛羊群赶回家。

若选择从1到3，则可以到达5，6：

选择5的话，吃完之后只能直接回家。若选择6，还可以再通过6回到3，再到5。

所以该图可以选择的路线有3条：

1->2->4 		total: 11
1->3->5 		total: 9
1->3->6->3->5: 		total: 13
  

所以最多能够吃到的牧草数量为13。

 

 

本题改编自USACO月赛金组

提示：强连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2行：N个正整数，第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000

第3..M+2行：2个正整数，u,v。表示存在一条从u到v的单向路径。1≤u,v≤N

输出

第1行：1个整数，最多能够吃到的牧草数量。

 

样例输入

6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3

样例输出 13

跑一遍tarjan，将同一个强连通变量里的点缩起来，建立一张新图，跑dfs。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define clr(a,b) memset(a,b,sizeof(a))
#define fir first
#define se second
#define pb(x) push_back(x)
#define ALL(V) (V).begin(), (V).end()
const int maxn = 1e5 + 10;
const int mod = 1000000007;
const int oo = 0x3f3f3f3f;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
typedef vector<int> vii;
//header 1.0

int n, m, t, id;
int a[maxn];
int na[maxn];
stack<int> s;
vii g[maxn], rg[maxn];
vii ng[maxn];
vii ans[maxn];
int chk[maxn];
int grp[maxn];

void init() {
    for(int i = 0; i < maxn; i++) g[i].clear();
    for(int i = 0; i < maxn; i++) rg[i].clear();
    for(int i = 0; i < maxn; i++) ng[i].clear();
    for(int i = 0; i < maxn; i++) ans[i].clear();
    clr(a, 0); clr(na, 0);
    clr(chk, 0); clr(grp, 0);
    while(!s.empty()) s.pop();
    id = 0;
}

void dfs(int x) {
    if(chk[x] == t) return;
    chk[x] = t;
    for(int i : g[x]) dfs(i);
    s.push(x);
}

void dfs2(int x) {
    if(chk[x] == t) return;
    chk[x] = t; ans[id].pb(x);
    grp[x] = id;
    for(int i : rg[x]) dfs2(i);
}

int fans;
int vis[maxn];
void dfs3(int x, int sum) {
    fans = max(fans, sum);
    for(int i : ng[x]) {
        dfs3(i, sum + na[i]);
    }
}

int main() {
    //freopen("d:/in.txt", "r", stdin);
    //freopen("d:/out2.txt", "w", stdout);
    while(~scanf("%d %d", &n, &m)) {
        init();
        for(int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
        }
        for(int i = 1; i <= m; i++) {
            int u, v;
            scanf("%d %d", &u, &v);
            g[u].pb(v), rg[v].pb(u);
        }
        t = 1;
        for(int i = 1; i <= n; i++) {
            if(chk[i] != t) {
                dfs(i);
            }
        }
        t = 2;
        for(int i = 1; i <= n; i++) {
            int tmp = s.top();
            if(chk[tmp] != t) {
                ++id;
                dfs2(tmp);
            }
            s.pop();
        }
        for(int i = 1; i <= id; i++) {
            int sum = 0;
            for(int j : ans[i]) {
                for(int k : g[j]) {
                    if(grp[k] != i)
                    ng[i].pb(grp[k]);
                }
                for(int k : rg[j]) {
                    if(grp[k] != i)
                    ng[grp[k]].pb(i);
                }
                sum += a[j];
            }
            na[i] = sum;
        }
        fans = 0;
        clr(vis, 0);
        //printf("check %d %d\n", grp[2], a[grp[2]]);
        dfs3(grp[1], na[grp[1]]);
        printf("%d\n", fans);
    }
}