BLAST.tv Paris Major 2023 观后感

摩尔投票

方法：

大概操作就是记录一个 \(major,cnt\) ，顺序遍历数组 \(a\)，假设遍历到了第 \(i\) 个，当 \(cnt=0\) 时让 \(major=a_i\) ， 当 \(cnt\) 不为 \(0\) 时，如果 \(a_i=major\) 让 \(cnt\) 加 \(1\) ，否则减 \(1\)

这样做的时间复杂度是 \(O(n)\) 的，空间复杂度是 \(O(1)\) 的。

注意这个是有绝对众数的时候才是对的。

拓展：

现在你要求出现次数超过 \(\frac{n}{k}\) 的，显然数的个数是小于 \(k\) 的，不然 \(n\) 个肯定不够

其实做法和上面差不多，现在要开两个数组 \(major_i,cnt_i\)

操作：

首先如果 \(x\) 本身是候选者的话，则对其出现次数加一

如果不是的话，如果有 \(cnt=0\) 的位置那么就让 \(x\) 成为候选者，出现次数变为 \(1\)，否则让所有候选者出现次数减 \(1\)

注意这个不一定所有都是对的，但是正确的答案一定包括

这个万一就感觉有点抽象了，所以还是证明一下吧

考虑反证法，假设 \(x\) 出现了 \(y>\frac{n}{k}\) 次，但是他不在答案里面

1. 他就没有进入过 \(major\) 数组：那么他肯定让所有候选者减去了 \(y\) 次，但是由 \(y>\frac{n}{k}\) 知 \(y\times k > n\) 不符合题意
2. 他进入过然后被干掉了：同理，他被干掉了说明肯定所有候选者都减去了 \(y\) 次，同上，还是寄

那么摩尔投票有什么用呢？

摩尔投票具有结合律，可以用 \(ds\) 乱搞

这玩意就和线性基很像，就直接把一个插进另一个就行了

CF643G Choosing Ads

就是板子

code

更加神奇的东西

其实感觉和摩尔投票没啥关系了

假设我现在猜一手区间众数为 \(x\) ，现在就可以把等于 \(x\) 的设为 \(1\) ，否则设为 \(-1\) ，这样 \(\text{chk}\) 一个区间是否众数是 \(x\) 就可以 \(O(1)\) 了

因为是绝对众数，所以我枚举一遍我猜的众数就可以求出所有区间的众数了，但是这是 \(O(n^2)\) 的

但是还有性质 😍😍😍

1. 当区间 \([l,r]\) 有绝对众数 \(x\) 时，区间 \([l,k],[k+1,r],k\in[l,r)\) 肯定有一个的有绝对众数并且他是 \(x\) 废话
2. 区间 \([l,l],[l,l+1],[l,l+2],…,[l,r]\) 的本质不同绝对众数个数只有 \(log_2\) 个，原因是我要是想成为绝对众数要大于区间一半，就比如假设现在序列长度为 \(n\) ，你至少要加 \(n+1\) 个数才能成为新的绝对众数

将上面两个结合起来后，就有了一个非常 😎 的结论，就是跨过区间 \([l,r]\) 中点 \(mid\) 的所有区间的绝对众数个数是 \(\log\) 级别的，具体来说，根据性质 \(1\)，就是区间 \([l,l],[l,l+1],…,[l,mid]\) 和 \([mid,mid],[mid,mid+1],…,[mid,r]\) 的绝对众数集合一定是包含所有上述区间的绝对众数的，又根据性质 \(2\) ，可以知道只有 \(\log\) 个

ARC159F Good Division

题意：定义可以每次删去一对相邻不同的数把序列删空，求将数组 \(A\) 划分成若干个合法的子串的方案数

首先转化一下题意，一个序列是好的当且仅当他没有绝对众数，这个显然是正确的，因为题目里面给的操作就是一个摩尔投票的过程。

然后我们就有 \(O(n^2)\) 的做法了，🐍 \(f_i\) 表示前 \(i\) 个数的方案数，转移就枚举最后一个序列长度就行了，好棒！但是过不了😔

考虑利用上面那个东西优化，搞一个类似 \(cdq\) 优化 \(dp\) 的东西

假设现在求的区间是 \([l,r]\) ，先递归 \([l,mid]\) 算出左边的值，考虑左边对右边的贡献，根据上面性质，跨过中点的区间只有 \(\log\) 个众数，发现一个区间只有一个绝对众数，所以可以先让所有 \([mid+1,r]\) 的 \(f\) 加上 \([l,mid]\) 的 \(f\)， 然后直接枚举众数减去不合法的，精细实现一下应该可以做到 \(O(n\log^2 n)\)

code (上面肯定 🤡 可能讲的不是很清楚)

但是我还想讲一个好玩的东西，虽然好像跟摩尔投票无关，但是跟上面的那个玩意有关，有了这个就很好做到 \(O(n\log^2n)\) 了

给定长度为 \(n\) 一个 \(0,1\) 序列 \(A\)，求 \(1\) 个数比 \(0\) 个数多的区间个数 \(n \le 反正单 \log 过不去\)

首先这个用 \(bit\) 很容易做到 \(O(n\log n)\) ，但是还不够优秀 😅

首先肯定的转化是把 \(0\) 改为 \(-1\) ，做一个前缀和，现在就是要对于每个 \(i\) 求 \(sum_i >sum_{j-1}\) 的 \(j\) 的个数了

现在有一个很 🤩 的做法，我们把 \(1,-1\) 看为折线

比如 \(101001\) 这个就长成这样

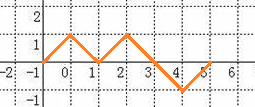
发现每次只会移动一位，也就是说我每移动一次就只有一个纵坐标加入或减去

算了上面的你一定没有听懂 🧐

其实就是你对 \([-n,n]\) 的每个位置开一个桶，统计 \([1,i]\) 有几个 \(sum_i\) 是当前纵坐标，然后你再记一个 \(pre\) 表示坐标有多少 \(j\) 满足 \(j<i,sum_j<sum_i\)，走上来就把桶贡献加进 \(pre\)，走下去就把桶从 \(pre\) 中删掉

应用：

Coming（coming）

这是 [生成函数] 的题看不了

题意也不能说

算了谁能看谁看吧

题解