七大经典排序(Java版)
.
冒泡排序:
通过相邻的两个数的比较, 根据需要决定是否将两个数互换位置, 然后将比较往前(或往后)推进. 最简单的排序算法,直接上代码。

for(i=0;i<length-1;i++) for(j=i+1;j<length;j++) if(arrayVal[i]>arrayVal[j]) { //置换位置 temp=arrayVal[i]; arrayVal[i]=arrayVal[j]; arrayVal[j]=temp; } }
选择排序:
"选择排序"就是第0个逐步和后面全部的比,比完0位置就得到最小的数,紧接着再从1位置对比后面的元素,以此类推,逐步得到从小到大的值.

for(int i = 0; i < arr.length - 1; i++) { int k = i; for(int j = k + 1; j < arr.length; j++){ if( arr[j] < arr[k]){ k =j; } //在内层循环结束,也就是找到本轮循环的最小的数以后,再进行交换 if( i != k) { int temp= arr[i]; arr[i] = arr[k]; arr[k] = temp; }
插入排序:
首先对数组的前两个数据进行从小到大的排序。
接着将第三个数据与排好序的两个数据比较,将第三个数据插入合适的位置。
然后将第四个数据插入到已排好序的前3个数据中。
....
// 第1个数肯定是有序的,从第2个数开始遍历,依次插入有序序列
public static void insertionSort(int[] a){
for(int i = 1 ; i < a.length; i++){
int temp = a[i];
int j = i - 1;
while( j >= 0 && temp < a[j]){
a[j+1] = a[j];
j--;
}
a[j+1] = temp;
}
Shell排序算法:(希尔排序、缩小增量排序):
Shell排序是基于插入排序的思想。
1.将有n个元素的数组分成n/2个数字序列,第1个数据和第n/2+1个数据为一对,...
2.一次循环使每一个序列对排好顺序。
3.然后,变为n/4个序列,在次排序。
4.直到序列变为1个。

//希尔排序
public static void shellSort(int a[]){
for(int r = a.length/2 ; r >= 1; r/=2 ){
for(int i = r; i < a.length ; i++){
int temp = a[i];
int j = i - r;
while(j >= 0 && temp < a[j]){
a[j+r] = a[j];
j -= r;
}
a[j+r] = temp;
}
}
}
快速排序算法
1.在待排序的元素任取一个元素作为基准(通常选第一个元素,但最的选择方法是从待排序元素中随机选取一个作为基准),称为基准元素;
2.将待排序的元素进行分区,比基准元素大的元素放在它的右边,比其小的放在它的左边;
3.对左右两个分区重复以上步骤直到所有元素都是有序的。
public static void quickSort3(int arr[],int _left,int _right){
int left = _left;
int right = _right;
int temp = 0;
if(left <= right){ //待排序的元素至少有两个的情况
temp = arr[left]; //待排序的第一个元素作为基准元素
while(left != right){ //从左右两边交替扫描,直到left = right
while(right > left && arr[right] >= temp){
right --; //从右往左扫描,找到第一个比基准元素小的元素
}
arr[left] = arr[right];
while(left < right && arr[left] <= temp){
left ++; //从左往右扫描,找到第一个比基准元素大的元素
}
arr[right] = arr[left];
}
arr[right] = temp; //基准元素归位
quickSort3(arr,_left,left-1); //对基准元素左边的元素进行递归排序
quickSort3(arr, right+1,_right); //对基准元素右边的进行递归排序
}
}
堆排序算法
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆:
堆是具有以下性质的完全二叉树:
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
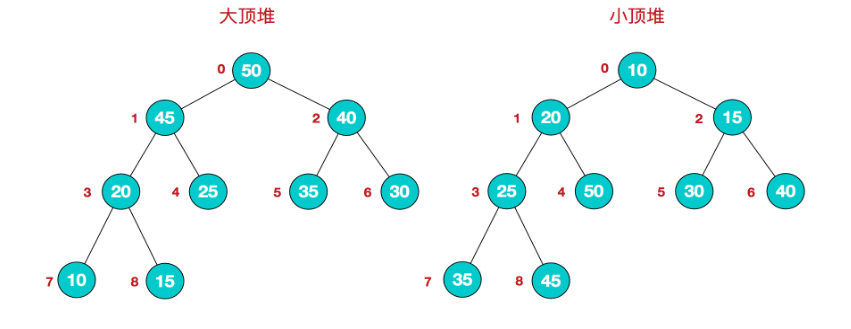
堆排序的基本思想:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
堆排序的基本步骤:
1.构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
2.将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
public class HeapSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
//1.构建大顶堆
for(int i=arr.length/2-1;i>=0;i--){
adjustHeap(arr,i,arr.length);
}
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);
adjustHeap(arr,0,j);
}
}
// 调整大顶堆
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];
for(int k=i*2+1;k<length;k=k*2+1){
if(k+1<length && arr[k]<arr[k+1]){
k++;
}
if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;
}
//交换元素
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
归并排序
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
public class MergeSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
int []temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
sort(arr,0,arr.length-1,temp);
}
private static void sort(int[] arr,int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;
sort(arr,left,mid,temp);//左边归并排序,使得左子序列有序
sort(arr,mid+1,right,temp);//右边归并排序,使得右子序列有序
merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;
int j = mid+1;
int t = 0;
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){
temp[t++] = arr[i++];
}
while(j<=right){
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left <= right){
arr[left++] = temp[t++];
}
}
}
各个排序算法比较:
| 排序算法 | 平均速度 | 最坏情况 | 是否稳定 |
| 冒泡排序 | O( n^2) | O( n^2) | 稳定 |
| 快速排序 | O(nlogn) | O( n^2) | 不稳定 |
| 选择排序 | O( n^2) | O( n^2) | 不稳定 |
| 插入排序 | O( n^2) | O( n^2) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | 不稳定 |
| Shell排序 | O( n^(3/2) ) | O( n^2) | 不稳定 |
| 合并排序 | O(nlogn) | O(nlogn) | 稳定 |




 浙公网安备 33010602011771号
浙公网安备 33010602011771号