重生之数据结构与算法----二叉树的变种
挖坑待埋
由于二叉树有很多变种,目前只提供逻辑概念,具体实现日后慢慢补充
二叉搜索树
上文简单的介绍了一下二叉搜索树(BST),这个树可以说是梦的起点。无数高性能搜索方案,底层核心都是基于BST来构建。
那二叉搜索树有什么优势呢?
它的优势即左小右大,左子树的每个节点都小于当前节点,右子树的每个节点都大于当前节点。
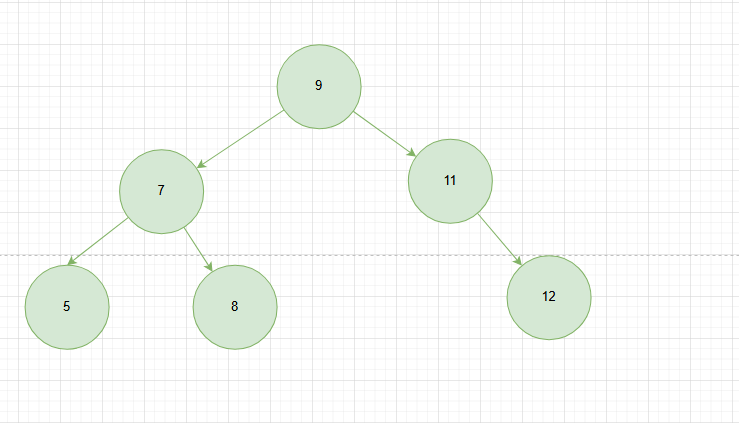
因为这个特性,我们可以使用最简单的二分法。来实现快速找到某个节点。
举个例子
假如我要找到节点11
使用标准的DFS算法(中序),遍历路径为5,7,8,9,11.时间复杂度O(N)
使用二叉搜索遍历,遍历路径为9,时间复杂度O(log N)
一个简单的二叉搜索树
点击查看代码
public class MySortList<K,V>
where K: IComparable<K>
{
public static void Run()
{
var list = new MySortList<int, string>();
////此写法会退化为链表
//for (int i = 0; i <= 100; i++)
//{
// list.Put(i, i.ToString());
//}
list.Put(50, "50");
list.Put(30, "30");
list.Put(20, "20");
list.Put(40, "40");
list.Put(70, "70");
list.Put(60, "60");
list.Put(80, "80");
list.Put(18, "18");
list.Put(55, "55");
list.Put(65, "65");
list.Put(75, "75");
list.Put(85, "85");
list.Treverse(list.Root,0);
list.Remove(70);
list.Treverse(list.Root, 0);
}
private TreeNode Root = null;
public MySortList()
{
}
/// <summary>
/// 增/改
/// O(logN)
/// </summary>
/// <param name="key"></param>
/// <param name="value"></param>
public void Put(K key, V value)
{
if (key == null)
throw new ArgumentNullException(nameof(key));
//var oldValue = Get(key);
Root = Put(Root, key, value);
}
private TreeNode Put(TreeNode? node,K key,V value)
{
if(node==null)
return new TreeNode(key,value);
int compare = key.CompareTo(node.Key);
//当前key大于左子树,去右子树
if (compare>0)
{
node.Right = Put(node.Right, key, value);
}
else if (compare < 0)
{
node.Left=Put(node.Left, key, value);
}
else
{
node.Value = value;
}
return node;
}
/// <summary>
/// 查
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
public V? Get(K key)
{
if(key==null)
throw new ArgumentNullException(nameof(key));
var node = Get(this.Root, key);
if (node == null)
return default;
return node.Value;
}
/// <summary>
/// 在BST中,二分法查找key
/// </summary>
/// <param name="node"></param>
/// <param name="key"></param>
/// <returns></returns>
private TreeNode? Get(TreeNode node,K key)
{
if (node == null)
return null;
var compare = key.CompareTo(node.Key);
//key大于当前节点,说明此节点左边都小于当前key.
if (compare > 0)
{
return Get(node.Right, key);
}
//key小于当前节点,key的节点在此节点的中
if (compare < 0)
{
return Get(node.Left, key);
}
return node;
}
public void Treverse(TreeNode node,int depth)
{
//if (node == null) return;
for (int i = 0; i < depth; i++)
{
Console.Write(" ");
}
Console.WriteLine($"Value: {node.Value}");
if (node.Left != null)
{
Treverse(node.Left,depth+1);
}
if (node.Right != null)
{
Treverse(node.Right,depth+1);
}
}
public void Remove(K key)
{
if (key == null)
throw new ArgumentNullException(nameof(key));
Remove(Root, key);
}
private TreeNode Remove(TreeNode? node,K key)
{
var compare=key.CompareTo(node.Key);
//大于当前节点,去右子树
if (compare>0)
{
node.Right = Remove(node.Right, key);
}
//小于当前节点,去左子树
else if (compare < 0)
{
node.Left = Remove(node.Left, key);
}
else
{
//情况1,当前节点为叶子节点,没有左右子树
if (node.Left == null && node.Right == null)
{
return node;
}
//情况2,左右子树有一个非空
if (node.Left == null || node.Right == null)
{
if (node.Left == null)
{
node = node.Right;
}
if (node.Right == null)
{
node = node.Left;
}
return node;
}
else
{
//情况3,左/右子树都非空
//得到左子树最大节点的指针
var leftMax = MaxNode(node.Left);
//删除左子树最大的那个节点
node.Left = RemoveMax(node.Left);
leftMax.Left = node.Left;
leftMax.Right = node.Right;
node = leftMax;
return node;
}
}
return node;
}
private TreeNode MaxNode(TreeNode node)
{
while (node.Right != null)
{
node = node.Right;
}
return node;
}
private TreeNode RemoveMax(TreeNode node)
{
if (node.Right ==null)
{
//右边为空,说明左边最大
return node.Left;
}
node.Right = RemoveMax(node.Right);
return node;
}
public class TreeNode
{
public K Key { get; set; }
public V Value { get; set; }
public int Size { get; set; }
public TreeNode? Left { get; set; }
public TreeNode? Right { get; set; }
public TreeNode(K key, V value)
{
this.Key = key;
this.Value = value;
this.Size = 1;
}
}
}
注意,它和上文讲到的双链表加强哈希的区别是,前者只是key插入顺序的排序,而不是key值大小的排序
平衡树
二叉搜索树的效率取决于树高,树结构越平衡,树高就接近O(log N),增删改查的效率也就越高。
二叉搜索树的缺点是不会对树进行平衡,在特殊情况下会退化为链表,增删改查复杂度就退化为Log(N),如果你的二叉搜索树是这种结构,就不太妙了。
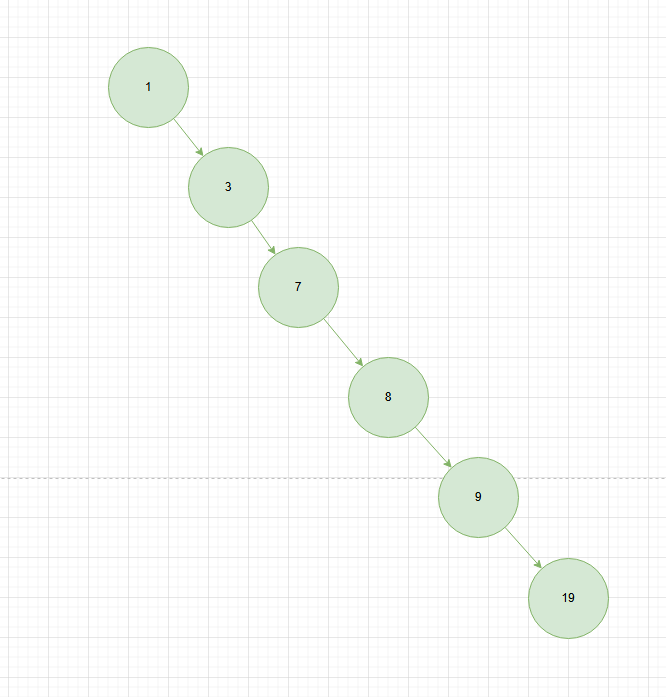
平衡树是一类特殊的二叉搜索树,它通过特定的机制(如旋转操作)来保持树的左右子树高度相对平衡,使得树的高度始终保持在 O(log N)级别,从而保证了查找、插入和删除操作的时间复杂度稳定。
一个简单的AVL树
//挖坑
一个简单的伸展树
红黑树
红黑树是一种自平衡的二叉搜索树,它在每个节点上增加了一个存储位来表示节点的颜色(红色或黑色)。通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。
虽然红黑树和一般的二叉平衡树(如 AVL 树)都旨在保持树的平衡以提高操作效率,但它们在平衡的实现方式和平衡程度上有所不同:
- AVL 树:是一种严格的二叉平衡树,它要求每个节点的左右子树的高度差不超过1
在插入和删除节点时,AVL 树可能需要进行更多的旋转操作来保持严格的平衡,因此在插入和删除操作频繁的场景下,性能可能会受到一定影响。 - 红黑树:并不追求严格的平衡,而是近似平衡。它在插入和删除节点时,通过颜色调整和较少的旋转操作来维护树的平衡,相对来说插入和删除操作的效率更高。
因此,红黑树在需要频繁进行插入、删除操作的场景中更为适用,例如在 C# 的 SortedDictionary<TKey, TValue>、Java 的 TreeMap 等数据结构中都使用了红黑树来实现。
一个简单的红黑树
挖坑待埋
B树
B树是一种多路平衡搜索树,它的每个节点可以有多个子节点(通常远大于 2)。B 树的节点中存储了多个键值对,并且这些键值对是有序排列的。
一个简单的B树
挖坑待埋
B+树
B + 树是 B 树的一种变种,它和 B 树的主要区别在于,B + 树的非叶子节点只存储索引信息,而所有的数据都存储在叶子节点中,并且叶子节点之间通过指针相连形成一个有序链表。
一个简单的B+树
挖坑待埋
字典树
字典树本质上是多叉树的变种,是一种针对字符串进行特殊优化的数据结构。
它在处理字符串时有如下优势
- 节省公共字符串前缀的内存空间
- 支持通配符
是不是不好理解?,让我们举个例子。
trie.add("that");
trie.add("the");
trie.add("their");
trie.add("thds");
trie.add("apple");
trie.add("them")
它的树结构会变成
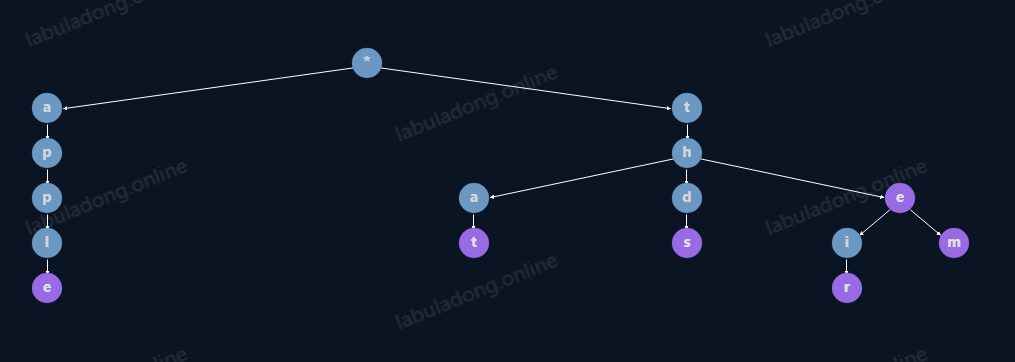
看到这个结构,你就能明白为什么它对字符串处理有得天独厚的优势了。
同样的存储方案,用数组/链表来处理。都占用了size*6的空间。
但使用字典树,底层会将公共前缀提取出来,从而减少内存占用。
因为这个特性,很容易就能推导出,它支持通配符,也能按照key顺序遍历.
这都是它的结构所决定的。
它的每个节点代表一个字符,从根节点到某个节点的路径上经过的字符连接起来就构成了一个字符串
一个简单的字典树
挖坑
二叉堆
二叉堆是一种二叉树结构的变种,同时也是一种完全二叉树。主要是能动态排序,实现优先级队列。
动态排序的数据结构其实只有两个,一个是二叉搜索树,另一个二叉堆了。
他们两者能做的事情都差不多,不过在实现上,二叉堆更简单。
其主要有两种类型
-
大顶堆
任意节点都大于等于左右子节点的值
![image]()
-
小顶堆
任意节点都小于等于左右子节点的值
![image]()
一个简单的小顶堆
点击查看代码
/// <summary>
/// 简单的小顶堆
/// </summary>
public class PriorityQueueSimple
{
public static void Run()
{
var pr = new PriorityQueueSimple(100);
pr.Push(3);
pr.Push(2);
pr.Push(1);
pr.Push(5);
pr.Push(4);
while (pr.Count > 0)
{
Console.WriteLine(pr.Pop());
}
}
private int[] _heap;
public int Count { get; private set; }
public PriorityQueueSimple(int capacity)
{
_heap = new int[capacity];
Count= 0;
}
/// <summary>
/// 先把新元素追加到二叉树底层,保持完全二叉树的结构。此时该元素的父节点可能比它大,不满足小顶堆的性质
/// 所以为了恢复小顶堆,将这个元素不断上浮(swim),直到父节点比它小为止。
/// </summary>
/// <param name="x"></param>
public void Push(int x)
{
//将新元素放到最后,实现插入的O(1)
_heap[Count] = x;
//然后再一步一步上浮到正确位置
Swim(Count);
Count++;
}
private void Swim(int currentIndex)
{
//如果父节点>当前节点,说明不符合小顶堆
while (currentIndex > 0 && _heap[Parent(currentIndex)] > _heap[currentIndex])
{
//将两者值交换,实现上浮
Swap(Parent(currentIndex), currentIndex);
currentIndex = Parent(currentIndex);
}
}
public int Pop()
{
//缓存堆顶,避免被覆盖
var head = _heap[0];
//把堆底元素放到堆顶
_heap[0] = _heap[Count - 1];
Count--;
//从堆顶开始下沉
Sink(0);
return head;
}
private void Sink(int currentIndex)
{
while (Left(currentIndex) < Count || Right(currentIndex) < Count)
{
var minIndex = currentIndex;
//当前节点的左节点
var currentLeftIndex = Left(currentIndex);
//对比左边节点,看谁最小
if (currentLeftIndex < Count && _heap[currentLeftIndex] < _heap[minIndex])
{
minIndex = currentLeftIndex;
}
//再对比右边节点,看谁最小
var currentRightIndex = Right(currentIndex);
if (currentRightIndex < Count && _heap[currentRightIndex] < _heap[minIndex])
{
minIndex= currentRightIndex;
}
//如果已经是最小了,说明完成了下沉
if (minIndex == currentIndex)
{
break;
}
//否则交换值
Swap(currentIndex, minIndex);
currentIndex = minIndex;
}
}
private void Swap(int i,int j)
{
int temp = _heap[i];
_heap[i]=_heap[j];
_heap[j] = temp;
}
/// <summary>
/// 查看堆顶
/// </summary>
/// <returns></returns>
public int Peek()
{
return _heap[0];
}
/// <summary>
/// 父节点的索引
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private int Parent(int node)
{
return (node - 1) / 2;
}
/// <summary>
/// 左节点的索引
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private int Left(int node)
{
return node * 2 + 1;
}
/// <summary>
/// 右节点的索引
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private int Right(int node)
{
return node * 2 + 2;
}
}
Q1:说好的二叉结构,怎么用数组实现?
- 链表节点需要一个额外的指针存储相邻节点的地址,所以相对数组,链表的内存消耗会大一些
- 链表查找复杂度太高,无法实现O(1)。只有数组支持O(1)。
想要用数组模拟二叉树,前提是这个二叉树必须是完全二叉树。完全二叉树的特性是紧密排列,完全可以用数组来存储
线段树
线段树它的每个节点代表一个区间。根节点代表整个区间,每个内部节点将其代表的区间分成两部分,分别由其左右子节点表示.
线段树主要用于高效解决区间查询和动态修改的问题,其区间查询复杂度为O(log N),动态修改的复杂度为O(log N)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号