DS博客作业04--图
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 李雷默 |
0.PTA得分截图

1.本周学习总结
1.1 图的存储结构

1.1.1 邻接矩阵
- 结构体定义
#define MAXV<最大顶点数>
typedef struct {
int no;//顶点编号
INfoType info;//顶点其他信息
}VertcxRype;
typedef struct {
int edges[MAXV][MAXV];//邻接矩阵
int n, e;//顶点数,边数
VertcxRype vexs[MAXV];//存放顶点信息
}MatGraph;
- 建图函数
void CreateAdj(AdjGraph*& G, int A[MAXV][MAXV], int n, int e)
{
int i, j;ArcNode* p;
G = (AdjGraph*)malloc(sizeof(AdjGraph));
for (i = 0;i < n;i++)
g->adjlist[i].firstarc = NULL;
for (i = 0;i < n;i++)
for(j=n-1;j>=0;j--)
if (A[i][j] != 0 && A[i][j] != INF)
{
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
p->weight = A[i][j];
p->nextarc = G->adjlist[i].firstarc;
G->adjlist[i].firstarc = p;
}
G->n = n; G->e = e;
}
1.1.2 邻接表

- 结构体定义
typedef struct ANode
{
int adjvex;//该边的终点编号
struct ANode *nextarc;//指向下一条边的指针
InfoType info;
}ArcNode;
typedef struct Vnode
{
Vertex data;
ArcNode *firstarc;//指向第一条边的顶点
}VNode;
typedef struct
{
VNode dajlist[MAXV];//邻接表
int n, e;
}AdjGraph;
- 建图函数
void CreateAdj(AdjGraph *&G, int n, int e)//创建图邻接表
{
int i, j, a, b;
G = new AdjGraph;
for (i = 1; i <= n; i++)//邻接表头结点置零
{
G->adjlist[i].firstarc = NULL;
}
for (j = 1; j <= e; j++)//无向图
{
cin >> a >> b;
ArcNode *p,*q;
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;//用头插法进行插入
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = q;
}
G->n = n;
G->e = e;
}
1.1.3 邻接矩阵和邻接表表示图的区别
邻接表的主要特点:邻接表表示不唯一,特别适合于稀疏图存储,时间复杂度为O(n+e).
邻接矩阵的主要特点:一个图的邻接矩阵表示是唯一的,特别适合与稠密图的存储,时间复杂度为O(n^2).
1.2 图遍历
1.2.1深度优先遍历
void DFSTraverse(MGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = FALSE;
for (v = 0; v < G.vexnum; v++)
if (!visited[v])
{
DFS(G, v);
}
}
void DFS(MGraph G, int v)
{
printf("%c ", G.Vex[v]); // 访问顶点v
visited[v] = TRUE; // 设已访问标记
int w;
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
{
if (!visited[w]) {
DFS(G, w);
}
}
}
适用于哪些问题求解:图的深度遍历可以找到两点之间的全部路径,以此可以找到迷宫问题的全部可能答案,同时可以判断是否有简单路径,测试图的结构是否正确。
1.2.2广度优先遍历
void BFSTraverse(MGraph G)
{
int i;
for (i = 0; i < G.vexnum; ++i)
visited[i] = FALSE; // 访问标记数组初始化
InitQueue(Q); // 初始化辅助队列
for (i = 0; i < G.vexnum; ++i) // 从0号顶点开始遍历
if (!visited[i]) // 对每个连通分量调用一次BFS
BFS(G, i); // vi为访问过,从vi开始访问BFS
}
void BFS(MGraph G, int v)
{
printf("%c ", G.Vex[v]); // 访问初始顶点v
visited[v] = TRUE; // 对v做已访问标记
EnQueue(Q, v);
int w;
while (!IsEmpty(Q))
{
DeQueue(Q, v);
for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
{
if (!visited[w])
{
printf("%c ", G.Vex[w]);
visited[w] = TRUE;
EnQueue(Q, w);
}
}
}
}
适用于哪些问题求解:图的广度遍历可以以层次型遍历图找到特定的第几个或者最近最远的顶点,可求解迷宫问题的最短路径。
1.3 最小生成树
一个图的极小连通子图的权值之和最小构造出的树为最小生成树,最小生成树是不唯一的,但权值之和一定一样。n个顶点的图构成n-1条边的最小生成树。
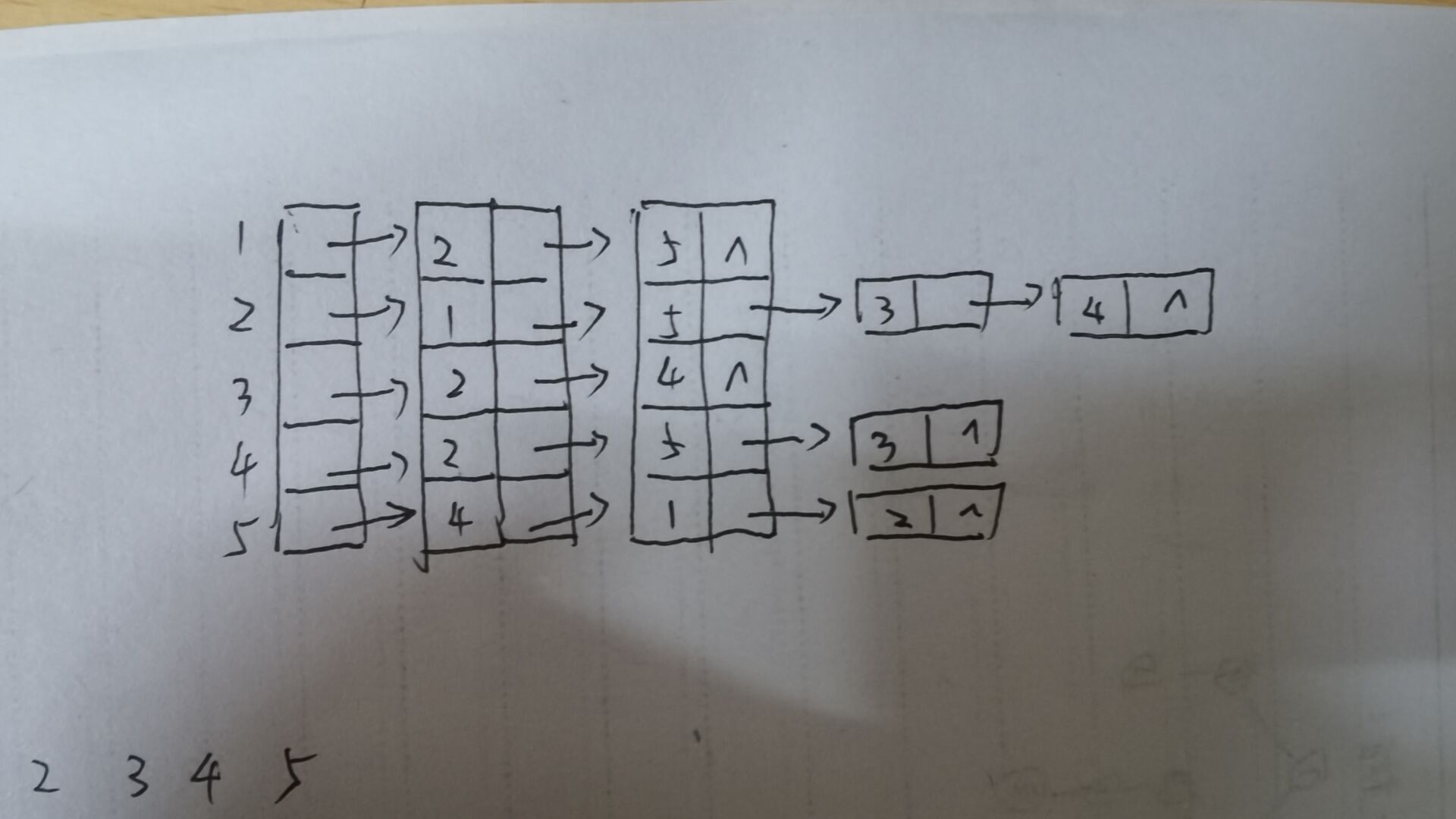
1.3.1 Prim算法求最小生成树
- 基于上述图结构求Prim算法生成的最小生成树的边序列:
假设从顶点0出发,0到3的权值最小,为3;继续找,3到1的权值最小为1,找到1;继续,1到2的权值最小,找到2;最后找到4。所以改图的一个Prim算法生成的最小生成树边序列: - 实现Prim算法的2个辅助数组是什么?其作用是什么?
1.closest[i]:最小生成树的边依附在U中顶点编号。
2.lowcost[i]表示顶点i到U中顶点的边权重,取最小权重的顶点k加入U。并规定lowcost[k]=0表示这个顶点在U中 - (closest[k],k)构造最小生成树的一条边。
- 代码:
void Prim(MatGraph g,int v)
{
int lowcost[MAXV];
int MIN;
int closest[MAXV],i,j,k;
for(i=0;i<g.n;i++)//给lowcost[]和closest[]置初值
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for(i=1;i<g.n;i++)//找出(n-1)个顶点
{
MIN=INF;
for(j=0;j<g.n;j++)//在(V-U)中找出离U最近的顶点k
if(lowcost[j]!=0&&lowcost[j]<MIN)
{
MIN=lowcost[j];
K=J;//K记录最近顶点的编号
}
printf("边(%d,&d)权为:%d\n",closest[k],k,MIN);//输出最小生成树的一条边
lowcost[k]=0;//标记k已经加入U
for(j=0;j<g.n;j++)//对(V-U)中的顶点j进行调整
if(lowcost[j]!=0&&g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j]
closest[j]=k;//修改数组lowcost和closest
}
}
}
时间复杂度为O(n^2)。
1.3.2 Kruskal算法求解最小生成树
- 基于上述图结构求Kruskal算法生成的最小生成树的边序列:
所有边按照权值大小排序,按照从小到大的顺序进行判断,首先最小是(0,3),其次是(1.2),然后是(1,3),两点不在同一棵树上,可以连接,然后是(2,4),同样不在一棵树上,进行连接。所以改图用Kruskal算法生成的最小生成树的边序列为{(0,3),(1,2),(1,3),(2,4)}。 - 实现Kruskal算法的辅助数据结构是什么?其作用是什么?
1.设置一个辅组数组vset[0,n-1],vset[i]用于记录一个顶点i所在的连通分量编号
2.用一个数组E[]存放图G中的所有边,要求它们是按照权值从小到大的顺序排序的,为此先从图G的邻接矩阵中获取所有边集E,再采用直接插入排序法对边集E按权值递增排序。 - 代码:
void Kruskal(AdjGraph *g)
{
int i,j,u1,v1,sn1,sn2,k;
int vest[MAXV];//集合辅组数组
Edge E[MaxSize];//存放所有边
k=0;//E数组的下标从0开始计
for(i=0;i<g.n;i++)
{
p=g->adjlist[i].firstarc;
while(p!=NULL)
{
E[k].u=i;E[k].v=p->adjlist;
E[k].w=p->weight;
k++;p=p->nextarc;
}
InsertSort(E,g.e);
for(i=0;i<g.n;i++)
vest[i]=i;
k=1;
j=0;
while(k<g.n)
{
u1=E[j].u;v1=E[j].v;
sn1=vset[u1];
sn2=vset[v1];
if(sn1!=sn2)
{
printf("(%d,%d):%d\n",u1,v1,E[j].w);
k++;
for(i=0;i<g.n;i++)
if(vest[i]==sn2)
vest[i]=sn1;
}
j++;
}
}
时间复杂度为O(e2)。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
- Dijkstra算法需要哪些辅助数据结构
1.数组dist[]:源点V0到每个终点的最短路径长度
2.数组path[]:最短路径序列的前一项点的序号;初值或无路径用-1表示
3.数组s[]:表示最短路径项点的集合 - 代码:
void Dijkstra(MatGraph g, int v)
{
int dist[MAXV],path[MAXV];
int s[MAXV];//判断是否访问
int mindis, i, j, u;
for (i = 0; i < g.n; i++)
{
dist[i] = g.edges[v][i];//初始化距离
s[i] = 0;
if (g.edges[v]]i] < INF)//v到i有边,初始化前继结点
{
path[i] = v;
}
else
{
path[i] = -1;
}
}
s[v] = 1;
for (i = 0; i < g.n; i++)//进行n-1次
{
mindis = INF;
for (j = 0; j < g.n; j++)//找到最小路径的长度
{
if (s[j] == 0 && dist[j] < mindis)
{
u = j;
mindis = dist[j];
}
}
s[u] = 1;
for (j = 0; j < g.n; j++)//修改改变结点后的路径长度
{
if (s[j] == 0)
{
if (g.edges[u][j] < INF&&dist[u] + g.edges[u][j] < dist[j])//修改此处可得到各种多种解法
{
dist[j] = dist[u] + g.edges[u][j];
path[j] = u;
}
}
}
}
}
- Dijkstra算法如何解决贪心算法无法求最优解问题?
贪心算法无法求最优解问题,在该代码中dist[u]+g.edges[u][j]<dist[j]此处的小于号将该题的解法固定唯一,若改为<=号则会出现多种解法。 - Dijkstra算法的时间复杂度,适用什么图结构,为什么。
Dijkstra算法的时间复杂度为O(n^2),其中n为图中顶点个数。更适用于求稠密图的最短路路径问题,因为稠密图的边数远远大于点数。
1.4.2 Floyd算法求解最短路径
- Floyd算法解决什么问题?
Floyd算法是解决给定的加权图中顶点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。 - Floyd算法需要哪些辅助数据结构
1.有向图G=(V,E)用邻接矩阵g表示。
2.设置一个二维数组A用于存放当前顶点之间的最短路径长度,即分量A[i][j]表示当前i->j的最短路径长度。
3.用二维数组path保存最短路径,它与当前迭代的次数有关。在算法结束时,由二维数组path的值追溯,可以得到从i->j的最短路径。 - Floyd算法优势。
Floyd算法容易理解,可以算出任意两个节点之间的最短距离,代码编写简单,但时间复杂度比较高,不适合计算大量数据。
1.5 拓扑排序
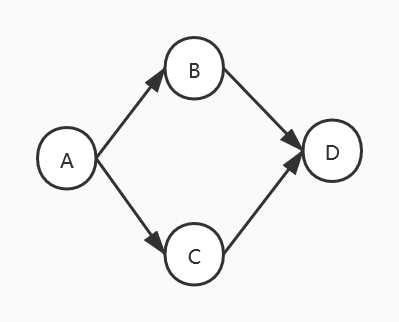
A->B->C->D或A->C->B->D
- 结构体:
typedef struct {
Vertex data;//顶点信息
int count;//存放入度
AreNode *firstarc;//头结点类型
}VNode;
- 代码:
void TopSort(AdjGraph *G)
{
int node[MAXV];
int counts = 0;
int top = -1;
int stacks[MAXV];
ArcNode *p;
int i, j, k = 0;
for (i = 0; i < G->n; i++)//初始化count
{
G->adjlist[i].count = 0;
}
for (i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
while (p)//计算每个结点入度
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (i = 0; i < G->n; i++)
{
if (G->adjlist[i].count == 0)//结点为0入栈
{
stacks[++top] = i;
}
}
while (top > -1)
{
i = stacks[top--];
node[k++] = i;//进入数组
counts++;
p = G->adjlist[i].firstarc;
while (p)
{
j = p->adjvex;
G->adjlist[j].count--;//该节点入度-1
if (G->adjlist[j].count == 0)
{
stacks[++top] = j;
}
p = p->nextarc;
}
}
if (counts < G->n)//判断个数是否符合
{
cout << "error!";
}
else
{
for (i = 0; i < k; i++)
{
cout << node[i];
if (i != k - 1)
{
cout << " ";
}
}
}
}
关键路径
- AOE网:带权的有向无环图,图中入度为0的顶点表示工程的开始事件,出度为0的顶点表示工程的结束事件,称这样的有向图为边表示活动的网(AOE网)。
- 通常每个工程都只有一个开始事件和结束事件,工程的AOE网都只有入度为0的顶点,称为源点,和一个出度为0的顶点,称为汇点。
- 关键路径:在AOE网中从源点到汇点的所有路径中最大路径长度的路径。
- AOE网中一条关键路径各活动持续时间的总和,把关键路径上的活动称为关键活动。
2.PTA实验作业
2.1 六度空间
2.1.1 伪代码
int main()
{
定义矩阵;
输入数据对矩阵的元素进行修改;
for (i = 1; i <= n; i++)
{
cout = BFS(i);
}
}
int BFS(int i)
{
static int visited[MAXV];//存放已访问过的结点
queue<int>q;
int level;
int last = i;//用于判断是否为该层最后一个
int tail;
int count = 0;
访问该结点并进队;
while (队不为空)
{
队头元素出;
for (遍历结点)
{
if (未访问过且边存在)
{
访问进队;
count++;
tail记录此时结点;
}
}
if (last == i)//为该层最后一个
{
level++;
last = j;//移动到下一层
}
if (达到6层)
{
return count;
}
}
}
2.1.2 提交列表

2.1.3 本题知识点
利用邻接矩阵进行广度遍历,通过广度遍历进行层数的判断,需要引入last和tail进行结点访问的层数判断以及结点层数的改变,通过比较last可以判断层数是否需要改变,并及时返回数量。
2.2 村村通或通信网络设计或旅游规划
2.2.1 伪代码
int main()
{
输入边数和顶点数;
Create(n, e);
int num=0;
num = Prim(n, e);
}
void Create(int n, int e)
{
对矩阵初始化;
修改矩阵;
}
int Prim(int n, int e)
{
int closet[];//保存顶点下标
int lowcost[];//保存权值
int cost = 0;
lowcost[1] = 0;
lowcost[1] = 0;
初始化lowcost[]和closet;
for (i = 2; i <= 2; i++)
{
初始化min,j,k;
while (j < n)
{
找到权值最小的点记录下标;
}
if (判断下标是否改变, 若有证明连通)
{
记录cost和访问顶点操作;
}
else return -1;
修改lowcost和closet;
}
}
2.2.2 提交列表

2.2.3 本题知识点
将村村通联想到最小二成树,最小二成树的两种算法,邻接矩阵的相关知识。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号