Z-algorithm
刚学Z算法1ms,把上次听课写的抄过来了
Z-algorithm
Z算法是用来 \(O(n)\) 求文本串 \(S\) 的每个后缀与 \(T\) 的最长公共前缀。
暴力做法是从每个点开始暴力往后匹配。时间复杂度 \(O(n^2)\),让我们考虑像 kmp 和 manacher 一样进行优化。
从左往右处理后缀,记从 \(i\) 开始的后缀与 \(T\) 的最长公共前缀为 \(ans_i\)。
记录下 \(p+ans_p\) 最大的 \(p\) 和 \(q=p+ans_p\)。
考虑当前处理的 \(i\) 小于 \(q\) 的情况,如果 \(i\ge q\) 那么直接暴力。
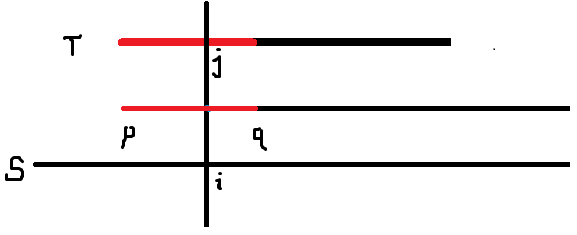
考虑 \(i\) 在 \(T\) 中对应 \(j\)。
我们记 \(next_j\) 表示 \(T_{j\sim }n\) 与 \(T\) 的最长公共前缀。(这就是为什么 Z-算法 被称为扩展kmp,虽然与kmp的 \(next\) 不同)
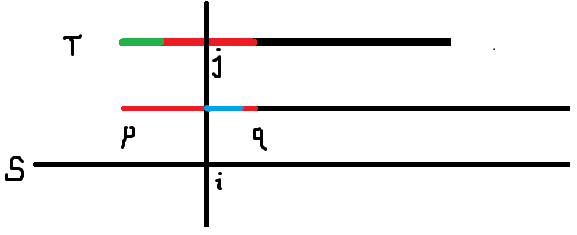
那么此时的 \(next_j\) 就意味着蓝色段和绿色段相匹配。
我们可以知道,如果蓝色段的末尾在 \(q\) 之前,那么必然不能再匹配,答案就可以确定了。
如果蓝色段的末尾在 \(q\) 或 \(q\) 之后,在 \(q\) 之后的信息我们还未能得知,那么我们直接暴力。
这样我们可以知道,在处理当前后缀时,如果 \(q\) 没有变,那么答案一定是 \(O(1)\) 得到的,如果 \(q\) 改变了,那么暴力的次数就是 \(q\) 右移的次数,又 \(q\) 是单调不降的,所以复杂度是 \(O(n)\) 的。
现在重点是如何求出 \(next\) 数组,它的定义是:\(next_j\) 表示 \(T_{j\sim n}\) 与 \(T\) 的最长公共前缀。这让我们想到 kmp 的 \(next\) 求法,所以我们把 \(T\) 和它自己做一次 Z-算法。
我们发现如果从头开始做,那么 \(p=1,q=n\),且上面的 \(j=i\),是无法计算的,所以我们刚开始就匹配 \(T_2\),大概是这样
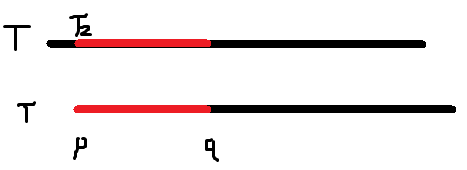
这样我们发现除了 \(next_1\) 和 \(next_2\) 其他的 \(next_i\) 都可以通过之前算出来的 \(next\) 来做到和上面一样的算法,所以我们只需要特殊处理一下 \(next_2\) 就好了,时间复杂度也是 \(O(n)\)。
例题
P5410 【模板】扩展 KMP(Z 函数)
code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define in read()
inline string read(){
string p;
char c=getchar();
while(!islower(c))c=getchar();
while(islower(c))p+=c,c=getchar();
return p;
}
const int N=2e7+10;
string a,b;
int lena,lenb,nxt[N],ans[N];
void getnxt(){
int p=1,q;nxt[0]=lenb;
for(int i=1;i<lenb;i++)
if(b[i]==b[i-1])nxt[p]++;
else break;
q=p+nxt[p];
for(int i=2,j;i<lenb;i++){
if(i<q){
nxt[i]=nxt[j=i-p];
if(i+nxt[i]<q)continue;
nxt[i]=q-i;
}
else nxt[i]=0;
while(b[i+nxt[i]]==b[nxt[i]])
nxt[i]++;
p=i,q=p+nxt[p];
}
}
void match(){
int p=0,q;
for(int i=0,r=min(lena,lenb);i<r;i++)
if(a[i]==b[i])ans[p]++;
else break;
q=p+ans[p];
for(int i=1,j;i<lena;i++){
if(i<q){
ans[i]=nxt[j=i-p];
if(i+ans[i]<q)continue;
ans[i]=q-i;
}
else ans[i]=0;
while(a[i+ans[i]]==b[ans[i]])
ans[i]++;
p=i,q=p+ans[p];
}
}
signed main(){
a=in,b=in;
lena=a.length();
lenb=b.length();
a+='#';getnxt();ll tmp=0;
for(int i=0;i<lenb;i++)
tmp^=ll(i+1)*(nxt[i]+1);
cout<<tmp<<'\n';tmp=0;
match();
for(int i=0;i<lena;i++)
tmp^=ll(i+1)*(ans[i]+1);
cout<<tmp;
return 0;
}
P7114 [NOIP2020] 字符串匹配
这题容易想到枚举分割后的一部分。
如果我们枚举 \(C\),那么我们就要判断前面是否是由循环节组成,再枚举循环节数量的因子作为 \(AB\) 再对 \(AB\) 进行拆分找出符合条件的 \(A\)。略显繁琐,但用 kmp 应该可以做。
换种想法,我们枚举 \(AB\),这样我们只需要找出这个 \(AB\) 能往后循环几段。并且我们发现由于题目性质,重复的两段循环节对于\(C\) 的出现奇数次的字符数并无影响,也就是说每个 \(AB\) 我们只需要分奇偶讨论循环节段数即可。
假设有奇数段循环节,那么 \(C\) 的出现奇数次的字符数等于从第一个 \(AB\) 往后的字符串的出现奇数次的字符数;假设有偶数段循环节,那么 \(C\) 的出现奇数次的字符数等于整个字符串的出现奇数次的字符数。
上面的 \(C\) 的出现奇数次的字符数是可以 \(O(n)\) 预处理,\(O(1)\) 查询的。于是我们需要求的是 \(AB\) 段的拆分方法,又发现此时 \(A\) 的左端一定是字符串首,故预处理出可能的 \(n\) 个 \(A\) 的出现奇数次的字符数,然后发现上个树状数组就可以了。
code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e6+10;
string b;
int lenb,z[N];
inline void getz(){
int p=1,q;z[0]=lenb,z[1]=0;
for(int i=1;i<lenb;i++)
if(b[i]==b[i-1])z[p]++;
else break;
q=p+z[p];
for(int i=2,j;i<lenb;i++){
if(i<q){
z[i]=z[j=i-p];
if(i+z[i]<q)continue;
z[i]=q-i;
}
else z[i]=0;
while(b[i+z[i]]==b[z[i]])z[i]++;
p=i,q=p+z[p];
}
}
int tong[30];
int lim[N],limre[N];
int c[30],ans;
inline int lowbit(int x){return x&(-x);}
inline void update(int x,int w){for(;x<=26;x+=lowbit(x))c[x]+=w;}
inline int query(int x){int res=0;for(;x;x-=lowbit(x))res+=c[x];return res;}
signed main(){
int T;
cin>>T;
while(T--){
cin>>b,lenb=b.length(),b+='#',getz();
for(int i=lenb-1;i>=0;i--)
limre[i]=limre[i+1],
limre[i]+=!(tong[b[i]-'a']%2),
limre[i]-=(tong[b[i]-'a']%2),
tong[b[i]-'a']++;
memset(tong,0,sizeof(tong));
lim[0]=1;tong[b[0]-'a']++;
for(int i=1;i<lenb;i++)
lim[i]=lim[i-1],
lim[i]+=!(tong[b[i]-'a']%2),
lim[i]-=(tong[b[i]-'a']%2),
tong[b[i]-'a']++;
memset(tong,0,sizeof(tong));
update(lim[0]+1,1);ans=0;
for(int i=1;i<lenb-1;i++){
int k=z[i+1]/(i+1)+1;if(k*(i+1)>=lenb)k--;
ans+=query(limre[i+1]+1)*(k/2+k%2);
ans+=query(limre[0]+1)*(k/2);
update(lim[i]+1,1);
}
for(int i=0;i<lenb-1;i++)
update(lim[i]+1,-1);
cout<<ans<<'\n';
memset(lim,0,sizeof(lim));
memset(limre,0,sizeof(limre));
}
return 0;
}
CF126B Password
CF432D Prefixes and Suffixes
CF526D Om Nom and Necklace
CF427D Match & Catch


 浙公网安备 33010602011771号
浙公网安备 33010602011771号