数位dp
8.29冯巨讲完没有写,10.15被叫上去讲课,于是花了一个上午看了一下。
数位dp
数位dp用于解决一类问题:求给定区间中,满足给定条件的某个 \(D\) 进制数或此类数的数量。给定条件往往与数位有关,例如数位之和、指定数码个数、数的大小顺序分组等等。题目给定的区间往往很大,无法采用朴素的方法求解。此时,由于数的位数是 \(\log(n)\) 级别,我们就需要利用数位的性质,设计 \(\log(n)\) 级别复杂度的算法。解决这类问题最基本的思想就是“逐位确定”的方法。
大多情况下,题目要求 \([l,r]\) 中符合要求的数的个数,
数位dp名义上是dp,实则不好用递推来解决,通常会使用记忆化搜索。
大多情况下,题目要求 \([l,r]\) 中符合要求的数的个数,直接写搜索非常不好写,既有上界又有下界。所以一般都会差分一下,求 \(solve(r)-solve(l-1)\),这样就只有上界,好写的多。
用记忆化搜索非常好写,首先写一个爆搜:
int dfs(int now/*当前在哪一位*/,/*为满足题目条件记录的有用值*/,bool limit/*是否顶到上界*/){
if(now==0)return ;//满足题目要求返回1,否则返回0
int res=0,end=limit?a[now]:9;//循环这一位,如果顶到上界就只能循环到a[now]
for(int i=0;i<=end;i++){
if()continue;//不满足题目条件的跳过
res+=dfs(now-1,/*记录有用值*/,limit&&i==end/*是否顶到上界*/);
}
return res;
}
显然复杂度是 \(O(ans)\),使用记忆化搜索:
int dfs(int now,,bool limit){
if(now==0)return ;
if(!limit&&f[now][...])return f[now][...];
int res=0,end=limit?a[now]:9;
for(int i=0;i<=end;i++){
if()continue;
res+=dfs(now-1,,limit&&i==end);
}
if(!limit)f[now][...]=res;
return res;
}
其中 \(f[now][...]\),代表的是不受限制,第 \(now\) 位,在 \(...\) 状态下的方案总数。
也就是说顶到上界的情况不能这样算。\(...\) 比较灵活,可以根据题目条件或你记录的有用值来设。
由于顶到上界或者受到限制的情况很少,所以这样的时间复杂度就是 \(f\) 的状态数。
不理解就先看题
例题
不要62
题目要求 \([l,r]\) 中不出现 \(62\) 和 \(4\) 的数的个数。
于是我们要求 \([0,n]\) 中不出现 \(62\) 和 \(4\) 的数的个数,对于 \(4\) ,我们只要搜索时不搜 \(4\) 即可,但对于 \(2\),我们需要知道这一位前面是不是 \(6\),所以搜索的第二个值就记录前一位是不是 \(6\) 就好了。
\(f[now]\) 就是第 \(now\) 位时的方案数。
看一下代码就懂了。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
int f[20];
int a[20],an;
int dfs(int now,bool is6,bool limit){
if(now==0)return 1;
if(!limit&&!is6&&f[now])return f[now];
int res=0,end=limit?a[now]:9;
for(int i=0;i<=end;i++){
if(i==4||(is6&&i==2))continue;
res+=dfs(now-1,i==6,limit&&i==end);
}
if(!limit&&!is6)f[now]=res;
return res;
}
int solve(int x){
an=0;
while(x){
a[++an]=x%10;
x/=10;
}
return dfs(an,false,true);
}
signed main(){
int n,m;
n=in,m=in;
while(n||m){
cout<<solve(m)-solve(n-1)<<endl;
n=in,m=in;
}
return 0;
}
windy 数
和上面差不多,记录的变成了前一个数是多少。
这题要注意前导 \(0\) 的情况,所以还要记录前面是否全是 \(0\)。
当前面全是 \(0\) 的时候,当前位不能受前一位的影响,所以把前一位随便设一个不会影响的值就好了,比如 11 或者114515也行
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
int a[20],an;
int f[15][2][20];
int dfs(int now,int last,bool all0,bool limit){
if(now==0)return 1;
if(!limit&&f[last][all0][now])return f[last][all0][now];
int res=0,end=limit?a[now]:9;
for(int i=0;i<=end;i++){
if(abs(i-last)<2)continue;
res+=dfs(now-1,(all0&&i==0)?11:i,all0&&i==0,limit&&i==end);
}
if(!limit)f[last][all0][now]=res;
return res;
}
int solve(int x){
an=0;
while(x){
a[++an]=x%10;
x/=10;
}
return dfs(an,11,1,1);
}
signed main(){
int n,m;
n=in,m=in;
cout<<solve(m)-solve(n-1);
return 0;
}
Amount of Degrees
这题有些需要思考的地方。
一个数要等于 \(K\) 个互不相等的 \(B\) 的整数次幂之和,那么在 \(B\) 进制下,它的表示中一定只有 \(0,1\) 且恰好有 \(K\) 个 \(1\),于是可以记录已经有多少个 \(1\) 然后按套路做。
注意这里的上界会有一定变化,将上界化为 \(B\) 进制后,找到他从高到低第一个大于 \(1\) 的位置,将这一位及更低位变成 \(1\) 就是这里的上界,想一下就知道这样很对。
上述做法:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
int k,b;
int a[50],an;
int f[50][20];
int dfs(int now,int had,bool limit){
if(now==0)return had==0;
if(!limit&&f[now][had])return f[now][had];
int res=0,end=limit?a[now]:1;
for(int i=0;i<=end;i++){
if(!had&&i==1)continue;
res+=dfs(now-1,had-(i==1),limit&&i==end);
}
if(!limit)f[now][had]=res;
return res;
}
int solve(int x){
an=0;
while(x){
a[++an]=x%b;
x/=b;
}
for(int i=an;i>=1;i--){
if(a[i]>1)
while(i)
a[i--]=1;
}
return dfs(an,k,1);
}
signed main(){
int n,m;
n=in,m=in,k=in,b=in;
cout<<solve(m)-solve(n-1);
return 0;
}
但对于数位dp,还有一种很有用的东西能够帮助你思考,就是模拟一颗完全二叉树,
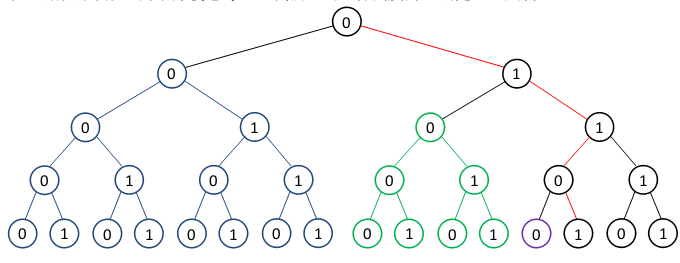
像这样,每层代表一位,每条路径代表一棵树,在这棵树上思考。
我们发现,从顶点向 \(n\) 走,一旦遇到 \(1\),就代表左子树内都可以被统计,因为每层代表每位,所以我们只需要在 \(x\) 层中有 \(y\) 个 \(1\) 的数量,发现其实就是组合数 \(\binom x y\),也就是说预处理出组合数之后就可以线性做,这样每次统计左子树的答案,会漏掉 \(n\) 自己,特殊处理一下即可。
上述做法:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
int p=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
return p*f;
}
int k,b;
int a[32],an;
int f[32][32];
void getf(){
f[0][0]=1;
for(int i=1;i<=31;i++)
for(int j=1;j<=i;j++)
f[i][j]=f[i-1][j-1]+f[i-1][j];
}
int solve(int x){
an=0;
while(x){
a[++an]=x%b;
x/=b;
}
for(int i=an;i>=1;i--){
if(a[i]>1)
while(i)
a[i--]=1;
}
int res=0,temp=0;
for(int i=an;i>=1;i--)
if(a[i]==1)res+=f[i][k-temp+1],temp++;
if(temp==k)res++;
return res;
}
signed main(){
int n,m;
n=in,m=in,k=in,b=in;
getf();
cout<<solve(m)-solve(n-1);
return 0;
}
可以找国集队爷刘聪的《浅谈数位类统计问题》来看。
8.29 笔记:
冯巨推题
https://blog.csdn.net/sslz_fsy/article/details/88618061
https://blog.csdn.net/sslz_fsy/article/details/87367688
https://blog.csdn.net/sslz_fsy/article/details/82284529
https://blog.csdn.net/sslz_fsy/article/details/95241942


 浙公网安备 33010602011771号
浙公网安备 33010602011771号