“你什么意思”之基于RNN的语义槽填充(Pytorch实现)
1. 概况
1.1 任务
口语理解(Spoken Language Understanding, SLU)作为语音识别与自然语言处理之间的一个新兴领域,其目的是为了让计算机从用户的讲话中理解他们的意图。SLU是口语对话系统(Spoken Dialog Systems)的一个非常关键的环节。下图展示了口语对话系统的主要流程。
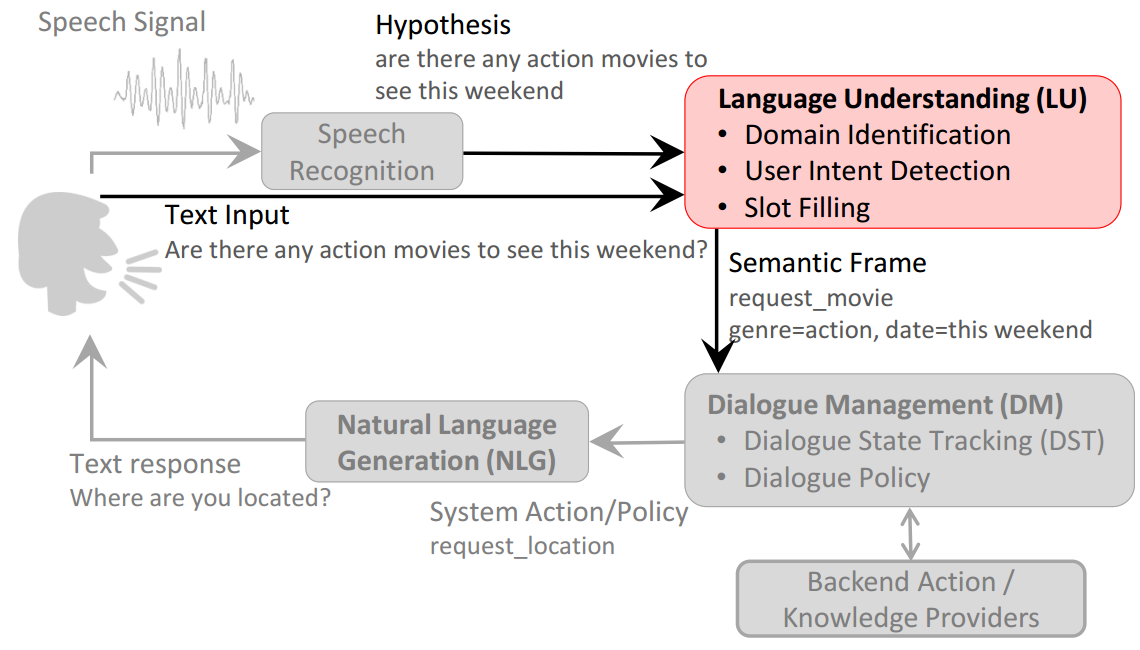
SLU主要通过如下三个子任务来理解用户的语言:
- 领域识别(Domain Detection)
- 用户意图检测(User Intent Determination)
- 语义槽填充(Semantic Slot Filling)
例如,用户输入“播放周杰伦的稻香”,首先通过领域识别模块识别为"music"领域,再通过用户意图检测模块识别出用户意图为"play_music"(而不是"find_lyrics" ),最后通过槽填充对将每个词填充到对应的槽中:"播放[O] / 周杰伦[B-singer] / 的[O] / 稻香[B-song]"。
从上述例子可以看出,通常把领域识别和用户意图检测当做文本分类问题,而把槽填充当做序列标注(Sequence Tagging)问题,也就是把连续序列中每个词赋予相应的语义类别标签。本次实验的任务就是基于ATIS 数据集进行语义槽填充。(完整代码地址:https://github.com/llhthinker/slot-filling)
1.2 数据集
本次实验基于ATIS(Airline Travel Information Systems )数据集。顾名思义,ATIS数据集的领域为"Airline Travel"。ATIS数据集采取流行的"in/out/begin(IOB)标注法": "I-xxx"表示该词属于槽xxx,但不是槽xxx中第一个词;"O"表示该词不属于任何语义槽;"B-xxx"表示该词属于槽xxx,并且位于槽xxx的首位。部分ATIS训练数据集如下:
what O
is O
the O
arrival B-flight_time
time I-flight_time
in O
san B-fromloc.city_name
francisco I-fromloc.city_name
for O
the O
DIGITDIGITDIGIT B-depart_time.time
am I-depart_time.time
flight O
leaving O
washington B-fromloc.city_name
ATIS数据集一共有83种语义槽,因此序列标注的标签类别一共有\(83+83+1=167\)个。ATIS数据集分为训练集和测试集,数据规模如下表:
| 训练集 | 测试集 | |
|---|---|---|
| 句子总数 | 4978个 | 893个 |
| 词语总数 | 56590个 | 9198个 |
| 句子平均词数 | 11.4个 | 10.3个 |
2. 模型
上文中提到,通常把槽填充当做序列标注问题。很多机器学习算法都能够解决序列标注问题,包括HMM/CFG,hidden vector state(HVS)等生成式模型,以及CRF, SVM等判别式模型。本次实验主要参考论文《Using Recurrent Neural Networks for Slot Filling in Spoken Language Understanding 》 ,基于RNN来实现语义槽填充。
RNN可以分为简单RNN(Simple RNN)和门控机制RNN(Gated RNN),前者的RNN单元完全接收上个时刻的输入;后者基于门控机制,通过学习到的参数自行决定上个时刻的输入量和当前状态的保留量。下面将介绍Elman-RNN, Jordan-RNN, Hybrid-RNN(Elman和Jordan结合)这三种简单RNN,以及经典的门控机制RNN:LSTM。
2.1 Elman-RNN
Elman-RNN将当前时刻的输入\(x_t\)和上个时刻的隐状态输出\(h_{(t-1)}\)作为输入,具体如下:
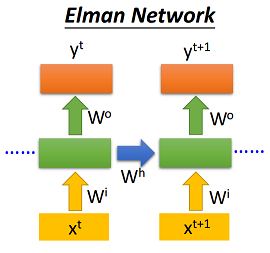
需要说明的是,Pytorch默认的RNN即为Elman-RNN,但是它只支持\(\tanh\)和ReLU两种激活函数。本次实验按照论文设置,激活函数均采取sigmoid函数,使用Pytorch具体实现如下:
class ElmanRNNCell(nn.Module):
def __init__(self, input_size, hidden_size):
super(ElmanRNNCell, self).__init__()
self.hidden_size = hidden_size
self.i2h_fc1 = nn.Linear(input_size, hidden_size)
self.i2h_fc2 = nn.Linear(hidden_size, hidden_size)
self.h2o_fc = nn.Linear(hidden_size, hidden_size)
def forward(self, input, hidden):
hidden = F.sigmoid(self.i2h_fc1(input) + self.i2h_fc2(hidden))
output = F.sigmoid(self.h2o_fc(hidden))
return output, hidden
2.2 Jordan-RNN
Jordan-RNN将当前时刻的输入\(x_t\)和上个时刻的输出层输出\(y_{(t-1)}\)作为输入,具体如下:
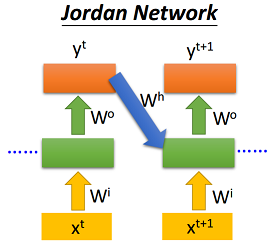
使用Pytorch具体实现如下,其中\(y_0\)初始化为可训练的参数:
class JordanRNNCell(nn.Module):
def __init__(self, input_size, hidden_size):
super(JordanRNNCell, self).__init__()
self.hidden_size = hidden_size
self.i2h_fc1 = nn.Linear(input_size, hidden_size)
self.i2h_fc2 = nn.Linear(hidden_size, hidden_size)
self.h2o_fc = nn.Linear(hidden_size, hidden_size)
self.y_0 = nn.Parameter(nn.init.xavier_uniform(torch.Tensor(1, hidden_size)), requires_grad=True)
def forward(self, input, hidden=None):
if hidden is None:
hidden = self.y_0
hidden = F.sigmoid(self.i2h_fc1(input) + self.i2h_fc2(hidden))
output = F.sigmoid(self.h2o_fc(hidden))
return output, output
2.4 Hybrid-RNN
Hybrid-RNN将当前时刻的输入\(x_t\),上个时刻的隐状态\(h_{(t-1)}\) 以及上个时刻输出层输出\(y_{(t-1)}\)作为输入,具体如下:
Pytorch已经实现了LSTM, 只需要调用相应的API即可,调用的代码片段如下:
self.rnn = nn.LSTM(input_size=embedding_dim,
hidden_size=hidden_size,
bidirectional=bidirectional,
batch_first=True)
3. 实验
3.1 实验设置
实验基于Python 3.6 和Pytorch 0.4.0,为进行对照实验,下列设置针对所有RNN模型:
- 所有RNN模型均只使用单层;
- 词向量维度设置为100维,并且随机初始化,在训练过程中进行调整;
- 隐状态维度设置为75维;
- 采用带动量的随机梯度下降(SGD),batch size为1,学习率(learning rate)为0.1,动量(momentum)为0.9并保持不变;
- epoch=10;
- 每种RNN模型都实现单向(Single)和双向(Bi-Directional),并分别训练。
3.2 实验结果
在使用CPU的情况下,不同模型在测试集的\(F_1\)得分以及平均一个epoch训练时长的结果如下:
| \(F_1(\%) / T(s)\) | Elman | Jordan | Hybrid | LSTM |
|---|---|---|---|---|
| Single | 87.26 / 438 | 87.90 / 487 | 88.46 / 494 | 92.16 / 3721 |
| Bi-Directional | 92.88 / 565 | 90.31 / 580 | 91.85 / 613 | 93.75 / 4357 |
从上表中可以看出:
- 基于门控机制的LSTM由于其参数和运算步骤的增加,一个epoch的训练时长是另外三种Simple RNN的9倍左右,而\(F_1\)得分也比Simple RNN高;
- 双向(Bi-Directional)RNN的\(F_1\)得分普遍比单向(Single)RNN高,而运行时间也多一些。
在使用同一块GPU的情况下,不同模型在测试集的\(F_1\)得分以及平均一个epoch训练时长的结果如下:
| \(F_1(\%) / T(s)\) | Elman | Jordan | Hybrid | LSTM |
|---|---|---|---|---|
| Single | 88.89 / 35.2 | 88.36 / 41.3 | 89.65 / 43.5 | 92.44 / 16.8 |
| Bi-Directional | 91.78 / 68.0 | 89.82 / 72.2 | 93.61 / 81.6 | 94.26 / 18.7 |
从上表中可以看出,即使是随机梯度下降(batch_size=1),GPU的加速效果仍然相当明显。值得指出的是,虽然LSTM的运算步骤比其他三种Simple-RNN多,但是用时却是最少的,这可能是由于LSTM是直接调用Pytorch的API,针对GPU有优化,而另外三种的都是自己实现的,GPU加速效果没有Pytorch好。
4. 总结与展望
总的来说,将槽填充问题当做序列标注问题是一种有效的做法,而RNN能够较好的对序列进行建模,提取相关的上下文特征。双向RNN的表现优于单向RNN,而LSTM的表现优于Simple RNN。对于Simple RNN而言,Elman的表现不比Jordan差(甚至更好),而用时更少并且实现更简单,这可能是主流深度学习框架(TensorFlow / Pytorch等)的simple RNN是基于Elman的原因。而Hybrid作为Elman和Jordan的混合体,其训练时间都多余Elman和Jordan,\(F_1\)得分略有提升,但不是特别明显(使用CPU时的双向Elman表现比双向Hybrid好),需要更多实验进行验证。
从实验设置可以看出,本次实验没有过多的调参。如果想取得更好的结果,可以进行更细致的调参,包括 :
- 改变词向量维度和隐状态维度;
- 考虑采用预训练词向量,然后固定或者进行微调;
- 采用正则化技术,包括L1/L2, Dropout, Batch Normalization, Layer Normalization等;
- 尝试使用不同的优化器(如Adam),使用mini-batch,调整学习率;
- 增加epoch次数。
此外,可以考虑在输入时融入词性标注和命名实体识别等信息,在输出时使用Viterbi算法进行解码,也可以尝试不同形式的门控RNN(如GRU,LSTM变体等)以及采用多层RNN,并考虑是否使用残差连接等。
参考资料
Mesnil G, Dauphin Y, Yao K, et al. Using recurrent neural networks for slot filling in spoken language understanding[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2015, 23(3): 530-539.
Wikipedia. Recurrent neural network. https://en.wikipedia.org/wiki/Recurrent_neural_network
PyTorch documentation. Recurrent layers. http://pytorch.org/docs/stable/nn.html#recurrent-layers
Hung-yi Lee. Machine Learning (2017,Spring). http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2017/Lecture/RNN.pdf
YUN-NUNG (VIVIAN) CHEN. Spring 105 - Intelligent Conversational Bot. https://www.csie.ntu.edu.tw/~yvchen/s105-icb/doc/170321_LU.pdf


 浙公网安备 33010602011771号
浙公网安备 33010602011771号