bzoj 1670: [Usaco2006 Oct]Building the Moat护城河的挖掘 -- 凸包
1670: [Usaco2006 Oct]Building the Moat护城河的挖掘
Time Limit: 3 Sec Memory Limit: 64 MBDescription
为了防止口渴的食蚁兽进入他的农场,Farmer John决定在他的农场周围挖一条护城河。农场里一共有N(8<=N<=5,000)股泉水,并且,护城河总是笔直地连接在河道上的相邻的两股泉水。护城河必须能保护所有的泉水,也就是说,能包围所有的泉水。泉水一定在护城河的内部,或者恰好在河道上。当然,护城河构成一个封闭的环。 挖护城河是一项昂贵的工程,于是,节约的FJ希望护城河的总长度尽量小。请你写个程序计算一下,在满足需求的条件下,护城河的总长最小是多少。 所有泉水的坐标都在范围为(1..10,000,000,1..10,000,000)的整点上,一股泉水对应着一个唯一确定的坐标。并且,任意三股泉水都不在一条直线上。 以下是一幅包含20股泉水的地图,泉水用"*"表示

图中的直线,为护城河的最优挖掘方案,即能围住所有泉水的最短路线。 路线从左上角起,经过泉水的坐标依次是:(18,0),(6,-6),(0,-5),(-3,-3),(-17,0),(-7,7),(0,4),(3,3)。绕行一周的路径总长为70.8700576850888(...)。答案只需要保留两位小数,于是输出是70.87。
Input
* 第1行: 一个整数,N * 第2..N+1行: 每行包含2个用空格隔开的整数,x[i]和y[i],即第i股泉水的位 置坐标
Output
* 第1行: 输出一个数字,表示满足条件的护城河的最短长度。保留两位小数
Sample Input
2 10
3 7
22 15
12 11
20 3
28 9
1 12
9 3
14 14
25 6
8 1
25 1
28 4
24 12
4 15
13 5
26 5
21 11
24 4
1 8
Sample Output
HINT
Source
凸包:
(1)找出点集p[]中最左下的点p1,把p1同点集中其他各点用线段连接,并计算这些线段的斜率,然后按斜率从小到大排序,得到新的节点序列p1,p2,...pn.依次连接这些点,得到一个多边形(已经逆时针,有所进展,但还需去掉不在凸包上的点)。此时p1是凸包的边界起点,p2和pn也是最终凸包的顶点,p[n+1]=p1(看成循环的)
(2)删除p3,p4,...p[n-1]中不在凸包上的点:
先把p1,p2,p3入栈S中,再依次循环(i = 3 -> n-1),若栈顶的两个点和当前的点p[i]这三点连线的方向向顺时针方向偏转,表明是凹的,应删除,则栈顶元素出栈(要循环判断,即可能前面的仍是凹的,还需再出栈,举例如下图),直到向逆时针方向偏转或者栈内只有2个元素了(p1p2),就把当前点p[i]入栈。
最后栈中的元素就是最终凸包上的点。
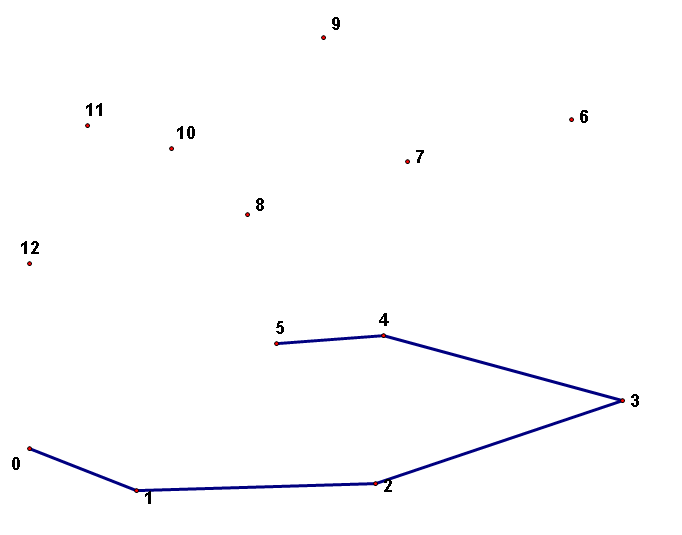
----------------
---------------
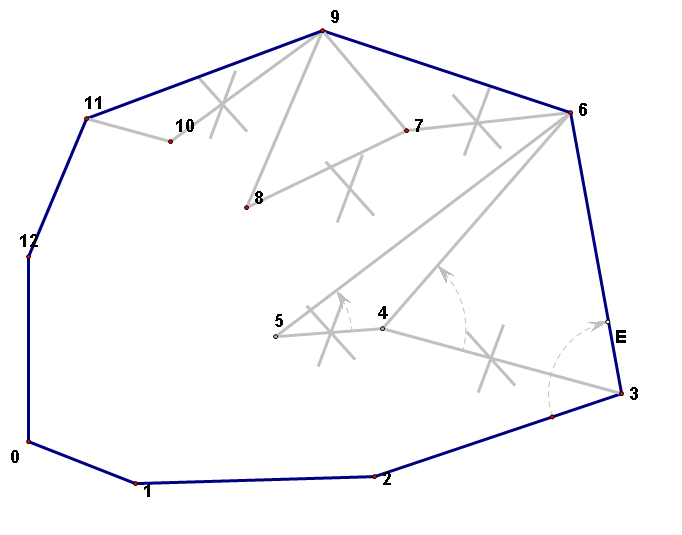
--------------------
#include<map> #include<cmath> #include<queue> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define ll long long #define db double #define N 5050 #define inf 100000009 char xB[1<<15],*xS=xB,*xTT=xB; #define getc() (xS==xTT&&(xTT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xTT)?0:*xS++) #define isd(c) (c>='0'&&c<='9') inline int read(){ char xchh; int xaa; while(xchh=getc(),!isd(xchh));(xaa=xchh-'0'); while(xchh=getc(),isd(xchh))xaa=xaa*10+xchh-'0';return xaa; } struct tb{db x,y,k;}p[N],s[N]; bool cmp(tb a,tb b){return a.k<b.k;} db mul(tb a,tb b,tb c){return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);} db dis(tb a,tb b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));} int n,x,y,tp=1; db ans; int main() { n=read(); for(int i=0;i<n;i++) { x=read();y=read(); p[i]=(tb){(db)x,(db)y}; if(x<p[0].x||(x==p[0].x&&y<p[0].y)) swap(p[0],p[i]); } for(int i=0;i<n;i++) p[i].k=(p[i].x==p[0].x?inf:(p[i].y-p[0].y)/(p[i].x-p[0].x)); sort(p+1,p+n,cmp); p[n]=p[0];s[0]=p[0];s[1]=p[1]; for(int i=2;i<=n;i++) { while(tp&&mul(p[i],s[tp],s[tp-1])>=0) tp--; s[++tp]=p[i]; } for(int i=0;i<tp;i++) ans+=dis(s[i],s[i+1]); printf("%.2lf\n",ans); return 0; }
版权声明:本文为博主原创文章,未经博主允许不得转载。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号