数据结构与算法——排序算法-基数排序
简单介绍
基数排序(radix sort)属于 分配式排序(distribution sort),又称 桶子法(bucket sort 或 bin sort),顾名思义,它是通过键值的各个位的值,将要排序的 元素分配 至某些「桶」中,达到排序的作用。基数排序是对 传统桶排序 的扩展。
基数排序属于 稳定性 的排序,基数排序法是效率高的稳定性排序法。
其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
稳定性简介
2,1,43,1 数组进行排序后变成:1,1,2,43
稳定性指的是:两个 1 的先后顺序不改变。
基数排序(Radix Sort)是 桶排序 的扩展。
基数排序是 1887 年赫尔曼·何乐礼发明的。实现方式:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
基本思想
- 将所有待比较数值 统一为同样的数位长度,数位较短的数 前面补零
- 然后从最低位开始(个位),依次进行一次排序
- 这样从最低位排序一直到最高位排序完成以后,序列就变成了一个有序序列
基本思想是抽象的,下面看看思路分析,你就明白是咋回事了。
思路分析

解析上面的图:
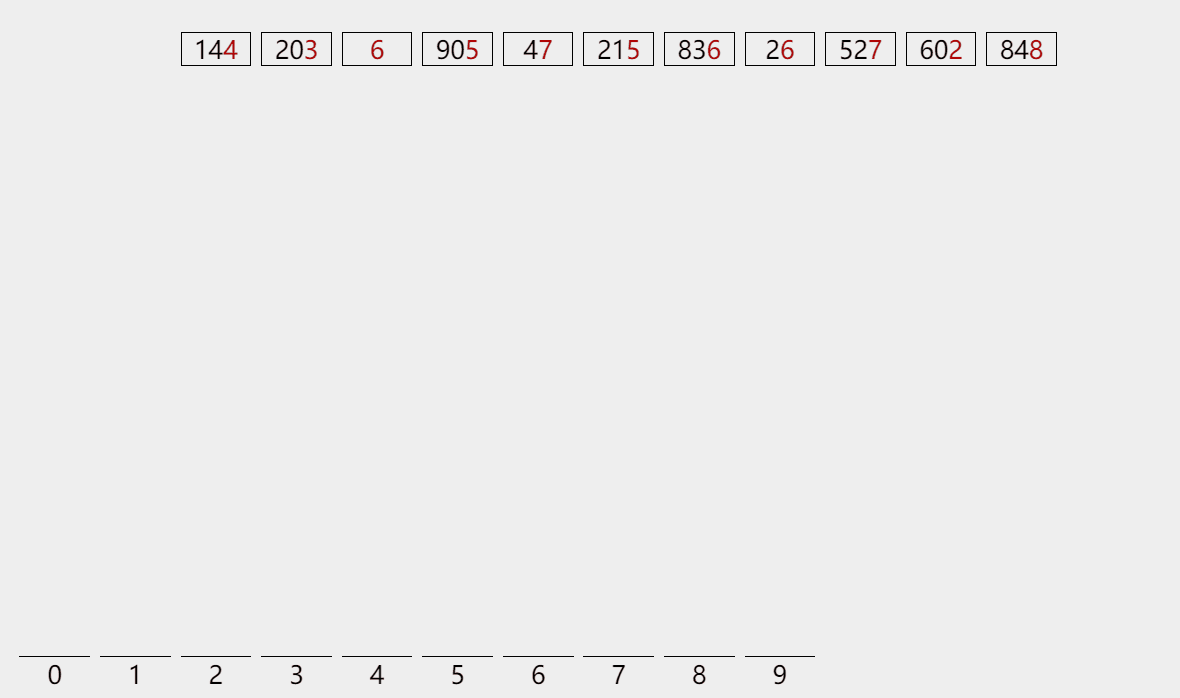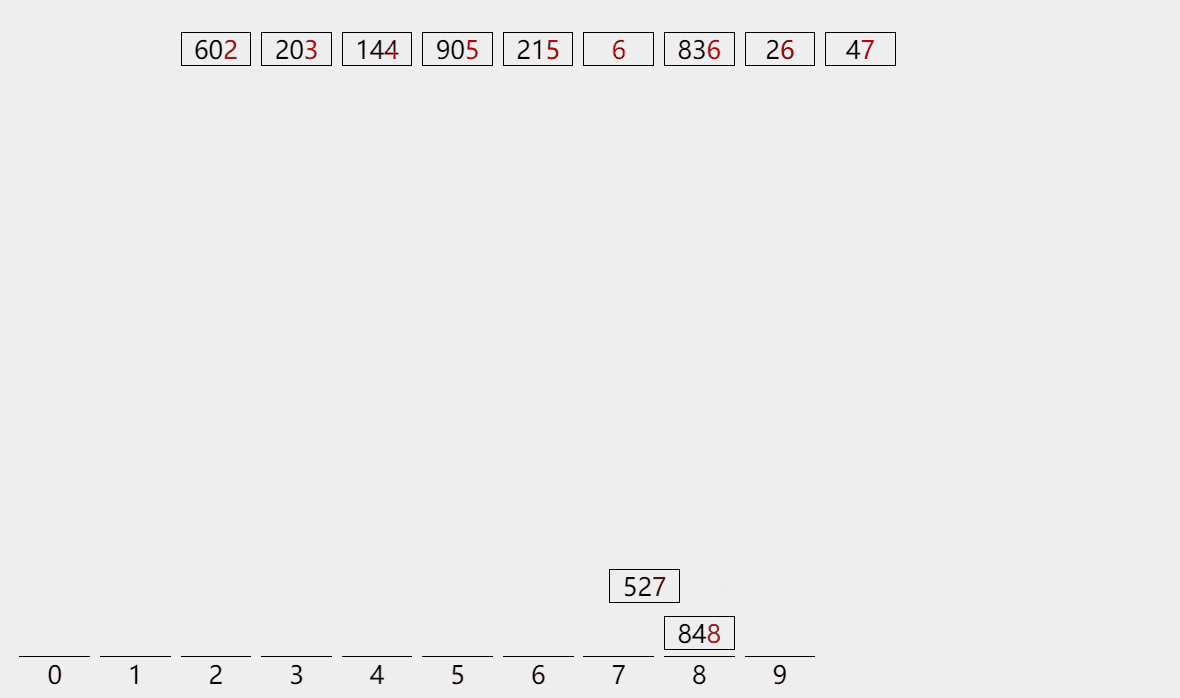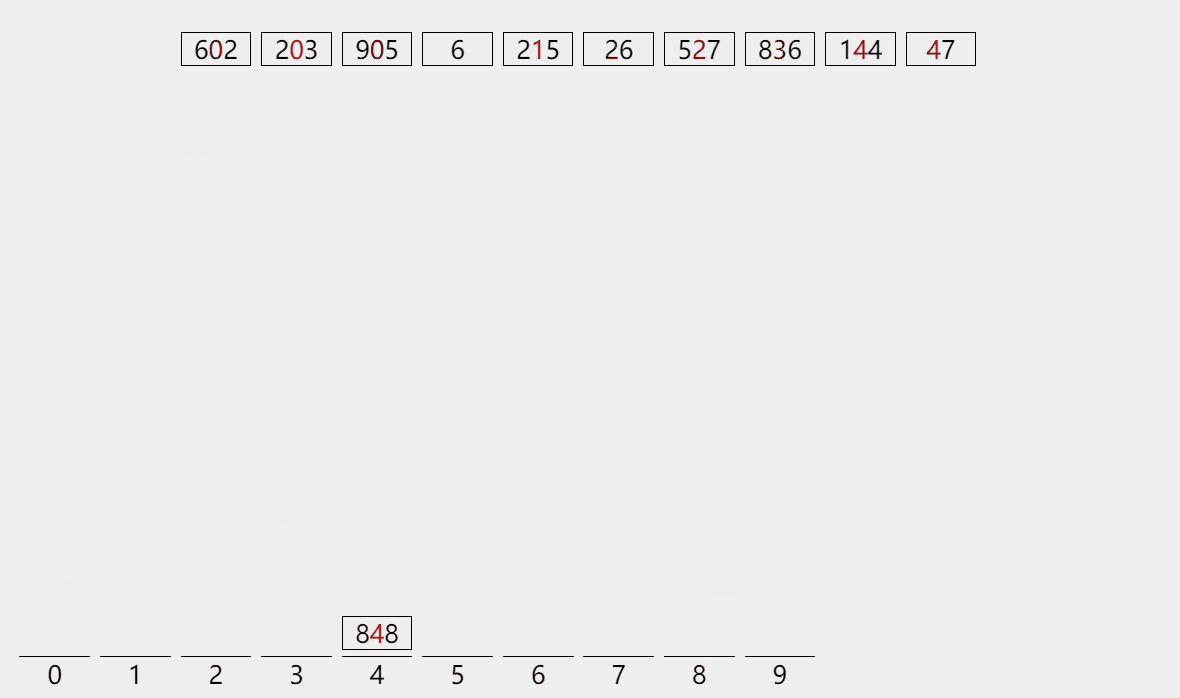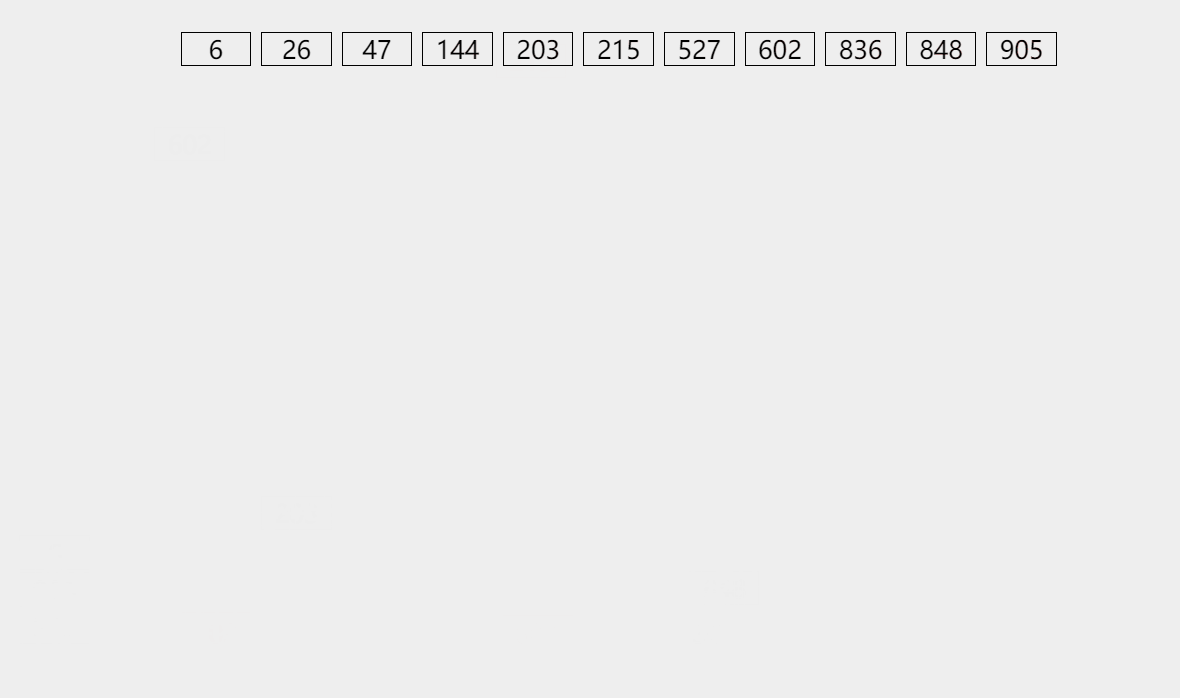
第一轮:判断 个位数
-
将每个元素的 个位数 取出,找到其 个位数 所对应的下标的桶,然后把这个数放到桶中(桶为一个一维数组)
-
按照这个桶的顺序,依次取出数据,放回原来的数组
注意:取出桶里的数据时,不仅要按桶的顺序依次来取,而且单个桶里的数据取出顺序也要按先放进去的先取出来的规则。
以上步骤中,每一轮除了用什么位数的值来判断放在哪个桶里不同外,其他的都相同。
第二轮:判断 十位数。
需要注意的是:
- 第一轮使用后的桶并未清理,上图为了讲解方便,并未展示桶中已有的数据,不过会进行覆盖。
- 长度不足的数,用零表示。如
3,没有十位数,则归类到第一个桶中(0),即该数看成03。
第三轮:判断 百位数
一个流程下来,你会发现,在第三轮排序后,数组已经是有序的了
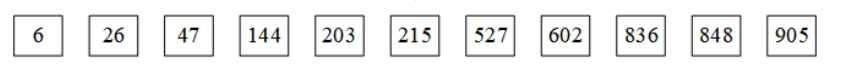
动图:
代码实现
推导实现
为了更容易理解,下面进行分步推导来找出里面的规律,从而实现算法。
/**
* 推导:推导每一步的状态,然后找规律
*/
@Test
public void processDemo() {
//这里我就随便一个数组了
int arr[] = {53, 3, 542, 748, 14, 214};
System.out.println("原始数组:" + Arrays.toString(arr));
processRadixSort(arr);
}
public void processRadixSort(int[] arr) {
// 第一轮
// 1. 将每个元素的 **个位数** 取出,找到其 个位数 所对应的下标的桶,然后把这个数放到桶中(**桶为一个一维数组**)
// 2. 按照这个桶的顺序,**依次取出数据**,放回原来的数组
// 定义 10 个桶,每个桶是一个一维数组
// 由于无法知道每个桶需要多少个元素,所以声明为数组长度
// 例如:加入10 个数字都是 1,那么只会分配到同一个通中
int[][] buckets = new int[10][arr.length];
// 定义每个桶中有效的数据个数
// 桶长度为数组大小,那么每一个桶中存放了几个有效的元素呢?就需要有这个变量来指示
int[] bucketCounts = new int[buckets.length];
// 开始第一轮的代码实现
// 1. 将每个元素的 **个位数** 取出,找到其 个位数 所对应的下标的桶,然后把这个数放到桶中(**桶为一个一维数组**)
for (int i = 0; i < arr.length; i++) {
// 获取到个位数
int temp = arr[i] % 10;
// 根据规则,将该数放到对应的桶中
buckets[temp][bucketCounts[temp]] = arr[i];
// 并将该桶的有效个数+1
bucketCounts[temp]++;
}
// 2. 按照这个桶的顺序,**依次取出数据**,放回原来的数组
int index = 0; // 原始数组下标索引
for (int i = 0; i < buckets.length; i++) {
if (bucketCounts[i] == 0) {
// 标识该桶无数据
continue;
}
for (int j = 0; j < bucketCounts[i]; j++) {
arr[index++] = buckets[i][j];
}
// 取完数据后,要重置每个桶的有效数据个数,注意,这里一步一定要做!!!
bucketCounts[i] = 0;
}
System.out.println("第一轮排序后:" + Arrays.toString(arr));
// 第 2 轮:判断 十位数
for (int i = 0; i < arr.length; i++) {
// 获取到十位数
int temp = arr[i] / 10 % 10;//就这一步不同
buckets[temp][bucketCounts[temp]] = arr[i];
bucketCounts[temp]++;
}
index = 0; // 原始数组下标索引
for (int i = 0; i < buckets.length; i++) {
if (bucketCounts[i] == 0) {
continue;
}
for (int j = 0; j < bucketCounts[i]; j++) {
arr[index++] = buckets[i][j];
}
bucketCounts[i] = 0;
}
System.out.println("第二轮排序后:" + Arrays.toString(arr));
// 第 3 轮:判断 百位数
for (int i = 0; i < arr.length; i++) {
// 获取到十位数
int temp = arr[i] / 100 % 10;//就这一步不同
buckets[temp][bucketCounts[temp]] = arr[i];
bucketCounts[temp]++;
}
index = 0; // 标识当前放回原数组的哪一个了
for (int i = 0; i < buckets.length; i++) {
if (bucketCounts[i] == 0) {
continue;
}
for (int j = 0; j < bucketCounts[i]; j++) {
arr[index++] = buckets[i][j];
}
bucketCounts[i] = 0;
}
System.out.println("第三轮排序后:" + Arrays.toString(arr));
}
测试输出
原始数组:[53, 3, 542, 748, 14, 214]
第一轮排序后:[542, 53, 3, 14, 214, 748]
第二轮排序后:[3, 14, 214, 542, 748, 53]
第三轮排序后:[3, 14, 53, 214, 542, 748]
根据前面的推导,整理发现有如下的规律:整体代码比较固定,少数变量在变化,即判断的位数
-
要循环几轮?这个与待排序数组中的最大值有几位数有关系
需要找到数组中的最大值,并且得到该值的位数
-
获取数组中每个数的个、十、百 位数的公式可以如下整理:
// 获取个位数 arr[i] % 10 -> arr[i] / 1 % 10 // 获取十位数 arr[i] / 10 % 10 // 获取百位数 arr[i] / 100 % 10可以发现规律,每一次变化的都是 10 的倍数
因此通过推到以及上面的分析整理,下面完成了该算法的具体代码
完整实现
@Test
public void radixSortTest() {
int arr[] = {53, 3, 542, 748, 14, 214};
System.out.println("原始数组:" + Arrays.toString(arr));
radixSort(arr);
System.out.println("排序后:" + Arrays.toString(arr));
}
/**
* 根据推导规律,整理出完整算法
*
* @param arr
*/
public void radixSort(int[] arr) {
// 1. 得到数组中的最大值,并获取到该值的位数。用于知道要循环几轮
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// 得到位数
int maxLength = (max + "").length();//这里很巧妙!
// 定义桶 和 标识桶中元素个数
int[][] bucket = new int[10][arr.length];
int[] bucketCounts = new int[bucket.length];
// 总共需要进行 maxLength 轮
for (int k = 1, n = 1; k <= maxLength; k++, n *= 10) {//注意看这里,有两个变量,k控制循环,n用于后面获取到对应的位数
// 进行桶排序
for (int i = 0; i < arr.length; i++) {
// 获取该轮的桶索引:n 每一轮按 10 的倍数递增,获取到对应数位数
// 这里额外使用一个步长为 10 的变量 n 来得到每一次递增后的值
int bucketIndex = arr[i] / n % 10;//这里很巧妙!
// 放入该桶中
bucket[bucketIndex][bucketCounts[bucketIndex]] = arr[i];
// 标识该桶元素多了一个
bucketCounts[bucketIndex]++;
}
// 将桶中元素获取出来,放到原数组中,注意,要按单个桶中的数据取出是先进先出的顺序
int index = 0;
for (int i = 0; i < bucket.length; i++) {
if (bucketCounts[i] == 0) {
// 该桶无有效元素,跳过不获取
continue;
}
// 获取桶中有效的个数
for (int j = 0; j < bucketCounts[i]; j++) {
arr[index++] = bucket[i][j];
}
// 取完后,重置该桶的元素个数为 0 ,下一次才不会错乱数据,这一步很重要!!!
bucketCounts[i] = 0;
}
System.out.println("第" + k + "轮排序后:" + Arrays.toString(arr));
}
}
测试输出
原始数组:[53, 3, 542, 748, 14, 214]
第1轮排序后:[542, 53, 3, 14, 214, 748]
第2轮排序后:[3, 14, 214, 542, 748, 53]
第3轮排序后:[3, 14, 53, 214, 542, 748]
排序后:[3, 14, 53, 214, 542, 748]
动图:

大数据量耗时测试
/**
* 大量数据排序时间测试
*/
@Test
public void bulkDataSort() {
int max = 80000;
// max = 8;
int[] arr = new int[max];
for (int i = 0; i < max; i++) {
arr[i] = (int) (Math.random() * 80000);
}
if (arr.length < 10) {
System.out.println("原始数组:" + Arrays.toString(arr));
}
Instant startTime = Instant.now();
radixSort(arr);
if (arr.length < 10) {
System.out.println("排序后:" + Arrays.toString(arr));
}
Instant endTime = Instant.now();
System.out.println("共耗时:" + Duration.between(startTime, endTime).toMillis() + " 毫秒");
}
多次测试输出信息
共耗时:31 毫秒
共耗时:29 毫秒
共耗时:22 毫秒
共耗时:39 毫秒
如果增加数据量到 800 万,也发现只会用时 400 毫秒左右,速度非常快。
但是,如果数据量增加到 8000 万,则会报错(这个就得看你的电脑内存大小了)
java.lang.OutOfMemoryError: Java heap space
at cn.mrcode.study.dsalgtutorialdemo.datastructure.sort.radix.RadixSortTest.radixSort(RadixSortTest.java:125)
这是为什么呢?原因就在于开启了 10 个桶,每个桶都是 8000 万个数据。那么换算下单位:
80000000 * 11 * 4 / 1024 /1024 / 1024 = 3.2 G 左右的堆空间
# 11 = 10 个桶 + 原始数组
# 4 :一个 int 占用 4 字节
也就是说,牺牲内存来提升速度。
注意事项
-
基数排序是对 传统桶排序 的扩展,速度很快
-
是经典的空间换时间的方式,占用内存空间很大
当数据量太大的时候,所耗费的额外空间较大。是原始数据的 10 倍空间
-
基数排序是稳定的
相同的数,排序之后,他们的先后顺序没有发生变化。
-
有负数时,不用基数排序来进行排序
如果要支持负数可以参考 中文维基百科
由于上述算法使用的按位比较,并未考虑负数,直接使用,将导致数组越界。
改造支持负数的核心思想是:将负数取绝对值,然后再反转成负数。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号