密码学习第3天-RSA(1)

RSA 加密算法，一种非对称加密算法，在各种场景与环境下都有它的身影，那么它和其它加密算法又有什么不同呢，以及什么是非对称加密算法？

• 非对称加密：传统的加密算法基于同一密钥进行加密和解密，此时我们会发现我们攻击的重点将落在通信双方的密钥到底是什么，因为即使你的加密算法天衣无缝，但是你的密钥泄露了，我便可以直接通过解密算法得到密钥。

  在一个不安全的通信环境中，你的信息需要经过很多节点（中间人）才能传输至目标，此时我们考虑两个问题：

  1. 如何保证发送的信息没有被窃取？
  2. 如何保证是可信的发送人（即别人不能伪造你的身份发送信息）？

  其实这便是信息安全等级保护中的CIA三要素的机密性（Confidentiality）和完整性（Integrity）要求。

  显然，依靠传统的对称密码我们没办法做到这两点，因为传统对称密码需要事先约定使用某个特定的密码进行通信。此时我们考虑这样一个加密算法，它拥有两组密钥

  公开密钥Pk（Public key）：又称公钥，可以公开给所有人进行存储。

  私有密钥Sk（Secret key）：又称私钥，只能是发送者自己保存。

• 如果我们规定加密时使用公钥，解密时使用私钥，那么似乎我们的第一个问题中的放窃取便有了解决方案

  我Xenny要给Soar发送信息，此时我只需要获取Soar的公开密钥（因为这会公开给所有人），然后用这个公钥将我们的信息进行加密，再发送给Soar即可，Soar收到信息后只需要用自己的私钥解密即可。

  为什么？

  考虑此时有一个中间节点获取了我们的信息，但是他只能得到加密的信息，而解密则需要私钥，故他没有窃取我们的消息。

• 那么如何保证可信呢，这里其实属于数字签名的内容，在后续的课程中我们会详细介绍各类签名、认证算法，那么在这里我们可以稍作提及，其实我们只需要使用私钥对数据进行签名，用公钥进行验签即可。

  此处若不能理解如何操作，可以暂时不用深究。

• 在刚才的内容中，我们提到了非常多的新名词

  公钥、私钥、非对称、签名等等…

  但我们如何实现这种算法呢，让我们回到本节内容的重点——RSA算法上，RSA 是 1977 年由罗纳德 · 李维斯特（Ron Rivest）、阿迪 · 萨莫尔（Adi Shamir）和伦纳德 · 阿德曼（Leonard Adleman）一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。

  整个密码学的基石都是基于一些数学难题，以RSA算法为例，其基于大整数分解难题（IFP），目前来说我们并没有什么有效的办法对一个极大整数做因式分解，再多的优化在极大整数面前都与爆破无异，这保障了RSA的安全性。

  接下来我们将学习RSA是如何工作的

生成公私钥

1. 选取两个不同的大素数 p 和 q ，计算 $N=p⋅q$ 。
2. 求欧拉函数值 $φ(N)=φ(p)φ(q)=(p−1)(q−1)$
3. 选择一个小于 $φ(N)$ 的整数 e ，并且满足 e 和 φ(N) 互质，求得 e在模 φ(N) 意义下的乘法逆元 dd ，有 $ed≡1(modφ(N))$。
4. 销毁 p 和 q 。

此时有 (N,e)为公钥， (N,d)为私钥。

可能此时你便已经开始看不懂了，没关系，让我们一一拆分解释，值得注意的是，你会发现不同的资料上的表述可能都不太一样，例如“素”和“质”的区分，实际上，这些内容因为在目前我们无须深究，所以只需要了解其含义即可，再之后的教程中我们会学习各类算法在不同环、域上的扩展，此时我们再来深究其数学意义。

• 互质：两个正整数只有一个公因数1时，则称其为互质。

• 欧拉函数 φ(N)φ(N)：小于或等于 N 的正整数中与 N 互质的数的数目

  若 p 为素数，则 φ(p)=p−1 (因为每一个小于 p 的数都与 p 互质。)

  又有若 N=p⋅q，则 φ(N)=φ(p)φ(q)。这里涉及到欧拉函数性质和计算方式，我们不在此深究，感兴趣的同学可以从 N 中有哪些和 N不互质的数来进行推导本公式。

  由此我们有在RSA中，φ(N)=(p−1)(q−1)。

• 乘法逆元：

  在加法中，我们有a+(−a)=0a+(−a)=0，我们称其互为相反数。
  在乘法中，我们有a⋅(1/a)=1a⋅(1/a)=1，我们称其互为倒数。
  在矩阵中，我们有M⋅M−1=EM⋅M−1=E，我们称其为逆矩阵。

  但是其实我们可以用一个统一的称呼：逆元，即某种运算下的逆元素，我们会发现，元素和其逆元素进行运算之后总是一个定值，实际上在代数中，他们构成了一个群（不用深究），而我们进行要了解则是在模意义下的乘法逆元。

  在模 p 意义下，指的是后续的所有运算都是在模 p 的条件下满足，例如 3⋅4≠1

  但 $(3⋅4)mod11=(1)mod11$，对于这种式子我们称其为同余式，并且有专门的同余符号进行表示
  $3⋅4≡1(mod11)3⋅4≡1(mod11)$
  所以参考上面乘法中的逆元运算规则，在模意义下则有

  $a⋅a^−1≡1(mod p)$

  我们称 a 和 $a^−1$ 互为在模 p 意义下的乘法逆元。例如上述中的 3 与 4 互为在模 11 下的乘法逆元。

• 至此你应该能够理解上述内容中的各项式子代表何意，那么如何用这些数字来进行加解密呢，我们继续往下学习。

加密

• RSA算法本质上都是基于数学运算，在加密时我们需要先将消息转化为一个数字 m（例如消息ASCII码的二进制排列转为数字），然后有

  $c≡m^e(modN)$

  此时得到的 c 便是我们的密文。

解密

• 加密时我们只用到了公钥 (N,e)，同理解密时我们也只需用到私钥 (N,d)。有

  $m≡c^d(modN)$

  此时得到的 m 便是我们的明文消息。

正确性证明

• 也许此时你不明白为什么 m 能经过不同的两次幂运算后会得到原始值，这其实就是为什么RSA中要用到欧拉函数，如果你还不能够理解上面的一切，下面的正确性证明可以先略过，不要给自己徒增压力

  转换为证明

  m≡cd≡(me)d≡med(modN)m​≡cd≡(me)d≡med(modN)​

  又有 ed≡1(modφ(N))ed≡1(modφ(N))，即ed=1+kφ(N)ed=1+kφ(N)。

1. 若gcd(m,N)=1gcd(m,N)=1，则med≡med−1⋅m≡mkφ(N)⋅m≡m(modN)med≡med−1⋅m≡mkφ(N)⋅m≡m(modN)。原始得证。（中间涉及到欧拉定理 aφ(n)≡1(modn)aφ(n)≡1(modn)）

2. 若gcd(m,N)≠1gcd(m,N)=1，则 mm 为 pp 或 qq 的整数，设 m=hpm=hp，有

   med≡med−1≡mk(p−1)(q−1)⋅m≡(1+xq)⋅m≡m+xq⋅hp≡m(modN)med​≡med−1≡mk(p−1)(q−1)⋅m≡(1+xq)⋅m≡m+xq⋅hp≡m(modN)​

   其中

   mk(p−1)(q−1)=(mk(p−1))q−1=1+xqmk(p−1)(q−1)=(mk(p−1))q−1=1+xq

   原式得证。

---

• 至此，我们用尽可能用简洁的内容将RSA的原理与作用简单描述了一遍，接下来我们便要开始正式进入CTF中的RSA算法学习了。

• 再上一节中我们学习了RSA的数学原理基础，本节课我们将了解如何具体实现RSA算法。

  注意，在大部分资料中，其他作者更喜欢使用举一些特定的数字带入运算，从而让读者明白整个流程或从数字上直观的得到不同算式之间的联系。但我不会在这里不会使用此方式来阐述RSA的算法流程，带入具体数值进行计算观察关系的方式在解题时非常有效，但更多的我希望各位能够理解一种抽象的思维，这对我们后续的学习非常有帮助，当然各位同学在学习过程中可以自行选择自己喜欢的方式进行操作。

  我们使用Python语言来实现一个RSA算法，首先你需要确保你已经安装好了Python执行环境以及编辑环境。（这一步如果有问题请自行搜索解决）

  我使用的环境为Python 3.9.12 + VSCode，你并不需要和我的环境保持一致，你可以选择自己熟悉或喜爱的环境进行操作，不过Python请使用3.8及以上版本，不然某些操作可能会得到不一样的结果。环境除了这二者之外还包括操作操作系统，我在平时工作中会使用很多不同的操作系统进行工作，对于CTF中密码学而言，这没那么重要，同时我也会尽量保持使用跨平台的代码。在特殊时候会进行进一步说明。

  因为课程设置关系，在后续的内容中，我默认你已经基本掌握了Python语法，我将只会解释代码中新出现的库、函数、类的用法和说明。

Python实现RSA

• 上一节我们发现RSA无外乎就是那几个参数之间的运算，而我们要做的便是使用Python实现这些算式，首先我们要做的第一步是

1. 生成两个大素数P，Q。

   这是一个很模糊的概念，我希望各位在学习中能够做到尽量严谨，很显然，这里定义的大素数到底多大才是大呢？

   10算大吗？100算吗？10000算吗？葛立恒数算吗？

   我们需要一个更加精确的说法，我们生成两个512位的素数（这里包括之后的内容中涉及到的位都是指二进制位而不是十进制），那么如何使用Python产生一个素数呢，如果不借助任何外力的情况，我们可以从1开始选择，2，3，4…直到某个数满足512位且为素数为止，但是既然我们都使用Python了，为何还要这样做呢？

   让我们来使用Python强大的开源库pycryptodome，一般来说你只需要使用

   pip3 install pycryptodome
   # 或
   python3 -m pip install pycryptodome
   

   便可以成功安装，然后在Python环境中执行以下代码

   import Crypto
   

   如果没有显示ModuleNotFoundError：等诸如此类的错误话，那么恭喜你成功的安装了本库。这里你可能会奇怪为什么安装使用pycryptodome，而引入时使用Crypto，这涉及到这的库和其他库的一些联系，有兴趣的可以自行去查找。
   然后我们就可以生成素数了，我们引入库中的子包Crypto.Util.number，这个子包中包含了大量的数学工具，之后我们会经常用到这个子包。

   from Crypto.Util.number import *
   p = getPrime(512)
   q = getPrime(512)
   print(p)
   print(q)
   

   执行上面的代码，你便可以得到两个512位的素数，这依赖于我们调用了包中的getPrime函数，它能够返回一个n位的素数，其中n是我们的传入参数。至此我们便完成了RSA的第一步。

2. n=p⋅q, φ(n)=(p−1)(q−1)
   后续的过程便简单了很多，我们只需要在之前的基础上完成运算即可，添加下列代码并执行

   n = p*q
   phi = (p-1)*(q-1)
   

3. 选取与φ(n)互素的e，计算满足$ed≡1(modφ(n))$
   这里我们要完成两个数学操作，一个是互素的判断，一个是求解e的乘法逆元。

   e = 65537
   assert GCD(e, phi) == 1, "该e不满足互素条件"
   d = inverse(e, phi)
   

   这里GCD函数能够求解最大公因数（Greatest Common Divisor），之前我们学习了互素的概念就是两个数的最大公因数为1，所以这里我们用断言表达式认定e一定是和phi互素的。为什么我们要选择65537作为e呢，实际上这并不是硬性规定，一些标准提供了一些e的参考值，65537在各类实现与标准中被广泛使用，但是这并不影响你可以将值改变为其他值进行后续的操作。
   求d的过程中，我们使用了inverse函数，该函数有两个参数(a,p)，作用便是求解a在模p意义下的乘法逆元，那么这里我们便是求解e在模phi下面的乘法逆元，结果为d。之前我们提到了逆元是互为逆元，所以你可以尝试下面的代码
   print(inverse(d, phi) == e)
   打印的结果将为True，从这里我们也可以看出在RSA中的关键点便是获取这个phi的值，因为得到的phi我们便可以求e或d的值，而这正是我们加解密的密钥参数。

4. (n,e)即为公钥，(n,d)即为私钥，此时我们便得到了一组RSA的公私钥，随后我们便可以开始用这组密钥来进行加解密操作。
   加密：
   假设我们要加密的消息为Hello，我们定义一个字符串进行存储

   message = b'hello'
   

   注意这里我们定义的是一个bytes类型字符串，它将每个字符用8位二进制进行存储，是字符串最原生的存储形式。你也可以直接定义'hello'，但在Python3中它是一个Unicode的字符串，需要进行编码操作才能转换为bytes类型进行后续的运算。
   但我们在RSA中是数与数的运算，该如何将字符串参与操作呢？
   我们使用包中的bytes_to_long函数，从函数名也可以猜出来，这个函数是将字符串转换为数字，运行下列代码

   m = bytes_to_long(message)
   print(m)
   

   此时，我们的消息已经被转换为一个字符串了。随后我们便可以对消息进行RSA加密

   c = pow(m, e, n)
   print(c)
   

   我们使用Python自带的pow函数进行幂运算，注意不要写成m**e % n，二者代表的意义相同，但是pow函数内置快速幂，可以快速得出结果，而m**e % n会将meme的结果先计算出来再取模，meme是一个非常大的数，这会消耗你计算机大量的运算和存储资源。
   至此，我们便完成了加密过程，得到了RSA的密文C。
   解密：
   我们执行

   msg = pow(c, d, n)
   print(msg)
   

   此时我们便完成了RSA的解密操作，随后你可以比较一下msg和m的值，他们会是一样的。

• 完整代码：

  from Crypto.Util.number import *
  p = getPrime(512)
  q = getPrime(512)
  
  n = p*q
  phi = (p-1)*(q-1)
  e = 65537
  assert GCD(e, phi) == 1, "该e不满足互素条件"
  d = inverse(e, phi)
  
  print(f'公钥：({e}, {n})')
  print(f'私钥：({d}, {n})')
  
  message = b'hello'
  m = bytes_to_long(message)
  print('消息：', m)
  
  c = pow(m, e, n)
  print('密文：', c)
  
  msg = pow(c, d, n)
  print('明文：', msg)
  
  assert msg == m, "解密失败"
  

1. 如果你用一个比较长的字符串，会发现解密后得到的值和原来的不一样，这其实是RSA的缺陷之一，你可以自行了解一下RSA的一些算法标准也可以继续关注我们之后的课程。
2. 如果我用一个不满足互素条件的e，你会发现求不出d，这是因为只有满足互素的数才存在逆元，那么此时我们考虑用一个不存在逆元的e来进行加密，是否有可能进行解密呢？我们后续课程会讨论这些情况。

• 本部分内容建议先做完P7，P8尝试自行推导wp中的公式再做查看。
• 之前的内容我们对于欧拉函数一节没有做详细的介绍，因为重点是先理解RSA的算法过程，但要想深入学习密码学各个攻击的原理，我们必须掌握欧拉函数及其性质，本篇将介绍欧拉函数涉及的数学定理以及运算。

欧拉函数计算

• 之前我们已经介绍过欧拉函数的定义了
  φ(n)为在小于n的正整数中与n互素的数的数目。
  此前我们只讨论了特殊的情况，当p为素数时，有φ(p)=p−1，现在我们来讨论更一般的情况，当nn是一个双因子合数时
  n=p⋅q
  我们考虑和n不互素的数有
  p,2p,3p,⋯ ,(q−1)p,q,2q,3q,⋯ ,(p−1)q
  因为只有这些数和nn的最大公因数不为1，则欧拉函数值应该为n−1n−1减去这些不互素的数的数目
  φ(n)=(pq−1)−(q−1)−(p−1)=(p−1)(q−1)
  显然对于三因子，多因子我们都可以得到上面的结论，即当
  n=p1p2⋯pr
  有
  φ(n)=(p1−1)(p2−1)⋯(pr−1)

• 现在我们考虑因子阶不为1的情况，还是先从双因子数讨论
  n=pk1qk2
  此时，和nn不互素的数有
  p,2p,⋯ ,(qk2−1)p,q,2q,⋯ ,(pk1−1)qp,2p,⋯,(qk2​−1)p,q,2q,⋯,(pk1​−1)q
  但我们会发现，上面的数中又可能会存在重复的数，例如
  p,2p,⋯ ,qp,⋯ ,2qp,⋯ ,(qk2pk1−1−1)p
  q,2q,⋯ ,pq,⋯ ,2pq,⋯ ,(pk1qk2−1−1)q
  
  

欧拉函数性质

• 欧拉函数在数论中有广泛的运用，在此我们并不会讨论完所有关于欧拉函数的性质，只会重点讲解一些于CTF中涉及的性质。

1. 积性函数

   积性函数：对于任意互质的整数 a和b有性质f (ab)=f (a)f (b)的 数论函数 。
   完全积性函数：对于任意整数 a和b有性质f (ab)=f (a)f (b)的 数论函数 。

   显然欧拉函数属于积性函数，因为其值来自每一个因子的乘积，而每个系数刚好又是每个因子的欧拉值，即

   φ(p^k1qk2)=φ(p^k1)φ(qk2)

   这个性质可以推广到rr个因子中，即

   φ(n)=φ(p1^k1)φ(p2k2)⋯φ(pr^kr)

2. 欧拉定理

   若(a,m)=1（我们一般用(a,b)代表gcd⁡(a,b)），则有aφ(m)≡1(modm)。

   欧拉定理我们可以用如下思路证明，设小于m中与m不互素的数集为

   s={x1,x2,⋯ ,xφ(m)}s={x1​,x2​,⋯,xφ(m)​}

   他们中任意两个值都满足（因为值本身不相等）

   又a与m互素，我们可知有

   (axi,m)=1

   因为他们中间不包含任何除1以外的公因子，那么此时我们有

   axi≡xj(modm), (xi,xj∈s)

   什么意思呢？就是说axiaxi​模mm的余数（设为rr）rr一定在集合ss中，这里大家应该能理解，因为ss中是所有小于mm且和mm互素的数，又rr也和mm互素，所以rr一定在ss中。并且我们还可以证明

   axi≢axj(modm)axi​≡axj​(modm)

   这里可以用反证法，如果他们同余，则说明a(xi−xj)≡0(modm)a(xi​−xj​)≡0(modm)，说明a∣ma∣m或者(xi−xj)∣m(xi​−xj​)∣m，（a∣ba∣b代表aa整除bb）而这显然是和互素矛盾的。

   进一步的我们可以得到

   x1x2⋯xφ(m)≡ax1⋅ax2⋯axφ(m)(modm)x1​x2​⋯xφ(m)​≡ax1​⋅ax2​⋯axφ(m)​(modm)

   这又是为何，因为我们不需要关心axiaxi​的余数到底是哪个xjxj​，我们只需要知道aa和不同的xixi​得到的余数各不相同即可，那么φ(m)φ(m)个相乘也会得到不同的φ(m)φ(m)个值，也就是覆盖了集合ss。

   两边消项，有

   1≡aφ(m)(modm)1≡aφ(m)(modm)

3. 扩展欧拉定理

   我们也称其为欧拉降幂，指的是
   
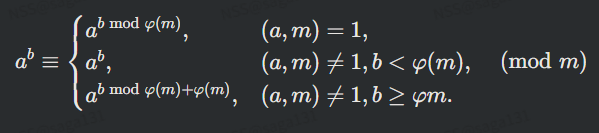
   即我们可以将幂指数模φ(m)φ(m)后处理，这里的证明可以参考OI-wiki。

• 在之前的内容中我们介绍了同余的概念，关于模运算后面会经常出现在我们的题目中，因为取模本质是一种信息丢失，所以使得正向运算非常简单，我们很容易计算一个值取模后的结果，但却很难从余数中恢复这个数的原始值，所以取模经常出现在密码学的运用之中。

模数利用方法

直接分解

对于一些不安全/位数比较小的素数,以当前的算法和算力很容易将其分解。通常300bit以下的模数均可在较短时间内被分解,一些不安全的素数也会很快被特定算法所分解。
CTF中常用的分解手法:

• 在线网站 http://factordb.com
• 在线网站 https://www.alpertron.com.ar/ECM.HTM
• 工具yafu
• SageMath内置的factor函数
  

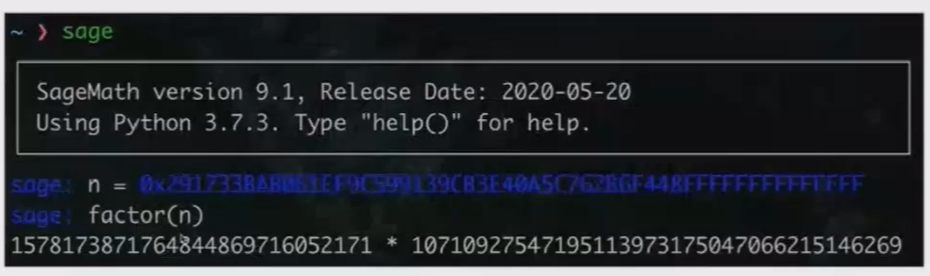
p、q相近

from Crypto.Util.number import getPrime, isPrime

def nextPrime(p):
	p = (p+2) | 1
	while not isPrime(p):
		p += 2
	return p

def genkey(bits):
	p = getPrime(bits)
	q = nextPrime(p)
	e = 65537
	n = p*q
	return n

相差只有几百或者几千
此时,有如下关系:
p^2<n<q2
如果对n开近似平方根:
p2<sqrt(n)<q2
则近似平方根必然落在p和q之间,且距离p和q很近,可以通过穷举的方式,找到p和q。

n=...
root = n.nth_root(..., truncate_mode=True)[0]  

for i in range(-1000,1000):
    pp = root + i
    if gcd(pp, n) != 1:
        print(pp, n // pp)
        break

模不互素

当两个模数共有同一个素数时,有如下关系:
n1=p · q1
n2=p . q2
可以对n1和n2求最大公约数(gcd),这两者的最大公约数即为其中的一个素因子p,从而可以分解这两个模数。
案例代码：

p = getPrime(1024)
q1 = getPrime(1024)
q2 = getPrime(1024)

n1 = p * q1
n2 = p * q2

解题代码：

from Crypto.Util.number import GCD

p = GCD(n1, n2)
q1 = n1 // p
q2 = n2 // p

共模

当两个用户共同使用相同的模数、不同的私钥,加密同一明文消息时即存在“共模”。

p = getPrime(512)
q = getPrime(512)
n = p*q
e1 = getPrime(64)
e2 = getPrime(64)
m = bytes_to_long(flag)

c1 = pow(m, el, n)
c2 = pow(m, e2, n)

RSA解密实际上可以看作是，对$c$开$e$次方根；或者说是，找到一个$d$，使得 $$m^{ed} \equiv m^1 \pmod{n}$$ 目的是为了让$m$的右上角指数变为1。 这在只有一个$c \equiv m^e \pmod{n}$时是很难的，被称为RSA Problem。
但是现在有两组这样关系： $$m^{e_1} \equiv c_1 \pmod{n}$$ $$m^{e_2} \equiv c_2 \pmod{n}$$ 可以通过扩展欧几里得算法计算出 $$r e_1 + s e_2 = 1$$ 从而有 $$c_1^r c_2^s \equiv m^{r e_1 + s e_2} \equiv m^1 \pmod{n}$$ 使得右上角的指数变为1。
解决代码：

def egcd(a, b):
	'''
	Extended Euclidean Algorithm.
	returns x, y, gcd(a,b) such that ax + by = gcd(a,b).
	'''
	
	u, ul = 1, 0
	v, vl = 0, 1
	while b:
	q, r = divmod(a, b)
	u, ul = ul, u - q * u1
	v, v1 = vl, v - q * v1
	a, b = b, r
	return u, v, a

r, s, _ = egcd(el, e2)
if r < 0:
	r = -r
	c1 = inverse(cl, n)
else:
	s = -s
	c2 = inverse(c2, n)

m= pow(cl, r, n) * pow(c2, s, n) % n
print(long_to_bytes(m))

指数利用方法

小公钥指数利用

RSA算法通过模幂运算对明文信息加密，当指数逐渐增大时，模运算将会发挥作用，将整数的幂运算的结果截断至有限范围内。 但是当指数太小时，模运算还未发挥作用，幂运算就已经结束了。此时的加密结果并没有被截断，即是原本的幂运算，此时就不存在“加密”效果了。 $$c \equiv m^e \pmod{n} \implies c = m^e$$
利用条件：加密指数e特别小,比如e为3。
利用原理:假设用户使用的密钥e=3,若m较小,模运算没有发挥作用,则有c=m^3
此时直接对密文c开3次方根,即可解密出明文m。
题目：

p = getPrime(512)
q = getPrime(512)
n = p * q
m = 123456789
pow(m, 3, n) == m ** 3
pow(m, 3, n)
结果：1881676371789154860897069

利用代码：

c=...
c.nth_root(3)

什么情况下会发生小公钥指数利用？ 当$m$较小时，即$m^e < n$时，就会存在这种利用。 另外，即使$m^e$稍比$n$大一点点，也可以通过穷举的方式对其尝试开根。 $$c \equiv m^e \pmod{n} \implies c = m^e - k \cdot n$$ 可以从0开始穷举$k$，并对$k \cdot n + c$尝试开$e$次方根，若可以开出来根，则说明成功解密。
（对于正常的RSA加密，$k$一般很大，无法被穷举 ）
代码实现：

C =...
e =...
n =...

for k in range(0, 1000000):
	tmp = k*n + c
	root, ok = tmp.nth_root(e, truncate_mode=True)
	if ok:
		print(root)
		break

已知e、d分解n

RSA算法若能够知道加密指数$e$和解密指数$d$，则可以完成对$n$的分解。 根据$e$和$d$的关系有 $$e \cdot d \equiv 1 \pmod{\phi(n)}$$ 同样可以化为 $$\implies e \cdot d = 1 + k \cdot \phi(n)$$ 其中$d < \phi(n)$，因此必有$k < e = 65537$，$k$可以穷举，从而可以得到$\phi(n) = (p - 1) \cdot (q - 1)$。
例题

from gmpy2 import invert
from md5 import md5
from secret import p, q

e = 65537
n = p * q
phi = (p - 1) * (q - 1)
d = invert(e, phi)

print(n, e, d)
print("Flag: flag{" + md5(str(p + q)).hexdigest() + "}")
'''
163525789637230613164207451567045337669117713835764919138975924589655440682968131227401265830
8206556271716296099516132028339626845634974789812858373221853516973250968457253813428505486
2962090824699811261298833275908218597248369932631547669384610688057047403431395257083906956228
48315322366375398232307468754197643541958599210127261345770914514679199047350857144036414690162129
58361895969784545241861560162677607648216337378443764188292654489343487631446165542988382677295
938499373829049502248616616207
914592837973667401308068520504381390923686253309725328965057798530443506221312139823187583226189
4458314629575455534857526856347342666543680295774020887572597763115856401485816534177577248411206
1585535808817167485533282657626883943034396738528623267975528644329172668776962878108764837084
58250159260840175705373263257606839439339687265082223797526432972668776962874160764353080
8235340864803776103524381462645277071034527339724107080190182918285547261656180371664408941407
83908475867205314326381975781806576626728869028362140775515945493072557602327492774111594121748
968079f091733f764549453
Flag: flag{xxxx}
'''

解题代码：

for k in range(1, e):
	if (exd-1)% k == 0: #k可以整除ed-1
	phi = (e*d - 1) // k
	if pow(123,phi,n) == 1:#满足欧拉定理
		var('p q')
		print(solve([(p-1)*(q-1) == phi, p*q == n], [p,q]))

Wiener利用

利用条件： 当$d$比较小（$d < \frac{1}{3} N^{\frac{1}{4}}$ ）时，对手可以使用Wiener利用来获取私钥$d$。
特征：通常出题人为了要使得生成的私钥$d$比较小，通常会先生成一个比较小的$d$，然后再去求$e$，从而使得$e$的取值范围位于（$1, \phi$ ）之间，会导致$e$看起来很大。
从$\phi(n)$和$e$、$d$的关系式出发，有 $$ed = 1 + k \cdot \phi(n)$$ 代入$\phi(n)$的表达式 $$\phi(n) = (p - 1) \cdot (q - 1) = n - (p + q) + 1$$ 有 $$ed = 1 + k \cdot (n - (p + q) + 1)$$ 两边同时除以$nd$，可得 $$\frac{e}{n} = \frac{k}{d} (1 - \delta)$$ 式子左边均已知，右边均未知。 右边的比值和左边的比值非常接近，这种情况可以使用连分数来将左边的比值展开，在连分数的展开式中，很大概率存在$k$和$d$。从而可以求出私钥$d$，进行解密。

def recover(e, N):
    cf = convergents(e / N)
    G, x = ZZ['x']()
    for index, k in enumerate(cf[1:]):
        d0 = k.denominator()
        k_num = k.numerator()
        if k_num != 0 and (e * d0 - 1) % k_num == 0:
            phi = (e * d0 - 1) // k_num
            s = (N - phi + 1)
            f = x^2 - s * x + N
            b = f.discriminant()
            if b > 0 and b.is_square():
                d = d0
                roots = list(zip(*f.roots()))[0]
                if len(roots) == 2 and prod(roots) == N:
                    print(f"[x] Recovered!\nd = {hex(d0)} {d0}")
                    return d
            else:
                continue
    print("[] Could not determine the value of d with the parameters given. Make sure that d < 1/3 * N ^ 0.25")
    return -1

LSB利用手法

假设现在有一个oracle(预言机),它会对一个给定的密文进行解密,但并不会直接返回解密结果,而是检验解密的明文的奇偶性,并根据奇偶性返回相应的值,比如1表示奇数,0表示偶数,即最低位( LSB, least significant bit ) .
那么给定任意一个消息被加密后的密文,只需要log(N)次oracle询问,就可以解密出明文消息。(例如当N是1024位时,只需要大约1024次左右的oracle询问,就可以解密出明文。)

Oracle代码

cc = int(raw_input('Your encrypted message:').strip())
mm = k.decrypt(cc)
if mm & 1 == 1:
	print 'The plain of your decrypted message is odd!'
else:
	print 'The plain of your decrypted message is even!'

RSA的积性（乘法同态）： $$Enc(P_1 \cdot P_2) = Enc(P_1) \cdot Enc(P_2)$$证明： $$(P_1 \cdot P_2)^e = P_1^e \cdot P_2^e \pmod{n}$$ 利用这个性质，可以选择一个$s$，并计算$c' \equiv c \cdot s^e \pmod{n}$，将$c'$发送给服务器，服务器会返回$c'$解密结果$m \cdot s$的奇偶性。通过不断巧妙地继续选取$s$，就可以恢复出$m$。
假设我们现在已经获取到了明文$m$加密所得的密文$c$。 第一次选择$s = 2$，并向服务器发送 $$c' \equiv c \cdot 2^e \pmod{n}$$ 服务器解密得到 $$m' \equiv 2 \cdot m \pmod{n}$$ 并会返回$2 \cdot m \pmod{n}$的奇偶性。
由于$m < n$，所以$2 \cdot m \pmod{n}$有两种情况： - 没有被$\text{mod } n$，就是$2 \cdot m$，此时服务器会返回“偶数”。这说明 $$2 \cdot m < n \text{，即 } 0 \leq m < \frac{n}{2}$$ - 被$\text{mod } n$了，解密结果为$2 \cdot m - n$，由于$2 \cdot m$为偶数且$n$为奇数，因此服务器必然会返回“奇数”。这说明 $$2 \cdot m > n \text{，即 } \frac{n}{2} < m < n$$

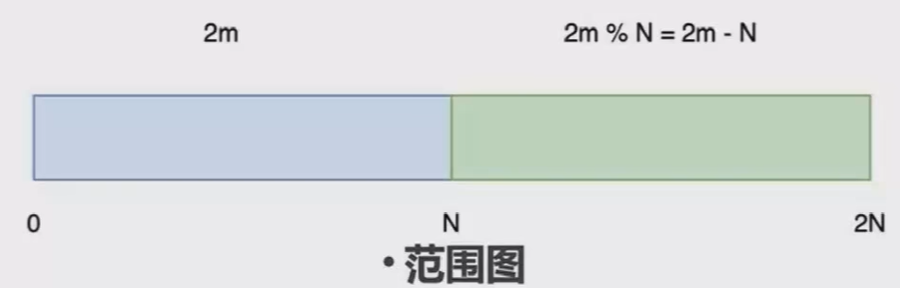
第二次选择$s=4$，并向服务器发送 $$c' \equiv c \cdot 4^e \pmod{n}$$ 服务器解密得到 $$m' \equiv 4 \cdot m \pmod{n}$$ 并会返回$4 \cdot m \pmod{n}$的奇偶性。
如果$0 \leq m < \frac{n}{2}$： - 服务器返回“偶数”，说明没有被$\text{mod } n$，有$4 \cdot m < n$，也就是说 $0 \leq m < n/4$

• 服务器返回“奇数”，说明$4 \cdot m > n$，只有 $\frac{n}{4} < m < \frac{n}{2}$
  如果$\frac{n}{2} \leq m < n$： - 服务器返回“偶数”，说明$4 \cdot m - 2 \cdot n < n$，即 $$0 \leq m < n/4$$ - 服务器返回“奇数”，说明$4 \cdot m - 3 \cdot n < n$，即 $\frac{3n}{4} < m < n$
  通过上述方法，可以将$m$的取值范围缩小一半。 之后，仍然可以继续类似的操作，通过选取$s = 2^i$，服务器会返回$m \cdot 2^i$的奇偶性，从而可以不断地将范围缩小一半，直至最后范围缩小到1，即为正确的$m$。
  例题：

p = getPrime(256)
q = getPrime(256)
n = p * q
e = 65537
m = 12345678
c = pow(m, e, n)

def oracle(cc):
    return pow(cc, inverse(e, (p-1)*(q-1)), n) % 2

解题代码：

L, H = 0, n
t = pow(2, e, n)
CC = C
for _ in range(n.bit_length()):
	cc = (t * cc) % n
	if oracle(cc) = 0:
		H = (L + H) // 2
	else:
		L = (L + H) // 2
	print(L, H)
m = L

# 结果并不一定精确,需要再附近找一下正确的
for x in range(-1000, 1000):
	if pow(x+m, e, n) == c:
		print(x+m)