密码学习第2天-分组密码的分组及其应用

分组与填充

分组密码算法只能加密固定长度(16字节)的分组,当我们需要加密的明文长度超过分组密码的块长度时,需要对分组密码算法迭代,以便将一段很长的明文全部加密,这就是分组密码的模式(mode)。

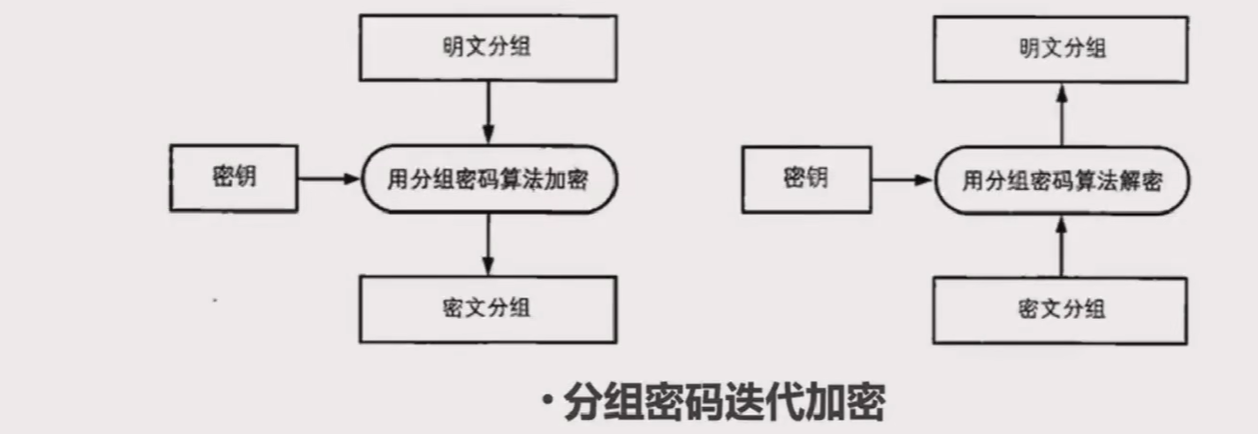
常见的分组模式有如下几种:

• ECB模式:Electronic Code Book mode(电子密码本模式)
• CBC模式:Cipher Block Chaining mode(密码分组链接模式)
• CFB模式:Cipher FeedBack mode(密文反馈模式)
• OFB模式:Output FeedBack mode(输出反馈模式)
• CTR模式:CounTeR mode(计数器模式)
• GCM模式:Galois/Counter Mode(伽罗瓦/计数器模式)
  填充：分组密码迭代加密要求每一个明文分组都是块长度(8或16字节),当分组到最后一组时,其长度不足块长度,就需要对其进行填充,将其长度扩展为块长度。
  
  常见的填充方式有如下几种:
• 补零:在末尾补上0x00字节
  ... | DD DD DD DD DD DD DD DD | DD DD DD DD 00 00 00 00 |
• 字节填充:先填充0×00字节,直至最后一字节填充值为填充长度
  ... | DD DD DD DD DD DD DD DD | DD DD DD DD 00 00 00 04 |
• PKCS7填充:若需填充N个字节,则每个填充字节值都是N
  ... | DD DD DD DD DD DD DD DD | DD DD DD DD 04 04 04 04 |

ECB模式

ECB(Electronic Code Book,电子密码本)模式是最简单的加密模式,明文消息被分成固定大小的块(分组),并且每个块被单独加密。

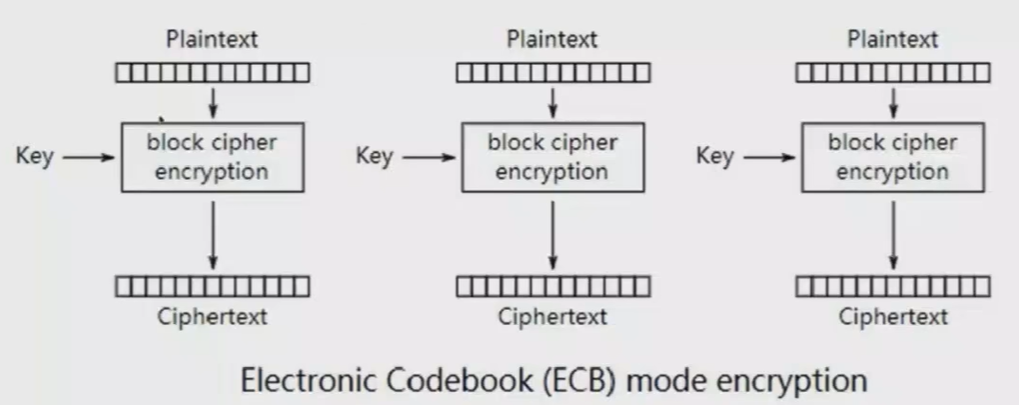
每个块的加密和解密都是独立的,且使用相同的方法进行加密,所以可以进行并行计算。
ECB模式中,明文分组与密文分组是一一对应的关系,因此,如果明文中存在多个相同的明文分组,则这些明文分组最终都将被转换为相同的密文分组。这样一来,只要观察一下密文,就可以知道明文中存在怎样的重复组合,并可以以此为线索来破译密码,因此ECB模式是存在一定风险的。

代码实现

from Crypto.Cipher import AES

def aes_ecb_encrypt(pt, key):
	aes = AES.new(key, AES.MODE_ECB)
	ct = aes.encrypt(pt)
	return ct

def aes_ecb_decrypt(ct, key):
	aes = AES.new(key, AES.MODE_ECB)
	pt = aes.decrypt(ct)
	return pt

CBC模式

CBC(Cipher Block Chaining,密文分组链接)模式中每一个分组要先和前一个分组加密后的数据进行XOR异或操作,然后再进行加密。这样每个密文块依赖该块之前的所有明文块,为了使得加密带有随机性,第一个数据块进行加密之前需要用初始化向量IV进行异或操作。


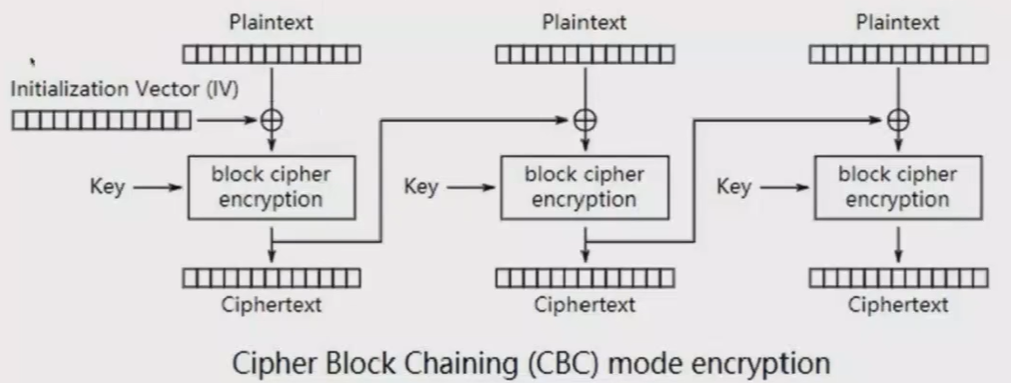
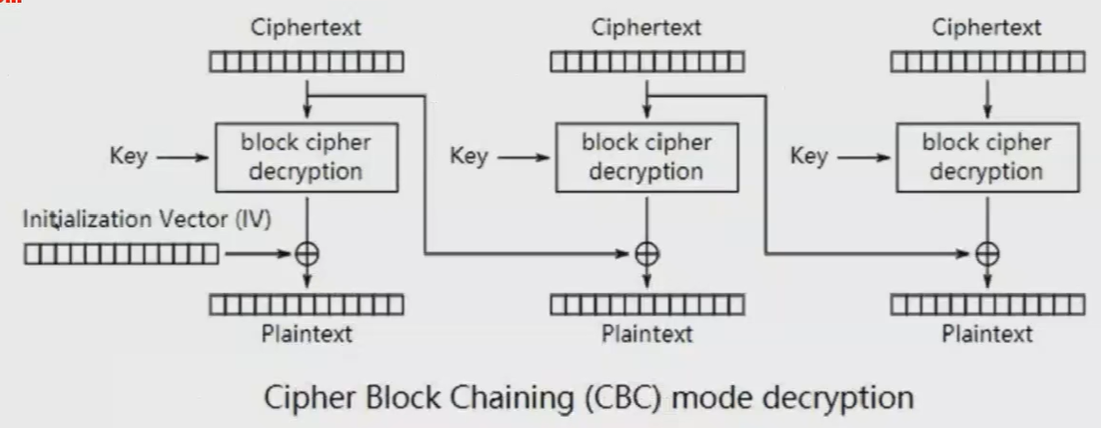
CBC模式是一种最常用的加密模式,它主要缺点是加密是连续的,不能井行处理,并且与ECB一样消息块必须填充到块大小的整倍数。
与ECB模式的区别:ECB模式只进行了加密,而CBC模式则在加密前进行了一次XOR,由于ⅣV的随机性,保证了相同的明文每次加密都会得到不同的密文。

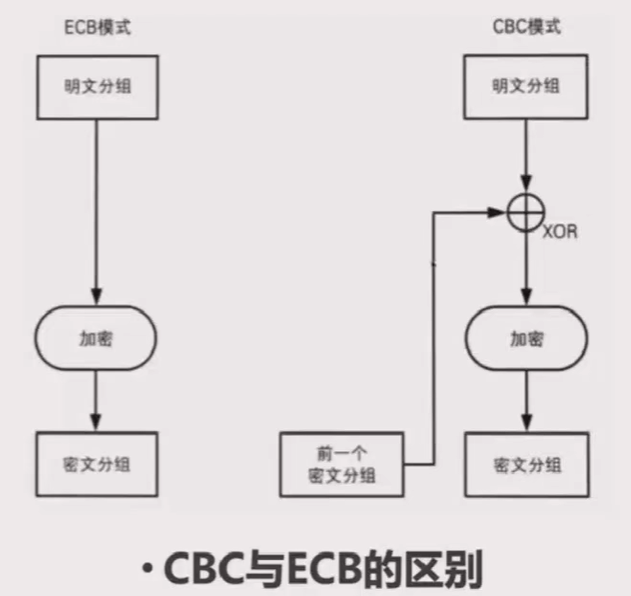
代码实现：

def aes_cbc_encrypt(pt, key, iv):
	aes = AES.new(key, AES.MODE_CBC, iv=iv)
	ct = aes. encrypt(pt)
	return ct

def aes_cbc_decrypt(ct, key, iv):
	aes = AES.new(key, AES.MODE_CBC, iv=iv)
	pt = aes.decrypt(ct)
	return pt

CFB模式

CFB(Cipher FeedBack,密文反馈)模式中,前一个分组的密文经过加密后再与当前分组的明文XOR异或操作生成当前分组的密文。
这里异或在加密之后


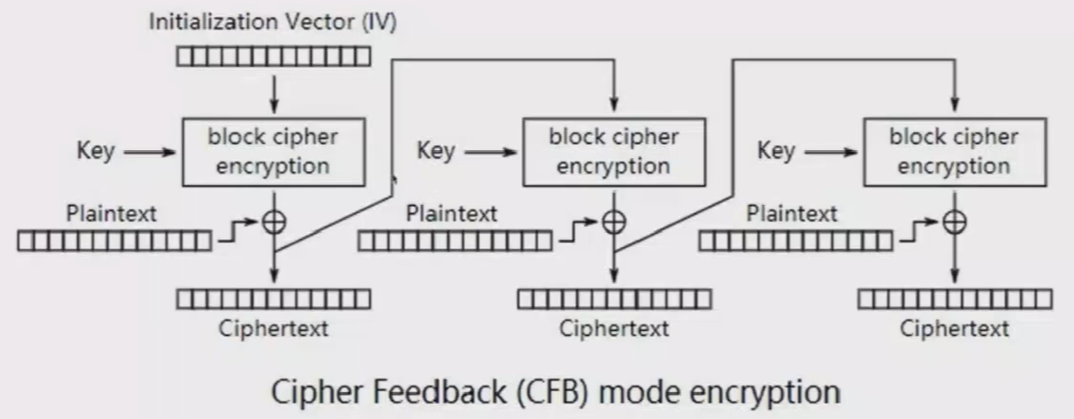
代码实现：

def aes_cfb_encrypt(pt, key, iv):
	aes = AES.new(key, AES.MODE_CFB, iv=iv)
	ct = aes.encrypt(pt)
	return ct

def aes_cfb_decrypt(ct, key, iv):
	aes = AES.new(key, AES.MODE_CFB, iv=iv)
	pt = aes. decrypt(ct)
	return pt

分组模式的利用

1.初始化向量IV的复用

在密码学的领域里,初始化向量(initialization vector,缩写为IV)是一个固定长度的输入值,一般的
使用上会要求它是随机数或拟随机数(pseudorandom)。
可用在CBC、CTR等模式中,为加密提供随机性,保证语义安全(已知某段未知明文的密文不会泄漏该
明文的其余任何信息)。
ECB模式中,由于没有Ⅳ,导致在密钥不变的情况下,相同的明文必然会加密生成相同的密文,会泄漏明文的部分信息。

CBC模式中,引入了Ⅳ,使得每一次加密都会生成不同的密文数据,并且IV的作用会影响到所有数据的加密结果。
CTR模式由,IV又称为nonce,也关乎到所有数据的加密结果,nonce直接影响到了生成出来的流
密钥的安全性。
对于IV,一般有如下几个要求:
随机生成
不可重复使用
如果IV重复使用不更新,则会导致严重的后果!

import os
#系统内置的密码学安全随机数生成器
iv = os.urandom(16)

CTR模式中,IV/nonce和计数器的组合是用于产生流密钥的关键,如果每一次加密的IV/nonce都是一样的,那么会导致生成的流密钥也是完全一样的。
如果对手已知一段明密文,则可以通过对明文和密文异或,恢复出密钥流,并用这个密钥流对其他
未知密文解密,或者对任意的明文进行加密。这就是“IV复用”。
例题：

import os
from Crypto.Cipher import AES

FLAG = b"flag{test_flag_}"  
KEY = os.urandom(16)  
NONCE = os.urandom(12)  

def aes_ctr_encrypt(pt):
    aes = AES.new(KEY, AES.MODE_CTR, nonce=NONCE)
    ct = aes.encrypt(pt)
    return ct

def aes_ctr_decrypt(ct):
    aes = AES.new(KEY, AES.MODE_CTR, nonce=NONCE)
    pt = aes.decrypt(ct)
    return pt

# 加密预设的 FLAG 并输出
print(f"flag: {aes_ctr_encrypt(FLAG)}")  

# 循环接收用户输入进行加密
while True:
    user_input = bytes.fromhex(input("Input a hex string to encrypt: "))
    ct = aes_ctr_encrypt(user_input)
    print(f"Your ciphertext: {ct}")

从题目中我们可以获取以下信息（其中$P_{flag}$和$K$均未知 ）

$$P_{flag} \oplus K = C_{flag}$$

我们可以任意选取一段明文$P_{user}$发送给服务端，并得到$C_{user}$满足

$$P_{user} \oplus K = C_{user}$$

从中可以解出$K$

$$K = P_{user} \oplus C_{user}$$

从而可以求出$P_{flag}$

$$P_{flag} = K \oplus C_{flag} = P_{user} \oplus C_{user} \oplus C_{flag}$$
解题代码：

def xor(a,b):
	return bytes(x^y for x,y in zip(a,b)]

C_flag =b'\x12\x844\x13%p\xa2j>\x85hc1\x10\xb9\xac'
P_user = b"\x77"*16
C_user =b'\x03\x9f"\x03)s\xb0n=\xadyx\'\x00\x91\xa6'

K = xor(P_user, C_user
P_flag = xor(K, C_flag
print P_flag
# b'flag{test_flag_}

ECB模式剪贴

ECB模式中,明文分组与密文分组是一一对应的关系,相同的明文将会被加密成相同密文。
例子：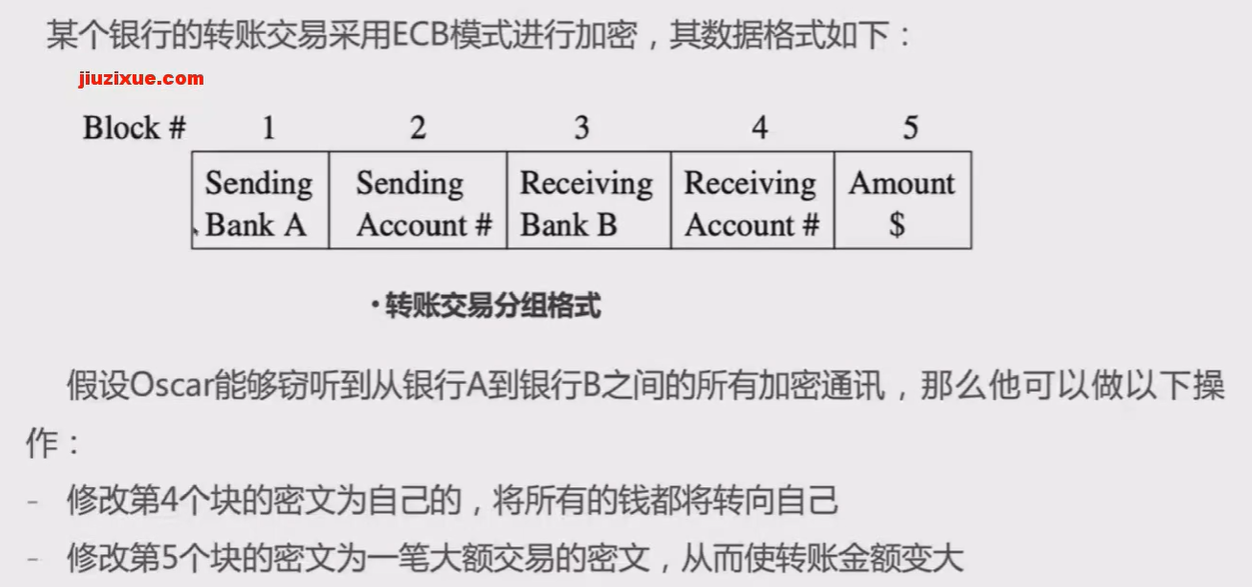
例子2：

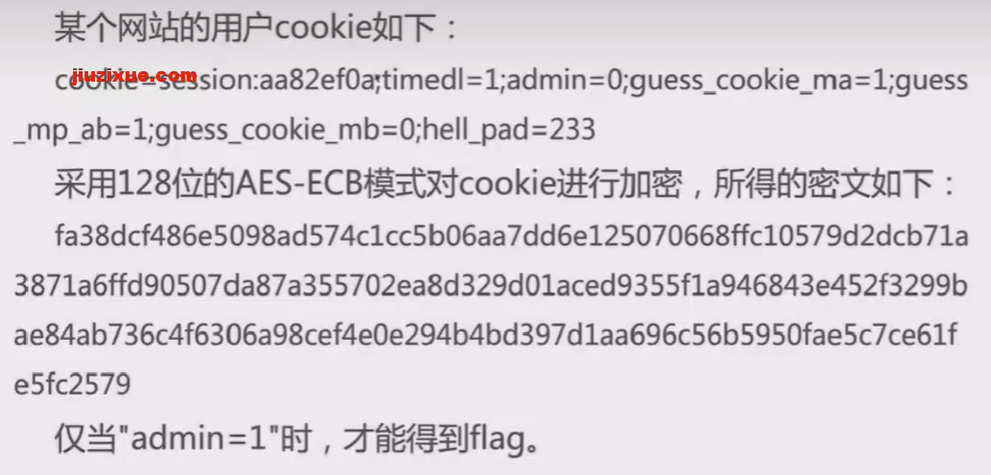
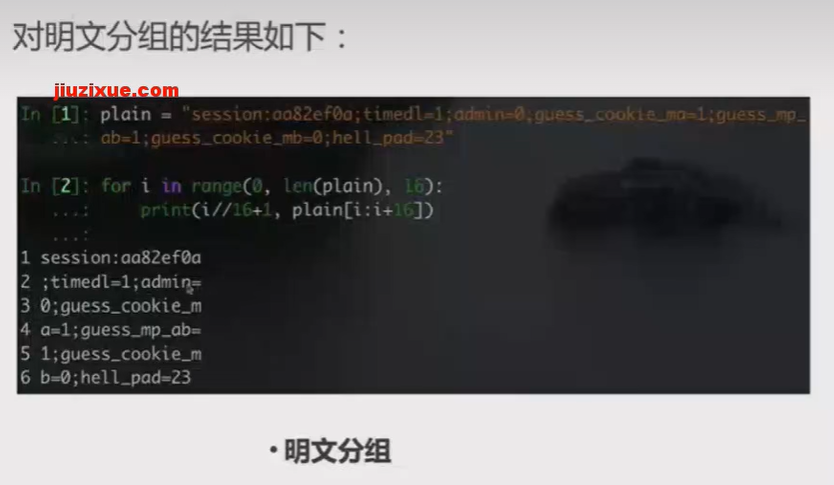
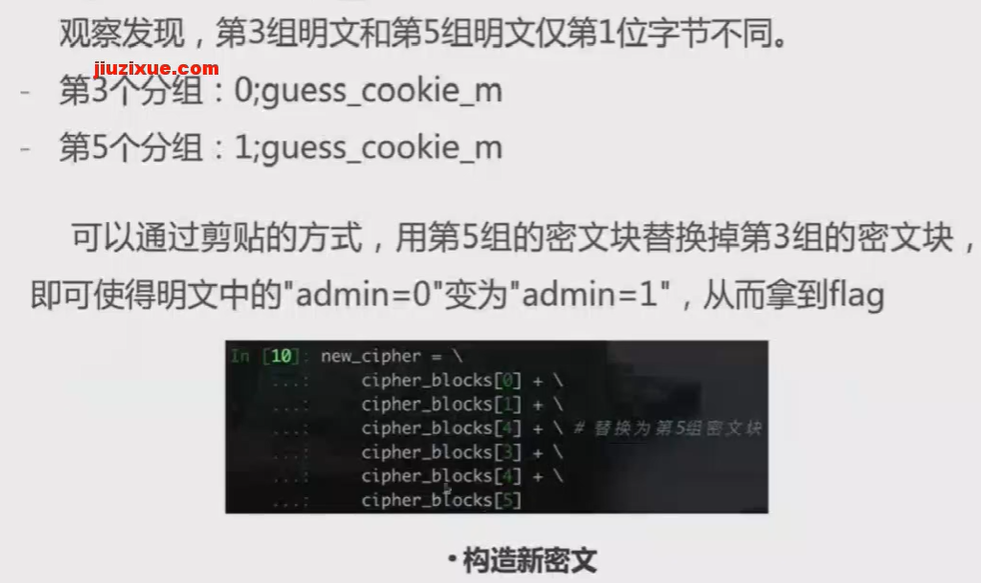
CBC模式字节翻转

CBC模式的解密过程可以由如下关系式来表示（其中nb是块的数量）： $$P_1 = Dec_k(C_1) \oplus IV$$ $$P_i = Dec_k(C_i) \oplus C_{i - 1}, \ 1 < i \leq nb,$$ - CBC模式加解密 从中可以看出，若修改某个密文块$C_{i - 1}$，则会影响到解密出来的下一个明文块$P_i$，即我们可以通过篡改密文来任意操纵明文。
假设对手想要控制某个块的明文,他可以通过修改前一块密文相应的字节来达到这个目的。若要修改
第3个明文块第i个字节的数值,则可以对第2个密文块第i个字节异或上相应的数值(但也会导致解密出来的第2块明文不可预测)。

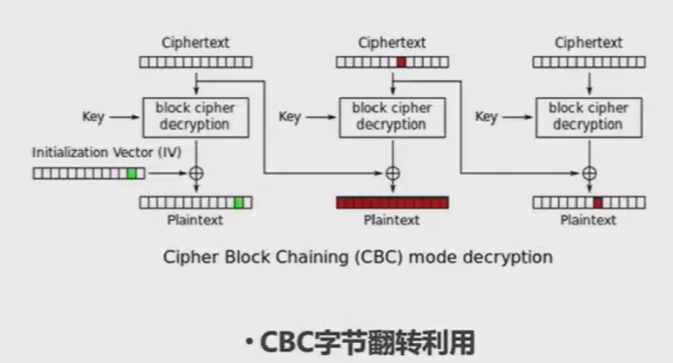
假设第3段的明文为admin=0;（块大小为8字节），第2段的密文为8563c9bdeac3f1b2，并想要通过字节翻转将解密第3段的明文修改为admin=1; 根据关系式 $$P_3 = Dec_k(C_3) \oplus C_2$$ $$P'3 = Dec_k(C_3) \oplus C'2$$ 可得只需
$$C'2 = P_3 \oplus P'3 \oplus C_2$$
在案例中，对于第7个字节位，有如下关系： $$P = 0x30$$ $$P' = 0x31$$ $$C = 0xf1$$ 可得只需 $$C' = 0x30 \oplus 0x31 \oplus 0xf1 = 0xf0$$ 因此只需将第2段密文修改为8563c9bdeac3f0b2，即可完成利用。
加密只能提供机密性,即对手无法从密文中得到任何和明文相关的信息,但是加密却无法保障密文不会
被任意篡改。
要想防御住剪贴利用和字节翻转利用,最关键的是要防止对手可以对密文的修改,即可以察觉到密文是
否被修改。
MAC(消息认证码)即为一种可以保护密文完整性的密码原语,在现实使用中,常常采用CBC+MAC的
方式来传输加密数据。

利用PKCS7

PKCS7是一种常用的填充方式,其具体的填充方式为:填充N个字节,且这N个填充字节的字节值均N。

例如,当块大小为16时,对"aaaabbbbcccc"进行填充。填充的结果为"aaaabbbbcccc\x04\x04\x04\x04"。

注意:即使最后一个块的长度为16,PKCS7填充方式仍然会对其进行填充,会在其后填充一块全为0x10的16字节块。

代码实现：

def pad(pt):
	pad_length = 16 - len(pt)%16
	pt += bytes([pad_length]) * pad_length
	return pt

def unpad(pt):
	pad_length = pt[-1]
	if not 1 ≤ pad_length ≤ 16:
		return None
	if pad(pt[ :- pad_length]) # pt:
		return None
	return pt[ :- pad_length]

服务器端进行AES-CBC解密的时候,会对解密的结果做解除填充(unpad)操作,如果解除填充
时校验到填充格式不合法,则会直接报错,通常会返回对应的错误消息"Padding Error!"。

def decrypt(cipher):
	# AES-CBC 解密
	decrypted_res = aes.decrypt(cipher
	# 解除填充
	plaintext = unpad(decrypted_res)
	if not plaintext: #填充格式错误,unpad函数返回None
		return "Padding Error!"
	# 继续执行
	# ...
	return "OK"

Padding Oracle
场景目标:对手获取到了一段密文,想要对其进行解密。
利用思路:可以通过字节翻转的手法来修改解密后的明文,并将其发送给服务端,若修改后的明文符合
填充格式,服务器返回OK,则对手可以从中获取到一些关于原始密文的一些信息。

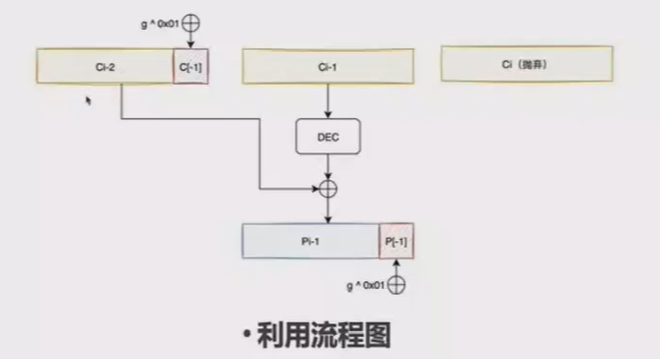
如何解密最后一个字节?,
我们要利用0x01这个合法的填充格式。假设g为最后一字节(共有256种可能性),对上一个密文块的最后一字节异或上g^{0x01,则解密后的最后一个明文块也会异或上g}0x01,若g正确,则最后一块格式为 ….... 0x01,服务器返回OK,否则服务器返回Padding Error。

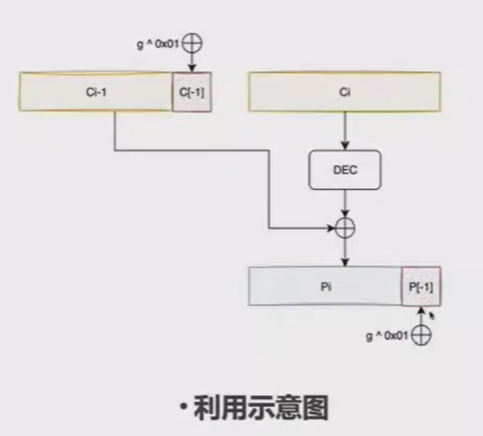
就是一直猜，猜测到合法为止
如何解密倒数第i个字节?
我们要利用0x0i这个合法的填充格式。
先通过已解出来倒数i-1个明文,通过字节翻转的方式将解密后的明文块后i-1修改为0xOi;然后继续使用解密倒数第1个字节的方式,尝试256种可能的g,直至服务器返回OK,说明g即为倒数第i个字节。

通过上述方法,可以解密出最后一个明文块的16个字节。
解密完之后,即可将最后16字节的密文抛弃,继续对倒数第二块密文块进行解密。依此方法,可以对所
有密文进行解密,恢复出整个明文信息。

利用代码：

# padding_oracle recovers the last 16 plaintext bytes of the given ciphertext
def padding_oracle(cipher):
    plaintext = b""
    for index in range(1, 17):
        print(f"[*] index: {index}")
        for byte in range(0, 256):
            bytes_xor = b"\x00"*(16-index)+bytes([byte]*index)+xor(plaintext,bytes([index]*(index-1)))
            new_cipher = cipher[:-32] + xor(cipher[-32:-16], bytes_xor) + cipher[-16:]

            if oracle(new_cipher) == "Padding Error!":
                print(f"[{byte:>3d}], Padding Error!")
            else:
                plaintext = bytes([byte]) + plaintext
                print(f"[{byte:>3d}] OK")
                print(f"plaintext: {plaintext}")
                break
    return plaintext