密码学习第1天——序列密码和分组密码

现代密码学

对称密码学

序列密码

OTP

序列密码(流密码)属于对称密码算法,加解密双方使用一串与明文长度相同的密钥流,与明文流组合(按位异或)来进行加解密。（中间的符号是异或）


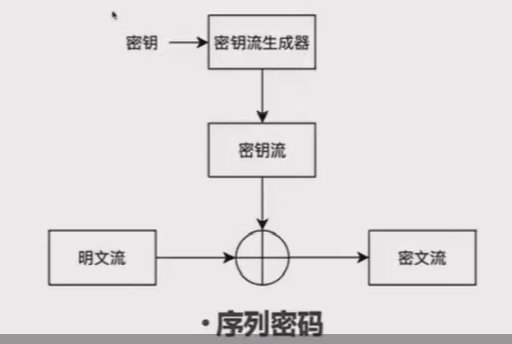
序列密码的安全性取决于密钥流的安全性,因此密钥流生成尤其关键。
通常使用伪随机数发生器(PRNG)来生成密钥流,对于密码学安全的伪随机数发生器,一般要求具有
以下特性:

• 所产生随机数的周期足够大
• 种子的长度足够大,以抵抗暴力枚举攻击
• 种子中1bit的改变会引起序列的极大改变(雪崩效应)
• 产生的密钥流能抵抗统计学分析
• 获取少量已知的密钥流时,无法还原整个发生器的状态
  一次性密码本(one-time pad,OTP)是一种“无法破解”的密码技术。在理论上,此种密码具有“完善保密性”,安全性已由香农证明。
  一次性密码本通过真随机数发生器(TRNG)（(微观层面)基于热力学噪声、光电效应等在理论上完全不可预测的物理过程,硬件通过重复采样这些随机的信号,并放大到宏观层面,从而生成随机数。(宏观层面)基于掷硬币、骰子、轮盘等,生成随机数。）生成的密钥流来进行加解密,生成的密钥流长度与明文
  流长度一致,且密钥流只能使用一次。
  
  但在来际操作中,一次性密码本存在以下问题:
• 密钥流必须保证真正的随机
• 密钥流至少要与明文长度等长
• 密钥流只能使用一次
  
  技巧：一个小写的英文字母(例如b=0x62),异或上空格(0x20),则会变成一个大写的英文字母(B=0x42)。反之亦然。
  对于p1 xor p2=c1 xor c2,如果其中某个位置的异或结果p1[i] xor p2[i]是一个大小写的字母,那
  么有很大概率另外一个明文字符就是空格(0x20),通过多个样本进行统计,可以近乎100%的概率确
  定此处是否为空格,进而能够获取到这个位置的密钥字节。
  剩余部分,只需再结合人工分析,即可恢复出所有的密钥,进而完成解密。
  利用：Many-Time-Pad 攻击

　　作为 MTP 攻击的范例，来看下面一道例题：

BUUCTF: [AFCTF2018]你听过一次一密么？

(原题有bug, 笔者有少量改动)
25030206463d3d393131555f7f1d061d4052111a19544e2e5d54
0f020606150f203f307f5c0a7f24070747130e16545000035d54
1203075429152a7020365c167f390f1013170b1006481e13144e
0f4610170e1e2235787f7853372c0f065752111b15454e0e0901
081543000e1e6f3f3a3348533a270d064a02111a1b5f4e0a1855
0909075412132e247436425332281a1c561f04071d520f0b1158
4116111b101e2170203011113a69001b47520601155205021901
041006064612297020375453342c17545a01451811411a470e44
021311114a5b0335207f7c167f22001b44520c15544801125d40
06140611460c26243c7f5c167f3d015446010053005907145d44
0f05110d160f263f3a7f4210372c03111313090415481d49530f

　　上述的每一个字符串 ，都是某个 key 异或上明文  得到的。我们的目标是获取这个 key. 已知明文是英文句子。

　　回顾异或运算的性质：结合律、交换律、逆元为其自身。这是非常好的性质，然而也为攻击者提供了方便。因为：

　　这表明，两个密文的异或，就等于对应明文的异或。这是很危险的性质，高明的攻击者可以通过频率分析，来破译这些密文。我们来看字符串  异或上其他密文会得到什么东西。以下只保留了英文字符，其余字符以 “.” 代替。

....S....N.U.....A..M.N...
...Ro..I...I....SE....P.I.
.E..H...IN..H...........TU
..A.H.R.....E....P......E.
...RT...E...M....M....A.L.
d...V..I..DNEt........K.DU
.......I....K..I.ST...TiS.
.....f...N.I........M.O...
.........N.I...I.S.I..I...
....P....N.OH...SA....Sg..

　　可以观察到，有些列上有大量的英文字符，有些列一个英文字符都没有。这是偶然现象吗？

ascii表

　　ascii 码表在 Linux 下可以通过 man ascii 指令查看。它的性质有：

• 0x20 是空格。 低于 0x20 的，全部是起特殊用途的字符； 0x20~0x7E 的，是可打印字符。
• 0x30~0x39 是数字 0,1,2...9。
• 0x41~0x5A 是大写字母 A-Z； 0x61~0x7A 是小写字母 a-z.

　　我们可以注意到一个至关重要的规律：小写字母 xor 空格，会得到对应的大写字母；大写字母 xor 空格，会得到小写字母！所以，如果  得到一个英文字母，那么  中的某一个有很大概率是空格。再来回头看上面  xor 其他密文——也就等于  xor 其他明文的表，如果第  列存在大量的英文字母，我们可以猜测  是一个空格。那一列英文字母越多，把握越大。

　　知道  的  位是空格有什么用呢？别忘了异或运算下， 的逆元是其自身。所以

　　于是，只要知道某个字符串的某一位是空格，我们就可以恢复出所有明文在这一列的值。

　　攻击过程显而易见：对于每一条密文，拿去异或其他所有密文。然后去数每一列有多少个英文字符，作为“在这一位是空格”的评分。

　　上面的事情做完时候，依据评分从大到小排序，依次利用 “某个明文的某一位是空格” 这种信息恢复出所有明文的那一列。如果产生冲突，则舍弃掉评分小的。不难写出代码：

import Crypto.Util.strxor as xo
import libnum, codecs, numpy as np

def isChr(x):
    if ord('a') <= x and x <= ord('z'): return True
    if ord('A') <= x and x <= ord('Z'): return True
    return False

def infer(index, pos):
    if msg[index, pos] != 0:
        return
    msg[index, pos] = ord(' ')
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(' ')

dat = []

def getSpace():
    for index, x in enumerate(c):
        res = [xo.strxor(x, y) for y in c if x!=y]
        f = lambda pos: len(list(filter(isChr, [s[pos] for s in res])))
        cnt = [f(pos) for pos in range(len(x))]
        for pos in range(len(x)):
            dat.append((f(pos), index, pos))

c = [codecs.decode(x.strip().encode(), 'hex') for x in open('Problem.txt', 'r').readlines()]

msg = np.zeros([len(c), len(c[0])], dtype=int)

getSpace()

dat = sorted(dat)[::-1]
for w, index, pos in dat:
    infer(index, pos)

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

　　执行代码，得到的结果是：

Dear Friend, T%is tim< I u
nderstood my m$stake 8nd u
sed One time p,d encr ptio
n scheme, I he,rd tha- it 
is the only en.ryptio7 met
hod that is ma9hemati:ally
 proven to be #ot cra:ked 
ever if the ke4 is ke)t se
cure, Let Me k#ow if  ou a
gree with me t" use t1is e
ncryption sche e alwa s...

　　显然这不是最终结果，我们得修正几项。把 "k#now" 修复成 "know"，把 "alwa s" 修复成 "always". 代码如下：

def know(index, pos, ch):
    msg[index, pos] = ord(ch)
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(ch)

know(10, 21, 'y')
know(8, 14, 'n')

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

　　结果得到：

Dear Friend, This time I u
nderstood my mistake and u
sed One time pad encryptio
n scheme, I heard that it 
is the only encryption met
hod that is mathematically
 proven to be not cracked 
ever if the key is kept se
cure, Let Me know if you a
gree with me to use this e
ncryption scheme always...

　　我们成功恢复了明文！那么 key 也很好取得了：把  异或上  即可。

key = xo.strxor(c[0], ''.join([chr(c) for c in msg[0]]).encode())
print(key)

# b'afctf{OPT_1s_Int3rest1ng}!'

　　Many-Time-Pad 是不安全的。我们这一次的攻击，条件稍微有点苛刻：明文必须是英文句子、截获到的密文必须足够多。但是只要攻击者有足够的耐心进行词频分析、监听大量密文，还是能够发起极具威胁性的攻击。如果铁了心要用直接xor来加密信息，应当采用一次一密(One-Time-Pad).

　　完整的解题脚本如下：

import Crypto.Util.strxor as xo
import libnum, codecs, numpy as np

def isChr(x):
    if ord('a') <= x and x <= ord('z'): return True
    if ord('A') <= x and x <= ord('Z'): return True
    return False


def infer(index, pos):
    if msg[index, pos] != 0:
        return
    msg[index, pos] = ord(' ')
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(' ')

def know(index, pos, ch):
    msg[index, pos] = ord(ch)
    for x in range(len(c)):
        if x != index:
            msg[x][pos] = xo.strxor(c[x], c[index])[pos] ^ ord(ch)


dat = []

def getSpace():
    for index, x in enumerate(c):
        res = [xo.strxor(x, y) for y in c if x!=y]
        f = lambda pos: len(list(filter(isChr, [s[pos] for s in res])))
        cnt = [f(pos) for pos in range(len(x))]
        for pos in range(len(x)):
            dat.append((f(pos), index, pos))

c = [codecs.decode(x.strip().encode(), 'hex') for x in open('Problem.txt', 'r').readlines()]

msg = np.zeros([len(c), len(c[0])], dtype=int)

getSpace()

dat = sorted(dat)[::-1]
for w, index, pos in dat:
    infer(index, pos)

know(10, 21, 'y')
know(8, 14, 'n')

print('\n'.join([''.join([chr(c) for c in x]) for x in msg]))

key = xo.strxor(c[0], ''.join([chr(c) for c in msg[0]]).encode())
print(key)

BUUCTF: [De1CTF2019]xorz

【附件】

　　给的是 , 其中  已知，故实际上我们拿到了 . 在这里  是有周期的，且周期不超过38。如果知道了  的周期，那么用 Many-Time-Pad 就可以成功攻击。由于 len(key) 并不大，从大到小枚举 len(key)，肉眼判断是否为flag即可。最后发现 len(key)=30 是满足要求的。

from itertools import cycle
import codecs, numpy as np
import Crypto.Util.strxor as xo

salt="WeAreDe1taTeam"
si=cycle(salt)


c = codecs.decode('49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c', 'hex')


a = [r ^ ord(next(si)) for r in c]  # a[i] = m[i] ^ k[i]

def div(sz):
    ret = [''.join([chr(ch) for ch in a[i*sz : (i+1)*sz]]).encode() for i in range(len(a)//sz)]
    # if len(a) % sz != 0:
        # ret.append(a[len(a)//sz*sz:])
    print('\n'.join(map(lambda x:codecs.encode(x, 'hex').decode(), ret)))
    return ret

sz = 30
t = div(sz)

➜  workspace python3 work.py > out.txt
➜  workspace python3 mtp.py
In faith I do not love thee wi
th mine eyes,For they in thee
a thousand errors note;But `ti
s my heart that loves what the
y despise,Who in despite of vi
ew is pleased to dote.Nor are
mine ears with thy tongue`s tu
ne delighted;Nor tender feelin
g to base touches prone,Nor ta
ste, nor smell, desire to be i
nvitedTo any sensual feast wit
h thee alone.But my five wits,
 nor my five senses canDissuad
e one foolish heart from servi
ng thee,Who leaves unswayed th
e likeness of a man,Thy proud
heart`s slave and vassal wretc
h to be.Only my plague thus fa
r I count my gain,That she tha
t makes me sin awards me pain.
b'W3lc0m3tOjo1nu55un1ojOt3m0cl3W'

LCG（线性同余生成器）

模运算：两个整 数a,b,若它们除以模数m所得到的余数相同,则称a,b对于模m同余,记作a≡b(mod m)，例如11 ≡ 2 (mod 9)
事实上,所有除以9余数为2的整数,都与2同余,为一个等价类:[2]={ …. ,2-2·9,2-9,2,2+9,2+2·9, ….. }
性质：
若两个整数a,b对于模m同余,则对于整数c有:a±c≡b±c(modm)，axc≡bxc (modm)
11±3≡2±3(mod9)
11x3 ≡ 2x3 ≡ 6 (mod 9)
问题：
3÷2≡? (mod 9)
除法可以用乘法来定义,找到c满足2xc≡1(mod9)
c≡ 5 (mod 9)
代入2×5≡1(mod 9)
3÷2×1≡?(mod 9)
3÷2×(2×5)≡?(mod 9)
3x5 ≡ 15 ≡ 6 (mod 9)
对于非零整数a,若a与模数m互质,则存在a的逆元a-1满足
a^-1*a≡1(mod m)
例如
2^-1 ≡5 (mod 9)
模运算中,除以某个数,等价于乘上这个数的逆元
b÷2 (mod9) ⇒bx2^-1(mod9)⇒b×5 (mod 9)
注意,并不是所有情况都存在逆元!例如2对于模10就不存在逆元。
如何计算模逆元?
暴力穷举法、辗转相除法、欧拉定理法
安装pyCrypto库:python3-m pip install pycryptodome
inverse(2,9) -> 5
2*5%9=1
线性同余生成器是一种生成伪随机数的算法

• 在已知常数A,B,M的前提下,若能捕获到线性同余生成器的一个输出,则可以恢复出状态,并通过递
  推式预测之后产生的所有随机数。
  Xn+1≡Axn+B(mod M)
  Xn≡(xn+1-B)A^-1(mod M)
  对于C语言标准库中的rand()函数,即为
  Xn =(xn+1-12345)×1857678181(mod 2147483648)
• 在已知常数M但未知A,B的条件下,若能捕获到线性同余生成器的连续两个输出,则可以建立一个
  关于A,B的同余方程:
  X(i+1) ≡Axi+B(mod M)
  获取2个同余方程,可以建立一个方程组,解方程组即可得到A,B:
  x(i+1) ≡Axi+B (mod M)
  x(j+1)≡Axj+B (mod M)
  
  

LFSR（线性反馈移位寄存器）

给定前一状态的输出，将该输出的线性函数作为输入的移位寄存器

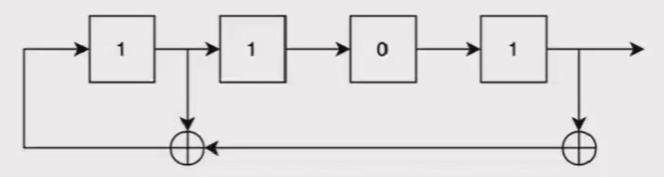
移位寄存器是指:若干个寄存器排成一行,每个寄存器中都存储着一个二进制数(0或1)。移位寄存器每次把最右端(末端)的数字输出,然后整体向右移一位。

只能输出内部状态
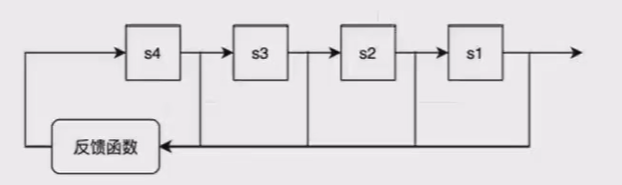
反馈移位寄存器:在移位寄存器向右移位一位后,左边会空出一位,此时可以采用一个反馈函数,将
寄存器中已有的某些状态作为反馈函数的输入,经过反馈函数运算,并将运算结果填充到移位寄存器的
最左端,这样移位寄存器就有源源不断的输入。

线性反馈移位寄存器:反馈函数是线性函数(只进行简单线性运算的函数)的反馈移位寄存器。
线性运算通常是简单地对某些位组合异或,并将异或的结果填充到LFSR的最左端。

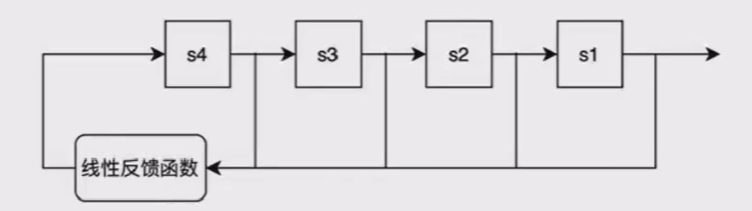
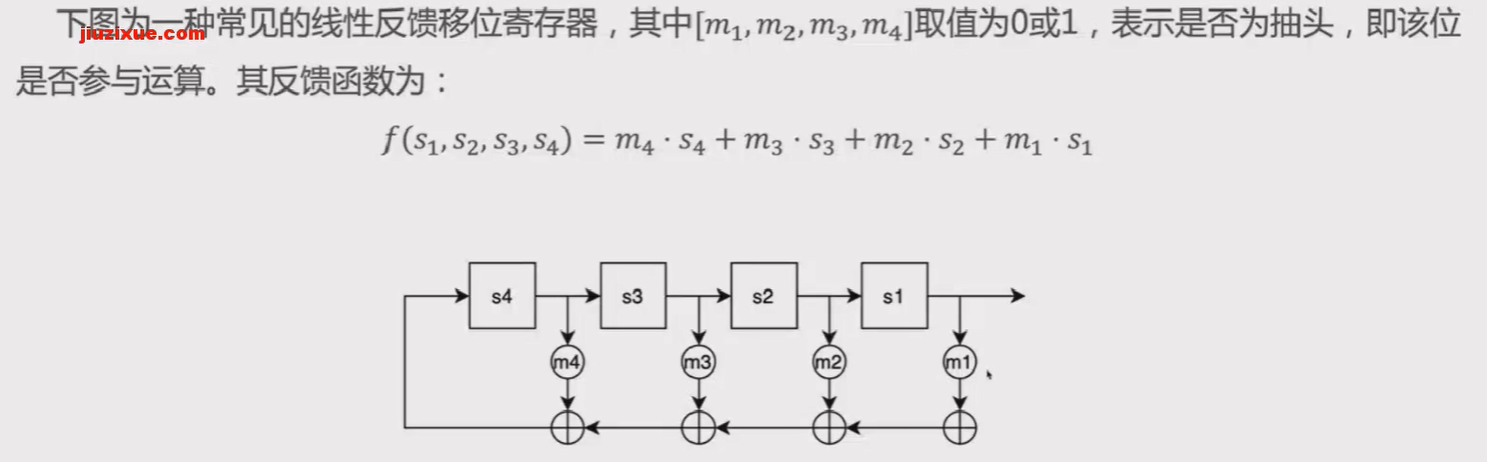
示例：


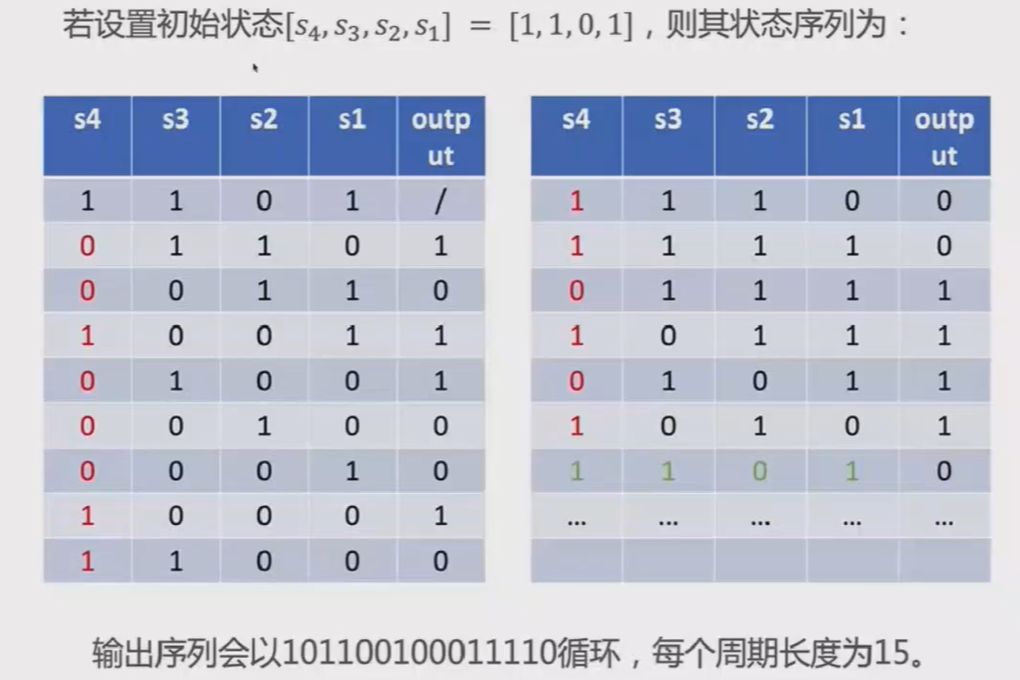
我们通常把LFSR中的寄存器个数称为LFSR的级数。
一个n级的LFSR最多可以存储2”-1种状态。(LFSR中的所有状态全为0时,其反馈函数的输出也永远是0,输出序列将一直是0,这种情况是不可用的)
例如,一个3级的LFSR最多可以遍历001,010,011,100,101,110,111共7种状态。
由于LFSR一个n级的LFSR最多可以存储2”-1种状态,因此当LFSR移位到一定程度时,一定会出现重复的状态。而相同状态生成的反馈函数结果总是相同的,因此LFSR会陷入一种循环,即LFSR存在周期。
LFSR的周期与其反馈函数是有密切关系的,反馈函数决定了LFSR的循环序列。

若LFSR中的值为[S1,S2,…,Sn],则第n+1位的值可以表示为:
Sn+1=mn·Sn+…+m2·S2+m1S1

此递推关系可以对应一个特征多项式:
f(x)=mn·x^n+…+m2·x2+m1·x+1

例如对于之前的例子中的4级LFSR,其特征多项式为:
f(x) = x^4+x + 1
为了能够产生足够安全的密钥,通常要求LFSR的周期要足够大。
一个n级的LFSR最多可以存储2n-1种状态,其最大周期也为2n-1。
m序列:周期为2n-1的LFSR所生成的序列。

Q:什么时候能产生最大周期?
A:当特征多项式为本原多项式时

在已知LFSR的反馈函数的前提下,如果对手已知连续n位明文和n位密文,则可以计算得出n位密钥,即为LFSR的一个状态。此时根据反馈函数,即可计算出LFSR的全部输出,即全部密钥流,从而破解LFSR。

在未知LFSR的反馈函数的前提下,对手依然通过获取连续2n位明文和2n位密文,计算得出2n位密钥[k1,k2,…,kn,…,k2n]。这2n位密钥中,蕴含着LFSR的n+1种状态,分别为
[k1, k2, ··. , kn], [k2, k3, ... ,kn+1], ··· , [kn+1, kn+2, ··· ,k2n]

这些状态之间存在着互相递推关系,例如kn+1就是由[k1,k2,…,kn]计算出来的。以此类推,kn+i就是由[ki,ki+1,…,ki+n-1]计算得出,从而可以得出n个线性方程,构成一个线性方程组。

其中c1为每个抽头的取值,n个方程,n个未知数,可以求出每一个抽头的唯一解,得到反馈函
数,从而攻破LFSR。

实现代码：

n = ...
k2n = [ ... ]

M = matrix(GF(2), n, n)
for i in range(n):
	for j in range(n):
		M[i,j] = k2n[i+j]

Y = vector (GF(2), n)
for i in range(n):
	Y[i] = k2n[n+i]

C = M.solve_right(Y)
print(C)

分组密码

DES

分组密码(又被称为块密码)与序列密码不同的地方在于,分组密码不是仅对一个比特位进行加密,而是对多个位组成的一个块(大小通常为8字节或16字节)进行整体的加密运算。

现代密码学中设计分组密码算法一般需要遵循如下两个原则:

• 混淆(confusion):模糊明文和密文之间的关系,常使用替换(substitution)的方式来实现
• 扩散(Diffusion):将明文中一位的影响扩散到多个密文,常使用置换(Permutation)的方式来实现
  
  现代密码学中通常采用多轮运算，每轮运算中都有若干层混淆变换和扩散变换
  DES（数据加密标准）
  DES是一种典型的分组密码,其块长度为64位,密钥长度为64位(其中有8位为校验位,实际有效的只有56位)。明文按照64位分组,经过加密运算,输出对应的64位密文。
  
  DES中对明文进行16轮的加密运算,每一轮运算都会有一个相应的子密钥参与(子密钥通过密钥扩展算法计算得出)。
  此外,在开头和结尾处还分别有初始置换和最终置换的操作,用于方便硬件电路的算法实现。
  
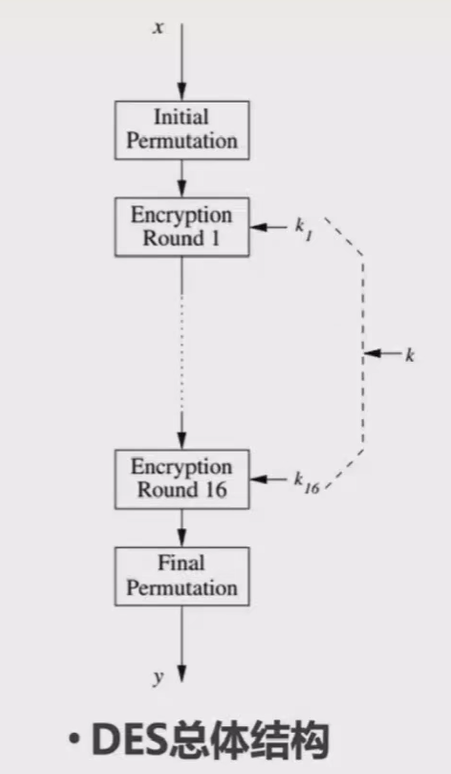
  初始置换和最终置换就是简单地根据置换表,来把长度为64比特的block中每一个位置进行变换。
  

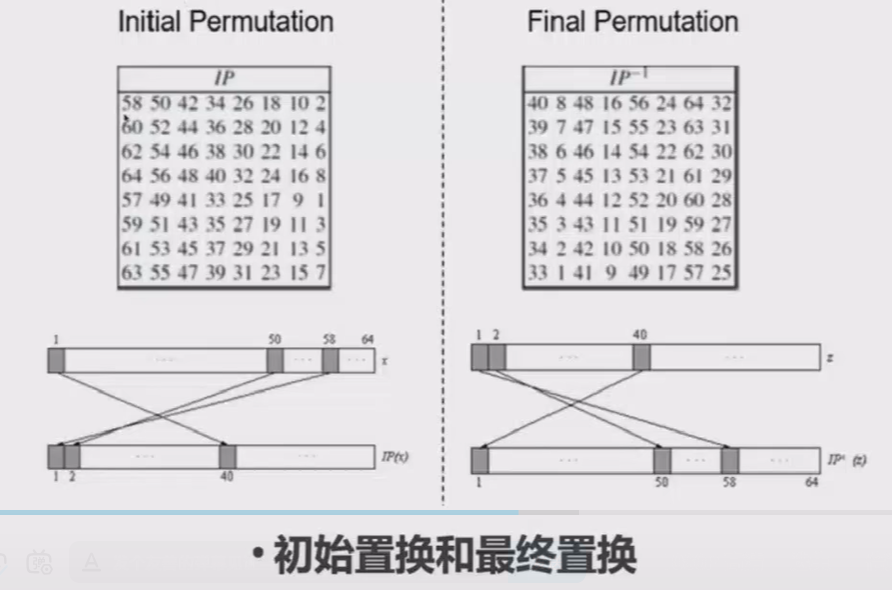
IP_table = [
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16,8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7
] # ok

FP_table = [
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25
] # ok

def IP(block):
	result = []
	for i in range(len(IP_table)):
		result.append(block[IP_table[i]-1])
	return result

def FP(block):
	result = []
	for i in range(len(FP_table)):
		result.append(block[FP_table[i]-1])
	return result

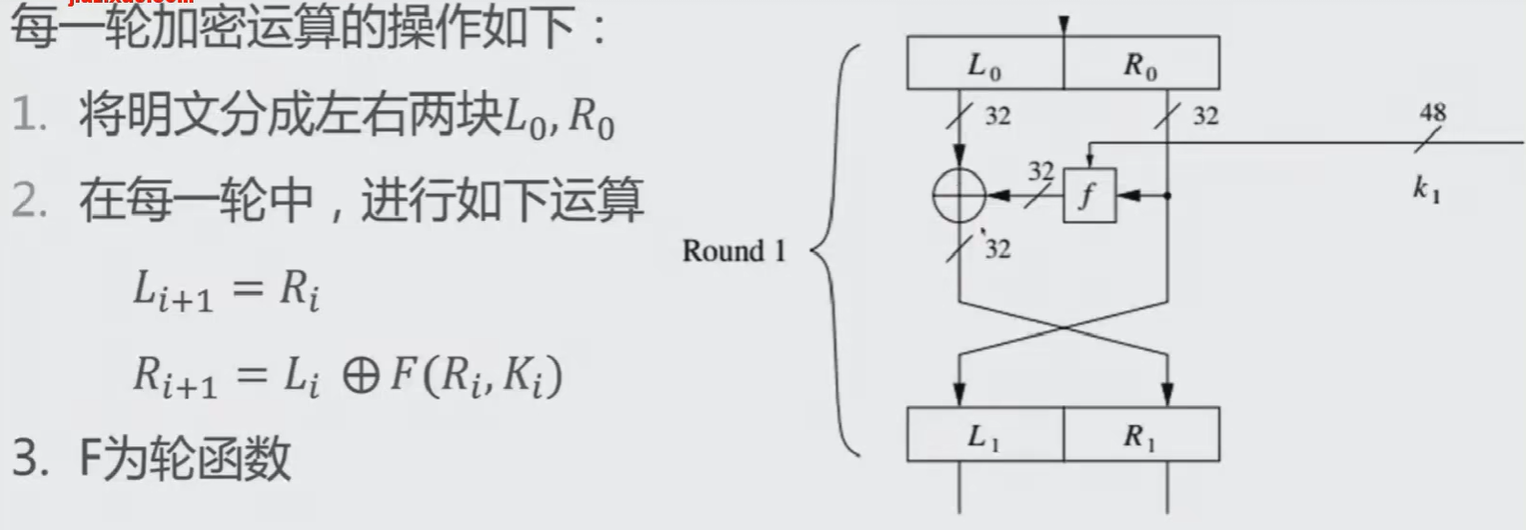
总体结构：

# Initial permutation
m = IP(m)
# divide the block into two 32-bit halves
Li, Ri = m[:32], m[32:]
# 16 rounds
for i in range(16):
	Li, Ri = Ri, BlockXor(Li, Feistel(Ri, subkey[i]))
# merge the two divided half block which is 32-bit into one 64-bit block
m = Ri + Li # There is a need to change order of the final two halves
# Final permutation
m = FP(m)

轮函数的具体运算如下:

1. 先通过Expansion将32比特输入扩展为48
   比特
2. 再与48比特的子密钥混合作异或运算
3. 然后48比特分别分为8组,每组6比特,经,过S盒替换,输出8组4比特,即32比特
4. 最后对这32比特进行移位置换P
   
   密钥扩展的具体运算如下:

ㅤ

1. 先通过PC-1置换去除64比特密钥中的校验位
2. 将56比特的密钥分成左右28比特两半
3. 连续16轮运算,每一轮分别先对左右两半循环移位,再经过PC-2置换生成一个48比特的子密钥
4. 最终得到16组48比特的字密钥,用于加解密

subkey = []
if len(bkey) == 64:
	# PC-1
	bkey = PC_1(bkey)
elif len(bkey) # 56:
	raise ValueError("key must be 56-bit or 64-bit in length")
# divide the block into two halves
Ci, Di = bkey[: 28], bkey[28:]
for i in range(16):
	# Left Rotation
	Ci, Di = LR(Ci, Di, i)
	# PC-2
	subkey.append(PC_2(Ci + Di))
return subkey # ok

调用crypto库：

In [1]: from Crypto.Cipher import DES

In [2]: key = b"01234567"

In [3]: des = DES.new(key, DES.MODE_ECB)

In [4]: msg = b"deadbeaf"

In [5]: cipher = des.encrypt(msg)

In [6]: print(cipher)
b'\x88\xbdV\xd3Y\x91\xd2t'

In [7]: des.decrypt(cipher)
b'deadbeaf'

AES

AES算法的块大小为128位,密钥长度可为128/192/256位,在加密过程中分别有相应的轮数,对应着不同的安全等级。

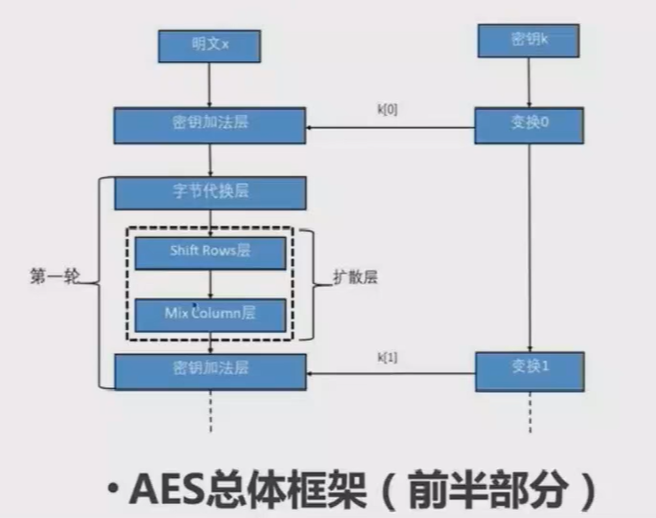
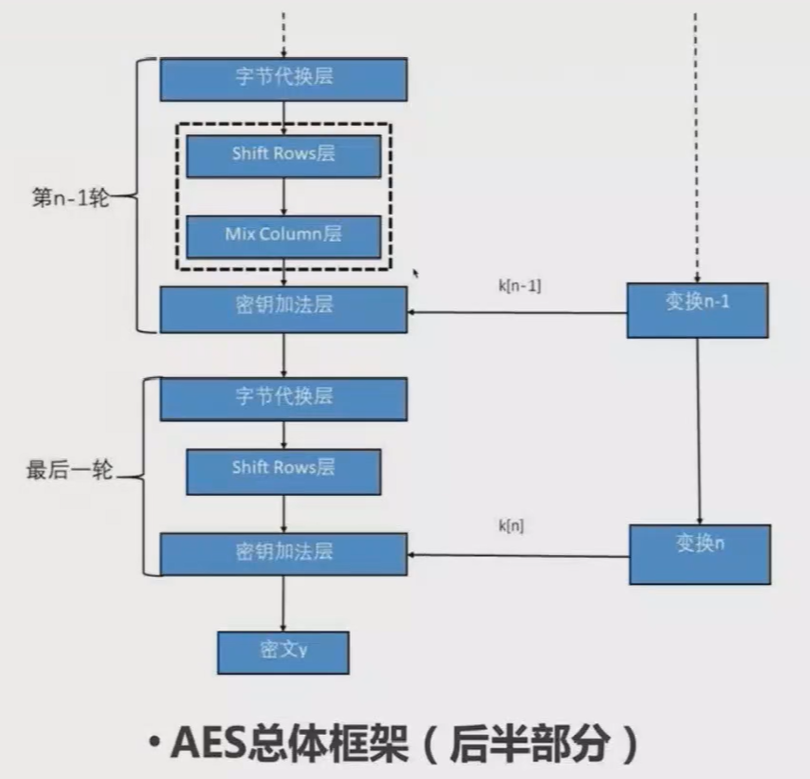
AES算法不同于DES,并没有采用Feistel结构。DES每一轮都是对64/2=32位的数据进行加密,而AES每一轮直接对整个128位进行加密,AES中使用“算法层”来对128位数据进行操作:


AES的代码实现

# start
r = 0
k_sch = self.subkeys[0] + self.subkeys[1] + self.subkeys[2] + self.subkeys[3]

state = list(msg)
AES.add_round_key(state, k_sch)

# round 1 ~ `rounds`-1
for r in range(1, self.rounds):
    AES.sub_bytes(state)
    AES.shift_rows(state)
    AES.mix_columns(state)
    k_sch = self.subkeys[4*r] + self.subkeys[4*r+1] + self.subkeys[4*r+2] + self.subkeys[4*r+3]
    AES.add_round_key(state, k_sch)

# the last round
r = self.rounds
AES.sub_bytes(state)
AES.shift_rows(state)
k_sch = self.subkeys[-4] + self.subkeys[-3] + self.subkeys[-2] + self.subkeys[-1]
AES.add_round_key(state, k_sch)

# convert `list` state to `bytes` output
output = bytes(state)
return output

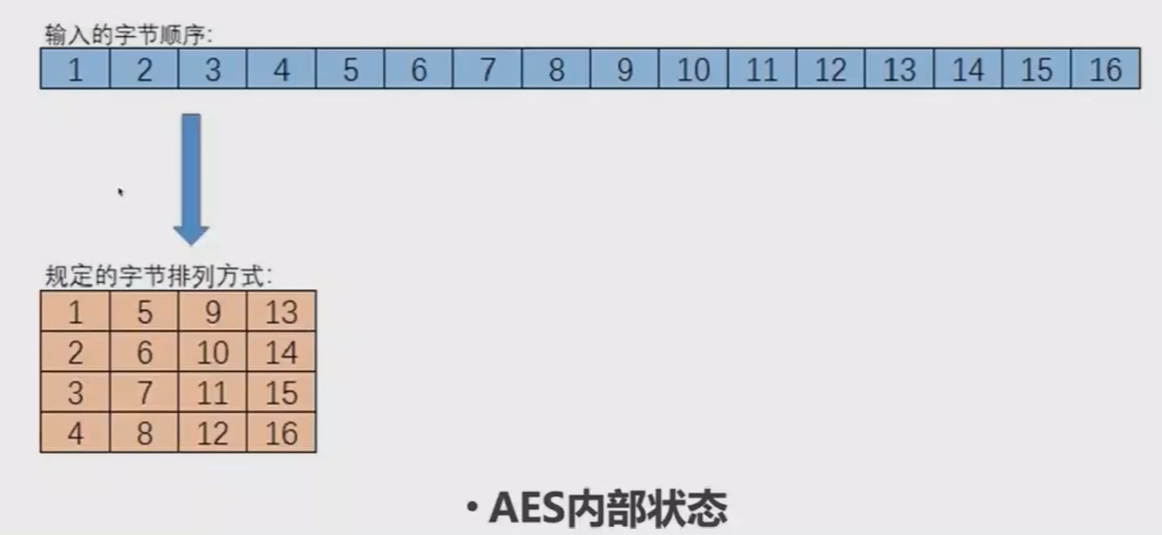
AES的内部状态是由4*4的字节矩阵来表示的。输入的16字节会按照如下的排列方式转换为字节矩阵,然后进行运算,最后再转换回。

密钥加法层(Key Addition Layer):输入16字节的明文和子密钥,对这两个输入逐字节异或,并将异或结果输出。

字节代换层(Byte Substitution Layer):让输入的每一个字节,通过S-Box代还(映射)到另外一个字节,此处的S-Box是可以根据某种方法计算出来的,也可以直接使用计算好的S-Box进行代换。


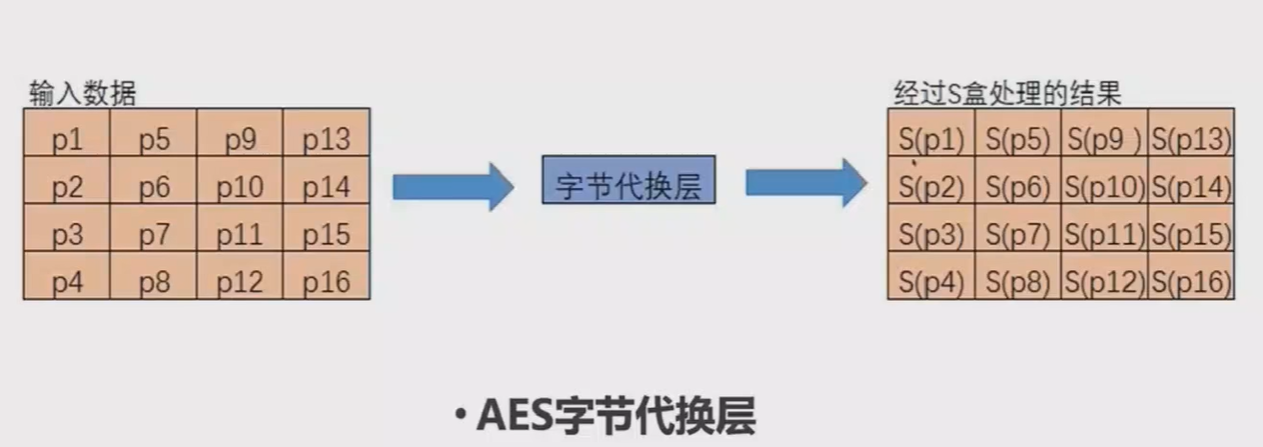
行移位层(Shift Rows Layer):对于4*4的字节矩阵,在做行移位时,第一行保持不变,第二行往左移动一格,第三行往左移动两格,第四行往左移动三格。

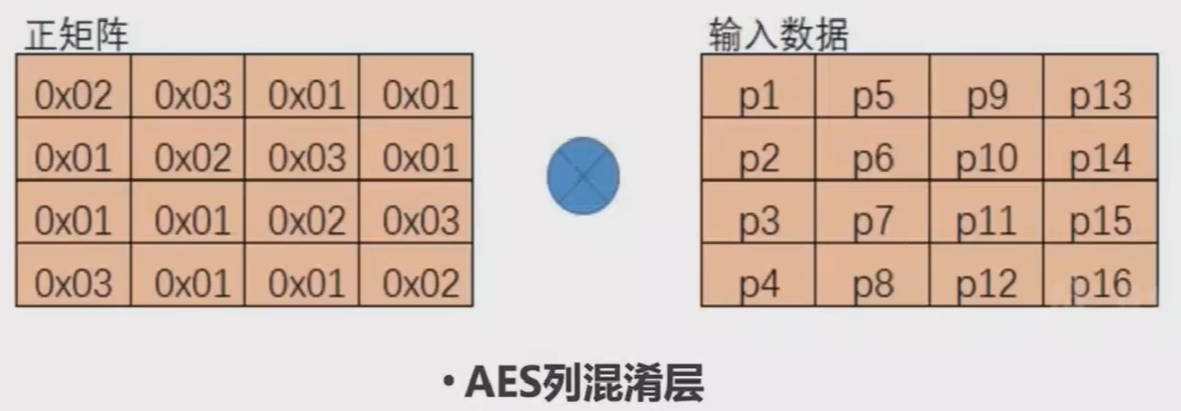
列混淆层(MixColumn Layer):将整个字节矩阵乘上一个列混淆矩阵(有限域上的矩阵运算)。行移位和列混淆操作是AES的混淆层,目的是为了将单个字节上的变换扩散到整个状态。

行移位层和列混淆层代码实现：

@staticmethod
def shift_rows(s):
    s = list(s[0::5] + s[4::5] + s[3:4:5] + s[8::5] + s[2:8:5] + s[12::5] + s[1:12:5])

@staticmethod
def mix_columns(s):
    # ref: https://github.com/bozhu/AES-Python/blob/master/aes.py
    def xtime(a):
        return (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)

    for i in range(4):
        t = s[4*i] ^ s[4*i+1] ^ s[4*i+2] ^ s[4*i+3]
        u = s[4*i]
        s[4*i] ^= t ^ xtime(s[4*i] ^ s[4*i+1])
        s[4*i+1] ^= t ^ xtime(s[4*i+1] ^ s[4*i+2])
        s[4*i+2] ^= t ^ xtime(s[4*i+2] ^ s[4*i+3])
        s[4*i+3] ^= t ^ xtime(s[4*i+3] ^ u)

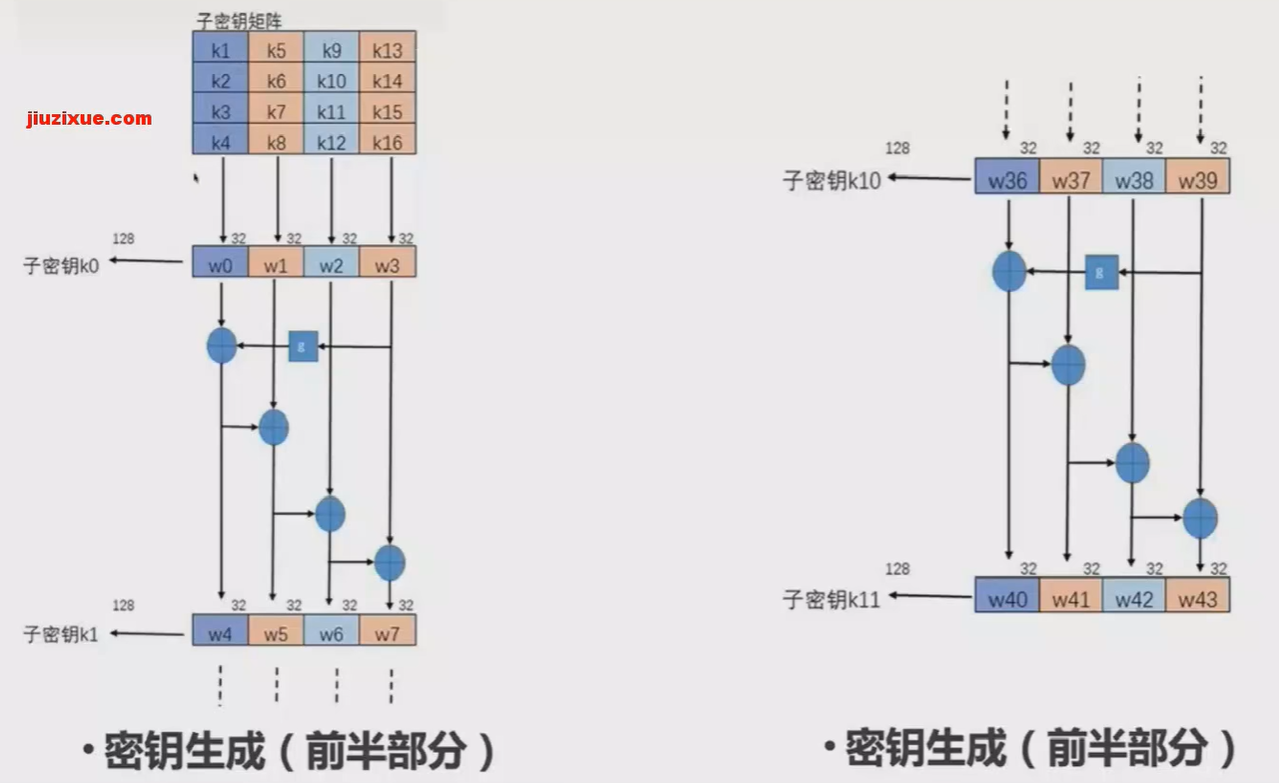
标准128位的AES密钥,对应共有11组子密钥,分别在一开始和每一轮(共10轮)中参与轮密钥加法层的运算。
子密钥的生成是以列为单位的,一列是4字节,32比特,四列构成一组子密钥。子密钥由专门的密钥扩展算法计算得出,存储在w[0],w[1], ….. ,W[43]的子密钥数组中。

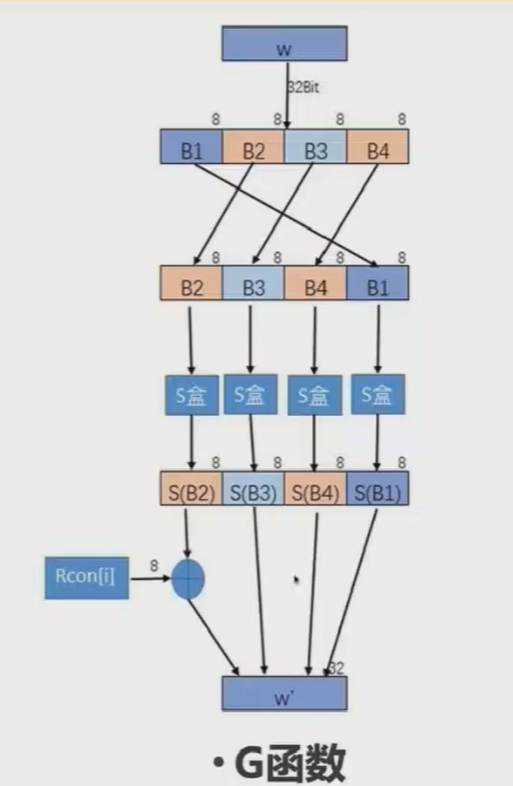
G函数进行了如下操作:

• 将输入的4个字节进行换位
• 逐字节经过S盒进行代换
• 用第一个字节和轮系数进行异或运算

G函数的目的有两个:

• 增加密钥扩展的非线性
• 消除AES中的对称性
  
  密钥扩展代码实现：

@staticmethod
def key_expansion(k, r):
    # fips-197 Figure 11
    k = list(k)  # in case k is bytes
    Nk = len(k) // 4
    subkeys = [k[i:i + 4] for i in range(0, 4 * Nk, 4)]

    i = Nk
    while i < 4 * (r + 1):
        t = subkeys[i - 1]
        if i % Nk == 0:
            tt = AES.sub_word(AES.rot_word(t))
            t = [tt[0] ^ AES.Rcon[i // Nk]] + tt[1:]
        elif Nk > 6 and i % Nk == 4:
            t = AES.sub_word(t)
        subkeys.append(AES.word_xor(subkeys[i - Nk], t))
        i += 1
    return subkeys

用python的aes库

from Crypto.Cipher import AES

# 密钥（需为 16、24 或 32 字节，此处 16 字节示例）
key = b"0123456789abcdef"  
# 创建 AES 加密对象，使用 ECB 模式
aes = AES.new(key, mode=AES.MODE_ECB)  
# 明文（需为 16 字节倍数，此处 16 字节示例）
plaintext = b"deadbeafcabebabe"  

# 加密
ciphertext = aes.encrypt(plaintext)  
print("加密结果:", ciphertext)

# 解密
decrypted_text = aes.decrypt(ciphertext)  
print("解密结果:", decrypted_text)

例题1

import time
import random
from Crypto.Cipher import AES
from Crypto.Util.number import *

random.seed(int(time.time()))
key = long_to_bytes(random.getrandbits(128))

aes = AES.new(key, mode=AES.MODE_ECB)
cipher = aes.encrypt(flag)
with open("cipher", "wb") as f:
    f.write(cipher)

getrandbits只要找到seed就能找到这个随机数（seed一定，随机数不会变），所以找到时间戳即可
从cipher文件找出来
解密：

import random
from time import time
from Crypto.Cipher import AES
from Crypto.Util.number import *

# 读取密文
cipher = open("cipher", "rb").read()

# 已知的时间戳（对应 09/20/2020 @ 12:26pm (UTC) ）
timestamp = 1600604760  

# 前后一天的时间戳范围遍历
for i in range(-3600 * 24, 3600 * 24):  
    random.seed(timestamp + i)
    # 生成 128 位随机密钥并转换为 16 字节的字节串
    key = random.getrandbits(128).to_bytes(16, 'big')  
    aes = AES.new(key, mode=AES.MODE_ECB)
    decrypted = aes.decrypt(cipher)
    # 检查解密后的内容是否包含 "flag"
    if b"flag" in decrypted:  
        print(decrypted)
        # b'flag{506F0547-571B-4362-9428-FDDAB535C5DA}\x00\x00\x00\x00\x00\x00'