daimayuan第二课(1.二叉树的遍历,2.二叉树的最近公共祖先,3.二叉搜索树)
二叉树的最近公共祖先:
1:概念:就是两个节点在这棵树上深度最大的公共的祖先节点。
换句话说,就是两个点在这棵树上距离最近的公共祖先节点。
2:因为是基础课,所以tarjan和倍增lca就留到中级课再写
有兴趣的可以看这个算法详解之最近公共祖先(LCA) - hulean - 博客园 (cnblogs.com)
3:简单的两种方法
a:用数组存相比
b:先到同一深度在往上找
代码题目看后面
二叉搜索树:
当然这个还是基础的,后续再更
1:若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。
2:若它的右子树不为空,则右子树上所有结点的值都大于根结点的值。
3:由于二叉搜索树中,每个结点左子树上所有结点的值都小于该结点的值,右子树上所有结点的值都大于该结点的值,因此对二叉搜索树进行中序遍历后,得到的是升序序列。
同时利用这个性质已知中序,后序,可以建立这个树
因为对于二叉搜索树左小右大的原则,其中序遍历即为树中的元素的升序排列;而后序遍历是按先左子右子再根节点的顺序输出;
因此 对于二叉搜索树而言
如果按照其后序遍历的颠倒后的顺序插入元素,就可以还原整棵树!
原因是在元素x被插入以前,x的父节点已经插入在树中(后序遍历的颠倒后的顺序),因此x一定会插入到原来的树中的位置上。
代码题目看后面
注意:不适合下标太大的;
前序,中序,后序 问题:
1:序转换问题
a:可以构建二叉搜索树(只适合已知中序,后序求前序)
b:递归处理,先找到根节点在分成两部分继续找根
递归处理可解决这两种,其中输出则是按前序,后序遍历的位置输出;
2:知道前序,后序,求中序的可能
我们首先可以明确的是,在一棵树上若有一个结点是只有一个子结点的那么这个子结点在左在右不影响先序后序的遍历顺序,那么总树数就要乘以2(乘法原理,这个子结点有两种选择,一种成为左子树,一种成为右子树),为了找到只有一个子结点的结点数,我们继续。。
我们可以得到一个规律,在先序遍历中某一元素A的后继元素B,如果在后序遍历中A的前驱元素是B,那么A只有一个子树
1:遍历一般二叉树
给你一棵n个节点的二叉树, 节点编号为1..n,要你求出这棵二叉树的先序、中序和后序遍历。
树的形式用以下方式给出:
- 输入第一行给出一个数n,表示节点数;
- 根节点编号为1;
- 后面n行,每行有两个数,第一个数为第i个节点的左儿子编号,第二个数为第i个节点的右儿子编号,如果编号为0表示没有这个子节点;
- 输入保证是一棵二叉树。
输入格式
见题面。
输出格式
输出三行,每行n个数代表一种遍历。 第一行为先序遍历,第二行为中序遍历,第三行为后序遍历。
#include <bits/stdc++.h> using namespace std; struct Tree{ int vaule; Tree *l,*r,*fa; }a[1025]; void front(Tree *x) { printf("%d ",x->vaule); if(x->l) front(x->l); if(x->r) front(x->r); } void mid(Tree *x) { if(x->l) mid(x->l); printf("%d ",x->vaule); if(x->r) mid(x->r); } void up(Tree *x) { if(x->l) up(x->l); if(x->r) up(x->r); printf("%d ",x->vaule); } int main() { int n; scanf("%d",&n); for(int i = 1;i <= n;i ++ ) { int x,y; scanf("%d %d",&x,&y); a[i].vaule = i; if(x) a[i].l = &a[x]; if(y) a[i].r = &a[y]; } front(&a[1]); printf("\n"); mid(&a[1]); printf("\n"); up(&a[1]); printf("\n"); }
2:二叉树的最近公共祖先
给你一棵n个节点的二叉树, 节点编号为1..n。
树的形式用以下方式给出:
- 输入第一行给出一个数n,表示节点数;
- 根节点编号为1;
- 后面n行,每行有两个数,第一个数为第i个节点的左儿子编号,第二个数为第i个节点的右儿子编号,如果编号为0表示没有这个子节点;
- 输入保证是一棵二叉树。
接下来一个给出两个节点编号u,v你需要求出这两个节点的最近公共祖先。
最近公共祖先(LCA)问题是指:对于两个节点u,v,找到一个深度最大的x是u,v的祖先。
输入格式
第一行一个整数n。 接下来n行,每行两个整数,表示第i个节点的儿子信息。 接下来一行两个整数u,v。
输出格式
输出一个数,代表u,v的最近公共祖先x。
1:解法一:数组
#include <bits/stdc++.h> using namespace std; struct Tree{ int vaule; Tree *l,*r,*fa; }a[1025]; int res[1025],pos[1025]; int main() { int n; scanf("%d",&n); for(int i = 1;i <= n;i ++ ) { int x,y; scanf("%d %d",&x,&y); a[i].vaule = i; if(x) a[i].l = &a[x],a[x].fa = &a[i]; if(y) a[i].r = &a[y],a[y].fa = &a[i]; } int x,y,cnt = 0,cnt1 = 0; scanf("%d %d",&x,&y); while(x != 1) { res[++ cnt] = x; // cout << x << ' '; x = a[x].fa->vaule; } // cout << '\n'; res[++cnt] = 1; while(y != 1) { pos[++ cnt1] = y; y = a[y].fa->vaule; } pos[++cnt1] = 1; int ans = 0; for(int i = cnt ,j = cnt1;i||j;i--,j--) { if(res[i] == pos[j]) ans = res[i]; else break; } printf("%d\n",ans); }
2:解法而:深度
#include <bits/stdc++.h> using namespace std; struct Tree{ int vaule; Tree *l,*r,*fa; }a[1025]; void front(Tree *x) { printf("%d ",x->vaule); if(x->l) front(x->l); if(x->r) front(x->r); } void mid(Tree *x) { if(x->l) mid(x->l); printf("%d ",x->vaule); if(x->r) mid(x->r); } void up(Tree *x) { if(x->l) up(x->l); if(x->r) up(x->r); printf("%d ",x->vaule); } int main() { int n; scanf("%d",&n); for(int i = 1;i <= n;i ++ ) { int x,y; scanf("%d %d",&x,&y); a[i].vaule = i; if(x) a[i].l = &a[x]; if(y) a[i].r = &a[y]; } front(&a[1]); printf("\n"); mid(&a[1]); printf("\n"); up(&a[1]); printf("\n"); }
3:求先序排列
题目描述
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示)。
输入格式
共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式
共一行一个字符串,表示一棵二叉树的先序。
1:解法一:二叉搜索树
#include <bits/stdc++.h> using namespace std; int n; char mid[1025],up[1025]; int p[1025]; char q[1025]; struct Tree{ int vaule; Tree *l,*r,*fa; }*head; Tree* buildtree(Tree *root,int num) { Tree *z = (Tree *)malloc(sizeof(Tree)); Tree *y = NULL; Tree *x = root; z->vaule = num; while(x != NULL) { y = x; if(num < x->vaule) x = x->l; else x = x->r; } z->fa = y; if(y == NULL) root = z; else if(num < y->vaule) y->l = z; else y->r = z; return root; } void prve(Tree * t) { if(t == NULL) return ; printf("%c",q[t->vaule]); prve(t->l); prve(t->r); } int main() { head = NULL; //cin>>mid>>pre; scanf("%s %s",mid,up); for(int i=0;mid[i]!='\0';i++)//建立字母与标号的双向联系 { p[mid[i]]=i; q[i]=mid[i]; } for(int i = strlen(up) - 1;i >= 0; i --) { head = buildtree(head,p[up[i]]); } prve(head); }
2:解法二:递归
#include<cstdio> #include<iostream> #include<cstring> using namespace std; void beford(string in,string after){ if (in.size()>0){ char ch=after[after.size()-1]; cout<<ch;//找根输出 int k=in.find(ch); beford(in.substr(0,k),after.substr(0,k)); beford(in.substr(k+1),after.substr(k,in.size()-k-1));//递归左右子树; } } int main(){ string inord,aftord; cin>>inord;cin>>aftord;//读入 beford(inord,aftord);cout<<endl; return 0; }
4.遍历问题
题目描述
我们都很熟悉二叉树的前序、中序、后序遍历,在数据结构中常提出这样的问题:已知一棵二叉树的前序和中序遍历,求它的后序遍历,相应的,已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历,你却不能确定其中序遍历序列,考虑如下图中的几棵二叉树:
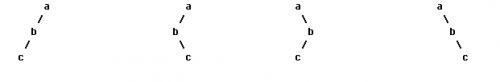
所有这些二叉树都有着相同的前序遍历和后序遍历,但中序遍历却不相同。
输入格式
输A数据共两行,第一行表示该二叉树的前序遍历结果s1,第二行表示该二叉树的后序遍历结果s2。
输出格式
输出可能的中序遍历序列的总数,结果不超过长整型数
#include <bits/stdc++.h> using namespace std; char pre[100001],up[100001]; int main() { scanf("%s %s",pre,up); int ans = 1; for(int i = 0;i <= strlen(pre) - 2; i ++ ) { for(int j = 0; j <= strlen(pre) - 1; j ++ ) if(pre[i] == up[j] && pre[i + 1] == up[j - 1]) ans*=2; } printf("%d\n",ans); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号