5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

 

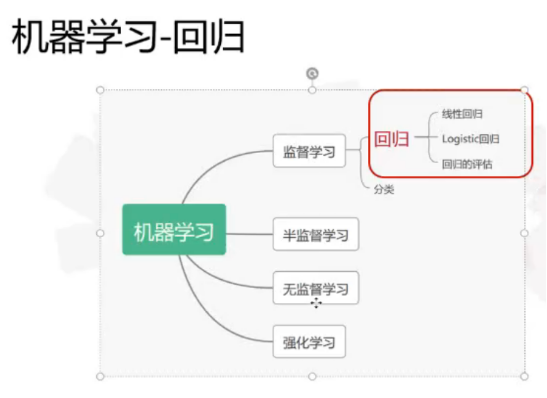
本节课学习了机器学习中的监督学习里的线性回归算法，回归是统计学中最有力的工具之一。机器学习监督学习算法分为分类算法和回归算法两种，其实就是根据类别标签分布类型为离散型、连续性而定义的。回归算法用于连续型分布预测，针对的是数值型的样本，使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。

监督学习：

 

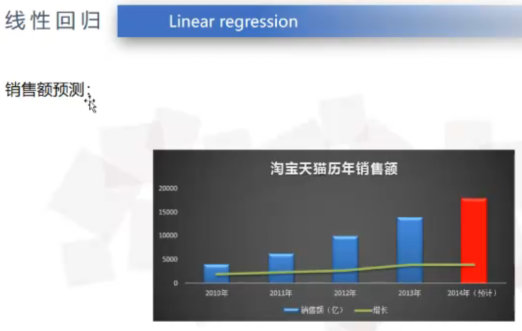
利用线性回归来进行销售额预测

我们把销售额当做目标值，把广告投入、公司收入、产品好坏等称为输入数据的特征，通过输入特征得到输出的目标值，我们知道输出的销售额是连续型的便可用回归来解决。

 

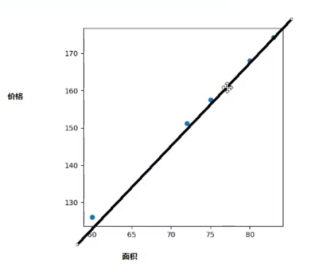
最重要的内容，求解这条线，线性回归模型

 

把线性回归问题转化为矩阵乘积的问题，矩阵在线性回归中扮演者非常重要的作用。矩阵:大多数算法的计算基础，矩阵的这种运算正好满足了线性回归的这种需求。

 

掌握数组的加法运算和乘法运算还有矩阵的乘法

 

找到一个合适的w（权值）和特征值相乘再加上添置就得到y，是一个连续性的值。（如果没有添置就无法画出上图红色那条线）

机器学习和预测值是存在一定误差的，需要使用迭代算法来减小误差，因此引入了损失函数。

 

线性回归算法的策略和优化

 

 

从下图可以看出随着训练次数的增加，loss不断下降，预测值越接近真实值。

 

 

 

 

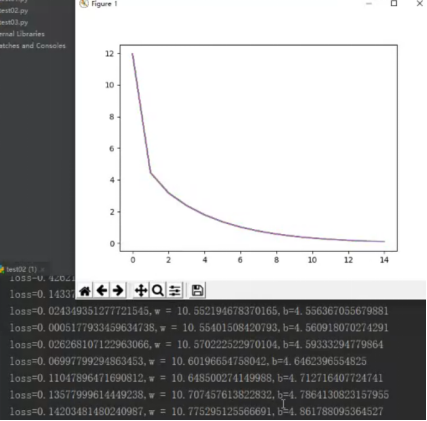
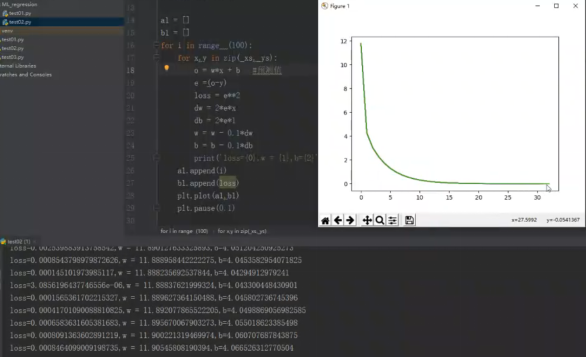
2.思考线性回归算法可以用来做什么？

线性回归算法可以用来：

①预测音乐流行趋势：以某音乐平台用户的历史播放数据为基础，期望通过对艺人的试听量的预测，挖掘出即将成为潮流的艺人，从而实现对一个时间段内音乐流行趋势的准确把控。

②对红酒品质评分：基于红酒的化学特性，例如酸性、含糖量、氯化物含量、硫含量、酒精度、PH值、密度等，构建机器学习模型，对红酒品质进行评分。

③预测电影票房：依据历史票房数据、影评数据、舆情数据等互联网公众数据，对电影票房进行预测。

 

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。

使用线性回归模型对红酒进行预测。

from sklearn.datasets import load_wine #导入数据集
#sklearn转换器处理wine数据集
wine = load_wine()
data = wine['data']
target = wine['target']
#数据集划分
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.2,random_state=5)#数据集划分为训练集，测试集
#（1）根据load_wine数据集处理的结果，构建线性回归模型。
from sklearn.linear_model import LinearRegression
model_1=LinearRegression()
model_1.fit(x_train,y_train)
pre1 = model_1.predict(x_test)
#（2）结合真实评分和预测评分，计算均方误差、中值绝对误差、可解释方差值。
from sklearn.metrics import explained_variance_score,median_absolute_error,mean_squared_error
print('--------线性回归模型--------')
print('线性回归模型的均方误差为：',mean_squared_error(y_test,pre1))
print('线性回归模型的中值绝对误差为：',median_absolute_error(y_test,pre1))
print('线性回归模型的可解释方差值为：',explained_variance_score(y_test,pre1))
#（3）根据得分，对模型的性能优劣进行评价
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.sans-serif'] = 'SimHei'
fig = plt.figure(figsize=(10,6)) ##设定空白画布，并制定大小
a=fig.add_subplot(1,2,1)
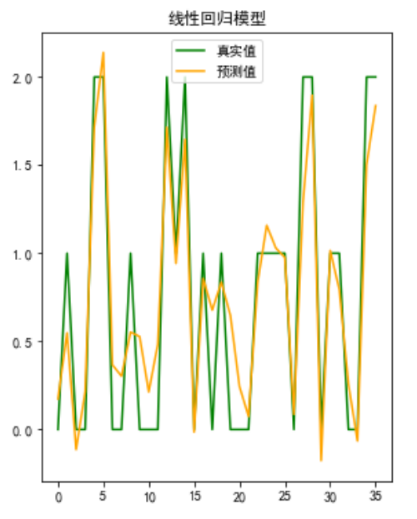
plt.title('线性回归模型')
plt.plot(range(y_test.size),y_test,color="green")
plt.plot(range(y_test.size),pre1,color="orange")
plt.legend(['真实值','预测值'],loc = 'upper center')
plt.show() ##显示图片