动态规划DP的优化

写一写要讲什么免得忘记了。DP的优化。

大概围绕着"是什么"，"有什么用"，"怎么用"三个方面讲.

主要是《算法竞赛入门经典》里的题目讲解，但是有些过于简单的删去了，添加了一些不怎么简单的省选题目作为例子

这里的DP优化都是涉及到O(n^k)到O(n^k-1)方法比较巧妙也有用到数学里面的定理之类。

所以秉着由易到难的原则，安排内容如下：

专题1：动态规划基础知识和计数DP、数位DP（几大类DP的类型介绍）

专题2：DP的简单优化（稍微提两句mjy大佬的任务）

专题3：单调队列优化DP和斜率优化（这个比较难也比较重要） blog

专题4：四边形不等式优化DP

专题5：习题课

专题1：动态规划基础知识和计数DP、数位DP（几大类DP的类型介绍）

专题2：DP的简单优化（稍微提两句mjy大佬的任务）

专题3：单调队列优化DP和斜率优化（这个比较难也比较重要）

斜率优化DP blog、

将这个DP的优化方法之前我们必须看一个例子，优化的前提一直是暴力DP不错！

P3195 [HNOI2008]玩具装箱TOY

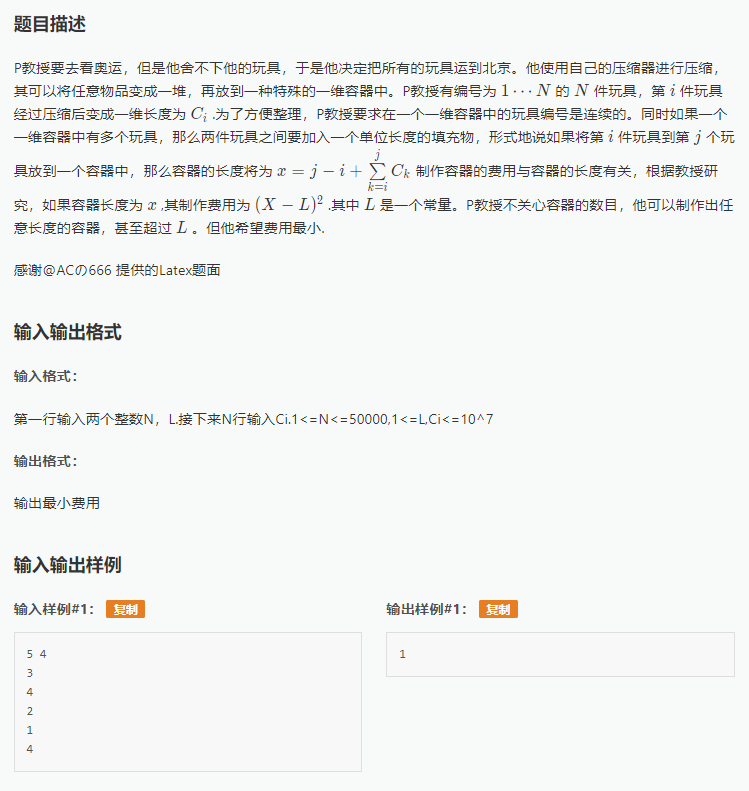
这个DP方程非常好想，F[i]从第1个到第i个物品放在箱子里的最小花费。

转移从第j个物品开始考虑在第j个物品放完之后的(i+1)到第j个物品放在一个容器中，每次决策一次那么得出方程式

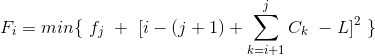
为了方便起见我们这里的L++，然后用sum[x]表示C的前缀和那么DP方程就可以改写为：

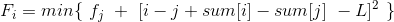
然后我们发现对于确定的i，sum[i]+i的值是一定的，我们用s[x]表示sum[i]+i

进一步改写DP方程：

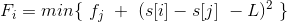
于是我们这个DP方程就显的优美了，不妨把暴力的代码打出来把：

# include<bits/stdc++.h>
# define int long long
# define SQR(x) ((x)*(x))
using namespace std;
const int MAXN=1e5+10;
int s[MAXN],f[MAXN];
int n,L;
signed main()
{
    scanf("%lld%lld",&n,&L); L++;
    int t;
    for (int i=1;i<=n;i++)
     scanf("%lld",&t),s[i]=s[i-1]+t;
    for (int i=1;i<=n;i++) s[i]+=i;
    memset(f,0x3f,sizeof(f)); f[0]=0;
    for (int i=1;i<=n;i++)
     for (int j=0;j<i;j++)
      f[i]=min(f[i],f[j]+SQR(s[i]-s[j]-L)); 
    printf("%lld\n",f[n]);  
    return 0;
 }

我们发现这样的算法时间完全承受不了，我们考虑优化！！！

优化用到的正是斜率优化。

为了O(1)转移我们必须寻求一种方法来找到最优的转移方案，

我们不妨把式子化简一下

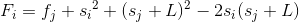
对于当前最优的决策方案Fi，我们的每一个j都可以表示一个Fi的取值，这里取到最值，这和直线非常相似我们不妨把带有j的当做变量分离一下试试

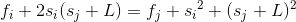
b + k * x = y

我们发现这样一个神奇的式子，对于每一个j的取值都有一个在J(s_j+L,f_j+s_i²+(s_j+L)²)与之对应，这个J就是坐标轴上离散的一个点，

就好比对于所有决策状态中的点J集合，一条直线（斜率K=2s_i已固定）经过这个J集合中至少一个点，使其截距b，尽可能小。

观察到题目中的c[i]都是正数意味着k=2*s[i]必然单调递增，我们承认的一个事实是在平面直角坐标系中一条直线k的值越大越陡，截距b越小

考虑怎样一个数据结构可以维护这样一个，单调递增k的特性呢？答案显然是单调队列，我们只要维护一个下凸包即可。

具体的解释是这样，考虑F[i]的斜率2*s_i如显然AB的斜率比F[i]的斜率小那么显然，A就是一个废弃的点（由于B的存在我宁可连B也不连A），我们就可以把它弹掉。

对于更新过的坐标集，第一个点的显然是最优的，由于满足下凸的性质，直线斜率不变，那么截距只能越来越大，这时候更新答案，更新完毕之后由于产生一个新的决策点J

我们需要对前面的点做一遍检查

对于新加进来的这个决策点new(就是当前的最优值)，我们判断他是不是有资格作为后续DP状态的来源点，

如果new这个点和A这个点的斜率比BC的斜率还要小，那么BC这两个点将会被清除由于后续来的斜率线段一定会选择过new而不是B或者C

这也是基于上面的下凸包的性质。

提醒一下对于当前需要转移的i，我们可以不作记录的原因在于

对于每一个和i有关的常数我们都会在作差之中消除，我们可以不用理他（抵消！），这样程序就没有了i的干扰了！

Code：

# include<bits/stdc++.h>
# define int long long
# define SQR(x) ((x)*(x))
using namespace std;
const int MAXN=5e4+10;
int sum[MAXN],F[MAXN],c[MAXN],s[MAXN],q[MAXN];
int n,L;
inline double X(int j){ return (double)s[j];}
inline double Y(int j){ return (double)F[j]+(s[j]+L)*(s[j]+L);}
//和i无关的每一个j点计算出他的横坐标和纵坐标
inline double R(int i,int j){return (Y(j)-Y(i))/(X(j)-X(i));}
//i下的两点斜率
# define Empty (head>=tail)
signed main()
{
    scanf("%lld%lld",&n,&L); L++; sum[0]=0;
    for (int i=1;i<=n;i++) 
        scanf("%d",&c[i]),
        sum[i]=sum[i-1]+c[i],
        s[i]=sum[i]+i;
    int head=1,tail=1; q[1]=0;
//涉及到取两个元素的队列还是手打比较好
    for (int i=1;i<=n;i++) {
        while (!Empty&&R(q[head],q[head+1])<2*s[i]) head++;
//不满足下凸的性质队头出
        int j=q[head]; F[i]=F[j]+SQR(s[i]-s[j]-L);
//转移
        while (!Empty&&R(q[tail-1],q[tail])>R(q[tail],i)) tail--; 
//不满足下凸性质的队尾出
q[++tail]=i;
//加入一个新的决策i
    }
    printf("%lld\n",F[n]);
    return 0;
 } 
//这个板子会在后面经常用到

这里还需要提高一下，我们其实不需要吧这个直线写出来就可以知道斜率，这样减少思维难度。

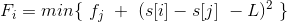
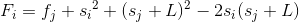
是这个方程，我们不妨考虑一个决策k在另一个决策j之前，但是k没有j优秀（对于更新外部循环变量i来说），

即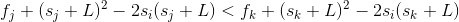

所以k这个决策无用抛弃。

可以化简为左边是s_i和s_j或s_k乘积形式除过去，就可以得到斜率

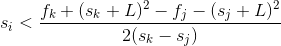
这个式子本质上是和上面是一样的，和R没有什么区别。

维护的话相似。

P2120 [ZJOI2007]仓库建设

考虑最简单的DP方程：

f[i]从山顶（1号）到第i号放完的最小代价

考虑f[i]从j转移过来。

设W_k表示如果将i这个地点作为建站处那么对于k<i的任意一个点，其代价

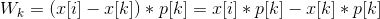
那么从1-j 已经处理完毕，考虑 j+1 到 i 这些物品的结构

转移方程：

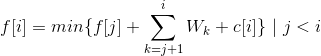
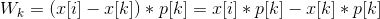
对于需要转移的每一个x[i]不变，转移方程可以改写为

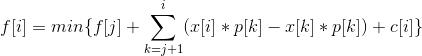
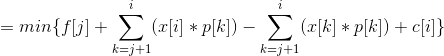
前缀和处理 -x[i]*p[i]和p[i]的前缀和分别为 g[i] 和 P[i]

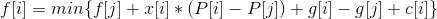
这样复杂度降到了O（n^2）

帖下代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+10;
int f[MAXN],x[MAXN],p[MAXN],P[MAXN],c[MAXN],g[MAXN];
int n;
signed main()
{
    scanf("%lld",&n);
    for (int i=1;i<=n;i++) 
        scanf("%lld%lld%lld",&x[i],&p[i],&c[i]),
        P[i]=P[i-1]+p[i],g[i]=g[i-1]-x[i]*p[i];
    memset(f,0x3f,sizeof(f)); f[0]=0;
    for (int i=1;i<=n;i++) 
     for (int j=0;j<i;j++)
      f[i]=min(f[i],f[j]+x[i]*P[i]-x[i]*P[j]+g[i]-g[j]+c[i]);
    printf("%lld\n",f[n]);  
    return 0;
}

接下来将斜率优化的部分：

f[i]=f[j]+x[i]*P[i]-x[i]*P[j]+g[i]-g[j]+c[i]

f[i]+x[i]*P[j] = f[j] + x[i]*P[i] +g[i] - g[j] + c[i]

b + k * x = y

由于斜率单调递增，那么x[i]单调递增所以斜率单调递增，所以处理方法同上！

#include <bits/stdc++.h>
#define int long long
#define Empty (head>=tail)
using namespace std;
const int MAXN=1e6+10;
int f[MAXN],x[MAXN],p[MAXN],P[MAXN],c[MAXN],g[MAXN],q[MAXN];
double X(int j) { return (double)P[j];}
double Y(int j) { return (double)f[j]-(double)g[j];}
double R(int i,int j){return (double)(Y(i)-Y(j))/(X(i)-X(j));}
int n;
signed main()
{
    scanf("%lld",&n);
    for (int i=1;i<=n;i++) 
        scanf("%lld%lld%lld",&x[i],&p[i],&c[i]),
        P[i]=P[i-1]+p[i],g[i]=g[i-1]-x[i]*p[i];
     int head=1,tail=1; q[1]=0;
    for (int i=1;i<=n;i++) {
        while (!Empty&&R(q[head],q[head+1])<x[i]) head++;
        int j=q[head]; f[i]=f[j]+x[i]*P[i]-x[i]*P[j]+g[i]-g[j]+c[i];
        while (!Empty&&R(q[tail-1],q[tail])>R(q[tail],i)) tail--; 
        q[++tail]=i;
    }
    printf("%lld\n",f[n]);
    return 0;
}

P3628 [APIO2010]特别行动队

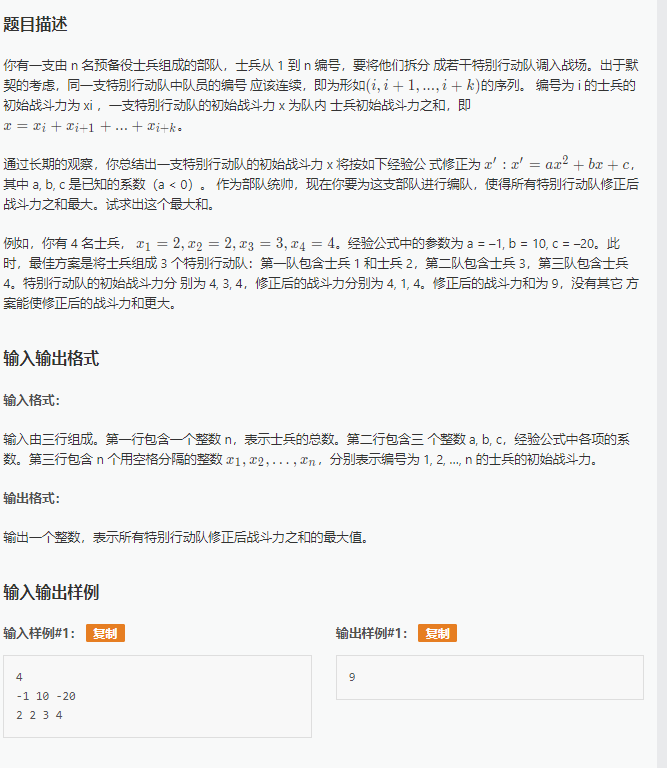
先考虑暴力DP+前缀和优化！

设F[i]表示前i个士兵安排任务最大化战斗力,sum[x]表示x的前缀和数组

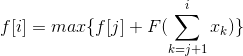
对于这个式子可以用前缀和表示，用F(x)=A*x*x+B*x+C代换可知

依然考虑斜率优化下，还是写成斜率的形式

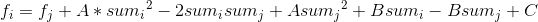
依旧把有斜率的东西放到左边，右边保留一个解析式，就像这样：

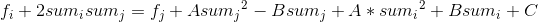
b + k * x = y

这里是斜率k单调递减然后求f_i最大值，其实只要向上面一样维护一个上凸包即可！

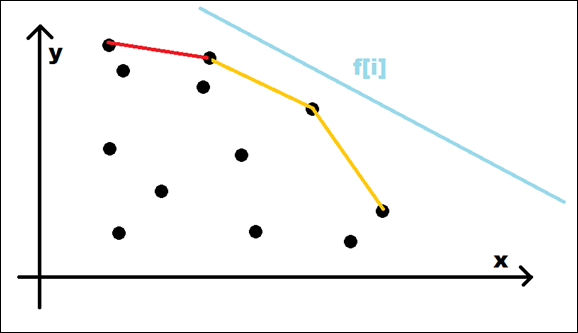
代码其实只要改两个符号就差不多了，理解就是取反然后按照斜率递增求Min一样就行。

code：

# include <bits/stdc++.h>
# define int long long
# define Empty (head>=tail)
using namespace std;
const int MAXN=2e6+10;
int sum[MAXN],f[MAXN],q[MAXN*2],A,B,C,n;
double X(int j){return sum[j];}
double Y(int j){return (double)f[j]+A*sum[j]*sum[j]-B*sum[j];} 
double R(int i,int j){return (double)(Y(i)-Y(j))/(double)(X(i)-X(j));}
int Fun(int x) {return A*x*x+B*x+C;}
signed main()
{
    scanf("%lld",&n);
    scanf("%lld%lld%lld",&A,&B,&C);
    int t;
    for (int i=1;i<=n;i++) 
     scanf("%lld",&t),sum[i]=sum[i-1]+t;
    int head=1,tail=1; q[1]=0;
    for (int i=1;i<=n;i++) {
        while(!Empty&&(R(q[head+1],q[head])>2*A*sum[i])) head++;
        int j=q[head];  f[i]=f[j]+Fun(sum[i]-sum[j]); 
        while (!Empty&&(R(q[tail],q[tail-1])<R(q[tail],i))) tail--;
        q[++tail]=i;
    } 
    printf("%lld\n",f[n]);
    return 0;
}

到这里我们已经完成了斜率优化的入门题型这里给出几个练习，有助于能力提升：

- [防御准备](入门难度) [题解]
- [土地购买](中等难度) [题解]
- [序列分割](中等难度) [题解]
- [货币兑换](进阶难度) [题解]

专题4：四边形不等式优化DP

四边形不等式：相交小于等于包含

设w(x,y)是定义在Z上的二元函数，对于a<=b<=c<=d属于Z，都有w(a,d)+w(b,c)>=w(a,c)+w(b,d)

或者定义a<b，有w(a,b+1)+w(a+1,b)>=w(a,b)+w(a+1,b+1)

这两种定义是等价的！

证明：对于a<c，有w(a,c+1)+w(a+1,c)>=w(a,c)+w(a+1,c+1) （第2种定义）

　　　对于a+1<=c，有w(a+1,c+1)+w(a+2,c)>=w(a+1,c)+w(a+2,c+1) （第2种定义）

　　　两式相加，得：w(a+1,c+1)+w(a+2,c)+w(a,c+1)+w(a+1,c)>=w(a+1,c)+w(a+2,c+1) + w(a,c)+w(a+1,c+1)

　　　消去相同项得：w(a+2,c)+w(a,c+1)>=w(a+2,c+1) + w(a,c)

　　　同理对于任意的a<=b<=c有w(a,c+1)+w(b,c)>=w(a,c)+w(b,c+1)

　　　同理对于任意的a<=b<=c<=d都有w(a,d)+w(b,c)>=w(a,c)+w(b,d)

证毕。

一维线性DP的四边形不等式优化：

对于形如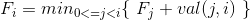的一维线性DP方程，记录P[i]表示F[i]取到最小值的j，

若P[i]单调不减，则F具有决策单调性

定理：若val满足四边形不等式即val为凸（以后为了方便，满足四边形不等式的性质一律叫凸）则F具有决策单调性

证明：令i在[1，N]，j在[0,P[i]-1]，i’在[i+1,N]

根据P[i]最优性，得F[P[i]]+val(P[i],i)<=F[j]+val(j,i)

由于val满足四边形不等式，有val(j,i)+val(P[i],i')<=val(j,i')+val(P[i],i)【相交小于等于包含】

两式相加，得：F[P[i]]+val(P[i],i)+val(j,i)+val(P[i],i')<=F[j]+val(j,i)+val(j,i')+val(P[i],i)

消去相同项，得：F[P[i]]+val(P[i],i')<=F[j]+val(j,i)　　

对于i'的最优决策P[i']在[P[i],i']不可能小于P[i],即P[i']>=P[i]

所以F满足决策单调性

在循环的任意时刻，数组中的情况一定是形如

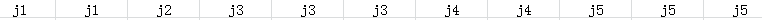
由于决策单调则j1<j2<j3<j4<j5

求出F[i]后考虑i可能作为F[i'] (i'>i)的决策，那借用单调队列的思想考虑一个位置pos，之前的决策都比i好，之后的决策都比i差，

我们需要快速找到上述位置并把之后的所有元素改为i，把[pos,i]改为i，

假设我们的位子在j3（中间那个），那么处理后的数组就变为：

显然直接修改效率太低，我们在队列中用若干个三元组(j,l,r)表示数组的[l,r]最优决策都是j

另外队列中无需保留小于P[1~i-1]的部分，（由于F的决策单调性）

队列头部就是最优决策

算法:

检查队头(j₀,l₀,r₀)，若r₀<=i-1，删除队头，否则l₀=i
取出队头的决策j作为最优决策，状态转移求出F[i]
尝试插入新决策i：
- （1）取出队尾(j_t,l_t,r_t)
- （2）对于F[l_t]来说i是比j_t更优的决策（由于决策单调对于l_t来说i都优于此时的决策那么在队尾整个区间都差于此时的决策），pos=l_t删除队尾,goto(1)
- （3）对于F[r_t]来说i不如j_t更优 goto(5)
- （4）不满足（2）和（3）的，在[l_t,r_t]二分查找到pos，使之前的决策比i更优，之后的决策i更优（就说对于F[mid]来说，i决策比jt决策更优最小化mid），goto(5)
- （5）把（i，pos，N）插入队尾

[诗人小G]

# include <bits/stdc++.h>
# define int long long
# define ld long double
using namespace std;
const int MAXN=1e6+10;
int N,P,L;
ld sum[MAXN],f[MAXN];
int last[MAXN],nxt[MAXN];
char s[MAXN][55];
struct node{ int j,l,r;};
deque<node>q;
void Print_B()
{
    puts("Too hard to arrange");
}
void Print_E()
{
    for (int i=1;i<=20;i++) putchar(45);
    putchar('\n');
}
void write(int x)
{
    if (x<0) { x=-x; putchar('-');}
    if (x>9) write(x/10);
    putchar('0'+x%10);
}
void writeln(int x)
{
    write(x);putchar('\n');
}
inline int read()
{
    int X=0,w=0; char c=0;
    while (!(c>='0'&&(c<='9'))) w|=c=='-',c=getchar();
    while ((c>='0'&&(c<='9'))) X=(X<<1)+(X<<3)+(c^48),c=getchar();
    return w?-X:X;
}
ld pow(ld x,int n)
{
    ld ans=1;
    while (n) {
        if (n&1) ans=ans*x;
        x=x*x;
        n>>=1;
    }
    return ans;
}
ld calc(int i,int j)
{
    return (ld)f[j]+pow(abs(sum[i]-sum[j]+(i-j-1)-L),P);
}
void Clear()
{
    memset(f,0,sizeof(f));
    deque<node>tmp; swap(q,tmp);
    memset(last,0,sizeof(last));
    memset(nxt,0,sizeof(nxt));
    sum[0]=0;
}
signed main()
{
    int T; T=read();
    while (T--) {
        Clear();
        N=read();L=read();P=read();
        for (int i=1;i<=N;i++) {
            cin>>s[i];
            int len=strlen(s[i]);
            sum[i]=sum[i-1]+(ld) strlen(s[i]);
        } 
        q.push_back((node){0,1,N});
        for (int i=1;i<=N;i++) {
            while (!q.empty()) {
                if (q.front().r<i) q.pop_front();
                else {
                    q.front().l=i; break;
                }
            }

            int j=q.front().j;
            last[i]=j;
            f[i]=calc(i,j);
            int pos=-1;
            while (!q.empty()) {
                int lt=q.back().l;
                int rt=q.back().r;
                int jt=q.back().j;
                if (calc(lt,i)<=calc(lt,jt)) {
                    pos=lt; q.pop_back(); continue;
                } else 
                if (calc(rt,jt)<=calc(rt,i))  break;
                else {
                    int l=lt,r=rt,ans=1;
                    while (l<r) {
                        int mid=(l+r)>>1;
                        if (calc(mid,i)<=calc(mid,jt)) r=mid;
                        else l=mid+1;
                    }
                    q.back().r=l-1; pos=l;  break;
                }
            }
            if (pos!=-1) q.push_back((node){i,pos,N});
        }
        if (f[N]>(1e18)*1ll) Print_B();
        else {
            printf("%lld\n",(int)(f[N]+0.5));
            for (int i=N;i;i=last[i]) nxt[last[i]]=i;
            int now=0;
            for (int i=1;i<=N;i++) {
                now=nxt[now];
                int tmp=now;
                for (int j=i;j<tmp;j++) printf("%s ",s[j]);
                puts(s[tmp]);
                i=tmp;
            }
        } 
        Print_E();
    }
    return 0;
}

二维区间DP 四边形不等式定理：

（特别的要求F[i][i]=w[i][i]=0）

如果有下面条件成立：

w为凸
对于任意的a<=b<-c<=d有w(a,d)>=w(b,c)

那么F也为凸。

由于我们定义二元函数的凸性是有两种定义方法，

我们就是要证明：对于任意 i< i+1<=j< j+1,满足f[i][j]+f[i+1][j+1]<=f[i][j+1]+f[i+1][j](交叉小于等于包含)

设f[i+1][j]取最小值的时候k=x，f[i][j+1]取最小值的时候k=y

f[i][j]=f[i][x]+f[x+1][j]+w(i,j)

f[i+1][j+1]=f[i+1][y]+f[y+1][j+1]+w(i+1,j+1)

所以左式取最值的时候，左式=f[i][x]+f[x+1][j]+w(i,j)+f[i+1][y]+f[y+1][j+1]+w(i+1,j+1)

由于w为凸，所以w(i,j)+w(i+1,j+1)<=w(i+1,j)+w(i,j+1)

f[i][x]+f[x+1][j]+w(i,j)+f[i+1][y]+f[y+1][j+1]+w(i+1,j+1)<=f[i][j+1]+f[i+1][j]

右式=f[i][y]+f[y+1][j+1]+w(i,j+1)+ f[i+1][x]+f[x+1][j]+w(i+1,j)

得：

f[i][x]+f[x+1][j]+w(i,j)+f[i+1][y]+f[y+1][j+1]+w(i+1,j+1)<=f[i][y]+f[y+1][j+1]+w(i,j+1)+ f[i+1][x]+f[x+1][j]+w(i+1,j)

展开得：

f[i][j]+f[i+1][j+1]<=f[i][j+1]+f[i+1][j]

证毕。

二维区间DP决策单调性定理：

如果 （特别的要求F[i][i]=w[i][i]=0）为凸

那么对于任意i<j都有P[i][j-1]<P[i][j]<P[i+1][j]

记p=P[i][j]，对于任意的i<k<=p,由于F为凸那么f[i][p]+f[i+1][k]>=f[i][k]+f[i+1][p]

移项可得：f[i+1][k]-f[i+1][p]>=f[i][k]-f[i][p]

由于p最优，得f[i][k]+f[k+1][j]>=f[i][p]+f[p+1][j]

(f[i+1][k]+f[k+1][j]+w(i+1,j))-(f[i+1][p]+f[p+1][j]+w(i+1,j))

= f[i+1][k]-f[i+1][p]+f[k+1][j]-f[p+1][j]

>=f[i][k]-f[i][p]+f[k+1][j]-f[p+1][j]

= f[i][k]+f[k+1][j]-(f[i][p]+f[p+1][j])>=0

所以对于f[i+1][j]，p比任何k<=p优所以P[i+1][j]>=P[i][j]

同理可知P[i][j-1]<=P[i][j]

四边形不等式优化定理总结

1.四边形不等式的定义：相交小于包含
两种等价定义：
对于a<=b<=c<=d属于Z，都有w(a,d)+w(b,c)>=w(a,c)+w(b,d)
对于a,b属于Z 若 a<b，有w(a,b+1)+w(a+1,b)>=w(a,b)+w(a+1,b+1)
2.一维线性DP决策单调定理
对于形如f[i]=min_{0<=j<i}{F[j]+w(j,i)}若w为凸那么F决策单调递增
3.二维区间DP决策单调性定理
对于形如F[i][j]=min_{i<=k<=j}{f[i][k]+f[k+1][j]+w(i,j)}
（特别的要求F[i][i]=w(i,i)=0）若w为凸则F为凸，
对于F理应满足决策P[i][j-1]<P[i][j]<P[i+1][j]
P[l][r]表示当[l,r]分为[l,k]和[k+1,r]两部分时F[l][r]最大

利用第二种等价定义，证明函数w(x,y)的凸性事实上只要
证明对于任意j<i,w(j,i+1)+w(j+1,i)>=w(j,i)+w(j+1,i+1)
只需证明：w(j+1,i)-w(j+1,i+1)>=w(j,i)-w(j,i+1)
代入换元函数单调性可知w(x,y)的凸性

更方便的方案：打表暴力DP验证决策单调！

石子合并弱化版本 https://www.luogu.org/problemnew/show/U58387
石子合并强化版本 GarsiaWachs算法（这里放过了GW的暴力O(n^2)那是因为数据随机）

专题5：习题课

posted @ 2018-12-18 15:25 ljc20020730 阅读(340) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

ljc20020730

hi！我回来啦！这次带来一个好消息！我回来啦作为一个ACMer. 我的新博客是cnblogs.com/maystern 做了美化哦！快来看看吧。

动态规划DP的优化

专题1：动态规划基础知识和计数DP、数位DP（几大类DP的类型介绍）

专题2：DP的简单优化（稍微提两句mjy大佬的任务）

专题3：单调队列优化DP和斜率优化（这个比较难也比较重要）

专题4：四边形不等式优化DP

专题5：习题课

公告